Как найти заряд прошедший через источник

Представлено решение, соответствующее одному из следующих случаев.

Дан правильный ответ на вопрос задания, и приведено объяснение, но в нём не указаны два явления или физических закона, необходимых для полного верного объяснения.

Указаны все необходимые для объяснения явления и законы, закономерности, но имеющиеся рассуждения, направленные на получение ответа на вопрос задания, не доведены до конца.

Указаны все необходимые для объяснения явления и законы, закономерности, но имеющиеся рассуждения, приводящие к ответу, содержат ошибки.

Источник

Найти ток через резистор сразу после замыкания ключа

Участок цепи, схема которого изображена на рисунке, до замыкания ключа К имел электрическую ёмкость 3 нФ. После замыкания ключа электроёмкость данного участка цепи стала равной 4 нФ. Чему равна электроёмкость конденсатора C_x (в нФ)?

При последовательном соединении конденсаторов их общая ёмкость находится по формуле:

Отсюда

После замыкания ключа, учитывая что при параллельном соединении конденсаторов их ёмкости складываются, получаем:

Находим отсюда

Из двух конденсаторов ёмкостями С = 6 мкФ и 2С, резистора, идеального источника с ЭДС В и ключа собрали электрическую цепь, схема которой показана на рисунке. Изначально ключ был разомкнут, конденсатор ёмкостью 2С не заряжен, а конденсатор ёмкостью С заряжен до напряжения и подключён к цепи в полярности, показанной на рисунке. Ключ замыкают и дожидаются окончания перераспределения зарядов в цепи. Какое количество теплоты выделится в резисторе после замыкания ключа?

1) Найдём установившиеся на конденсаторах напряжения после перераспределения зарядов (см. рис.).

При последовательном соединении сумма напряжений на конденсаторах и резисторе равна напряжению источника питания. Так как в установившемся режиме ток в цепи отсутствует, по закону Ома для участка цепи напряжение на резисторе равно нулю. Тогда для суммы напряжений на конденсаторах:

2) По закону сохранения электрического заряда суммарный заряд обведенных пунктиром обкладок конденсаторов сохраняется. Запишем условие равенства исходного заряда конечному, выразив заряды через соответствующие напряжения на конденсаторах:

Решая записанную систему уравнений, найдём установившиеся заряды на конденсаторах:

3) Найдём заряд, прошедший через источник, как разность конечного и начального заряда на конденсаторе ёмкостью С:

4) Запишем закон сохранения энергии для электрической цепи, связывая состояния системы до замыкания ключа и после установления окончательных напряжений на конденсаторах (с учётом работы источника, равной

Окончательно для выделившегося количества теплоты:

Ответ:

Из двух конденсаторов ёмкостями С = 6 мкФ и 2С, резистора, идеального источника с ЭДС В и ключа собрали электрическую цепь, схема которой показана на рисунке. Изначально ключ был разомкнут, конденсатор ёмкостью С не заряжен, а конденсатор ёмкостью 2С заряжен до напряжения и подключён к цепи в полярности, показанной на рисунке. Ключ замыкают и дожидаются окончания перераспределения зарядов в цепи. Какое количество теплоты выделится в резисторе после замыкания ключа?

1) Найдём установившиеся на конденсаторах напряжения после перераспределения зарядов (см. рис.).

При последовательном соединении сумма напряжений на конденсаторах и резисторе равна напряжению источника питания. Так как в установившемся режиме ток в цепи отсутствует, по закону Ома для участка цепи напряжение на резисторе равно нулю. Тогда для суммы напряжений на конденсаторах:

2) По закону сохранения электрического заряда суммарный заряд

обведенных пунктиром обкладок конденсаторов сохраняется. Запишем

условие равенства исходного заряда конечному, выразив заряды через

соответствующие напряжения на конденсаторах:

Решая записанную систему уравнений, найдём установившиеся заряды на конденсаторах:

3) Найдём заряд, прошедший через источник, как разность конечного и начального заряда на конденсаторе ёмкостью 2С:

4) Запишем закон сохранения энергии для электрической цепи, связывая состояния системы до замыкания ключа и после установления окончательных напряжений на конденсаторах (с учётом работы источника, равной

Окончательно для выделившегося количества теплоты:

Ответ:

На рисунке изображена схема электрической цепи, содержащей резистор сопротивлением R = 2 Ом, два резистора сопротивлением 2R, незаряженный конденсатор ёмкостью 25 мкФ, ключ и источник постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением.

Установите соответствие между физическими величинами и их значениями через достаточно большое время после замыкания ключа. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

А) сила электрического тока, текущего через резистор 3

Б) напряжение на резисторе 2

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

После замыкания ключа К в цепи пойдёт ток, и конденсатор C постепенно зарядится до напряжения U. Напряжение на концах параллельно соединённых проводников одно и то же. Так как сопротивления резисторов в нижней ветке равны, то на каждом из них будет падать одинаковое напряжение

Соответственно через резистор 3 потечет ток

На рисунке изображена схема электрической цепи, содержащей резистор сопротивлением R = 2 Ом, два резистора сопротивлением 2R, незаряженный конденсатор ёмкостью 25 мкФ, ключ и источник постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением.

Установите соответствие между физическими величинами и их значениями через достаточно большое время после замыкания ключа. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

А) сила электрического тока, текущего через резистор 1

Б) напряжение на конденсаторе

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

После замыкания ключа К в цепи пойдёт ток, и конденсатор C постепенно зарядится до напряжения U. Напряжение на концах параллельно соединённых проводников одно и то же.

Соответственно через резистор 1 потечет ток

Аналоги к заданию № 10190: 10259 Все

На рисунке изображена схема электрической цепи, состоящей из последовательно соединённых источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, резистора сопротивлением 2 Ом, конденсатора ёмкостью 4 мкФ и ключа.

В начальный момент времени ключ разомкнут, конденсатор не заряжен. Определите электрическую энергию конденсатора через большое время, прошедшее после замыкания ключа. Ответ запишите в микроджоулях.

Сразу после замыкания ключа по цепи пойдет ток зарядки. Поскольку конденсатор включен последовательно с резистором, ток в цепи прекратится, как только конденсатор зарядится. Причем, напряжение на конденсаторе станет равным ЭДС источника тока. Тогда энергия заряженного конденсатора через длительное время будет равной

На рисунке изображена схема электрической цепи, состоящей из последовательно соединённых источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, резистора сопротивлением 2 Ом, конденсатора ёмкостью 4 мкФ и ключа.

В начальный момент времени ключ разомкнут, конденсатор не заряжен. Определите заряд конденсатора через большое время, прошедшее после

замыкания ключа. Ответ запишите в микрокулонах.

Сразу после замыкания ключа по цепи пойдет ток зарядки. Поскольку конденсатор включен последовательно с резистором, ток в цепи прекратится, как только конденсатор зарядится. Причем, напряжение на конденсаторе станет равным ЭДС источника тока. Тогда заряд конденсатора найдем по формуле

В электрической цепи, схема которой изображена на рисунке, сила тока через источник сразу после замыкания ключа в n = 3 раза больше силы тока, установившейся спустя большое время после этого замыкания. Установившийся заряд на конденсаторе ёмкостью C = 0,5 мкФ равен q = 2 мкКл. Найдите ЭДС ℰ источника.

1. Сразу после замыкания ключа К ток пойдет только через конденсатор С, поскольку он ещё не заряжен, и напряжение на нём и на резисторе R равно нулю, откуда по закону Ома для участка цепи следует, что и ток через резистор в первый момент равен нулю. Поэтому по закону Ома для замкнутой цепи где r — внутреннее сопротивление источника тока.

2. В установившемся режиме ток через конденсатор не идёт, и по закону Ома для замкнутой цепи причём по условию

3. Установившееся падение напряжения на резисторе равно напряжению на конденсаторе

согласно формуле для связи заряда и напряжения на конденсаторе.

4. Из написанных уравнений получаем, что

откуда Cледовательно,

5. Таким образом,

В электрической цепи, схема которой изображена на рисунке, сила тока через источник сразу после замыкания ключа в n = 2 раза больше силы тока, установившейся спустя большое время после этого замыкания. Установившийся заряд на конденсаторе ёмкостью C = 1 мкФ равен q = 1,75 мкКл. Найдите ЭДС ℰ источника.

1. Сразу после замыкания ключа К ток пойдет только через конденсатор С, поскольку он ещё не заряжен, и напряжение на нём и на резисторе R равно нулю, откуда по закону Ома для участка цепи следует, что и ток через резистор в первый момент равен нулю. Поэтому по закону Ома для замкнутой цепи где r — внутреннее сопротивление источника тока.

2. В установившемся режиме ток через конденсатор не идёт, и по закону Ома для замкнутой цепи причём по условию

3. Установившееся падение напряжения на резисторе равно напряжению на конденсаторе

согласно формуле для связи заряда и напряжения на конденсаторе.

4. Из написанных уравнений получаем, что

откуда Cледовательно,

5. Таким образом,

Аналоги к заданию № 10965: 11006 Все

Непосредственно над неподвижно закреплённой проволочной катушкой на её оси на пружине подвешен полосовой магнит (см. рис.). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы вы использовали для объяснения

Решение (см. также Правило ниже).

1. Когда ключ разомкнут, тока в катушке нет, магнит висит неподвижно, и пружина растянута.

2. После замыкания ключа в катушке потечёт ток (от плюса к минусу источника напряжения) и индукция магнитного поля катушки (вблизи её оси) будет направлена вниз (правило буравчика).

3. Катушка с током аналогична полосовому магниту, северный полюс которого в данном случае расположен у её нижнего торца, а южный — у верхнего. Поскольку разноименные полюса магнитов притягиваются друг к другу, значит, магнит будет притягиваться к катушке (опускаться вниз)

Линии магнитной индукции направлены от севера к югу, значит сверху север, а снизу юг, следовательно магнит будет двигаться вверх.

Линии маг­нит­ной ин­дук­ции выходят из се­ве­рного полюса магнита и входят в южный, внутри магнита они идут от южного полюса к северному.

Заряженный конденсатор С₁ = 1 мкФ включён в последовательную цепь из резистора R = 300 Ом, незаряженного конденсатора C₂ = 2 мкФ и разомкнутого ключа К (см. рис.). После замыкания ключа в цепи выделяется количество теплоты Q = 30 мДж. Чему равно первоначальное напряжение на конденсаторе С₁?

Первоначальный заряд конденсатора В результате перезарядки конденсаторов после замыкания ключа их заряды равны соответственно и причём (по закону сохранения электрического заряда). В результате перезарядки на конденсаторах устанавливаются одинаковые напряжения, так как ток в цепи прекращается и напряжение на резисторе R становится равным нулю. Поэтому По закону сохранения энергии выделившееся в цепи количество теплоты равно разности значений энергии конденсаторов в начальном и конечном состояниях:

Решая систему из уравнений, написанных выше, получаем:

Конденсатор подключен к источнику тока последовательно с резистором R = 20 кОм (см. рис.). В момент времени t = 0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи, выполненных с точностью ±1 мкА, представлены в таблице

t, с	0	1	2	3	4	5	6
I, мкА	300	110	40	15	5	2	1

Выберите все верные утверждения о процессах, наблюдаемых в опыте.

1) Ток через резистор в процессе наблюдения уменьшается.

2) Через 2 с после замыкания ключа конденсатор остаётся полностью разряженным.

3) ЭДС источника тока составляет 12 В.

4) В момент времени t = 3 с напряжение на резисторе равно 0,3 В.

5) В момент времени t = 3 с напряжение на конденсаторе равно 6 В.

Проверим справедливость предложенных утверждений.

1) Из таблицы ясно, что ток через резистор в процессе наблюдения уменьшается.

2) Ток через резистор со временем уменьшается, следовательно, возникает напряжение противоположное напряжению на источнике тока. Это напряжение возникает из-за зарядки конденсатора. При t = 2 с конденсатор уже не является полностью разряженным.

3) В момент замыкания ключа, то есть при t = 0 напряжение на резисторе равно ЭДС источника. Напряжение на резисторе в этот момент равно:

4) В момент времени напряжение на резисторе равно:

5) Напряжение на конденсаторе равно разности ЭДС источника тока и напряжения на резисторе. При t = 3 с напряжение на конденстаторе равно 6 В − 0,3 В = 5,7 В.

Таким образом, верными являются утверждения под номерами 1 и 4.

Почему через резистор идет ток? Ведь конденсатор — это разрыв цепи.

Кон­ден­са­тор пропускает переменный ток.

На рисунке приведена схема электрической цепи, состоящей из конденсатора ёмкостью С, резистора сопротивлением R и ключа К. Конденсатор заряжен до напряжения U = 20 В. Заряд на обкладках конденсатора равен q = 10 –6 Кл. Какое количество теплоты выделится в резисторе после замыкания ключа К? Ответ выразите в микроджоулях.

После замыкания ключа конденсатор полностью разрядится и вся запасённая в нём энергия выделится в виде теплоты в резисторе:

На рисунке приведена схема электрической цепи, состоящей из конденсатора ёмкостью С, резистора сопротивлением R и ключа К. Емкость конденсатора C = 1 мкФ, и он заряжен до напряжения U = 10 В. Какое количество теплоты выделится в резисторе после замыкания ключа К? Ответ выразите в микроджоулях.

После замыкания ключа конденсатор полностью разрядится и вся запасённая в нём энергия выделится в виде теплоты в резисторе:

Аналоги к заданию № 9151: 9182 Все

На рисунке изображена схема электрической цепи. Что произойдет с общим сопротивлением цепи при замыкании ключа К? Сопротивление цепи

1) увеличится при любых значениях и

2) уменьшится при любых значениях и

3) уменьшится, только если

4) увеличится, только если

При замыкании ключа два резистора окажутся подключенными параллельно. При параллельном соединении двух резисторов общее сопротивлении всегда меньше, чем сопротивление любого из них. Проверим это, например для сопротивления для второго проверяется аналогично. Рассмотрим разность

Какой заряд установится на конденсаторе С ёмкостью 1 мкФ после замыкания ключа К в цепи, схема которой изображена на рисунке? Параметры цепи: U = 12 В, R₁ = 3 Ом, R₂ = 1 Ом, R₃ = 2 Ом, R₄ = 4 Ом. Внутреннее сопротивление батареи равно нулю.

1. После замыкания ключа К в цепи пойдёт ток, и конденсатор C постепенно зарядится до напряжения U_С и заряда q = CU_С, после чего ток через конденсатор прекратится.

2. Пусть токи через резисторы и равны и Тогда, по закону сохранения заряда, в каждом узле сумма входящих в него токов равна сумме выходящих:

3. По закону Ома для полной цепи где по правилам вычисления сопротивлений для параллельного и последовательного соединения резисторов суммарное сопротивление

4. По закону Ома для участка цепи

5. Кроме того, падение напряжения на резисторе должно равняться падению напряжения на резисторах и соединённых с ним параллельно:

6. Решая полученную систему уравнений, получим:

Ответ:

Источник

Adblock
detector

При отключении конденсатора от источника тока напряжение

Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением Таким образом, напряжение уменьшается.

Источник

Действия с конденсатором

9. Емкость плоского конденсатора С₁ = 10 -10 Ф. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U₁ = 600 В и отключили от источника. Какую работу необходимо совершить, чтобы вынуть диэлектрик из конденсатора? Трением пренебречь.

Если конденсатор отключили от источника, то напряжение уменьшается, но остается q = const.Энергия конденсатора: 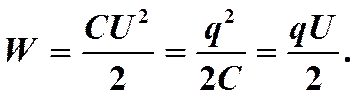Т.к. q=const, то необходимо использовать формулу 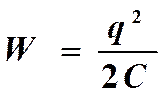. А_внеш. = W₂ – W₁

.

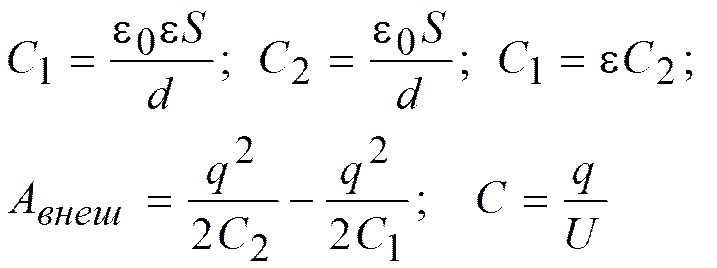
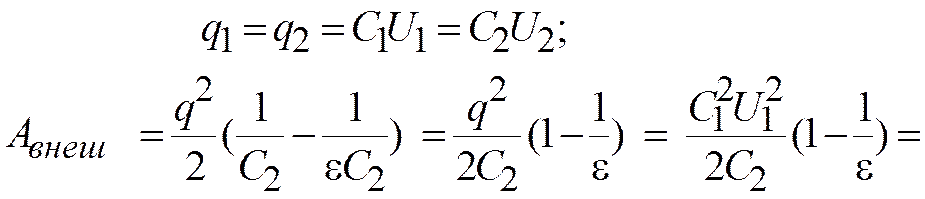
Если конденсатор остается подключенным к источнику, то q ≠ const, а

U = const = q₁/C₁ = q₂/C₂и W = ½ (CU 2 ).

10.Плоский конденсатор электроемкостью 4нФ подсоединен к источнику напряжения 10 В. Затем, не отключая конденсатор от источника, расстояние между его обкладками увеличили в 2 раза.

1) Найти, во сколько раз изменились следующие величины: а) электроемкость конденсатора, б) заряд на его обкладках, в) напряжение на конденсаторе, г) поверхностная плотность заряда, д) напряженность электростатического поля, е) поток Е через пластину конденсатора,

ж) электрическая индукция D, з) плотность энергии электрического поля в конденсаторе,

и) энергия конденсатора.

2) Рассчитать работу, затраченную на изменение расстояния между обкладками.

3) Найти заряд, прошедший через источник.

1) а) 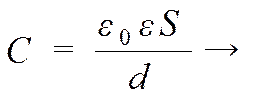если С₁ = 4 нФ, то

в) Т.к. конденсатор от источника не отключается, то U₂ = U₁ = U =10 B, но изменяется заряд:

г) 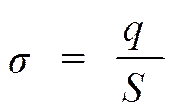→ σ₂ / σ₁ = ½. д) 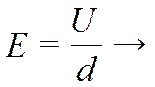Е₂ / Е₁ = ½.

е)N_E = ES , N_E2 / N_E1 = ½. ж) 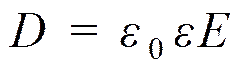→ D₂ /D₁ = ½.

и)Когда U = const, то W = ½CU 2 ,

2) Работа внешних сил, затраченная на изменение расстояние между обкладками, рассчитывается как изменение энергии конденсатора:

3) Найдем заряд, прошедший через источник:

Источник

При отключении конденсатора от источника тока напряжение

Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением Таким образом, напряжение уменьшается.

Источник

Физика дома

Одной из тем, изучаемых в курсе физики 10-го класса, является тема «Конденсаторы». Сама по себе тема не сложная, но решение задач по этой теме вызывает вопросы. Давайте разберём некоторые задачи и те нюансы, на которые необходимо обращать внимание.

Теорию Вы можете прочитать в учебнике. Поэтому сразу перейдём к задачам — к практике. Рассмотрим несколько задач.

1) Как изменится электроёмкость конденсатора при увеличении заряда на его обкладках в n раз?

Ёмкость конденсатора зависит от геометрических размеров пластин, их взаимного расположения и электрических свойств среды. Ни один из этих параметров здесь не изменяется. Следовательно электроёмкость конденсатора не изменится. При увеличении заряда на пластинах — увеличится напряжение между обкладками.

2) Плоский воздушный конденсатор, площадь каждой пластины которой равна S, а расстояние между ними d₁, зарядили до напряжения U и отключили от источника напряжения . После этого увеличили расстояние между пластинами до d₂. Как изменится при этом энергия конденсатора ?

При увеличении расстояния между пластинами, электроёмкость конденсатора уменьшается в 2 раза. Это — во-первых. Во-вторых. Для решения этой задачи большинство используют формулу для определения энергии электрического поля заряженного конденсатора. После подстановки получается, что энергия уменьшается в 2 раза. Этот ответ будет не верный.

Для ответа на вопрос этой задачи следует воспользоваться другой формулой для определения энергии. Поскольку после отключения конденсатора от источника напряжения, постоянным остаётся заряд на конденсаторе! Следовательно энергия заряженного конденсатора увеличивается в 2 раза!

3) Тот же самый вопрос, но конденсатор остаётся подключённым к источнику напряжения .

Если конденсатор остаётся подключённым к источнику напряжения, то напряжение между обкладками остаётся неизменным, какие бы изменения не производились с конденсатором. И для ответа на вопрос необходимо воспользоваться первой формулой.

4) Конденсатор ёмкостью С₁, заряженный до разности потенциалов U₁ соединили одноимённо заряженными обкладками с конденсатором ёмкостью С₂, заряженным до напряжения U₂. Найдите разность потенциалов между обкладками конденсаторов после их соединения.

В основе решения задач подобного типа лежит закон сохранения электрического заряда. Заряд конденсаторов до соединения равен заряду системы после соединения. То есть, записав закон сохранения заряда и расписав заряды конденсаторов, определить неизвестную величину уже не вызывает никаких трудностей.

5) Как изменится ёмкость плоского конденсатора, если между его обкладками поместить стеклянную пластинку, толщина которой равна половине расстояния между обкладками? Какая работа совершается при этом, если конденсатор остаётся подсоединён к источнику напряжения U?

Для начала необходимо понять, а что происходит с конденсатором. Если сделать рисунок, то это выглядит примерно следующим образом:

И если мысленно между воздушным зазором и диэлектриком пометить тонкий проводник, то получившийся конденсатор будет представлять собой два последовательно соединенные конденсатора, с расстояние между пластинами d/2. Просчитав ёмкость получившейся системы, отвечаем на первый вопрос задачи.

Чтобы ответить на вопрос с энергией, рассчитываем энергию системы до и после введения диэлектрика. Разность энергий будет показывать работу, совершённую при этом.

Конденсатор может быть заполнен диэлектриком таким образом, что диэлектрик заполняет конденсатор на половину площади пластин. Тогда конденсатор разрезаем на пополам и решаем задачу, как будто имеем два параллельно соединённых конденсатора с площадью пластин S/2.

6) Конденсатор подключили к источнику тока через резистор сопротивлением 5 кОм. Результаты измерений напряжения между обкладками конденсатора представлены в таблице:

Источник

35. Электродинамика Читать 0 мин.

35.441. Цепи

Через конденсатор постоянный ток не течёт.

Напряжение на параллельных участках цепи одинаково.

В системе отключенных конденсаторов заряд всегда остаётся постоянным. Напряжение и ёмкость может меняться.

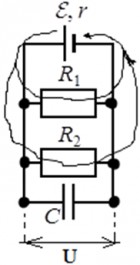
Выделившееся количество теплоты равно разности начальной и конечной энергии:

Eн ― начальная энергия системы [Дж];

Ек ― конечная энергия системы [Дж].

Начальные и конечные энергии определяются энергиями конденсаторов и катушек индуктивности входящих в цепь.

После установления равновесия, напряжение есть только на конденсаторах, не подключенных параллельно к резисторам.

Конденсатор в цепи постоянного тока

Плоский конденсатор представляет собой пластинки, на которых может скапливаться заряд. Между пластинками находится пространство, заполненное диэлектриком (или воздухом в роли диэлектрика). Поскольку диэлектрики ― вещества, плохо проводящие ток, от одной пластины конденсатора через слой диэлектрика на другую пластину заряд перейти не может, а значит, через конденсатор ток не проходит. Если на участке цепи находится такой конденсатор ― этот участок «заблокирован», тока в нем нет.

Если на участке цепи находится конденсатор не заряженный, или заряженный частично, а цепь подключают к источнику тока ― на обкладках конденсатора начинает скапливаться заряд. Это означает, что на этом участке цепи до конденсатора есть ток ― до тех пор, пока конденсатор не заряжен полностью.

Если цепь от источника тока отключить, и в ней есть заряженный конденсатор ― конденсатор начинает разряжаться. Заряды с одной обкладки конденсатора пытаются перейти на другую, по «длинному пути» ― через всю цепь, создавая, таким образом, ток. Ток в такой цепи будет до тех пор, пока конденсатор не разрядится.

Пример: Пусть в цепи есть два резистора с сопротивлениями R1 и R2, источник ЭДС ε, и конденсатор емкостью C:

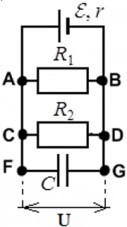
Конденсатор C полностью заряжен. В этом случае токи в цепи не проходят через участок цепи FG ― его словно нет в цепи, и в расчетах параметров цепи он не учитывается. Ток считается выходящим из положительно заряженной клеммы источника ЭДС (тонкая и длинная) к входящим в отрицательно заряженную клемму (жирная короткая черта):

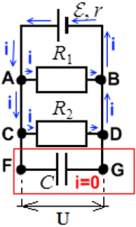
Конденсатор разряжен или заряжен не док конца. В этом случае конденсатор только заряжается, и ток в цепи через точку F проходит — вплоть до обкладки конденсатора – но дальше, в точку G ток не проходит.

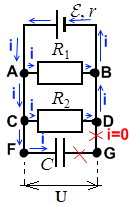
Конденсатор заряжен, но от источника ЭДС цепь отключена. В этом случае ток идет через всю цепь ― пока конденсатор может служить источником зарядов и пока полностью не разрядится. Когда конденсатор разрядится ― ток в цепи прекратится.

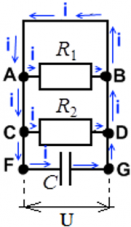
Напряжения на всех параллельных участках цепи равны ― это основное свойство параллельного подключения. Вне зависимости от того, находится на ветви резистор, или конденсатор. Таким образом, во всех случаях для примера выше, напряжение на конденсаторе C равно напряжению на резисторе R1, и равно напряжению на резисторе R2. Благодаря этому свойству, зная, например, энергию, скопившуюся на заряженном конденсаторе, или его заряд, можно вычислить напряжение на резисторах.

Заряженный конденсатор, отключенный от цепи. У заряженного конденсатора на обкладках находится определенное количество заряда. Если конденсатор отключить от цепи ― заряду некуда переместиться, и он остается на конденсаторе неизменным. Получить дополнительный заряд, если он заряжен не до конца, конденсатору тоже неоткуда. Заряд конденсатора, отключенного от цепи, постоянен.

Электроемкость конденсатора ― это его физико-геометрическая характеристика, показывающая, как много заряда он может скопить. Электроемкость конденсатор не зависит ни от заряда на его обкладках, ни от напряжения в цепи.

Электроемкость конденсатора равна C = $frac <varphi_2 – varphi_1>= frac$ , где

C ― электроемкость конденсатора, [Ф];

(φ2 – φ1) ― разность потенциалов на обкладках конденсатора, [В];

U ― напряжение на обкладках конденсатора [В].

Электроемкость плоского конденсатора зависит от размеров его пластин, расстояния между ними, а также типа диэлектрика, который заполняет пространство между пластинами.

Электроемкость плоского конденсатора равна C = $frac<varepsilonvarepsilon_0 S>$ , где

C ― ёмкость конденсатора [Ф];

ε ― диэлектрическая проницаемость;

ε0 ― электрическая постоянная;

S ― площадь обкладок конденсатора [м2];

d ― расстояние между обкладками [м].

В электрической цепи за счет сопротивления, которое преодолевают движущиеся в материале заряды, выделяется тепло. Количество теплоты, которая выделяется в цепи, равно разности начальной и конечной энергии всей системы Q = Eн – Eк¸ где

Eн ― начальная энергия системы [Дж];

Eк ― конечная энергия системы [Дж].

В цепи энергия скапливается на конденсаторах (энергия электрического поля) и на катушках индуктивности (энергия магнитного поля). Поэтому энергия электромагнитных сил в цепи в любой момент равна сумме энергий на конденсаторах и на катушках, которые входят в цепь.

Энергия электрического поля заряженного конденсатора равна We = $frac <2>= frac <2>= frac<2C>$ , где

We ― энергия электрического поля конденсатора, [Дж];

C ― электроемкость конденсатора, [Ф];

U ― напряжение на обкладках конденсатора, [В];

q ― заряд на обкладках конденсатора, [Кл].

Энергия магнитного поля катушки индуктивности равна E = $frac<2>$ , где

E ― энергия магнитного поля катушки [Дж];

L ― индуктивность катушки [Гн];

Состояние равновесия и зарядка конденсаторов

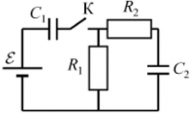
Пример 1: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, оба конденсатора емкостями C1 и C2 разряжены.

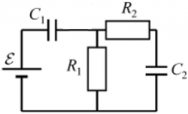
Ток от источника ЭДС до конденсатора C1 будет идти до тех пор, пока конденсатор C1 не будет полностью заряжен. При этом от конденсатора C1 дальше заряды не проходят ― ни на резисторы R1 и R2, ни на конденсаторC2. Как только конденсатор C1 полностью заряжается, в системе наступает состояние равновесия ― напряжение на конденсаторе становится равным ЭДС, весь возможный заряд конденсатор принял. Поскольку ток через него не прошел до конденсатора C2 ― этот конденсатор так и остался незаряженным. Напряжение есть лишь на конденсаторе C1, а на конденсаторе C2напряжение равно нулю. Зарядка конденсатораC1:

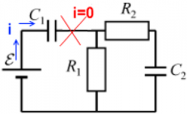
После того, как конденсатор C1 заряжен, ток в цепи прекращается.

Пример 2: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, все три конденсатора емкостями C1, C2 и C3 разряжены.

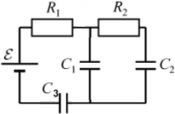
Ток, выходя из источника ЭДС, разделяется на два тока ― один питает подзарядку конденсатораC1, а другой ― конденсатораC2. Состояние равновесия наступает, когда оба конденсатора полностью заряжены ― в цепи ток больше не проходит. Но так как ток дальше конденсаторов не проходит ― конденсатор C3 не получает заряд, и остается разряженным. Напряжение на конденсаторе C3 равно нулю.

Зарядка конденсаторов C1 иC2:

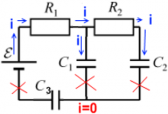
После того, как конденсаторыC1 и C2 заряжены, ток в цепи прекращается.

Источник

На этой странице вы узнаете

• Где самое большое сопротивление в теле человека?
• Какой ученый променял бильярд на физику?
• К чему может привести авария среди электронов?

Весь современный мир держится на электричестве. Наряду с глобальной интернет-сетью, наш мир «опутан» сетью электрических проводов. Что такого происходит в этих тоненьких проводах, что от них зависит жизнь целого города? Давайте поближе познакомимся с электрическим током и узнаем, откуда он появляется.

Мы с вами уже познакомились с электрическими схемами в теме «Законы постоянного тока», где  выяснили, какие приборы существуют и как используются в схемах. В этой статье мы поговорим о том, как в элементарных электрических цепях появляется ток. Начало положено, сопротивление бесполезно.  

Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.

Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение. 

Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока). 

Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?

Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.

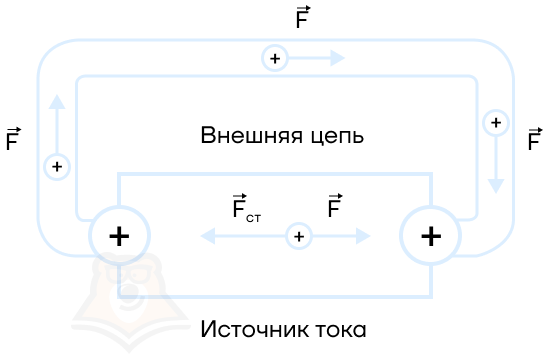
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_{ст})), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)). 

Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_{ст})), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда. 

После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.

Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.

Основные параметры источника тока

Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление. 

ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_{ст})), затраченную на перемещение зарядов (q) внутри источника.

Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока. 

Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление. 

Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.

Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.

Закон Ома для участка цепи

Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.

Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и напряжение. Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:

U_r = Ir.

Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:

U_R = IR.

Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:

Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи: 

Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.

Короткозамкнутая цепь

Рассмотрим частный случай электрической цепи, в котором источник тока будет подключен сам на себя. Иначе говоря, он будет короткозамкнутым.

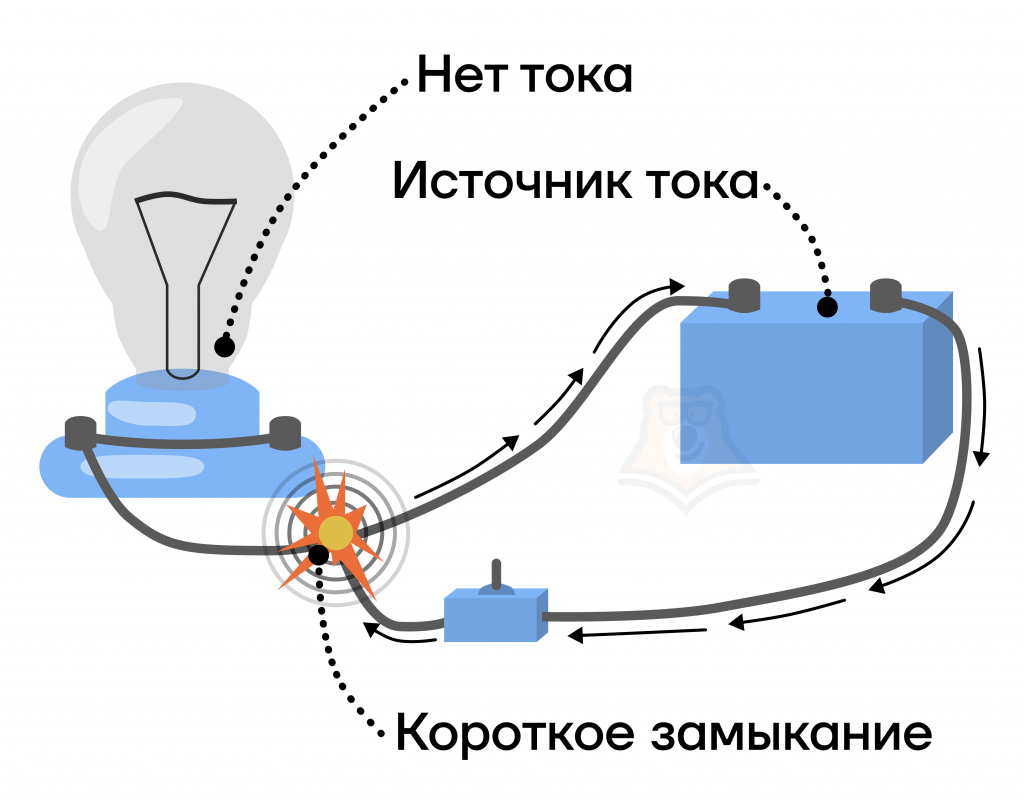
В этом случае отсутствует сопротивление внешней цепи и закон Ома для цепи будет выглядеть так:

Короткое замыкание — это такой случай соединения проводов, при котором практически весь ток проходит по пустому проводу и возвращается в источник тока. 

Короткое замыкание приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам. 

Теперь, когда мы уже рассмотрели основные характеристики источника тока, можем перейти к мощности и КПД источника тока.

Мощность и КПД источника тока

Мы уже не раз говорили о том, что при протекании тока выделяется энергия. Источники тока не исключение. При подключении их к цепи на них выделяется энергия. При этом энергия выделяется и в самой цепи.

Чтобы найти мощность передачи энергии (P), выделяемой источником тока, необходимо умножить силу тока на ЭДС этого источника тока. Тогда получим:

При этом часть этой мощности уходит на элементы внешней цепи, а другая часть – на преодоление внутреннего сопротивления источника тока:

(εI = I^2R + I^2r).

Тогда мощность, выделяемая на внешней цепи:

(P_R=I^2R).

А мощность, которая теряется на внутреннее сопротивление источника тока:

(P_r=I^2r).

Теперь давайте рассмотрим коэффициент полезного действия (КПД, ) источника тока. Как мы уже говорили ранее, часть ЭДС источника тока уходит на внутреннее сопротивление, а часть – на внешнюю цепь. При этом вспомним, что КПД – это отношение полезной мощности к затраченной.

Запишем формулы для мощности:

(P_{ист}=εI=I^2(R+r)),
(P_R=IU =I^2R).

Тогда КПД:

Мы с вами выяснили, что источники тока – элементы электрической цепи, без которых самой цепи не существовало бы. Хотя, конечно, она бы существовала, но была бы бесполезной. Однако и они «не без греха», так как существует опасное внутреннее сопротивление, которое является головной болью для многих инженеров. А все потому, что оно снижает КПД источников тока. Дальше вы можете ознакомиться с полноценными электрическими схемами и посмотреть, как ток ведет себя за пределами источника тока.

Термины

Напряжение – произведение сопротивления элемента и протекающего через него тока.

Резистор (или резистивный элемент) – элемент электрической цепи, который может только потреблять энергию и не может ее создавать.

Сторонние силы — это все внешние силы, воздействующие на заряд.

Электростатическое поле — невидимое поле, создаваемое постоянными электрическими зарядами.

Фактчек

• ЭДС источника тока (ε) — это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами: (ε =frac{А_{cт}}{q}).
• Внутреннее сопротивление (r) — определяет количество потерь энергии при прохождении тока через источник тока.
• Закон Ома для полной цепи: Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению: (I =frac{ε}{R + r}).
• Предельное значение силы тока для данного источника тока называется током короткого замыкания: (I_{кз} =frac{ε}{r}).
• Полная мощность цепи — это есть мощность источника тока: (P_ист=εI).

Проверь себя

Задание 1.
Как рассчитывается ЭДС источника тока?

1. (ε =frac{А_{ст}}{q})
2. (ε =frac{U}{q})
3. (ε =frac{А_{ст}}{I})
4. (ε =frac{А_{ст}}{qt})

Задание 2.
Короткое замыкание — это:

1. Соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи. 
2. Соединение концов участка цепи проводником, сопротивление которого очень велико по сравнению с сопротивлением участка цепи. 
3. Соединение концов участка цепи проводником, сопротивление которого не зависит от сопротивления участка цепи. 
4. Отсутствие электрического тока в цепи.

Задание 3.
Чему равно ЭДС источника тока?

1. (ε = U_R- U_r)
2. (ε = U_R+ U_r)
3. (ε = U_R U_r)
4. (ε = U_R)

Задание 4.
От чего зависит сила тока в цепи с заданным источником тока?

1. от внутреннего сопротивления цепи
2. от внутреннего сопротивления источника тока
3. от внешнего сопротивления цепи
4. не зависит ни от каких величин

Задание 5.
Где самое большое сопротивление в человеке?

1. в сердце
2. в пищеварительной системе
3. на коже
4. в голове

Ответы: 1. — 1; 2. — 1; 3. — 2; 4. — 3; 5. — 3.