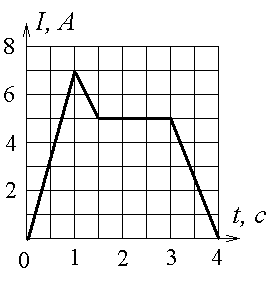Вычислить величину электрического заряда, проходящего через поперечное сечение проводника площадью 2 мм² за 10 секунд, при этом плотность тока равномерно возрастает от 0 до 106 а/м².
Дано: S=2×10-6м² t=10 с; j1=0; j2=106 а/м².
Найти: q-?
Решение:
Определяем количество электричества q, прошедшее через поперечное сечение проводника за время t, по следующей формуле:
q=Iср×t,
где Iср — среднее значение величины тока.
Из формулы I=j×S определяем среднее значение величины тока:
Тогда электрический заряд равен:

Ответ: величина электрического заряда равна 10 кулонам
При
перемещении электрического заряда q
из точки 1 в точку 2 электрическое поле
совершает работу
,
(7.1)
где
– разность потенциалов или напряжение
.
Как известно,
сила тока определяется, как заряд,
протекающий через поперечное сечение
провода за единицу времени, т.е.
. (7.2)
Если известна
зависимость силы тока
,
то из (7.2) можно выразить заряд, протекающий
за малый промежуток времени:
, (7.3)
и преобразовать
формулу (7.1) следующим образом:
, (7.4)
где
– электрическая мощность.
Используя
закон Ома для однородного участка цепи
,
и подставляя его в (7.4), получим закон
Джоуля-Ленца:
(7.5)
В формуле
(7.5) учтено то обстоятельство, что работа
электрического поля, совершенная над
электрическими зарядами, не приводит
к увеличению их кинетической энергии,
а выделяется в виде тепла
.
Таким образом,
из (7.5) можно рассчитать тепло, выделившееся
в сопротивлении
за любой промежуток времени:
(7.6)
Задача 9.
По проводу
сопротивлением
= 20 Ом течет переменный электрический
ток. Сила тока изменяется по закону
,
где А = 3
А, = 1 с. Чему равно
количество теплоты, выделившейся в
проводе за промежуток времени от
до
= 2 с?
Решение:
Подставим
функцию силы тока от времени в формулу
(7.6):
Дж
Ответ: Q = 18 МДж
Задача 10.
По проводу
сопротивлением
= 20 Ом течет переменный электрический
ток. Сила тока изменяется по закону
,
где А = 3
А/с,
рад/с. Чему равно количество теплоты,
выделившейся в проводе за промежуток
времени от
до
= 2 с?
Решение:
Подставим
функцию силы тока от времени в формулу
(7.6):
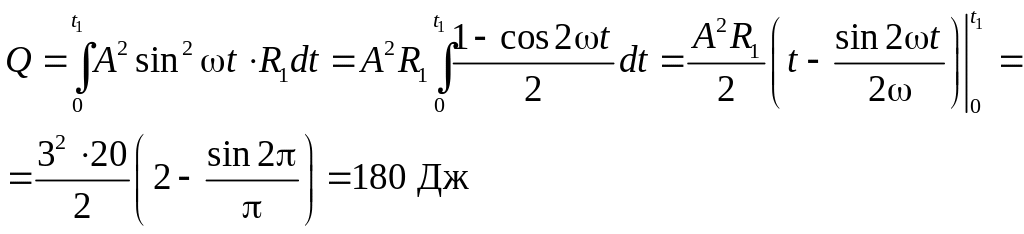
Ответ: Q = 180 Дж
7.1 По проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
.
А,
Ом,
с, = 1 с.
Чему равно
количество теплоты, выделившейся в
проводе за время
?
Ответы: а) 0,33
Дж; б) 0,20 Дж; в) 0,14 Дж; г) 0,11 Дж;
д) 250 мДж; е) 167 мДж; ж) 50 мДж;
7.2 По
проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
а)
;
б)
.
Чему равно
количество теплоты, выделившейся в
проводе за время
?
А,
Ом,
рад/с,
с
Ответы: а) 500 мДж; б) 500 мДж
7.3 По
проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
.
Чему равно количество теплоты, выделившейся
в проводе за время
?
А,
Ом,
с–1,
с
Ответ: 432 мДж
7.4э. Напряженность
электрического поля в проводнике
увеличили в 2 раза. Как изменилась
удельная тепловая мощность (тепло,
выделяющееся за единицу времени в
единице объема)?
а) увеличилась
в 2 раза; б) увеличилась в 4 раза;
в) увеличилась
в 8 раз; г) уменьшилась в 2 раза.
8. Заряд, прошедший через поперечное сечение проводника
Используя
формулу (7.3), можно найти количество
электричества, т.е. электрический заряд,
прошедший через поперечное сечение
провода за любой промежуток времени
(8.1)
Задача 11.
Используя
условие задачи 9, найти полный заряд,
прошедший через поперечное сечение
провода за промежуток времени от
до
с.
Решение:
Используем
формулу (8.1):
Кл.
Ответ: q
= 559 Кл
Задача 12
Используя
условие задачи 10, найти полный заряд,
прошедший через поперечное сечение
провода за промежуток времени от
до
с.
Решение:
Используем
формулу (8.1):
Кл.
Ответ: q
= 3,82 Кл
8.1 По проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
а)
;
б)
;
в)
г)
.
Чему равен
заряд, прошедший через поперечное
сечение провода за время
?
А,
А,
Ом, t1 =
= 1 с
Ответы: а) 833 мКл б) 750 мКл; в) 583 мКл; г) 367
мКл
8.2 По
проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
а)
;б)
.
Чему равен
заряд, прошедший через поперечное
сечение провода за время
?
А,
рад/с,
Ом,
с
Ответы: а) 477 мКл; б) 0,83 Кл
8.3 По
проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
а)
;
б)
.
Чему равен заряд, прошедший через
поперечное сечение провода за время
?
А,
рад/с,
Ом,
с
Ответы: а) 500 мКл; б) 0,50 Кл
8.4 По
проводу сопротивлением
течет переменный электрический ток.
Сила тока изменяется по закону
.
Чему равен заряд, прошедший через
поперечное сечение провода за время
?
А,
с–1,
Ом,
с
Ответ: 632 мКл
8.5э. Сила тока, текущего по проводнику,
меняется во времени, как показано на
рисунке. Какой заряд протечет сквозь
поперечное сечение проводника в
промежуток времени
о
т
t1 = 1 c
до t2 = 3 c?
а) 7 Кл; б) 12 Кл; в) 10,5 Кл; г) 1,5 Кл.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Времена, когда ток обнаруживался с помощью личных ощущений ученых, пропускавших его через себя, давно миновали. Теперь для этого применяют специальные приборы, называемые амперметрами.
Амперметр — это прибор, служащий для измерения силы тока. Что понимают под силой тока?
Обратимся к рисунку 21, б. На нем выделено поперечное сечение проводника, через которое проходят заряженные частицы при наличии в проводнике электрического тока. В металлическом проводнике этими частицами являются свободные электроны. В процессе своего движения вдоль проводника электроны переносят некоторый заряд. Чем больше электронов и чем быстрее они движутся, тем больший заряд будет ими перенесен за одно и то же время.
Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за 1 с.
Пусть, например, за время t = 2 с через поперечное сечение проводника носители тока переносят заряд q = 4 Кл. Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
I — сила тока.
Итак, чтобы найти силу тока I, надо электрический заряд q, прошедший через поперечное сечение проводника за время t, разделить на это время:
I = q/t (10.1)
Единица силы тока называется ампером (А) в честь французского ученого А. М. Ампера (1775—1836). В основу определения этой единицы положено магнитное действие тока, и мы на нем останавливаться не будем.
Если сила тока I известна, то можно найти заряд q, проходящий через сечение проводника за время t. Для этого надо силу тока умножить на время:
q = It. (10.2)
Полученное выражение позволяет определить единицу электрического заряда — кулон (Кл):
1 Кл = 1 А · 1 с = 1 А·с.
1 Кл — это заряд, который проходит за 1 с через поперечное сечение проводника при силе тока 1 А.
Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например миллиампер (мА) и микроампер (мкА):
1 мА = 0,001 А, 1 мкА = 0,000001 А.
Как уже говорилось, измеряют силу тока с помощью амперметров (а также милли- и микроамперметров). Демонстрационный гальванометр, о котором упоминалось выше, представляет собой обычный микроамперметр.
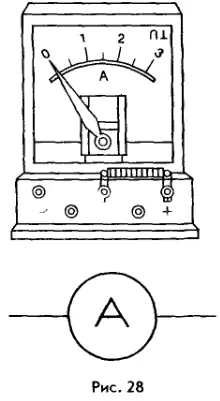
Существуют разные конструкции амперметров. Амперметр, предназначенный для демонстрационных опытов в школе, изображен на рисунке 28. На этом же рисунке приведено его условное обозначение (кружок с латинской буквой «А» внутри).
При включении в цепь амперметр, как и всякий другой измерительный прибор, не должен оказывать заметного влияния на измеряемую величину. Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется.
В зависимости от назначения в технике используют амперметры с разной ценой деления. По шкале амперметра видно, на какую наибольшую силу тока он рассчитан. Включать его в цепь с большей силой тока нельзя, так как прибор может испортиться.
Для включения амперметра в цепь ее размыкают и свободные концы проводов присоединяют к клеммам (зажимам) прибора. При этом необходимо соблюдать следующие правила:
1) амперметр включают последовательно с тем элементом цепи, в котором измеряют силу тока;
2) клемму амперметра со знаком «+» следует соединять с тем проводом, который идет от положительного полюса источника тока, а клемму со знаком «–» — с тем проводом, который идет от отрицательного полюса источника тока.
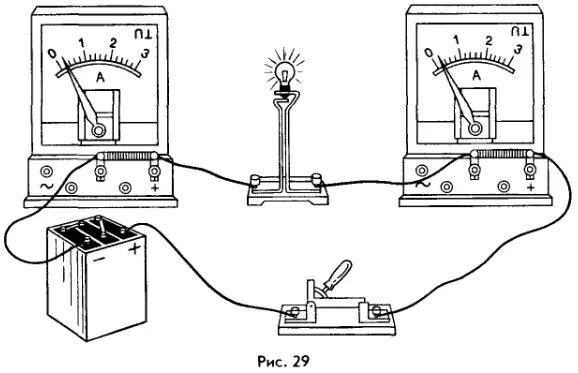
При включении амперметра в цепь не имеет значения, с какой стороны (слева или справа) от исследуемого элемента его подключать. В этом можно убедиться на опыте (рис. 29). Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение.
??? 1. Что такое сила тока? Какой буквой она обозначается? 2. По какой формуле находится сила тока? 3. Как называется единица силы тока? Как она обозначается? 4. Как называется прибор для измерения силы тока? Как он обозначается на схемах? 5. Какими правилами следует руководствоваться при включении амперметра в цепь? 6. По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
Сила тока I для тока, протекающего через некоторую площадь сечения проводника S эквивалентна производной заряда q по времени t и количественно характеризует электрический ток.
Таким образом выходит, что сила тока — это поток заряженных частиц через некоторую поверхность S.
Электрический ток является процессом движения как отрицательных, так и положительных зарядов.
Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков (dq+ и dq−), справедливым будет заключение о том, что сила тока равна следующему выражению:
I=dq+dt+dq-dt.
В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:
I=q∆t,
где сила тока определена в качестве заряда, который пересекает некоторую поверхность S в единицу времени. В системе СИ роль основной единицы измерения силы тока играет Ампер (А).
1A=1 Кл1 с.
Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью
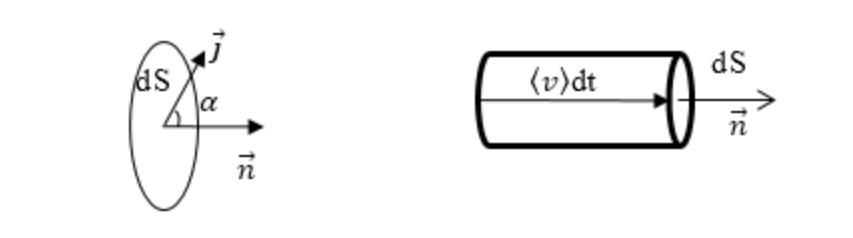
Выделим в проводнике, в котором протекает ток, малый объем dV случайной формы. С помощью следующего обозначения υ определим среднюю скорость движения носителей зарядов в проводнике. Пускай n0 представляет собой концентрацию носителей заряда. На поверхности проводника выберем пренебрежительно малую площадку dS, которая расположена ортогонально скорости υ (рис. 1).
Рисунок 1
Проиллюстрируем на поверхности площадки dS очень короткий прямой цилиндр, имеющий высоту υdt. Весь массив частиц, которые располагались внутри такого цилиндра за время dt пересекут плоскость dS и перенесут через нее, в направлении скорости υ, заряд, выражающийся в виде следующего выражения:
dq=n0qeυdSdt,
где qe=1,6·10-19 Кл является зарядом электрона, другими словами отдельной частицы или же носителя тока. Разделим приведенную формулу на dSdt и получим:
j=dqdSdt,
где j представляет собой модуль плотности электрического тока.
j=n0qeυ,
где j является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:
j=∑niqiυii,
где i представляет собой носитель заряда. Плотность тока — это векторная величина. Снова обратим внимание на рисунок 1. Пускай n→ представляет собой единичный перпендикуляр к плоскости dS. В случае, если частицы, переносящие заряд, являются положительными, то переносимый ими заряд в направлении нормали больше нуля. В общем случае переносимый в единицу времени элементарный заряд может быть записана в следующем виде:
dqdt=j→n→dS=jndS.
Формула приведенная выше справедлива также в том случае, когда плоскость площадки dS неортогональная по отношению к вектору плотности тока. По той причине, что составляющая вектора j→, направленная под прямым углом к нормали, через сечение dS электричества не переносит. Исходя из всего вышесказанного, плотность тока в проводнике окончательно запишем, применяя формулу j=n0qeυ в таком виде:
j→=-n0qeυ→.
Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:
j=IS∆t,
где S играет роль площади сечения проводника. Плотность постоянного тока равна по всей площади сечения проводника. Для двух разных сечений проводника (S1,S2) с постоянным током справедливо следующее равенство:
j1j2=S2S1.
Основываясь на законе Ома для плотности токов можно записать такое выражение:
j→=λE→,
где λ обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:
I=∫SjndS,
где интегрирование происходит по всей поверхности S любого сечения проводника. Единица плотности тока Aм2.
Линии тока
Линии, вдоль которых движутся заряженные частицы, носят название линий тока.
Направления движения положительных зарядов также определяются в качестве направлений линий тока. Изобразив линии тока, можно получить наглядное представление о движении электронов и ионов, которые формируют собой ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность данной трубки. Такую трубка представляет собой так называемую трубку тока. К примеру, поверхность металлической проволоки в изоляторе будет определяться как труба тока.
Сила тока в проводнике равномерно возрастает от 0 до 5 А на протяжении 20 с. Определите заряд, который прошел через поперечное сечение проводника за данный отрезок времени.
Решение
В качестве основы решения данной задачи возьмем формулу, которая характеризует собой силу тока, то есть:
I=dqdt.
Таким образом, заряд будет найден как:
q=∫t1t2Idt.
В условии задачи сказано, что сила тока изменяется равномерно, а это означает то, что мы можем записать закон изменения силы тока в следующем виде:
I=kt.
Найдем коэффициент пропорциональности в приведенном выражении, для чего необходимо запишем закон изменения силы тока еще раз для момента времени, при котором сила тока эквивалентна I2=3А (t2):
I2=kt2→k=I2t2.
Подставим выражение выше в I=kt и проинтегрируем в соответствии с q=∫t1t2Idt, получим формулу такого вида: q=∫t1t2ktdt=∫t1t2I2t2tdt=I2t2∫t1t2tdt=t22t1t2=I22t2t22-t12.
В качестве начального момента времени возьмем момент, когда сила тока эквивалентна нулю, другими словами t1=0, I1=0 A; t2=20, I2=5 А. Проведем следующие вычисления:
q=I22t2t22=I2t22=5·202=50 (Кл).
Ответ: q=50 Кл.
Определите среднюю скорость движения электронов в проводнике, молярная масса вещества которого эквивалентна μ, поперечное сечение проводника S. Сила тока в проводнике I. Примем, что на каждый атом вещества в проводнике приходится два свободных электрона.
Решение
Силу тока (I) в проводнике можно считать постоянной, что позволяет нам записать следующее выражение:
I=q∆t=Nqe∆t,
где заряд q определим как произведение числа электронов проводимости в проводнике, на заряд одного электрона qe, представляющего собой известную величину. ∆t играет роль промежутка времени, за который через поперечное сечение проводника проходит заряд q. Найти N можно, если применять известное в молекулярной физике соотношение:
N’NА=mμ=ρVμ,
где N′ играет роль количества атомов в проводнике, объем которого V, плотность ρ, а молярная масса μ. NA представляет собой число Авогадро. По условию задачи N=2N′. Найдем из N’NА=mμ=ρVμ число свободных электронов: N=2ρVμNA.
Подставим выражение, приведенное выше, в I=q∆t=Nqe∆t, в результате чего получим:
I=2ρVμNAqe∆t=2ρqeNASlμ∆t,
где объем проводника найден как V=Sl, где l – длина проводника. Выразим ее.
l=μ∆tI2ρqeNAS.
Среднюю скорость движения электронов или, другими словами, скорость тока в проводнике можно определить следующим образом: υ=l∆t=μI2ρqeNAS.
Ответ: υ=μI2ρqeNAS.
При прохождении электрического тока по цепи мы можем наблюдать различные его действия: тепловое, химическое, магнитное, световое.
Возьмем, к примеру, тепловое действие. Вы можете уверенно сказать, что оно точно может проявляться в разной степени. Это подтверждали наши опыты. Натянутая медная проволока просто нагревалась, а вот вольфрамовая спираль в электрической лампе уж точно нагревалась сильнее. Ведь она накалилась настолько, что начинала излучать свет. Значит, мы могли накалить до похожего состояния и медную проволоку. Что же для этого нужно сделать? Как контролировать силу действия тока? Что эта сила вообще из себя представляет?
На данном уроке вы узнаете ответы на все эти вопросы. Мы рассмотрим, как заряд перемещается по проводнику при прохождении тока. С помощью этих знаний мы подойдем к определению новой силы и ее свойств — силы тока.
Перемещение заряда по проводнику
Как вы уже знаете, электрический ток представляет собой упорядоченное движение заряженных частиц. Мы говорим, что частицы “заряженные” — это означает, что они имеют какой-то определенный заряд $q$.
Соответственно, при движение таких частиц происходит перенос некоторого заряда. Каждый свободный электрон в металле переносит заряд. Каждый ион в растворе кислот, солей или щелочей тоже переносит заряд.
Логично, что чем больше частиц переместится от одного участка цепи к другому, тем больший общий заряд будет ими перенесен.
От чего же зависит интенсивность действий электрического тока? Опытным путем было доказано, что интенсивность (степень действия) электрического тока зависит как раз от величины этого переносимого заряда.
Сила тока
Электрический заряд, проходящий через поперечное сечение проводника в $1 space с$, будет определять такую величину, как сила тока в цепи (рисунок 1).
Сила тока — это физическая величина, равная отношению электрического заряда $q$, прошедшего через поперечное сечение проводника, ко времени его прохождения $t$:
$I = frac{q}{t}$,
где $I$ — сила тока.
Сила взаимодействия проводников с током как основа для определения единицы силы тока
Для того, чтобы определить единицу измерения силы тока, были проведены опыты, которые мы сейчас и рассмотрим. Опыты эти заключались в явлении взаимодействия двух проводников с током.
Возьмем два гибких прямых проводника. Расположим их параллельно друг другу. Подсоединим их к источнику тока (рисунок 2).
После замыкания цепи по ней пойдет электрический ток. Ток будет идти и по нашим подопытным проводникам.
Что мы увидим? Они начнут взаимодействовать друг с другом. А именно, они будут притягиваться друг к другу (рисунок 2, а) или отталкиваться друг от друга (рисунок 2, б). Это будет зависеть от направления тока в них.
Тут же встает вопрос о том, как же измерить эту силу, с которой взаимодействуют проводники? Опыты показали следующее.
Сила взаимодействия между проводниками с током зависит от:
длины проводников;
расстояния между ними;
среды, в которой находятся проводники;
силы тока в проводниках.
Для нас сейчас имеет значение самый последний пункт. Возьмем проводники, для которых все остальные условия будут одинаковы, кроме силы токов. Окажется, что, чем больше сила тока в каждом проводнике, тем с большей силой они взаимодействуют между собой.
Единица измерения силы тока
А теперь представьте себе очень тонкие и очень длинные проводники. Расположены они параллельно друг другу. Расстояние между ними — $1 space м$. Сила тока в них одинакова. И все это в вакууме! Вот здесь и появляется единица измерения силы тока (рисунок 3).
За единицу силы тока принимаю такую силу тока, при которой отрезки параллельных проводников длиной $1 space м$ взаимодействуют с силой $2 cdot 10^{-7} space Н$ ($0.0000002 space Н$).
Имя этой единицы — ампер ($А$). Она названа в честь французского физика Андре Ампера (рисунок 4).

Дольные и кратные единицы силы тока
На практике вы часто можете увидеть следующие единицы: миллиампер ($мА$), микроампер ($мкА$), килоампер ($кА$).
$1 space мА = 0.001 space А = 1 cdot 10^{-3} space А$;
$1 space мкА = 0.000001 space А = 1 cdot 10^{-6} space А$;
$1 space кА = 1000 space А = 1 cdot 10^3 space А$.
Сила тока некоторых электроприборов
Для лучшего понимания, сколько же составляет один ампер на практике, в таблице 1 приведены средние значения силы тока для некоторых электроприборов.
| Устройство | Значение силы тока $I$, А |
| Лампочка карманного фонаря | 0,1 |
| Обычная лампа накаливания | 0,3 — 0,5 |
| Холодильник | 0,8 — 1 |
| Телевизор | 1,2 — 2 |
| Электрический утюг | 3 |
| Пылесос | 4 — 9 |
| Стиральная машина | 6 — 10 |
| Двигатель троллейбуса | 160 — 220 |
| Молния | более 400 000 |
Связь единицы измерения заряда и единицы измерения силы тока
Хоть мы уже и говорили о заряде и единице его измерения (кулон) ранее, в физике принято определять его через ампер.
Выразим из определения силы тока ($I = frac{q}{t}$) сам заряд и получим следующую формулу.
$q = It$.
Если $I = 1 space А$, а $t = 1 space с$, то мы получим единицу электрического заряда — $1 space Кл$.
$1 space кулон = 1 space ампер cdot 1 space с$, или
$1 space Кл = 1 space А cdot 1 space с = 1 space А cdot с$.
За единицу электрического заряда принимают электрический заряд, проходящий сквозь поперечное сечение проводника при силе тока $1 space А$ за время $1 space с$.
Электрический заряд и его зависимость от силы тока и времени
Мы получили формулу, позволяющую по-новому взглянуть на определение электрического заряда: $q = It$.
Делаем вывод:
электрический заряд, проходящий через поперечное сечение проводника зависит от силы тока и времени его прохождения.
Эти знания пригодятся в решении задач. Обратите внимание, что электрический заряд иногда называют количеством электричества.
Например, давайте найдем количество электричества, которое проходит сквозь поперечное сечение спирали лампы за $1 space мин$. Сила тока лампы равна $400 space мА$.
Дано:
$I = 400 space мА$
$t = 1 space мин$
СИ:
$I = 0.4 space А$
$t = 60 space с$
$q — ?$
Показать решение и ответ
Скрыть
Решение:
Используем формулу для электрического заряда, полученную из определения силы тока:
$q = It$.
Рассчитаем этот заряд:
$q = 0.4 space А cdot 60 space с = 24 space Кл$.
Ответ: $q = 24 space Кл$.
Упражнения
Упражнение №1
Выразите в амперах силу тока, равную $2000 space мА$; $100 space мА$; $55 space мА$; $3 space кА$.
Дано:
$I_1 = 2000 space мА$
$I_2 = 100 space мА$
$I_3 = 55 space мА$
$I_4 = 3 space кА$
Показать решение и ответ
Скрыть
Решение:
$I_1 = 2000 space мА = 2000 cdot 10^{-3} space А = 2 space А$.
$I_2 = 100 space мА = 100 cdot 10^{-3} space А = 0.1 space А$.
$I_3 = 55 space мА = 55 cdot 10^{-3} space А = 0.055 space А$.
$I_4 = 3 space кА = 3 cdot 10^3 space А = 3000 space А$.
Ответ: $I_1 = 2 space А$, $I_2 = 0.1 space А$, $I_3 = 0.55 space А$, $I_4 = 3000 space А$.
Упражнение №2
Сила тока в цепи электрической плитки равна $1.4 space А$. Какой электрический заряд проходит через поперечное сечение ее спирали за $10 space мин$?
Дано:
$t = 10 space мин$
$I = 1.4 space А$
СИ:
$t = 600 space с$
$q — ?$
Показать решение и ответ
Скрыть
Решение:
Используем формулу: $q = It$.
$q = 1.4 space А cdot 600 space с = 840 space Кл$.
Ответ: $q = 840 space Кл$.
Упражнение №3
Сила тока в цепи электрической лампы равна $0.3 space А$. Сколько электронов проходит через поперечное сечение спирали за $5 space мин$?
Маленькое напоминание:
заряд одного электрона по модулю равен $|q_e| = 1.6 cdot 10^{-19} space Кл$.
Дано:
$t = 5 space мин$
$I = 0.3 space А$
$|q_e| = 1.6 cdot 10^{-19} space Кл$
СИ:
$t = 300 space с$
$n_e — ?$
Показать решение и ответ
Скрыть
Решение:
Для начала определим суммарный заряд, который проходит через поперечное сечение спирали лампы за указанное время:
$q = It$,
$q = 0.3 space А cdot 300 space с = 90 space Кл$.
А теперь найдем количество электронов, которые в сумме несут этот заряд:
$n_e = frac{q}{|q_e|}$,
$n_e = frac{90 space Кл}{1.6 cdot 10^{-19} space Кл} approx 56 cdot 10^{19}$.
Вот такое огромное количество электронов проходит через поперечное сечение спирали всего за 5 минут.
Ответ: $n_e = 56 cdot 10^{19}$.