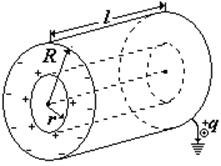
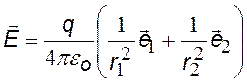Электроемкость сферического конденсатора

.

концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
.
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть , а следовательно можно считать, что
емкость сферического конденсатора будет равна
. Площадь сферы S = 4πr2 следовательно формула будет совпадать с формулой емкости плоского конденсатора
.
Формулы:
Энергия конденсатора: .
Ёмкость конденсатора: 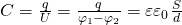
Ёмкость цилиндрического конденсатора: .
Ёмкость плоского конденсатора: 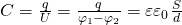
Обозначения в формулах:
C — электрическая ёмкость (ёмкость конденсатора);
g — заряд;
U — потенциал проводника (напряжение);
φ — потенциал;
ε — относительная диэлектрическая проницаемость;
— электрическая постоянная;
S — площадь одной обкладки;
d — расстояние между обкладками;
r2— Больший радиус (от центра, до края конденсатора);
r1 — Малый радиус (Его может и не быть — это пустота).
вернутся в раздел: электрическая ёмкость
A capacitor is simply an electric device that consists of two terminals that have the ability to store energy in the form of an electric charge. It can be designed by simply placing two electrical conductors at a distance from each other. The empty space between the conductors may be filled by vacuum(or air) or with an insulating material known as a dielectric. The ability of the capacitor to store charges is known as capacitance.
In a capacitor, the two terminals having opposite charges are placed at a distance from each other which allows it to generate(store) energy. The simplest design for a capacitor is a parallel plate, which consists of two metal plates with a gap between them. It should be noted that a capacitor can be of any shape or size or be made of any material until its terminals store opposite charges and thus store energy.
Capacitance of a capacitor
Consider a capacitor whose positive and negative plates hold +q and -q charge respectively. A DC voltage source is applied across it which gives it a potential difference of V across the plates. Now as we know,
Q α V
Putting a constant C in this relation.
Q=CV.
Note: The capacitance of every material is unique and its SI unit is Farad(F).
Working of a capacitor
Let’s suppose that we are given the most basic form of the capacitor, which is a parallel plate capacitor. It consists of two parallel plates separated by a small distance and that gap is filled by a dielectric. Next, we are given a DC voltage source that is linked across the capacitor, where one plate is attached to the positive end (plate I) and the other plate is connected to the negative end (plate II). When the battery’s potential is applied across the capacitor, plate I become positive in relation to plate II. At steady-state, current attempts to pass through the capacitor from the positive plate to the negative plate. However, because of a gap between them with an insulating layer(dielectric), it is unable to flow.
Structure of a simple capacitor.
For some time the capacitor continues to get charged by the incoming flow of the current. But after some time it reaches a state where it holds the maximum amount of charge that it can possibly hold. This is how a capacitor stores energy The time taken to reach this state of maximum charge is called the charging time of the capacitor. Later we disconnect the voltage source from the circuit and insert a load resistor in it. Now the current starts flowing from the positively charged terminal of the capacitor to the negatively charged terminal and loses all of its energy in the process. This time period is called the discharging time of the capacitor.
Discharging of a capacitor.
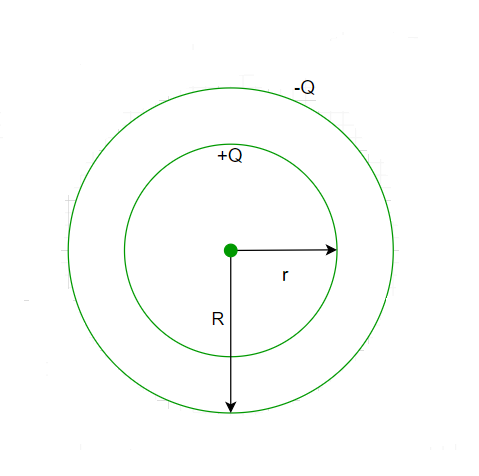
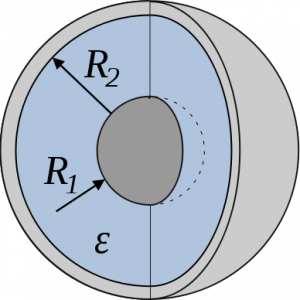
Spherical Capacitor Formula
As mentioned earlier capacitance occurs when there is a separation between the two plates. So for constructing a spherical capacitor we take a hollow sphere such that the inner surface is positively charged and the outer surface of the sphere is negatively charged. The inner radius of the sphere is r and the outer radius is given by R. The distance of R-r between the two oppositely charged surfaces acts as the dielectric. Let’s assume that the inner spherical surface has a potential of V1 and V2.
A spherical capacitor
Next, the electric field generated by a charged sphere (hollow) of radius r having charge Q is given by,
E=
. ⇢ (1)
Also, we know that the Electric field generated is related to the potential difference as,
E=
. ⇢ (2)
Comparing (1) and (2),

Integrating on both sides within the limits V, V and r, R.
⇢ (3)
is the change in potential as we move from inside the sphere to outside. Now the capacitance of a capacitor is given by,
⇢ (4)
Comparing (3) and (4),

![Rendered by QuickLaTeX.com C = frac{Q4π∈_0}{Q[frac{1}{R} - frac{1}{r}]}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20136%2045'%3E%3C/svg%3E)
Simplifying further we get,
Since capacitance can’t be negative the positive value is taken. This is the expression for the capacitance of a spherical capacitor.
Sample Questions
Question 1: A spherical capacitor has an inner radius of 7 cm and an outer radius of 10 cm. Find the capacitance of the sphere. Assume the dielectric in between to be air.
Solution:
The capacitance of the sphere is given by,
C =

Here ∈0 = 8.85 × 10-12, r = 7, R = 10
C=
C = 2.593 × 10-12F
Question 2: In the above problem find how much charge will it take for the capacitor to raise its potential from 0 to10,000 V.
Solution:
The capacitance of the spherical capacitor is C = 2.593 × 10-12F.
The charge required can be found by using Q = CV. where V is the potential difference.
Potential difference V in this case is 1000-0 = 1000V
Therefore, Q = 3.7052 × 10-12 × 1000
Q = 2.593 × 10-9C
Question 3: The inner radius of a spherical capacitor is x m and its outer radius is 5/4 x m if the outer radius is increased to 3/2x m, find by what ratio its capacitance is changed.
Solution:
In this case

=

= 20 πεox F

= 20 πεox F


So the capacitance decreases as the external radius is increased.
Question 4: A sphere has a radius of 10 cm. find the capacitance on it and also find the potential difference required to give it a charge of 10^-8 C.
Solution:
C = 4 πεox F
C = 4 × 3.14 × 8.85 × 10−12 × 10 × 10−2
C = 111.156 × 10−13
C = 1.11 × 10−11 F
Now Q = CV
Therefore

Hence V = 900.9 V
Question 5: The outer radius of a spherical capacitor is 10 % bigger than its inner radius. The capacitance of this capacitor is 10-8 F. Find the value of its inner and outer radii.
Answer:

Here r = x, R = 1.1x and C= 10-8 F
So,



x = 0.009 m
So the inner radius is 0.09 cm and the outer radius is 0.099 cm.
Question 6: The inner and outer radii of a spherical capacitor are 5cm and 6cm. Find the energy of the capacitor if a potential difference of 1000V is applied to it.
Solution:
The capacitance of this capacitor is calculated as,

C = 3.3363 × 10−12 F
U = 1/2 CV2
U = 21 × 3.3363 × 10−12 × (1000)2
U = 1.66815 × 10−9 J
Question 7: A spherical capacitor of inner and outer radii 8cm and 10cm has an energy of 10-8 J . Find its Voltage.
Solution:
Lets find the capacitance first,

C = 4.446 × 10-9 F
U = 1/2 CV2

V = 2.12 V
Last Updated :
01 May, 2022
Like Article
Save Article
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
При малой величине зазора, то есть , а следовательно можно считать, что
емкость сферического конденсатора будет равна
. Площадь сферы
следовательно формула будет совпадать с формулой емкости плоского конденсатора
Так же есть:
Энергия конденсатора:
Ёмкость конденсатора :
Ёмкость цилиндрического конденсатора :
Емкость плоского конденсатора : ;
В Формуле мы использовали :
— Электроемкость сферического конденсатора
— Относительная диэлектрическая проницаемость
— Электрическая постоянная
— Больший радиус (от центра, до края конденсатора)
— Малый радиус (Его может и не быть — это пустота)
-
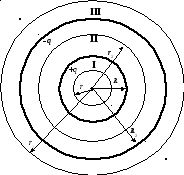
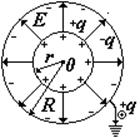
Поле сферического конденсатора
Обкладками сферического конденсатора
являются две концентрические сферы (R1иR2). Сообщим
этим поверхностям одинаковые по величине,
но разноимённые заряды+qи–qи вычислим
электрическое поле, создаваемое этими
зарядами в пространстве (рис. 2.10.).
Сферы делят пространство на 3 области:
I— внутри первой сферы
(r1<R1),
II— между обкладками (R1r2<R2),
III— за пределами
конденсатора (r3>R2).
Рис. 2.10.
Область I.
Выберем замкнутую гауссову поверхность
внутри первой области. Разумно,
руководствуясь соображениями симметрии,
эту поверхность выбрать сферической
(r1).
Поток вектора напряжённости через эту
поверхность (по определению потока)
равен:
Этот поток, согласно теореме Гаусса,
пропорционален заряду, заключённому
внутри поверхности. Но внутри сферы
радиуса r1заряд
отсутствует. Поэтому и поток равен нулю
(!)
Отсюда заключаем, что в области Iполе равно нулю
0 < r<R1,E= 0 (2.18)
Область II.
Вновь в качестве замкнутой поверхности
выберем сферу, но теперь её радиус r2лежит в пределах отR1доR2.
Вычислим поток вектора напряжённости
поля через эту гауссову поверхность.
Воспользуемся теорией Гаусса:
:
Оказывается, что электрическое поле
между обкладками сферического конденсатора
неотличимо от поля точечного заряда
. (2.19)
Посмотрим теперь, как выглядит поле в
области III.
Вновь выберем замкнутую гауссову
сферическую поверхность (радиус r3>R2). Вычисляем
поток вектора напряжённости
Этот поток равен нулю, так как он
пропорционален алгебраической сумме
зарядов, заключённых внутри этой
поверхности. Но алгебраическая сумма
одинаковых разноимённых зарядов равна
нулю
Отсюда следует, что Е = 0 (r3R2)/
График Е=Е(r)
приведён на рисунке 2.11.
Рис. 2.11.
Лекция 3 «Потенциал электростатического поля»
План лекции
3.1. Работа сил электростатического поля
при перемещении заряда. Потенциал и
разность потенциалов.
3.2. Теорема о циркуляции вектора
напряжённости электростатического
поля.
3.3. Связь напряжённости и потенциала
электростатического поля.
3.4. Примеры расчёта потенциала
электростатического поля.
3.4.1. Потенциал поля точечного заряда.
3.4.2. Разность потенциалов на обкладках
сферического конденсатора.
Существуют две характеристики
электрического поля. В любой точке
пространства поле можно задать либо
вектором напряжённости — это «силовая»
характеристика поля, либо потенциалом
— это его энергетическая характеристика.
Потенциал — энергетическая характеристика
поля, связанная и с энергией заряда в
электростатическом поле и с работой,
совершаемой электрической силой при
перемещении заряда.
-
Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
Рассмотрим произвольное перемещение
(1–а–2) зарядаqв
электростатическом поле. Пусть поле
создаётся неподвижным точечным зарядомQ(рис. 3.1.). В процессе
перемещения на зарядq
действует кулоновская сила:
. (3.1)
Рис. 3.1.
Её работа на перемещении
равна:
. (3.2)
Здесь dr=dlсos— толщина сферической оболочки,
окружающей зарядQ.
Полная работа электрической силы равна
сумме работ на всех участках траектории:
. (3.3)
Теперь несложно показать, что эта работа
не зависит от формы траектории и остаётся
неизменной, если начальная и конечная
точки траектории не меняют своего
положения. Рассмотрим, например,
перемещение того же заряда q
из начальной точки 1 в конечную 2 по
новой траектории 1–b–2.
При преодолении прежнего сферического
слоя на перемещенииэлектрическая сила совершит работу:
. (3.4)
Но ведь эта работа в точности совпадает
с работой на перемещении dl(3.2) по первоначальной траектории 1–а–2.
Полная работа, равная сумме элементарных
работ на всех участках новой траектории,
будет равна работе электрической силы
на траектории 1–а–2:
. (3.5)
Вспомним, что силы, работа которых не
зависит от вида траектории и определяется
только положением её начальной и конечной
точек, называются консервативными.
Мы пришли к выводу, что кулоновская
сила консервативна. Впрочем, ничего
неожиданного в этом выводе нет: ведь
сила взаимодействия двух точечных
зарядов может быть отнесена к классу
центральных сил, а все центральные силы,
как было установлено в механике,
консервативны.
Итак, вычислим работу кулоновской силы
при перемещении заряда qиз точки 1 в положение 2 (по любой
траектории):

Как и следовало ожидать, величина работы
никак не связана с видом траектории.
Она зависит только от положения её
начальной (r1) и
конечной (r2)
точек.
В механике было показано, что работа
консервативной силы равна убыли
потенциальной энергии системы:
. (3.7)
Присмотримся внимательнее к результату
(3.6):
.
Сопоставив этот результат с теоремой
о работе консервативной силы (3.7), запишем
уравнение:
,
из которого следует, что потенциальная
энергия системы:
+const. (3.9)
Это потенциальная энергия системы двух
точечных зарядов, или, что то же самое,
энергия заряда qв
электрическом поле точечного зарядаQ.
Константа в выражении (3.9) принимается
обычно равной нулю. Это означает, что
принимается равной нулю энергия
взаимодействия зарядов qиQна бесконечном удалении
их друг от друга (приr= ∞).Тогда на расстоянииrэнергия взаимодействия равна. (3.10)
Потенциальная энергия заряженной
частицы в электрическом поле зависит,
таким образом, от величины заряда qи от его положения в поле относительно
зарядаQ, создающего
поле.
Энергия единичного (q= 1) точечного заряда уже не будет связана
с величиной этого пробного зарядаqи может быть принята в качестве
энергетической характеристики данной
точки электростатического поля:
.
Эта энергетическая характеристика поля
получила название потенциал — .
Потенциал произвольной точки
электростатического поля равен энергии
единичного положительного заряда,
помещённого в эту точку.
Можно придать потенциалу и иной физический
смысл.
Поместим заряд qв
поле точечного зарядаQ.
Первоначально расстояние между зарядами
—r. Отпустим зарядq. Под действием
электрической силы отталкивания зарядqудалится в бесконечность
(рис. 3.2.). На этом перемещении кулоновская
сила совершит работу:
. (3.11)
Эта работа не зависит от формы траектории,
поэтому мы её вычислили, считая, что
заряд qудаляется по
радиусу.
Рис. 3.2.
Сравнивая (3.10) и (3.11), заключаем, что:
. (3.12)
Потенциал некоторой точки
электростатического поля равен работе,
совершаемой электрической силой при
эвакуации единичного положительного
заряда из этой точки в бесконечность.
Теперь вычислим потенциал поля, созданного
системой точечных зарядов Q1,Q2, …,QN.
При перемещении заряда qиз точки 1 в бесконечность электрическая
сила совершит работу, равную алгебраической
сумме работ сил, действующих на движущийся
заряд со стороны зарядовQ1,Q2, …,QN(рис. 3.3.):
Рис. 3.3.
Согласно (3.12) работа каждой силы равна:
. (3.13)
Здесь
— потенциал поля, создаваемого в точке
1 зарядомQi.
Таким образом, суммарная работа равна:
,
где
.
Потенциал поля, созданного системой
точечных зарядов, равен алгебраической
сумме потенциалов, создаваемых в
рассматриваемой точке каждым из зарядов
в отдельности:
. (3.14)
Результат (3.14) известен как «принцип
суперпозиции для потенциала». Это
очень важный вывод, позволяющий
использовать понятие потенциала не
только для характеристики полей точечных
зарядов, но и для любых произвольных
электростатических полей.
Ещё раз обратимся к вычислению работы
электрической силы при перемещении
заряда qиз точки 1
теперь уже произвольного электростатического
поля в бесконечность. Поскольку эта
работа не зависит от формы траектории,
унося заряд в бесконечность, пройдём
предварительно точку 2 электростатического
поля (рис. 3.4.).
Рис. 3.4.
Ясно, что вся работа на этом перемещении
складывается из двух частей:
.
Разделив это равенство на величину
переносимого заряда q,
получим:
,
или:
. (3.15)
Здесь
—разность потенциаловдвух точек
поля. Она равна работе, совершаемой
электрической силой при перемещении
единичного заряда из первой точки во
вторую:
. (3.16)
Таким образом, зная разность потенциалов
двух точек поля, легко вычислить работу
электрического поля, совершаемую при
перемещении заряда qмежду этими точками:
. (3.17)
В международной системе единиц СИ
потенциал (и разность потенциалов)
измеряется в вольтах:
.
Разность потенциалов двух точек
электростатического поля равна одному
вольту, если при переносе заряда q= 1Кл между этими точками, электрическая
сила совершает работуА(Fэл.)
= 1 Дж.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
разность потенциалов между обкладками, t — линейная плотность заряда, q – заряд на всей длине l. Подставив в (§§), получим: |
|
|
|
емкость цилиндрического конденсатора длиной l |
Сферический конденсатор. Это две металлические концентрические сферы, разделенные сферическим слоем диэлектрика. Если внутренней обкладке сообщить заряд +q, на внутренней поверхности внешней обкладки индуцируется заряд —q, а на внешней ее поверхности +q. Этот заряд отводится в землю за счет заземления (см. рис.). Поле такого конденсатора сосредоточено только между обкладками.
|
|
разность потенциалом между обкладками. Подставив в (§§), получим: |
|
|
|
емкость сферического конденсатора |
|
При наличии диэлектрика с диэлектрической проницаемостью e во всех формулах надо заменить (см. ниже — диэлектрики): |
e0 ® ee0 |
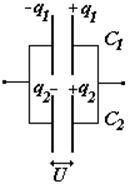
Соединения конденсаторов.
Конденсаторы можно соединять параллельно или последовательно, или смешанным образом: часть параллельно, часть последовательно. При параллельном соединении емкость системы увеличивается и становится равной сумме емкостей. При последовательном соединении емкость системы всегда уменьшается. Последовательное соединение применяют не для уменьшения емкости, а главным образом для уменьшения разности потенциалов на каждом конденсаторе, чтобы не было пробоя конденсатора.
|
|
||
|
|
запишем формулу (§§) для каждого конденсатора и для всей системы (заменив Dj®U); подставляя q в последнюю формулу, получим: С паралл=С1 + С2 Обобщим на случай 3-х и более конденсаторов |
параллельное соединение |
|
|
емкость системы при параллельном соединении конденсаторов (i=1,2,…,n) n — число конденсаторов |
|
|
Заряды на всех обкладках по величине одинаковые. Запишем формулы аналогично предыдущему случаю, произведем те же действия и найдем |
последовательное соединение |
|
|
для 2-х конденсаторов |
|
|
|
емкость системы при последовательном соединении конденсаторов |
|
Электростатика в веществе
Диполь, его поле.
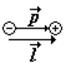
Диполем называется система, состоящая из двух одинаковых по величине, но различных по знаку зарядов q, расположенных на определенном расстоянии l друг от друга. Если это расстояние не меняется, диполь называют жестким. Если расстояние меняется пропорционально напряженности внешнего поля, диполь называют упругим.
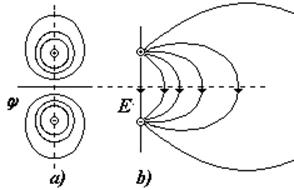
Изучение поля диполя и его поведения во внешнем электрическом поле имеет большое значение, так как диполь может служить моделью молекул. На легких частицах, оказавшихся в электрическом поле, возникают индуцированные заряды, и частицы становятся диполями. С помощью достаточно большого количества таких частиц можно наблюдать силовые линии поля, т. к. частички-диполи будут располагаться по силовым линиям поля.
Диполь характеризуют дипольным (электрическим) моментом (см. рис.):
|
|
|
дипольный (электрический) момент диполя – это вектор, проведенный от отрицательного заряда к положительному |
Для определения потенциала j и напряженности Е поля диполя можно воспользоваться принципом суперпозиции:
|
|
Электростатическое поле диполя имеет сложный вид (см. рис.): a) эквипотенциальные поверхности, b) силовые линии (половина поля) |
|
|
|
||
|
|
Из формулы (©) можно получить потенциал поля диполя для расстояний r, существенно превышающих размер диполя. Для этого в формуле (©) приведем к общему знаменателю, примем r1×r2 » r2, (r1 – r2 ) = l×cos q и введем 

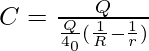

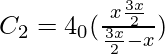






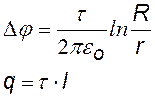
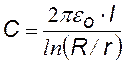
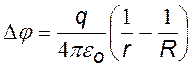
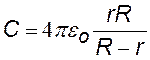
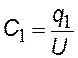
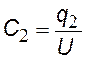
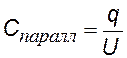
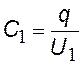
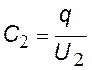
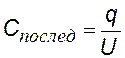
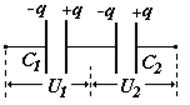
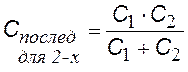
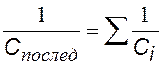
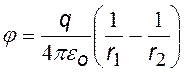 (©)
(©)