Содержание:
- Последовательное соединение конденсаторов
- Параллельное соединение конденсаторов
- Смешанное соединение конденсаторов
- Пример расчета
В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.
-
Последовательное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.
Схема последовательного соединения конденсаторов будет иметь следующий вид:

Фактически последовательное соединение конденсаторов имеет следующий вид:

При данной схеме соединения заряды на конденсаторах будут одинаковы:
Qобщ=Q1=Q2=Q3,
где: Q1, Q2, Q3 — соответственно заряд на первом, втором, третьем и т.д. конденсаторах
Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:
U1=Q/C1; U2=Q/C2; U3=Q/C3, где:
- U1, U2, U3 — соответственно напряжение на первом, втором, третьем конденсаторах
- C1, C2, C3 — соответственно емкости первого, второго, третьего конденсаторов
При этом общее напряжение составит:
Uобщ=U1+U2+U3+…+Un
Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:
- При последовательном соединении двух конденсаторов:
Собщ=(C1*C2)/(C1+C2)
- При последовательном соединении трех и более конденсаторов:
1/Собщ=1/C1+1/C2+1/C3+…+1/Cn
-
Параллельное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.
Схема параллельного соединения конденсаторов будет иметь следующий вид:

Таким образом параллельное соединение конденсаторов будет иметь следующий вид:

При данной схеме напряжение на всех конденсаторах будет одинаково:
U=U1=U2=U3
Заряд же на каждом из конденсаторов будет зависеть от его емкости:
Q1=U*C1; Q2=U*C2; Q3=U*C3
При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:
Qобщ=Q1+Q2+Q3…+…Qn.
Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:
Собщ=C1+C2+C3+…+Cn
-
Смешанное соединение конденсаторов
Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.
Приведем пример такой схемы:

Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.
Для наглядности приведем пример расчета общей емкости данной схемы.
-
Пример расчета
Условно разделив схему на группы получим следующее:

Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.
Произведем расчет каждой группы:
- Группа 1 — последовательное соединение трех конденсаторов:
1/C1,2,3 = 1/C1+1/C2+1/C3 = 1/5+1/15+1/10=0,2+0,067+0,1 = 0,367 → C1,2,3 = 1/0,367 = 2,72 мкФ
- Группа 2 — последовательное соединение двух конденсаторов:
С4,5 = (C4*C5)/(C4+C5)= (20*30)/(20+30) = 600/50 = 12 мкФ
- Группа 3 — параллельное соединение трех конденсаторов:
С6,7,8 = C6+C7+C8 = 5+25+30 = 60 мкФ
В результате расчета схема упрощается:

Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:
- Группа 4 — параллельное соединение двух групп конденсаторов:
С1,2,3,4,5 = C1,2,3+C4,5 = 2,72+12 = 14,72 мкФ
В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:

Теперь можно определить общую емкость схемы:
Собщ = (C1,2,3,4,5*C6,7,8)/(C1,2,3,4,5+C6,7,8) = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ
Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!
Не нашли на сайте статьи на интересующую Вас тему касающуюся электрики? Напишите нам здесь. Мы обязательно Вам ответим.
↑ Наверх
Цель: закрепить знания методов расчета электрической емкости и зарядов конденсаторов при их смешанном соединении.
Теоретические сведения
Электрический конденсатор — это система из двух проводников (обкладок, пластин), разделенных диэлектриком.
Конденсаторы обладают свойством накапливать на своих обкладках электрические заряды, равные по величине и противоположные по знаку.
Электрический заряд q каждой из обкладок пропорционален напряжению U между ними:

Величину С, равную отношению заряда одной из обкладок конденсатора к напряжению между ними, называют электрической емкостью конденсатора и выражают в фарадах (Ф).
Емкость конденсатора зависит от геометрических размеров, формы, взаимного расположения и расстояния между обкладками, а также от свойств диэлектрика.
Конденсаторы могут быть соединены последовательно, параллельно и смешанно (последовательно-параллельно).
Последовательное соединение

При таком на обкладках всех конденсаторов будут одинаковые по величине заряды:

Напряжения на конденсаторах будут различны, так как они зависят от их емкостей:

Общее напряжение:

Общая, или эквивалентная, емкость

Параллельное соединение

При параллельном соединении напряжение на всех конденсаторах одинаковое.
Заряды на обкладках отдельных конденсаторов при различной их емкости:

Заряд, полученный всеми параллельно соединенными конденсаторами:

Общая (эквивалентная) емкость:


Задание

1. Определить эквивалентную емкость батареи конденсаторов, соединенных по схеме, при соответствующих положениях ключей.

2. Для случая, когда ключи К1, К2 и К3 разомкнуты, найти заряды на каждом конденсаторе и общий заряд схемы.

Порядок выполнения расчета
Задание 1
1. Для своих данных начертить исходную схему.

2. Рассчитать последовательное соединение С3-С7:

3. Рассчитать параллельное соединение С4-С5:

4. Рассчитать последовательное соединение С2-С45:

5. Найти эквивалентную емкость, рассчитав параллельное соединение С245-С37:

Задание 2
1. Для своих данных начертить исходную схему.

2. Рассчитать заряды на каждом конденсаторе:

3. Рассчитать общий заряд схемы:

4. Проверка:



При
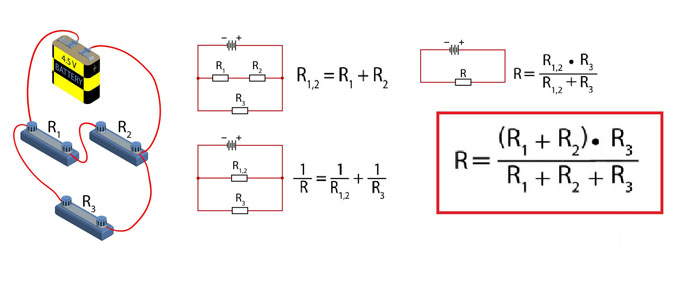
решении задач на смешанное соединение проводников обычно составляют так
называемые эквивалентные схемы, выделяя участки с последовательным и
параллельным соединением.
Пример
1.

Сопротивление R1,2 заменило
выделенный участок цепи, в котором два проводника соединены параллельно.
Тогда
мы можем найти сопротивление этого участка с параллельным соединением
проводников:
![]()
А теперь видно,
что проводники R1,2 и R3 соединены
последовательно. Общее сопротивление равно R = R1,2 + R3 = 4 +
2 = 6.
Пример
2.

В данном случае
нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема
разветвляется, а в точке В ветви соединяются. Таким образом,
эквивалентные схемы будут иметь вид:


R2, R3 и R4 соединены
последовательно. Поэтому R2,3,4 = R2 + R3 + R4 = 1 + 10
+ 1 = 12
R2,3,4 и R5 соединены
параллельно. Поэтому

И в последней
схеме проводники соединены последовательно. R = R2-5 + R1 + R6 = 1 + 4,8
+ 1 = 6,8.
Пример
3.
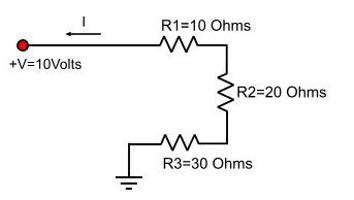
Найти распределение токов и напряжений в цепи.

Решение.
Так
как известны сила тока и сопротивление на первом участке, то можно найти
напряжение на нем: U1 = I1 R1 = 1 ∙ 10
= 10 B.
Первый
и второй проводники соединены параллельно. Значит, напряжение на них одинаково,
т.е. U1 = U2 = 10 В. Так
как первый и второй проводники имеют одинаковое сопротивление, то сила
тока на них одинакова: I2 = 1 А. При
параллельном соединении I1,2 = I1 + I2 = 2 А.
Участки
1-2, 3-4-5 и 6-7 соединены последовательно между собой, значит I3,4,5 = I6,7 = I1,2 = 2 A.
Найдем
общее сопротивление участка 3-4-5:

R3,4,5
= 3 Ом.
Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно
одинаково на всех участках. U3,4,5 = I3,4,5 ∙R3,4,5 = 2 ∙ 3 =
6 В.
U3 = U4 = U5 = 6 В. Зная
напряжение на каждом из участков и сопротивление, можно найти силу тока на
каждом участке.

Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
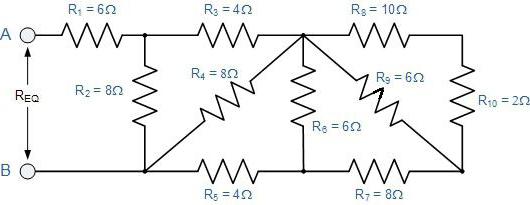
Рассмотрим пример смешанного соединения проводников (рис. ).
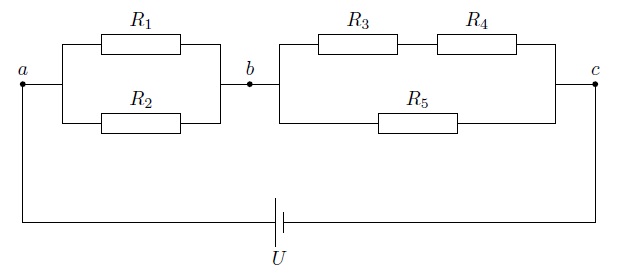
Рис. Смешанное соединение
Пусть
В,
Ом,
Ом,
Ом,
Ом,
Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков
и
. Сопротивление участка
:
Ом.
Участок
является параллельным соединением: два последовательно включённых резистора
и
подключены параллельно к резистору
. Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

B.
(Заметим попутно, что сумма этих напряжений равна
В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора
и
находятся под напряжением
, поэтому:

A.
(В сумме имеем
А, как и должно быть при параллельном соединении.)
Сила тока в резисторах
и
одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор
течёт ток
A.
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Последовательное и параллельное соединение резисторов
Напряжение при последовательном и параллельном соединении резисторов
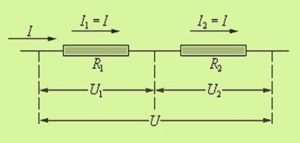
Какое соединение проводников называется параллельным
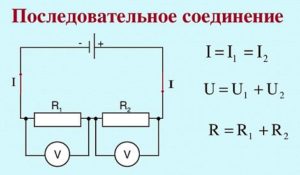
Сопротивление при последовательном и параллельном соединении резисторов
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
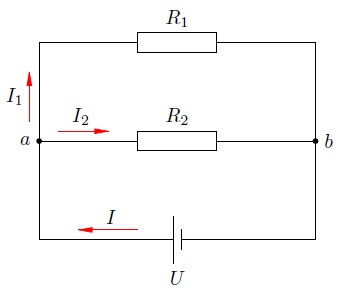
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам:
и
. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от
к
(по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения
и
на резисторах
и
равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку
за время
из неразветвлённого участка поступает заряд
. За это же время
из точки
к резистору
уходит заряд
, а к резистору
— заряд
.
Ясно, что
. В противном случае в точке
накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть
— сопротивление разветвлённого участка
. Напряжение на участке
равно 
. Поэтому:
Сокращая на
, получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами
, но разными поперечными сечениями
и
. Тогда это соединение можно рассматривать как проводник той же длины
, но с площадью сечения
. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти
:
(2)
К сожалению, в общем случае
параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех
резисторов одинаковы и равны
. Тогда:
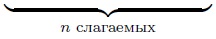
откуда
Мы видим, что сопротивление участка из
параллельно соединённых одинаковых проводников в
раз меньше сопротивления одного проводника.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора
и
, соединённых последовательно и подключённых к источнику постоянного напряжения
(рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
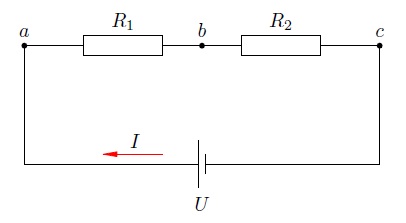
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение
на участке
— это работа поля по переносу единичного заряда из точки
в точку 
на участке
— это работа поля по переносу единичного заряда из точки
в точку
. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки
в точку
, то есть напряжение
на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть
— сопротивление участка
. По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения
, но с разными длинами
и
.
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной
и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Разница между последовательным и параллельным соединением, преимущества и недостатки
Принципиальные отличия между последовательным и параллельным соединение проводников по ключевым электротехническим параметрам приведены в таблице:
| Параметр/тип соединения | Последовательное | Параллельное |
| Электросопротивление | Равняется сумме электросопротивлений всех электропотребителей. | Меньше значения электросопротивления каждого отдельного из подключенных электроприборов. |
| Напряжение | Равняется совокупному вольтажу всех электропотребителей. | Одинаковая величина на всех участках электроцепи. |
| Сила тока | Одинаковая величина на всех участках электроцепи. | Равняется совокупному значению токов на каждом из приборов. |
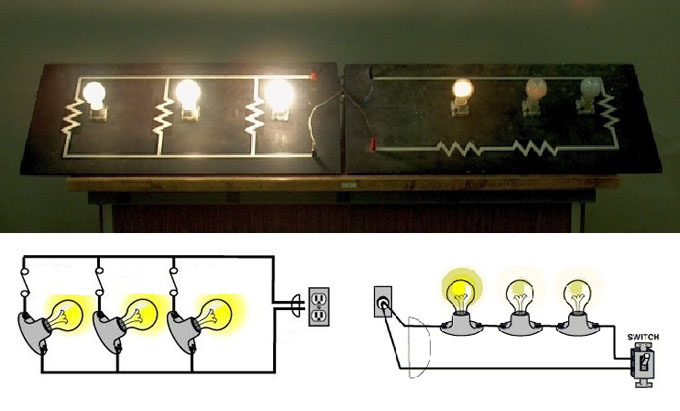
За счет своих особенностей каждый из типов сборки цепей имеет свои преимущества и недостатки. Это позволяет использовать данные способы для решения разных электротехнических задач.
Плюсы и минусы последовательного соединения
Основными преимуществам электроцепей из последовательно соединенных приборов являются их следующие особенности:
- простота проектирования и построения схемы;
- низкая стоимость комплектации;
- возможность подключения приборов, рассчитанных на меньшее рабочее напряжение, по сравнению с номинальным напряжением сети;
- выполнение функции регулирования тока – обеспечивает равномерные нагрузки на все приборы.
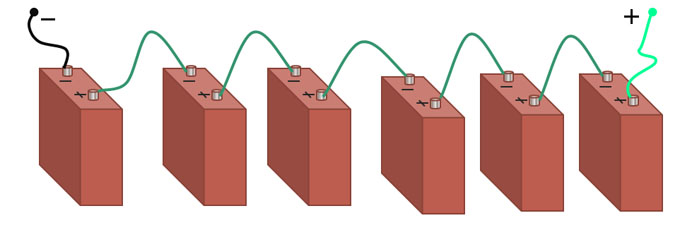
Однако у этого способа компоновки электросхемы есть и серьезные недостатки. Главным из них является ненадежность цепи из последовательно соединенных проводников. При выходе из строя любого из подключенных приборов, происходит отключение всей цепи.
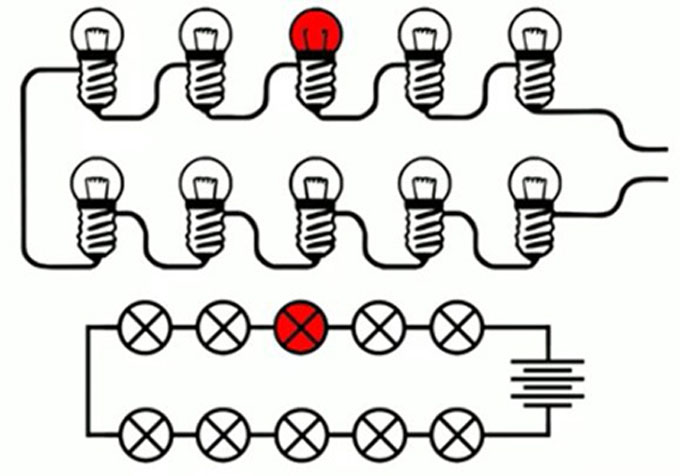
Кроме того, минусом является снижение напряжения при увеличении количества подключенных потребителей. Примером может служить последовательное соединение нескольких ламп. Чем больше осветительных приборов подключено таким способом к источнику электропитания, тем менее яркий свет они будут давать.
Плюсы и минусы параллельного соединения
При использовании параллельного соединения проводников обеспечиваются такой набор преимуществ:
- стабильность напряжения на электроприборах, вне зависимости от их числа;
- возможность включения или отключения отдельных участков в нужный момент без нарушения работы всей электроцепи;
- надежность – при выходе одного или нескольких компонентов из строя сама электроцепь продолжает сохранять работоспособность.

Недостатком является более сложный расчет и сложная схема, использование которой повышает стоимость комплектации электросети.
Не допускается подключение приборов, с номинальным рабочим вольтажом меньше сетевого. Параллельное соединение аккумуляторов с разным значением вольтажа связано с перетеканием тока в АКБ с меньшей его величиной, что может вызывать ускоренный износ батареи.
Закон Ома для участка цепи
Одним из ключевых электротехнических законов можно назвать закон Ома для участка цепи. Именно этим законом объясняются отличия, которые существуют для параллельного и последовательного соединения проводников.
Формулируется он таким образом:
Сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника.
Записывается он следующей формулой:
I = U/R, где
I – сила тока, (А);
U – вольтаж, (В);
R – электросопротивление, (Ом).
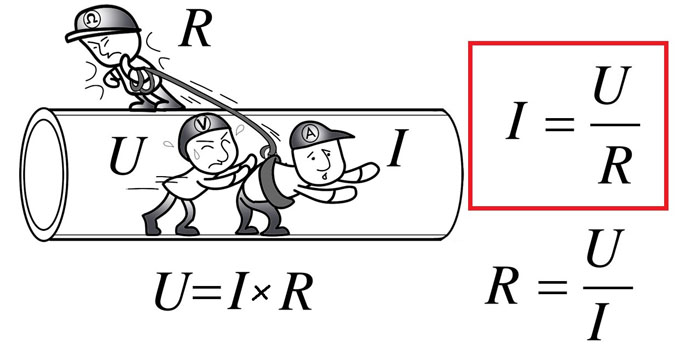
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
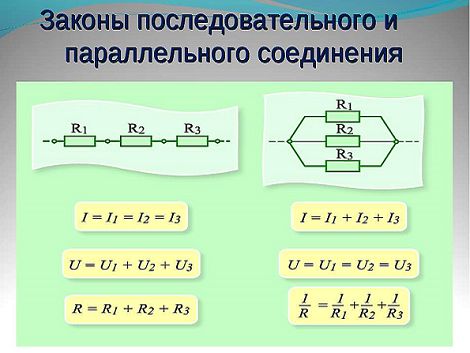
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- Закон ома параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
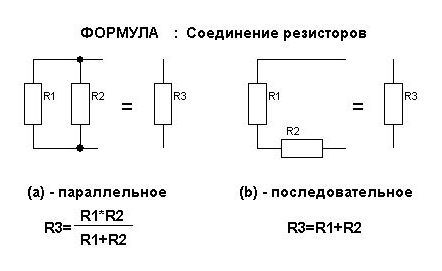
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
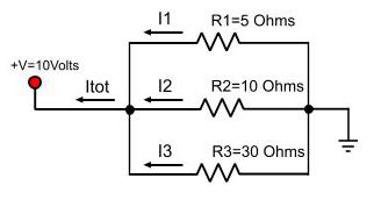
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — Iобщ * Rобщ = I1 * R1 + I2 * R2;
- параллельно необходимо пользоваться формулой для силы тока — Uобщ / Rобщ = U1 / R1 + U2 / R2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
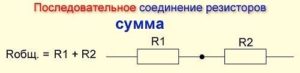
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2.
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2.
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Смешанное соединение проводников в электрической цепи
На практике сборку электроцепей, как правило, проводят таким метод, который предусматривает смешанное соединение проводников. Это комбинированное решение, которое сочетает оба способа. Обычно для монтажа основной сети используют параллель, а отдельные потребители при необходимости объединяют в последовательную сеть.
При расчете и сборке смешанных соединений сопротивлений обязательно должны учитываться особенности, преимущества и недостатки обоих методов подключения. В ходе проектирования, схему целесообразно разбить на отдельные части и выполнить расчет в по физическим законам, которые справедливы для последовательного и параллельного соединения. После этого, составные части объединяют в единую схему.
Способы соединения резисторов, решение задачи смешанного соединения проводников: видео
Смешанное соединение резисторов
Смешанное соединение резисторов – это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
Определяется общее сопротивление участков с параллельным соединением резисторов.Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.Определяется общее сопротивление участков с параллельным соединением резисторов.Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.
PS:
Параллельное соединение резисторов используется для получения меньшего сопротивления из имеющихся простейших радиоэлектронных элементов. При таком способе соединения складываются проводимости. Поэтому чем больше параллельно включенных резисторов, тем ниже получается общее сопротивление или выше проводимость соответственного участка электрической цепи – носителям электрических зарядов легче его преодолеть.
Последовательное соединение резисторов используется с целью большего ограничения протеканию электрическому току, то есть приводит к повышению сопротивления соответственного участка электрической цепи или для снижения ее проводимости.
Важнейшим параметром резистора является мощность рассеивания. При любом способе соединения, не важно, при последовательном, при параллельном или при смешанном, происходит сложение мощностей рассеивания отдельных резисторов. Поэтому все вместе они способны рассеять больше тепла, а соответственно и пропустить большие токи не перегреваясь, что широко применяется в радиолюбительской практике.
Предыдущая
РазноеЭлектромагнитное излучение – невидимый убийца.
Следующая
РазноеКак правильно соединить провода между собой
Смешанное соединение конденсаторов


4.2
Средняя оценка: 4.2
Всего получено оценок: 141.
4.2
Средняя оценка: 4.2
Всего получено оценок: 141.
Основными типами соединений в электротехнике являются последовательные и параллельные соединения. Если элементы схемы соединены одновременно обоими типами соединений, говорят о смешанном соединении. Найдем электрические характеристики смешанного соединения конденсаторов.
Соединение конденсаторов в батарею
В электротехнике иногда требуется соединение нескольких конденсаторов. При параллельном соединении выводы каждого конденсатора присоединяются к выводам цепи. При последовательном соединении к выводам цепи подсоединяются только выводы первого и последнего конденсаторов. Из остальных же конденсаторов создается «цепочка», так, чтобы первый вывод очередного конденсатора подсоединялся ко второму выходу предыдущего.
Большое число конденсаторов можно соединить в несколько последовательных цепей, эти цепи могут быть соединены параллельно, образующиеся новые цепи можно опять соединять последовательно — и так из большого числа конденсаторов можно создать большую параллельно-последовательную батарею. Как найти характеристики такой батареи?
Поскольку в такой батарее существуют только конденсаторы, следовательно, в ней не происходит ни потерь энергии, ни ее преобразования. Электрический заряд, проходящий по батарее, лишь распределяется между ее элементами. То есть батарея, состоящая из одних конденсаторов, с точки зрения внешней цепи представляет собой конденсатор некоторой емкости.
Найдем ее.
Емкость соединенных конденсаторов
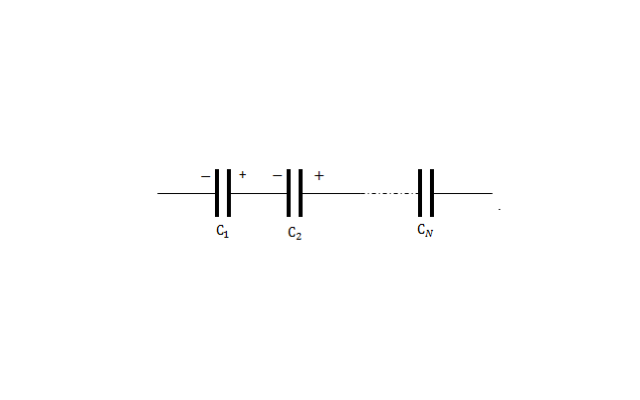
Для расчета смешанного соединения конденсаторов требуется знать две формулы: емкость чисто параллельного и чисто последовательного соединения. При чисто параллельном соединении конденсаторов их емкость складывается:
$$C_{пар}=C_1+C_2+…+C_n$$
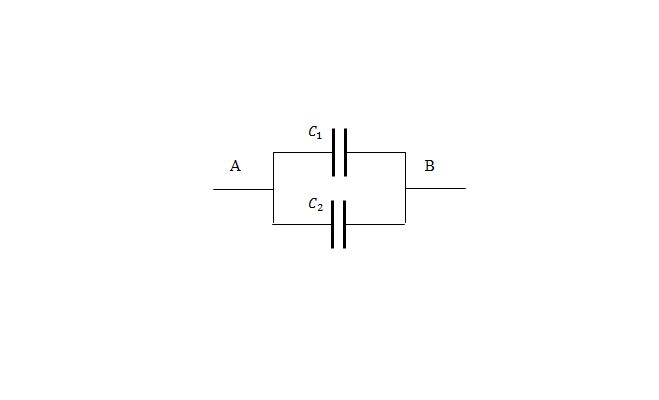
Если конденсаторы соединяются последовательно, то складывается напряжение на них, зарядить их труднее, следовательно, емкость уменьшается. Величина, обратная суммарной емкости, равна сумме обратных величин отдельных емкостей конденсаторов:
$${1over C_{посл}}={{1over C_1}+{1over C_1}+…{1over C_n}}$$
Анализ схемы смешанного соединения
Теперь можно приступать к анализу схемы смешанного соединения.
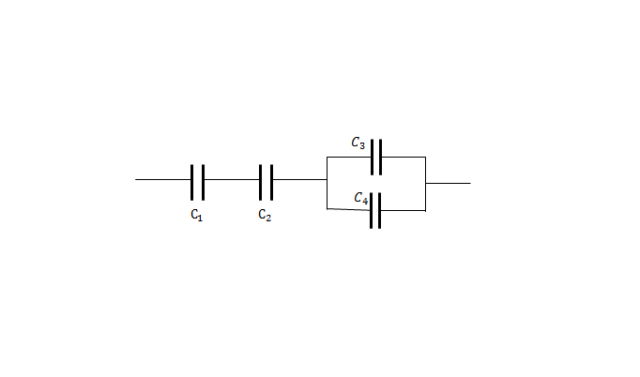
В схеме необходимо выделить узлы — точки цепи, к которым присоединены три и более звеньев. Даже в очень сложной схеме найдутся такие узлы, между которыми соединение конденсаторов будет только последовательным или только параллельным. Эти конденсаторы в схеме заменяются одним эквивалентным, имеющим емкость, для определения которой используется соответствующая формула.
После замены схема снова анализируется. В ней снова выделяются узлы, между которыми конденсаторы соединены только одним из двух способов. Снова проводится замена конденсаторов эквивалентом.
Так делается до тех пор, пока схема максимально не упростится. Чаще всего при этом остается только один эквивалентный конденсатор, емкость которого и будет равна емкости всей батареи конденсаторов в смешанном соединении.
Иногда, в сложных случаях, невозможно упростить схему до одного эквивалентного конденсатора с помощью указанных двух преобразований. В этом случае для расчета смешанного соединения конденсаторов используются более сложные методы, например, метод узловых потенциалов. Кроме того, существуют особые эквивалентные преобразования, например, преобразование треугольника конденсаторов в трехлучевую звезду и обратно. Все эти методы изучаются в вузовском курсе теории цепей.

Что мы узнали?
Для нахождения эквивалентной емкости смешанного соединения конденсаторов в схеме выделяются узлы, звенья между соседними узлами заменяются эквивалентными элементами с помощью формул последовательного или параллельного соединения. В результате схема упрощается. Такие упрощения проводятся, пока не останется один эквивалентный конденсатор, имеющий емкость, равную емкости исходного соединения.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 141.
А какая ваша оценка?
