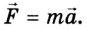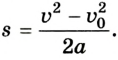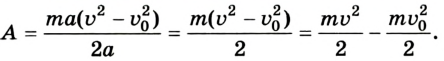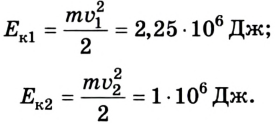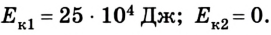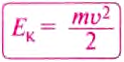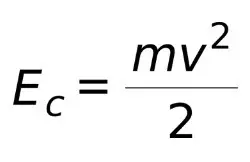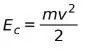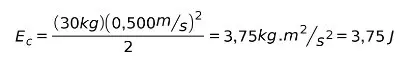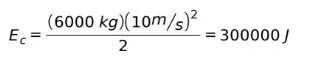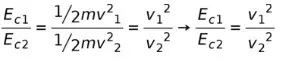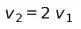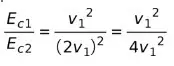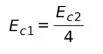Как найти зависимость кинетической энергии от времени

На тело массой m действует сила F. Установить зависимость кинитеческой енергии тела от времени, если t=0 ,v (начальная скорость)=0

Кинетическая энергия определяется формулой:

$K=frac{mv^2}{2}$        (1)

Если на тело постоянно действует сила, то оно движется равноускоренно и скорость в любой момент времени определяется формулой:

$v=v_0+at$          

 В нашем случае:

$v=at$                 (2)

Для определения ускорения воспользуемся вторым законом Ньютона:

$a=frac{F}{m}$               (3)

Если подставить (3) в (2):

$v=frac{Ft}{m}$             (4)

Подставив (4) в (1) находим искомую зависимость кинетической энергии от времени:

$K=frac{mv^2}{2}=frac{mF^2t^2}{2m^2}=frac{F^2t^2}{2m}$

Кинетическая энергия в физике – формулы и определения с примерами

Содержание:

Кинетическая энергия:

Иногда значение работы можно найти, не используя понятия силы и перемещения, на основании характеристики изменения энергии тела.

Рассмотрим тело массой m, на которое действует сила F. Направление действия силы совпадает с направлением перемещения. Работа, которую выполняет эта сила,

A = Fs.
Согласно второму закону механики Ньютона значение силы

Как известно, модуль перемещения равен:

Поэтому

Как известно, выражение 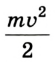называется кинетической энергией. Следовательно, для расчета работы достаточно определить только массу тела и его начальную и конечную скорости, т. е. знать изменение кинетической энергии тела. Такой метод удобен, поскольку им можно пользоваться даже в случае переменной силы и произвольной траектории.

Физическая величина, описывающая состояние движущегося тела и изменение которой определяет работу, называется кинетической энергией.

Для измерения энергии, как и работы, используется единица джоуль (Дж), названная в честь английского ученого Д. Джоуля.

Кинетической энергией обладает тело, движущееся в данной системе отсчета с определенной скоростью: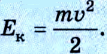
Скорость тела, измеренная в разных системах отсчета, будет иметь разное значение, т. е. она является относительной величиной. Поэтому кинетическая энергия тела постоянной массы тоже величина относительная и в разных системах отсчета имеет разное значение.

Рассмотрим, например, два железнодорожных вагона, массы которых составляют по 2 • 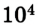кг, движущиеся в одном направлении со скоростями 15 м/с и 10 м/с относительно железнодорожного полотна, причем первый догоняет второго. Их кинетическая энергия соответственно будет:

Если же систему отсчета связать со вторым вагоном, то первый будет двигаться со скоростью 5 м/с , а второй – со скоростью v = 0. В этом случае

Следовательно, при расчетах в разных инерциальных системах отсчета следует учитывать, что кинетическая энергия в случае перехода из одной системы в другую будет изменяться.

Что такое кинетическая энергия

Кинетическая энергия (от греческого слова кинетикос – тот, что приводит в движение) – это энергия, которой тело обладает вследствие собственного движения.

Кинетической энергией обладает ветер, её используют для сообщения движения ветряным двигателям. Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их вращаться. На рисунке 175, а изображена ветряная мельница, в которой за счёт энергии ветра мелют зерно. Современные довольно мощные ветряные двигатели (рис. 175, б) используют для того, чтобы вырабатывать электроэнергию, качать из скважин воду и подавать её в водонапорные башни.

Движущаяся вода или нагретый пар, вращая турбины электростанции, теряет часть своей кинетической энергии и выполняет работу. Самолёт, летящий высоко в небе, кроме потенциальной обладает и кинетическуй энергией. Если тело находится в состоянии покоя, т. е. его скорость относительно Земли равна нулю, то и его кинетическая энергия относительно Земли будет равна нулю.

Опытами установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия. Выявленная зависимость математически выражается такой формулой:

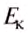
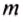
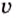
где — кинетическая энергия тела; — масса тела; — скорость движения тела.

Определение кинетической энергии

Наблюдения явлений природы показывают, что работа может выполняться при движении тел. Так, движущийся тепловоз, стыкуясь с вагоном, перемещает его на некоторое расстояние. Выполняется работа и в том случае, когда брошенный камень разбивает лед. Выстреленная из ружья пуля пробивает доску и т. п. Если потенциальной энергией обладают тела, на которые действует сила, то в упомянутых выше случаях работа выполняется потому, что они осуществляли перемещение, двигались.

Какой энергией обладают движущиеся тела

Энергию движущегося тела называют кинетической энергией.

Кинетическая энергия является физической величиной ее значение можно рассчитывать. Для этого необходимо знать, от каких физических величин она зависит.

Как рассчитывают кинетическую энергию

Поставим желоб под некоторым углом к поверхности стола. На некотором расстоянии от его нижнего конца поставим брусок. На средней части желоба разместим маленький стальной шарик и отпустим его. Скатившись по желобу, шарик ударится о брусок и переместит его на некоторое расстояние. Отметим расстояние, на которое сместился брусок.

Поместим шарик в верхней части желоба и отпустим его. В этом случае, скатившись желобом к основе, шарик приобрел большую скорость, чем раньше. Ударившись в брусок, он переместит его на большее расстояние, чем в предыдущем опыте, соответственно выполнив большую работу.

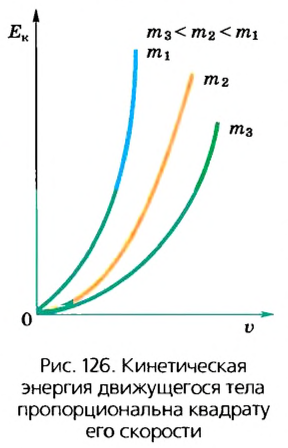
Таким образом, кинетическая энергия тела зависит от его скорости. Эта зависимость нелинейная, что заметно на графике зависимости кинетической энергии тела от его скорости. График имеет вид кривой линии (рис. 126).

Кинетическая энергия тела относительна

Как известно, скорость тела является относительной величиной и зависит от выбора тела отсчета. Поэтому и кинетическая энергия является величиной относительной. Если артиллерийский снаряд, попав в стену, причиняет значительные разрушения, то снаряд, посланный вдогонку сверхзвуковому самолету, не причинит ему существенных повреждений, поскольку скорость снаряда относительно самолета будет небольшой.

Последствия столкновения автомобилей в случае их движения навстречу друг другу будут всегда более ощутимы, чем тогда, когда один автомобиль догоняет другой.

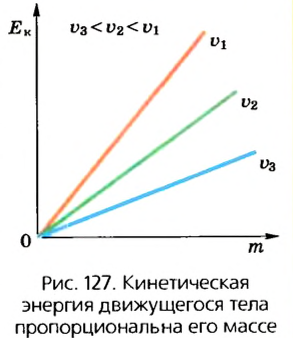
Кинетическая энергия зависит и от массы тела. Если повторим предыдущие опыты с шариком большей массы, то увидим, что перемещения бруска в этом случае будет большим. Эта зависимость линейная, поэтому можно сказать, что кинетическая энергия тела пропорциональна его массе (рис. 127).

Как рассчитать кинетическую энергию

Чтобы рассчитать кинетическую энергию, используют формулу:

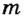
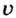
где — масса тела; — скорость тела.

Кинетическая энергия разных физических тел используется для выполнения механической работы. Так, опытные водители автомобилей время от времени отсоединяют двигатель от колес, выключая сцепление, и этим экономят топливо. Работа по преодолению сил трения выполняется за счет кинетической энергии автомобиля. Конструкторы работают над моделью городского автобуса, который начинает движение за счет энергии раскрученного во время стоянки большого маховика. Это дает возможность существенно уменьшить выбросы вредных газов в атмосферу и экономить топливо.

В южных областях Украины, в частности на Крымском полуострове, используют ветряные электростанции, которые работают за счет кинетической энергии потоков воздуха — ветра (рис. 128).

Кинетическая энергия тела

Рассмотрим движение тела массой т под действием нескольких сил, например движение санок (см. рис. 124). Предположим также, что сила натяжения веревок постоянна, а следовательно, постоянной будет и результирующая сила 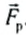. Она совпадает по направлению с перемещением тела или противоположна ему. Эта сила, естественно, вызывает ускорение санок, т. е. изменяет их скорость. Кроме того, она совершает работу. Следовательно, между работой результирующей силы и изменением скорости санок должна существовать связь.

Рассмотрим случай, когда проекция результирующей силы на направление движения положительна, т. е. санки движутся равноускоренно с ускорением а, которое находится из второго закона Ньютона:
(1)

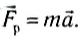
Работа результирующей силы:
A = F_p△r, (2)
где △r— модуль перемещения тела за некоторый промежуток времени. Подставим выражение (1) в (2). В результате получим:
A = ma△r. (3)

При равноускоренном одномерном движении модуль перемещения △r и изменение скорости связаны соотношением:
(4)
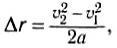
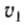
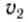
где и — начальная и конечная скорости тела, которое совершило перемещение △r с ускорением а.

Соотношение (3) с учетом (4) примет вид:
(5)

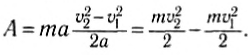
Полученная формула связывает работу результирующей силы, действующей на тело, с изменением величины 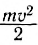. Эта величина называется кинетической энергией тела и обычно обозначается К.
Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости:
(6)

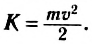
Тогда формула (5) примет вид:
(7)

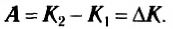
Итак, работа результирующей силы, действующей на тело, равна изменению кинетической энергии тела. Как вы уже знаете, изменение какой-то величины равно разности конечного значения и начального. Из формулы (7) очевидно следует, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в СИ в джоулях.

Когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то K₂>K₁. Это означает, что кинетическая энергия тела увеличивается. Понятно, что, если результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. Следует отметить, что, хотя мы получили формулу (7) для частного случая равноускоренного и прямолинейного движения, она справедлива и в случае изменяющейся во времени результирующей силы. Поэтому формулу (7) часто называют теоремой о кинетической энергии.

Итак, любое движущееся тело (рис. 127, 128) обладает кинетической энергией. Поскольку скорость тела зависит от выбора инерциальной системы отсчета, то и кинетическая энергия также зависит от выбора системы отсчета. Очевидно, что, как и работа, кинетическая энергия является скалярной физической величиной. Она не зависит от направления движения тела, а определяется его массой и квадратом скорости.

Главные выводы:

1. Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости и зависит от выбора системы отсчета.
2. Изменение кинетической энергии равно работе всех сил, действующих на тело.
3. Кинетическая энергия измеряется в тех же единицах, что и работа.

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Закон сохранения и превращения механической энергии
• Работа, мощность и энергия
• Движение и силы
• Давление в физике
• Взаимодействие тел
• Механическая энергия и работа
• Золотое правило механики
• Потенциальная энергия

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Кинетическая и потенциальная энергии

Энергия – важнейшее понятие в механике. Что такое энергия. Существует множество определений, и вот одно из них.

Что такое энергия?

Энергия – это способность тела совершать работу.

Кинетическая энергия

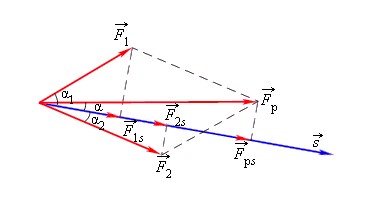
Рассмотрим тело, которое двигалось под действием каких-то сил изменило свою скорость с v 1 → до v 2 → . В этом случае силы, действующие на тело, совершили определенную работу A .

Работа всех сил, действующих на тело, равна работе равнодействующей силы.

F р → = F 1 → + F 2 →

A = F 1 · s · cos α 1 + F 2 · s · cos α 2 = F р cos α .

Установим связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F → , направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F → , v → , a → , s → совпадают по направлению и их можно рассматривать как алгебраические величины.

Работа силы F → равна A = F s . Перемещение тела выражается формулой s = v 2 2 – v 1 2 2 a . Отсюда:

A = F s = F · v 2 2 – v 1 2 2 a = m a · v 2 2 – v 1 2 2 a

A = m v 2 2 – m v 1 2 2 = m v 2 2 2 – m v 1 2 2 .

Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.

Определение. Кинетическая энергия

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Кинетическая энергия – энергия движения тела. При нулевой скорости она равна нулю.

Теорема о кинетической энергии

Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.

Теорема о кинетической энергии

Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.

A = E K 2 – E K 1 .

Таким образом, кинетическая энергия тела массы m , движущегося со скоростью v → , равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.

A = m v 2 2 = E K .

Чтобы остановить тело, нужно совершить работу

A = – m v 2 2 =- E K

Потенциальная энергия

Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще потенциальная энергия, то есть энергия взаимодействия тел, которая зависит от их положения.

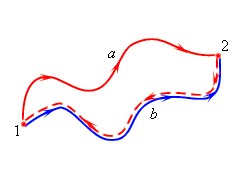
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.

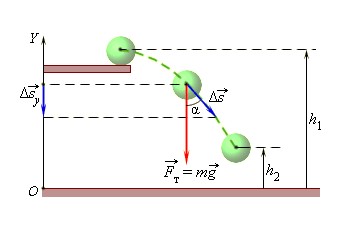
Рассмотрим пример, когда шар переместился из точки с высотой h 1 в точку с высотой h 2 .

При этом сила тяжести совершила работу, равную

A = – m g ( h 2 – h 1 ) = – ( m g h 2 – m g h 1 ) .

Эта работа равна изменению величины m g h , взятому с противоположным знаком.

Величина Е П = m g h – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальная энергия тела равна нулю.

Определение. Потенциальная энергия

Потенциальная энергия – часть полной механической энергии системы, находящейся в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему.

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A = – ( E П 2 – E П 1 ) .

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

Здесь G – гравитационная постоянная, M – масса Земли.

Потенциальная энергия пружины

Представим, что в первом случае мы взяли пружину и удлинили ее на величину x . Во втором случае мы сначала удлинили пружину на 2 x , а затем уменьшили на x . В обоих случаях пружина оказалась растянута на x , но это было сделано разными способами.

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

A у п р = – A = – k x 2 2 .

Величина E у п р = k x 2 2 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Что такое кинетическая энергия

Кинетическая энергия — это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия — это работа, которую тело выполняет, когда оно движется.

Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра — это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении.

Кинетическая энергия в физике измеряется в джоулях, сокращенно буквой J.

Формула кинетической энергии

Для расчета кинетической энергии тел используется уравнение:

Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2.

Мы можем сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя.

Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м/с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх.

Кинетическая энергия зависит от массы и скорости.

Гоночные машины спроектированы с наименьшей массой для улучшения характеристик.

Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит.

Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией.

А теперь представьте: две одинаковые машины едут, одна со скоростью 50 км/ч, а другая со скоростью 100 км/ч. Чем выше скорость, тем серьезнее авария.

Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза.

Автомобиль, движущийся со скоростью 60 км/ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км/ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии.

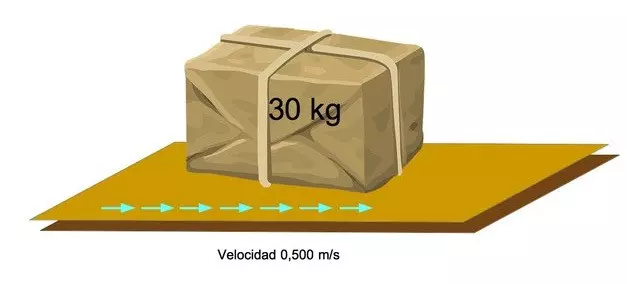
Как рассчитать кинетическую энергию тела?

В аэропорту хотят рассчитать кинетическую энергию 30-килограммовой упаковки в системе, которая движется со скоростью 0,500 м/с. Как мы это делаем?

Решение

Мы знаем массу и скорость упаковки, поэтому используем формулу:

Подставляя значения, имеем:

Рассуждение

Единицей кинетической энергии является джоуль, которая является той же для единицы работы. Обратите внимание, что, несмотря на то, что он тяжелый, его кинетическая энергия не так велика из-за его низкой скорости.

Ключевые моменты для запоминания

• Тело имеет кинетическую энергию, только если оно находится в движении.
• Кинетическая энергия зависит от массы и скорости тела.

Задачи на кинетическую энергию и решение

Задача 1 на нахождение кинетической энергии

Слон в 6000 кг бежит со скоростью 10 м/с. Какова его кинетическая энергия? Какова скорость пушечного ядра весом 1 кг, если у него была та же самая кинетическая энергия слона?

Ответ

Используя уравнение кинетической энергии, энергия слона равна:

Рассчитав кинетическую энергию, мы можем получить скорость пули, очистив v:

Это означает, что скорость пули равна 775 м/с. Сравните это со скоростью слона: вот это разница!

Задача 2

Мужчина врезался в столб на своей машине. Когда он пошел, чтобы сообщить о катастрофе, он сказал, что ехал с допустимой скоростью во время аварии. Но следователь помнил физику 7 и 8 класса и установил, что скорость транспортного средства была в два раза выше, чем утверждал водитель. Какова взаимосвязь между кинетической энергией и скоростью, сообщаемой человеком, и кинетической энергией со скоростью, рассчитанной следователем?

Ответ

Мы будем рассматривать Ec1 как кинетическую энергию транспортного средства на скорости v1, сообщаемой человеком, и Ec2 как кинетическую энергию со значением скорости v2, рассчитанным исследователем. Соотношение между кинетическими энергиями рассчитывается путем деления энергий следующим образом:

Следователь сказал, что скорость во время аварии была вдвое выше, чем сообщал человек, то есть:

Подставим значение скорости в уравнение:

Исключая похожие термины, мы имеем:

Это означает, что кинетическая энергия в соответствии со скоростью, сообщаемой человеком, составляет четверть кинетической энергии по расчетам следователя. Проще говоря, ущерб, нанесенный автомобилем, был в четыре раза больше, чем сообщал мужчина.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/fizika/zakony-sohranenija-v-mehanike/kineticheskaja-i-potentsialnaja-energii/

[/spoiler]

Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).

Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.

Определяют кинетическую энергию по формуле:

Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:

С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия. 

Если масса увеличивается в (2) раза, тогда кинетическая энергия увеличивается также в (2) раза.

Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной (2  м/с).

Рис. (1). График, зависимость кинетической энергии от массы

Рис. (2). График, зависимость кинетической энергии от скорости движения