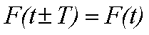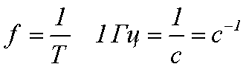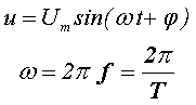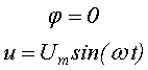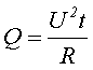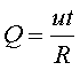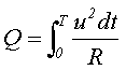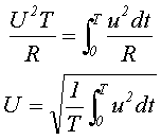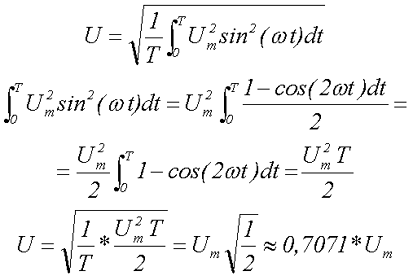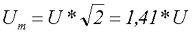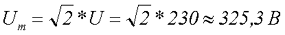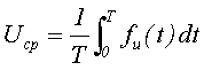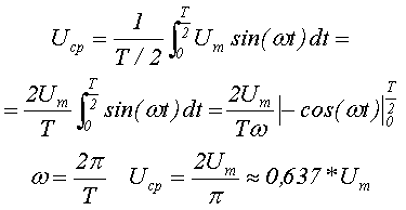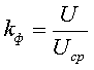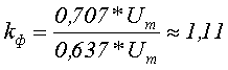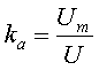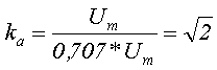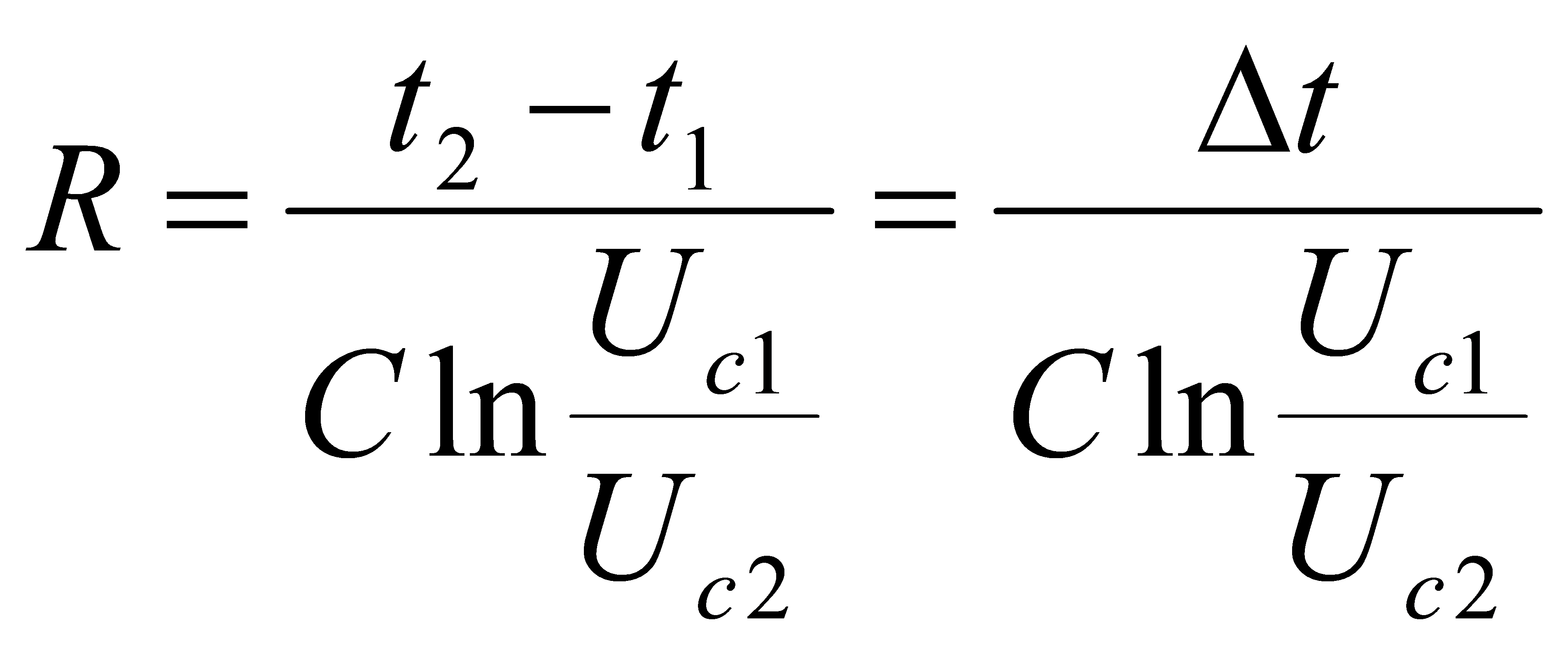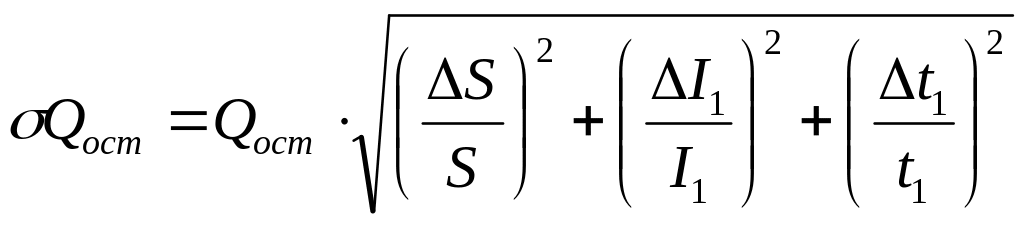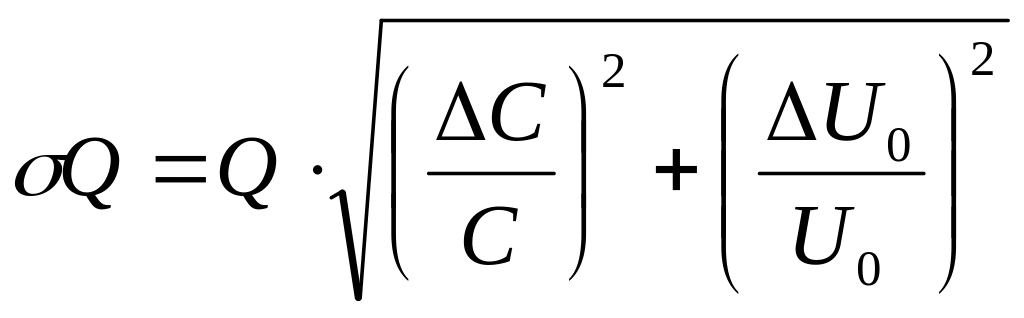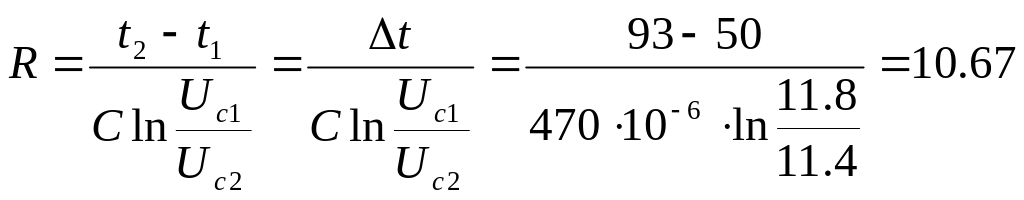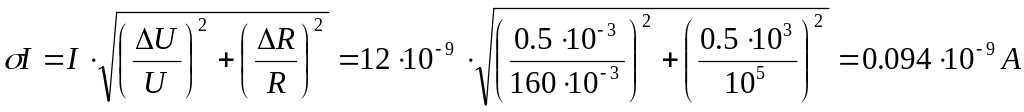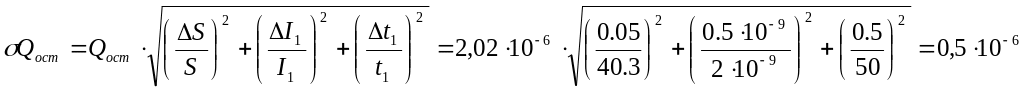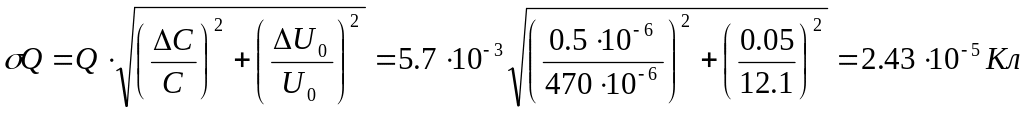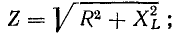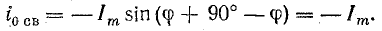ElectronicsBlog
Обучающие статьи по электронике
Переменное напряжение и его параметры
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
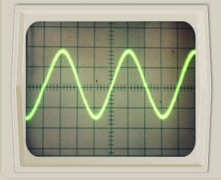
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
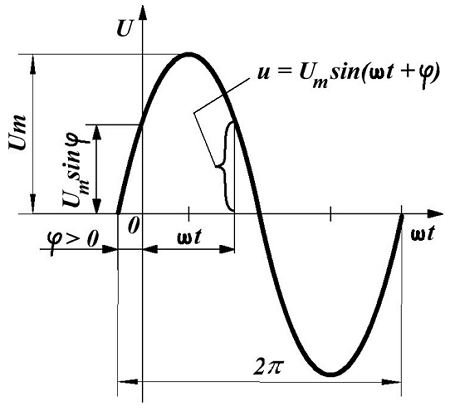
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
Для переменного напряжения мгновенное значение выделяемой энергии составит
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
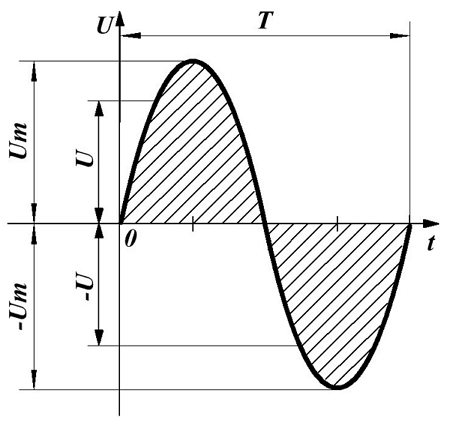
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
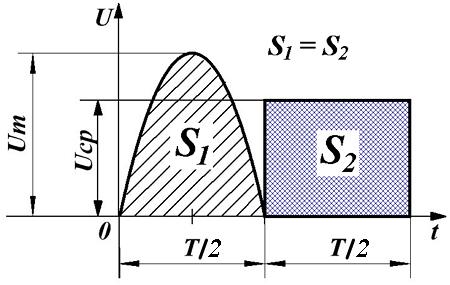
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
Так для синусоидального напряжения коэффициент формы составит
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
Так для синусоидального напряжения коэффициент амплитуды составит
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Источник
Решение задач по теме «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ
Презентация к уроку
Цели урока:
- Образовательные: обобщение и систематизация знаний по теме, проверка знаний, умений, навыков. В целях повышения интереса к теме работу вести с помощью опорных конспектов.
- Воспитательные: воспитание мировоззренческого понятия (причинно-следственных связей в окружающем мире), развитие у школьников коммуникативной культуры.
- Развивающие: развитие самостоятельности мышления и интеллекта, умение формулировать выводы по изученному материалу, развитие логического мышления, развитие грамотной устной речи, содержащей физическую терминологию.
Тип урока:систематизация и обобщение знаний.
Техническая поддержка урока:
- Демонстрации:
- Плакаты.
- Показ слайдов с помощью информационно – компьютерных технологий.
- Дидактический материал:
- Опорные конспекты с подробными записями на столах.
- Оформление доски:
- Плакат с кратким содержанием опорных конспектов (ОК);
- Плакат – рисунок с изображением колебательного контура;
- Плакат – график зависимости колебаний заряда конденсатора, напряжения между обкладками конденсатора, силы тока в катушке от времени, электрической энергии конденсатора, магнитной энергии катушки от времени.
1. Этап повторения пройденного материала. Проверка домашнего задания.
Четыре группы задач по теме:
- Электромагнитные колебания.
- Колебательный контур.
- Свободные колебания. Свободные колебания – затухающие колебания
- Характеристика колебаний.
2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.
Учитель: Темой урока является «Решение задач по теме: «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ»
К доске вызываются 3 ученика для проверки домашнего задания.
– Задания по этой теме можно разделить на четыре группы.
Четыре группы задач по теме:
1. Задачи с использованием общих законов гармонических колебаний.
2. Задачи о свободных колебаниях конкретных колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.
– Мы остановимся на решении задач 1 и 2 групп.
Урок начнем с повторения необходимых понятий для данной группы задач.
Электромагнитные колебания – это периодические и почти периодические изменения заряда, силы тока и напряжения.
Колебательный контур – цепь, состоящая из соединительных проводов, катушки индуктивности и конденсатора.
Свободные колебания – это колебания, происходящие в системе благодаря начальному запасу энергии с частотой, определяемой параметрами самой системы: L, C.
Скорость распространения электромагнитных колебаний равна скорости света: С = 3 . 10 8 (м/с)
Основные характеристики колебаний
Амплитуда (силы тока, заряда, напряжения) – максимальное значение (силы тока, заряда, напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда, напряжения) – i, q, u
Схема колебательного контура
Учитель: Что представляют электромагнитные колебания в контуре?
Электромагнитные колебания представляют периодический переход электрической энергии конденсатора в магнитную энергию катушки и наоборот согласно закону сохранения энергии.
Задача №1 (д/з)
Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?
Задача № 2 (д/з)
Колебательный контур состоит из конденсатора емкостью С и катушки индуктивности индуктивностью L. Как изменится период свободных электромагнитных колебаний в этом контуре, если электроемкость конденсатора и индуктивность катушки увеличить в 3р.
Задача № 3 (д/з)
Амплитуда силы тока при свободных колебаниях в колебательном контуре 100 мА. Какова амплитуда напряжения на конденсаторе колебательного контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1 Гн? Активным сопротивлением пренебречь.
Схема электромагнитных колебаний
Ученик 1 наглядно описывает процессы в колебательном контуре.
Ученик 2 комментирует электромагнитные колебания в контуре, используя графическую зависимость заряда, напряжения. Силы тока, электрической энергии конденсатора, магнитной энергии катушки индуктивности от времени.
Уравнения, описывающие колебательные процессы в контуре:
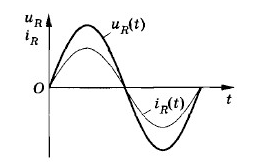
Обращаем внимание, что колебания силы тока в цепи опережают колебания напряжения между обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы тока по гармоническому закону, необходимо учитывать связь между функциями синуса и косинуса.
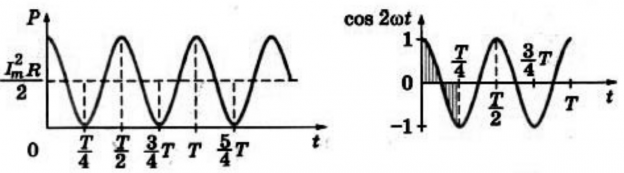
По графику зависимости силы тока от времени в колебательном контуре определите, какие преобразования энергии происходят в колебательном контуре в интервале времени от 1мкс до 2мкс?
1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.
По графику зависимости силы тока от времени в колебательном контуре определите:
а) Сколько раз энергия катушки достигает максимального значения в течение первых 6 мкс после начала отсчета?
б) Сколько раз энергия конденсатора достигает максимального значения в течение первых 6 мкс после начала отсчета?
в) Определите по графику амплитудное значение силы тока, период, циклическую частоту, линейную частоту и напишите уравнение зависимости силы тока от времени.
Задача № 3 (д/з)
Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите, какое преобразование энергии происходит в интервале времени от 0 до 2 мкс?
1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.
Задача № 4 (д/з)
Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите: сколько раз энергия конденсатора достигает максимального значения в период от нуля до 2мкс? Сколько раз энергия катушки достигает наибольшего значения от нуля до 2 мкс? По графику определите амплитуду колебаний напряжений, период колебаний, циклическую частоту, линейную частоту. Напишите уравнение зависимости напряжения от времени.
К доске вызываются 2 ученика
Задача № 5, 6
Заряд на обкладках конденсатора колебательного контура изменяется по закону
q = 3·10 –7 cos800πt. Индуктивность контура 2Гн. Пренебрегая активным сопротивлением, найдите электроемкость конденсатора и максимальное значение энергии электрического поля конденсатора и магнитного поля катушки индуктивности.
В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменяется заряд конденсатора в колебательном контуре с течением времени.
1. Напишите уравнение зависимости заряда от времени. Найдите амплитуду колебаний заряда, период, циклическую частоту, линейную частоту.
2. Какова энергия магнитного поля катушки в момент времени t = 5 мкс, если емкость конденсатора 50 пФ.
Домашнее задание. Напишите уравнение зависимости силы тока от времени. Найдите амплитуду колебаний силы тока. Постройте графическую зависимость силы тока от времени.
Источник
Расчетные формулы:
1)
зависимость
напряжения на конденсаторе от времени
в процессе его заряда
где:
Uc
– мгновенное значение напряжения на
конденсаторе (В), R
– сопротивление
цепи (Ом), С – электроемкость конденсатора
(Ф).
2)
зависимость
напряжения на конденсаторе от времени
в процессе его разряда
где
Uнач
–
начальное
напряжение (В)
3)
Где:
–
постоянной времени RC – цепи,
R
– сопротивление
цепи (Ом), С – электроемкость конденсатора
(Ф).
4)
где:
– интервал времени между измерениями
напряжений
и
на емкости в процессе ее разрядки.
.
Где:
Uc
– мгновенное значение напряжения на
конденсаторе (В), R
– сопротивление
цепи (Ом)
.
Нахождение
заряда, оставшегося в диэлектрике, при
известной зависимости I(t)
за очень большое время наблюдения.
где:
– оставшийся в диэлектрике заряд, S
–
площадь под графиком I(t),
а I1
и
t1
–масштабы по осям тока и времени
соответственно.
.
Полный
заряд заряженного конденсатора.
Формулы погрешностей косвенных измерений:
–
среднеквадратичная погрешность тока
разряда конденсатора во внешней цепи;
– среднеквадратичная
погрешность заряда, оставшегося в
диэлектрике после исчезновения
поляризационного заряда;
–
среднеквадратичная
погрешность полного заряда заряженного
конденсатора.
Таблица исходных
данных
Таблица 1.
Зависимость напряжения на конденсаторе от времени его заряда
U0= 12,1В, R=100кОм,
С=470мкФ,
|
t,c |
6 |
12 |
19 |
28 |
38 |
51 |
67 |
92 |
134 |
|
Uc,B |
1,2 |
2,4 |
3,6 |
4,8 |
6 |
7,2 |
8,4 |
9,6 |
10,8 |
|
Uc |
1,294348 |
2,433572 |
3,591284 |
4,847559 |
5,988372 |
7,151049 |
8,20389 |
9,27484 |
10,17595 |
– пример расчета
мгновенного значения напряжения на
конденсаторе для первого значения
времени (остальные значения приведены
в таблице 1).
Таблица 2.
Зависимость
напряжения на конденсаторе от времени
его разряда
Uнач=
10,8В,
R=100кОм,
С=470мкФ,
|
t,c |
6 |
13 |
22 |
32 |
45 |
59 |
85 |
127 |
180 |
|
Uc,B |
9,6 |
8,4 |
7,2 |
6 |
4,8 |
3,6 |
2,4 |
1,2 |
0 |
|
Uc |
9,505652 |
8,190299 |
6,762962 |
5,466809 |
4,145815 |
3,077837 |
1,770099 |
0,724277 |
0,234514 |
– пример расчета
мгновенного значения напряжения на
конденсаторе для первого значения
времени (остальные значения приведены
в таблице 2).
Таблица 3.
Зависимость
напряжения на конденсаторе от времени
его разряда через искомое входное
сопротивление вольтметра Rв
Uнач=
11,9В, С=470мкФ
-
№ измерения
1
2
3
4
5
6
7
8
9
t,
c50
93
136
177
223
169
317
365
413
Uс,B
11,8
11,7
11,6
11,5
11,4
11,3
11,2
11,1
11
Пара №-в измер., выбр. Для расч.
1 и 5
3 и 7
2 и 8
4 и 8
5 и 9
1 и 6
2 и 7
3 и 8
4 и 9
Rв,МОм
10,67
10,97
10,99
11,30
11,32
6,34
10,91
11,06
11,30
–
расчет теоретического
значения постоянной времени.
МОм
– пример расчета
первого значения сопротивления цепи
(остальные значения приведены в таблице
3).
Таблица 4.
Зависимость
напряжения на конденсаторе от времени
после его разряда закорачиванием.
U0=
190 мВ, R=100кОм, С=470мкФ,
-
t,c
11
22
44
61
100
124
153
234
403
Uс,мB
160
130
100
70
40
30
20
10
0
I,
нА16
13
10
7
4
3
2
1
0
–
пример расчета
первого значения тока разряда конденсатора
во внешней цепи (остальные значения
приведены в таблице 4).
–
расчет заряда,
оставшегося в диэлектрике после
исчезновения поляризационного заряда;
–
расчет полного
заряда заряженного конденсатора.
Расчет погрешностей
косвенных измерений:
–
значение среднеквадратичной погрешности
тока разряда конденсатора во внешней
цепи;
– значение
среднеквадратичной погрешности заряда,
оставшегося в диэлектрике после
исчезновения поляризационного заряда;
–
значение
среднеквадратичная погрешность полного
заряда заряженного конденсатора.
Графический
материал
График 1.
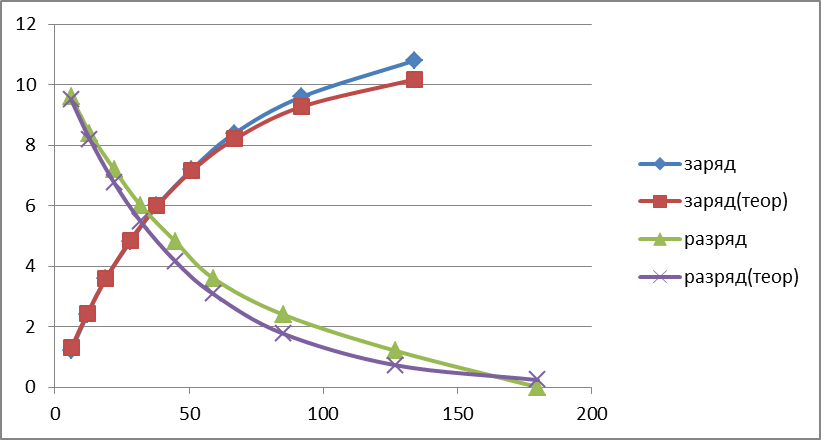
График 2.

Окончательный
результат:
А
– окончательный результат значения
тока разряда
конденсатора во внешней цепи для первого
значения в таблице 4;
–
окончательный результат значения
заряда, оставшегося
в диэлектрике после исчезновения
поляризационного заряда;
–
окончательный результат значения
полного заряда заряженного конденсатора.
Вывод:
В результате
расчетов полученные значения тока
разряда конденсатора во внешней цепи
удовлетворяют ожидаемым, погрешность
составила не более 8%, что делает результаты
допустимыми. Из чего можно сделать вывод
о высокой точности используемых
измерительных приборов. Так же расчеты
подтвердили что
значения полного заряда заряженного
конденсатора значительно больше заряда,
оставшегося в диэлектрике после
исчезновения поляризационного заряда,
это обусловлено свойством материи, все
выше перечисленное характеризует
свойства диэлектрика и называется
диэлектрической
проницаемостью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чем больше напряжение тем меньше сила тока в цепи


Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.
Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Подтверждение закона Ома
Бум исследования электрических явлений пришёлся на конец XVIII – начало XIX веков. Такие учёные, как Фарадей, Ампер, Вольт, Эрстед, Кулон, Лачинов, Ом провели ряд экспериментов, которые позволили Максвеллу создать теорию электромагнитных явлений.
Огромную роль в открытии новых знаний сыграл опыт Ома исследовавшего, от чего зависит сила тока в цепи. Немецкий физик ставил опыты над проводимостью различных материалов. Для этого он использовал электрическую цепь, в разрыв которой подключал проводники разной длины и замерял силу тока.
Изначально учёный не смог установить закономерность. Всё дело в том, что для своих опытов Ом использовал химическую батарею. Друг учёного Поггендорф предложил взять термоэлектрический источник тока. В итоге физик смог проследить зависимость. Описал он её так: частное от a, разделённого на l + b, где b определяет интенсивность воздействия на проводника длиною l, причём a и b — постоянные, зависящие соответственно от действующей силы и сопротивления элементов цепи.
Обычно при изучении закона в седьмом классе средней школы учитель демонстрирует эту зависимость на практических уроках. Для этого чтобы ученики удостоверились в справедливости утверждения, преподаватель собирает электрическую цепь, в состав которой входят:
- вольтметр – прибор для измерения напряжения, включается параллельно измеряемому проводнику;
- амперметр – устройство для замера тока, подключается последовательно с измеряемым телом;
- регулируемый источник электродвижущей силы (ЭДС).
Суть опыта заключается в подключении проводников с разной длиной. Измеренные результаты заносят в таблицу. Она должна иметь примерно следующий вид:
| Первое тело | Второе тело | Третье тело | |||
| U, В | I, А | U, В | I, А | U, В | I, А |
| 1 | 0,5 | 1 | 0,4 | 1 | 0,2 |
| 2 | 1 | 2 | 0,6 | 2 | 0,3 |
| 3 | 1,5 | 3 | 0,8 | 3 | 0,4 |
| 4 | 2 | 4 | 1 | 4 | 0,5 |
Проведя анализ таблицы, можно сделать вывод. Если для любого тела напряжение разделить на соответствующую ему силу тока, то получится одно и то же число. Следовательно, это отношение является свойством проводника. Для первого оно равно двум, второго – пяти, а третьего – десяти. При одинаковых токах в третьем случае число больше, значит, это тело оказывает большее сопротивление току.
Полученные значения по факту и являются величинами, обратными проводимости. Обозначают их буквой R (resistance).
Разбираемся что такое ток и сопротивление
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.
Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.
Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.
График зависимости
По результатам эксперимента Ом построил график зависимости силы тока от сопротивления, который напоминает собой левую часть параболы. Современная запись закона Ома имеет вид: I = U / R. Звучит она следующим образом: ток прямо пропорционален напряжению и обратно пропорционален электрическому сопротивлению.
Но при разработке приборов или исследовании участка цепи перед учёными и инженерами стоит задача, прежде всего, выяснить зависимость тока от напряжения. Поэтому ими строится график, в котором по оси абсцисс откладывают значение потенциала, а ординат — силы тока. В итоге если отложить соответствующие точки, то должна получиться прямая линия. Это говорит о том, что зависимость величин линейная. То есть во сколько раз увеличивается напряжение, во столько же возрастает сила тока.
Такого вида график называется вольт-амперной характеристикой (ВАХ). Но при реальных измерениях изменение ток зависит ещё от температуры. Установлено, что при нагреве сопротивление проводника увеличивается. Поэтому прямая на ВАХ будет иметь меньший угол наклона. Кроме того, ток может быть двух видов:
- постоянный – сила не изменяется от времени;
- переменный – изменяющийся по синусоидальному закону.
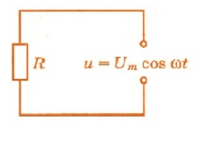
Поток носителей заряда для второго вида описывается гармоническим законом: I(t) = Im * cos (wt + f), где: w – циклическая частота, f – сдвиг фаз относительно напряжения, Im – наибольшее значение тока. Тогда изменение напряжения во времени можно записать так: U(t) = Um * cos (wt). В этом случае закон Ома примет вид: I = U / Z, где Z – полное сопротивление цепи.
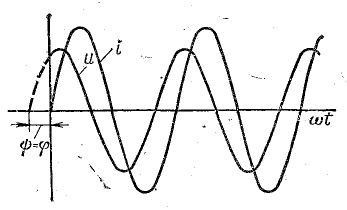
График зависимости силы тока от времени, впрочем, как и напряжения, будет представлять собой синусоиду. Если отложить их на одном рисунке, то при активном сопротивлении (резистор) фазы величин будут совпадать друг с другом. В схеме, содержащей реактивные составляющие, а это ёмкость, и индуктивность, фаза тока соответственно будет опережать и отставать от напряжения. Угол изменения составит девяносто градусов.
Графики зависимости позволяют определить мощность. Сделать это можно, воспользовавшись формулой: P = U * I * cos(f). Чтобы построить график мощности, нужно аппроксимировать на ось t точки синусоиды I(t) и U(t), в которых параметры изменяют свой знак.
Характеристика P(t) будет также описываться по гармоническому закону. Причём в каждой этой точке линя изменит направление.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.
Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.
Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Величина силы тока
По определению силой тока называется физическая величина равная величине заряда q, прошедшего через поперечное сечение проводника за время t:
Если сила тока не зависит от времени, то такой электрический ток называется постоянным. Рассмотрим далее именно такой случай, когда ток постоянен. Измерить величину заряда чрезвычайно трудно, поэтому в 1826 г. немецкий физик Георг Ом поступил следующим образом: в электрической цепи, состоящей из источника напряжения (батареи) и сопротивления, он измерял величину тока при разных значениях сопротивления. Затем, не меняя величину сопротивления, он стал изменять параметры источника напряжения, подключая сразу, например, два-три источника. Измеряя величину тока в цепи, он получил зависимости силы тока от напряжения U и от сопротивления R.
Рис. 1. Схема измерений тока и напряжения Георга Ома.
Что изменится для полной цепи
В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.
Полная цепь включает в себя источник питания
Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).
Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:
Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.
Вроде не слишком сложно, но можно попробовать еще проще:
- Чем выше ЭДС источника тока, тем больше ток.
- Чем больше суммарное сопротивление, тем ток меньше.
Как найти сопротивление, напряжение
Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.
Формула напряжения и сопротивления по закону Ома
Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.
С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
Уравнение зависимости изменения напряжения от времени
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
- Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
- Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
- Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
- Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
Классический метод расчета
Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.
Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи

при наличии магнитной связи с катушкой, обтекаемой током 

Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать
| Резистор (идеальное активное сопротивление) |
| Катушка индуктивности (идеальная индуктивность) |
| Конденсатор (идеальная емкость) |
 . . |
(1) |
Подставив в (1) значение тока через конденсатор

получим линейное дифференциальное уравнение второго порядка относительно

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:
 , , |
(2) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); 

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением
 , , |
(3) |
где 



Наличие индуктивных связей на порядок дифференциального уравнения не влияет.
Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение 

Частное решение 

Вторая составляющая 

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид
 |
(4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей 


Таблица 2. Законы коммутации
Первый закон коммутации (закон сохранения потокосцепления)
Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Второй закон коммутации (закон сохранения заряда)
Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения 

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:
первый закон коммутации – в ветви с катушкой индуктивности ток в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
второй закон коммутации – напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа 

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для 

Пример. Определить токи и производные 

В соответствии с законами коммутации


На основании второго закона Кирхгофа для момента коммутации имеет место

и 
Для известных значений 

определяется 
Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей 
Таблица 3. Выражения свободных составляющих общего решения
Вид корней характеристического уравнения
Выражение свободной составляющей
Корни 
Корни 
Пары комплексно-сопряженных корней
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях 
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

которое называется декрементом колебания, или натуральным логарифмом этого отношения

называемым логарифмическим декрементом колебания, где 
Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Переходные процессы в электрических цепях с сосредоточенными параметрами
Содержание:
Переходные процессы в электрических цепях с сосредоточенными параметрами:
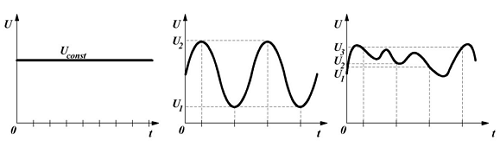
В предыдущих главах электрические цепи постоянного и переменного токов и их расчет рассмотрены в установившемся режиме, т. е. при установившихся напряжениях и токах.
В установившемся режиме напряжения и токи во всех участках электрической цепи остаются неизменными в течение сколь угодно большого промежутка времени. В понятие неизменных напряжений и токов в данном случае включаются не только постоянные, но и синусоидальные напряжения и токи с постоянными амплитудой и частотой.
По условиям эксплуатации и характеру работы электроустановок или по другим (в том числе случайным) причинам изменяются режимы в электрических цепях.
Для перехода от одного установившегося режима к другому требуется некоторый переходный период, в течение которого изменяются величины токов и напряжений в электрической цепи. С большей или меньшей скоростью эти величины приходят в соответствие с условиями нового режима.
В последующих параграфах для переходных периодов в некоторых простых цепях найдены зависимости тока и напряжения от времени, позволяющие определить их величины в любой момент.
Общие сведения о переходных процессах
Для изучения переходных процессов в простой или сложной цепи необходимо рассмотреть общие сведения о них. В числе таких сведений отметим причины возникновения переходных процессов, основные определения и два закона коммутации, на которых основаны исследования переходных процессов.
Причины возникновения переходных процессов
Переходные процессы возникают вследствие изменения э. д. с. в цепи, напряжения, приложенного к цепи, или в связи с изменением ее параметров — сопротивления, индуктивности или емкости.
Непосредственными причинами возникновения переходных процессов могут быть: коммутационные изменения режимов, т.е. включение и выключение источников питания, приемников энергии; короткие замыкания на участках электрических цепей; изменения механической нагрузки электродвигателей и др.
Электромагнитные процессы, происходящие в электрических целях при переходе от одного установившегося режима к другому, называют переходными процессами.
Электрические токи, напряжения в цепи во время переходного процесса называют переходными токами или напряжениями.
Продолжительность переходных процессов в электрических цепях (переходный период) чаще всего составляет десятые и сотые доли секунды. Однако знание характера их очень важно, так как и за малое время возможны резкие увеличения токов и напряжений, которые могут оказаться опасными для электрических установок.
В устройствах связи, автоматики, счетно-решающей техники, радиотехники с помощью переходных процессов формируются импульсы — сигналы, несущие определенную информацию.
Изучение переходных процессов в этих устройствах необходимо для оценки тех изменений, которые они могут внести в электрические сигналы.
Соотношение длительностей установившихся и переходных режимов может быть самым различным и зависит от условий эксплуатации и назначения электрических цепей. Одни из них по продолжительности практически все время работают в установившемся режиме (двигатели с длительной неменяющейся нагрузкой, лампы электрического освещения), другие, наоборот, непрерывно находятся в переходном режиме (двигатели с повторно-кратковременной нагрузкой, линии связи во время передачи информации, импульсные устройства автоматики, счетно-решающие машины в период работы).
Первый закон коммутации
Первый закон коммутации применяется к цепям, обладающим индуктивностью.
Ток в индуктивности не может измениться скачком. Поэтому мгновенный ток в ветви с индуктивностью в первый момент переходного периода остается таким, каким он был в последний момент предшествующего установившегося режима.
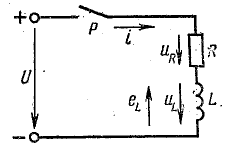
Справедливость первого закона коммутации следует из простых рассуждений, которые изложим применительно к случаю включения катушки индуктивности на постоянное напряжение U (рис. 25.1).
До замыкания рубильника Р установившийся режим характеризуется тем, что ток в цепи, напряжения активное uR и индуктивное uL равны нулю.
С момента замыкания рубильника возникает переходный процесс, в течение которого ток в катушке увеличивается до некоторой величины i = I, изменяются и напряжения uR и uL. Электрическое состояние цепи по схеме рис. 25.1 в любой момент переходного периода характеризуется уравнением
В установившемся режиме при замкнутом рубильнике Р ток в цепи постоянный, т. е. скорость изменения тока равна нулю: 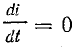

Предположим, что переходный период отсутствует и ток в катушке мгновенно (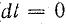
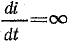
Но это противоречит уравнению (25.1), в котором напряжение источника U — конечная величина. Изменение тока скачком означало бы также, что энергия магнитного поля катушки увеличилась скачком от 0 до 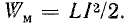
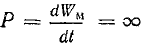
Из первого закона коммутации следует, что в начальный момент после замыкания рубильника (при t = 0) ток в цепи равен нулю (i0 = 0), падение напряжения в сопротивлении i0R = 0, а индуктивное напряжение — напряжению источника u0L = U и цепь как бы разомкнута индуктивностью.
Второй закон коммутации
Второй закон коммутации применяется к цепям, обладающим емкостью.
Напряжение на емкости не может измениться скачком. Поэтому напряжение на емкости в первый момент переходного периода остается таким, каким оно было в последний момент предшествующего установившегося режима.
Рассуждения, подтверждающие второй закон коммутации, приведем применительно к случаю зарядки конденсатора через резистор (включение цепи с R и С на постоянное напряжение, рис. 25.2). До замыкания рубильника Р установившийся режим характеризуется тем, что ток в цепи на резисторе и конденсаторе равны нулю.
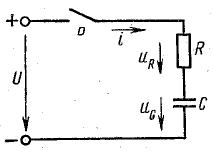
Рис. 25.2. Ко второму закону коммутации
С момента замыкания рубильника возникает переходный процесс, в течение которого напряжение на конденсаторе увеличивается до напряжения источника U (конденсатор заряжается), изменяются ток в цепи и напряжение на резисторе.
Электрическое состояние цепи (рис. 25.2) в любой момент переходного периода характеризуется уравнением, составленным по второму закону Кирхгофа: 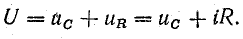
Ток в цепи пропорционален скорости изменения напряжения на конденсаторе: 
Учитывая это, получаем 
Приложенное к цепи напряжение (напряжение источника) делится на две части: одна из них (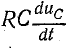
В установившемся режиме при замкнутом рубильнике Р напряжение на конденсаторе не изменяется, т. е. скорость изменения напряжения на конденсаторе равна нулю (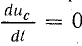
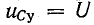
Доказательства существования переходного периода при зарядке конденсатора аналогичны тем, которые были ранее приведены для цепи с катушкой индуктивности.
Предположим, что в момент замыкания рубильника Р напряжение на конденсаторе изменилось скачком от 0 до U. Такое предположение означает конечное изменение напряжения за время, равное нулю, т. е. 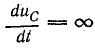
Включение катушки индуктивности на постоянное напряжение
После включения катушки к источнику постоянного напряжения ток в цепи рис. 25.1 увеличивается, но не мгновенно. Перейдем к более подробному анализу переходного процесса.
График переходного тока
Закон изменения тока в катушке после замыкания рубильника в схеме рис. 25.1 можно выяснить, используя уравнение (25.1) в преобразованном виде: 
В первый момент переходного периода ток в цепи с R и L равен нулю (i0 = 0).
Поэтому независимо от величины сопротивления R скорость изменения тока в начальный момент переходного периода выражается отношением величины напряжения к индуктивности: 
Из этого выражения следует, что сразу после включения цепи ток начинает увеличиваться по линейному закону с наибольшей в данных условиях скоростью.
Но так происходит лишь в начальный момент переходного периода. Как только в цепи появился ток, хоть и малой величины, одновременно возникло падение напряжения iR [см. уравнение (25.1)], а индуктивное напряжение соответственно уменьшилось. Уменьшение индуктивного напряжения немедленно вызовет снижение скорости изменения тока.
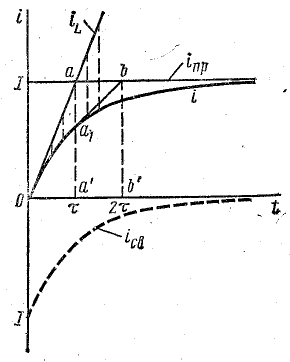
Рис. 25.3. График переходного тока после включения цепи на постоянное напряжение
Таким образом, рассматриваемый переходный процесс в катушке (при постоянных величинах U, R, L) отличается тем, что с увеличением тока уменьшается скорость его изменения. По этой причине график тока (кривая i на рис. 25.3) с течением времени все более отклоняется от прямой iL, которая соответствует начальной скорости переходного процесса. Прямая iL, как нетрудно заметить, является касательной к кривой переходного тока i реальной цепи, а наклон ее к оси абсцисс характеризует наибольшую скорость изменения тока, возможную при заданных условиях.
Теоретически переходный процесс продолжается бесконечно долго, а ток в цепи асимптотически стремится к установившемуся I = U/R.
Постоянная времени электрической цепи
Если предположить, что при наличии в цепи сопротивления R ток изменялся бы по линейному закону с наибольшей скоростью (прямая iL), то установившейся величины I он достиг бы за наименьшее время t = τ. Этот промежуток времени является важной характеристикой и называется постоянной времени электрической цепи.
Постоянную времени можно определить графически (рис. 25.3). Для этого нужно провести касательную Оа к кривой тока в начале координат; точку 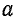
Такую же длину имеет отрезок 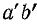
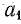
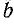
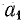
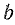
Из рис. 25.3 можно получить аналитическое выражение для определения постоянной времени. Прямая 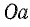
Это следует из уравнения (25.5): при R = 0
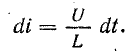
Отсюда 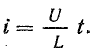
По графику 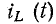
Так как U = IR, то постоянная времени 
Постоянная времени, как видно из последней формулы, определяется только параметрами R, L данной цепи.
Уравнение кривой переходного тока
Уравнение кривой переходного тока в катушке после замыкания рубильника в схеме рис. 25.1 можно получить, используя уравнение (25.1) в таком виде: 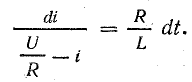
Проинтегрируем обе части этого дифференциального уравнения: 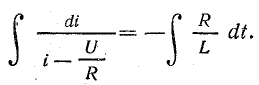
В результате интегрирования получим 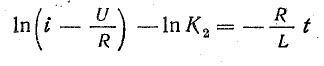
или 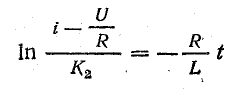
(постоянная интегрирования взята в форме 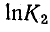
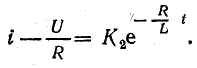
Постоянная интегрирования К2 определяется из начальных условий: согласно первому закону коммутации, в начальный момент переходного периода ток в цепи равен нулю, так как он был равен нулю в последний момент до включения рубильника.
Подставив в последнее равенство t = 0 и i = 0, найдем
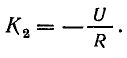
Определив К2 из начальных условий, получим окончательно уравнение для переходного тока 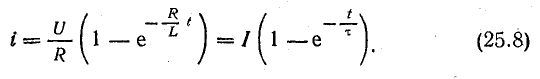
В этом уравнении τ = L/R — уже известная постоянная времени цепи.
Уравнению (25.8) соответствует график переходного тока (кривая i на рис. 25.3).
Как было отмечено, переходный процесс продолжается бесконечно долго. Это подтверждается уравнением (25.8), согласно которому ток устанавливается при t = ∞. В практике переходный период считается законченным по истечении времени, равном (4 ÷ 5)τ, когда ток отличается от установившегося примерно на 1%.
Принужденная и свободная составляющие переходного тока
Из уравнения (25.8) видно, что переходный ток можно рассматривать как алгебраическую сумму двух составляющих: 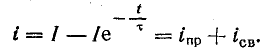
Первая составляющая представляет собой ток, установившийся в цепи по окончании переходного процесса (прямая iпр на рис. 25.3): 
Этот ток определяется непрерывным действием постоянного напряжения U в переходном и установившемся режимах. Его принято называть принужденным током.
Вторая составляющая возникает в начале переходного процесса и постепенно затухает до нуля, после чего переходный процесс считается законченным (кривая iсв на рис. 25.3). Эта составляющая переходного тока называется свободным током. Он изменяется по закону 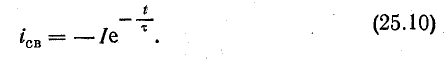
Из уравнения (25.10) следует:
постоянная времени электрической цепи равна интервалу времени, в течение которого свободный ток в этой цепи убывает в е раз.
График переходного тока (рис. 25.3) можно получить, сложив графики принужденного и свободного токов. Однако нужно помнить, что физически реальным в течение переходного процесса является общий ток, постепенно нарастающий от начального (i = 0) до установившегося (i = I).
Одновременно с увеличением тока происходит процесс постепенного изменения (в данном случае накопления) энергии 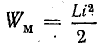
Влияние величины напряжения и параметров цепи на переходный процесс
Переходный процесс при включении цепи с R и L на постоянное напряжение U характеризуют три показателя: установившийся ток, начальная скорость изменения тока и постоянная времени цепи [см. формулы (25.2), (25.6), (25.7)].
Используя эти выражения, можно проследить влияние величины напряжения источника и параметров цепи на переходный процесс (имеются в виду изменения напряжения или параметров цепи до начала переходного процесса).
Установившийся ток и начальная скорость изменения тока зависят от напряжения, а постоянная времени цепи, характеризующая продолжительность переходного процесса, не зависит.
Эти заключения отражены на рис. 25.4: графики установившегося тока проведены на разном уровне, а касательные к кривой тока наклонены к оси времени под разными углами. При этом постоянная времени не изменилась (τ2 = τ1).
Продолжительность переходного процесса в обоих случаях одинакова, несмотря на то что скорость изменения тока разная. Это обстоятельство не должно вызывать сомнения: при изменении напряжения ток увеличивается с другой скоростью, но и стремится к другой установившейся величине.
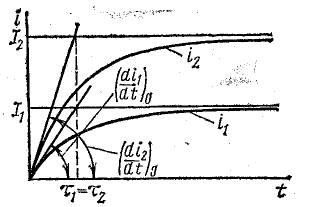
Рис. 25.4. Графики переходного тока при различных напряжениях на зажимах цепи
При изменении сопротивления R в цепи изменяются установившийся ток и постоянная времени. Начальная скорость изменения тока от сопротивления R не зависит.
В соответствии с этими выводами на рис. 25.5 проведены две асимптоты (I1 и I2) и одна общая касательная к графикам переходного тока в начале координат: 
Касательная пересекает асимптоты в точках с разными координатами не только по оси токов, но и по оси времени, что подтверждает предыдущий вывод о зависимости постоянной времени от сопротивления R.
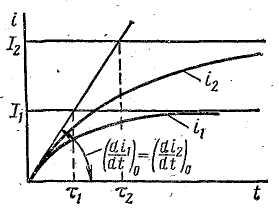
Рис. 25.5. Графики переходного тока при различных сопротивлениях цепи
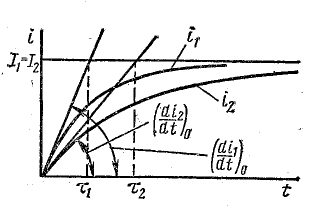
Рис. 25.6. Графики переходного тока при различных индуктивностях цепи
Из этого нетрудно сделать заключение о том, как влияет сопротивление на продолжительность переходного процесса.
Изменение индуктивности не сказывается на величине установившегося тока, но начальная скорость изменения тока и постоянная времени изменяются. Поэтому на рис. 25.6 проведены одна (общая) асимптота и две касательные в начале координат к графикам переходного тока. Касательные пересекают асимптоту в двух точках и отмечают величины постоянных времени τ1 и τ2, соответствующих двум величинам индуктивности цепи.
В данном случае переходные токи стремятся к одинаковой установившейся величине с разной скоростью, поэтому продолжительность переходного процесса неодинакова.
Отключение катушки индуктивности от источника постоянного напряжения
Отключение приемников электрической энергии от источника или от сети осуществляется в большинстве случаев разрывом цепи в одной или нескольких точках. Встречаются случаи, когда элементы цепи, обладающие большой индуктивностью, при разрыве цепи одновременно замыкаются накоротко или на разрядное сопротивление.
Размыкание электрической цепи с катушкой индуктивности
При размыкании электрической цепи с катушкой индуктивности (рис. 25.7, а) в момент разрыва цепи напряжение между расходящимися контактами выключателя В резко увеличивается от нуля до U + uL. Скорость изменения тока в момент разрыва цепи 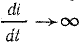
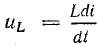
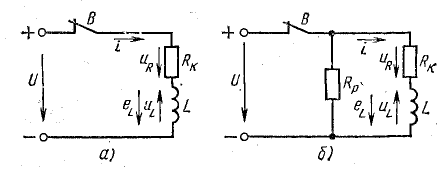
Рис. 25.7. Схемы размыкания цепи с индуктивностью
В некоторых случаях (например, при выключении обмоток возбуждения электрических машин) напряжение может достигать величин, опасных для изоляции. Значительного повышения напряжения можно избежать, если одновременно с отключением индуктивной катушки от источника замкнуть ее на разрядное сопротивление (рис. 25.7, б). По подобной схеме работают, например, автоматы гашения поля (АГП) генераторов на электростанциях. При внутренних повреждениях в генераторе необходимо как можно скорее отключить его от сети и «погасить» магнитное поле. Для этого и служит АГП, с помощью которого обмотка возбуждения замыкается на разрядное сопротивление и отключается от возбудителя.
Изменение тока в катушке, замкнутой на разрядное сопротивление
Переходный процесс в замкнутом контуре катушка — разрядное сопротивление отличается от процесса в цепи рис. 25.7, а тем, что скорость изменения тока 
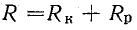
При включении катушки на постоянное напряжение по схемам рис. 25.1 или 25.7, б катушка является приемником энергии. Ток i и э. д. с. самоиндукции еL имеют противоположные направления, что соответствует накоплению энергии в магнитном поле катушки за счет энергии источника.
После отключения цепи от источника энергии (рис. 25.7, б) в образовавшемся короткозамкнутом контуре ток не может уменьшиться мгновенно до нуля, а поддерживается в течение переходного периода, пока имеется энергия в магнитном поле катушки.
Запас энергии в магнитном поле непрерывно уменьшается, так как в активном сопротивлении цепи R совершается необратимый процесс превращения электрической энергии в тепловую.
Таким образом, во время переходного процесса катушка является источником электрической энергии с электродвижущей силой самоиндукции еL, которая возникает и поддерживается в связи с уменьшением тока. Это подтверждается и изменением направления э. д. с. самоиндукции, которое теперь совпадает с направлением тока.
Закон изменения тока при выключении катушки (как и при ее включении) определяется параметрами R и L. Еще до подробного анализа уравнения тока, который приведен далее, можно отметить обстоятельства, позволяющие судить о характере уменьшения тока в катушке.
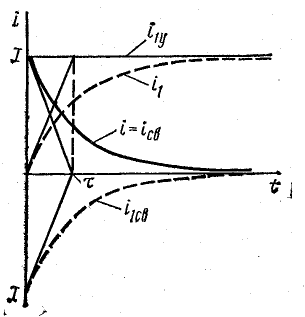
Рис. 25.8. График переходного тока в катушке индуктивности, замкнутой на сопротивление
В начальный момент переходного периода величина тока 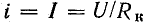
Предположим, что сопротивление 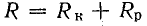
Касательная к графику тока (рис. 25.8) в точке с координатами t = 0, i = I отсечет на оси времени отрезок τ, выражающий постоянную времени цепи, которая и в данном случае аналитически определяется формулой (25.7).
Уравнение переходного тока
Величину переходного тока в короткозамкнутой катушке можно определить из уравнения (25.1), если учесть, что U = 0: 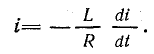
После разделения переменных получим 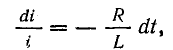
а после интегрирования обеих частей уравнения — 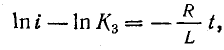
где К3 — постоянная интегрирования, отсюда 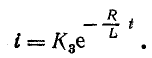
В установившемся режиме, предшествующем отключению катушки от источника, и в начальный момент переходного периода (t = 0) ток i0 = I = U/R.
Учитывая это, из начальных условий найдем K3: 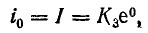
а 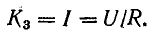
Таким образом, уравнение тока в переходный период имеет вид 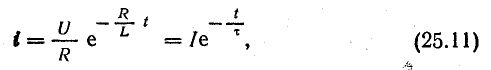
где 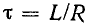
В короткозамкнутой катушке ток уменьшается по экспоненциальному закону от i0 = I до установившегося iy = 0.
Сравнивая (25.11) с выражением свободного тока в катушке при ее включении на постоянное напряжение (25.10), убеждаемся, что они одинаковы, если не учитывать изменение знака.
Длительность переходного процесса, как и при включении катушки, теоретически равна бесконечности, а практически ток принимается равным нулю при t = (4 ÷ 5)τ.’
Вопрос о влиянии величины начального тока I и параметров цепи на продолжительность переходного процесса можно проанализировать аналогично тому, как это сделано для случая включения катушки.
Основными характеристиками переходного процесса являются:
начальный ток I = U/R; начальная скорость изменения тока 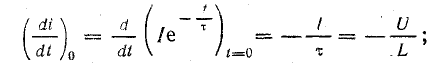
постоянная времени цепи τ = L/R.
Нетрудно заметить, что выражения этих характеристик совпадают соотвественно с формулами (25.2), (25.6) и (25.7). Изменился лишь знак в формуле начальной скорости изменения тока. Но это объясняется просто: ток теперь не увеличивается, а уменьшается, и касательная к кривой тока наклонена к оси времени под утлом, большим 90°.
Изменение сопротивления в цепи с индуктивностью
При включении катушки индуктивности, обладающей параметрами R, L, сопротивление цепи уменьшается скачком от ∞ до R, а при выключении оно увеличивается от R до ∞.
В соответствии с такими изменениями сопротивления ток в цепи за время переходного периода увеличивается от 0 до I или уменьшается от I до 0.
При скачкообразном изменении сопротивления цепи в конечных пределах тоже возникает переходный процесс, который в общих чертах подобен уже рассмотренным процессам.
Некоторые особенности его обусловлены тем, что при уменьшении сопротивления ток увеличивается начиная с некоторой конечной величины, а при увеличении сопротивления ток уменьшается не до нуля.
Уменьшение сопротивления в цепи
При разомкнутом рубильнике Р в цепи с последовательно соединенными сопротивлением R1 и катушкой R2, L (рис. 25.9) установившийся ток 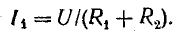
После замыкания рубильника сопротивление в цепи внезапно уменьшается до R2, а ток постепенно увеличивается до 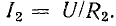
Переходный процесс от первого режима ко второму отличается от рассмотренного тем, что ток в цепи увеличивается не от нуля, а от величины I1. Однако закон изменения тока от I1 до I2 такой же. 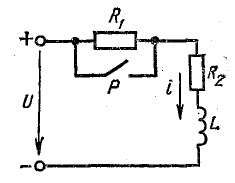
25.9. Схема изменения скачком сопротивления в цепи
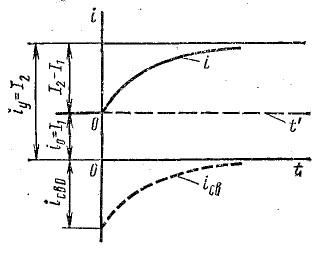
Рис. 25.10. График переходного тока после уменьшения сопротивления
Вследствие уменьшения сопротивления в цепи возникает добавочный свободный ток, начальная величина которого определяется в соответствии с первым законом коммутации: 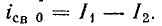
Если к принужденному току 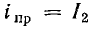
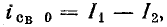
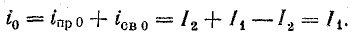
Свободный ток уменьшается в течение переходного процесса до нуля по известному закону (рис. 25.10). По аналогии с формулой (25.11) имеем 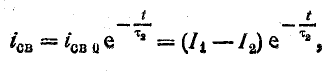
или 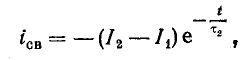
где 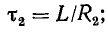
Увеличение сопротивления в цепи
Обратный переход от второго режима к первому совершается после размыкания рубильника. Сопротивление цепи внезапно увеличивается, а ток от I2 уменьшается по экспоненциальному закону, стремясь к установившейся величине I1 (рис. 25.11).
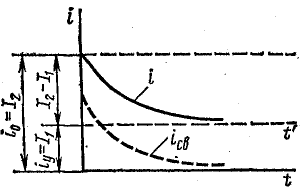
Рис. 25.11. График переходного тока после увеличения сопротивления
Принужденная составляющая переходного тока iпр = I1.
Свободная составляющая, по аналогии с формулой (25.11), 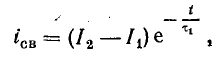
где 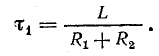
Уравнение переходного тока
Зарядка конденсатора
Анализ процесса зарядки конденсатора от источника постоянного напряжения во многом совпадает с анализом переходного процесса после включения катушки на постоянное напряжение, так как исходные уравнения (25.1) и (25.4) по своей структуре аналогичны.
Уравнение кривых переходного тока и напряжения на конденсаторе
Закон изменения напряжения на конденсаторе и зарядного тока можно найти, решив дифференциальное уравнение (25.4). Путем разделения переменных это уравнение приводится к виду, удобному для интегрирования: 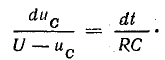
Интегрирование и последующие преобразования, выполненные в том же порядке, как для цепи с катушкой индуктивности, приводят к решению уравнения в виде 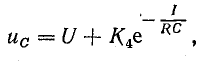
где К4 — постоянная интегрирования.
Из начальных условий (t = 0, uC0 — 0) находим 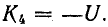
Уравнение кривой напряжения на конденсаторе принимает вид 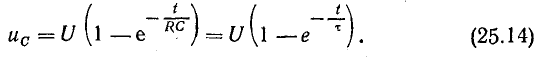
Уравнение зарядного тока легко найти из предыдущего уравнения (25.14), если учесть выражение (25.3): 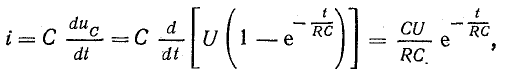
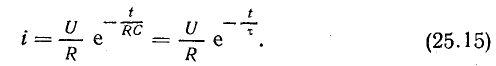
В дальнейшем для анализа переходных процессов при зарядке конденсаторов потребуется выражение скорости изменения напряжения на конденсаторе в начальный момент времени. Это выражение нетрудно получить, используя формулы (25.3) и (25.15): 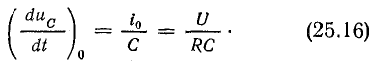
Графики зависимости напряжения на конденсаторе uC и зарядного тока i3 от времени изображены на рис. 25.12.
Как видно из этих графиков, скорость увеличения напряжения на конденсаторе и скорость уменьшения зарядного тока непрерывно снижаются.
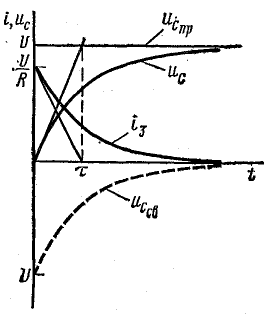
Рис. 25.12. Графики переходных тока и напряжения при зарядке конденсатора
Напряжение uC и зарядный ток асимптотически стремятся к своим пределам: uC— к величине напряжения источника U, а ток i — к нулю. Теоретически переходный процесс продолжается бесконечно долго, что подтверждают уравнения (25.14) и (25.15) (uC = U и i = 0 при t = ∞). Однако практически считают, что переходный процесс заканчивается за время, равное (4 ÷ 5)τ. Величина τ в уравнениях (25.14) и (25.15) — постоянная времени цепи: 
Постоянная времени, которая зависит от параметров цепи R, С, как и в цепи с индуктивностью, является показателем продолжительности переходного процесса.
В уравнении (25.14) можно выделить принужденную и свободную составляющие напряжения на конденсаторе: 


Зарядный ток состоит только из свободной составляющей 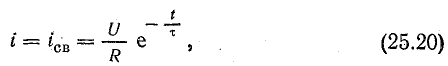
а принужденная составляющая
Влияние величины напряжения источника и параметров цепи на переходный процесс
Переходный процесс при зарядке конденсатора от источника постоянного напряжения характеризуют три показателя: установившееся напряжение на конденсаторе; начальная скорость изменения напряжения; постоянная времени [см. формулы (25.18), (25.16), (25.17)].
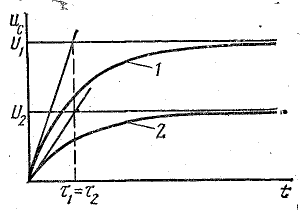
Рис. 25.13. Графики переходного напряжения на конденсаторе при различных напряжениях источника
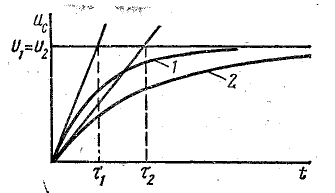
Рис. 25.14. Графики переходного напряжения на конденсаторе при различных сопротивлениях цепи
Используя их выражения, можно проследить влияние величины напряжения заряжающего источника и параметров цепи на переходный процесс (имеется в виду изменение напряжения или параметров цепи до начала переходного процесса).
При изменении напряжения источника изменяются установившееся напряжение на конденсаторе и начальная скорость изменения напряжения, а постоянная времени цепи, характеризующая длительность переходного процесса, от напряжения не зависит. На рис. 25.13 построены соответственно двум различным напряжениям источника U1 и U2 два графика изменения напряжения на конденсаторе 1 и 2 и две касательные к ним в начале координат, имеющие разные углы наклона к оси времени.
Продолжительность переходного периода в обоих случаях одинакова, так как напряжения на конденсаторе изменяются с разными скоростями, стремясь к разным установившимся величинам.
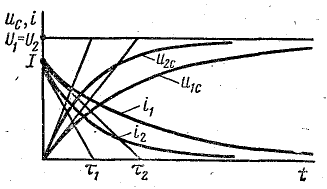
Рис. 25.15. Графики переходных напряжений и тока конденсатора при различных величинах емкости
Сопротивление входит в выражения начальной скорости изменения напряжения на конденсаторе (25.16) и постоянной времени цепи (25.17), а установившееся напряжение на конденсаторе от сопротивления не зависит. В соответствии с этим на рис. 25.14 проведены одна общая асимптота (U1 = U2) и две касательные в начале координат к графикам переходного напряжения на конденсаторе.
Касательные пересекают асимптоту в двух точках, при этом отмечают две величины постоянной времени: τ1 и τ2. На том же рисунке показаны кривые 1 и 2 изменения напряжения на конденсаторе uC, соответствующие двум величинам сопротивления в цепи. По этим графикам нетрудно сделать заключение о влиянии сопротивления на переходный процесс заряда конденсатора. Изменение емкости влияет на продолжительность переходного процесса так же, как изменение сопротивления (рис. 25.15) К такому заключению можно прийти, применяя для анализа те же выражения (25.16), (25.17), (25.18). Однако имеется разница в энергетической характеристике процесса: при изменении емкости меняется конечный запас энергии в электрическом поле цепи, а при изменении сопротивления — количество электрической энергии, преобразованной в тепло.
Задача 25.13.
Конденсатор емкостью С = 10 мкФ заряжается через резистор, сопротивление которого R = 9 Ом, по схеме рис. 15.16 (переключатель П в положении 1) от источника электрической энергии с э. д. с. Е = 100 В и внутренним сопротивлением r = 1 Ом (на схеме не показано). Через промежуток времени, равный удвоенной величине постоянной времени цепи зарядки, переключатель П переведен в положение 2.
Определить энергию, израсходованную в резисторе за время зарядки конденсатора.
Решение. Закон изменения напряжения на конденсаторе в процессе зарядки 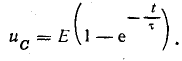
К моменту переключения рубильника напряжение uC достигает величины 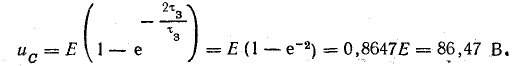
Закон изменения тока в процессе зарядки конденсатора 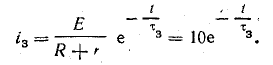
Энергия, израсходованная в сопротивлении R при зарядке конденсатора, 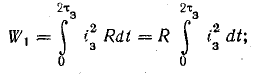
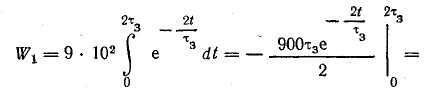
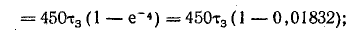
Разрядка конденсатора на сопротивление
Переходный процесс при разрядке конденсатора рассмотрим по схеме рис. 25.16, предполагая, что заряженный до напряжения uСУ = U конденсатор емкостью С отключается от источника энергии и его обкладки замыкаются на сопротивление R (переключатель П в положении 2).
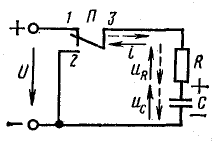
Рис. 25.16. Схема разрядки конденсатора
Переходный процесс при разрядке конденсатора
После переключения по схеме рис. 25.16 конденсатор не может разрядиться мгновенно, т. е. напряжение uC не может уменьшиться скачком до нуля, а поддерживается в течение переходного периода за счет энергии, накопленной в электрическом поле конденсатора.
При этом в активном сопротивлении R совершается необратимый процесс превращения электрической энергии в тепловую. Запас энергии в электрическом поле непрерывно сокращается, а вместе с этим уменьшается и напряжение на конденсаторе. Во время переходного периода конденсатор является источником энергии.
Характер изменения напряжения на конденсаторе при его разрядке можно установить пока без математического анализа несложными рассуждениями, предположив, что конденсатор замкнут на то же сопротивление R, через которое он заряжается.
В начальный момент переходного периода величина напряжения на конденсаторе сохраняется, как и следует из второго закона коммутации. В дальнейшем закон уменьшения напряжения uC будет определяться изменением энергии в электрическом поле конденсатора, подобно тому как при зарядке изменением энергии электрического поля определяется свободная составляющая напряжения на конденсаторе (см. рис. 25.12).
Отличие заключается лишь в том, что при зарядке энергия в электрическом поле накапливалась, а при разрядке она расходуется. Выражением этого отличия служит изменение направления разрядного тока в конденсаторе по сравнению с зарядным током (на рис. 25.16 направления тока, напряжений на конденсаторе и резисторе при разрядке показаны сплошными, а при зарядке — пунктирными стрелками).
График разрядного тока можно получить, повернув график зарядного тока на 180° вокруг оси времени (рис. 25.17).
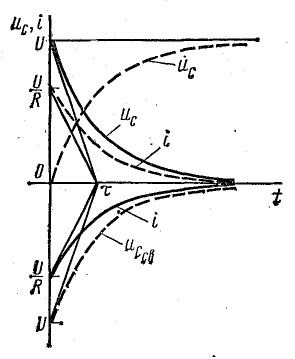
Рис. 25.17. Графики переходных напряжений и тока при разрядке конденсатором
Так же можно получить график напряжения на конденсаторе, который по форме повторяет график свободной составляющей напряжения на конденсаторе при зарядке (на рис. 25.17 графики, относящиеся к процессу зарядки, показаны пунктиром, а графики при разрядке — сплошными линиями). Касательная к графику uC в точке с координатами t = 0, uC = U отсечет на оси времени отрезок τ, выражающий постоянную времени цепи, которая и при разрядке алгебраически определяется формулой (25.17).
Уравнение напряжения на конденсаторе и тока в цепи при разрядке конденсатора
Для математического анализа переходного процесса при разрядке конденсатора исходным является уравнение (25.4), в котором для этого случая напряжение источника нужно считать равным нулю: 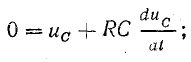
отсюда 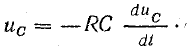
После разделения переменных получим 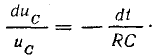
После интегрирования 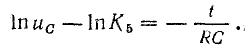
Отсюда 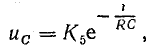
где К5 — постоянная интегрирования, определяемая из начальных условий: при t = 0 и uC0 = U.
Подставляя начальные условия в последнее уравнение, найдем
К5 = U.
Следовательно, напряжение на конденсаторе при разрядке выражается уравнением 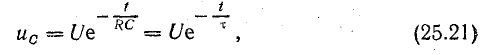
где τ = RC — постоянная времени цепи при разрядке конденсатора.
Итак, напряжение на конденсаторе при разрядке уменьшается по экспоненциальному закону от uC0 = U до установившегося uCУ = 0.
Сравнивая формулу (25.21) с выражением свободного напряжения на конденсаторе при зарядке [см. формулу (25.19)], убеждаемся в том, что они одинаковы, если не учитывать изменения знака.
Длительность переходного процесса, как и при зарядке, теоретически равна бесконечности, а практически разрядка считается законченной при t = (4 ÷ 5)τ.
Для разрядного тока выражение получается на основе закона Ома: 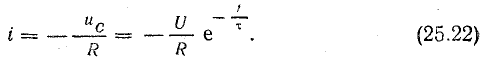
Вопрос о влиянии величины начального напряжения и параметров цепи на продолжительность переходного процесса можно проанализировать, используя три основные характеристики переходного процесса: начальное напряжение на емкости 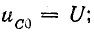
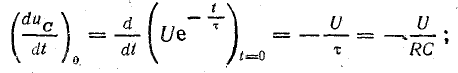
постоянную времени 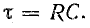
Эти выражения совпадают соответственно с формулами (25.16), (25.17), (25.18). Только знак в формуле начальной скорости изменился на обратный. Объясняется это тем, что конденсатор теперь разряжается, а не заряжается, и напряжение uC уменьшается, а не увеличивается, поэтому касательная к кривой uC в начальный момент наклонена к оси времени под углом, большим 90°.
Задача 25.15.
Согласно условию задачи 25.13, после периода зарядки конденсатора 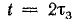
Определить энергию, израсходованную в цепи за время разрядки конденсатора.
Решение. При разрядке конденсатора энергия, израсходованная в элементе цепи с сопротивлением R, равна убыли энергии электрического поля конденсатора в одно и то же время.
Энергия электрического поля к концу зарядки конденсатора 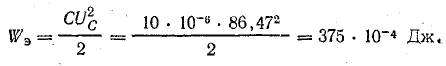
Вся эта энергия выделяется в виде тепла в сопротивлении при разрядке конденсатора. Таким образом, общая энергия, выделенная в сопротивлении R при зарядке и разрядке, составляет
Включение катушки индуктивности на синусоидальное напряжение
Изменение напряжения источника во время переходного процесса влияет на характер переходного тока. При анализе переходного процесса в цепи переменного тока приходится, кроме того, учитывать сдвиг фаз между напряжением и установившимся током, начальную фазу напряжения или, иначе говоря, мгновенное напряжение источника в момент включения цепи.
Однако переходные процессы в цепях постоянного и переменного токов одинаковы: они возникают при переходе от одного установившегося режима к другому при несоответствии запасов энергии в электрическом и магнитном полях цепи условиям нового режима. В течение переходного режима это несоответствие устраняется изменением энергии полей.
Уравнение переходного тока
После включения участка электрической цепи с активным сопротивлением R и индуктивностью L на синусоидальное напряжение (рис. 25.18) начинается переходный период, к концу которого в цепи устанавливается синусоидальный ток.
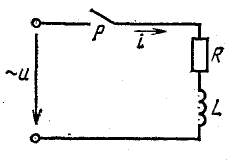
Рис. 25.18. Схема катушки индуктивности, включенной на переменное напряжение
Момент включения цепи будем полагать началом отсчета времени (t = 0).
Пусть приложенное напряжение изменяется по закону 
где ψ — начальная фаза.
В момент включения цепи напряжение имеет величину 
Ток в цепи после ее включения представляется суммой принужденной и свободной составляющих: 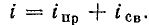
В установившемся режиме синусоидальный ток в катушке сдвинут по фазе относительно напряжения на угол φ, определяемый соотношением активного и индуктивного сопротивлений катушки. Установившийся ток, как известно, является принужденной составляющей переходного тока: 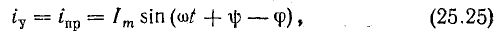
где
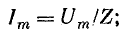
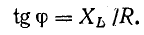
Свободная составляющая переходного тока не зависит от формы приложенного напряжения и изменяется по такому же закону [см. формулу (25.10)], что и при включении катушки на постоянное напряжение, равное мгновенному напряжению источника (u0) в момент включения цепи (t = 0): 
где К6 — постоянная интегрирования, равная свободной составляющей тока при t = 0, т. е. 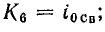
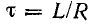
Таким образом, переходный ток 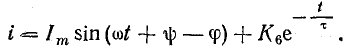
Постоянную К6 находят с помощью первого закона коммутации: в начальный момент (t = 0) ток в цепи равен нулю, так как ранее цепь была разомкнута и ток в катушке скачком измениться не может.
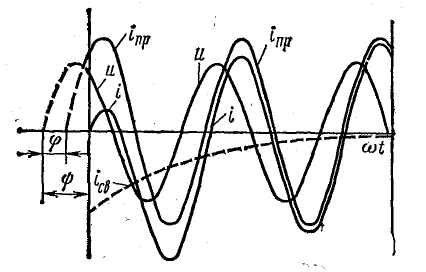
Рис. 25.19. Графики переходного процесса в катушке индуктивности после включения на переменное напряжение
Поэтому 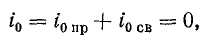
отсюда следует, что 
Bp (25.25) 
Следовательно, 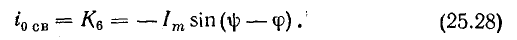
Уравнение свободной составляющей 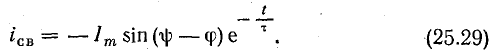
Переходный ток 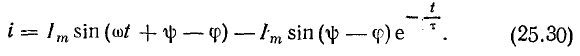
Графики переходного тока и его составляющих показаны на рис. 25.19.
Влияние на переходный процесс начальной фазы приложенного напряжения
Рассматривая рис. 25.19, можно заметить, что изменения установившегося и переходного токов носят колебательный характер, причем колебания установившегося тока совершаются около оси ωt, а переходного тока — около кривой iсв(t). Обусловлено это тем, что свободная составляющая переходного тока, внося искажения, как бы смещает график синусоидального тока и искривляет его ось. Степень искажения зависит от того, в какой момент включена цепь, так как в выражение свободной составляющей (25.29) входит начальная фаза приложенного к цепи напряжения.
Рис. 25.20. Графики переходного процесса после включения катушки индуктивности (при ψ = φ)
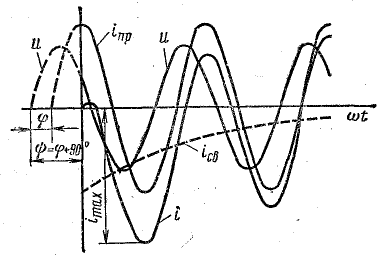
Рис. 25.21. Графики переходного процесса после включения катушки индуктивности (при ψ = φ + 90°)
Если включение катушки произошло в момент, когда принужденная составляющая переходного тока равна нулю [т. е. при ψ = φ, см. формулу (25.27)], то свободная составляющая не возникает: согласно (25.27), при ψ = φ iсв = 0. Иначе говоря, в этом случае переходный период отсутствует и в цепи с первого момента после включения наступает установившийся режим (рис. 25.20).
Наибольшая величина свободного тока в начальный момент времени может быть равна амплитуде установившегося тока. Это имеет место при ψ = φ + 90°, когда в момент включения цепи принужденная составляющая тока равна амплитуде Im (рис. 25.21):
В этом случае свободная составляющая переходного тока затухает быстрее или медленнее в зависимости от величины постоянной времени цепи, а переходный ток в соответствии с этим приближается к установившемуся.
В цепях с большой постоянной времени (с большой индуктивностью и малым сопротивлением) свободная составляющая переходного тока затухает медленно, поэтому переходный ток в течение первого полупериода достигает величины, равной почти удвоенной амплитуде установившегося тока:
Короткое замыкание в цепи переменного тока
При внезапном коротком замыкании скачком уменьшается сопротивление цепи Z. Переходный процесс, возникающий в результате изменения сопротивления, рассмотрим на схеме рис. 25.22, где электрическая нагрузка, представленная сопротивлением Zн, подключена через сопротивление Zл к источнику синусоидального напряжения с постоянной амплитудой и неизменной частотой. Такой схемой замещения можно представить реальную
цепь, в которой к шинам трансформаторной подстанции через линию (Zл) подключена группа потребителей электрической энергии (Zн).
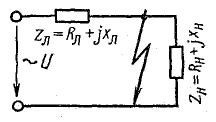
Рис. 25.22. Схема короткого замыкания в цепи переменного тока
Уравнение кривой переходного тока
Предположим, что сопротивление цепи изменилось в результате короткого замыкания в конце линии, как показано на рис. 25.22. При этом будем считать, что синусоидальное напряжение источника остается неизменным по амплитуде (принятое условие неизменности амплитуды напряжения соответствует короткому замыканию на участке, отделенном от мощных источников питания большим сопротивлением).
До короткого замыкания установившийся режим характеризуется напряжением 
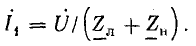
Уравнение напряжения, приложенного к цепи, 
где ψ— фазовый угол, определяющий напряжение в начальный момент короткого замыкания (t = 0).
Установившийся ток до короткого замыкания отстает от напряжения на угол 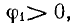
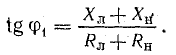
В этом случае уравнение тока 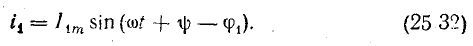
Установившийся режим после короткого замыкания характеризуется тем же напряжением U и током 
Уравнение установившегося тока 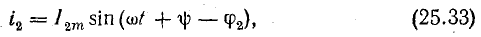
где φ2 — угол сдвига фаз напряжения и установившегося тока короткого замыкания, определяемый соотношением активного и реактивного сопротивлений короткозамкнутой цепи: 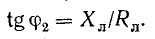
Переходный ток в короткозамкнутой линии представим суммой принужденной и свободной составляющих: 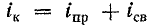
( 
Свободная составляющая тока изменяется по тому же закону, по которому она изменяется в цепи по схеме рис. 25.9 при уменьшении сопротивления: 
где τ2 — постоянная времени короткозамкнутой цепи:
K7 — постоянная величина, определяемая из начальных условий.
В начальный момент переходного периода, согласно первому закону коммутации, следовательно,
Отсюда
Свободная составляющая переходного тока, согласно уравнению (25.34)
Переходный ток короткого замыкания выражается уравнением
На рис. 25.23 показаны графики напряжения и тока в цепи до и после короткого замыкания.
Влияние начальной фазы напряжения на переходный процесс короткого замыкания
Ток короткого замыкания, как уже отмечено, складывается из двух составляющих — принужденной составляющей, равной установившемуся току короткого замыкания, и свободной составляющей, затухающей благодаря наличию в цепи активного сопротивления.
Принужденная составляющая изменяется по синусоидальному закону, и поэтому ее называют периодической составляющей, а свободная составляющая не изменяет знака, и ее называют апериодической составляющей тока короткого замыкания.
Начальную величину свободной составляющей определяют из уравнения (25.36):
Она зависит от начальной фазы напряжения ψ, т. е. от момента возникновения короткого замыкания.
Рис. 25.23. Графики переходного процесса при коротком замыкании в цепи переменного тока (при )
Рис. 25.24. Графики переходного процесса при коротком замыкании в цепи переменного тока (при )
Наиболее тяжелым случаем является короткое замыкание в момент, когда мгновенное напряжение на зажимах цепи равно нулю (), а сопротивление цепи короткого замыкания чисто индуктивное (). Соответствующий график тока короткого замыкания показан на рис. 25.24.
В реальных электрических сетях индуктивное сопротивление цепи короткого замыкания во многих случаях значительно больше активного, поэтому при расчете токов короткого замыкания активное сопротивление часто не учитывают. При этом условии свободная составляющая переходного тока в момент t = 0 близка к наибольшей возможной величине, равной амплитуде периодической составляющей. Если активное сопротивление цепи короткого замыкания мало, свободная составляющая затухает медленно, поэтому в самом неблагоприятном случае за время, приблизительно равное полупериоду, ток короткого замыкания достигает своей наибольшей величины, близкой к удвоенной амплитуде установившегося тока короткого замыкания.
Наибольший мгновенный ток короткого замыкания называют ударным током (iуд).
Свободная составляющая тока короткого замыкания затухает тем быстрее, чем меньше постоянная времени цепи короткого замыкания τ2, т. е. чем больше активное сопротивление и меньше индуктивность.
Параметры цепей короткого замыкания в реальных электроустановках обычно такие, что свободная составляющая тока короткого замыкания заметно проявляется в течение 0,1—0,2 с.
Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами
Как отмечено ранее, в установившемся режиме токи и напряжения всех ветвей электрической цепи изменяются по периодическому закону или, в частном случае, сохраняют неизменные значения. Всякое изменение как топологии цепи, так и параметров входящих в нее элементов: подключение или отключение отдельных ветвей, изменение параметров пассивных элементов или параметров источников энергии, нарушает периодический характер изменения токов и напряжений ветвей, т. е. приводит к тому, что режим работы цепи становится неустановившимся. Любое скачкообразное изменение в цепи, приводящее к нарушению установившегося режима, будем называть коммутацией. Если внешнее воздействие на цепь и после коммутации имеет периодический характер, то с течением времени (теоретически через бесконечно большой промежуток времени) цепь перейдет в новый установившийся режим. Неустановившиеся процессы, которые имеют место в цепи при переходе от одного установившегося режима к друюму, называются переходными.
При анализе переходных процессов в цепи, как правило, можно пренебречь длительностью процесса коммутации, т. е. считать, что коммутация осуществляется практически мгновенно. Начало отсчета времени переходного процесса обычно совмещают с моментом коммутации, причем через t=0_ обозначают момент времени, непосредственно предшествующий коммутации, а через или — момент времени, следующий непосредственно за коммутацией (начальный момент времени после коммутации).
Переходные процессы, связанные с изменением топологии цепи или различными коммутациями пассивных элементов, присущи в основном устройствам производства, передачи и преобразования электрической энергии. Для радиотехнических устройств более характерен режим, когда топология цепи и параметры пассивных элементов неизменны, а внешнее воздействие на цепь изменяется по произвольному (чаще всего непериодическому) закону. Понятие коммутации в том виде, как оно было сформулировано ранее, по сути дела, теряет смысл, так как изменение параметров источников энергии происходит практически непрерывно. При анализе неустановившихся процессов в радиотехнических цепях начало отсчета времени выбирают исходя из постановки задачи, независимо от того, находилась ли цепь до этого момента времени в установившемся режиме или нет. Для единства терминологии начало отсчета времени неустановившихся процессов, имеющих место в радиотехнических цепях, обычно также называют моментом коммутации.
Законы коммутации
Переход реальной электрической цепи от одного установившегося режима к другому не может происходить мгновенно, скачком. Это объясняется тем, что каждому установившемуся состоянию соответствует определенное значение энергии, запасенной в электрическом и магнитном полях. Скачкообразный переход от одного установившегося режима к другому потребовал бы скачкообразного изменения запасенной энергии,- что, учитывая выражение (1.5), возможно только, если источники энергии обладают бесконечно большой мощностью, т. е. отдаваемые ими токи или напряжения могут принимать бесконечно большие значения. В связи с тем что любой реальный источник энергии может отдавать только конечную мощность, суммарная энергия, запасенная в цепи, может изменяться только плавно, т. е. представляет собой непрерывную функцию времени. Принимая во внимание, что запасенная в цепи энергия определяется суммарными зарядом всех конденсаторов и потокосцеплением всех индуктивных катушек, приходим к выводу, что суммарные потокосцепление и заряд цепи также являются непрерывными функциями времени, в частности после коммутации они равны суммарному потокосцеплению и суммарному заряду цепи в момент времени
Это положение известно под названием принципа непрерывности во времени суммарного потокосцепления и суммарного электрического заряда цепи. В реальных цепях в момент коммутации возможны коммутационные потери энергии, например потери энергии за счет искры или электрической дуги между контактами переключателей, поэтому суммарная энергия цепи после коммутации может быть несколько меньше суммарной энергии цепи до коммутации.
Если электрическая цепь не содержит энергоемких элементов, то процесс ее перехода от одного установившегося режима к другому должен происходить мгновенно. Такие безреактивные цепи можно рассматривать только в качестве весьма упрощенных моделей реальных цепей.
Если коммутация идеализированной электрической цепи не затрагивает ветвей, содержащих реактивные элементы, т. е. в процессе коммутации не производится подключения или отключения ветвей, содержащих емкости и индуктивности, и не происходит скачкообразного изменения их параметров, то из принципа непрерывности суммарных потокосцепления и заряда цепи следует непрерывность токов индуктивностей и напряжений емкостей. Вывод о непрерывности токов индуктивностей и напряжений емкостей формулируется в виде законов (правил) коммутации.
Первый закон коммутации: в начальный момент времени после коммутации ток индуктивности сохраняет такое же значение, как и непосредственно перед коммутацией:
а затем плавно изменяется, начиная с этого значения.
Второй закон коммутации: в начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией:
а затем плавно изменяется, начиная с этого значения.
Законы коммутации не накладывают ограничений на характер изменения токов емкостей, напряжений индуктивностей и токов или напряжений сопротивлений, которые могут изменяться произвольным образом, в том числе и скачкообразно.
Как известно, в теории цепей рассматриваются процессы, имеющие место в идеализированных цепях при идеализированных внешних воздействиях. Применение чрезмерно упрощенных моделей элементов цепей и внешних воздействий может привести к нарушению предпосылок, использованных при формулировании законов коммутации, и вследствие этого к нарушению самих законов. Так, представляют интерес случаи, когда идеализированные источники энергии в течение бесконечно короткого промежутка времени могут отдавать бесконечно большой ток или напряжение, т. е. развивать бесконечно большую мощность. При таких внешних воздействиях законы коммутации нарушаются и токи индуктивностей или напряжения емкостей изменяются скачкообразно.
Законы коммутации могут не выполняться и при некоторых коммутациях, затрагивающих ветви, содержащие реактивные элементы. Коммутации такого типа называются некорректными. Анализ процессов в цепях при некорректных коммутациях производят с использованием принципа непрерывности суммарных потокосцепления и электрического заряда цепи, который имеет более общий характер, чем законы коммутации.
Следует подчеркнуть, что некорректность коммутации возникает вследствие излишне упрощенного рассмотрения процесса коммутации или в результате применения чрезмерно упрощенных моделей элементов и может быть устранена при более строгом анализе.
Таким образом, термин «некорректная коммутация» является не вполне удачным: правильнее говорить не о некорректной коммутации, а о некорректной постановке задачи коммутации.
Пример 6.1.
Рассмотрим процесс зарядки конденсатора от гальванического элемента. Если использовать последовательные схемы замещения конденсатора и источника энергии (рис. 6.1, а), то переключение ключа S из положения 1 в положение 2 (или наоборот) является корректной коммутацией.
Действительно, пусть в исходном состоянии ключ находится в ,положении 1 и емкость С полностью разряжена, а в момент времени t = 0 ключ перебрасывается в положение 2. Если бы в результате коммутации напряжение та емкости возросло скачком, то в соответствии с компонентным уравнением емкости (1.13) ток цепи достиг бы бесконечно большого значения, что привело бы к .тому, что левая часть уравнения баланса напряжений для цепи, получающейся после коммутации не равнялась бы правой части.
Таким образом, предположение о том, что в рассматриваемой цепи нарушается второй закон коммутации, приводит к явно неправильному результату. Следовательно, в начальный момент времени после коммутации напряжение на емкости сохраняет то же значение, что и в момент времени, непосредственно предшествующий коммутации: а затем плавно увеличивается, стремясь в пределе к новому установившемуся значению, роемому э.д.с. источника напряжения (в установившемся режиме ток через емкость равен нулю, и из уравнения баланса напряжений следует, что = Е).
Если в исходном состоянии ключ находится в положении 2, а емкость С заряжена до напряжения Е, то при перебросе ключа в положение 1 напряжение на емкости в начальный момент времени после коммутации сохраняет значение, которое было в момент времени, непосредственно предшествующий коммутации, напряжение на сопротивлении скачком становится равным — (0+) = —Е, а ток сопротивления скачком возрастает до значения (0+)= Затем напряжение и ток емкости плавно уменьшаются, стремясь в пределе к нулю.
Если упростить схему замещения конденсатора и исключить из нее последовательное сопротивление (рис. 6.1, б), то перевод ключа из положения 1 в положение 2 будет по-прежнему оставаться корректной коммутацией в то время, как перевод ключа из положения 2 в положение 1 — станет некорректной коммутацией (некорректность коммутации объясняется тем, что рассматриваемая схема замещения цепи не учитывает потерь энергии в конденсаторе и соединительных проводах, а также энергию, выделяющуюся вместе с искрой между контактами ключа. В зависимости от требуемой точности анализа необходимо либо принять, что напряжение на емкости скачком изменилось от одного установившегося значения до другого, либо применить более сложную схему замещения цепи с учетом ключа и соединительных проводников).
Если упрощать и далее схему замещения цепи (исключив из нее внутреннее сопротивление источника (рис. 6.1, в), то перевод ключа из одного положения в другое всегда будет представлять собой некорректную коммутацию.
Пример 6.2.
Рассмотрим идеализированную цепь (рис. 6.2). Пусть в исходном состоянии ключ S находится в положении 1, через индуктивность протекает постоянный ток а ток индуктивности равен нулю:
Если в момент времени t=0 ключ S перебросить из положения 1 в положение 2, то индуктивности окажутся включенными последовательно и их токи должны мгновенно уравняться (для соблюдения уравнения баланса токов). Очевидно, что такая коммутация некорректна, причем начальное значение тока индуктивностей после коммутации может быть определено из принципа непрерывности потокосцепления: откуда
При анализе такой цепи обычно принимается, что токи индуктивностей скачком изменяются до уровня а затем плавно увеличиваются, начиная с этого уровня, до установившегося значения
Можно убедиться, что энергия данной цепи непосредственно после коммутации
меньше, чем энергия, запасенная в индуктивности до коммутации:
причем разность между этими величинами равна энергии коммутационных потерь. Рассмотренная коммутация может быть сделана корректной, если при анализе принять во внимание конечное время коммутации, применить более точные модели индуктивных катушек, содержащие не только сопротивления потерь, но и паразитные емкости, и учесть явления, имеющие место в искре или дуге между контактами. Разумеется, учет этих явлений существенно усложняет анализ.
Общий подход к анализу переходных процессов
Задача анализа переходных процессов заключается в общем случае в определении мгновенных значений токов и напряжений всех или части ветвей электрической цепи в произвольный момент времени после коммутации. Для этого необходимо найти общее решение основной системы уравнений электрического равновесия цепи или системы уравнений электрического равновесия, составленной любым другим способом, при t> 0. Исключая из системы уравнений все неизвестные величины, кроме одной, получают дифференциальное уравнение цепи, составленное относительно этой величины. Таким образом, задача анализа переходных процессов может быть сведена к решению дифференциального уравнения цепи при t > 0. В частности, задача анализа переходных процессов в линейной инвариантной во времени цепи с сосредоточенными параметрами -ro порядка сводится к нахождению об
щего решения линейного неоднородного дифференциального уравнения -ro порядка вида (1.61).
Общее решение такого уравнения содержит v произвольных постоянных, для нахождения которых необходимо задать значения искомой функции у и ее — 1 первых производных в начальный момент времени после коммутации, т. е. при t = Эти величины определяют с помощью законов коммутации на основании анализа процессов, имеющих место в рассматриваемой цепи перед коммутацией. В результате анализа цепи до коммутации рассчитывают значения токов всех индуктивностей и напряжения всех емкостей в момент времени, непосредственно предшествующий коммутации. Далее, используя законы коммутации (в более общем случае — принцип непрерывности потокосцепления и электрического заряда цепи), находят значения токов индуктивностей и напряжений емкостей в начальный момент времени после коммутации. Очевидно, что для определения v начальных условий требуется применить законы коммутации к v независимо включенным реактивным элементам, т. е. к реактивным элементам, включенным таким образом, что их энергетическое состояние может быть задано независимо. Следовательно, порядок сложности цепи, равный порядку дифференциального уравнения цепи определяется числом независимо включенных реактивных элементов. Совокупность начальных значений токов независимо включенных индуктивностей и напряжений независимо включенных емкостей представляет собой независимые начальные условия цепи. Используя независимые начальные условия и уравнения электрического равновесия цепи после коммутации, находят зависимые начальные условия, т. е. значения токов и напряжений любых ветвей и их производных в момент времени t =
Если энергия, запасенная в цепи в момент времени, непосредственно предшествующий коммутации, равна нулю, то говорят, что цепь анализируется при нулевых начальных условиях. Если начальный запас энергии не равен нулю, то цепь анализируется при ненулевых начальных условиях (в первом случае все независимые начальные условия равны нулю, во втором случае хотя бы одно из них имеет ненулевое значение).
Следует обратить внимание на то, что независимые начальные условия, а следовательно, токи и напряжения ветвей цепи после коммутации определяются исходя из энергетического состояния цепи только в момент времени, непосредственно предшествующий коммутации (t = 0_), и не зависят от характера процессов, имеющих место в рассматриваемой цепи до коммутации (при ).
Определение порядка сложности цепи
В некоторых случаях порядок сложности электрической цепи v бывает желательно выяснить еще до составления уравнений электрического равновесия. Очевидно, что значение не может превышать общего числа реактивных элементов цепи В связи с тем что последовательно или параллельно включенные реактивные элементы одного типа не являются энергетически независимыми, при подсчете необходимо объединять такие элементы и заменять их эквивалентным элементом соответствующего типа.
Если в цепи имеется так называемый емкостный контур, т е. контур, образованный только емкостями и, может быть, независимыми источниками напряжения, то напряжение любой из емкостей такого контура выражают через напряжения других емкостей с помощью уравнения баланса напряжений, составленного для данного емкостного контура. Таким образом, наличие в цепи емкостного контура уменьшает на единицу число независимо включенных емкостей и снижает порядок сложности цепи.
Число независимо включенных индуктивностей снижается при наличии в цепи так называемого индуктивного сечения, т. е. сечения, в которое входят только индуктивности, и, может быть, независимые источники тока. Частным случаем индуктивного сечения является индуктивный узел (узел, к которому подключены только индуктивности и независимые источники тока). Ток, а следовательно, и энергия любой из индуктивностей, входящей в индуктивное сечение, могут быть выражены через токи других индуктивностей на основании уравнений баланса токов, составленного для данного сечения.
Если в состав цепи входит несколько емкостных контуров или индуктивных сечений, то при оценке числа независимо включенных реактивных элементов учитывают только независимые емкостные контуры и независимые индуктивные сечения, т. е. такие контуры и сечения, уравнения баланса напряжений и токов которых независимы.
Таким образом, порядок сложности линейной цепи, составленной только из идеализированных пассивных элементов и независимых источников тока или напряжения:
Где — общее число реактивных элементов; — число независимых емкостных контуров; — число независимых индуктивных сечений.
Следует иметь в виду, что порядок сложности цепи зависит также от соотношений между параметрами входящих в нее элементов, поэтому выражение (6.4) позволяет оценить только максимально возможное значение порядка сложности цепи (в том числе и цепи с управляемыми источниками).
Пример 6.3.
Определим порядок сложности цепи, схема которой приведена на рис. 6.3, а.
Преобразуя участки цепи, содержащие последовательно и параллельно включенные однотипные реактивные элементы (рис. 6.3, б), определяем общее число реактивных элементов цепи = 6. Рассматриваемая цепь содержит один емкостной контур, образованный емкостями и источником напряжения е, и одно индуктивное сечение (индуктивности поэтому порядок сложности данной цепи не может превышать четырех.
Классический метод анализа переходных процессов
Свободные и принужденные составляющие токов и напряжений:
Классический метод анализа переходных процессов в линейных инвариантных во времени цепях с сосредоточенными параметрами основан на классическом методе решения обыкновенных дифференциальных уравнений. Как известно, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами [см. (1.61)]
равно сумме частного решения этого уравнения и общего решения однородного дифференциального уравнения
которое получается из (1.61) при f(t) = 0.
Общее решение однородного дифференциального уравнения (6.5) характеризует так называемые свободные процессы в цепи, т. е. процессы в цепи после коммутации в отсутствие внешних источников энергии (напомним, что функция f (t) обращается в нуль при выключении всех независимых источников тока и напряжения).
Таким образом, характер свободных процессов ие зависит от вида внешнего воздействия на цепь, а определяется только параметрами пассивных элементов и линейно управляемых источников, а также топологией цепи после коммутации.
Свободные процессы в цепи протекают за счет разности энергий, соответствующих установившимся режимам работы цепей до и после коммутации. В связи с тем что эта разность имеет конечное значение, свободные процессы в цепях с потерями с течением времени затухают (в идеализированных цепях без потерь свободные процессы имеют незатухающий характер).
Частное решение уравнения (1.61) определяет принужденный режим работы цепи, т.е. режим, задаваемый действующими в цепи независимыми источниками энергии.
Если внешнее воздействие иа цепь после коммутации изменяется по периодическому закону (сохраняет неизменное значение), то частное решение уравнения (1.61) характеризует установившийся режим цепи после коммутации.
Итак, при использовании классического метода анализа переходных процессов искомая реакция цепи у (ток или напряжение какойлибо ветви после коммутации) представляется в виде суммы свободной и принужденной составляющих:
Свободная составляющая реакции цепи с течением времени затухает поэтому принужденная составляющая реакции представляет собой установившееся значение искомого тока или напряжения после коммутации
Для определения принужденной составляющей реакции цепи можно воспользоваться рассмотренными ранее методами анализа линейных цепей в установившемся режиме. Если после коммутации токи всех независимых источников тока и напряжения всех независимых источников напряжения не изменяются, то с течением времени в цепи после коммутации установится режим постоянного тока. Очевидно, что принужденная составляющая реакции цепи в этом случае будет являться постоянным током или напряжением.
Если после коммутации цепь находится под гармоническим воздействием определенной частоты, то принужденная составляющая реакции цепи также будет гармонической функцией времени и для определения можно воспользоваться методом комплексных амплитуд.
Если цепь после коммутации находится под воздействием нескольких источников гармонических колебаний различной частоты, то, используя принцип наложения, мгновенное значение можно найти как сумму мгновенных значений частичных токов или напряжений, вызванных в установившемся после коммутации режиме каждым из источников в отдельности. Применяя принцип наложения, можно найти принужденную составляющую реакции цепи и тогда, когда внешнее воздействие на цепь х (t) описывается периодической функцией более сложного вида, удовлетворяющей условиям Дирихле, т. е. имеющей на конечном интервале конечное число максимумов и минимумов и конечное число разрывов первого рода. В этом случае Функция х (t) может быть разложена в ряд Фурье (представлена в виде суммы гармонических колебаний кратных частот), а мгновенное значение может быть найдено как сумма мгновенных значений частичных токов или напряжений, вызванных в установившемся после коммутации режиме каждой из гармонических составляющих внешнего воздействия в отдельности.
Для определения свободной составляющей реакции цепи необходимо найти корней характеристического уравнения
соответствующего однородному уравнению (6.5). Когда все корни уравнения (6.6) простые (различные), свободная составляющая реакции имеет вид
т. е. каждому простому корню соответствует слагаемое свободной составляющей вида
где —постоянная интегрирования.
Если какой-либо корень характеристического уравнения (6.6) имеет кратность n, то этому корню соответствует слагаемое свободной составляющей вида
Характеристическое уравнение (6.6) может иметь вещественные или комплексные корни, причем все корни характеристического уравнения линейной цепи, составленной из идеализированных пассивных элементов и независимых источников энергии, расположены в левой полуплоскости комплексного переменного р (включая и мнимую ось): так как только в этом случае свободные процессы в цепи имеют затухающий (точнее, ненарастающий) характер.
Общая схема применения классического метода анализа переходных процессов
Наметим основные этапы классического метода анализа переходных процессов в линейных инвариантных во времени цепях с сосредоточенными параметрами.
1. Анализ цепи до коммутации. В результате этого анализа определяют токи индуктивностей и напряжения емкостей в момент времени, непосредственно предшествующий коммутации (t= 0_).
2. Определение независимых начальных условий. Независимые начальные условия представляют собой токи индуктивностей и напряжения емкостей в момент времени (t = ). Независимые начальные условия находят с помощью законов коммутации или принципа непрерывности потокосцепления и электрического заряда цепи.
3. Составление дифференциального уравнения цепи после коммутации (при Дифференциальное уравнение цепи получают из системы уравнений электрического равновесия цепи, составленной любым методом, путем исключения всех неизвестных величин, кроме одной, представляющей собой Ток или напряжение какой-либо ветви.
4. Анализ установившегося процесса в цепи после коммутации (при В результате анализа установившегося процесса в цепи после коммутации находят принужденную составляющую реакции цепи (частное решение дифференциального уравнения цепи).
5. Определение свободной составляющей реакции цепи. На этом этапе составляют характеристическое уравнение цепи, находят его корни и определяют общий вид свободной составляющей реакции цепи (общее решение однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации).
6. Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального уравнения цепи) находят путем суммирования свободной и принужденных составляющих реакции цепи.
7. Определение постоянных интегрирования. Постоянные интегрирования находят по зависимым начальным условиям (значениям искомых токов или напряжений и их — 1 первых производных в начальный момент времени после коммутации). Для определения зависимых начальных условий используют независимые начальные условия и уравнения электрического равновесия цепи после коммутации.
8. Определение реакции цепи, соответствующей заданным начальным условиям. Подставляя постоянные интегрирования в общее решение дифференциального уравнения цепи после коммутации, находят частное решение дифференциального уравнения, соответствующее заданным начальным условиям, т. е. искомый ток или напряжение одной из ветвей при t>0.
Переходные процессы в последовательной RС-цепи при скачкообразном изменении э. д. с.
Рассмотрим переходные процессы в последователоной RС-цепи (рис. 6.4, а) при скачкообразном изменении э. д. с. идеализированного источника постоянного напряжения
Такое изменение э. д. с. источника напряжения происходит наприМеР, когда в цепи, схема которой приведена на рис. 6.4, б, ключ S в момент времени t = 0 перебрасывают из положения 1 в положение 2.
Очевидно, что в момент времени, непосредственно предшествовавший коммутации, напряжение на емкости равнялось напряжению на зажимах источника энергии при t 0 приведена на рис. 6.5, а. В этом случае ток индуктивности в момент времени, непосредственно предшествующий коммутации, (0_) = 0.
Дифференциальное уравнение цепи, составленное относительно тока при имеет вид
Принужденная составляющая тока может быть найдена с помощью метода комплексных амплитуд
где —модуль и аргумент комплексного входного сопротивления рассматриваемой цепи. Характеристическое уравнение цепи
имеет единственный корень = —R/L, поэтому свободная составляющая тока содержит один экспоненциальный член
где = L/R — постоянная времени последовательной RL-цепи.
Суммируя свободную и принужденную составляющие, находим общее решение дифференциального уравнения цепи (6.18) после коммутации:
Для определения постоянной интегрирования воспользуемся первым законом коммутации, в соответствии с которым начальное значение тока рассматриваемой цепи должно равняться нулю:
Подставляя (6.20) в выражение (6.19), получаем откуда
С учетом (6.21) выражение для тока рассматриваемой цепи после коммутации принимает вид
Характер переходных процессов зависит от соотношения между начальной фазой э. д. с. идеализированного источника напряжения и аргументом входного сопротивления цепи. Если выбирают таким образом, что начальные значения принужденной и свободной составляющих равны нулю то свободная составляющая тока тождественно равна нулю. Переходные процессы в цени в этом случае отсутствуют, т. е. установившийся режим наступает сразу же после коммутации. При или начальные значения свободной и принужденной составляющих максимальны, и отличие в форме кривых выражено наиболее резко (рис. 6.5, б).
Как и для последовательной RC-цепи, скорость затухания свободной составляющей тока рассматриваемой цепи не зависит от характера внешнего воздействия, а определяется только постоянной времени За промежуток времени t = свободная составляющая тока уменьшается в е раз и к моменту времени после коммутации переходные процессы в цепи можно считать практически закончившимися.
Подключение к последовательной RLC-цепи источника постоянного напряжения
Последовательная RLС-цепь содержит два независимо включенных реактивных элемента, поэтому процессы в ней описываются дифференциальным уравнением второго порядка, а для определения постоянных интегрирования необходимо задать два независимых начальных условия. Если э. д. с. идеального источника напряжения изменяется во времени по закону
то независимые начальные условия цепи имеют нулевые значения
Составим уравнение электрического равновесия цепи по методу токов ветвей
Дифференцируя правую и левую части (6.23), получаем дифференциальное уравнение рассматриваемой цепи после коммутации
Для определения единственного решения этого уравнения, соответствующего заданному режиму работы цепи до коммутации, необходимо определить начальные значения тока цепи и его первой производной по времени. Начальное значение тока цепи совпадает с начальным значением тока индуктивности
а начальное значение первой производной тока цепи по времени может быть найдено с использованием независимых начальных условий (6.22) и уравнения электрического равновесия цепи (6.23) при
В связи с тем что установившееся значение тока этой цепи после коммутации равно нулю, ток при содержит только свободную составляющую:
Характеристическое уравнение последовательной RLC-цепи
имеет два корня
где – коэффициент затухания; – резонансная частота цепи. В зависимости от соотношения между величинами и или, что то же самое, в зависимости от добротности цепи,
корни характеристического уравнения (6.27) могут быть вещественными различными, комплексно-сопряженными или вещественными одинаковыми (кратными). Рассмотри каждый из этих случаев.
Вещественные различные корни. При малой добротности последовательной RLC-цепи (Q 2p) характеристическое уравнение (6.27) имеет два различных вещественных отрицательных корня, а выражение для тока цепи после коммутации содержит два экспоненциальных члена:
Дифференцируя правую и левую части выражения (6.29)
и используя зависимые начальные условия (6.25), (6.26), составляем уравнения для определения постоянных интегрирования и откуда
С учетом (6.30) выражение для тока цепи после коммутации принимает вид
Расположение корней характеристического уравнения в плоскости комплексного переменного р и зависимость нормированного тока рассматриваемой цепи от времени
приведены на рисунке 6.6,а. Переходный процесс в цепи носит апериодический (неколебательный) характер, причем вследствие того, что вторая составляющая нормированного тока цепи затухает быстрее, чем первая
Комплексно-сопряженные корни добротности последовательной RLС-цепи (Q> 1/2, т. е. R внешнего воздействия близка к частоте свободных колебаний, а добротность Q настолько велика, что практически совпадает с резонансной частотой цепи С учетом этих допущений, которые незначительно уменьшают общность получаемых результатов, выражение (6.41) существенно упрощается:
Таким образом, в последовательной 7?£С-цепи, удовлетворяющей принятым допущениям, свободная составляющая тока является затухающей гармонической функцией времени. В начальный момент времени амплитуда свободной составляющей тока равна амплитуде принужденной составляющей, а затем уменьшается по экспоненциальному закону. Через промежуток времени, равный после коммутации, амплитуда свободной составляющей становится пренебрежительно малой по сравнению с амплитудой принужденной составляющей, и переходной процесс в цепи можно считать практически закончившимся.
Ток цепи после коммутации равен сумме свободной и принужденной составляющих:
Если частота внешнего воздействия в точности совпадает с резонансной частотой цепи озо, то входное сопротивление цепи имеет чисто резистивный характер и выражение (6.42) принимает вид (рис. 6.7, а)
Как видно из рисунка, амплитуда тока цепи при плавно увеличивается во времени, стремясь в пределе к установившемуся значению Ни при каких значениях t амплитуда тока после коммутации не превышает этого значения.
При включении в последовательную RLС-цепь источника гармонического напряжения, частота которого близка к резонансной, но не равна ей, в цепи наблюдаются биения, заключающиеся в периодическом увеличении амплитуды тока или напряжения до значения, значительно превышающего амплитуду принужденной составляющей (рис. 6.7, б). Если пренебречь затуханием свободной составляющей тока то из выражения (6.42) получаем
Как видно из этого выражения, ток цепи имеет частоту, близкую к резонансной, а амплитуда тока медленно изменяется во времени:
причем максимальное значение тока в переходном режиме в два раза превышает амплитуду принужденной составляющей.
Возникновение биений при включении источника гармонического напряжения в последовательную RLC-цепь объясняется тем, что вследствие несовпадения частот внешнего воздействия и свободных колебаний фазовые соотношения между свободной и принужденной составляющими тока непрерывно изменяются, а разность мгновенных фаз этих колебаний линейно нарастает во времени. В те моменты времени, когда разность мгновенных фаз будет равна где k = 0,1, 2, . сумма мгновенных значений будет максимальна, а в те моменты времени, когда разность фаз будет равна — минимальна. Частотой биений называют частоту повторения максимумов огибающей тока (6.45). Угловая частота биений, таким образом, равна абсолютному значению разности угловых частот свободной и принужденной составляющей
В реальных колебательных контурах коэффициент затухания имеет малое, но конечное значение. Свободная составляющая тока в таких контурах экспоненциально уменьшается во времени, а биения носят затухающий характер.
Операторный метод анализа переходных процессов
Преобразование Лапласа и его применение к решению дифференциальных уравнений:
Классический метод анализа переходных процессов применяют в основном тогда, когда исследуемая цепь имеет невысокий порядок сложности, а внешнее воздействие на нее после коммутации является гармонической функцией времени либо постоянно. Если внешнее воздействие на цепь после коммутации имеет более сложный характер, то определение принужденной составляющей реакции цепи существенно затруднено, а при повышении порядка цепи усложняется определение постоянных интегрирования. Значительно большие возможности представляет операторный метод анализа переходных процессов, основанный на применении преобразования Лапласа. Подобно ранее рассмотренному методу комплексных амплитуд, операторный метод относится к символическим методам, в которых операции над функциями времени заменяются операциями над их символами (изображениями). Взаимное соответствие между функцией времени a (t) и ее изображением А (р) в операторном методе устанавливается с помощью прямого
преобразований Лапласа и указывается знаком соответствия
Функция А (р) называется операторным изображением функции а (t) или изображением функции р (t) по Лапласу. Исходная функция времени a (t) по отношению к своему операторному изображению является оригиналом. Комплексное число р будем называть оператором преобразования Лапласа или комплексной частотой (смысл последнего понятия будет пояснен в следующем параграфе).
Из курса высшей математики известно, что для функций а (t), равных нулю при t 0 и удовлетворяющих неравенству
где К и — некоторые постоянные числа, интеграл (6.46) абсолютно сходится при Re (р) > . Изображение А (р) в полуплоскости Re (р) > является аналитической функцией р, которая стремится к нулю при Re(p) На практике к интегрированию по формулам (6.46), (6.47) приходится прибегать сравнительно редко, так как для большинства часто употребляемых функций разработаны таблицы прямого и обратного преобразований Лапласа [6, 7]. Операторные изображения некоторых функций приведены в приложении 1. Следует иметь в виду, что в ряде справочников, в частности в [6], приведены таблицы преобразовании Карсона—Хевисайда
которое отличается от преобразования Лапласа только наличием множителя р.
Напомним некоторые свойства преобразования Лапласа. Изображение по Лапласу постоянной величины К равно этой величине, деленной на р:
Умножение функции времени а (t) на постоянное число К соответствует умножению на это же число ее изображения:
Изображение суммы функций времени равно сумме изображений этих функций:
где
Если начальное значение функции a (t) равно нулю а = 0, то дифференцированию функции а (y) соответствует умножение изображения этой функции на р (теорема дифференцирования)
при
Повторным применением теоремы дифференцирования, можно выражения для производных высших порядков:
Интегрированию функции времени в пределах от 0 до t соответствует деление изображения этой функции на р (теорема интегрирования:
смещению функции времени на соответствует умножение изображения на (теорема запаздывания):
а смещению изображения А (р) в комплексной плоскости на комплексное число соответствует умножение оригинала на (теорема смещения):
Значения функции времени при t = 0 и t = могут быть найдены с помощью предельных соотношений
предполагается, что соответствующие пределы существуют).
Если изображение А (р) может быть представлено в виде отношения двух полиномов от р, не имеющих общих корней:
причем степень полинома М (р) выше, чем степень полинома N (р), а уравнение
не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться теоремой разложения
где — корни уравнения (6.56).
Теорема разложения может быть сформулирована также для случая, когда уравнение (6.56) имеет кратные корни, и может быть распространена на случай, когда А (р) является произвольной мероморфной функции р, т. е. функцией, не имеющей иных особых точек, кроме полюсов [7].
Как известно, преобразование Лапласа лежит в основе операторного метода решения линейных дифференциальных уравнений, разработанного в середине прошлого века русским математиком М. Е. Ващенко-Захарченко. Независимо, но значительно позднее известный английский ученый О. Хевисайд применил операторный метод к анализу переходных процессов в электрических цепях с сосредоточенными и распределенными параметрами. Значительный вклад в развитие и обоснование операторного метода внесли советские ученые К. А. Круг, В. С. Игнатовский, А. М. Эфрос, А. М. Данилевский, А. И. Лурье, М.И. Конторович и зарубежные ученые Д. Р. Карсон, Я. Минусинский, Б. ван дер Поль, П. Леви.
При использовании операторного метода решения дифференциальных уравнений неизвестные токи и напряжения ветвей электрической цепи, а также заданные токи и напряжения независимых источников заменяют их операторными изображениями. При этом система интегродифференциальных уравнений электрического равновесия, составленная относительно мгновенных значений токов и напряжений ветвей, преобразуется в систему алгебраических уравнений, составленных относительно операторных изображений соответствующих токов и напряжений. Решая эту систему уравнений, можно найти изображения искомых токов и напряжений ветвей электрической цепи после коммутации. Далее, применяя обратное преобразование Лапласа, можно перейти от изображений искомых токов и напряжений к оригиналам.
Уравнения электрического равновесия цепи в операторной форме. Операторные схемы замещения идеализированных двухполюсных элементов
Итак, используя преобразование Лапласа, каждому уравнению, входящему в систему уравнений электрического равновесия цепи, можно поставить в соответствие уравнение, составленное относительно операторных изображений токов и напряжений. Уравнениям баланса мгновенных значений токов и напряжений соответствуют уравнения баланса операторных изображений токов и напряжений, а компонентным уравнениям, описывающим соотношения между мгновенными значениями токов и напряжений отдельных ветвей, соответствуют уравнения, связывающие операторные изображения токов и напряжений тех же ветвей. Вследствие того что изображение суммы функций времени равно сумме изображений этих функций (6.50), для перехода от уравнений баланса мгновенных значений токов и напряжений ветвей к уравнениям баланса операторных изображений токов и напряжений достаточно в уравнениях (1.37), (1.40) заменить мгновенные значения токов и напряжений их операторными изображениями
Если уравнения баланса напряжений формировались относительно мгновенных значений напряжений отдельных элементов (1.42), то в операторной форме эти уравнения принимают вид
Уравнения (6.58) и (6.59) или (6.60) будем называть уравнениями баланса токов и напряжений в операторной форме, а операторные изображения токов и напряжений— операторными токами и напряжениями.
По аналогии с ранее рассмотренными понятиями комплексного входного сопротивления и комплексной входной проводимости введем понятия операторного входного сопротивления Z (р) и операторной входной проводимости Y (р).
Операторным входным сопротивлением пассивного линейного двухполюсника называется отношение операторного напряжения на входе двухполюсника к операторному току при нулевых начальных условиях
где — операторные изображения тока и напряжения на входе некоторого пассивного двухполюсника при и нулевых начальных условиях.
Величина, обратная Z (р), называется операторной входной проводимостью
Операторное входное сопротивление и операторная входная проводимость пассивного линейного двухполюсника, подобно его комплексному входному сопротивлению и комплексной входной проводимости, не зависят от интенсивности внешнего воздействия и определяются только параметрами входящих в двухполюсник идеализированных пассивных элементов и схемой их соединения.
Как следует из выражений (6 .61), (6.62), каждому пассивному линейному двухполюснику при нулевых начальных условиях может быть поставлена в соответствие операторная схема замещения, на которой рассматриваемый двухполюсник представляется своим операторным входным сопротивлением или операторной входной проводимостью, а токи и напряжения на его зажимах — их операторными изображениями. Если в рамках решаемой задачи двухполюсник не находится при нулевых начальных условиях, то его операторная эквивалентная схема должна содержать независимый источник тока или напряжения, характеризующий начальные запасы энергии в цепи.
Рассмотрим операторные компонентные уравнения и операторные схемы замещения идеализированных пассивных двухполюсников.
Сопротивление. Соотношения между мгновенными значениями тока и напряжения на зажимах сопротивления устанавливаются выражениями (1.9), (1.10):
Учитывая, что умножению функции времени на постоянное число соответствует умножение изображения функции на это же число (6.49), получения компонентных уравнений сопротивления в операторной форме достаточно в выражениях (1.9), (1.10) заменить мгновенные значения токов и напряжений их операторными изображениями
Подставляя соотношения (6.63), (6.64) в (6.61), (6.62), находим выражения для операторного входного сопротивления и операторной входной проводимости
Операторная эквивалентная схема сопротивления приведена на рис. 6.8.
Емкость. Напряжение и ток емкости связаны соотношениями (1.13), (1.16):
Используя теоремы дифференцирования (6.52) и интегрирования (6.53), получаем
Операторные компонентные уравнения емкости (6.66) и (6.67) являются равносильными и могут быть получены одно из другого. При нулевых начальных условиях они принимают вид
Таким образом, операторное входное сопротивление (p) и операторная входная проводимость емкости (р) определяются выражениями
Операторным компонентным уравнениям (6.66) и (6.67) соответствуют параллельная и последовательная схемы замещения емкости (рис. 6.9, а, б), содержащие независимый источник тока или напряжения . При нулевых начальных условиях независимые источники тока или напряжения, характеризующие начальный запас энергии в емкости, выключаются, и в операторной эквивалентной схеме емкости остается только один элемент — операторное входное сопротивление или операторная входная проводимость емкости (рис. 6.9 в).
Индуктивность. Мгновенные значения тока и напряжения индуктивности связаны между собой соотношениями (1.22) и (1.23):
Применяя к этим выражениям теоремы дифференцирования (6.52) и интегрирования (6.53), получаем компонентные уравнения индуктивности в операторной форме:
Уравнения (6.69), (6.70) равносильные и могут быть получены одно из другого с помощью элементарных преобразований. Используя их, определяем комплексное входное сопротивление и комплексную входную проводимость индуктивности
и строим ее последовательную и параллельную схемы замещения (рис. о. 10, а, б). Как и операторные схемы замещения емкости, операторные схемы замещения индуктивности содержат независимый источник напряжения или тока характеризующий начальный запас энергии в индуктивности. Операторная эквивалентная схема индуктивности при нулевых начальных условиях приведена на рис. 6.10, в.
Анализируя полученные результаты, нетрудно установить, что выражения для операторных входных сопротивлений (проводимостей) идеализированных пассивных элементов имеют такую же структуру, как и выражения для комплексных входных сопротивлений (проводимостей) этих же элементов, и могут быть получены одно из другого путем замены на р.
Аналогичным образом может быть получено выражение для операторного входного сопротивления (проводимости) произвольного линейного двухполюсника, составленного из идеализированных пассивных
элементов. Поэтому для преобразования операторных схем замещения линейных пассивных двухполюсников при нулевых начальных условиях можно использовать все рассмотренные ранее (см. гл. 2) правила преобразования линейных пассивных цепей при гармоническом воздействии, а для преобразования операторных схем замещения тех же участков цепей при ненулевых начальных условиях — правила преобразования активных двухполюсников. В частности, последовательная и параллельная схемы замещения емкости или индуктивности могут быть преобразованы одна в другую с помощью рассмотренных ранее (см. гл. 2) приемов преобразования активных двухполюсников.
Используя операторные эквивалентные схемы идеализированных пассивных элементов, можно получить операторную эквивалентную схему произвольного участка линейной цепи или всей цепи в целом. С этой целью каждый идеализированный пассивный элемент, изображенный на эквивалентной схеме цепи для мгновенных значений, должен быть заменен операторной эквивалентной схемой, а токи и напряжения идеализированных источников тока или напряжения — представлены операторными изображениями соответствующих функций.
Операторная эквивалентная схема цепи имеет такую же структуру, как и эквивалентная схема цепи для мгновенных значений, но содержит дополнительные независимые источники энергии, определяющие запасы энергии цепи в момент времени, непосредственно предшествовавший коммутации.
Используя операторную схему замещения цепи, можно с помощью любого из известных методов сформировать систему уравнений ее электричесхого равновесия в операторной форме, которая будет равносильна основной системе уравнений электрического равновесия цпи после коммутации.
В связи с тем что операторная схема замещения цепи может быть построена непосредственно по эквивалентной схеме цепи для мгновенью значении, этап формирования дифференциальных уравнений цепи может быть исключен. Метод анализа переходных процессов в линейных цепях, основанный на формировании операаторных уравнений электрического равновесия цепей по их операторным эквивалентным схемам, получил название операторного метода анализа переходных процессов. Этот метод представляет собой дальнейшее развитие операторного метода решения дифференциальных уравнений и позволяе анализировать процессы в цепи после коммутации, минуя этап формирования уравнений электрического равновесия цепи для мгновенных значений токов и напряжений.
Общая схема применения метода
Наметим основные этапы анализа переходных процессов в линейных цепях с помощью операторного метода.
- Анализ цепи до коммутации и определение независимых начальных условий. Выполняются так же, как и при использовании классического метода анализа переходных процессов.
- Составление операторной эквивалентной схемы цепи после коммутации. Составление операторной эквивалентной схемы цепи производится непосредственно по эквивалентной схеме цепи для мгновенных значений путем замены каждого идеализированного пассивного элемента его операторной схемой замещения и представления токов и напряжений идеализированных источников тока или напряжения их операторными изображениями.
- Составление уравнений электрического равновесия цепи в операторной форме. Система уравнений электрического равновесия цепи в операторной форме может быть сформирована любым из рассмотренных в гл.4 методов непосредственно по операторной схеме замещения цепи.
- Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений. Может производиться любым методом, в том числе путем использования рассмотренного ранее метода сигнальных графов.
- Определение оригиналов искомых токов и напряжений. Как правило, производится путем применения таблиц обратного преобразования Лапласа [6] и использования основных свойств преобразования Лапласа. Если изображение интересующей функции представляет собой отношение двух полиномов р, для выполнения обратного преобразования Лапласа можно воспользоваться теоремой разложения.
Пример 6.4.
Для цепи, схема которой приведена на рис. 6.11, а, найдем зависимость тока и напряжения индуктивности от времени при Э.д.с. идеализированного источника постоянного напряжения е (t) при t = 0 скачком изменяется от
Анализируя процессы в цепи до коммутации, находим начальное значение тока индуктивности
Для построения операторной эквивалентной схемы цепи после коммутации (рис. 6.11, б) заменяем все идеализированные пассивные элементы их операторными схемами замещения, а э. д. с. идеализированного источника напряжения
— операторной э.д.с., Используя метод контурных токов, составляем систему уравнений электрического равновесия цепи в операторной форме
где
Решая эту систему уравнений, находим операторные изображения искомого тока
Преобразуем полученные выражения к такому виду, чтобы для выполнения обратного преобразования Лапласа можно было непосредственно воспользоваться таблицами, приведенными в приложении 1:
Учитывая, что получаем .выражения для искомых тока и напряжения индуктивности при
где — постоянная времени рассматриваемой цепи. Как видно из полученных соотношений, в начальный момент времени ток индуктивности сохраняет то же значение, что и до коммутации а затем плавно изменяется, стремясь в пределе к Напряжение индуктивности в начальный момент времени скачком изменяется от нуля до и а затем плавно уменьшается до нуля.
Нетрудно заметить, что в начальный момент времени (t = ток и напряжение индуктивности принимают такие значения, которые они имели бы в случае, если индуктивность была заменена идеализированным источником тока (рис. 6.11, в), ток которого равен
Таким образом, в начальный момент после коммутации индуктивность ведет себя подобно идеализированному источнику тока (при нулевых начальных условиях ток этого источника равен нулю, и, следовательно, ветвь, содержащую индуктивность, в начальный момент времени можно считать разомкнутой).
Операторные характеристики линейных цепей
Реакция цепи на экспоненциальное воздействие:
Выясним, какой физический смысл имеет оператор р, входящий в выражения для операторных сопротивлений и проводимостей. С этой целью найдем реакцию цепи на экспоненциальное внешнее воздействие
где — некоторые комплексные числа.
Коэффициент имеет размерность внешнего воздействия и называется обобщенной комплексной амплитудой, величина – имеет размерность и называется обобщенной (комплексной) частотой.
Заметим, что многие встречающиеся на практике внешние воздействия можно рассматривать как частный случай экспоненциального воздействия или как сумму некоторого их количества. Действительно, при выражение (6.72) описывает экспоненциально затухающее экспоненциально нарастающее или неизменное внешнее воздействие. Сумма экспоненциальных воздействий с комплексно-сопряженными амплитудами и комплексно-сопряженными частотами представляет собой гармоническое колебание
амплитуда которого нарастает , затухает или неизменна во времени . Как видно из выражения (6.73), мнимую часть комплексной частоты можно рассматривать как угловую частоту некоторого гармонического колебания, а вещественную часть— как коэффициент, определяющий характер изменения огибающей этого колебания. Вследствие того что интегрирование и дифференцирование экспоненциальной функции не изменяют ее вида, реакция линейной цепи на экспоненциальное внешнее воздействие определенной комплексной частоты является экспоненциальной функцией той же частоты, причем отношение реакции цепи к внешнему воздействию в этом случае не зависит от времени.
Пусть напряжение, приложенное к зажимам идеализированного пассивного элемента изменяется во времени по закону
В этом случае ток сопротивления
и ток индуктивности
Входным сопротивлением пассивного линейного двухполюсника при экспоненциальном внешнем воздействии называется отношение мгновенного значения напряжения на зажимах этого двухполюсника к мгновенному значению тока:
Используя выражения (6.74) — (6.78), найдем входные сопротивления идеализированных пассивных элементов при экспоненциальном внешнем воздействии
Полагая в выражениях (6.79) получаем рассмотренные ранее выражения для операторных входных сопротивлений идеализированных пассивных элементов, а полагая — выражения для комплексных входных сопротивлений тех же элементов при гармоническом внешнем воздействии. Таким образом, комплексные сопротивления идеализированных пассивных элементов при гармоническом внешнем воздействии численно равны входным сопротивлениям тех же элементов при экспоненциальном внешнем воздействии а операторные входные сопротивления рассматриваемых элементов — входному сопротивлению этих элементов при экспоненциальном внешнем воздействии
Следовательно, оператор преобразования Лапласа р, входящий в выражения для операторных входных сопротивлений и проводимостей идеализированных пассивных элементов, можно рассматривать как обобщенную (комплексную) частоту экспоненциального воздействия вида (6.80).
Переходя от идеализированных пассивных элементов к участкам цепей, составленным из таких элементов, и, далее, к произвольным линейным цепям, убеждаемся, что отношение двух любых токов или напряжений этих цепей при экспоненциальном внешнем воздействии вида (6.80) численно равно отношению операторных изображений соответствующих токов или напряжений при нулевых начальных условиях.
Понятие об операторных характеристиках
Рассмотрим идеализированную линейную цепь, не содержащую независимых источников тока и напряжения, у которой выделены пара входных v — v’ и пара выходных k — k’ зажимов.
Операторной, или обобщенной, частотной характеристикой линейной цепи называется отношение операторного изображения реакции цепи к операторному изображению внешнего воздействия при нулевых начальных условиях:
где
Учитывая, что отношение двух любых токов и напряжений линейной цепи, находящейся под экспоненциальным воздействием, численно равно отношению операторных изображений соответствующих величин при нулевых начальных условиях, устанавливаем, что операторная характеристика линейной цепи численно равна отношению реакции цепи к внешнему воздействию при внешнем воздействии вида (6.80)
Для перехода от операторной характеристики цепи к ее комплексной частотной характеристике достаточно в выражении (6.81) заменить р на Следовательно, комплексную частотную характеристику можно рассматривать как частный случай обобщенной частотной характеристики при
Подобно комплексной частотной характеристике, операторная характеристика линейной цепи не зависит от действующих в цепи токов и напряжений, а определяется только топологией цепи и параметрами входящих в нее элементов. В связи с тем что выражения для операторных сопротивлений и проводимостей идеализированных пассивных элементов (6.65), (6.68), (6.71) были получены безотносительно к виду внешнего воздействия, операторные характеристики описывают свойства линейных цепей при произвольных внешних воздействиях.
Как и комплексные частотные характеристики, операторные характеристики цепи делятся на входные и передаточные, причем каждой комплексной частотной характеристике соответствует операторная. В зависимости оттого, какая величина выступаете качестве внешнего воздействия на цепь, а какая рассматривается в качестве отклика цепи, различают:
операторное входное сопротивление
операторную входную проводимость
операторные коэффициенты передачи по напряжению
операторное передаточное сопротивление
и операторную передаточную проводимость
Операторные коэффициенты передачи по напряжению и току являются безразмерными величинами, операторные входное и передаточное сопротивления имеют размерность сопротивления, а операторные входная и передаточная проводимости — размерность проводимости.
Определение операторных характеристик
Для определения операторной характеристики цепи с заданной комплексной частотной характеристикой достаточно в соответствующем аналитическом выражении заменить на р. В общем случае выражения для любых операторных характеристик сколь угодно сложной линейной цепи, не содержащей независимых источников энергии, могут быть получены из рассмотрения узловых или контурных уравнений цепи, составленных по ее операторной схеме замещения при нулевых начальных условиях.
Пусть необходимо найти операторные входное сопротивление и входную проводимость цепи со стороны зажимов v — v’. Подключим к этим зажимам идеализированный источник напряжения (t) и построим операторную схему замещения цепи при нулевых начальных условиях. Выбирая систему независимых контуров таким образом, чтобы ветвь, содержащая источник явилась главной ветвью v-гo контура, составим систему контурных уравнений цепи в операторной форме. Далее, используя формулы Крамера (4.14), найдем ток v-й ветви, совпадающий с током v-гo контура:
Здесь — определитель системы контурных уравнений, составленных в операторной форме; — алгебраическое дополнение элемента
Используя выражение (6.88), находим операторное входное сопротивление и операторную входную проводимость цепи со стороны зажимов v — v’:
Аналогичным образом можно найти и передаточные функции цепи. С этой целью, используя (4.14), определяем ток
ветви, содержащей сопротивление и являющейся главной ветвью k-го контура. Далее, подставляя выражения (6.88), (6.89), (6.90) в (6.84) — (6.87), находим операторный коэффициент передачи цепи по напряжению
операторный коэффициент передачи по току
операторную передаточную проводимость
и операторное передаточное сопротивление
В связи с тем что определитель представляют собой полиномы от собственных и взаимных операторных сопротивлений независимых контуров цепи, а сопротивления контуров являются рациональными функциями р с вещественными коэффициентами, любая операторная характеристика линейной электрической цепи не содержащей независимых источников энергии, также является рациональной функцией р с вещественными коэффициентами, т. е. может быть представлена в виде отношения двух полиномов
Здесь — вещественные коэффициенты, значения которых опре деляются параметрами идеализированных пассивных элементов и управляемых источников.
Напомним, что значения аргумента при которых N (р) = О, называются нулями, а значения аргумента при которых М (р) = 0, — полюсами функции Решая уравнения N (р) = 0; М (р) = 0 и разлагая полиномы N (р) и М (р) на множители, выражение (6.91) можно преобразовать к виду
Здесь — вещественное число, называемое масштабным коэффициентом.
Из выражения (6.92) следует, что нули и полюсы функции определяют значения этой функции с точностью до постоянного коэффициента K. Зная расположение нулей и полюсов операторной характеристики цепи в плоскости комплексной частоты р, можно получить полную информацию о свойствах этой цепи, в частности с точностью до постоянного множителя найти реакцию цепи на заданное воздействие. Графическое изображение расположения нулей и полюсов функции в плоскости комплексной частоты называется диаграммой нулей и полюсов или полюсно-нулевой диаграммой функции. При пoстроении полюсно-нулевых диаграмм мнимую и вещественную оси плоскости р обозначают соответственно нули изображают кружками, а полюсы — крестиками.
Пример 6.5.
Для цепи, схема которой приведена на рис. 3.12, а, найдем операторное входное сопротивление со стороны зажимов 1—1′ и операторный коэффициент передачи по напряжению от зажимов 1—1′ к зажимам 2—2′ в режиме холостого хода на зажимах 2—2′. Построим диаграммы нулей и полюсов функций
Ранее были получены выражения для комплексного входного сопротивления (3.12) и комплексного коэффициента передачи (3.16) данной цепи
Заменяя в этих выражениях на р, находим операторное входное сопротивление и операторный коэффициент передачи цепи по напряжению:
Можно убедиться, что аналогичные результаты получаются и при рассмотрении операторной схемы замещения цепи (рис. 6.12, а).
Полюсно-нулевые диаграммы функций изображены на рис. 6.12, б,в соответственно. Функция имеет один нуль = —RL, функция имеет один нуль = 0 и один полюс v = — R/L.
Пример 6.6.
Найдем операторное входное сопротивление последовательного колебательного контура (см. рис. 3.21, а) в режиме холостого хода на выходе. Построим полюсно-нулевую диаграмму функции .
Операторное входное сопротивление последовательного колебательного контура равно сумме операторных сопротивлений входящих в контур элементов
Используя введенные ранее обозначения запишем выражение для операторного входного сопротивления контура в виде
В зависимости от соотношения между величинами операторное входное сопротивление может иметь два различных вещественных нуля
два одинаковых вещественных нуля
или два комплексно-сопряженных нуля
Во всех случаях функция имеет один полюс
Диаграммы нулей и полюсов функции для изображены на рис. 6.13, а, б, в соответственно. Очевидно, что нули функции являются полюсами функции а полюсы — нулями
Из примеров 6.5 и 6.6 видно, что нули операторного входного сопротивления цепи (полюсы операторной входной проводимости) совпадают с корнями характеристического уравнения, определяющего характер свободных процессов в цепи. Этот результат имеет весьма общий характер и позволяет находить корни характеристического уравнения по выражению для входного сопротивления (входной проводимости) цепи, не прибегая к составлению дифференциального уравнения.
Временные характеристики линейных цепей
Единичные функции и их свойства:
Важное место в теории линейных цепей занимает исследование реакции этих цепей на идеализированные внешние воздействия, описываемые так называемыми единичными функциями.
Единичной ступенчатой функцией (функцией Хевисайда) называется функция
При = 0 для единичной ступенчатой функции используют обозначение l (t) (рис. 6.14, б). График функции l (t— ) имеет вид ступеньки или скачка, высота которого равна l (рис. 6.14, а). Скачок такого типа будем называть единичным. Функцию Хевисайда
l удобно использовать для аналитического представления различных внешних воздействий на цепь, значение которых скачкообразно изменяется в момент коммутации:
где f (t) — ограниченная функция времени.
При подключении цепи к источнику постоянного тока или напряжения значение внешнего воздействия на цепь
где — момент коммутации.
Внешнее воздействие такого вида называется неединичным скачком. Используя функцию Хевисайда, выражение (6.95) можно представить в виде
Если при t = в цепь включается источник гармонического тока или напряжения
то с использованием функции l (t — внешнее воздействие на цепь можно представить в форме
Если внешнее воздействие на цепь в момент времени t = скачкообразно изменяется от одного фиксированного значения до другого то
Внешнее воздействие на цепь, имеющее форму прямоугольного импульса высотой X и длительностью (рис. 6.15, а), можно представить в виде разности двух одинаковых скачков
сдвинутых во времени на (рис. 6.15, б, в):
Рассмотрим прямоугольный импульс длительностью и высотой 1/ (рис. 6.16, а). Очевидно,что площадь этого импульса равна 1 и не зависит от . При уменьшении длительности импульса его высота возрастает, причем при она стремится к бесконечности, но площадь остается равной 1. Импульс бесконечно малой длительности, бесконечно большой высоты, площадь которого равна 1 будем называть единичным импульсом. Функция, определяющая единичный импульс, обозначается и называется –функцией или функцией Дирака.
При = 0 для -функции используется обозначение (t). При построении временных диаграмм функции и (t) будем изображать в виде вертикальной стрелки со значком оо около острия (рис.6.16, б, в).
Для установления связи между -функцией и единичной ступенчатой функцией воспользуемся выражением (6.96). Полагая X = 1/ и устремляя к нулю, получаем
Таким образом, -функция представляет собой производную от единичной ступенчатой функции, а единичная ступенчатая функция — интеграл от -функции.
Строгое обоснование операций над единичными функциями, в том числе операции дифференцирования единичной ступенчатой функции, дано в теории обобщенных функций. Для качественного обоснования таких операций функции и 6 удобно рассматривать в качестве предельных значений некоторых более простых функций, для которых соответствующие операции являются определенными. Рассмотрим, например, функцию (t) (рис. 6.17, а), удовлетворяющую условиям
Производная функция (t) по времени (рис. 6.17, б) имеет вид прямоугольного импульса длительностью и высотой 1/:
При функция (t) вырождается в единичную ступенчатую функцию, а функция — в -функцию:
откуда непосредственно следует, что
При выполнении различных операций над единичными функциями момент коммутации удобно расчленять на три различных момента: _ момент времени, непосредственно предшествовавший коммутации
— собственно момент коммутации и —момент времени, следующий непосредственно после коммутации. С учетом этого интеграл (6.98) можно заменить на
Произведение произвольной ограниченной функции времени f(t) на 6
Из выражений (6.102) и (6.103) следует, что интеграл от произведения произвольной ограниченной функции f (t) на равен либо значению этой функции при (если точка принадлежит интервалу интегрирования), либо нулю (если не принадлежит интервалу интегрирования):
Таким образом, с помощью -функции можно выделять значения функции f (t) в произвольные моменты времени Эту особенность – функции обычно называют фильтрующим свойством.
Для определения реакции линейных электрических цепей на внешнее воздействие в виде единичного скачка или единичного импульса необходимо найти изображения единичных функций по Лапласу. Используя рассмотренные свойства единичных функций, получаем
При операторные изображения единичных функций имеют простой вид:
Переходная и импульсная характеристики линейных цепей
Рассмотрим линейную электрическую цепь, не содержащую независимых источников тока и напряжения. Пусть внешнее воздействие на Цепь представляет собой неединичный скачок а реакция цепи на это воздействие при нулевых начальных условиях
Переходной характеристикой линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие неединичного скачка тока или напряжения к высоте этого скачка при нулевых начальных условиях:
Из выражения (6.107) видно, что если X =1, следовательно, переходная характеристика цепи численно равна реакции цепи на воздействие единичного скачка тока или напряжения. Размерность переходной характеристики равна отношению размерности отклика к размерности внешнего воздействия, поэтому переходная характеристика может иметь размерность сопротивления, проводимости или быть безразмерной величиной.
Пусть внешнее воздействие на цепь имеет форму бесконечно короткого импульса бесконечно большой высоты и конечной площади
Реакцию цепи на это воздействие при нулевых начальных условиях обозначим
Импульсной характеристикой ) линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие бесконечно короткого импульса бесконечно большой высоты и конечной площади к площади этого импульса при нулевых начальных условиях:
Как следует из выражения (6.108), импульсная характеристика цепи численно равна реакции цепи на воздействие единичного импульса = 1), а размерность импульсной характеристики равна отношению размерности отклика цепи к произведению размерности внешнего воздействия на время.
Подобно комплексной частотной и операторной характеристикам цепи, переходная и импульсная характеристики устанавливают связь между внешним воздействием на цепь и ее реакцией, однако в отличие от первых характеристик аргументом последних является время t, а не угловая или комплексная р частота. Так как характеристики цепи, аргументом которых является время , называются временными, а аргументом которых является частота (в том числе и комплексная) — частотными характеристиками, то переходная и импульсная характеристики относятся к временным характеристикам цепи.
Каждой операторной характеристике цепи можно поставить в соответствие переходную и импульсную характеристики. Для установления связи между ними найдем операторные изображения переходной и импульсной характеристик. Используя выражения (6.107), (6.108), запишем
Здесь — операторные изображения реакции цепи на внешние воздействия соответственно. Выражая через операторные изображения внешних воздействий получаем
При = 0 операторные изображения переходной и импульсной характеристик имеют простой вид
Таким образом, импульсная характеристика цепи — это функция, изображение которой, по Лапласу, представляет собой операторную характеристику цепи а переходная характеристика цепи — функция, операторное изображение которой равно Выражения (6.109), (6.110) устанавливают связь между частотными и временнйми характеристиками цепи. Зная, например, им. пульсную характеристику можно с помощью прямого преобразования Лапласа найти соответствующую операторную характеристику цепи
а по известной операторной характеристике с помощью обратного преобразования Лапласа определить импульсную характеристику цепи
Используя выражения (6.109) и теорему дифференцирования (6.51), нетрудно установить связь между переходной и импульсной характеристиками
Следовательно, импульсная характеристика цепи равна первой производной переходной характеристики по времени. В связи с тем что переходная характеристика цепи численно равна реакции цепи на воздействие единичного скачка напряжения или тока, приложенного к цепи с нулевыми начальными условиями, значения функции при равны нулю. Поэтому, строго говоря, переходную характеристику цепи следует записывать как а не Заменяя в выражении (6.111) на и используя соотношение (6.103), получаем
Выражение (6.112) известно под названием формулы обобщенной производной. Первое слагаемое в этом выражении представляет собой производную переходной характеристики при t> а второе слагаемое содержит произведение -функции на значение переходной характеристики в точке . Если при функция изменяется скачкообразно, то импульсная характеристика цепи содержит -функцию, умноженную на высоту скачка переходной характеристики в точке Если функция не претерпевает разрыва при т. е. значение переходной характеристики в точке равно нулю, то выражение для обобщенной производной совпадает с выражением для обычной производной.
Определение временных характеристик линейных цепей
Для определения переходных (импульсных) характеристик линейной цепи в общем случае необходимо рассмотреть переходные процессы, имеющие место в данной цепи при воздействии на нее единичного скачка (единичного импульса) тока или напряжения. Это может быть выполнено с помощью классического или операторного методов анализа переходных процессов. На практике для нахождения временных характеристик линейных цепей удобно использовать другой путь, основанный на применении соотношений, устанавливающих связь между частотными и временными характеристиками. Определение временных характеристик в этом случае начинается с составления операторной схемы замещения цепи для нулевых начальных условий. Далее, используя эту схему, находят операторную характеристику соответствующую заданной паре: внешнее воздействие на цепь — реакция цепи Зная операторную характеристику цепи и применяя соотношения (6.109) или (6.110), определяют искомые временные характеристики.
При качественном рассмотрении реакции линейной цепи на воздействие единичного импульса тока или напряжения переходной процесс в цепи разделяют на два этапа. На первом этапе (при [цепь находится под воздействием единичного импульса, сообщающего цепи определенную энергию. Токи индуктивностей и напряжения емкостей, при этом скачком изменяются на значение, соответствующее поступившей в цепь энергии. На втором этапе (при ) действие приложенного к цепи внешнего воздействия закончилось (при этом соответствующие источники энергии выключены, т. е. представлены внутренними сопротивлениями), и в цепи возникают свободные процессы, протекающие за счет энергии, запасенной в реактивных элементах на первой стадии переходного процесса. Таким образом, импульсная характеристика цепи, численно равная реакции на воздействие единичного импульса тока или напряжения, характеризует свободные процессы в рассматриваемой цепи. Следовательно, при переходе цепи от исходного состояния к первой стадии переходного процесса, законы коммутации не выполняются, а при переходе от первой стадии переходного процесса ко второй – выполняются.
Пример 6.7.
Для цепи, схема которой приведена на рис. 3.12, а, найдем переходную и импульсную характеристики в режиме холостого хода на зажимах 2 —2′. Внешнее воздействие на цепь — напряжение на зажимах 1 —1′ х (t)= реакция цепи — напряжение на зажимах 2—2′ у (t) =
Операторная характеристика данной цепи, соответствующая указанной паре’ внешнее воздействие на цепь — реакция цепи, была получена в примере 6.5:
Следовательно, операторные изображения переходной и импульсной характеристик цепи имеют вид
Используя таблицы обратного преобразования Лапласа (см. приложение 1), переходим от изображения искомых временных характеристик к оригиналам (рис. 6.18, а, б):
Заменяя в полученных выражениях t на t — находим временные характеристики цепи при
Отметим, что выражение для импульсной характеристики рассматриваемой цепи (t) могло быть получено и другим путем с помощью формулы (6.112), примененной к выражению для переходной характеристики цепи
Для качественного объяснения вида переходной и импульсной характеристик цепи в рассматриваемом включении, подсоединим к зажимам независимый источник напряжения е (t) = (рис. 6.18, в). Переходная характеристика данной цепи численно равна напряжению на зажимах при воздействии на цепь единичного скачка напряжения е (t) = 1 (t), В, и нулевых начальных условиях.
В начальный момент времени после коммутации сопротивление индуктивности бесконечно велико, поэтому при t – = 0 напряжение на выходе цепи равно напряжению на зажимах 1—1′:
С течением времени напряжение на индуктивности уменьшается, стремясь к нулю при Все это объясняет, почему переходная характеристика начинается от значения и стремится к нулю при
Импульсная характеристика цепи численно равна напряжению на зажимах при приложении к входу цепи единичного импульса напряжения
е (t) =
При все входное напряжение оказывается приложенным к индуктивности, и ток индуктивности скачком увеличивается от нуля до
При источник напряжения может быть заменен короткозамыкаюшей перемычкой, а ток индуктивности плавно уменьшается от до нуля. Напряжение на индуктивности равно напряжению на сопротивлении R, поэтому при выходное напряжение цепи изменяется от ) — R/L до нуля.
Применение принципа наложения для анализа переходных процессов в линейных цепях
Определение реакции цепи на произвольное внешнее воздействие:
Наиболее общий подход к анализу переходных процессов в линейных цепях основан на использовании принципа наложения. Внешнее воздействие на цепь х = х (t) в этом случае представляют в виде линейной комбинации однотипных элементарных составляющих
а реакцию цепи на такое воздействие ищут в виде линейной комбинации частичных реакций (t) на воздействие каждой из элементарных составляющих внешнего воздействия в отдельности:
В качестве элементарных составляющих (t) можно выбирать внешние воздействия, описываемые различными классами функций, реакция цепи на которые может быть найдена с помощью рассмотренных ранее методов. Наиболее широкое распространение получили элементарные (пробные) воздействия в виде гармонической функции времени, единичного скачка или единичного импульса.
Метод анализа переходных процессов в линейных цепях, основанный на представлении внешнего воздействия в виде конечной или бесконечной суммы гармонических функций времени, получил название спектрального.
Определение реакции цепи на произвольное внешнее воздействие по ее переходной характеристике
Рассмотрим произвольную линейную электрическую цепь, не содержащую независимых источников энергии, переходная характеристика которой (t) известна. Пусть внешнее воздействие на цепь задается в виде произвольной функции х = х (t), равной нулю при t
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://toehelp.ru/theory/toe/lecture24/lecture24.html
http://www.evkova.org/perehodnyie-protsessyi-v-elektricheskih-tsepyah-s-sosredotochennyimi-parametrami
[/spoiler]
2018-05-14
Найти зависимость от времени $t$ напряжения на конденсаторе $C$ (рис.) после замыкания в момент $t = 0$ ключа К.
Решение:
Пусть в любой момент времени заряд на пластинах равен $+ q$ и $-q$ соответственно, тогда напряжение на конденсаторе $phi = q / C$ (1)
Тогда $i = i_{1} + i_{2}$, где $i_{2} = frac{dq}{dt}$ (2)
В цепи 65146, используя $- Delta phi = 0$.
$frac{q}{C} + left ( i_{1} + frac{dq}{dt} right ) R – mathcal{E} = 0$ (3)
[используя (1) и (2)]
В цепи 25632, используя $- Delta phi = 0$
$- frac{q}{C} + i_{1}R = 0$ или $i_{1}R = frac{q}{C}$ (4)
Из (1) и (2),
$frac{dq}{dt} R = mathcal{E}_{1} – frac{2q}{C}$ или, $frac{dq}{ mathcal{E} – frac{2q}{C} } = frac{dt}{R}$ (5)
При интегрировании выражения (5) между подходящими пределами,
$int_{0}^{q} frac{dq}{ mathcal{E} – frac{2q}{C} } = frac{1}{R} int_{0}^{t}dt$ или, $- frac{C}{2} ln frac{ mathcal{E} – frac{2q}{C} }{ mathcal{E} } = frac{t}{R}$
Таким образом $frac{q}{C} = V = frac{1}{2} mathcal{E} (1 – e^{ – 2t/RC} )$
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
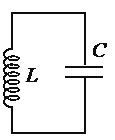
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
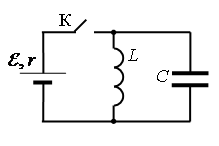
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
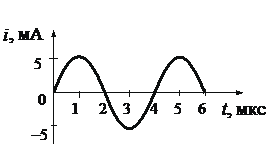
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.5k