Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Содержание
- Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
- Как найти время, зная скорость и расстояние?
- Как найти скорость, если известно время и расстояние?
- Как найти расстояние, если известно время и скорость?
- Единицы измерения
- График зависимости скорости тела от времени: фото
- Таблица 4 класс: скорость, время, расстояние
- Примеры решения задач на скорость, время, расстояние за 4 класс
- ВИДЕО: Задачи на движение
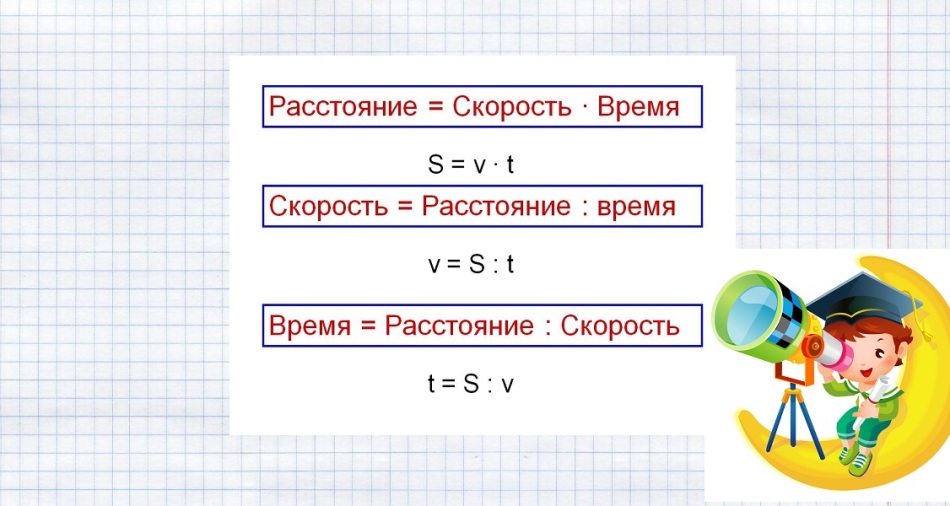
Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S. Скорость обозначается буквой v. А время, за которое пройден путь, обозначается буквой t.
- Путь — S
- Скорость — v
- Время — t
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.

Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту . Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?

Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.

Пишем в черновик эти данные например так:
Расстояние до норы — 3 километра
Скорость Зайца — 1 километр за 1 минуту
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S — 3 километра
V — 1 км/мин
t — ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S : v
Теперь запишем решение задачи цифрами:
t = 3 : 1 = 3 минуты
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.
- Из условия задачи определяем, что нужно найти скорость
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S — 3 километра
t — 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S : t
Теперь запишем решение задачи цифрами:
v = 3 : 3 = 1 км/мин

Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Расстояние — неизвестно
Теперь, то же самое запишем математическими знаками:
v — 1 км/мин
t — 3 минуты
S — ?
Вспоминаем формулу для нахождения расстояния:
S = v ⋅ t
Теперь запишем решение задачи цифрами:
S = 3 ⋅ 1 = 3 км

Как научиться решать более сложные задачи?
Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.

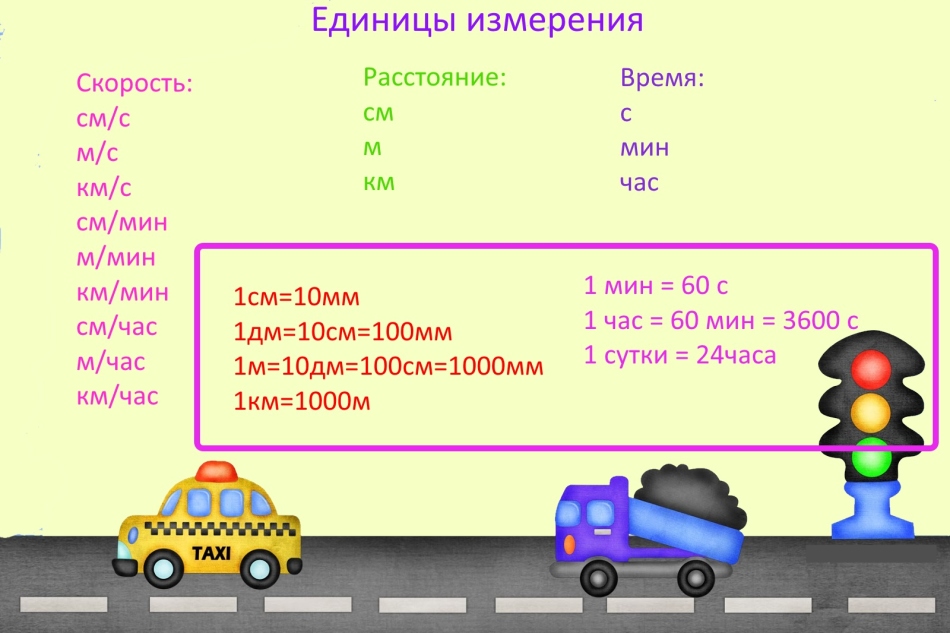
Единицы измерения
Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.
ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.
Для любознательных: Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.

Задача про удава: Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)

Решение:
Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
Запишем эти данные:
Скорость мартышки — 60 см/сек
Скорость слоненка — 20 см/сек
Время — 5 секунд
Расстояние неизвестно
Запишем эти данные математическими знаками:
v1 — 60 см/сек
v2 — 20 см/сек
t — 5 секунд
S — ?
Запишем формулу для расстояние, если известна скорость и время:
S = v ⋅ t
Посчитаем, какое расстояние прошла мартышка:
S1 = 60 ⋅ 5 = 300 см
Теперь посчитаем, сколько прошел слоненок:
S2 = 20 ⋅ 5 = 100 см
Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
S = S1 + S2 = 300 + 100 = 400 см
График зависимости скорости тела от времени: фото
Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
- Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?

Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.

Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)

Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
- 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
- 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
- Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
- Ответ: 24 км, 36 км.
Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.
ВИДЕО: Задачи на движение
Формулы скорости, времени, расстояния?
Как выразить эти понятия друг одно через другие?
Анонимный вопрос
2 ноября 2018 · 236,9 K
Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.
Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).
Выразить скорость из этой формулы можно следующим образом: v=S/t
А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v
204,2 K
Комментировать ответ…Комментировать…
V = S : t
t = S : V
S = V * t
S = расстояние
V = скорость
t = время
: = деление
* = умножение
Пример :
Решил найти расстояние ( S)
Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа
Ответ : 16 км Читать далее
21,3 K
Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?
Комментировать ответ…Комментировать…
Учусь в гимназии №17. Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.) Читать далее
20,1 K
Комментировать ответ…Комментировать…
Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
5,7 K
Комментировать ответ…Комментировать…
Короче!
Если у вас расстояние нужно найти то:
S=t*v, S=50*20(пример)
Если нужно найти время то:
t=S:V
Если нужно найти скорость то :
V=S:T.
Это все формулы. Читать далее
59,9 K
спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!
Комментировать ответ…Комментировать…
Вычисление перемещения по графику проекции скорости
Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»
Теория
Пусть задан график зависимости проекции скорости от времени t (рис. 1).
Проекция перемещении тела за промежуток времени от
до
численно равна по величине площади фигуры, ограниченной графиком
, осью времени 0t и перпендикулярами к
и
(см. рис. 1, площадь выделена штриховкой).

Проекцию перемещения на ось 0Х будем считать:
— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);
— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).
Путь s может быть только положительным:

Напоминаем формулы для расчета площадей фигур:
— прямоугольника –
— треугольника –
— трапеции –
Задачи
Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.
Ответ: ____ м.

Решение. Проекция перемещения за промежуток времени Δt=–
=5с–1с=4c численно равна площади фигуры, ограниченной графиком
, осью времени 0t и перпендикулярами к
с и
с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна
где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения , т.к. проекция скорости
.
м.
Ответ: 16.

Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.
| Интервал времени | Путь |
| от 0 до 10 с | Ответ: м. |
| от 30 до 40 с | Ответ: м. |
В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.

Решение. Путь за промежуток времени Δt = –
численно равна площади фигуры, ограниченной графиком
осью времени 0t и перпендикулярами к
и
.
На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).
,
где a = 20 м/c, . Тогда
м.
Путь равен значению площади (путь всегда положительный, т.е. s > 0).
м.
На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).
,
где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда м.
Ответ: 100125.

Задача 3. Определите за первые 4 с (рис. 7):
а) проекцию перемещения тела;
б) пройденный путь.
Ответ: а) ____ м; б) ____ м.

Решение. Проекция перемещения за время (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком
, осью времени 0t и перпендикулярами к
с и
с (рис. 8, площадь выделена штриховкой).
Так как при с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:
,
где
м/с,
=|-10 м/c|=10 м/c,
.
Тогда м,
м.
а) Проекция перемещения , т.к. проекция скорости
; проекция перемещения
, т.к. проекция скорости
. В итоге получаем:
45м – 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).
, s = 45 м + 5 м = 50 м.
Ответ: а) 40; б) 50.

Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.
Ответ: ____ м.

Решение. Проекция перемещения за время (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком
, осью времени 0t и перпендикулярами к
и
(рис. 10, площадь выделена штриховкой).
Так как при и
проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:
где
м/с,
|-2 м/c| = 2 м/с,
3м/c,
.
Тогда м,
м,
м.
Проекция перемещения , т.к. проекция скорости
.
Проекция перемещения , т.к. проекция скорости
. Проекция перемещения
, т.к. проекция скорости
. В итоге получаем:
3 м – 2 м + 3 м = 4 м.
Ответ: 4.

Задача 5. На рисунке приведен график зависимости скорости тела от времени
.

Определите путь, пройденный телом в интервале времени от 0 до 5 с.
Ответ: ____ м.
Решение. Решение любых графических задач основывается на умении «читать» графики. В данной задаче рассматривается зависимость проекции скорости тела от времени. На интервале от 0 до 3с проекция скорости уменьшается от значения 15 м/с до 0. На интервале от 3 до 5с модуль проекции начинает возрастать от нулевого значения до 10 м/с. Причем важно «увидеть», что тело в этом временном интервале начинает движение в направлении, противоположном оси ОХ.
Пройденный путь будет определяться площадью геометрической фигуры, образованной под графиком проекции скорости.
Рис.1

Дальнейшее решение задачи сводится к нахождению площадей двух треугольников, заштрихованных на рис.1
(м).
(м).
Тогда, общий путь в интервале времени от 0 до 5с будет определяться суммой отдельных путей и
.
(м).
Ответ: 32,5 м
По условию этой задачи можно поставить второй вопрос: найти проекцию перемещения в интервале времени от 0 до 5с.
В этом случае надо учесть, что проекция перемещения в интервале времени от 0 до 3 с положительная и её значение равно пройденному пути на этом интервале.
(м).
В интервале времени от 3 с до 5 с проекция перемещения отрицательная, так как тело движется в направлении противоположном оси ОХ.
(м).
Проекция перемещения за весь интервал времени будет равна
(м).
Ответ: 12,5 м
Задача 6. На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.

Ответ: ____ м.
Решение. Для нахождения пройденного пути в интервале времени от 1с до 5с необходимо рассчитать площадь геометрической фигуры под графиком модуля скорости.
Рис.1

Дальнейшее решение сводится к расчету площади трапеции, заштрихованной на графике (см. рис.1).
(м).
Особенностью подобной задачи является то, что при решении, необходимо внимательно отследить временной интервал, на котором требуется рассчитать пройденный путь.
Ответ: 30 м.
Задача 7. Из двух городов навстречу друг другу с постоянной скоростью двиижутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля равна 15 м/с. Какова скорость второго автомобиля?

Ответ: ____ м.
Решение. При движении навстречу друг к другу расстояние между двумя автомобилями уменьшается от значения 144 км до 0. На графике видно, что встреча автомобилей произошла в момент времени 60 минут, так как расстояние между автомобилями стало равным 0. Расчеты в этой задаче требуют обязательного применения системы «СИ».
144 км = 144000 м; 60 мин = 3600 с.
Используя эти данные, можно рассчитать скорость сближения автомобилей.
м/с
Так как автомобили движутся навстречу друг другу, то отсюда скорость второго автомобиля можно выразить как
(м/с)
Ответ: 25 м/с.
Задача 8. На рисунке представлен график зависимости модуля скорости тела от времени. Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

Ответ: ____ м.
Решение. Для нахождения пройденного пути необходимо рассчитать площадь геометрической фигуры (трапеции) под графиком модуля скорости (см.рис.1). Это относится к интервалу времени от 0 до 3 с. От 3 с до 5 с скорость тела равна 0, следовательно, тело находилось в состоянии покоя и пройденный путь в этом интервале равен 0.
Рис.1

(м).
(м).
Сакович А.Л., 2020
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вычисление перемещения по графику проекции скорости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
План урока:
Среднее значение
Скорость. Время. Расстояние
Взаимосвязь между скоростью, временем и расстоянием
Задачи на движение
На уроке узнаем, что означает «среднее арифметическое» и как его находят, будем решать задачи с величинами «скорость», «время», «расстояние».
Начнем урок с небольшой тренировки ума! Игра называется «Тройка». Вам нужно собрать в левой части три слагаемых так, чтобы получилось число за красной чертой. Считайте устно. Образец дан в первой строке: 18 + 34 + 16 = 68
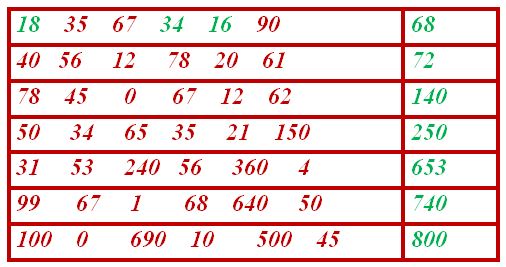
Проверь себя.
40 + 20 + 12 = 72
78 + 0 + 62 = 140
65 + 35 + 150 = 250
53 + 240 +360 = 653
99 + 1 + 640 = 740
690 + 10 + 100 = 800
Среднее значение
Каждый из нас в жизни встречается с выражениями «в среднем», «средняя температура», «средний заработок». Что это значит?
Рассмотрим на конкретной задаче.

Три друга Иван, Костя и Владимир каждую среду идут вместе от школы до музыкальной студии, где учатся игре на гитаре. Иван от школы до студии насчитал 251 шаг. Костя – 248 шагов, а Владимир насчитал 254 шага. Сколько в среднем шагов от школы до музыкальной студии?
В математике существует понятие «среднее арифметическое». Чтобы найти среднее арифметическое в этой задаче, нужно сложить количество шагов трех друзей, а затем полученную сумму разделить на 3 (по количеству слагаемых).
251 + 248 + 254 = 753 шага.
753 : 3 = 251 шаг
Можно сказать, что от школы до музыкальной студии в среднем 251 шаг.
Составим алгоритм.

Например, найти среднее арифметическое чисел: 5, 8, 7, 4.
Находим сумму чисел 5 + 8 + 7 + 4 = 24
Количество слагаемых – 4, значит, полученную сумму разделим на 4.
24 : 4 = 6
Среднее арифметическое – 6.
Пользуясь алгоритмом, найдите среднее арифметическое чисел: 12, 10, 8.
Проверь себя.
12 + 10 + 8 = 30
30 : 3 = 10
Среднее арифметическое – 10.
Рассмотрим более сложную задачу на нахождение среднего арифметического.
Задача
В столовой детского сада для приготовления завтраков малышам расходовали молоко три дня по 20 л и два дня по 25 л. Сколько в среднем расходовали молока в день?
Решим задачу вместе.

Сначала узнаем, сколько всего молока израсходовали.
20 ∙ 3 + 25 ∙ 2 = 110 (л) – израсходовали всего.
Затем узнаем, сколько дней расходовали молоко на завтрак.
3 + 2 = 5(дн.) – расходовали молоко.
Осталось количество израсходованного молока разделить на число дней.
110 : 5 = 22 (л) – расходовали в среднем за день.
Попробуйте самостоятельно решить подобную задачу.
Задача
Для игрового уголка в классе родители закупили 3 настольные игры: «Пазлы», «Домино», «Математический тренажер». Игра «Пазлы» стоила 160 р., «Домино» – 210 р., а «Математический тренажер» – 230 р.. Найди среднюю стоимость настольной игры.
Проверь себя.
- 160 + 210 + 230 = 600 (р.) – заплатили за все игры.
- 600 : 3 = 200 (р.) – стоит в среднем одна настольная игра.
- Ответ: 200 рублей
Скорость. Время. Расстояние
Скорость
Вы наблюдали, что вокруг нас постоянно что-то или кто-то движется. Некоторые объекты – быстро, а некоторые – совсем медленно. Например, по лесной тропе прогуливается человек, по шоссе едет автомобиль, по воздуху летит вертолет. Все они движутся. Но автомобиль движется быстрее, чем человек, а вертолет – быстрее автомобиля.
В математике, величиной характеризующей быстроту движения объектов называют скоростью.
Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть: 1 секунда, 1 минута, 1 час.
Давайте вместе разберем две простые задачи.

Легковая машина прошла 120 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько км прошла машина за 1 час?
120 : 2 = 60 (км) – пройдет машина за 1 час.
Таким образом, скорость движения машины 60 км в час. Сокращенно запишем так:
60 км/ч.
Космический корабль пролетает 8 000 м за 1 секунду. Как по-другому записать его скорость?
Его скорость можно записать так: 8 000 м/с. Мы знаем, что 1 км = 1000 м, поэтому скорость корабля можно записать по-другому: 8 км/с.
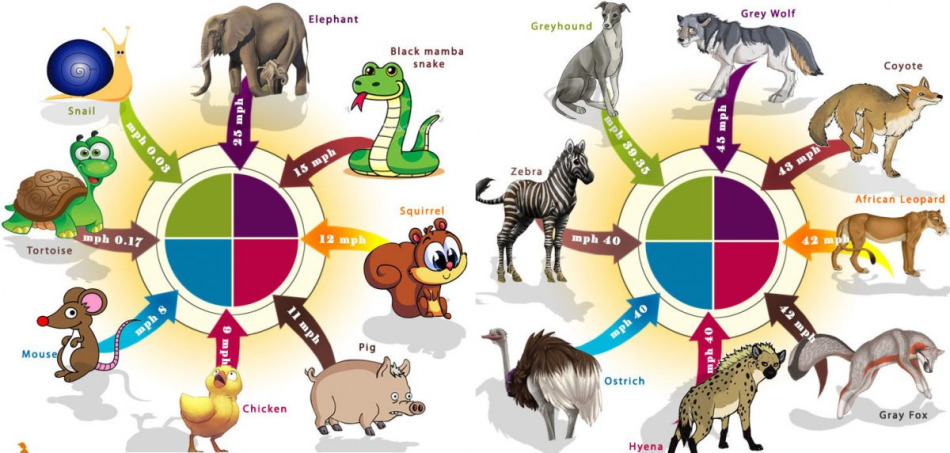
Посмотрите скорость движения некоторых животных. Какое животное самое медленное, самое быстрое? Обратите внимание, что скорость можно записать по-разному: в зависимости от того, сколько сантиметров, метров, километров кто-то пролетает, проползает или пробегает за секунду, минуту, час.

Время

С единицами времени вы уже знакомы. Это: секунда, минута, час, сутки, неделя, месяц, год, век.
Расстояние
Расстояние – это длина дороги, соединяющая начало и конец пути.

Расстояние измеряется в следующих единицах:
Миллиметр
Сантиметр
Дециметр
Метр
Километр
Взаимосвязь между скоростью, временем и расстоянием
Как же связаны между собой эти величины?
Давайте запомним условные обозначения, принятые в математике:
Скорость – v,
Время – t,
Расстояние – S.

Ребята, это три ключевых формулы для решения задач на движение, которые нужно знать назубок!
Задачи на движение
С задачами на движение мы встречаемся каждый день в обычной жизни.
Расстояние – самое большое из трех величин в задачах на движение. То есть, скорость и время всегда меньше расстояния.
Запомнили формулы, которые являются ключами к правильному решению задач?
Заполните пустые окошки в формулах:
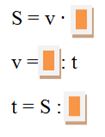
Решим задачи на движение.
Плот двигался по реке со скоростью 5 км/ч, а катер – со скоростью 20 км/ч. Какое расстояние преодолеет плот, и какое катер за 3 часа?
Выделяем величины, чертим таблицу. Читаем задачу по частям и записываем каждую величину в нужную ячейку таблицы.
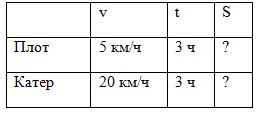
Какую из трех величин нужно найти? Верно, расстояние. Вспомним формулу: S = v ∙ t
5 ∙ 3 + 15 (км) – пройдет плот.
20 ∙ 3 = 60 (км) – пройдет катер.
Ответ: 15 км, 60 км.
Ребята участвовали в соревнованиях по бегу. Максим пробежал 200 м за 40 с, а Артем это же расстояние пробежал за 50 с. С какой скоростью бежал каждый из мальчиков?
Начертите таблицу, как в предыдущей задаче. Запишите величины в нужные ячейки. Поставьте знак вопроса. Пользуясь формулой, решите задачу самостоятельно.
Проверь себя.
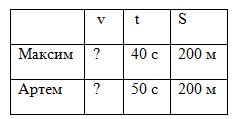
v = S : t
200 : 40 = 5 (м/с) – скорость движения Максима.
200 : 5 = 4 (м/с) – скорость движения Артема.
Ответ: 5 м/с, 4 м/с.
Решим еще одну задачу.
Два всадника отправились на прогулку на лошадях Рада и Снежка. Лошади преодолели одинаковое расстояние 30 км. Но двигались с разной скоростью. Рада бежала со скоростью 10 км/ч, а Снежка – 15 км/ч. Сколько времени длилась прогулка на Раде, и сколько времени – на Снежке?
Начертите таблицу, заполните ее ячейки. Пользуясь формулой, запишите решение.
Проверь себя.
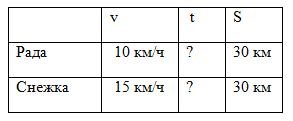
t = S : v
30 : 10 = 3 (ч) – прогулка на Раде.
30 : 15 = 2 (ч) – прогулка на Снежке.
Ответ: 3 ч, 2 ч.
Сегодня на уроке мы запомнили формулы-ключи для решения задач на движение, узнали о скорости самых медленных и самых быстрых животных, научились находить среднее арифметическое. До скорых встреч, ребята!
Предыдущий урок: Физика для чайников. Урок 3. Кинематика
Говорю сразу, будут формулы. Потом не говорите, что не предупреждал :). Итак, на прошлом уроке мы изучили основные понятие кинематки, такие как относительность движения, материальная точка. Вернемся к нашему примеру с автомобилем, который из города А выехал в город Б. Мы сделали допущение что дорога абсолютно прямая, и уходит в бесконечность в обе стороны. А город А – точка начала отчета. Тогда расстояние от точки А в сторону Б – некое положительное число, а в обратную сторону – отрицательное. И это число мы обозначим S. Если принять допущение, что скорость автомобиля постоянная, то расстояние от точки А будет выражено формулой:
В этой формуле S – это пройдённое расстояние, v – скорость, t – время. То есть при скорости, например, 60 км/ч за полчаса автомобиль проедет 60*0.5=30 км.
Но так же не бывает, чтобы скорость была постоянная. Автомобиль разгоняется, тормозит. Где-то стоит на светофоре, где-то знак ограничение скорости и нарисованная камера, а водитель боится штрафов и соблюдает скоростной режим. А где-то дорога хорошая и камер нет, там водитель может гнать все 150 км/ч а то и 200 км/ч. А еще он может остановиться на заправке. В общем, скорость постоянно меняется со временем. Если мы знаем зависимость скорости от времени, то мы можем сказать, что есть функция скорости от времени, и тогда расстояние от начальной точки можно вычислить вот по такой «страшной», на первый взгляд формуле:
Закорючка называется интеграл. В нем нет ничего страшного, он означает, что надо суммировать все бесконечно малые расстояния, пройденные автомобилем за все бесконечно малые отрезки времени до момента времени t. Выражение v(t) означает, что v (скорость) это функция от t (от времени). Иными словами, скорость меняется со временем. Еще тут есть некое dt – он обозначает бесконечно малый отрезок времени. Таким образом, мы суммируем все расстояния, которые прошла материальная точка за все бесконечно малые моменты времени. Это и есть интеграл. Звучит страшно, но не пугайтесь, для многих функций существуют готовые формулы интегралов. Их легко нагуглить. Если скорость одинакова, то тут все просто – используем предыдущую формулу. А если автомобиль разгоняется или тормозит? Значит, он движется с укореняем. Если ускорение одинаковое, то:
Здесь a – это ускорение – величина, показывающая как быстро менятся скорость. Решив интеграл, мы получим формулу пройденного расстояния:
Это, кстати, очень важная формула. Запомните ее. Очень многие формулы из физики на нее похожи, и я не раз потом будут ссылаться на нее.
А теперь попробуем решить задачку. Нужно рассчитать тормозной путь автомобиля, который движется со скоростью 72 км/ч, ускорение -5 м/с^2. Цифра взята со знаком минус, потому что ускорение против скорости движения. Тогда мы можем вычислить по такой формуле:
Переводим 72 км/ч в м/с. Это будет 72*1000/3600=20 м/с, тогда машина остановиться за 4 секунды, вычисляем:
Таким образом, при данных условиях тормозной путь будет 40 метров.
Следующий урок: Физика для чайников. Урок 5. Криволинейное движение.
