Как найти зависимость случайных величин - Сайт, где вы сможете решить свои вопросы

Понятие «зависимость»
случайных величин в теории вероятностей
отличается от понятия функциональной
зависимости. Если случайная величина
X
находится
в вероятностной зависимости от случайной
величины Y,
то это означает, что с изменением величины
Y
случайная величина X
имеет
тенденцию к изменению. В ряде случаев
вероятностная зависимость бывает
настолько слаба, что ею пренебрегают,
в других же случаях, наоборот, зависимость
между величинами настолько тесная, что,
зная значения одной из них, можно указать
значения другой.

Случайная величина
X,
входящая в систему (X,
Y)
является независимой от случайной
величины Y,
если ее закон распределения не зависит
от того, какое частное значение приняла
случайная величина
Y.

Для случайных
непрерывных величин условие независимости
случайной величины X
от Y
записывается в виде

при
любом y.
Это означает, что у этих распределений
одинаковая форма кривых и одинаковые
параметры.

Случайная величина
X,
входящая в систему (X,
Y)
является зависимой от случайной величины
Y,
если ее закон распределения зависит от
того, какое частное значение приняла
случайная величина
Y.

Условие же
зависимости случайной величины X
от Y
записывается в виде

что означает или
несоответствие форм кривых распределения
или неравенство параметров.

Теорема.
Зависимость
и независимость случайных величин,
входящих в систему, всегда взаимна,
т.е., если величина X
не зависит от Y,
то и величина Y
не зависит от X.

Рекомендуется
доказать теорему о взаимности
зависимости
и независимости случайных величин X
и Y
самостоятельно
ввиду простоты.

Для случайных
дискретных величин условие независимости
случайной величины X
от Y
определяется
равенством безусловной и условной
вероятностей друг другу

а условие зависимости
– неравенством их, т.е.

Пример 4.
В условиях примера 3 определить зависимость
или независимость случайных величин
X
и Y.

Решение.

Так как

,
а

,
то

,
что указывает на зависимость случайных
величин X
и Y.

В связи с тем, что
из равенства

следует равенство

,
поскольку

,
то выражение

называют условием
независимости случайных величин.

3.8 Числовые характеристики системы двух случайных величин

В качестве числовых
характеристик системы случайных величин
принимают начальные и центральные
моменты системы.

Начальные моменты
системы.

Начальным моментом

порядка k,
s
системы (X,
Y)
называют математическое ожидание
произведения

.

Для системы
случайных дискретных величин

где

– вероятность того, что система (X,
Y)
примет
значение

,
а суммирование распространяется по
всем возможным значениям случайных
величин X
и Y.

Для системы
случайных непрерывных величин

где f(x,
y)
– плотность распределения системы (X,
Y).

На практике чаще
всего применяются начальные моменты
первого порядка:

Они являются
математическими ожиданиями случайных
величин X
и Y,
входящих в систему и характеризуют
положение системы, представляя собой
координаты средней точки (центра
рассеивания) системы на плоскости.

На основе определения
начальных моментов можно записать
формулы для математических ожиданий
M(X)
и M(Y)
случайных величин X
и Y,
входящих в систему, в случае:

а) дискретных
величин

б) непрерывных
величин

Пример 5.
Система двух случайных дискретных
величин задана таблицей распределения:

	X1=3	X2=6	X3=9
Y1=4	0,1	0,2	0,3
Y2=8	0,2	0,1	0,1

Найти математическое
ожидание случайных величин X
и Y,
входящих в систему.

Решение.

;

Вывод: центр
группирования этой системы случайных
величин находится в точке с координатами

.

Центральные
моменты системы.

Центральным
моментом системы
(X,
Y)
порядка k,
s
называют математическое ожидание
произведения

:

для дискретных
величин и

для непрерывных
величин.

Среди центральных
моментов большое практическое значение
имеют вторые центральные моменты
системы:

и

.

Эти моменты являются
дисперсиями случайных величин X
и Y,
входящих в систему, и характеризуют
рассеивание случайных точек в направлении
осей 0x
и
0y.

Формулы дисперсий
случайных величин X
и Y,
входящих в систему,

а) для дискретных
величин:

;

,

б) для непрерывных
величин:

;

.

Для характеристики
системы случайных величин важную роль
играет второй
смешанный центральный момент

т.е. математическое
ожидание произведения центрированных
величин.

Эта характеристика
называется корреляционным
моментом или
ковариацией:

Корреляционный
момент кроме рассеяния случайных величин
X
и Y
характеризует еще и связь их между
собой.

Корреляционный
момент вычисляется по формуле:

а) для системы
дискретных величин

;

б) для системы
непрерывных величин

При решении многих
задач, в которых требуется определить
корреляционный момент, удобнее
пользоваться следующей формулой:

Она вытекает из
определения корреляционного момента.

Определение.
Случайные
величины являются связанными между
собой, если при изменении одной из них
другая реагирует изменением своего
условного математического ожидания.

Условное
математическое ожидание случайной
непрерывной величины можно определить
по формуле

где M(X/Y)
– условное математическое ожидание
случайной величины X
при условии, что случайная величина Y
приняла
частное значение y.

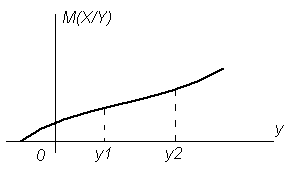
Рисунок 3.9 Графическая
интерпретация условного математического
ожидания M(X/Y)

Условное
математическое ожидание M(X/Y)
является функцией случайной величины
Y
(рис. 3.9). Если

,
то случайные величины X
и
Y
считаются
связанными. Связанность случайных
величин является частным случаем их
зависимости.

На практике чаще
всего M(X/Y)
имеет вид
прямой линии, которую называют линией
регрессии,
описываемой уравнением

Положение линии
регрессии зависит от величины и знака
корреляционного момента (рис. 3.10). Если
значение корреляционного момента
случайных величин X
и
Y
меньше нуля,
то регрессия отрицательная, а если
значение корреляционного момента больше
нуля, то регрессия положительная. Если
значение корреляционного момента равно
нулю, то случайные величины X
и
Y
между собой не связаны.

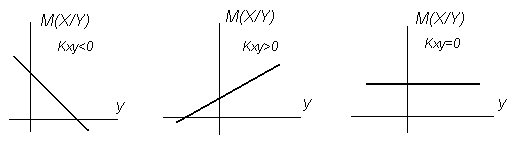
Рисунок 3.10 Положение
линии регрессии в зависимости от величины
и знака корреляционного момента

Свойства
корреляционного момента:

а)

;

б)

;

в)

– корреляционная матрица.

Для системы двух
случайных величин числовыми характеристиками
являются:

Из определения
корреляционного момента следует, что
размерность его равна размерности
произведения случайных величин X
и
Y.
Поэтому для одних и тех же величин
значения его будут зависеть от единиц
измерения случайных величин.

Эта особенность
корреляционного момента является его
недостатком, так как вызывает затруднения
при сравнении корреляционных моментов
различных пар случайных величин. Для
устранения этого недостатка вводят
новую числовую характеристику –
коэффициент
корреляции
или нормированный корреляционный
момент.

Коэффициентом
корреляции

случайных величин
X
и Y
называют
отношение корреляционного момента

к произведению средне – квадратичных
отклонений этих величин:

Для независимых
величин

;
для величин, связанных между собой
линейной зависимостью,

или

.
Равенство нулю коэффициента корреляции
еще не свидетельствует о том, что
случайные величины являются независимыми.

Система
произвольного числа случайных величин.
В тех случаях, когда изучаются процессы
с относительно большим числом n
случайных переменных

целесообразно пользоваться корреляционной
матрицей:

где

представляет собой корреляцию (смешанный
момент второго порядка) между величинами

.

К числовым
характеристикам системы n
случайных переменных относят их
математические ожидания и корреляционную
матрицу. Математические ожидания
определяют положение центра группирования
системы, а корреляционная матрица
характеризует разброс или рассеяние
случайных точек около центра группирования
и попарную связанность случайных
величин. Если случайные величины будут
не коррелированны между собой, то эта
матрица будет иметь нули везде кроме
диагонали.

Вопросы для
повторения

1 Что называется
системой двух случайных величин?
Приведите примеры.

2 Что понимают под
функцией распределения системы двух
случайных величин? Какими свойствами
она обладает?

3 Как определяется
вероятность попадания случайной точки
заданную область, если известна функция
распределения системы двух случайных
величин?

4 Что называется
плотностью распределения системы двух
непрерывных случайных величин? Каковы
ее свойства?

5 По каким формулам
определяются плотности распределений
составляющих системы?

6 Что понимают под
условным законом распределения случайной
величины?

7 Какая связь между
плотностью распределения системы,
условной плотностью и плотностью
составляющей системы?

8 Сформулируйте
теоремы, устанавливающие необходимые
и достаточные условия независимости
случайных величин.

9 Что собой
представляют начальные моменты первого
порядка и как они рассчитываются?

10 Что собой
представляют вторые центральные моменты
и как они рассчитываются?

11 Корреляционный
момент системы двух случайных величин
и его свойства.

12 Что понимают под
условным математическим ожиданием?

13 Чем отличается
коэффициент корреляции от корреляционного
момента?

14 Как по коэффициенту
корреляции установить степень связанности
случайных величин, входящих в систему?

15 Какими числовыми
характеристиками характеризуется
система n
случайных величин?

Упражнения

3.1 Система
случайных величин (x,y)
задана рядом распределения. Определите
вероятность того, что случайная величина
x
примет значение равное двум, т.е. P(x=2).

0,1

0,2

0,1

0,2

0,3

0,1

3.2 Значения
числовых характеристик системы случайных
величин X
и Y

;

.
Требуется рассчитать корреляционный
момент.

3.3 Система случайных
величин (X,Y)
задана рядом распределения. Определите
М (X) и М(y):

_yi^xi	2	3	5
2	0.1	0.2	0.1
4	0.2	0.3	0.1

3.4 Плотность
совместного распределения системы двух
случайных величин (X,Y)

Найти: а) постоянный
множитель C;
б) плотности распределения составляющих;
в) условные плотности распределения
составляющих.

3.5 При
каком значении коэффициента корреляции
функция условного математического
ожидания M(X/Y)
отображается прямой, параллельной оси
абсцисс?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Функции случайных величин

Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей и плотности для функции двух случайных аргументов.

Закон распределения вероятностей функции одной случайной величины

При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.

Таким образом, возникает задача, которую можно сформулировать так.

Дана система случайных величин (X_1,X_2,ldots,X_n) , закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:

Y=varphi(X_1,X_2,ldots,X_n).

(6.1)

Требуется определить закон распределения случайной величины , зная вид функций (6.1) и закон совместного распределения ее аргументов.

Рассмотрим задачу о законе распределения функции одного случайного аргумента

Y=varphi(X).

Пусть — дискретная случайная величина, имеющая ряд распределения

$begin{array}{|c|c|c|c|c|}hline{X}&x_1&x_2&cdots&x_n\hline{P}&p_1&p_2&cdots&p_n\hlineend{array}$

Тогда Y=varphi(X) также дискретная случайная величина с возможными значениями y_1=varphi(x_1),y_2=varphi(x_2),ldots,y_n=varphi(x_n) . Если все значения y_1,y_2,ldots,y_n различны, то для каждого k=1,2,ldots,n события ${X=x_k}$ и ${Y=y_k=varphi(x_k)}$ тождественны. Следовательно,

$P{Y=y_k}=P{X=x_k}=p_k$

и искомый ряд распределения имеет вид

$begin{array}{|c|c|c|c|c|}hline{Y}&y_1=varphi(x_1)&y_2=varphi(x_2)&cdots&y_n=varphi(x_n)\hline{P}&p_1&p_2&cdots&p_n\hlineend{array}$

Если же среди чисел y_1=varphi(x_1),y_2=varphi(x_2),ldots,y_n=varphi(x_n) есть одинаковые, то каждой группе одинаковых значений y_k=varphi(x_k) нужно отвести в таблице один столбец и соответствующие вероятности сложить.

Для непрерывных случайных величин задача ставится так: зная плотность распределения f(x) случайной величины , найти плотность распределения g(y) случайной величины Y=varphi(X) . При решении поставленной задачи рассмотрим два случая.

Предположим сначала, что функция y=varphi(x) является монотонно возрастающей, непрерывной и дифференцируемой на интервале (a;b) , на котором лежат все возможные значения величины . Тогда обратная функция x=psi(y) существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем

g(y)=fbigl(psi(y)bigr)cdot |psi'(y)|.

(6.2)

Пример 1. Случайная величина распределена с плотностью

$f(x)=frac{1}{sqrt{2pi}}e^{-x^2/2}$

Найти закон распределения случайной величины , связанной с величиной зависимостью Y=X^3 .

Решение. Так как функция y=x^3 монотонна на промежутке (-infty;+infty) , то можно применить формулу (6.2). Обратная функция по отношению к функции varphi(x)=x^3 есть psi(y)=sqrt[LARGE{LARGE{3}}]{y} , ее производная $psi'(y)=frac{1}{3sqrt[LARGE{LARGE{3}}]{y^2}}$ . Следовательно,

$g(y)=frac{1}{3sqrt{2pi}}e^{-sqrt[LARGE{LARGE{3}}]{y^2}/2}frac{1}{sqrt[LARGE{LARGE{3}}]{y^2}}$

Рассмотрим случай немонотонной функции. Пусть функция y=varphi(x) такова, что обратная функция x=psi(y) неоднозначна, т. е. одному значению величины соответствует несколько значений аргумента , которые обозначим x_1=psi_1(y),x_2=psi_2(y),ldots,x_n=psi_n(y) , где — число участков, на которых функция y=varphi(x) изменяется монотонно. Тогда

$g(y)=sumlimits_{k=1}^{n}fbigl(psi_k(y)bigr)cdot |psi'_k(y)|.$

(6.3)

Пример 2. В условиях примера 1 найти распределение случайной величины Y=X^2 .

Решение. Обратная функция x=psi(y) неоднозначна. Одному значению аргумента соответствуют два значения функции

$begin{gathered}x_1=psi_1(y)=+sqrt{y};\x_2=psi_2(y)=-sqrt{y}.end{gathered}$

Применяя формулу (6.3), получаем:

$begin{gathered}g(y)=f(psi_1(y))|psi'_1(y)|+f(psi_2(y))|psi'_2(y)|=\\=frac{1}{sqrt{2pi}},e^{-left(-sqrt{y^2}right)^2/2}!left|-frac{1}{2sqrt{y}}right|+frac{1}{sqrt{2pi}},e^{-left(sqrt{y^2}right)^2/2}!left|frac{1}{2sqrt{y}}right|=frac{1}{sqrt{2pi{y}}},e^{-y/2}.end{gathered}$

Закон распределения функции двух случайных величин

Пусть случайная величина является функцией двух случайных величин, образующих систему (X_1;X_2) , т. е. Y=varphi(X_1;X_2) . Задача состоит в том, чтобы по известному распределению системы найти распределение случайной величины .

Пусть f(x_1;x_2) — плотность распределения системы случайных величин . Введем в рассмотрение новую величину Y_1 , равную X_1 , и рассмотрим систему уравнений

$left{!begin{gathered}y=varphi(x_1;x_2);hfill\y_1=x_1.hfillend{gathered}right.$

Будем полагать, что эта система однозначно разрешима относительно x_1,x_2

$left{!begin{gathered}x_2=psi(y;y_2);hfill\x_1=y_1.hfillend{gathered}right.$

и удовлетворяет условиям дифференцируемости.

Плотность распределения случайной величины

$g_1(y)=intlimits_{-infty}^{+infty}f(x_1;psi(y;x_1))!left|frac{partialpsi(y;x_1)}{partial{y}}right|dx_1.$

Заметим, что рассуждения не изменяются, если введенную новую величину Y_1 положить равной X_2 .

Математическое ожидание функции случайных величин

На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.

Пусть случайная величина является функцией случайного аргумента с заданным законом распределения

Y=varphi(X).

Требуется, не находя закона распределения величины , определить ее математическое ожидание

M(Y)=M[varphi(X)].

Пусть — дискретная случайная величина, имеющая ряд распределения

$begin{array}{|c|c|c|c|c|}hline{x_i}&x_1&x_2&cdots&x_n\hline{p_i}&p_1&p_2&cdots&p_n\hlineend{array}$

Составим таблицу значений величины и вероятностей этих значений:

$begin{array}{|c|c|c|c|c|}hline{y_i=varphi(x_i)}&y_1=varphi(x_1)&y_2=varphi(x_2)&cdots&y_n=varphi(x_n)\hline{p_i}&p_1&p_2&cdots&p_n\hlineend{array}$

Эта таблица не является рядом распределения случайной величины , так как в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины можно определить по формуле

$M[varphi(X)]=sumlimits_{i=1}^{n}varphi(x_i)p_i,$

(6.4)

так как величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен.

Формула (6.4) не содержит в явном виде закон распределения самой функции varphi(X) , а содержит только закон распределения аргумента . Таким образом, для определения математического ожидания функции Y=varphi(X) вовсе не требуется знать закон распределения функции , а достаточно знать закон распределения аргумента .

Для непрерывной случайной величины математическое ожидание вычисляется по формуле

$M[varphi(X)]=intlimits_{-infty}^{+infty}varphi(x)f(x),dx,$

где f(x) — плотность распределения вероятностей случайной величины .

Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знание даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сформулируем эти случаи в виде теорем.

Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:

M(X+Y)=M(X)+M(Y).

Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

$M(XY)=M(X)M(Y)+mu_{xy}.$

Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Дисперсия функции случайных величин

По определению дисперсии имеем D[Y]=M[(Y-M(Y))^2]. . Следовательно,

D[varphi(x)]=M[(varphi(x)-M(varphi(x)))^2] , где M(varphi(x))=M[varphi(X)] .

Приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента Y=varphi(X) дисперсия выражается формулой

$D[varphi(x)]=intlimits_{-infty}^{+infty}(varphi(x)-M(varphi(x)))^2f(x),dx,$

(6.5)

где M(varphi(x))=M[varphi(X)] — математическое ожидание функции ; f(x) — плотность распределения величины .

Формулу (6.5) можно заменить на следующую:

$D[varphi(x)]=intlimits_{-infty}^{+infty}varphi^2(x)f(x),dx-M^2(X)$

Рассмотрим теоремы о дисперсиях, которые играют важную роль в теории вероятностей и ее приложениях.

Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:

$D!left[sumlimits_{i=1}^{n}X_iright]=sumlimits_{i=1}^{n}D[X_i]+2sumlimits_{i<j}mu_{x_ix_j}$

Следствие 6.3. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых:

$D!left[sumlimits_{i=1}^{n}X_iright]=sumlimits_{i=1}^{n}D[X_i]$

Теорема 6.4. Дисперсия произведения двух независимых случайных величин вычисляется по формуле

D[XY]=D[X]D[Y]+M^2(X)D[Y]+M^2(Y)D[X].

Корреляционный момент функций случайных величин

Согласно определению корреляционного момента двух случайных величин и , имеем

$mu_{xy}=M[(X-M(X))(Y-M(Y))].$

Раскрывая скобки и применяя свойства математического ожидания, получаем

$mu_{xy}=M(XY)-M(X)M(Y).$

(6.6)

Рассмотрим две функции случайной величины

Y_1=varphi_1(X);qquad Y_2=varphi_2(X).

Согласно формуле (6.6)

$mu_{y_1y_2}= M(Y_1Y_2)-M(Y_1)M(Y_2).$

отсюда

$mu_{y_1y_2}=M(varphi_1(X)varphi_2(X))-M(varphi_1(X))M(varphi_2(X)).$

т.е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.

Рассмотрим основные свойства корреляционного момента и коэффициента корреляции.

Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не изменяются.

Свойство 2. Для любых случайных величин и абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин:

$|mu_{xy}|leqslantsqrt{D[X]cdot D[Y]}=sigma_xcdot sigma_y,$

где sigma_x,sigma_y — средние квадратические отклонения величин и .

Следствие 6.5. Для любых случайных величин и абсолютная величина коэффициента корреляции не превосходит единицы:

$|r_{xy}|leqslant1.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

При
изучении систем случайных величин всегда следует обращать внимание на степень и
характер их зависимости. Эта зависимость может быть более или менее ярко
выраженной, более или менее тесной. В некоторых случаях зависимость между
случайными величинами может быть настолько тесной, что, зная значение одной
случайной величины, можно в точности указать значение другой. В другом крайнем
случае зависимость между случайными величинами является настолько слабой и
отдаленной, что их можно практически считать независимыми.

Понятие
о независимых случайных величинах – одно их важных понятий теории вероятностей.

Случайная
величина называется
независимой от случайной величины , если закон распределения величины не зависит от того,
какое значение приняла величина .

Для
непрерывных случайных величин условие независимости от может быть записано в виде:

при любом .

Напротив,
в случае, если зависит
от , то

Докажем,
что зависимость или независимость случайных величин всегда взаимны: если
величина не
зависит от .

Действительно,
пусть не
зависит от :

. (8.5.1)

Из формул
(8.4.4) и (8.4.5) имеем:

откуда, принимая
во внимание (8.5.1), получим:

что и
требовалось доказать.

Так
как зависимость и независимость случайных величин всегда взаимны, можно дать
новое определение независимых случайных величин.

Случайные
величины и называются
независимыми, если закон распределения каждой из них не зависит от того, какое
значение приняла другая. В противном случае величины и называются зависимыми.

Для
независимых непрерывных случайных величин теорема умножения законов
распределения принимает вид:

, (8.5.2)

т. е. плотность
распределения системы независимых случайных величин равна произведению
плотностей распределения отдельных величин, входящих в систему.

Условие
(8.5.2) может рассматриваться как необходимое и достаточное условие
независимости случайных величин.

Часто
по самому виду функции можно заключить, что случайные величины , являются независимыми, а
именно, если плотность распределения распадается на произведение двух функций,
из которых одна зависит только от , другая – только от , то случайные величины
независимы.

Пример.
Плотность распределения системы имеет вид:

Определить,
зависимы или независимы случайные величины и .

Решение.
Разлагая знаменатель на множители, имеем:

Из
того, что функция распалась
на произведение двух функций, из которых одна зависима только от , а другая – только от
, заключаем,
что величины и
должны быть
независимы. Действительно, применяя формулы (8.4.2) и (8.4.3), имеем:

;

аналогично

откуда
убеждаемся, что

и, следовательно,
величины и независимы.

Вышеизложенный
критерий суждения о зависимости или независимости случайных величин исходит из
предположения, что закон распределения системы нам известен. На практике чаще
бывает наоборот: закон распределения системы не известен; известны только законы
распределения отдельных величин, входящих в систему, и имеются основания
считать, что величины и независимы. Тогда можно написать
плотность распределения системы как произведение плотностей распределения
отдельных величин, входящих в систему.

Остановимся
несколько подробнее на важных понятиях о «зависимости» и «независимости»
случайных величин.

Понятие
«независимости» случайных величин, которым мы пользуемся в теории вероятностей,
несколько отличается от обычного понятия «зависимости» величин, которым мы
оперируем в математике. Действительно, обычно под «зависимостью» величин
подразумевают только один тип зависимости – полную, жесткую, так называемую –
функциональную зависимость. Две величины и называются функционально зависимыми,
если, зная значение одной из них, можно точно указать значение другой.

В
теории вероятностей мы встречаемся с другим, более общим, типом зависимости — с
вероятностной или «стохастической» зависимостью. Если величина связана с величиной вероятностной зависимостью,
то, зная значение ,
нельзя указать точно значение , а можно указать только ее закон
распределения, зависящий от того, какое значение приняла величина .

Вероятностная
зависимость может быть более или менее тесной; по мере увеличения тесноты
вероятностной зависимости она все более приближается к функциональной. Таким
образом, функциональную зависимость можно рассматривать как крайний, предельный
случай наиболее тесной вероятностной зависимости. Другой крайний случай –
полная независимость случайных величин. Между этими двумя крайними случаями
лежат все градации вероятностной зависимости – от самой сильной до самой
слабой. Те физические величины, которые на практике мы считаем функционально
зависимыми, в действительности связаны весьма тесной вероятностной
зависимостью: при заданном значении одной из этих величин другая колеблется в
столь узких пределах, что ее практически можно считать вполне определенной. С
другой стороны, те величины, которые мы на практике считаем независимыми, и
действительности часто находятся в некоторой взаимной зависимости, но эта
зависимость настолько слаба, что ею для практических целей можно пренебречь.

Вероятностная
зависимость между случайными величинами очень часто встречается на практике.
Если случайные величины и находятся в вероятностной зависимости,
это не означает, что с изменением величины величина изменяется вполне определенным образом;
это лишь означает, что с изменением величины величина имеет тенденцию также изменяться
(например, возрастать или убывать при возрастании ). Эта тенденция соблюдается лишь «в
среднем», в общих чертах, и в каждом отдельном случае от нее возможны
отступлении.

Рассмотрим,
например, две такие случайные величины: – рост наугад взятого человека, – его вес. Очевидно,
величины и находятся в
определенной вероятностной зависимости; она выражается в том, что в общем люди
с большим ростом имеют больший вес. Можно даже составить эмпирическую формулу,
приближенно заменяющую эту вероятностную зависимость функциональной. Такова,
например, общеизвестная формула, приближенно выражающая зависимость между
ростом и весом:

Формулы
подобного типа, очевидно, не являются точными и выражают лишь некоторую
среднюю, массовую закономерность, тенденцию, от которой в каждом отдельном
случае возможны отступления.

В
вышеприведенном примере мы имели дело со случаем явно выраженной зависимости.
Рассмотрим теперь такие две случайные величины: – рост наугад взятого человека; – его возраст.
Очевидно, для взрослого человека величины и можно считать практически независимыми;
напротив, для ребенка величины и являются зависимыми.

Приведем
еще несколько примеров случайных величин, находящихся в различных степенях
зависимости.

1.
Из камней, составляющих кучу щебня, выбирается наугад один камень. Случайная
величина –
вес камня; случайная величина – наибольшая длина камня. Величины и находятся в явно выраженной
вероятностной зависимости.

2.
Производится стрельба ракетой в заданный район океана. Величина – продольная ошибка
точки попадания (недолет, перелет); случайная величина – ошибка в скорости ракеты в
конце активного участка движения. Величины и явно зависимы, так как ошибка является одной из
главных причин, порождающих продольную ошибку .

3.
Летательный аппарат, находясь в полете, измеряет высоту над поверхностью Земли
с помощью барометрического прибора. Рассматриваются две случайные величины: – ошибка измерения
высоты и –
вес топлива, сохранившегося в топливных баках к моменту измерения. Величины и практически можно считать
независимыми.

В
следующем мы
познакомимся с некоторыми числовыми характеристиками системы случайных величин,
которые дадут нам возможность оценивать степень зависимости этих величин.

Источник

Две случайные величины X и Y называют коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю.

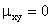
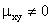
Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что , а это противоречит условию, так как для коррелированных величин .

Обратное предположение не всегда имеет место, т. е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.

Убедимся на примере, что две зависимые величины могут быть некоррелированными.

ПРИМЕР 13.1.60 Двумерная случайная величина (X, Y) задана плотностью распределения:

Доказать, что X и Y — зависимые некоррелированные величины.

Решение. Воспользуемся ранее вычисленными плотностями распределения составляющих X и Y (см. пример прим.13.1.55):

внутри заданного эллипса и

вне его.

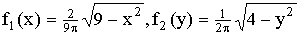
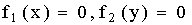
Так как 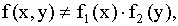, то X и Y — зависимые величины.

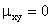
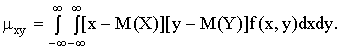
Для того, чтобы доказать некоррелированность X и Y , достаточно убедиться в том, что . Найдем корреляционный момент

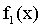
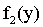
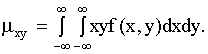
Поскольку функция симметрична относительно оси Oy, то M(X)=0; аналогично M(Y)=0 в силу симметрии относительно оси Ox. Следовательно,

Вынося постоянный множитель f(x,y) за знак интеграла, получим

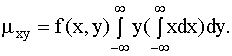
Внутренний интеграл равен нулю (подынтегральная функция нечетна, пределы интегрирования симметричны относительно начала координат), следовательно, 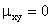, т.е. зависимые случайные величины X и Y некоррелированы.

Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их коррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Заметим, однако, что из некоррелированности нормально распределенных величин вытекает их независимость. Это утверждение доказывается в следующем разделе.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

3.8 Числовые характеристики системы двух случайных величин

Функции случайных величин

Закон распределения вероятностей функции одной случайной величины

Закон распределения функции двух случайных величин

Математическое ожидание функции случайных величин

Дисперсия функции случайных величин

Корреляционный момент функций случайных величин

Вам также может понравиться

Как составить аналитический баланс предприятия это

Как найти фотки в инстаграме в архиве

Huawei как найти в нем облако

Добавить комментарий Отменить ответ