План статьи
- Постановка задачи.
- Формальное описание задачи.
- Примеры задач.
- Несколько примеров на синтетических данных со скрытыми линейными зависимостями.
- Какие ещё скрытые зависимости могут содержаться в данных.
- Автоматизация поиска зависимостей.
- Число признаков меньше пороговой величины.
- Число признаков превышает пороговую величину.
Постановка задачи
Нередко в машинном обучении встречаются ситуации, когда данные собираются априори, и лишь затем возникает необходимость разделить некоторую выборку по известным классам. Как следствие часто может возникнуть ситуация, когда имеющийся набор признаков плохо подходит для эффективной классификации. По крайней мере, при первом приближении.
В такой ситуации можно строить композиции слабо работающих по отдельности методов, а можно начать с обогащения данных путём выявления скрытых зависимостей между признаками. И затем строить на основе найденных зависимостей новые наборы признаков, некоторые из которых могут потенциально дать существенный прирост качества классификации.
Формальное описание задачи
Перед нами ставится задача классификации L объектов, заданных n вещественными числами. Мы будем рассматривать простой двухклассовый случай, когда метки классов — это −1 и +1. Наша цель — построить линейный классификатор, то есть такую функцию, которая возвращает −1 или + 1. При этом набор признаковых описаний таков, что для объектов противоположных классов, измеренных на данном множестве признаков, практически не работает гипотеза компактности, а разделяющая гиперплоскость строится крайне неэффективно.
Иными словами, всё выглядит так, будто задача классификации на данном множестве объектов не может быть решена эффективно.
Итак, мы имеем столбец ответов, содержащий числа -1 или 1, и соответствующую ему матрицу значений признаков X1…Xn, состоящую из L строк и n столбцов.
Мы ставим перед собой подзадачу найти такие зависимости F(Xi,Xj), которые бы могли выступить в роли новых признаков для классифицируемых объектов и помочь нам построить оптимальный классификатор.
Примеры задач
Давайте рассмотрим нашу задачу по нахождению функций F(Xi,Xj) на примерах. Разумеется, весьма жизненных.
Примеры будут связаны с лепреконами. Лепреконы, если кто не в курсе, существуют где-то рядом с нами, хоть их практически никто и не видел. И у них, как и у людей, есть свои компьютеры, интернет и соцсети. Большую часть времени они посвящают поискам золота и складированию его в свои мешки. Однако же помимо честных лепреконов попадаются и такие, которые пытаются отлынить от этой важной работы. Их называют лепреконами-диссидентами. И именно из-за них скорость прироста объёмов золота у лепреконов никак не может достигнуть нужной величины!
Так как в мире лепреконов так же есть машинное обучение, их научились находить исходя из их поведения в крупных соцсетях. Но есть проблема! Каждый год появляется много молодых соцсетей, пытающихся захватить рынок, но ещё не умеющих собирать достаточно данных о своих пользователях для анализа! А тех данных, что они собирают, ну никак не достаточно, чтобы отличить порядочного лепрекона от лепрекона-диссидента! И тут то мы и сталкиваемся с необходимостью искать скрытые зависимости в имеющихся признаковых описаниях, чтобы на основе недостаточных на первый взгляд данных суметь построить оптимальный классификатор.
Однако пример с соцсетями будет вероятно чересчур сложным для разбора, так что давайте попробуем решить подобную задачу на примере ядерных процессоров лепреконов. Они характеризуются 4мя основными признаками:
a) Скорость вращения реактора (млн об/сек)
b) Вычислительная мощность (трл вычислений/сек)
c) Скорость вращения реактора под нагрузкой (млн об/сек) и
d) Вычислительная мощность под нагрузкой (трл вычислений/сек)
Ядерные процессоры производят 2 основные фирмы: 0 и 1 (‘Black Zero’ и ‘The First’). При этом у Black Zero цены вдвое ниже, но и ресурс также ниже впятеро! Однако главный гос. поставщик ядерных процессоров постоянно пытается обмануть заказчика и вместо оплаченных машин фирмы The First поставить более дешёвые и ненадёжные машины фирмы Black Zero. При этом разброс рабочих параметров реакторов настолько велик, что по основным характеристикам отличить одни от других для большинства измерений невозможно. В таблице 1 приведены характеристики 50ти случайно выбранных машин для каждой из фирм:
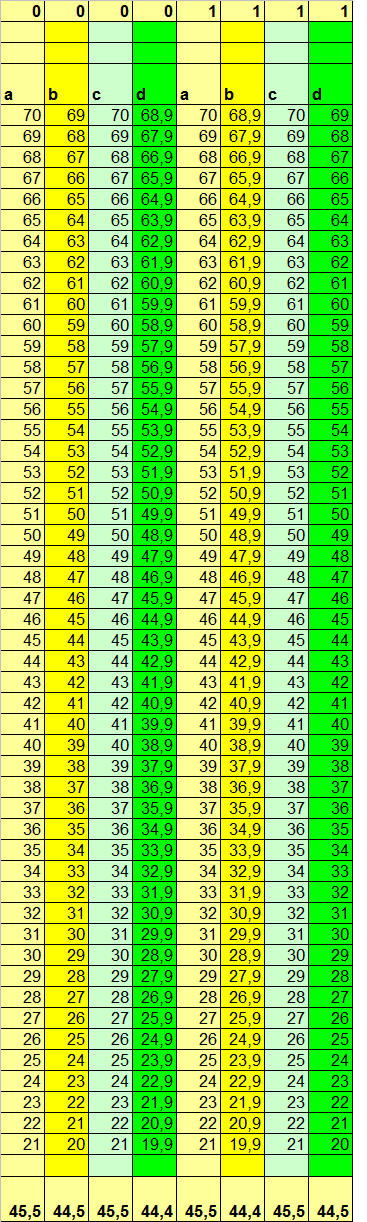
Таблица 1
Для удобства сравнения объекты классов 1 и 0 расположены не вертикально, а сбоку друг относительно друга. В приведённом примере видно, что в целом параметры вычислительной мощности зависят от оборотов реактора, причём, для машин разных производителей зависят несколько по-разному: для машин Black Zero в сравнении с машинами The First число вычислений выше при нормальных условиях для схожих оборотов реактора, но ниже под нагрузкой. Конечно, это потому, что машины фирмы The First без нагрузки входят в режим экономии плазмы, следствием чего является небольшое снижение производительности. Зато под нагрузкой они явно опережают конкурента.
Вот только мы видим эту зависимость, потому что данные специально так подобраны, чтобы эта зависимость была видна. В реальности же среди многих тысяч измерений и десятков (если не сотен) признаков, которые не могут быть так красиво отсортированы, как в этом придуманном примере, увидеть глазами такого рода зависимости обычно просто невозможно. А если ещё и не до конца ясна вся бизнес-специфика каждого признака, то пытаться найти глазами такие закономерности – занятие как минимум низкоэффективное.
Поэтому то, двигаясь в рамках парадигмы автоматизации обучения алгоритма, нам бы хотелось по максимуму исключить из процесса нахождения зависимостей между признаками человеческий фактор. Давайте рассмотрим несколько вариантов скрытых зависимостей и подумаем, как лучше всего организовать процесс их обнаружения.
Несколько примеров на синтетических данных со скрытыми линейными зависимостями
Вариант зависимости 1. Xj = K*Xi + C, K = 1
Первый вариант зависимости говорит: j-тый признак объекта линейно зависим от i-того признака, а также от свободного члена, представленного константой.
В нашем узком примере коэффициент пропорциональности будет равен единице, чтобы лучше можно было увидеть вклад свободного члена.
Пусть b = a — 1, d = c – 1.1 для класса 0 и наоборот для класса 1 (b = a – 1.1, d = c – 1)
В данном случае, конечно же, очевидно, что новый столбец со значениями
(d – b)
даст для объектов 0-го и 1-го классов соответственно значения
(c – 1.1) – (a – 1) = c – a – 0.1
и
(c – 1) – (a – 1.1) = c – a + 0.1
соответственно. А это, в свою очередь, при однородности данных в колонках A и C (а это одно из условий в нашей задаче), даёт нам неплохой инструмент для разделения объектов. И мы как минимум можем рассчитывать на позитивный вклад данного нового столбца в итоговую классификацию.
Результат подобного вычисления на наших придуманных данных вы можете посмотреть в таблице 2:

Таблица 2
Подобная ситуация, несмотря на кажущуюся надуманность, в действительности имеет место быть в жизни. Примером может служить необходимость для реализации некоего условия выполнить ряд регламентированных действий, имеющих константный набор сайд-эффектов. В случае с ядерными процессорами в нашем примере константная деградация вычислительной мощности может быть связана с необходимостью запуска фиксированного процесса для выхода на работу под нагрузкой. В жизни – запуск дополнительного генератора, фиксированное выделение ресурсов в резерв, энергия для запуска ДВС или промышленного генератора на ТЭС и т.д.
Однако выбор именно данной функции F(d, b) в реальной задаче конечно же не будет очевидным. Поэтому давайте рассмотрим для начала, к каким результатам приведёт нас иной выбор F(Xi, Xj)
F(Xi, Xj) = Xi/Xj
Говоря в терминах признаков нашей задачи, здесь мы можем попытаться измерить например деградацию вычислительной мощности под нагрузкой (B/D). Причём, исходя из предположения, что такая деградация не зависит от константы, а является полностью относительной величиной.
Давайте посмотрим, что получится в результате.
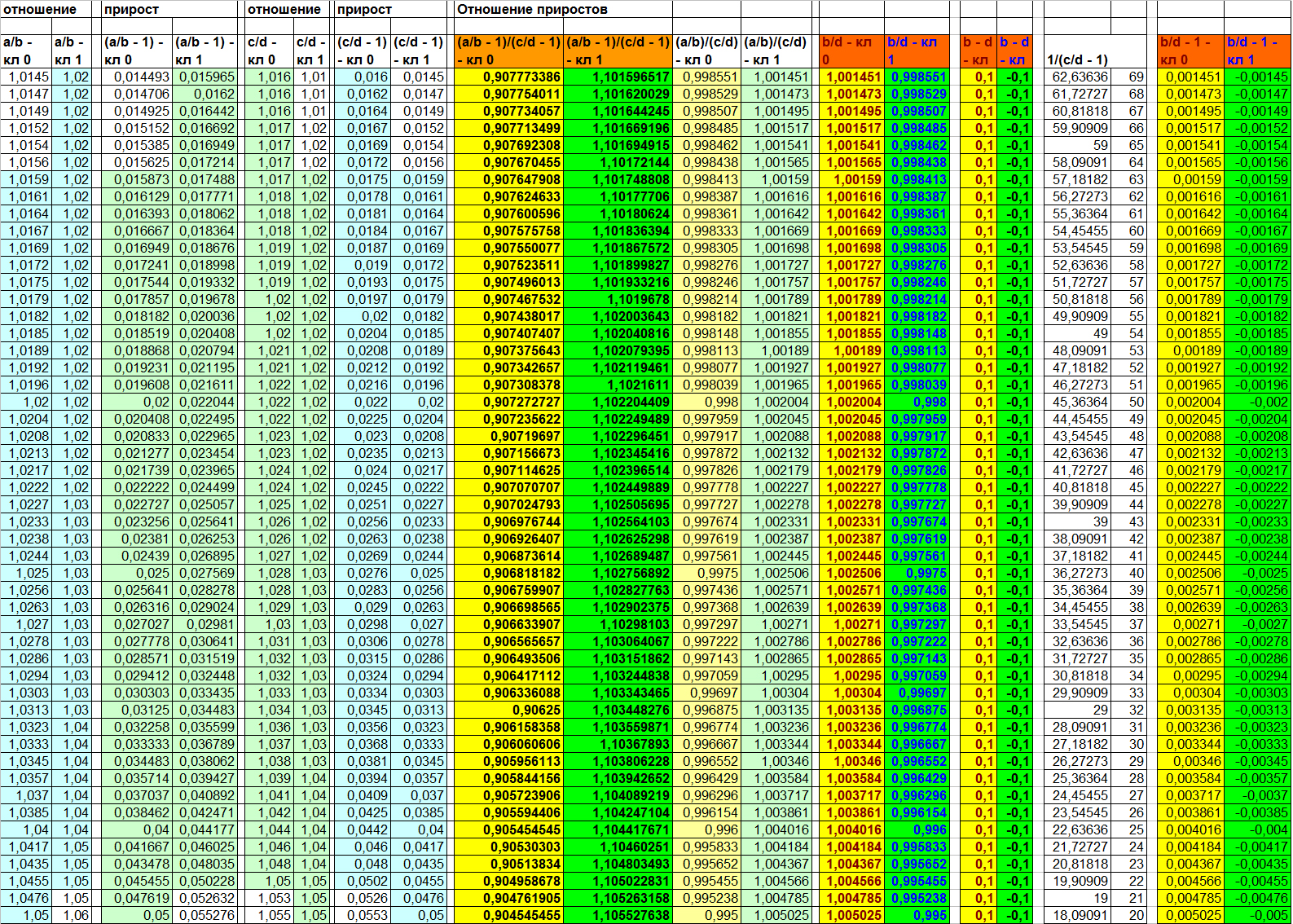
Таблица 3
Как можно увидеть в таблице 3, отношения (A/B) и (C/D) информативными не являются. Объекты противоположных классов на них по прежнему сильно перемешаны. А вот отношение B/D ожидаемо делает выборку линейно разделимой. Прямо как и в случае (B – D). Однако, забегая немного вперёд, скажу, что причина данной линейной разделимости по данному признаку всё же несколько иная, нежели для функции разности. Это будет наглядно видно на следующем примере.
Пока же давайте опустим этот нюанс и подумаем, что может быть не так в данном варианте зависимости. Для алгоритма — скорее всего ничего. А вот для человека визуально признаки для обоих классов могут показаться очень близкими. Конечно, в данном примере все значения красиво распределились по разные стороны от единицы, но в жизни такой наглядности может и не быть. Как же решить данную косметическую проблемку? Один из простых вариантов – посчитать прирост значения в числителе относительно величины значения в знаменателе. Что это значит?
Вычисляя отношение (X/Y), мы получаем ответ на вопрос «Сколько раз Y поместится в величину X». Однако же порой выгоднее решить вопрос «Сколько Y-ов нужно прибавить к величине Y, чтобы получился X». Во втором случае мы ищем прирост. Прирост может быть положительным и отрицательным и выражается простой формулой (X/Y – 1). Минус один – потому что за единицу измерения мы берём один Y.
Давайте ещё раз посмотрим в таблицу 3 (на две самые правые колонки) и обратим внимание на то, что теперь мы наглядно видим, что прирост для объектов разных классов есть величина разнознаковая. Стало быть, мы можем говорить о разнонаправленности прироста B от D для разных классов. И именно этот фактор в данном случае в действительности и играет ключевую роль в том, что признак (B/D) делает выборку линейно разделимой. Вывод: каждая из функций: (B – D) и (B/D) (или B/D — 1) делает выборку линейно разделимой несколько иным способом, а значит, возможны ситуации, когда лишь одна из них будет продуктивной для некоторой пары признаков. Но об этом более подробно чуть позже. Сейчас же давайте перейдём к третьей функции – последней для первого примера.
(A/B) / (C/D) – отношение линейных связей
или
(A/B — 1) / (C/D — 1) – отношение приростов
Что может побудить нас считать отношения линейных связей или отношения приростов? В нашем примере двух разных производителей техники такое вычисление имеет следующий смысл: «насколько изменится зависимость производительности от оборотов при подключении нагрузки».
Что ж, вполне законный вопрос. Учитывая, что речь идёт о разных производителях, разное поведение техники при повышении нагрузки вполне ожидаемо. В жизненных же ситуациях мы можем вести речь о том, что есть две взаимосвязи: F(Xi, Xj) и F(Xii, Xjj), и каждая из них в действительности есть функция от неизвестного нам набора параметров: F(M) и F’(M). И если такая гипотеза верна, мы можем предполагать, что даже если каждая из функций F и F’ одинаково проявляет себя для объектов разных классов, их композиция F”(F, F’) может проявляться различно на объектах разных классов, так как в действительности у этих разных классов значимо различны неизвестные нам параметры из множества M.
В нашем примере, конечно, мы изначально знаем, откуда растут ноги у такой взаимосвязи второго порядка, так как сами и составляли соответствующим образом данные. В жизни же мы можем этого не знать и рассчитывать лишь на то, что такая взаимосвязь существует. И следовательно пытаться её найти.
Давайте вернёмся к таблице 3 (четыре центральных колонки) и посмотрим, как проявляют себя данные функции для пар (A/B) и (C/D). Мы видим, что обе они делают выборку линейно разделимой. Как и рассмотренные ранее (B – D) и (B/D).
Единственным важным различием в данном примере является то, что значения функции (A/B) / (C/D) лежат весьма близко друг к другу, а вот ширина разделяющей полосы для объектов при использовании функции (A/B — 1) / (C/D — 1) значительно шире. Глядя на такой результат, можно задаться двумя вопросами:
- Так ли важно это различие?
- Всегда ли обе функции показывают одинаковую разделяющую способность?
Ответ на первый вопрос: Да, если мы планируем так или иначе включать в композицию метрические методы классификации. Ведь при более широкой разделяющей полосе лучше срабатывает гипотеза компактности. К тому же мы можем вести речь и о качестве визуализации. Справедливости ради стоит, конечно, отметить, что в данном примере метрические методы после обучения всё равно безошибочно разделят выборку по признаку (A/B) / (C/D). Однако в жизни взаимопроникновение при использовании метрики может оказаться куда более существенным.
Ответ же на второй вопрос для данного примера, пожалуй, не является достаточно очевидным. Поэтому давайте оставим его висящим в воздухе до рассмотрения следующего примера.
Вариант зависимости 2. Xj = K*Xi + C, K = 1, C – однознаковый для обоих классов
Данный пример – частный случай первого, в котором свободный член принимает для всех объектов значение либо больше, либо меньше нуля. Посмотрим, к каким эффектам это приведёт.
Пусть b = a — 1 для обоих классов, а вот d = c – 1.2 для класса 0 и c – 1.3 для класса 1)
В данном случае, конечно же, очевидно, что новый столбец со значениями
(B — D) даст для объектов 0-го и 1-го классов соответственно значения
(c – 1) – (a – 1.2) = c – a + 0.2
и
(c – 1) – (a – 1.3) = c – a + 0.3
соответственно. А это, в свою очередь, при однородности данных в колонках A и C (а это одно из условий в нашей задаче), даёт нам неплохой инструмент для разделения объектов. И мы опять как минимум можем рассчитывать на позитивный вклад данного нового столбца в итоговую классификацию.
Результат подобного вычисления на наших придуманных данных вы можете посмотреть в таблице 4:
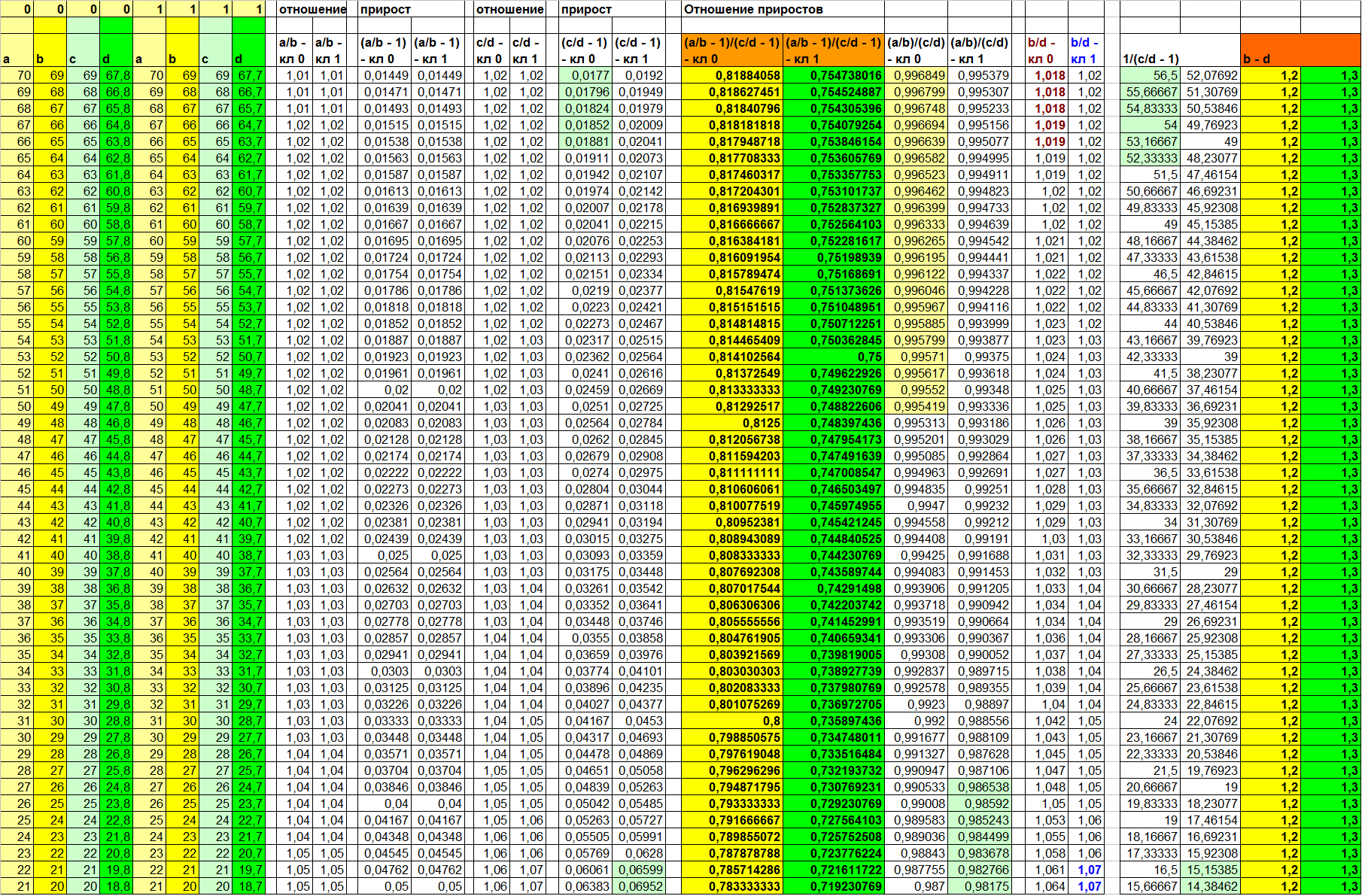
Таблица 4
Левые 8 колонок — актуальные значения признаков a, b, c, d для классов 0 и 1. Значения в остальных колонках — вычисленные в соответствии с функцией в заголовке. Значения (B — D) в двух правых колонках.
Итак, давайте посмотрим, что даст нам применение уже известных функций, которые в примере 1 смогли сделать выборку линейно разделимой.
F(Xi, Xj) = Xi/Xj
Как можно видеть в таблице 4, информативных отношений в данном случае найти не удаётся. И даже отношение (B/D) – колонок, значения в которых вычислены нами разными способами, не даёт нам сколь бы то ни было удовлетворительного результата (5-ая и 6-ая колонки справа). Но в чём же дело? Мы же всего лишь немного изменили значение свободного члена! Причина в том, что в первом примере свободный член для разных классов имел разный знак. И именно это и делало выборку линейно разделимой на признаке (B/D).
(A/B) / (C/D) – отношение линейных связей или
(A/B — 1) / (C/D — 1) – отношение приростов
Напомню, что в нашем надуманном примере про компьютеры лепреконов такое вычисление имеет смысл: «насколько изменится зависимость производительности от оборотов под нагрузкой».
На наших специально подогнанных и отсортированных данных мы невооружённым глазом видим, что деградация производительности под нагрузкой у машин фирмы The First немного выше, чем у машин фирмы Black Zero. (Но почему же тогда они стоят дороже? Очевидно, Black Zero пытается выжать из своих ядерных процессоров больше, чем те могут потянуть, сохранив при этом надёжность. Поэтому то они и служат в пять раз меньше, чем процессоры The First! Негоже жертвовать качеством в угоду маркетингу, Black Zero!)
Ну да вернёмся к нашим взаимосвязям. Если вновь заглянуть в таблицу 4, можно заметить одну очень интересную вещь!
Отношение приростов (A/B — 1) / (C/D — 1) делает выборку линейно разделимой, в то время как отношение линейных связей (A/B) / (C/D) оставляет довольно большой диапазон неопределённости! К слову говоря, вот и ответ на вопрос «Всегда ли обе функции показывают одинаковую разделяющую способность?»
(В таблице 4 это колонки с 7-ой по 10-ую справа. Непересекающиеся значения выделены цветом)
Что ж. Самое время перейти к третьему примеру, а пока просто запомнить следующее:
- функции отношения линейных связей и отношения приростов не всегда показывают одинаковую разделяющую способность;
- в примере, когда разделяющая способность функции отношения приростов была выше разделяющей способности функции отношения линейных связей, также стопроцентную разделяющую способность проявила функция разности, а вот отношения пар признаков были мало информативны для построения оптимального классификатора.
Вариант зависимости 3. Xj = K*Xi + C, K != 1, C = 0
Ещё один частный случай, но в котором в неизвестной зависимости играет роль коэффициент, а не свободный член.
Пусть b = a — 1 для обоих классов, а вот d = (c * 0.99) для класса 0 и (c * 0.98) для класса 1)
Результаты вычислений приведены в таблице 5. Рассмотрим их бегло.
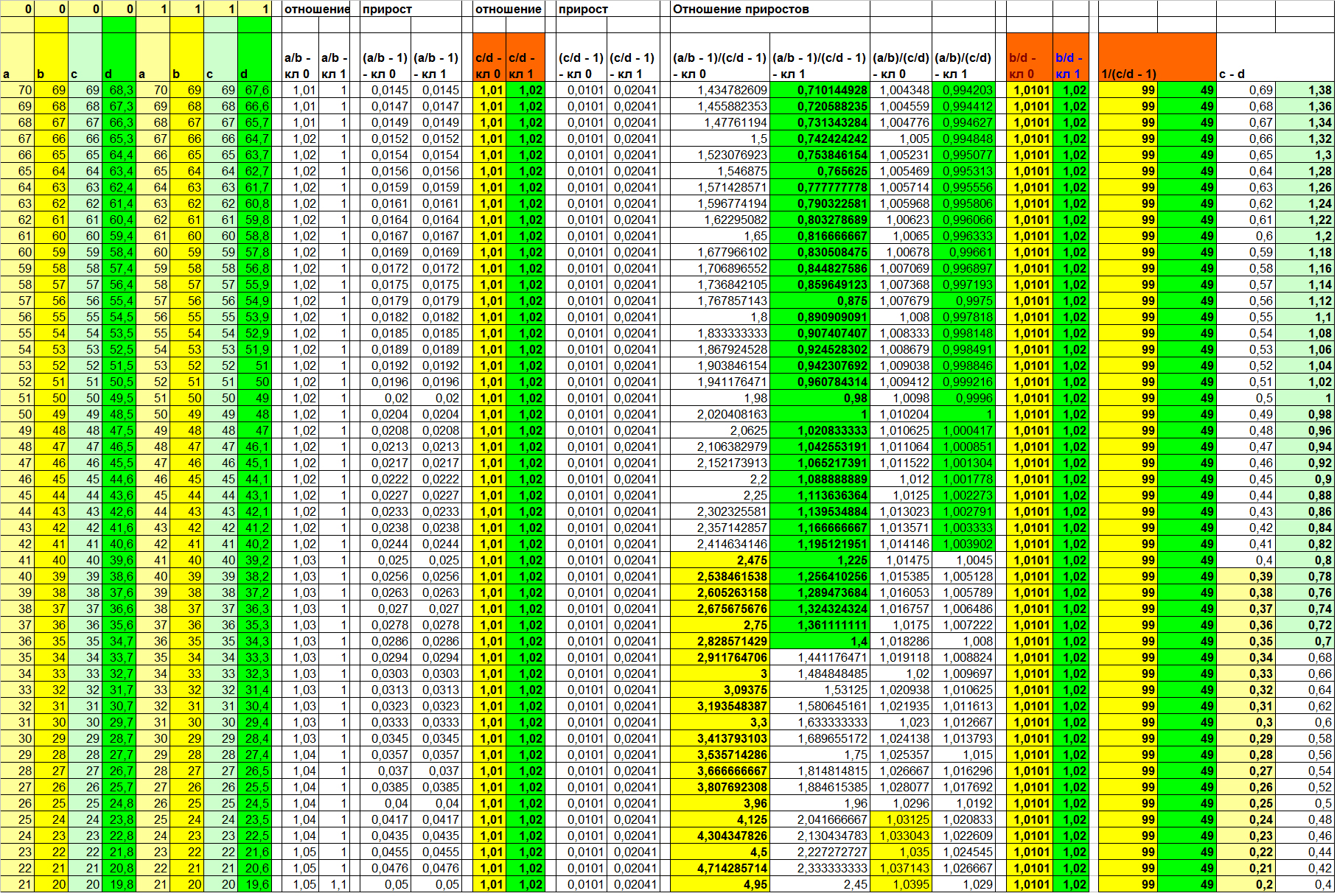
Таблица 5
Поскольку вклад в зависимость в этом примере вносит именно (и только!) коэффициент, ожидаемо сто процентную разделимость даёт функция отношения F(Xi, Xj) = Xi / Xj. А обратная к приросту (3-я и 4-ая колонки справа) ещё и улучшает визуализацию. Отношение линейных зависимостей вновь показывает результат, отличный от отношения приростов. Причём, опять в худшую сторону.
А вот бывшая в прошлых примерах стабильно информативной функция разности (две правые колонки) на этот раз оставляет довольно широкую зону неопределённости. И примечательно то, что она совпадает с зоной неопределённости функции отношения приростов. Сравните сами (колонки 1, 2 и 9, 10 справа; непересекающиеся значения разных классов выделены цветом).
Какова же будет картина, если вклад внесёт как коэффициент, так и свободный член? Ожидаемо ни одно из рассмотренных нами отношений в отдельности не делает выборку линейно разделимой. Однако диапазоны неопределённости для разных вычисленных колонок включают в себя разные подмножества объектов выборки! Что конечно же значит, что на множестве вычисленных признаков скорее всего возможно построить разделяющую гиперплоскость, на сто процентов разделяющую объекты разных классов.
Давайте на примере данных в таблице 6 рассмотрим, как проявила себя та или иная функция при заданных нами при формировании данных зависимостях:
для класса 0:
B = A - 1
D = 0,95*B - 0,55
для класса 1:
B = A - 1,1
D = 0,965*B - 0,5

Таблица 6
Для вычисленных значений функций от B и D мы видим, что простое отношение, отношение линейных связей, прирост и обратная к приросту дали очень схожие результаты. При этом, как мы помним, в прошлом примере (таблица 5) простое отношение сделало выборку линейно разделимой, тогда как отношение линейных связей оставило весьма широкую зону неопределённости (что, к слову, обусловлено избыточностью применения для ситуации в прошлом примере функции отношения линейных связей).
Также мы видим, что отношение приростов, в отличие от прошлых примеров, разделило выборку хуже отношения линейных связей. А функция разности дала ещё худшую результативность, нежели отношение приростов (напомню, что во всех прошлых примерах их эффективности были одинаковыми). Это говорит о многом.
Во-первых, отношение приростов не обязательно должно показывать ту же результативность, что и простая разность.
Во-вторых, разные функции могут оставлять зоны неопределённости разной ширины — в зависимости от истинной природы искомой скрытой зависимости.
В-третьих, в зависимости от истинной природы искомой скрытой зависимости разные функции могут дать наилучший результат разделения объектов разных классов.
Перед тем, как перейти к тому, какие ещё могут существовать скрытые взаимосвязи и как лучше организовать их поиск, приведу ещё один пример синтетических данных с зависимой колонкой D. Но на этот раз я намеренно не буду приводить истинную функцию D(a, b, c). Взгляните на таблицу 7 и ещё раз убедитесь в верности трёх выводов, приведённых немного выше.
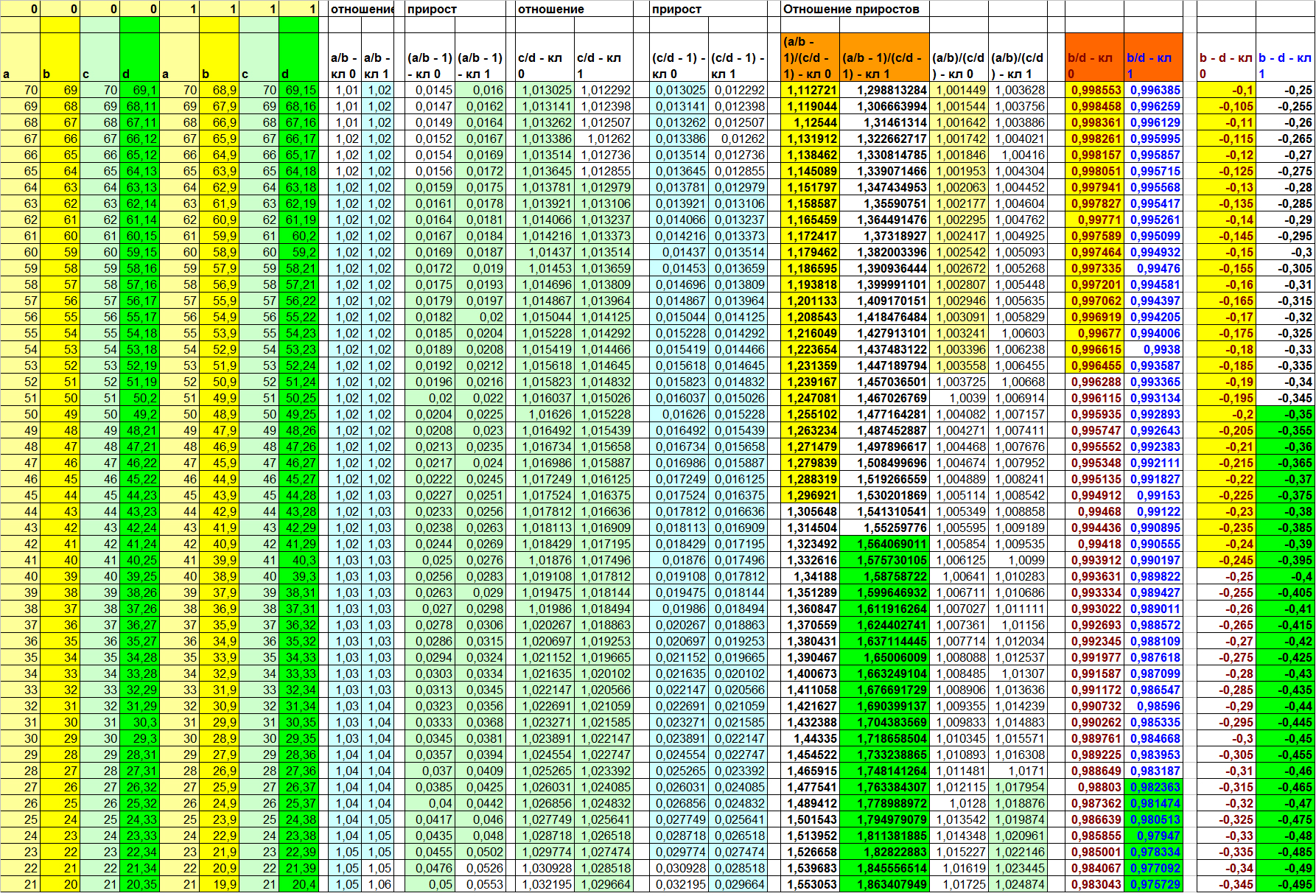
Таблица 7
Какие ещё скрытые зависимости могут содержаться в данных
В примерах выше мы использовали довольно примитивную линейную зависимость между признаками. Но может ли быть такое, что зависимость будет выражена не линейной функцией, а какой-то иной, более сложной?
Почему бы и нет. Например, представьте себе данные, собираемые датчиками в среде размножения колонии зелёных микроорганизмов. Если предположить, что фиксируется концентрация продуктов жизнедеятельности M, а также ряд объективных физических параметров среды, включая освещённость lx, то мы можем полагать, что присутствует зависимость M(lx). Но линейна ли такая зависимость. Если положить, что освещённость линейно влияет на скорость размножения бактерий, а концентрация ПЖД — линейно зависит от численности колонии, то зависимость должна быть квадратичной. Причина — способ размножения одноклеточных. А именно — деление клеток. Думаю, здесь излишне доказывать, что увеличение скорости деления одноклеточных квадратично (от скорости) повлияет на их численность через время t. Следовательно, мы можем пытаться например вычислить отношение (√M / lx), полагаемое нами как некоторая аппроксимация искомой линейной зависимости скорости размножения зелёных бактерий от освещённости. И если два вида зелёных бактерий и впрямь различаются тем, насколько освещённость влияет на их скорость размножения, то данный новый признак наверняка сможет внести свой полезный вклад в качество итогового алгоритма классификации.
Конечно, зависимости могут быть самыми разными, и в основе лежит смысл, вложенный в тот или иной признак. Однако же давайте уйдём от смысловой нагрузки признаков, которыми описаны объекты выборки, а вместо этого подумаем, как можно автоматизировать процесс поиска скрытых зависимостей.
Автоматизация поиска зависимостей
Итак, мы хотим определить, есть ли в нашем признаковом описании скрытые зависимости. Положим, мы решили не искать сложных алгоритмов выбора пар признаков, и просто проверить нашу гипотезу о наличии связи для всего множества признаков N: {X1… Xn}. Начать мы решаем с пар признаков, и для каждой пары вычислить некоторое значение — результат применения для данной пары некоторой функции из множества M: {F1(Xi, Xj)… Fm(Xi, Xj)}. При этом мы полагаем, что функции множества уже отобраны нами с учётом некоторой специфики нашей задачи.
Несложно догадаться, что число пар, для каждой из которых мы хотим применить m функций из множества M, есть число сочетаний из n по 2, то есть:
n! / (2! * (n - 2)!) = n * (n - 1) / 2 = (n² - n) / 2 = ½ n² - ½ n
Видно, что мы имеем дело с асимптотической сложностью O(n²).
А из этого вытекает два вывода:
- Такой полный перебор допустим только для выборки с числом признаков, не превышающим некоторой пороговой величины, вычисленной заранее.
- Вычисление зависимостей второго порядка, в которых участвуют уже вычисленные на основе первичных данных колонки (как отношение приростов), допустимо лишь в том случае, если существует строгий алгоритм отбора пар для таких проверок. В противном случае алгоритм полного прохода будет иметь сложность O(n⁴). Хотя в общем случае зависимости второго порядка так или иначе основаны пусть и на порой более слабых, но всё же достаточно информативных зависимостях первого порядка.
Соответственно, из сказанного выше следует, что возможны два случая:
- Число признаков меньше пороговой величины, и мы можем позволить себе проверку гипотезы на каждой паре.
- Число признаков превышает пороговую величину, и нам необходима стратегия отбора пар, на которых мы будем полноценно проверять гипотезу.
Рассмотрим сначала первый случай.
Число признаков меньше пороговой величины
Строго говоря, для нас не столько важно выявление некоей зависимости само по себе, сколько её разное поведение на объектах разных классов. Поэтому мы можем просто опустить момент проверки на предмет наличия зависимости, а вместо этого сразу провести проверку на предмет полезности новой колонки. Для этого достаточно применить один из известных быстрых классификаторов для данной колонки, измерив среднюю величину интересующей нас метрики качества на скользящем контроле. И затем, если показатель интересующей нас метрики качества выше заданной нами пороговой величины, оставить новую колонку, либо удалить её, если качество не дотянуло до требуемого.
Конечно же, здесь читателю в голову может прийти мысль: а что, если новая колонка вычислена на основе изначального признака, и без того имеющего высокую полезность для итогового алгоритма классификации? Ведь в этом случае получится, что мы просто создали лишний признак, опирающийся на уже имевшийся! Порождение мультиколлинеарности в чистом виде! Так вот именно на это мы и задаём порог метрики качества классификации для производных признаков. Несложно догадаться, что поскольку мы вычисляем функцию от пары признаков (а не от одного!), итог может быть и просто шумом, даже если на входе обе колонки были весьма информативными.
В этом несложно убедиться на примере синтетических данных, где значения в каждом признаке — независимо сгенерированные величины с заданными средней и отклонением. Причём, так, чтобы между средними разных классов было различие, а распределение на объектах каждого класса — нормальное (например, с помощью numpy.random.normal). Так вот поскольку мы априори генерируем значения признаков независимо друг от друга, попытка найти зависимости приводит лишь к зашумлённости, а производные признаки не дают удовлетворительного качества классификации.
Так вот приведённый выше пример говорит в пользу того, что если производный признак оказался информативным, мы можем судить о наличии взаимосвязи.
Пороговую величину для производных признаков можно выбирать разными способами. Либо разом для всей выборки, что явно проще, либо индивидуально для каждой пары. Во втором случае мы можем варьировать значение порога входа в зависимости от показателей интересующих нас метрик качества на каждой из колонок, поданных на вход.
Однако несмотря на кажущуюся логичность второго варианта выбора порога, в нём есть очень неприятный подводный камень. Речь о том, что не совсем верно выбирать в качестве порога величину метрики качества на одном из родительских столбцов. Причина в том, что может случиться и так, что производный признак с несколько более низкой величиной качества будет и впрямь аппроксимацией новой зависимости, и как следствие, может ошибаться на ином, нежели родители, множестве объектов. А это значит, что его включение в множество признаков для анализа может радикально повысить итоговое качество классификации!
Что же касается выбора общего порога входа для всех производных признаков, то здесь на мой взгляд весьма удобно выбрать порог исходя из того, какие значения интересующей нас метрики качества имеют (при применении по отдельности!) исходные колонки. Так, если для простоты примера взять Accuracy, то для его значений на исходных колонках [0.52, 0.53, 0.53, 0.54, 0.55, 0.57, 0.59, 0.61, 0.63] оптимальный порог для производных данных скорее всего будет лежать где-то в районе 0,6 (как показывает практика). Так или иначе, это не столь важно, ведь параметр является обучаемым, а его обучение повысит сложность алгоритма только линейно. При обучении же этого параметра так или иначе можно отталкиваться от плотности распределения Accuracy исходных признаков (Accuracy здесь только потому, что на нём данный пример!).
В принципе, здесь всё просто. Поэтому перейдём ко второму случаю.
Число признаков превышает пороговую величину
Данное условие означает, что мы не можем позволить себе проводить полноценный замер полезности для каждого производного признака. Либо даже больше: не можем позволить себе для каждой пары признаков генерировать производный. Оно и понятно: просто представьте, что признаков у нас тысяча. В этом случае число сочетаний будет равно
999 * 1000 / 2 = 499 500
И это ещё умножить на число тестируемых функций!
И даже если наш сервер способен посчитать качество классификации выбранным алгоритмом по отдельно взятому признаку 100 раз в секунду, ждать почти полтора часа, пока отработает алгоритм генерации признаков только для одной из выбранных нами функций — занятие как минимум странное. Хотя, с другой стороны порождающее немало свободного времени =)
Ну да вернёмся к нашим баранам. Как можно решать данную задачу?
Попытка уменьшить число исходных признаков на основе их полезности для классификации может оказаться не лучшей идеей, ведь на примере синтетических данных в первой части статьи было наглядно показано, что производный признак, каждый из родителей которого в чистом виде совершенно непригоден для задачи классификации, при идеальных условиях способен сделать выборку линейно разделимой.
Как же тогда быть? Видимо, вычислять производные признаки всё же придётся, правда, с некоторыми ограничениями.
Во-первых, в зависимости от того, насколько превышен порог по числу исходных признаков, мы можем для оценки полезности производных признаков генерировать их лишь для части исходных объектов выборки. Не буду вдаваться в то, какого размера подвыборки следует брать — на этот вопрос неплохо отвечает математическая статистика.
Во-вторых, оценку полезности каждого производного признака следует проводить по урезанному функционалу. Опять же, в зависимости от степени превышенности порога числа исходных. То есть, если до этого мы использовали для оценки качества производного признака, к примеру, метод k ближайших соседей с урезанным функционалом обучения, то теперь мы можем использовать его же, но с фиксировано заданными параметрами. Или применить для взвешивания полученного набора признаков метод опорных векторов с параметрами по умолчанию, и затем отбросить колонки с весом ниже определённого. Или же для более экстремальных случаев (с количеством исходных признаков) можно просто применить один из статистических критериев, например, простой Q-критерий Розенбаума. К сожалению, применение такого рода критериев не сможет помочь нам отобрать признаки, имеющие перемежающиеся пики в их распределениях плотности вероятности или просто разнонаправлено смещённые медианы.
Например, пусть значения получившегося признака для классов 1 и -1 равны соответственно:
[9,9,9,9,9,8,8,8,8,8,8,8,8,7,7,7,7,6,6,5,4,3,2,2,1,1,1,1,1,0,0,0,0,0,0,0,0,0]
[9,8,8,7,7,6,6,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,3,3,3,3,3,2,2,1,0]
или (для смещённых средних):
[1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6] VS [1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,5,5,6]
Очевидно, что в обоих случаях критерий Розенбаума посчитает, что выборки не различаются вообще. Конечно, в данном случае превосходно сработает критерий Пирсона, так как он предусматривает разбиение на некоторое число непересекающихся интервалов и подсчёт числа значений для каждого интервала в отдельности. Однако при этом критерий Пирсона потребует и больше времени на выполнение, а это именно тот параметр, который мы пытаемся оптимизировать при первом — грубом приближении.
В-третьих, по причине того, что мы допускаем снижение качества оценки полезности производных признаков, мы также немного снижаем порог входа.
Таким образом, мы сравнительно малой кровью избавляемся от внушительного числа самых неинформативных признаков. А вот на оставшихся (опять же, в зависимости от их числа) можем применить методы более качественной оценки полезности признака.
Если подытожить, то мы говорим о деградации качества оценки для первичного быстрого отбрасывания самых неинформативных признаков для последующего более качественного оценивания оставшихся.
Что ж, пора, пожалуй, завершать. Если коротко подытожить всё вышесказанное, стоит отметить следующие моменты.
Выводы
- Часто для признакового описания данных в задачах классификации бывает возможно найти скрытые зависимости F(Xi, Xj), которые способны выступить в роли самостоятельных признаков и повысить качество классификации.
- Скрытые зависимости между признаками могут описываться разными функциями, и в разных случаях разные функции могут проявить себя лучше остальных.
- Для автоматизации процесса нахождения скрытых зависимостей стоит изначально выбрать набор функций, адекватность применения которых зависит от специфики задачи.
- Число производных столбцов для анализа равно k*(n² — n) / 2, где k — число выбранных функций, n — число исходных признаков.
- Для не очень большого числа признаков можно позволить себе полный перебор всех пар с полноценной проверкой полезности для каждого полученного признака.
- Если число исходных признаков превышает некоторую пороговую величину, проверку производных признаков стоит проводить в два этапа: быстрое отбрасывание самых неинформативных производных признаков и последующий более качественный разбор оставшихся. Гипотетически есть возможность вычисления производных признаков F(Xi, Xj) от множества признаков M’, которые даст нам применение метода главных компонент на исходное множество признаков M, но встаёт вопрос о том, все ли скрытые зависимости в этом случае могут быть проявлены.
Что ж, на этом на этот раз всё. И да, теперь то уж мы точно сможем помочь лепреконам более эффективно находить диссидентов среди своих сородичей!
Исследуем отношение между переменными¶
В этой главе исследуются отношения между переменными.
-
Мы будем визуализировать отношения с помощью диаграмм рассеяния (scatter plots), диаграмм размаха (box plots) и скрипичных диаграмм (violin plots),
-
И мы будем количественно определять отношения, используя корреляцию (correlation) и простую регрессию (simple regression).
Самый важный урок этой главы заключается в том, что вы всегда должны визуализировать взаимосвязь между переменными, прежде чем пытаться ее количественно оценить; в противном случае вас могут ввести в заблуждение.
In [1]:
from os.path import basename, exists def download(url): filename = basename(url) if not exists(filename): from urllib.request import urlretrieve local, _ = urlretrieve(url, filename) print('Downloaded ' + local) download('https://github.com/AllenDowney/' + 'ElementsOfDataScience/raw/master/brfss.hdf5')
Изучение отношений¶
В качестве первого примера мы рассмотрим взаимосвязь между ростом и весом.
Мы будем использовать данные из Системы наблюдения за поведенческими факторами риска (BRFSS), которая находится в ведении Центров по контролю за заболеваниями по адресу https://www.cdc.gov/brfss.
В опросе приняли участие более 400 000 респондентов, но, чтобы произвести анализ, я выбрал случайную подвыборку из 100 000 человек.
In [2]:
import pandas as pd brfss = pd.read_hdf('brfss.hdf5', 'brfss') brfss.shape
Out[3]:
| SEX | HTM4 | WTKG3 | INCOME2 | _LLCPWT | _AGEG5YR | _VEGESU1 | _HTMG10 | AGE | |
|---|---|---|---|---|---|---|---|---|---|
| 96230 | 2.0 | 160.0 | 60.33 | 8.0 | 1398.525290 | 6.0 | 2.14 | 150.0 | 47.0 |
| 244920 | 2.0 | 163.0 | 58.97 | 5.0 | 84.057503 | 13.0 | 3.14 | 160.0 | 89.5 |
| 57312 | 2.0 | 163.0 | 72.57 | 8.0 | 390.248599 | 5.0 | 2.64 | 160.0 | 42.0 |
| 32573 | 2.0 | 165.0 | 74.84 | 1.0 | 11566.705300 | 3.0 | 1.46 | 160.0 | 32.0 |
| 355929 | 2.0 | 170.0 | 108.86 | 3.0 | 844.485450 | 3.0 | 1.81 | 160.0 | 32.0 |
BRFSS включает сотни переменных. Для примеров в этой главе я выбрал всего девять.
Мы начнем с HTM4, который записывает рост каждого респондента в см, и WTKG3, который записывает вес в кг.
In [4]:
height = brfss['HTM4'] weight = brfss['WTKG3']
Чтобы визуализировать взаимосвязь между этими переменными, мы построим диаграмму рассеяния (scatter plot).
Диаграммы рассеяния широко распространены и понятны, но их на удивление сложно правильно построить.
В качестве первой попытки мы будем использовать функцию plot с аргументом o, который строит круг для каждой точки.
см. документацию по plot
In [5]:
import matplotlib.pyplot as plt %matplotlib inline plt.plot(height, weight, 'o') plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Похоже, что высокие люди тяжелее, но в этом графике есть несколько моментов, которые затрудняют интерпретацию.
Первый из них – перекрытие (overplotted), то есть точки данных накладываются друг на друга, поэтому вы не можете сказать, где много точек, а где только одна.
Когда это происходит, результаты могут вводить в заблуждение.
Один из способов улучшить график – использовать прозрачность (transparency), что мы можем сделать с помощью ключевого аргумента alpha. Чем ниже значение alpha, тем прозрачнее каждая точка данных.
Вот как это выглядит с alpha=0.02.
In [6]:
plt.plot(height, weight, 'o', alpha=0.02) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Уже лучше, но на графике так много точек данных, что диаграмма рассеяния все еще перекрывается. Следующим шагом будет уменьшение размеров маркеров.
При markersize=1 и низком значении alpha диаграмма рассеяния будет менее насыщенной.
Вот как это выглядит.
In [7]:
plt.plot(height, weight, 'o', alpha=0.02, markersize=1) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Уже лучше, но теперь мы видим, что точки строятся отдельными столбцами. Это потому, что большая часть высоты была указана в дюймах и преобразована в сантиметры.
Мы можем разбить столбцы, добавив к значениям некоторый случайный шум; по сути, мы заполняем округленные значения.
Такое добавление случайного шума называется дрожанием (jittering).
Дрожание – это добавление случайного шума к данным для предотвращения перекрытия статистических графиков. Если непрерывное измерение округлено до некоторой удобной единицы, может произойти перекрытие. Это приводит к превращению непрерывной переменной в дискретную порядковую переменную. Например, возраст измеряется в годах, а масса тела – в фунтах или килограммах. Если вы построите диаграмму разброса веса в зависимости от возраста для достаточно большой выборки людей, там может быть много людей, записанных, скажем, с 29 годами и 70 кг, и, следовательно, в этой точке будет нанесено много маркеров (29, 70).
Чтобы уменьшить перекрытие, вы можете добавить к данным небольшой случайный шум. Размер шума часто выбирается равным ширине единицы измерения. Например, к значению 70 кг вы можете добавить количество u , где u – равномерная случайная величина в интервале [-0,5, 0,5]. Вы можете обосновать дрожание, предположив, что истинный вес человека весом 70 кг с равной вероятностью находится в любом месте интервала [69,5, 70,5].
Контекст данных важен при принятии решения о дрожании. Например, возраст обычно округляется в меньшую сторону: 29-летний человек может праздновать свой 29-й день рождения сегодня или, возможно, ему исполнится 30 завтра, но ей все равно 29 лет. Следовательно, вы можете изменить возраст, добавив величину v , где v – равномерная случайная величина в интервале [0,1]. (Мы игнорируем статистически значимый случай женщин, которым остается 29 лет в течение многих лет!)
Источник: Jittering to prevent overplotting in statistical graphics
Мы можем использовать NumPy для добавления шума из нормального распределения со средним 0 и стандартным отклонением 2.
см. документацию NumPy
In [8]:
import numpy as np noise = np.random.normal(0, 2, size=len(brfss)) height_jitter = height + noise
Вот как выглядит график с дрожащими (jittered) высотами.
In [9]:
plt.plot(height_jitter, weight, 'o', alpha=0.02, markersize=1) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Столбцы исчезли, но теперь мы видим, что есть строки, в которых люди округляют свой вес. Мы также можем исправить это с помощью дрожания веса.
In [10]:
noise = np.random.normal(0, 2, size=len(brfss)) weight_jitter = weight + noise
In [11]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Наконец, давайте увеличим масштаб области, где находится большинство точек данных.
Функции xlim и ylim устанавливают нижнюю и верхнюю границы для осей $x$ и $y$; в данном случае мы наносим рост от 140 до 200 сантиметров и вес до 160 килограмм.
Вот как это выглядит.
In [12]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Теперь у нас есть достоверная картина взаимосвязи между ростом и весом.
Ниже вы можете увидеть вводящий в заблуждение график, с которого мы начали, и более надежный, которым мы закончили. Они явно разные, и они предлагают разные истории о взаимосвязи между этими переменными.
In [13]:
# Set the figure size plt.figure(figsize=(8, 3)) # Create subplots with 2 rows, 1 column, and start plot 1 plt.subplot(1, 2, 1) plt.plot(height, weight, 'o') plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height') # Adjust the layout so the two plots don't overlap plt.tight_layout() # Start plot 2 plt.subplot(1, 2, 2) plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height') plt.tight_layout()
Смысл этого примера в том, что для создания эффективного графика разброса требуются некоторые усилия.
Упражнение: Набирают ли люди вес с возрастом? Мы можем ответить на этот вопрос, визуализировав взаимосвязь между весом и возрастом.
Но прежде чем строить диаграмму рассеяния, рекомендуется визуализировать распределения по одной переменной за раз. Итак, давайте посмотрим на возрастное распределение.
Набор данных BRFSS включает столбец AGE, который представляет возраст каждого респондента в годах. Чтобы защитить конфиденциальность респондентов, возраст округляется до пятилетних интервалов. AGE содержит середину интервалов (bins).
-
Извлеките переменную
'AGE'из фрейма данныхbrfssи присвойте ееage. -
Постройте функцию вероятности (Probability mass function, PMF) для
ageв виде гистограммы, используяPmfизempiricaldist.
empiricaldist– библиотека Python, представляющая эмпирические функции распределения.
In [14]:
try: import empiricaldist except ImportError: !pip install empiricaldist
In [15]:
from empiricaldist import Pmf
Упражнение: Теперь давайте посмотрим на распределение веса.
Столбец, содержащий вес в килограммах, – это WTKG3. Поскольку этот столбец содержит много уникальных значений, отображение его как функции вероятности (PMF) работает плохо.
In [17]:
Pmf.from_seq(weight).bar() plt.xlabel('Weight in kg') plt.ylabel('PMF') plt.title('Distribution of weight');
Чтобы получить лучшее представление об этом распределении, попробуйте построить график функции распределения (Cumulative distribution function, CDF).
Вычислите функцию распределения (CDF) нормального распределения с тем же средним значением и стандартным отклонением и сравните его с распределением веса.
Подходит ли нормальное распределение для этих данных? А как насчет логарифмического преобразования весов?
Упражнение: Теперь давайте построим диаграмму разброса (scatter plot) для weight и age.
Отрегулируйте alpha и markersize, чтобы избежать наложения (overplotting). Используйте ylim, чтобы ограничить ось y от 0 до 200 килограммов.
Упражнение: В предыдущем упражнении возрасты указаны в столбцах, потому что они были округлены до 5-летних интервалов (bins). Если мы добавим дрожание (jitter), диаграмма рассеяния покажет взаимосвязь более четко.
- Добавьте случайный шум к
ageсо средним значением0и стандартным отклонением2.5. - Создайте диаграмму рассеяния и снова отрегулируйте
alphaиmarkersize.
Визуализация отношений¶
В предыдущем разделе мы использовали диаграммы разброса для визуализации взаимосвязей между переменными, а в упражнениях вы исследовали взаимосвязь между возрастом и весом. В этом разделе мы увидим другие способы визуализации этих отношений, в том числе диаграммы размаха и скрипичные диаграммы.
Я начну с диаграммы разброса веса в зависимости от возраста.
In [23]:
age = brfss['AGE'] noise = np.random.normal(0, 1.0, size=len(brfss)) age_jitter = age + noise plt.plot(age_jitter, weight_jitter, 'o', alpha=0.01, markersize=1) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.ylim([0, 200]) plt.title('Weight versus age');
В этой версии диаграммы разброса я скорректировал дрожание весов, чтобы между столбцами оставалось пространство.
Это позволяет увидеть форму распределения в каждой возрастной группе и различия между группами.
С этой точки зрения кажется, что вес увеличивается до 40-50 лет, а затем начинает уменьшаться.
Если мы пойдем дальше, то сможем использовать ядерную оценку плотности (Kernel Density Estimation, KDE) для оценки функции плотности в каждом столбце и построения графика. И для этого есть название – скрипичная диаграмма (violin plot).
Библиотека Seaborn предоставляет функцию, которая создает скрипичную диаграмму, но прежде чем мы сможем ее использовать, мы должны избавиться от любых строк с пропущенными данными.
Вот так:
In [24]:
data = brfss.dropna(subset=['AGE', 'WTKG3']) data.shape
dropna() создает новый фрейм данных, который удаляет строки из brfss, где AGE или WTKG3 равны NaN.
Теперь мы можем вызвать функцию violinplot.
см. документацию по violinplot
In [25]:
import seaborn as sns sns.violinplot(x='AGE', y='WTKG3', data=data, inner=None) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Аргументы x и y означают, что нам нужно AGE на оси x и WTKG3 на оси y.
data – это только что созданный фрейм данных, который содержит переменные для отображения.
Аргумент inner=None немного упрощает график.
На рисунке каждая фигура представляет собой распределение веса в одной возрастной группе. Ширина этих форм пропорциональна предполагаемой плотности, так что это похоже на две вертикальные ядерные оценки плотности (KDE), построенные вплотную друг к другу (и залитые красивыми цветами).
Другой, связанный с этим способ просмотра данных, называется диаграмма размаха (ящик с усами, box plot).
Код для создания диаграммы размаха очень похож.
см. документацию по boxplot
In [26]:
sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Я включил аргумент whis=10, чтобы отключить функцию, которая нам не нужна.
Каждый прямоугольник представляет распределение веса в возрастной группе. Высота каждого прямоугольника представляет собой диапазон от 25-го до 75-го процентиля. Линия в середине каждого прямоугольника – это медиана. Шипы, торчащие сверху и снизу, показывают минимальное и максимальное значения.
На мой взгляд, этот график дает лучшее представление о взаимосвязи между весом и возрастом.
-
Глядя на медианы, кажется, что люди в возрасте от 40 лет являются самыми тяжелыми; люди младшего и старшего возраста легче.
-
Глядя на размеры ящиков, кажется, что люди в возрасте от 40 также имеют наибольший разброс в весе.
-
Эти графики также показывают, насколько искажено распределение веса; то есть самые тяжелые люди намного дальше от медианы, чем самые легкие.
Для данных, которые склоняются к более высоким значениям, иногда полезно рассматривать их в логарифмической шкале.
Мы можем сделать это с помощью Pyplot-функции yscale.
In [27]:
sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10) plt.yscale('log') plt.xlabel('Age in years') plt.ylabel('Weight in kg (log scale)') plt.title('Weight versus age');
Чтобы наиболее четко показать взаимосвязь между возрастом и весом, я бы использовал этот рисунок.
В следующих упражнениях у вас будет возможность создать скрипичную диаграмму и диаграмму размаха.
Упражнение: Ранее мы рассмотрели диаграмму рассеяния (scatter plot) по росту и весу и увидели, что более высокие люди, как правило, тяжелее. Теперь давайте более подробно рассмотрим диаграмму размаха (box plot).
Фрейм данных brfss содержит столбец с именем _HTMG10, который представляет высоту в сантиметрах, разбитую на группы по 10 см.
-
Составьте диаграмму размаха, показывающую распределение веса в каждой группе роста.
-
Постройте ось Y в логарифмическом масштабе.
Предложение: если метки на оси x сталкиваются, вы можете повернуть их следующим образом:
plt.xticks(rotation='45')Упражнение: В качестве второго примера давайте посмотрим на взаимосвязь между доходом (income) и ростом.
В BRFSS доход представлен как категориальная переменная; то есть респондентов относят к одной из 8 категорий доходов. Имя столбца – INCOME2.
Прежде чем связывать доход с чем-либо еще, давайте посмотрим на распределение, вычислив функцию вероятности (PMF).
-
Извлеките
INCOME2изbrfssи присвойте егоincome. -
Постройте функцию вероятности (PMF) для
incomeв виде гистограммы (bar chart).
Примечание: вы увидите, что около трети респондентов относятся к группе с самым высоким доходом; лучше, если бы было больше лидирующих групп, но мы будем работать с тем, что у нас есть.
Упражнение: Создайте скрипичную диаграмму (violin plot), которая показывает распределение роста в каждой группе дохода.
Вы видите взаимосвязь между этими переменными?
Корреляция¶
В предыдущем разделе мы визуализировали отношения между парами переменных. Теперь мы узнаем о коэффициенте корреляции, который количественно определяет силу этих взаимосвязей.
Когда люди говорят “корреляция”, они имеют в виду любую связь между двумя переменными. В статистике обычно это означает коэффициент корреляции Пирсона, который представляет собой число от -1 до 1, которое количественно определяет силу линейной связи между переменными.
Для демонстрации я выберу три столбца из набора данных BRFSS:
In [31]:
columns = ['HTM4', 'WTKG3', 'AGE'] subset = brfss[columns]
Результатом является фрейм данных только с этими столбцами.
С этим подмножеством данных мы можем использовать метод corr, например:
Out[32]:
| HTM4 | WTKG3 | AGE | |
|---|---|---|---|
| HTM4 | 1.000000 | 0.474203 | -0.093684 |
| WTKG3 | 0.474203 | 1.000000 | 0.021641 |
| AGE | -0.093684 | 0.021641 | 1.000000 |
Результатом является корреляционная матрица. В первой строке корреляция HTM4 с самим собой равна 1. Это ожидаемо; корреляция чего-либо с самим собой равна 1.
Следующая запись более интересна; соотношение роста и веса составляет около 0.47. Коэффициент положительный, это означает, что более высокие люди тяжелее, и он умеренный по силе, что означает, что он имеет некоторую прогностическую ценность. Если вы знаете чей-то рост, вы можете лучше предположить его вес, и наоборот.
Корреляция между ростом и возрастом составляет примерно -0.09. Коэффициент отрицательный, это означает, что пожилые люди, как правило, ниже ростом, но он слабый, а это означает, что знание чьего-либо возраста не поможет, если вы попытаетесь угадать их рост.
Корреляция между возрастом и весом еще меньше. Напрашивается вывод, что нет никакой связи между возрастом и весом, но мы уже видели, что она есть. Так почему же корреляция такая низкая?
Помните, что зависимость между весом и возрастом выглядит так.
In [33]:
data = brfss.dropna(subset=['AGE', 'WTKG3']) sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Люди за сорок – самые тяжелые; люди младшего и старшего возраста легче. Итак, эта связь нелинейна.
Но корреляция измеряет только линейные отношения. Если связь нелинейная, корреляция обычно недооценивает ее силу.
Чтобы продемонстрировать, я сгенерирую несколько поддельных данных: xs содержит точки с равным интервалом между -1 и 1.
ys – это квадрат xs плюс некоторый случайный шум.
In [34]:
xs = np.linspace(-1, 1) ys = xs**2 + np.random.normal(0, 0.05, len(xs))
Вот диаграмма рассеяния для xs и ys.
In [35]:
plt.plot(xs, ys, 'o', alpha=0.5) plt.xlabel('x') plt.ylabel('y') plt.title('Scatter plot of a fake dataset');
Понятно, что это сильная связь; если вам дано x, вы можете гораздо лучше догадаться о y.
Но вот корреляционная матрица:
Out[36]:
array([[1. , 0.01135475],
[0.01135475, 1. ]])
Несмотря на то, что существует сильная нелинейная зависимость, вычисленная корреляция близка к 0.
В общем, если корреляция высока, то есть близка к
1или-1, вы можете сделать вывод, что существует сильная линейная зависимость.
Но если корреляция близка к0, это не означает, что связи нет; может быть связь нелинейная.
Это одна из причин, по которой я считаю, что корреляция не является хорошей статистикой.
В частности, корреляция ничего не говорит о наклоне. Если мы говорим, что две переменные коррелируют, это означает, что мы можем использовать одну для предсказания другой. Но, возможно, это не то, о чем мы заботимся.
Например, предположим, что нас беспокоит влияние увеличения веса на здоровье, поэтому мы строим график зависимости веса от возраста от 20 до 50 лет.
Я создам два поддельных набора данных, чтобы продемонстрировать суть дела. В каждом наборе данных xs представляет возраст, а ys – вес.
Я использую np.random.seed для инициализации генератора случайных чисел, поэтому мы получаем одни и те же результаты при каждом запуске.
In [37]:
np.random.seed(18) xs1 = np.linspace(20, 50) ys1 = 75 + 0.02 * xs1 + np.random.normal(0, 0.15, len(xs1)) plt.plot(xs1, ys1, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #1');
А вот и второй набор данных:
In [38]:
np.random.seed(18) xs2 = np.linspace(20, 50) ys2 = 65 + 0.2 * xs2 + np.random.normal(0, 3, len(xs2)) plt.plot(xs2, ys2, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #2');
Я построил эти примеры так, чтобы они выглядели одинаково, но имели существенно разные корреляции:
In [39]:
rho1 = np.corrcoef(xs1, ys1)[0][1] rho1
In [40]:
rho2 = np.corrcoef(xs2, ys2)[0][1] rho2
В первом примере сильная корреляция, близкая к 0.75. Во втором примере корреляция умеренная, близкая к 0.5. Поэтому мы можем подумать, что первые отношения более важны. Но посмотрите внимательнее на ось y на обоих рисунках.
В первом примере средняя прибавка в весе за 30 лет составляет менее 1 килограмма; во втором больше 5 килограммов!
Если нас беспокоит влияние увеличения веса на здоровье, второе соотношение, вероятно, более важно, даже если корреляция ниже.
Статистика, которая нас действительно волнует, – это наклон линии, а не коэффициент корреляции.
В следующем разделе мы увидим, как оценить этот наклон. Но сначала давайте попрактикуемся с корреляцией.
Упражнения: Цель BRFSS – изучить факторы риска для здоровья, поэтому в него включены вопросы о диете.
Столбец _VEGESU1 представляет количество порций овощей, которые респонденты ели в день.
Посмотрим, как эта переменная связана с возрастом и доходом.
- Во фрейме данных
brfssвыберите столбцы'AGE',INCOME2и_VEGESU1. - Вычислите корреляционную матрицу для этих переменных.
Упражнение: В предыдущем упражнении корреляция между доходом и потреблением овощей составляет около 0.12. Корреляция между возрастом и потреблением овощей составляет примерно -0.01.
Что из следующего является правильной интерпретацией этих результатов?
- A: люди в этом наборе данных с более высоким доходом едят больше овощей.
- B: Связь между доходом и потреблением овощей линейна.
- C: Пожилые люди едят больше овощей.
- D: Между возрастом и потреблением овощей может быть сильная нелинейная зависимость.
Упражнение: В общем, рекомендуется визуализировать взаимосвязь между переменными перед вычислением корреляции. В предыдущем примере мы этого не делали, но еще не поздно.
Создайте визуализацию взаимосвязи между возрастом и овощами. Как бы вы описали отношения, если они есть?
Простая регрессия¶
В предыдущем разделе мы видели, что корреляция не всегда измеряет то, что мы действительно хотим знать. В этом разделе мы рассмотрим альтернативу: простую линейную регрессию.
Давайте еще раз посмотрим на взаимосвязь между весом и возрастом. В предыдущем разделе я создал два фальшивых набора данных, чтобы доказать свою точку зрения:
In [44]:
plt.figure(figsize=(8, 3)) plt.subplot(1, 2, 1) plt.plot(xs1, ys1, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #1') plt.tight_layout() plt.subplot(1, 2, 2) plt.plot(xs2, ys2, 'o', alpha=0.5) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake dataset #2') plt.tight_layout()
Тот, что слева, имеет более высокую корреляцию, около 0,75 по сравнению с 0,5.
Но в этом контексте статистика, которая нас, вероятно, волнует, – это наклон линии, а не коэффициент корреляции.
Чтобы оценить наклон, мы можем использовать linregress из SciPy-библиотеки stats.
см. документацию по scipy.stats.linregress
In [45]:
from scipy.stats import linregress res1 = linregress(xs1, ys1) res1._asdict()
Out[45]:
{'slope': 0.018821034903244396,
'intercept': 75.08049023710964,
'rvalue': 0.7579660563439407,
'pvalue': 1.8470158725245546e-10,
'stderr': 0.002337849260560816,
'intercept_stderr': 0.08439154079040351}
Результатом является объект LinregressResult, содержащий пять значений: slope – наклон линии, наиболее подходящей для данных; intercept – это пересечение линии регрессии.
Для фальшивого набора данных 1 расчетный наклон составляет около 0,019 кг в год или около 0,56 кг за 30-летний период.
Вот результаты для фальшивого набора данных 2.
In [47]:
res2 = linregress(xs2, ys2) res2._asdict()
Out[47]:
{'slope': 0.17642069806488858,
'intercept': 66.60980474219305,
'rvalue': 0.47827769765763184,
'pvalue': 0.0004430600283776228,
'stderr': 0.046756985211216295,
'intercept_stderr': 1.6878308158080693}
Расчетный наклон почти в 10 раз выше: около 0,18 килограмма в год или около 5,3 килограмма за 30 лет:
То, что здесь называется rvalue, – это корреляция, которая подтверждает то, что мы видели раньше; первый пример имеет более высокую корреляцию, около 0,75 по сравнению с 0,5.
Но сила эффекта, измеренная по наклону линии, во втором примере примерно в 10 раз выше.
Мы можем использовать результаты linregress для вычисления линии тренда: сначала мы получаем минимум и максимум наблюдаемых xs; затем мы умножаем на наклон и добавляем точку пересечения.
Вот как это выглядит для первого примера.
In [49]:
plt.plot(xs1, ys1, 'o', alpha=0.5) fx = np.array([xs1.min(), xs1.max()]) fy = res1.intercept + res1.slope * fx plt.plot(fx, fy, '-') plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake Dataset #1');
То же самое и со вторым примером.
In [50]:
plt.plot(xs2, ys2, 'o', alpha=0.5) fx = np.array([xs2.min(), xs2.max()]) fy = res2.intercept + res2.slope * fx plt.plot(fx, fy, '-') plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Fake Dataset #2');
Визуализация здесь может ввести в заблуждение, если вы не посмотрите внимательно на вертикальные шкалы; наклон на втором рисунке почти в 10 раз больше.
Рост и вес¶
Теперь рассмотрим пример с реальными данными.
Вот еще раз диаграмма рассеяния для роста и веса.
In [51]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Теперь мы можем вычислить линию регрессии. linregress не может обрабатывать значения NaN, поэтому мы должны использовать dropna для удаления строк, в которых отсутствуют нужные нам данные.
In [52]:
subset = brfss.dropna(subset=['WTKG3', 'HTM4']) height_clean = subset['HTM4'] weight_clean = subset['WTKG3']
Теперь мы можем вычислить линейную регрессию.
In [53]:
res_hw = linregress(height_clean, weight_clean) res_hw._asdict()
Out[53]:
{'slope': 0.9192115381848256,
'intercept': -75.12704250330165,
'rvalue': 0.47420308979024434,
'pvalue': 0.0,
'stderr': 0.005632863769802997,
'intercept_stderr': 0.960886026543318}
Наклон составляет около 0,92 килограмма на сантиметр, а это означает, что мы ожидаем, что человек выше на один сантиметр будет почти на килограмм тяжелее. Это довольно много.
Как и раньше, мы можем вычислить линию тренда:
In [54]:
fx = np.array([height_clean.min(), height_clean.max()]) fy = res_hw.intercept + res_hw.slope * fx
In [55]:
plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1) plt.plot(fx, fy, '-') plt.xlim([140, 200]) plt.ylim([0, 160]) plt.xlabel('Height in cm') plt.ylabel('Weight in kg') plt.title('Scatter plot of weight versus height');
Наклон этой линии соответствует диаграмме рассеяния.
Линейная регрессия имеет ту же проблему, что и корреляция; она только измеряет силу линейной связи.
Вот диаграмма рассеяния веса по сравнению с возрастом, которую мы видели ранее.
In [56]:
plt.plot(age_jitter, weight_jitter, 'o', alpha=0.01, markersize=1) plt.ylim([0, 160]) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Люди в возрасте от 40 – самые тяжелые; люди младшего и старшего возраста легче. Так что отношения нелинейные.
Если мы не посмотрим на диаграмму рассеяния и вслепую вычислим линию регрессии, мы получим вот что.
In [57]:
subset = brfss.dropna(subset=['WTKG3', 'AGE']) age_clean = subset['AGE'] weight_clean = subset['WTKG3'] res_aw = linregress(age_clean, weight_clean) res_aw._asdict()
Out[57]:
{'slope': 0.023981159566968686,
'intercept': 80.07977583683224,
'rvalue': 0.021641432889064033,
'pvalue': 4.3743274930078674e-11,
'stderr': 0.003638139410742186,
'intercept_stderr': 0.18688508176870167}
Расчетный уклон составляет всего 0,02 килограмма в год или 0,6 килограмма за 30 лет.
А вот как выглядит линия тренда.
In [58]:
plt.plot(age_jitter, weight_jitter, 'o', alpha=0.01, markersize=1) fx = np.array([age_clean.min(), age_clean.max()]) fy = res_aw.intercept + res_aw.slope * fx plt.plot(fx, fy, '-') plt.ylim([0, 160]) plt.xlabel('Age in years') plt.ylabel('Weight in kg') plt.title('Weight versus age');
Прямая линия плохо отражает взаимосвязь между этими переменными.
Давайте попрактикуемся в простой регрессии.
Упражнение: Как вы думаете, кто ест больше овощей, люди с низким доходом или люди с высоким доходом? Давайте выясним.
Как мы видели ранее, столбец INCOME2 представляет уровень дохода, а _VEGESU1 представляет количество порций овощей, которые респонденты ели в день.
Постройте диаграмму рассеяния порций овощей в зависимости от дохода, то есть с порциями овощей по оси y и группой доходов по оси x.
Вы можете использовать ylim для увеличения нижней половины оси y.
Упражнение: Теперь давайте оценим наклон зависимости между потреблением овощей и доходом.
-
Используйте
dropnaдля выбора строк, в которыхINCOME2и_VEGESU1не равныNaN. -
Извлеките
INCOME2и_VEGESU1и вычислите простую линейную регрессию этих переменных.
Каков наклон линии регрессии? Что означает этот наклон в контексте изучаемого нами вопроса?
Упражнение: Наконец, постройте линию регрессии поверх диаграммы рассеяния.
Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.
- Назначение корреляционного анализа
-
Выполняем корреляционный анализ
- Метод 1: применяем функцию КОРРЕЛ
- Метод 2: используем “Пакет анализа”
- Заключение
Назначение корреляционного анализа
Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:
- если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.
- если коэффициент положительный – зависимость прямая, т.е. увеличение одного показателя приводит к увеличению второго и наоборот.
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.

Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
КОРРЕЛ(массив1;массив2).
Порядок действий при работе с данным инструментом следующий:
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.

- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.

- На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab. Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.

- Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.

Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.

- В перечне слева выбираем пункт “Параметры”.

- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.

- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.

Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.

- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.

- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
- Когда все готово, щелкаем OK.

- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.

Заключение
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.



После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).



В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.

Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» – первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» – второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:

- Строим корреляционное поле: «Вставка» – «Диаграмма» – «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».




Теперь стали видны и данные регрессионного анализа.
Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е. 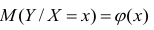
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину 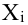 (число страниц) и
(число страниц) и 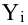 (средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (
(средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (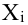 ,
,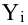 ) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.
) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.
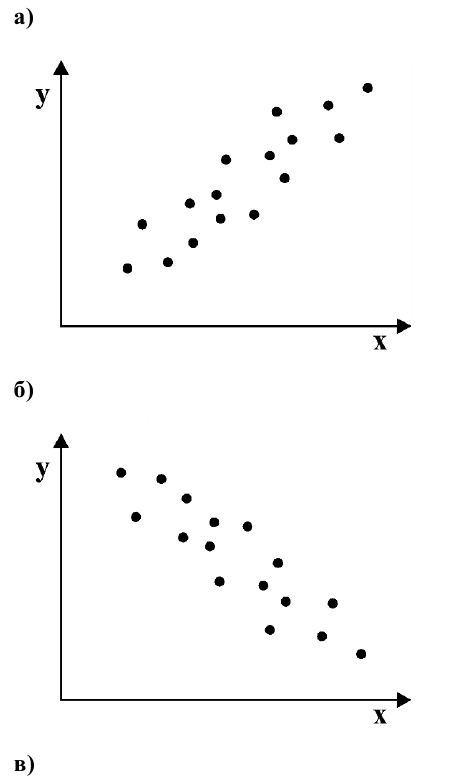
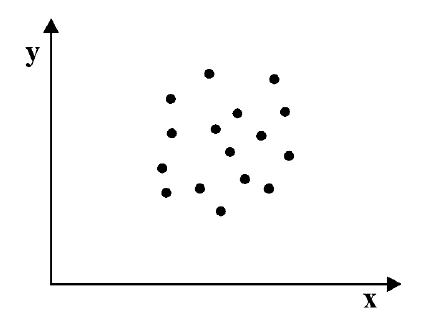
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) – корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика – это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице:  Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции:
Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции: 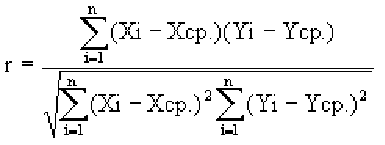
Коэффициент r мы считаем в Excel, с помощью функции 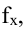 далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.
далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% – другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь – случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку: 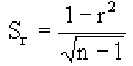
Связь нельзя считать случайной, если: 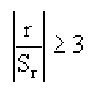
В то время как задача корреляционного анализа – установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа – описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 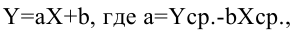
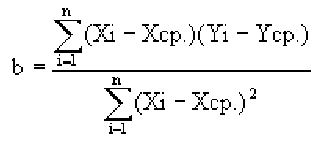
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y – нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 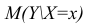 случайной переменной К, рассматриваемое как функция х, т.е.
случайной переменной К, рассматриваемое как функция х, т.е. 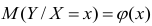 , называется
, называется
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
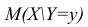 случайной переменной X, т.е.
случайной переменной X, т.е. 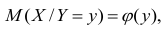 называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).
называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек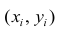 на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.
на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
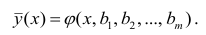
Аналогично определяется кривая регрессии X по Y (X на Y):
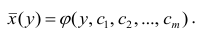
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее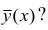 Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е.
Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е. 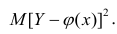 . Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является
. Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является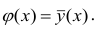 Это следует из свойств минимальности рассеивания около центра распределения
Это следует из свойств минимальности рассеивания около центра распределения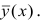
Если рассеивание вычисляется относительно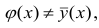 то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как
то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как 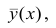 минимизирует среднеквадратическую погрешность прогноза величины Y по X.
минимизирует среднеквадратическую погрешность прогноза величины Y по X.
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
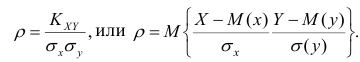 (1.1)
(1.1)
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 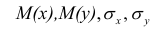 . Наилучшей оценкой
. Наилучшей оценкой
математического ожидания является среднее арифметическое, т.е.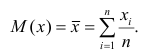
Оценкой дисперсии служит выборочная дисперсия, т.е.
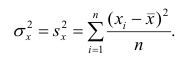
Тогда выборочный коэффициент корреляции
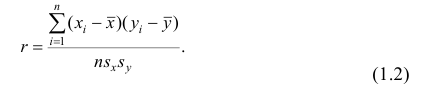
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
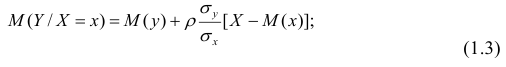
функция регрессии X на Y — следующий вид:
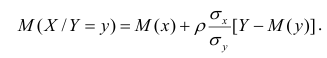
Выражения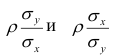 — называют коэффициентами регрессии.
— называют коэффициентами регрессии.
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 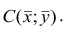 Запишем уравнение регрессии у на х и х на у:
Запишем уравнение регрессии у на х и х на у:
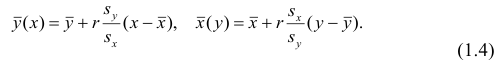
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
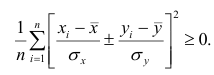
Возведём выражение под знаком суммы в квадрат:
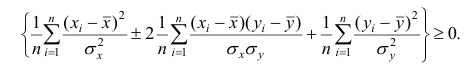
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что 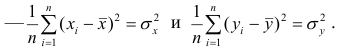
Таким образом, окончательно получаем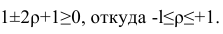
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных 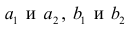 таких, что
таких, что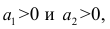 т.е.
т.е.
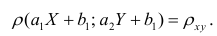
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции 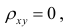 то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.
то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
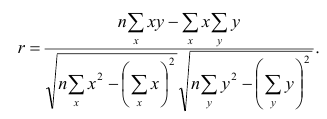
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
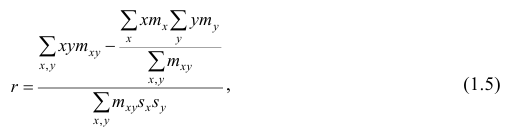
где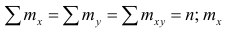 — суммарная частота наблюдаемого значенияпризнака х при всех значениях
— суммарная частота наблюдаемого значенияпризнака х при всех значениях 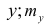 — суммарная частота наблюдаемого значения признака упри всех значениях х;
— суммарная частота наблюдаемого значения признака упри всех значениях х; 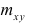 — частота появления пары признаков (x, у).
— частота появления пары признаков (x, у).
Из формулы (1.2) очевидно, что 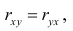 т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.
т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.
Поле корреляции. Вычисление оценок параметров двумерной модели
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 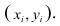 Считаем, что предпосылки корреляционного анализа выполнены.
Считаем, что предпосылки корреляционного анализа выполнены.
Пару случайных чисел 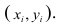 можно изобразить графически в виде точки с координатами
можно изобразить графически в виде точки с координатами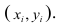 . Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.
. Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
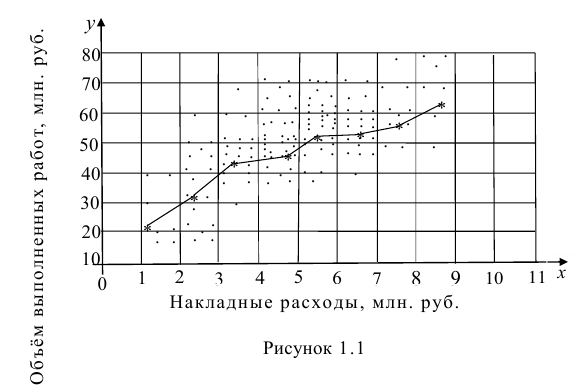
Если вычислить средние значения у в каждом интервале изменения х [обозначим их 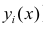 )], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.
)], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.
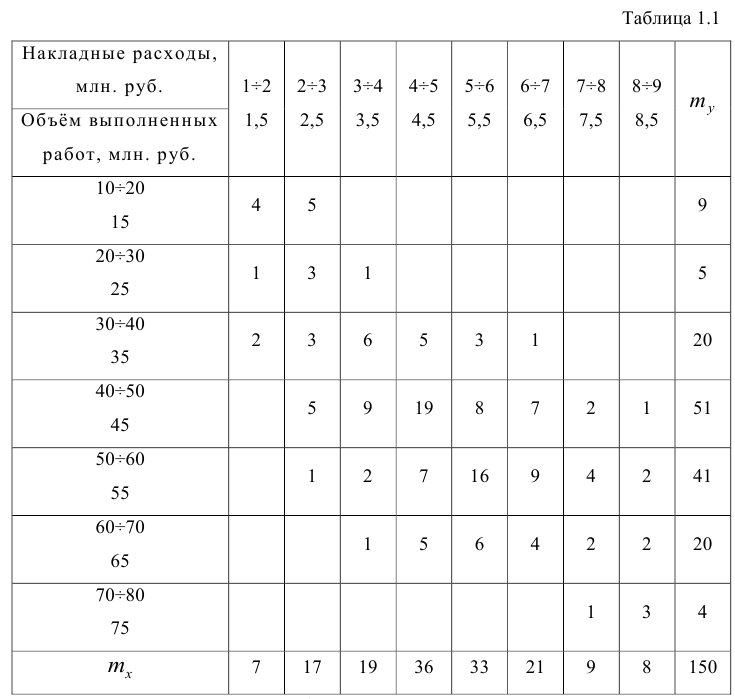
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают 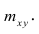 В 9-й строке и 10-м столбце находятся значения
В 9-й строке и 10-м столбце находятся значения 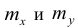 – суммы
– суммы 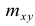 по соответствующим столбцу и строке.
по соответствующим столбцу и строке.
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
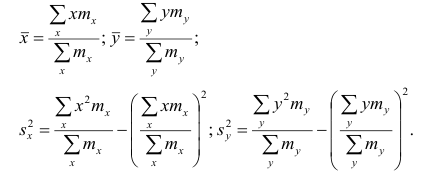 (1.6)
(1.6)
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 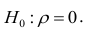 . Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют
. Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют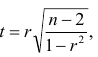
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение 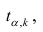 удовлетворяющее условию
удовлетворяющее условию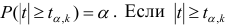 , то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При
, то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При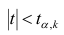 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
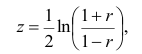
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
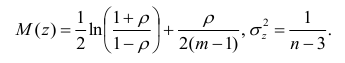
В этом, случае доверительный интервал для римеетвид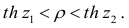 Величины
Величины 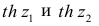 находят по таблицам по следующим значениям:
находят по таблицам по следующим значениям:
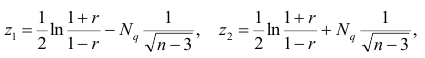
где 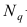 — нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции
— нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции 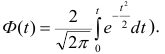
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
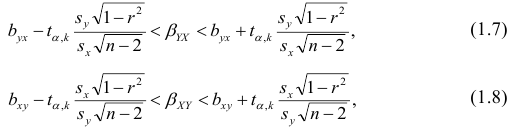
где 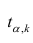 имеет распределение Стьюдента с k=n—2 степенями свободы.
имеет распределение Стьюдента с k=n—2 степенями свободы.
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 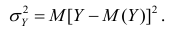 Дисперсию
Дисперсию 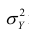 можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.
можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 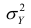 в следующем виде:
в следующем виде:
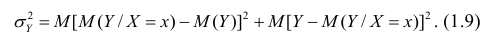
Первое слагаемое обозначим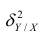 Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим
Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим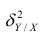 . Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией
. Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией 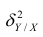 измеряет влияние на Y прочих факторов.
измеряет влияние на Y прочих факторов.
Покажем, что 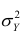 действительно можно разложить на два таких слагаемых:
действительно можно разложить на два таких слагаемых:
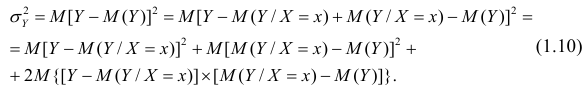
Для простоты полагаем распределение дискретным. Имеем 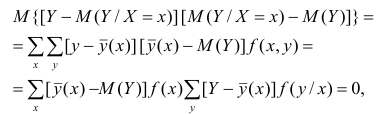
так как при любом х справедливо равенство
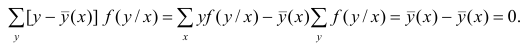
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии 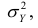 т.е. рассматривать отношение
т.е. рассматривать отношение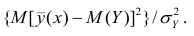 . Эту величину обозначают
. Эту величину обозначают 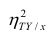 и называют теоретическим корреляционным отношением. Таким образом,
и называют теоретическим корреляционным отношением. Таким образом,
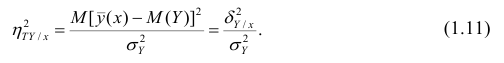
Разделив обе части равенства (1.9) на 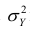 получим
получим
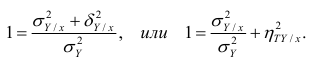
Из последней формулы имеем

Поскольку 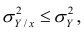 так как
так как 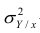 — составная часть
— составная часть 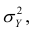 то из равенства (1.12) следует, что значение
то из равенства (1.12) следует, что значение 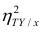 всегда заключено между нулем и единицей.
всегда заключено между нулем и единицей.
Все сделанные выводы справедливы и для 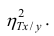 Из равенства (1.12)
Из равенства (1.12)
следует, что 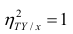 только тогда, когда
только тогда, когда 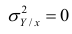 , т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии
, т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии 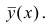 . В этом случае между Y и X существует функциональная зависимость.
. В этом случае между Y и X существует функциональная зависимость.
Далее, из равенства (1.12) следует, что 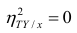 тогда и только тогда, когда
тогда и только тогда, когда
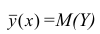 = const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).
= const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).
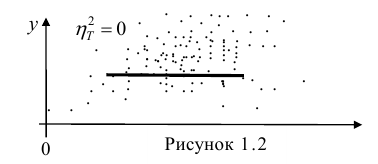
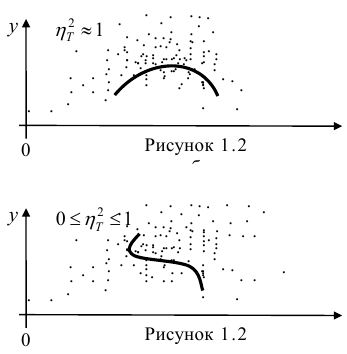
Аналогичными свойствами обладает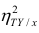 — показатель тесноты связи между X и У.
— показатель тесноты связи между X и У.
Часто используют величину

Считают, что она не может быть отрицательной. Значения величины 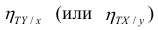 также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).
также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).
Значения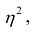 лежащие в интервале
лежащие в интервале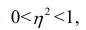 являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение
являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение 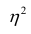 связано
связано 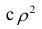 следующим образом:
следующим образом: 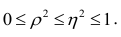 В случае линейной зависимости между переменными
В случае линейной зависимости между переменными 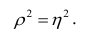
Разность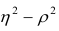 может быть использована как показатель нелинейности связи между переменными.
может быть использована как показатель нелинейности связи между переменными.
При вычислении 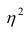 по выборочным данным получаем выборочное корреляционное отношение. Обозначим его
по выборочным данным получаем выборочное корреляционное отношение. Обозначим его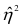 . Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид
. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид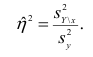
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
Пусть имеется многомерная нормальная совокупность с m признаками 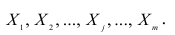 В этом случае взаимозависимость между признаками
В этом случае взаимозависимость между признаками
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где 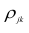 — парные коэффициенты корреляции; m — порядок матрицы.
— парные коэффициенты корреляции; m — порядок матрицы.
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
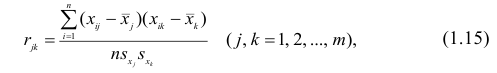
где 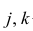 — порядковые номера признаков.
— порядковые номера признаков.
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между 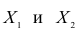 при фиксированном значении признака
при фиксированном значении признака 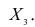 В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.
В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 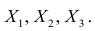 . Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков
. Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков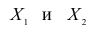 при фиксированном значении
при фиксированном значении 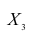 выражается через парные коэффициенты
выражается через парные коэффициенты
корреляции и имеет вид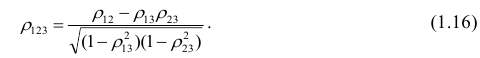
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при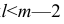 — подматрица порядкаl+2, составленная из элементов матрицы
— подматрица порядкаl+2, составленная из элементов матрицы 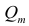 , которые отвечают индексам коэффициента частной
, которые отвечают индексам коэффициента частной
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
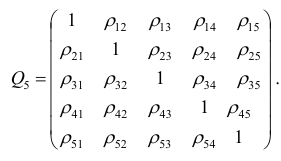
Для определения частного коэффициента корреляции второго порядка, например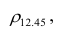 следует использовать подматрицу четвертого порядка,
следует использовать подматрицу четвертого порядка,
вычеркнув из исходной матрицы 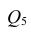 третью строку и третий столбец, так как признак
третью строку и третий столбец, так как признак 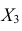 не рассматривают.
не рассматривают.
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
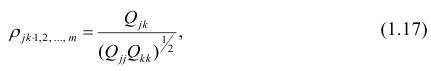
где 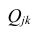 — алгебраические дополнения к элементу
— алгебраические дополнения к элементу 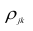 корреляционной
корреляционной
матрицы 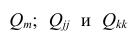 — алгебраические дополнения к элементам
— алгебраические дополнения к элементам 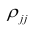 и ркк корреляционной матрицы
и ркк корреляционной матрицы 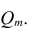
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу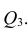
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
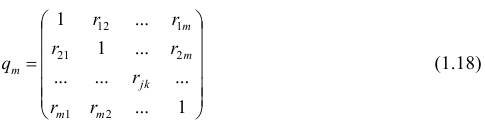
Формула выборочного частного коэффициента корреляции имеет вид

где 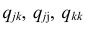 — алгебраические дополнения к соответствующим элементам матрицы (1.18).
— алгебраические дополнения к соответствующим элементам матрицы (1.18).
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 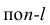 наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.
наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции

где 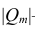 —определитель корреляционной матрицы
—определитель корреляционной матрицы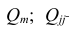 —алгебраическое
—алгебраическое
дополнение к элементу 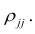
Квадрат коэффициента множественной корреляции 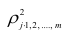 называется
называется
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале Оценками этих
Оценками этих
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 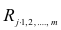 и
и
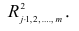 Формула для вычисления выборочного множественного коэффициента корреляции имеет вид
Формула для вычисления выборочного множественного коэффициента корреляции имеет вид

где 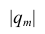 —определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции;
—определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции; 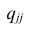 алгебраическое дополнение к элементу
алгебраическое дополнение к элементу 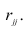
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
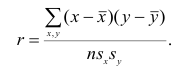
Пусть 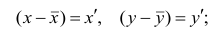 тогда, учитывая,
тогда, учитывая,
что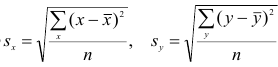 ,можно записать
,можно записать

В зависимости от того, что принять за меру различия между величинами 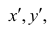 можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла
можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла 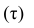 и коэффициент корреляции рангов Спирмэна р.
и коэффициент корреляции рангов Спирмэна р.
Введём следующую меру различия между объектами: будем считать 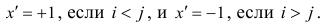 Поясним сказанное на примере. Имеем две последовательности:
Поясним сказанное на примере. Имеем две последовательности:
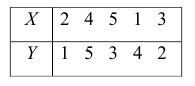
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как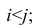 второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку
второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку 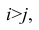 и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1; 2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.
и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1; 2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.
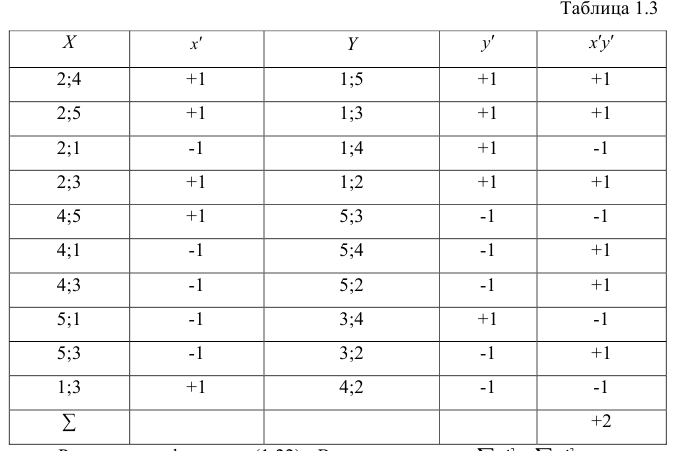
Рассмотрим формулу ( 1 .22). В нашем случае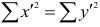 и равна
и равна
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.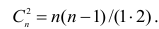 Обозначая
Обозначая 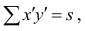 получаем формулу коэффициента корреляции рангов Кэнделла:
получаем формулу коэффициента корреляции рангов Кэнделла:
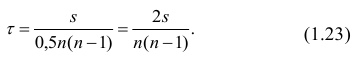
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 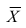 средний ранг последовательности X, через
средний ранг последовательности X, через 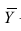 — средний ранг последовательности Т, то
— средний ранг последовательности Т, то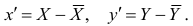 Поскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна
Поскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна 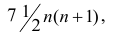 а средний ранг
а средний ранг 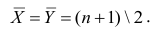
Тогда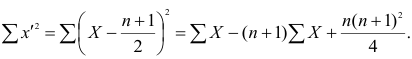 Сумма
Сумма
чисел натурального ряда равна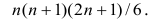
Тогда 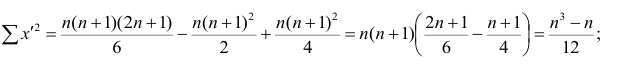
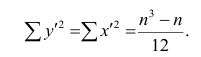
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину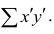 . Имеем:
. Имеем: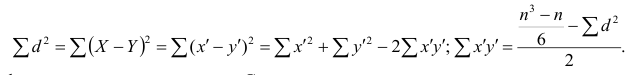
Коэффициент корреляции рангов Спирмэна

У коэффициентов 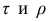 разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает
разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает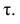 Выведены неравенства, связывающие
Выведены неравенства, связывающие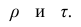 Например, при больших n можно пользоваться следующим приближённым соотношением:
Например, при больших n можно пользоваться следующим приближённым соотношением: 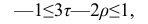 или
или
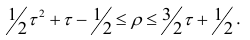 Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент
Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент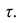
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму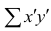 можно подсчитывать лишь по последовательности К, так как все
можно подсчитывать лишь по последовательности К, так как все 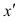 равны +1.
равны +1.
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 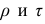 в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,
в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,
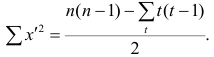 Соответственно для другой последовательности
Соответственно для другой последовательности
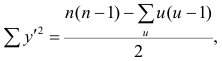
где t и u—число связанных пар в последовательностях.
Обозначая 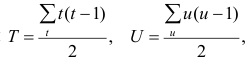 получаем
получаем
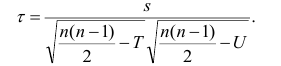
Аналогично находим выражение для р. Только в этом случае
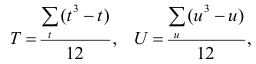 , где е и г – число связанных пар в
, где е и г – число связанных пар в
последовательностях, а
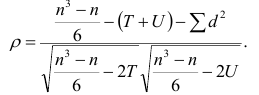
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации

где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
Пример:
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне 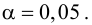
Решение. Для вычислений составим таблицу. Находим суммы
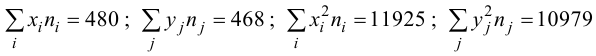 и заносим их в таблицу. Вычислим
и заносим их в таблицу. Вычислим
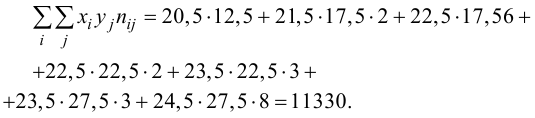
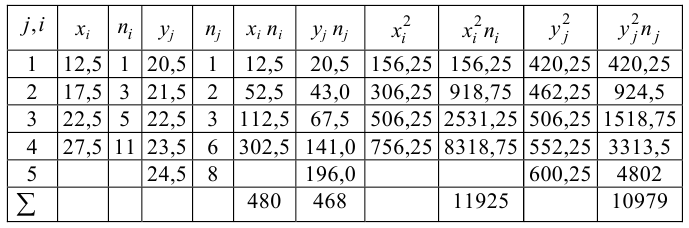
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
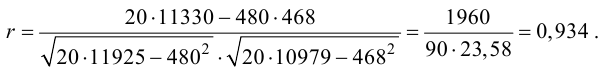
Проверим значимость 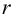 на уровне
на уровне 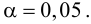 Для этого вычислим статистику
Для этого вычислим статистику
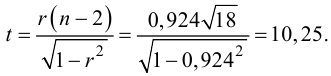
По таблице распределения П6 Стьюдента 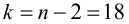 находим критическое значение
находим критическое значение 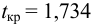 Так как
Так как 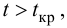 то считаем
то считаем 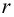 значимым.
значимым.
Пример:
Для данных табл. 13 найти корреляционное отношение 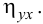
Для вычисления эмпирического корреляционного отношения найдем групповые средние 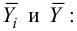
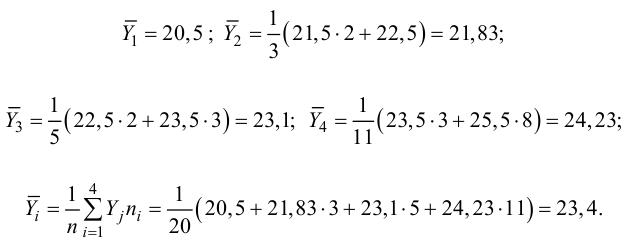
Тогда
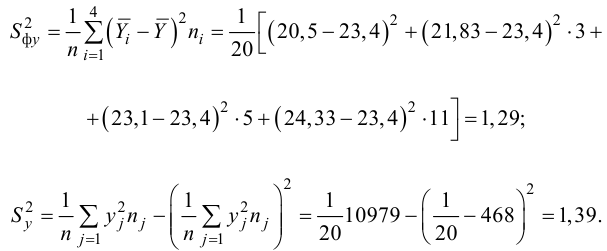
Вычисляем корреляционное отношение
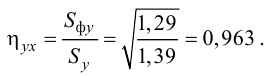
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ
