Как найти зависимость в физике - Сайт, где вы сможете решить свои вопросы

Рассмотрим движение тела из точки (A) в точку (B) (рис. (1)). Траектория (AB) является криволинейной.

Введём понятие «средняя скорость».

На рисунке (1) показаны вектора перемещений тела (Delta{vec{r_3}}), (Delta{vec{r_2}}) и (Delta{vec{r_1}}) за различные сокращающиеся промежутки времени (Delta{t_3}), (Delta{t_2}) и (Delta{t_1}).

Рис. (1). Перемещения тела при криволинейном движении

Средняя скорость равна отношению перемещения за конечный промежуток времени:

Средняя скорость является векторной величиной:

направление средней скорости υ ср→↑↑Δr→ находится согласно математической формуле определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу средней скорости);
числовое значение средней скорости (модуль, проекции на координатные оси) определяется согласно геометрическим правилам работы с векторами;
физические понятия отличаются от математических понятий наличием единиц измерения ([(v_{ср})] (=) [(frac{м}{с})]).

Участки траектории (AB), (AD) и (AE) (рис. (1)) характеризуются, соответственно, средними скоростями:

(vec{v_{ср3}}), (vec{v_{ср2}}), (vec{v_{ср1}}).


(vec{v_{ср3}}) = (frac{Delta{vec{r_3}}}{Delta{t_3}})	(vec{v_{ср2}}) = (frac{Delta{vec{r_2}}}{Delta{t_2}})	(vec{v_{ср1}}) = (frac{Delta{vec{r_1}}}{Delta{t_1}})

Если уменьшать неограниченно промежуток времени (Delta{t}), то быстрота движения тела характеризуется понятием «мгновенная скорость» (или «скорость»).

Математическая запись уменьшения промежутка времени:

Δt→0

(в математике существует понятие «предел», символ данного понятия — «lim»).

Физический смысл принципа уменьшения промежутка времени: на определённом этапе данной процедуры значения средней скорости будут приблизительно одинаковыми и определение физического понятия «средняя скорость» изменится на физическое понятие «мгновенная скорость»

υ→=limΔt→0υ ср→=limΔt→0Δr→Δt

Мгновенная скорость является векторной величиной:

вектор мгновенной скорости (далее — скорости) направлен по касательной к траектории в исследуемой точке (проверь, как на рисунке (1) «хорды — перемещения (Delta{vec{r_3}}), (Delta{vec{r_2}}) и (Delta{vec{r_1}})» при уменьшении промежутков времени (Delta{t_3}), (Delta{t_2}) и (Delta{t_1}) изображаются касательными, которые соответствуют векторам скоростей (vec{v_3}), (vec{v_2}), (vec{v_1})).

На рисунке (1) тело движется из точки (E) в точку (D), изменяя скорость от (v_2) до (v_3). Параллельным переносом перенесём вектор (vec{v_{3}}) к (vec{v_{2}}), тогда изменение скорости за промежуток времени (Delta{t}) равно разности векторов

((vec{v_{3}})(-)(vec{v_{2}})), что на рисунке (1) соответствует вектору ускорения (vec{a_{2}}).

Среднее ускорение равно отношению изменения скорости к промежутку времени:

Примечание:

1) в физических задачах при написании символа aср → индекс «ср», как правило, не прописывается;

2) в ситуации прямолинейного неравномерного движения используется термин «ускорение».

Характеристики физического понятия «среднее ускорение»:

направление вектора среднего ускорения определяется согласно правилу aср→↑↑Δυ→;
числовое значение ускорения (модуль, проекции на координатные оси) определяется согласно геометрическим правилам работы с векторами;
единица измерения ([(a_{ср})] (=) [(frac{м}{с^2})]).

Участки траектории (AB), (AD) и (AE) (рис. (1)) характеризуются, соответственно, средними ускорениями (vec{a_{3}}), (vec{a_{2}}), (vec{a_{1}}).


(vec{a_{3}}) (=) (frac{Delta{vec{v_3}}}{Delta{t_3}})	(vec{a_{2}}) (=) (frac{Delta{vec{v_2}}}{Delta{t_2}})	(vec{a_{1}}) (=) (frac{Delta{vec{v_1}}}{Delta{t_1}})

Если уменьшать неограниченно промежуток времени (Delta{t}), то изменение скорости движения тела в конкретный момент времени характеризуется физическим понятием «мгновенное ускорение».

Вектор мгновенного ускорения при движении тела по криволинейной траектории представляет векторную сумму компонентов данного вектора, которые направлены по касательной и нормали (перпендикуляр к касательной).

Векторное и скалярное уравнения скорости материальной точки

1) Общий вид:

векторное уравнение — (vec{v}) (=) (vec{v}(t));
числовые (скалярные) уравнения — (v_x) (=) (v_x(t)), (v_y) (=) (v_y(t)), (v_z) (=) (v_z(t)).

2) Прямолинейное равноускоренное движение:

векторное уравнение — (vec{v}(t)) (=) (vec{v}{_0}) (+) (vec{a}(t – t_0)),

где (vec{v}{_0}) — скорость тела в начальный момент времени ({t_0}), (vec{v}(t)) — скорость тела в произвольный момент

времени (t);

числовые (скалярные) уравнения — (v_x(t)) (=) (v_{0x}) (+) (a_x(t – t_0)), (v_y(t)) (=) (v_{0y}) (+) (a_y(t – t_0)),

(v_z(t)) (=) (v_{0z}) (+) (a_z(t – t_0)).

Графическое изображение зависимости проекции скорости от времени ({v_х}(t))

При движении тела с постоянным ускорением проекция скорости изменяется по линейному закону в зависимости от времени (t): (v_x(t)) (=) (v_{0x}) (+) (a_x(t – t_0)) (рис. (2)).

Рис. (2). График зависимости проекции скорости от времени

Значение проекции ускорения по графику определяется как тангенс угла: (a_x) (=) (tgα) (=) (frac{Delta{v}}{Delta{t}}).

Перемещение

Проекции перемещений при равнопеременном движении в момент времени (t) определяются формулами:

(s_x(t)=x(t) – x_0), (s_y(t)=y(t) -y_0), (s_z(t)=z(t) – z_0).

(A)

(B)

Рис. (3). Определение модуля и проекций перемещения по графику зависимости проекции скорости от времени

Модуль и проекции перемещения тела определяются графическим способом с

использованием графика зависимости (v_x(t)).

Рисунок (3) (A) ((v_0) (=) (0))

Рисунок (3) (B) ((v_0) (≠) (0))

Модуль перемещения определяется как площадь прямоугольного треугольника (ABC) с катетами

Модуль перемещения определяется как площадь трапеции (ABCD) с основаниями (d) (=) (v_0), (b) (=) (v_0+at) и высотой (h) (=) (t).

S=12b+dh⇒S=υ0⋅t+a⋅t22

Проекция перемещения: (s_x) (=) (S)

Примечание: если график проекции скорости состоит из участков, где площадь трапеции имеет отрицательное значение (например, (s_{x1}) (>) (0), (s_{x2}) (<) (0)), то модуль перемещения тела равен:

s=sx1+sx2

Источники:

Рис. 1. Перемещения тела при криволинейном движении. © ЯКласс.

Рис. 2. График зависимости проекции скорости от времени. © ЯКласс.

Рис. 3. Определение модуля и проекций перемещения по графику зависимости проекции скорости от времени. © ЯКласс.

Источник

Перемещение, координата и путь при равнопеременном движении в физике с примерами

Перемещение, координата и путь при равнопеременном движении:

Мы знаем, что при равнопеременном движении скорость тела линейно зависит от времени. А как зависит от времени перемещение? Координата? Пройденный путь?

В предыдущем параграфе для равнопеременного движения была найдена зависимость проекции скорости от времени:

и получена формула для проекции перемещения:

Подставляя 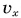из равенства (1) в (2), находим зависимость проекции перемещения от времени:

Отметим, что при движении с постоянным ускорением соотношения (1) и (3) выполняются и для векторов скорости и перемещения:

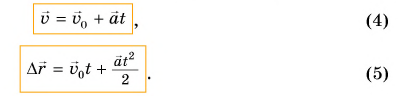
Учитывая, что проекция перемещения 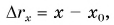из формулы (3) находим координату:

Формула (6) выражает кинематический закон равнопеременного движения. Функции (3) и (6) называются квадратичными. Следовательно, при равнопеременном движении проекция перемещения тела и его координата квадратично зависят от времени.

Сравним зависимости основных кинематических величин от времени для двух видов прямолинейного движения: равномерного и равнопеременного (табл. 1).

Таблица 1

Из таблицы видно, что при 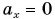формулы равнопеременного движения переходят в формулы равномерного.

Рассмотрим графики проекций 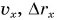и координаты х на конкретном примере: три тела (0, 1 и 2) движутся вдоль оси Ох. Их начальные скорости одинаковы 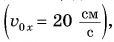проекции ускорения различны: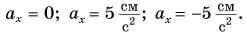

По формуле (1) 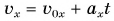построим графики проекции скорости этих тел (графики 0, 1, 2 на рис. 79). Графики прямолинейны, а их наклон определяется значением проекции ускорения 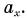График 2 пересекает ось времени в момент поворота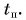

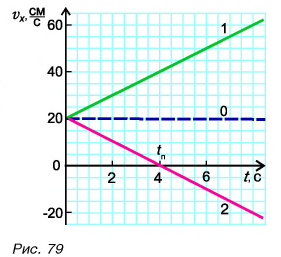
Перейдем к графикам проекции перемещения 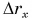(рис. 80).

Как мы знаем, при 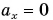(т. е. для равномерного движения) 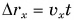и график 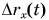— наклонная прямая линия (график 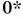на рис. 80).

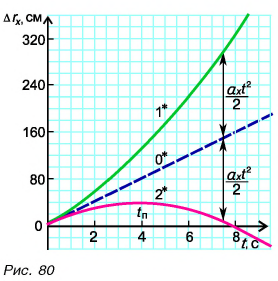
Из таблицы 1 видно, что формулы для проекции перемещения 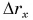при равномерном и равнопеременном движениях отличаются только на слагаемое 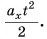Поэтому при 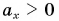точки графика 0* для каждого значения t следует поднять на 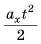(график 1*), а при 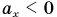(график 2*) — настолько же опустить (рис. 80).

Так как 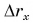квадратично зависит от времени (см. формулу (3)), графики проекции перемещения при равнопеременном движении являются участками парабол (рис. 80).

Обратите внимание на поведение графиков 2 и 2* в момент поворота 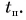График 2 для 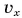(рис. 79) в этот момент проходит через нуль, а график 2* для 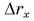(рис. 80) при 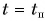достигает максимума, а затем начинает опускаться. Графики подтверждают: в момент поворота направление движения тела изменяется на противоположное.

А каким будет график пути? Для движения, при котором направление скорости не изменяется, график пути 1б (рис. 81) совпадает с графиком проекции перемещения 1а. Если же скорость меняет свое направление, то график пути s (2б) и график проекции перемещения 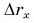(2а) будут совпадать лишь до момента поворота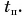

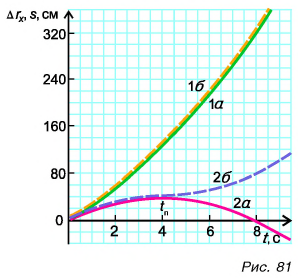
При 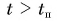проекция перемещения 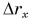начинает уменьшаться, а путь s продолжает расти. Он увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.

От графика проекции перемещения 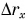легко перейти к графику координаты х (рис. 82).

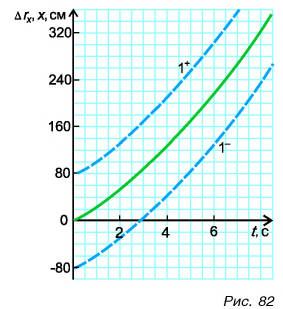
Так как, согласно формуле (6), 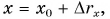то графики координаты х (параболы 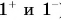) получаются путем смещения графика 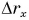на величину 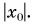Смещение вверх происходит при 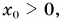а вниз — при 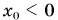(рис. 82). Выведем еще две формулы, полезные для решения задач о равнопеременном движении.

Выразим время из формулы проекции скорости (1): 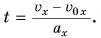Подставив это выражение в формулу (2), получим: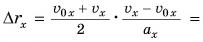
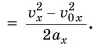Следовательно, при равнопеременном движении

В случае когда начальная скорость и ускорение одинаково направлены, из равенства (7) следует:

где s — пройденный путь.

Главные выводы:

При равнопеременном движении тела его перемещение и координата — квадратичные функции времени.
Графики зависимости проекции перемещения и координаты от времени для равнопеременного движения являются участками парабол.
Вершина параболы на графике проекции перемещения соответствует моменту времени, при котором мгновенная скорость равна нулю.

Пример решения задачи:

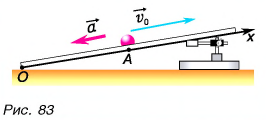
Шарику, находящемуся в точке А, расположенной посередине наклонного желоба длиной 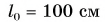(рис. 83), сообщили начальную скорость 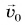вдоль наклонного желоба вверх. Ускорение шарика 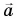направлено вдоль желоба вниз. Найдите координату точки поворота 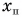и время 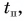за которое шарик ее достигнет, если

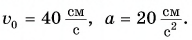
Определите время, когда шарик вернется в точку А, и время, когда он окажется в точке О. Постройте графики проекций скорости и перемещения, а также координаты шарика.

Пример решения задачи:

Решение

Выберем ось Ох, как показано на рисунке 83. Тогда проекция скорости 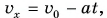проекция перемещения 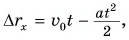координата 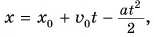где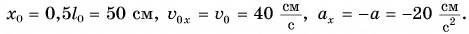
По этим формулам для моментов времени 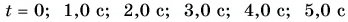найдем значения 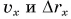и занесем результаты в таблицу.

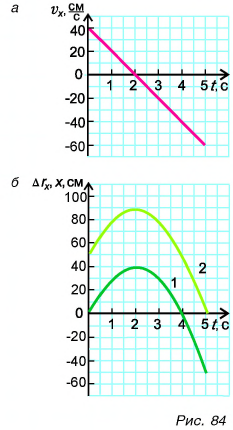
Используя полученные значения, строим графики проекций скорости (рис. 84, а) и перемещения (рис. 84, б, график 1) за промежуток времени от 0 до 5 с.

График координаты получим, сдвинув график проекции перемещения на 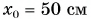вверх (график 2 на рис. 84, б). Из графиков и таблицы находим: координата точки поворота 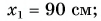шарик достиг ее в момент 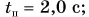в точке А шарик оказался при 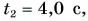а в точке О — при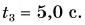

Ответ: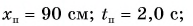

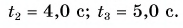
Рекомендую подробно изучить предметы:

Физика
Атомная физика
Ядерная физика
Квантовая физика
Молекулярная физика

Ещё лекции с примерами решения и объяснением:

Криволинейное движение
Ускорение точки при ее движении по окружности
Инерциальные системы отсчета
Энергия в физике
Прямолинейное равноускоренное движение
Сложение скоростей
Ускорение в физике
Скорость при равнопеременном движении

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Равнопеременное прямолинейное движение

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости на ось ОХ:

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
Построить уравнение вида x₁ = x₂.
Найти время встречи двух тел t_встр.
Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Построить графики x1(t) и x2(t).
Найти точку пересечения графиков.
Пустить перпендикуляр из этой точки к оси ОХ.
Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

Определить характер движения материальной точки.
Записать уравнение координаты материальной точки.
С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать исходные данные.
Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
Выразить скорость грузовика из уравнения его движения.
Записать уравнение движения мотоциклиста.
Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
Подставить время в формулу скорости грузовика и вычислить ее.

Решение

Координата встречи грузовика и мотоциклиста: x = 150 м.
Время запаздывания мотоциклиста: t_запазд = 5 с.
Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

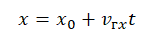
Так как начальная координата равна нулю, это уравнение примет

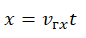
Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

[spoiler title=”источники:”]

Равнопеременное прямолинейное движение

Уравнение координаты при равноускоренном прямолинейном движении

[/spoiler]

Источник

В данной статьи изложены мысли, которые возникали при решении задач с сайта “Решу ЕГЭ” в разделе – https://phys-ege.sdamgia.ru/test?theme=204. Рисунки взяты оттуда же.

1. Общий подход

Анализ и использование данного графика базируется на формуле перемещения тела S, м:

Формула 1

Как видно из формулы площадь под графиком равна перемещению тела. Например, тело с 1 по 2 секунду на графике, представленном на рис. 1 прошло S = V * t = 2м/с * (2с – 1с) = 2м/с *1с = 2м

Рис. 1. График зависимости скорости от времени

2. Чуть посложнее

Если мы захотим найти перемещение тела с начала движения t = 0c до 4-ой секунды движения тела согласно графику на рис. 2, то нам необходимо найти сумму площадей трех геометрических фигур: с 0с по 1с – треугольник, с 1с по 2с прямоугольник, со 2с по 4с – трапеция.

Рис. 2. Находим перемещение как сумму площадей геометрических фигур

S треугольника = (1/2) * длину высоты треугольника * длину сторону треугольника, к которой проведена высота =
=(1/2) * 2м/с * (1с – 0с) = 1/2 * 2м/с * 1с = 1м
S прямоугольника мы находили в начале статьи = 2м
S трапеции = (1/2) * сумму оснований трапеции * высоту трапеции =
=(1/2) * (2м/с + 6м/с) * (4с – 2с) = (1/2) * 8м/с * 2с = 8м
Итого S = 1м + 2м + 8м = 11м

3. А если скорость равна нулю?

Не стоит пугаться нулевых скоростей на каком-либо интервале времени. Например с 3с по 5с на графике, представленном на рис. 3 перемещение тела равно 0м, т. к. площадь фигуры с 3с по 5с равна 0.

Рис. 3. Нулевое перемещение

4. А если скорость ушла “в минус”?

Рис. 4. Отрицательная скорость

А вот отрицательная скорость может вызвать некоторые затруднения. Здесь надо очень внимательно читать задание и не перепутать очень похожие физические величины: путь и перемещение. Путь – величина скалярная и поэтому для ее нахождения с помощью графика на рис. 4 надо зеркально отобразить отрицательные участки скорости и сложить площади фигур (см. Рис. 5)

Рис. 5. Зеркальное отображение отрицательных участков

Перемещение – величина векторная и поэтому при определении этой величины необходимо учитывать знак площади. Например, если нужно найти перемещение тела с 0с по 10с (см. рис. 5), то нужно площадь треугольника с 0с по 4с сложить с площадью треугольника с 8с по 10с и из полученного результата вычесть площадь треугольника с 4с по 8с.

5. Когда можно и не считать!

Рис. 6. Анализ графиков

Иногда требуется визуальный анализ графиков. Например, необходимо определить какой автомобиль из 4-х с 0с до 15с проехал наибольшее расстояние?
Рассматривая площади геометрических фигур под графиками (см. рис. 6) видим, что площадь больше у графика (и машины) №3.

6. Переходим к ускорению

До сих пор мы на линейных графиках с координатами скорости и времени (см. рис. 7) видели скорость, время и перемещение (или путь).

Рис. 7. Ищем на графике ускорение

А тут ещё прячется ускорение. Давайте попробуем его найти. Вспоминаем формулу равноускоренного движения

Формула 2 . Формула равноускоренного движения

Рассматривая график на рис. 7 определим Vo при t = 0с => Vo = 2м/с.
А теперь возьмём на графике точку в момент времени t = 1c и определим по графику скорость в этот момент времени => V = 4м/с.
Подставляем найденные значения в формулу 2 =>
4м/с = 2м/с + a * 1c => а = (4м/с – 2м/с) / 1с = 2м/с2

Возвращаемся к графику (см. рис. 8)

Рис. 8. Находим уравнение графика

Теперь мы можем сказать, что на рис. 8 представлен график линейного уравнения V = Vo + a*t = 2 + 2*t. Эти знания расширяют область использования графика на рис. 8. Например мы можем сказать, что при
t = 10c скорость будет равна V = 2м/с + 2м/с2*10с = 22м/с

7. Ищем ускорение на произвольном прямолинейном участке графика

Нас могут попросить найти ускорение тела на произвольном прямолинейном участке графика. Например с 6с по 10с на графике, представленном на рис. 9.

Рис. 9. Находим ускорение на произвольном прямолинейном участке графика

Для этого получим формулу для ускорения, усложнив формулу 2 заменив t на (t – to):

Формула 3. Формула для определения ускорения

Возвращаемся к поиску ускорения:
а = (5м/с – (-5м/с))/(10с – 6с) = 10м/с / 4с = 2.5м/с2

8. Ищем координаты тела

Зная начальные координаты тела, начальную скорость, ускорение тела и время перемещения можем найти координаты тела в любой момент времен (формула 4)

Формула 4. Уравнение для координаты тела

9. Ищем скорость в пространстве

Рис. 10. Скорость в пространстве

Мы можем знать значение проекций скорости на оси: х, y и z. Нас могут попросить найти модуль скорости. Ищем по формуле 5:

Формула 5. Формула для модуля скорости

Для понимания формулы 5 можно представить модуль скорости диагональю параллелепипеда, а проекции скорости сторонами параллелепипеда (см. рис. 11)

рис. 11 Расшифровка формулы 4

Заключение

Пока, это все мысли, которые появлялись во время решения задач в разделе сайта “Решу ЕГЭ” по адресу https://phys-ege.sdamgia.ru/test?theme=204. Пишите в комментариях, если что-то напрашивается добавить.

Автор с благодарностью примет любые пожертвования на развитие канала “От сложного к простому” https://money.yandex.ru/to/4100170126360.

Источник

Если траектория движения точки известна, то зависимость пути

, пройденного точкой, от истекшего промежутка времени

дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.2). Связь между

и

для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид

. Составим таблицу пути и времени такого движения:

t, с	1	2	3	4	5	6	…
s, м	2	4	6	8	10	12	…

Зависимость одной величины от другой часто бывает удобно изображать не формулами или таблицами, а графиками, которые более наглядно показывают картину изменения переменных величин и могут облегчать расчеты. Построим график зависимости пройденного пути от времени для рассматриваемого движения. Для этого возьмем две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс) назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для изображения промежутков времени и пути и примем точку пересечения осей за начальный момент и за начальную точку на траектории. Нанесем на осях значения времени и пройденного пути для рассматриваемого движения (рис. 18). Для «привязки» значений пройденного пути к моментам времени проведем из соответственных точек на осях (например, точек 3 с и 6 м) перпендикуляры к осям. Точка пересечения перпендикуляров соответствует одновременно обеим величинам: пути

и моменту

, — этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных путей, получая для каждой такой пары значений время — путь одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.

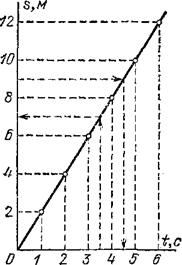
Рис. 18. График пути равномерного движения со скоростью 2 м/с

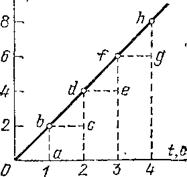
Рис. 19. К упражнению 12.1

В нашем случае график пути оказался прямой линией. Можно показать, что график пути равномерного движения всегда есть прямая линия; и обратно: если график зависимости пути от времени есть прямая линия, то движение равномерно.

Повторяя построение для другой скорости движения, найдем, что точки графика для большей скорости лежат выше, чем соответственные точки графика для меньшей скорости (рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.

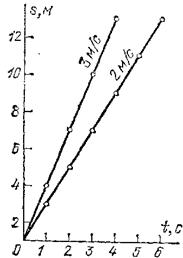
Рис. 20. Графики пути равномерных движений со скоростями 2 и 3 м/с

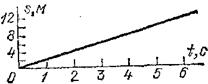
Рис. 21. График того же движения, что на рис. 18, вычерченный в другом масштабе

Наклон графика зависит, конечно, не только от числового значения скорости, но и от выбора масштабов времени и длины. Например, график, изображенный на рис. 21, дает зависимость пути от времени для того же движения, что и график рис. 18, хотя и имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков можно только в том случае, если они вычерчены в одном и том же масштабе.

С помощью графиков пути можно легко решать разные задачи о движении. Для примера на рис. 18 штриховыми линиями показаны построения, необходимые для того, чтобы решить следующие задачи для данного движения: а) найти путь, пройденный за время 3,5 с; б) найти время, за которое пройден путь 9 м. На рисунке графическим путем (штриховые линии) найдены ответы: а) 7 м; б) 4,5 с.

На графиках, описывающих равномерное прямолинейное движение, можно откладывать по оси ординат вместо пути

координату

движущейся точки. Такое описание открывает большие возможности. В частности, оно позволяет различать направление движения по отношению к оси

. Кроме того, приняв начало отсчета времени за нуль, можно показать движение точки в более ранние моменты времени, которые следует считать отрицательными.

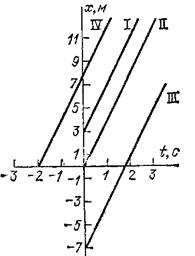
Рис. 22. Графики движений с одной и той же скоростью, но при различных начальных положениях движущейся точки

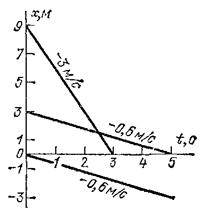
Рис. 23. Графики нескольких движений с отрицательными скоростями

Например, на рис. 22 прямая I есть график движения, происходящего с положительной скоростью 4 м/с (т. е. в направлении оси

), причем в начальный момент движущаяся точка находилась в точке с координатой

м. Для сравнения на том же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в точке с координатой

(прямая II). Прямая. III соответствует случаю, когда в момент

движущаяся точка находилась в точке с координатой

м. Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела координату

в момент

с.

Мы видим, что наклоны всех четырех графиков одинаковы: наклон зависит только от скорости движущейся точки, а не от ее начального положения. При изменении начального положения весь график просто переносится параллельно самому себе вдоль оси

вверх или вниз на соответственное расстояние.

Графики движений, происходящих с отрицательными скоростями (т. е. в направлении, противоположном направлению оси

), показаны на рис. 23. Они представляют собой прямые, наклоненные вниз. Для таких движений координата

точки с течением времени уменьшается.

12.3.
График пути для точки, движущейся со скоростью

, отсекает на оси ординат отрезок

. Как зависит от времени расстояние

от начальной точки? Напишите формулу этой зависимости.

12.4.
Точка, движущаяся со скоростью

, в момент

находится на расстоянии

от начальной. Как зависит от времени расстояние

?

12.5.
Точка, двигаясь равномерно вдоль оси

, имела координаты

м и

м в моменты времени

с и

с соответственно. Найдите графически, в какой момент точка проходила через начало координат и какова была координата

в начальный момент. Найдите проекцию скорости на ось

.

12.6.
Найдите при помощи графика пути, когда и на каком расстоянии от точки А автомашину, вышедшую из точки А, догонит вторая автомашина, вышедшая из той же точки через 20 мин после первой, если первая машина движется со скоростью 40 км/ч, а вторая — со скоростью 60 км/ч.

12.7.
Найдите при помощи графика пути, где и когда встретятся автомашины, вышедшие одновременно навстречу друг другу со скоростями 40 и 60 км/ч из пунктов А и В, лежащих на расстоянии 100 км друг от друга.

Графики пути можно строить и для случаев, в которых тело движется равномерно в течение определенного промежутка времени, затем движется равномерно, но с другой скоростью в течение другого промежутка времени, затем снова меняет скорость и т. д. Например, на рис. 26 показан график движения, в котором тело двигалось в течение первого часа со скоростью 20 км/ч, в течение второго часа — со скоростью 40 км/ч и в течение третьего часа — со скоростью 15 км/ч.

12.8.
Постройте график пути для движения, в котором за последовательные часовые промежутки тело имело скорости 10, -5, 0, 2, -7 км/ч. Чему равно суммарное перемещение тела?

Источник

Ответы Mail.ru

Домашние задания

Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика

Другие предметы

Вопросы – лидеры.