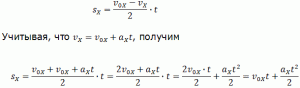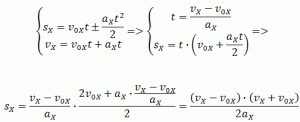В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Рассмотрим движение тела из точки (A) в точку (B) (рис. (1)). Траектория (AB) является криволинейной.
Введём понятие «средняя скорость».
На рисунке (1) показаны вектора перемещений тела (Delta{vec{r_3}}), (Delta{vec{r_2}}) и (Delta{vec{r_1}}) за различные сокращающиеся промежутки времени (Delta{t_3}), (Delta{t_2}) и (Delta{t_1}).
Рис. (1). Перемещения тела при криволинейном движении
Средняя скорость равна отношению перемещения за конечный промежуток времени:
Средняя скорость является векторной величиной:
- направление средней скорости υ ср→↑↑Δr→ находится согласно математической формуле определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу средней скорости);
- числовое значение средней скорости (модуль, проекции на координатные оси) определяется согласно геометрическим правилам работы с векторами;
- физические понятия отличаются от математических понятий наличием единиц измерения ([(v_{ср})] (=) [(frac{м}{с})]).
Участки траектории (AB), (AD) и (AE) (рис. (1)) характеризуются, соответственно, средними скоростями:
(vec{v_{ср3}}), (vec{v_{ср2}}), (vec{v_{ср1}}).
| (vec{v_{ср3}}) = (frac{Delta{vec{r_3}}}{Delta{t_3}}) | (vec{v_{ср2}}) = (frac{Delta{vec{r_2}}}{Delta{t_2}}) | (vec{v_{ср1}}) = (frac{Delta{vec{r_1}}}{Delta{t_1}}) |
Если уменьшать неограниченно промежуток времени (Delta{t}), то быстрота движения тела характеризуется понятием «мгновенная скорость» (или «скорость»).
Математическая запись уменьшения промежутка времени:
Δt→0
(в математике существует понятие «предел», символ данного понятия — «lim»).
Физический смысл принципа уменьшения промежутка времени: на определённом этапе данной процедуры значения средней скорости будут приблизительно одинаковыми и определение физического понятия «средняя скорость» изменится на физическое понятие «мгновенная скорость»
.
Мгновенная скорость является векторной величиной:
- вектор мгновенной скорости (далее — скорости) направлен по касательной к траектории в исследуемой точке (проверь, как на рисунке (1) «хорды — перемещения (Delta{vec{r_3}}), (Delta{vec{r_2}}) и (Delta{vec{r_1}})» при уменьшении промежутков времени (Delta{t_3}), (Delta{t_2}) и (Delta{t_1}) изображаются касательными, которые соответствуют векторам скоростей (vec{v_3}), (vec{v_2}), (vec{v_1})).
На рисунке (1) тело движется из точки (E) в точку (D), изменяя скорость от (v_2) до (v_3). Параллельным переносом перенесём вектор (vec{v_{3}}) к (vec{v_{2}}), тогда изменение скорости за промежуток времени (Delta{t}) равно разности векторов
((vec{v_{3}})(-)(vec{v_{2}})), что на рисунке (1) соответствует вектору ускорения (vec{a_{2}}).
Среднее ускорение равно отношению изменения скорости к промежутку времени:
Примечание:
1) в физических задачах при написании символа aср → индекс «ср», как правило, не прописывается;
2) в ситуации прямолинейного неравномерного движения используется термин «ускорение».
Характеристики физического понятия «среднее ускорение»:
- направление вектора среднего ускорения определяется согласно правилу aср→↑↑Δυ→;
- числовое значение ускорения (модуль, проекции на координатные оси) определяется согласно геометрическим правилам работы с векторами;
- единица измерения ([(a_{ср})] (=) [(frac{м}{с^2})]).
Участки траектории (AB), (AD) и (AE) (рис. (1)) характеризуются, соответственно, средними ускорениями (vec{a_{3}}), (vec{a_{2}}), (vec{a_{1}}).
| (vec{a_{3}}) (=) (frac{Delta{vec{v_3}}}{Delta{t_3}}) | (vec{a_{2}}) (=) (frac{Delta{vec{v_2}}}{Delta{t_2}}) | (vec{a_{1}}) (=) (frac{Delta{vec{v_1}}}{Delta{t_1}}) |
Если уменьшать неограниченно промежуток времени (Delta{t}), то изменение скорости движения тела в конкретный момент времени характеризуется физическим понятием «мгновенное ускорение».
Вектор мгновенного ускорения при движении тела по криволинейной траектории представляет векторную сумму компонентов данного вектора, которые направлены по касательной и нормали (перпендикуляр к касательной).
Векторное и скалярное уравнения скорости материальной точки
1) Общий вид:
- векторное уравнение — (vec{v}) (=) (vec{v}(t));
- числовые (скалярные) уравнения — (v_x) (=) (v_x(t)), (v_y) (=) (v_y(t)), (v_z) (=) (v_z(t)).
2) Прямолинейное равноускоренное движение:
- векторное уравнение — (vec{v}(t)) (=) (vec{v}{_0}) (+) (vec{a}(t – t_0)),
где (vec{v}{_0}) — скорость тела в начальный момент времени ({t_0}), (vec{v}(t)) — скорость тела в произвольный момент
времени (t);
- числовые (скалярные) уравнения — (v_x(t)) (=) (v_{0x}) (+) (a_x(t – t_0)), (v_y(t)) (=) (v_{0y}) (+) (a_y(t – t_0)),
(v_z(t)) (=) (v_{0z}) (+) (a_z(t – t_0)).
Графическое изображение зависимости проекции скорости от времени ({v_х}(t))
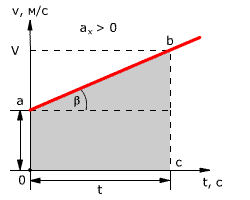
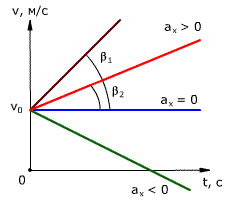
При движении тела с постоянным ускорением проекция скорости изменяется по линейному закону в зависимости от времени (t): (v_x(t)) (=) (v_{0x}) (+) (a_x(t – t_0)) (рис. (2)).
|
|
|
Рис. (2). График зависимости проекции скорости от времени
Значение проекции ускорения по графику определяется как тангенс угла: (a_x) (=) (tgα) (=) (frac{Delta{v}}{Delta{t}}).
Перемещение
Проекции перемещений при равнопеременном движении в момент времени (t) определяются формулами:
(s_x(t)=x(t) – x_0), (s_y(t)=y(t) -y_0), (s_z(t)=z(t) – z_0).
|
(A) |
(B) |
Рис. (3). Определение модуля и проекций перемещения по графику зависимости проекции скорости от времени
Модуль и проекции перемещения тела определяются графическим способом с
использованием графика зависимости (v_x(t)).
|
Рисунок (3) (A) ((v_0) (=) (0)) |
Рисунок (3) (B) ((v_0) (≠) (0)) |
|
Модуль перемещения определяется как площадь прямоугольного треугольника (ABC) с катетами (c) и (b), где (b) (=) (t), (c) (=) (at). |
Модуль перемещения определяется как площадь трапеции (ABCD) с основаниями (d) (=) (v_0), (b) (=) (v_0+at) и высотой (h) (=) (t). S=12b+dh⇒S=υ0⋅t+a⋅t22 |
|
Проекция перемещения: (s_x) (=) (S) |
Проекция перемещения: (s_x) (=) (S) |
Примечание: если график проекции скорости состоит из участков, где площадь трапеции имеет отрицательное значение (например, (s_{x1}) (>) (0), (s_{x2}) (<) (0)), то модуль перемещения тела равен:
s=sx1+sx2
.
Источники:
Рис. 1. Перемещения тела при криволинейном движении. © ЯКласс.
Рис. 2. График зависимости проекции скорости от времени. © ЯКласс.
Рис. 3. Определение модуля и проекций перемещения по графику зависимости проекции скорости от времени. © ЯКласс.
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
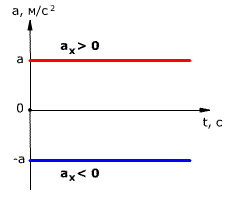
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
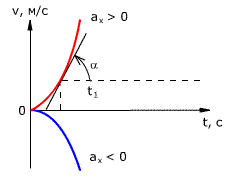
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
Графическое представление
равномерного прямолинейного движения
Механическое движение представляют графическим
способом. Зависимость физических величин выражают при помощи функций.
Обозначают:
V(t) – изменение
скорости со временем
S(t) –
изменение перемещения (пути) со временем
a(t) –
изменение ускорения со временем
Зависимость ускорения от времени.
Так как при равномерном движении ускорение равно нулю, то зависимость a(t) –
прямая линия, которая лежит на оси времени.
Зависимость скорости от времени.
Так как тело движется прямолинейно и равномерно (v = const), т.е. скорость со временем не изменяется,
то график с зависимостью скорости от времени v(t) – прямая линия, параллельная
оси времени.
Проекция перемещения тела
численно равна площади прямоугольника АОВС под графиком, так как величина
вектора перемещения равна произведению вектора скорости на время, за которое
было совершено перемещение.
Правило определения пути по графику v(t):
при прямолинейном равномерном движении модуль вектора перемещения равен площади
прямоугольника под графиком скорости.
Зависимость перемещения от
времени. График s(t) – наклонная линия:
Из графика видно, что
проекция скорости равна:
Рассмотрев эту формулу, мы
можем сказать, чем больше угол, тем быстрей движется тело и оно проходит
больший путь за меньшее время.
Правило
определения скорости по графику s(t): Тангенс угла наклона графика к оси
времени равен скорости движения.
Неравномерное
прямолинейное движение.
Равномерное
движение это движение с постоянной скоростью. Если скорость тела меняется,
говорят, что оно движется неравномерно.
Движение, при
котором тело за равные промежутки времени совершает неодинаковые перемещения,
называют неравномерным или переменным движением.
Для
характеристики неравномерного движения вводится понятие средней скорости.
Средняя
скорость движения равна отношению всего пути, пройденного материальной
точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не
средняя, а мгновенная скорость, которая определяется как
предел, к которому стремится средняя скорость за бесконечно малый промежуток
времени Δt:
Мгновенной скоростью переменного
движения называют скорость тела в данный момент времени или в данной точке
траектории.
Мгновенная скорость тела в любой точке
криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями
показано на рисунке.
Движение тела, при котором его скорость за
любые равные промежутки времени изменяется одинаково, называют равноускоренным
или равнопеременным движением.
Ускорение — это
векторная физическая величина, характеризующая быстроту изменения скорости,
численно равная отношению изменения скорости к промежутку времени, в течение
которого это изменение произошло.
Если скорость изменяется
одинаково в течение всего времени движения, то ускорение можно рассчитать по
формуле:
Обозначения:
Vx — Скорость
тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как
быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость
тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит
скорость уменьшается, движение замедленное.
Единица измерения ускорения в
СИ [м/с2].
Ускорение измеряют акселерометром
Уравнение скорости для
равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного
движения (перемещение при равноускоренном движении):
Обозначения:
Sx—
Перемещение тела при равноускоренном движении по прямой
Vx o —
Начальная скорость тела
Vx — Скорость тела при равноускоренном
движении по прямой
ax — Ускорение тела
t— Время
движения тела
Еще формулы, для нахождения перемещения при
равноускоренном прямолинейном движении, которые можно использовать при решении
задач:
–
если известны начальная, конечная скорости движения и ускорение.
–
если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного
прямолинейного движения
Механическое
движение представляют графическим способом. Зависимость физических величин
выражают при помощи функций. Обозначают:
V(t) – изменение
скорости со временем
S(t) –
изменение перемещения (пути) со временем
a(t) –
изменение ускорения со временем
Зависимость ускорения от времени.
Ускорение со временем не изменяется, имеет постоянное значение, график a(t) –
прямая линия, параллельная оси времени.
Зависимость скорости от времени. При
равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt .
Графиком является наклонная линия.
Правило определения пути по графику v(t):
Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t):
Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело
замедляет движение, ускорение отрицательное, угол графика тупой, поэтому
находим тангенс смежного угла.
Зависимость пути от времени. При
равноускоренном движении путь изменяется, согласно квадратной зависимости:
.
В координатах зависимость имеет
вид:
Графиком является ветка параболы.