Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.
Теоремы сложения вероятностей
Найдем вероятность суммы событий и
(в предположении их совместности либо несовместности).
Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:
Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.
Решение. Искомое событие произойдет, если будет продана пара обуви 44-го размера (событие
) или 45-го (событие
), или не меньше 46-го (событие
), т. е. событие
есть сумма событий
. События
,
и
несовместны. Поэтому согласно теореме о сумме вероятностей получаем
Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.
Решение. События “очередной будет продана пара обуви меньше 44-го размера” и “будет продана пара обуви размера не меньше 44-го” противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события
поскольку , как это было найдено в примере 1.
Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой “Electra Ltd” оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим
. Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события
являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.
Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).
Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:
Зависимые и независимые события. Условная вероятность
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или не появления “герба” во втором испытании (событие
). В свою очередь, вероятность появления “герба” во втором испытании не зависит от результата первого испытания. Таким образом, события
и
независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события
, называется условной вероятностью события
и обозначается
.
Условие независимости события от события
записывают в виде
, а условие его зависимости — в виде
. Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим извлечение изношенного резца в первом случае, а
— извлечение нового. Тогда
. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события зависит от того, произошло или нет событие
.
Формулы умножения вероятностей
Пусть события и
независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий
и
.
Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие ),
. Вероятность того, что из второго ящика взята стандартная деталь (событие
),
. Вероятность того, что из третьего ящика взята стандартная деталь (событие
),
. Так как события
,
и
независимые в совокупности, то искомая вероятность (по теореме умножения)
Пусть события и
зависимые, причем вероятности
и
известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие
, и событие
.
Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие
) и при третьем — синий (событие
).
Решение. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность
. Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный,
. Искомая вероятность
Формула полной вероятности
Теорема 2.5. Если событие наступает только при условии появления одного из событий
, образующих полную группу несовместных событий, то вероятность события
равна сумме произведений вероятностей каждого из событий
на соответствующую условную вероятность события
:
(2.1)
При этом события называются гипотезами, а вероятности
— априорными. Эта формула называется формулой полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.
Решение. Обозначим событие, означающее годность собранного узла;
,
и
— события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
Искомая вероятность
Формула Байеса
Эта формула применяется при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий
, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез
. Априорные (до опыта) вероятности
известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности
. Для гипотезы
формула Байеса выглядит так:
Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.
Решение. Рассчитаем условные вероятности по формуле Байеса:
для первого станка
для второго станка
для третьего станка
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение.
Два события называют независимыми,
если вероятность появления одного из
них не зависит от того, произойдет другое
событие или нет.
Например, опыт
состоит в бросании двух монет. Пусть А
и В
– события, состоящие в том, что герб
появится соответственно на первой и
второй монете. В данном случае вероятность
события А
не зависит от того, произошло событие
В
или нет. Следовательно, событие А
независимо от события В.
Определение.
Несколько событий называют попарно
независимыми,
если каждые два из них независимы.
Например, опыт
состоит в бросании трех монет. Пусть А,
В,
С
– события, состоящие в том, что герб
появится соответственно на первой,
второй и третьей монете. В данном случае
каждые два из рассматриваемых событий
(т.е. А
и В,
А
и С,
В
и С)
– независимы. Следовательно, события
А, В и С – попарно независимые. ◄
Определение.
Два события называют зависимыми,
если вероятность появления одного из
них меняется в зависимости от того,
произойдет другое событие или нет.
Например, в урне
3 белых и 2 черных шара. Наудачу берут
один шар, не возвращая его в урну. Если
появился белый шар (событие А),
то вероятность появления белого шара
во втором испытании (событие В)
Р(В)
=
![]() .
.
Если же в первом испытании появился
черный шар (т.е. событиеА
не произошло), то вероятность Р(В)
=
![]() .
.
Т.е. вероятность событияВ
зависит от того, произошло событие А
или нет. Следовательно, события А
и В
– зависимые.
Отметим, что
зависимость
и независимость событий всегда взаимны,
т.е. если событие В
не зависит от события А,
то и событие А
не зависит от события В.
2.4. Теорема умножения вероятностей независимых событий
Сформулируем
теорему умножения вероятностей
независимых событий.
Теорема.
Вероятность
совместного появления двух независимых
событий А и В равна произведению
вероятностей этих событий:
|
Р(АВ) = Р(А)·Р(В). |
(2.5) |
Для того чтобы
обобщить теорему умножения на несколько
событий, введем понятие независимости
событий в совокупности.
Определение.
Несколько событий называют независимыми
в совокупности,
если каждое из них и любая комбинация
остальных событий (содержащих либо все
остальные события, либо часть из них)
есть события независимые.
Например, если
события А1,
А2
и А3
независимые в совокупности, то независимыми
являются события: А1
и А2,
А1
и А3,
А2
и А3,
А1А2
и А3,
А1А3
и А2,
А2А3
и А1.
Подчеркнем, что
если несколько событий независимы
попарно, то из этого еще не следует их
независимость в совокупности. В этом
смысле требование независимости событий
в совокупности сильнее требования их
попарной независимости.
Теперь мы можем
сформулировать следствие из теоремы
умножения вероятностей, обобщающее
теорему умножения на несколько событий.
Следствие.
Вероятность
совместного появления нескольких
событий, независимых в совокупности,
равна произведению вероятностей этих
событий.
|
Р(А1А2…Аn) |
(2.6) |
Пример 2.4.
Имеется три урны, содержащих по 10 шаров.
В первой урне 5 шаров красного цвета, во
второй – 4, в третьей – 6. Из каждой урны
наудачу вынимают по одному шару. Найти
вероятность того, что все три шара
окажутся красного цвета.
Решение.
Вероятность того, что из первой урны
вынут шар красного цвета (событие А)
Р(А)
=
![]() = 0,5. Вероятность того, что из второй урны
= 0,5. Вероятность того, что из второй урны
вынут шар красного цвета (событиеВ)
Р(В)
=
![]() = 0,4. Вероятность того, что из третьей
= 0,4. Вероятность того, что из третьей
урны вынут шар красного цвета (событиеС)
Р(С)
=
![]() = 0,6.
= 0,6.
Так как события
А,
В
и С
независимые в совокупности, то искомая
вероятность (по теореме умножения) равна
Р(АВС)
= Р(А)·Р(В)·Р(С)
= 0,5·0,4·0,6 = 0,12. ◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгебра и начала математического анализа, 11 класс
Урок №34. Условная вероятность. Независимость событий.
Перечень вопросов, рассматриваемых в теме:
– Условная вероятность
– Совместные и несовместные события
– Схема решения задач на вычисление условной вероятности события;
– Задачи на определение независимости событий.
Глоссарий по теме
Совместные события – события, одновременное появление которых возможно.
Несовместные события – события, одновременное появление которых невозможно.
События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.
Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается PA(B).
Условная вероятность – вероятность наступления одного события при условии, что другое событие уже произошло.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 186-194.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе.
Рассмотрим примерную задачу:
Из колоды карт извлекают четыре карты. Первые две оказались семёрками. Какова вероятность, что одна или обе оставшиеся карты окажутся семёрками? (колода содержит 36 карт)
1. 1/561
2. 65/561
3. 1/105
4. 17/518
Теоретическая часть
События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример совместных событий: выпадение чётного числа и выпадение числа, кратного трём, при броске игрального кубика. Когда выпадает шесть, реализуются сразу оба события.
События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Пример несовместных событий: выпадение чётного числа и выпадение нечётного числа при броске игрального кубика.
Теорема о сумме двух событий:
Вероятность суммы любых двух событий А и В равна сумме вероятностей этих событий без вероятности их совместного осуществления: Р(А+В) = Р(А)+Р(В)-Р(АВ)
Рассмотрим пример.
В лотерее выпущено 10 000 билетов, из них: 10 выигрышей по 200 рублей, 100 выигрышей по 100 рублей, 500 выигрышей по 50 рублей и 1000 выигрышей по 10 рублей. Какова вероятность того, что человек, купивший билет, выиграет не менее 50 рублей?
Решение: Введем для удобства обозначение событий А – «человек выиграл 50 рублей», В – «человек выиграл 100 рублей», С – «человек выиграл 200 рублей», D – «человек выиграл не менее 50 рублей». Событие D означает, что выигрыш может составлять 50 и более рублей, то есть 50, 100 или 200 рублей: М=А+В+С. События А, В, С – попарно несовместны.
Воспользуемся теоремой: Р(М)=Р(А)+Р(В)+Р(С)=0,061.
Задача.
Дана вероятность исходного события. Чему равна вероятность противоположного события?
Вероятность исходного события А обозначим Р(А). Вероятность противоположного события Р(Ᾱ).
Решение:
События А и Ᾱ образуют полную группу событий, вероятность которой равна 1.
Тогда вероятность противоположного события находится по формуле:
P(Ᾱ)=1-P(A)
- События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.
Например, монета брошена два раза.
A – выпала «Решка»
B – выпал «Орёл»
Вероятность появления «Орла» во втором испытании не зависит от результата первого испытания.
Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:
Р(АВ)=Р(А)·Р(В)
Рассмотрим пример.
Задача.
Подбрасываются две монеты. Найдите вероятность выпадения двух орлов.
Решение:
Введем обозначение событий:
A1– на 1-й монете выпадет орёл;
A2– на 2-й монете выпадет орёл.
Событие “выпадение двух орлов” заключается в том, что на 1-й монете появится орёл и на 2-й монете появится орёл, следовательно, это произведение событий A1A2. Вероятность выпадения орла на одной монете не зависит от результата броска другой монеты, следовательно, события A1 и A2 независимы. По теореме умножения вероятностей независимых событий получим:
P(A1A2) = P(A1)· P(A2) = 1/2 · 1/2 = 1/4.
- Событие B называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события B, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается PA(B).
Отыскать вероятность совместного появления зависимых событий помогает теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: P(AB) = P(A)·PA(B).
Связь теории вероятностей с теорией множеств.
В математике принято устанавливать связи между различными разделами. Связь между теорией вероятностей и теорией множеств устанавливается следующим образом: события отождествляются с множествами. В таком случае понятию исход будет эквивалентно понятие элемент множества. При таком подходе выберите из списка, какому понятию из теории множеств соответствует данное понятие из теории вероятностей:
– Невозможное событие (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
– Сумма событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
– Произведение событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
Примеры и разбор решения заданий тренировочного модуля
1. В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара без возврата. Найдите вероятность того, что первый шар окажется черным, второй – красным и третий – белым.
Решение.
А – первый шар окажется черным
В – второй шар красный
С – третий шар белый
 .
.
Ответ: 4/91.
2. Колю отпускают гулять при условии сделанных уроков с вероятностью 0,8. Папа выдает ему деньги на мороженое с вероятностью 0,6. С какой вероятностью Коля пойдет гулять без мороженого?
Решение.
A – папа выдал Коле денег на мороженое
B – Колю отпустили гулять
Вероятность того, что Коля пойдёт гулять, есть в условии задачи P(B) = 0,8. Вероятность, что папа не выдаст ему деньги на мороженое, равна P(Ᾱ) = 1 – P(A) = 1 – 0,6 = 0,4. Вероятность одновременного осуществления двух независимых событий – произведение их вероятностей P(ᾹB) = P(Ᾱ)·P(B) = 0,8·0,4 = 0,32.
Ответ: 0,32.
На этой странице вы узнаете
- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.

Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
(P = frac{m}{n})
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
(P = frac{m}{n} * 100%)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?
)frac{1}{2} + frac{1}{2} = 1)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
(P(A) + P(overline{A}) = 1)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac{1}{6}).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).
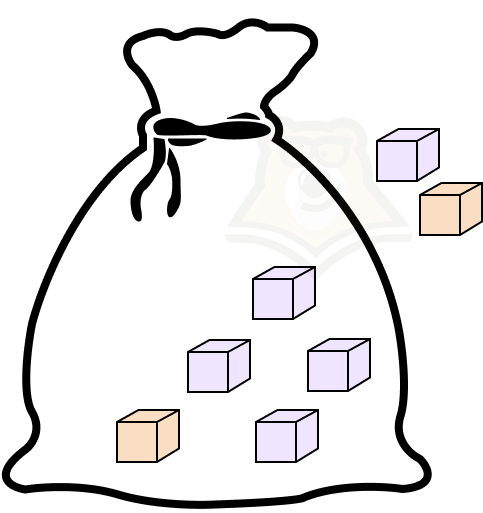
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
(P_n(k) = C_n^k * p^k * q^{n — k})
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
Продолжение статьи «Теория вероятности. Классическое определение».
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Итак, теория.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).
 Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.
Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.
Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.

Подборку задач на отработку темы смотрите здесь.
