Содержание
- – Как определяется зенитное расстояние?
- – Как определить горизонтальные координаты?
- – Как определить горизонтальную координату высоту?
- – Как определить координаты небесных тел?
- – Какие координаты составляют горизонтальную систему координат?
- – Как определить высоту полюса мира над горизонтом?
- – Какие бывают небесные координаты?
- – Чем определяется положение точки на Земле?
- – Что лежит в основе экваториальной системы координат?
- – Как определить высоту светила?
- – Чему равна высота точки зенита над горизонтом?
- – Как строят экваториальную систему координат?
- – Как найти прямое восхождение звезды?
- – Как определить координаты звезд?
- – Как определить координаты Солнца?
зенитное расстояние — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180º. С высотой h связано соотношением z = 90º – h.
Как определяется зенитное расстояние?
Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру. Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Как определить горизонтальные координаты?
Горизонта́льные координа́ты — в астрономии зенитное расстояние z небесного светила (иногда высота h светила) и азимут А. Поскольку обе указанные плоскости перпендикулярны плоскости математического горизонта, мерой двугранного угла может служить соответствующий угол между их следами в горизонтальной плоскости.
Как определить горизонтальную координату высоту?
Например, если светило “касается” горизонта, то его высота 0°, если же светило находится прямо над нами, то его высота – 90°. Точка, которая у нас над головой, называется зенит и обозначается “Z”.
Как определить координаты небесных тел?
Небесные координаты вводятся на геометрически правильной поверхности небесной сферы координатной сеткой, подобной сетке меридианов и параллелей на Земле. Координатная сетка определяется двумя плоскостями: плоскостью экватора системы и связанными с ним двумя полюсами, а также плоскостью начального меридиана.
Какие координаты составляют горизонтальную систему координат?
В горизонтальной системе координат одной координатой является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A. Высотой h светила называется дуга вертикала светила от плоскости математического горизонта до направления на светило.
Как определить высоту полюса мира над горизонтом?
Поскольку ось мира параллельна оси вращения Земли, высота полюса мира hP над горизонтом всегда равна географической широте φ места наблюдения, а наклон небесного экватора к истинному горизонту определяется углом 90° – φ.
Какие бывают небесные координаты?
Системы небесных координат: а – горизонтальная, б – экваториальная, в – эклиптическая, г – галактическая. N, S, W, E – точки севера, юга, запада, востока; Z – зенит… Выбранным направлением в этой системе является направление отвесной линии; осн. плоскость системы перпендикулярна отвесной линии.
Чем определяется положение точки на Земле?
Положение точки на земной поверхности определяется с помощью трех координат: широты (центральный угол, образованный отвесной линией в данной точке с плоскостью экватора, отсчитывается к северу или к югу от экватора), долготы (угол между плоскостью меридиана, проходящего через данную точку, и плоскостью начального …
Что лежит в основе экваториальной системы координат?
Экваториальная система координат — одна из систем небесных координат. В этой системе основной плоскостью является плоскость небесного экватора. Одной из координат при этом является склонение δ (реже — полярное расстояние p).
Как определить высоту светила?
h = φ + δ – 90°. Верхняя кульминация соответствует максимальной высоте светила над горизонтом, нижняя – минимальной (при этом светило может находиться под горизонтом).
Чему равна высота точки зенита над горизонтом?
Высота светила над горизонтом, h, – это угловое расстояние от истинного горизонта, измеряемое по вертикалу светила (аналог широты). Высота светила может изменяться в пределах от -90o до 90o. Отрицательная высота означает, что светило находится под горизонтом. Пример: высота зенита равна 90o.
Как строят экваториальную систему координат?
В экваториальной системе координат основными кругами являются: экватор, от которого отсчитываются склонения, небесный меридиан, круг склонений. Основные точки — это полюсы мира, точка весеннего равноденствия — начало отсчета прямых восхождений — и высшая точка экватора — начало отсчета часовых углов.
Как найти прямое восхождение звезды?
Прямое восхождение равно длине дуги небесного экватора от точки весеннего равноденствия до круга склонения светила, причём оно отсчитывается против часовой стрелки, если смотреть со стороны северного полюса мира.
Как определить координаты звезд?
Для того, чтобы найти звезду, используя бесплатное приложение Google Earth, выполните следующие действия:
- Загрузите и установите приложение
- В верхней панели наведите на значок ‘Планета’ и из выпадающего списка выберите ‘Небо’
- Слева в поисковом окне введите координаты звезды в следующем формате: 13:03:33.35 -49:31:38.1.
Как определить координаты Солнца?
Координаты Солнца
Z ~ f — d и H = 90° — Z. Например, 25 декабря d = 23,2° S. В широте f = 45,5° N; Z = 45,5° — (— 23,2°) = 68,7°; H = 21,3°. Легко найти и даты начала и конца полярного дня и ночи.
Интересные материалы:
Как поставить Гифку на обои iPhone?
Как поставить хэштег в инстаграме под фото?
Как поставить микрофон в телеграмме?
Как поставить нижний индекс на клавиатуре?
Как поставить пароль на папку в Windows 10?
Как поставить пароль на планшете Samsung?
Как поставить плюс перед цифрой в Экселе?
Как поставить шапку на канал на YouTube на Android?
Как поставить символ ударения в ворде?
Как поставит скобки в ворде?
Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.
Системы небесных координат отличаются друг от друга выбором основной плоскости и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.
Содержание
- 1 Горизонтальная система координат
- 2 Первая экваториальная система координат
- 3 Вторая экваториальная система координат
- 4 Эклиптическая система координат
- 5 Галактическая система координат
- 6 Изменения координат при вращении небесной сферы
- 7 История и применение
- 8 Использование различных систем координат
- 9 Примечания
- 10 См. также
Горизонтальная система координат
В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.
Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.
Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)
Первая экваториальная система координат
В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.
Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.
Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.
Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу и от 0° до −180° (от 0h до −12h) к востоку.
Вторая экваториальная система координат

Использование экваториальной системы координат.
В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.
Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).
RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.
Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.
- Объект на небесном экваторе имеет склонение 0°
- Склонение северного полюса небесной сферы равно +90°
- Склонение южного −90°
У склонения всегда указывается знак, даже если склонение положительно.
Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ < −90° + φ , то объект называется невосходящим, а значит он ненаблюдаем на широте φ.[1]
Эклиптическая система координат
В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
Галактическая система координат
В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.
Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.
Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.
Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.
Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).
Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:

Изменения координат при вращении небесной сферы
Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
История и применение
Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.
Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.
Использование различных систем координат
Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.
Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.
Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.
Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.
Примечания
- ↑ Зигель Ф. Ю. Сокровищница звёздного неба — путеводитель по созвездиям и Луне / Под ред. Г. С. Куликова. — 5-е изд. — М.: Наука, 1986. — С. 57—58. — 296 с. — 200 000 экз.
См. также
- Небесная сфера
Wikimedia Foundation.
2010.

Иногда вместо высоты h используется зенитное расстояние – угол между отвесной линией и направлением на светило ZОσ, или дуга вертикала Zσ. Зенитное расстояние есть дополнение до 900 высоты h:
z = 900 – h.
Зенитное расстояние светила отсчитывается от зенита и может принимать значения
00 ≤ z ≤ 1800.
Вторая координата горизонтальной системы – азимут – двугранный угол SZZ’σ между плоскостью небесного меридиана (начального круга) и плоскостью вертикала светила, обозначаемый буквой А:
А= двугр.угол SZZ’σ = SOM = SM = сф.угол SZM.
Вастрономии азимуты отсчитываются от точки юга S по ходу часовой стрелки в пределах
00 ≤ А ≤ 3600.
Вследствие суточного вращения небесной сферы горизонтальные координаты светила меняются в течение суток. Поэтому, фиксируя положение светил в этой системе координат, нужно отмечать момент времени, к которому относятся координаты h, z, A. Кроме того, горизонтальные координаты являются не только функциями времени, но и функциями положения места наблюдения на земной поверхности. Эта особенность горизонтальных координат обусловлена тем, что отвесные линии в разных точках земной поверхности имеют разное направление.
В горизонтальной системе координат ориентируются геодезические инструменты и выполняются измерения.
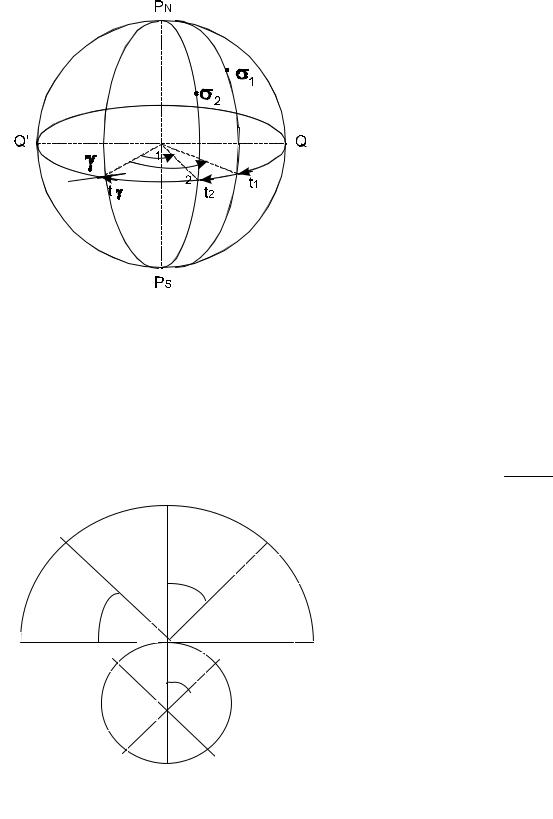
1.3.2 Первая экваториальная система координат
Первая экваториальная система координат
показана на рис. 6.
Основной круг первой экваториальной
системы координат есть небесный экватор
Q’KQ. Геометрические полюса небесного

 экватора – северный и южный полюсы мира, РN
экватора – северный и южный полюсы мира, РN
и РS.
Начальный круг системы – небесный меридиан РNQ’РSQ.
Рис. 6 Первая экваториальная система координат
Начальная точка системы – верхняя точка экватора Q.
Определяющий круг системы – круг склонения РNσРS.
Первая координата первой экваториальной системы – склонение светила δ, угол между плоскостью небесного экватора и направлением на светило КОσ, или дуга круга склонения Кσ. Склонение отсчитывается от экватора к полюсам и может принимать значения
-900 ≤ δ ≤ 900.
Иногда используется величина = 900 – δ, где 00 ≤ ≤1800, называемая
полярным расстоянием.
Склонение не зависит ни от суточного вращения Земли, ни от географических координат пункта наблюдения φ, λ.
Вторая координата первой экваториальной системы − часовой угол светила t − двугранный угол между плоскостями небесного меридиана и круга склонения светила, или сферический угол при северном полюсе мира:
t =дв.угол QРNРSσ = сф.угол QРNσ = QК = QOK.
Часовой угол отсчитывается от верхней точки экватора Q в направлении суточного вращения небесной сферы от 00 до 3600, 00 ≤ t ≤ 3600.
Часовой угол часто выражают в часовой мере, 0h ≤ t ≤ 24h.
Градусы и часы связаны соотношениями:
3600 = 24h, 150 = 1h, 15′ = 1m, 15″ = 1s.
Вследствие видимого суточного движения небесной сферы часовые углы светил постоянно изменяются. Часовой угол t отсчитывается от небесного меридиана, положение которого определяется направлением отвеса (ZZ’) в данном пункте и, следовательно, зависит от географических координат пункта наблюдения на Земле.
1.3.3 Вторая экваториальная система координат
Вторая экваториальная система координат изображена на рис. 7.
Основной круг второй экваториальной системы – небесный экватор QγQ’.
Начальный круг системы – круг склонений точки весеннего равноденствия РNγРS, называемый колюром равноденствий.
Начальная точка системы – точка весеннего равноденствия γ.
Определяющий круг системы – круг склонения РNσРS.
Первая координата – склонение светила δ.

Рис. 7 Вторая экваториальная система координат
Вторая координата – прямое восхождение α, двугранный угол между плоскостями колюра равноденствия и круга склонения светила, или сферический
угол γРNσ, или дуга экватора γК:
α =дв.угол γРNРSσ = сф.угол γPNσ = γК = = γOK.
Прямое восхождение α выражается в
часовой мере и отсчитывается от точки γ


 против хода часовой стрелки в направлении,
против хода часовой стрелки в направлении,
противоположном видимому суточному движению светил,
0h ≤ α ≤ 24h.
Во второй экваториальной системе координаты α и δ не зависят от суточного вращения светил. Так как эта система не связана
ни с горизонтом, ни с меридианом, то α и δ не зависят от положения точки наблюдения на Земле, то есть от географических координат φ и λ.
При выполнении астрономо-геодезических работ координаты светил α и δ должны быть известны. Они используются при обработке результатов наблюдений, а также для вычисления таблиц координат A и h, называемых эфемеридами, с помощью которых можно отыскать астрономическим теодолитом светило в любой заданный момент времени. Экваториальные координаты светил α
иδ определяются из специальных наблюдений на астрономических обсерваториях
ипубликуются в звездных каталогах.
1.4 Географическая система координат
|
Z |
Если спроектировать |
точку М |
|||||||
|
PN |
|||||||||
|
λ |
земной |
поверхности |
на |
небесную |
|||||
|
E |
Q |
сферу |
по |
направлению |
отвесной |
||||
|
• G |
φ |
линии ZZ’ |
(рис.8), |
то |
сферические |
||||
|
координаты |
зенита |
Z |
этой |
точки |
|||||
|
φ |
|||||||||
|
называются |
географическими |
||||||||
|
M |
|||||||||
|
N |
S |
координатами: |
географической |
||||||
|
p |
|||||||||
|
q |
широтой |
φ и |
географической |
||||||
|
O |
λ |
||||||||
|
q′ |
p′ |
долготой λ. |
|||||||
|
В |
географической |
системе |
|||||||
|
Q′ |
W |
||||||||
|
g |
координат |
задается |
положение |
||||||
|
PS |
|||||||||
|
пунктов |
на поверхности |
Земли. |
Z′
Рис.8. Географическая система координат
Географические координаты могут быть астрономическими, геодезическими и геоцентрическими. Методами геодезической астрономии определяют астрономические координаты.
Основной круг астрономической географической системы координат – земной экватор, плоскость которого перпендикулярна оси вращения Земли. Ось вращения Земли непрерывно совершает колебания в теле Земли (см. раздел “Движение земных полюсов”), поэтому различают мгновенную ось вращения (мгновенный экватор, мгновенные астрономические координаты) и среднюю ось вращения (средний экватор, средние астрономические координаты).
Плоскость астрономического меридиана, проходящего через произвольную точку земной поверхности, содержит отвесную линию в данной точке и параллельна оси вращения Земли.
Начальный меридиан – начальный круг системы координат – проходит через Гринвичскую обсерваторию (согласно международному соглашению 1883г).
Начальная точка астрономической географической системы координат – точа пересечения начального меридиана с плоскостью экватора.
В геодезической астрономии определяются астрономические широта и долгота, φ и λ, а также астрономический азимут направления A.
Астрономическая широта φ есть угол между плоскостью экватора и отвесной линией в данной точке. Широта отсчитывается от экватора к северному полюсу от 00 до +900 и к южному полюсу от 00 до -900.
Астрономическая долгота λ – двугранный угол между плоскостями начального и текущего астрономических меридианов. Долгота отсчитывается от гринвичского меридиана к востоку (λE– восточная долгота) и к западу (λW– западная долгота) от 00 до 1800 или, в часовой мере, от 0 до 12 часов (12h). Иногда долготу считают в одну сторону от 0 до 3600 или, в часовой мере, от 0 до 24 часов.
Астрономический азимут направления А – двугранный угол между плоскостью астрономического меридиана и плоскостью, проходящей через отвесную линию и точку, на которую измеряется направление.
Если астрономические координаты связаны с отвесной линией и осью вращения Земли, то геодезические – с поверхностью относимости (эллипсоидом) и с нормалью к этой поверхности. Подробно геодезическая система координат рассматривается в разделе “Высшая геодезия”.
1.5 Связь между координатами различных систем
1.5.1 Связь между координатами первой и второй экваториальных систем. Формула звездного времени
В первой и второй экваториальных системах склонение δ измеряется одним и тем же центральным углом и одной и той же дугой большого круга, значит, в этих системах δ одно и то же.
Рис. 9 Связь между первой и второй экваториальными системами координат
Рассмотрим связь между t и α. Для этого определим часовой угол точки γ − ее положение в первой экваториальной системе координат:
tγ = QOγ = Qγ.
Из рис. 9 видно, что для любого светила справедливо равенство
tγ = t + α.
Часовой угол точки весеннего равноденствия является мерой звездного времени s:
s = tγ = t + α.
Последняя формула называется формулой звездного времени: сумма
часового угла и прямого восхождения светила равна звездному времени.
1.5.2 Связь между небесными и географическими координатами. Основные теоремы курса сферической астрономии
|
Z |
||||
|
PN |
δz=φ |
Q |
||
|
Небесный экватор |
||||
|
hp=φ |
M |
Горизонт |
||
|
N |
S |
|||
|
p |
φ |
q |
||
|
o |
||||
|
Экватор |
p’ |
Земля |
||
|
Рис. 10 – К теореме о высоте полюса |
||||
|
Мира над горизонтом |
Теорема 1. Географическая широта места наблюдения численно равна склонению зенита в точке наблюдения и равна высоте полюса мира над горизонтом:
φ = δz = hp.
Доказательство следует из рис. 10. Географическая широта φ есть угол между плоскостью земного экватора и отвесной линией в пункте наблюдения,Moq. Склонение зенита δz есть
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Горизонтальная система координат
(перенаправлено с «Зенитное расстояние»)
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 сентября 2022 года; проверки требует 1 правка.
Горизонтальная система координат[1]:40, или горизонтная система координат[2]:30 — это система небесных координат, в которой основной плоскостью является плоскость математического горизонта, а полюсами — зенит и надир. Она применяется при наблюдениях звёзд и движения небесных тел Солнечной системы на местности невооружённым глазом, в бинокль или телескоп с азимутальной установкой[1]:85. Горизонтальные координаты не только планет и Солнца, но и звёзд непрерывно изменяются в течение суток ввиду суточного вращения небесной сферы.
ОписаниеПравить
Горизонтальная система координат.
Линии и плоскостиПравить
Горизонтальная система координат всегда топоцентрическая. Наблюдатель всегда находится в фиксированной точке на поверхности земли (отмечена буквой O на рисунке). Будем предполагать, что наблюдатель находится в Северном полушарии Земли на широте φ. При помощи отвеса определяется направление на зенит (z), как верхняя точка, в которую направлен отвес, а надир (Z’) — как нижняя (под Землёй)[1]:38. Поэтому и линия (ZZ’), соединяющая зенит и надир называется отвесной линией[3]:12.
Плоскость, перпендикулярная к отвесной линии в точке O называется плоскостью математического горизонта. На этой плоскости определяется направление на юг (географический, не магнитный!) и север, например, по направлению кратчайшей за день тени от гномона. Кратчайшей она будет в истинный полдень, и линия (NS), соединяющая юг с севером, называется полуденной линией[1]:39. Точки востока (E) и запада (W) берутся отстоящими на 90 градусов от точки юга соответственно против и по ходу часовой стрелки, если смотреть из зенита. Таким образом, NESW — плоскость математического горизонта.
Плоскость, проходящая через полуденную и отвесную линии (ZNZ’S) называется плоскостью небесного меридиана, а плоскость, проходящая через небесное тело — плоскостью вертикала данного небесного тела. Большой круг, по которому она пересекает небесную сферу, называется вертикалом небесного тела[1]:40.
КоординатыПравить
В горизонтальной системе координат одной координатой является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.
Высотой h светила называется дуга вертикала светила от плоскости математического горизонта до направления на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру[1]:40.
Зенитным расстоянием z светила называется дуга вертикала светила от зенита до светила. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимутом A светила называется дуга математического горизонта от точки юга до вертикала светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°[1]:41. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии и навигации азимуты отсчитываются от точки севера[4].)
Особенности изменения координат небесных телПравить
За сутки звезда (а также в первом приближении — тело Солнечной системы) описывает круг, перпендикулярный оси мира (PP’), которая на широте φ наклонена к математическому горизонту на угол φ. Поэтому она будет двигаться параллельно математическому горизонту лишь при φ равном 90 градусов, то есть на Северном полюсе. Поэтому все звёзды, видимые там, будут незаходящими (в том числе и Солнце на протяжении полугода, см. долгота дня) а их высота h будет постоянной. На других широтах доступные для наблюдений в данное время года звёзды делятся на
- заходящие и восходящие[3]:16 (h в течение суток проходит через 0)
- незаходящие[3]:16 (h всегда больше 0)
- невосходящие[3]:16 (h всегда меньше 0)
Максимальная высота h звезды будет наблюдаться раз в день при одном из двух её прохождений через небесный меридиан — верхней кульминации, а минимальная — при втором из них — нижней кульминации. От нижней до верхней кульминации высота h звезды увеличивается, от верхней до нижней — уменьшается.
Переход к первой экваториальнойПравить
В дополнение к плоскости горизонта NESW, отвесной линии ZZ’ и оси мира PP’ начертим небесный экватор, перпендикулярный к PP’ в точке O. Обозначим t — часовой угол светила, δ — его склонение, R — само светило, z — его зенитное расстояние. Тогда горизонтальную и первую экваториальную систему координат свяжет сферический треугольник PZR, называемый первым астрономическим треугольником[1]:68, или параллактическим треугольником[2]:36. Формулы перехода от горизонтальной системы координат к первой экваториальной системе координат имеют следующий вид[5]:18:
Вывод формул перехода
Первый астрономический треугольник, горизонтальная и первая экваториальная системы координат.
Последовательность применения формул сферической тригонометрии к сферическому треугольнику PZR такая же, как при выводе подобных формул для эклиптической системы координат: теорема косинусов, теорема синусов и формула пяти элементов[2]:37. По теореме косинусов имеем:
Первая формула получена. Теперь к тому же сферическому треугольнику применяем теорему синусов:
Вторая формула получена. Теперь применяем к нашему сферическому треугольнику формулу пяти элементов:
Третья формула получена. Итак, все три формулы получены из рассмотрения одного сферического треугольника.
Переход от первой экваториальнойПравить
Формулы перехода от первой экваториальной системы координат к горизонтальной системе координат выводятся при рассмотрении того же сферического треугольника, применяя к нему те же формулы сферической тригонометрии, что и при обратном переходе[2]:37. Они имеют следующий вид[5]:17:
ПримечанияПравить
- ↑ 1 2 3 4 5 6 7 8 Цесевич В.П. Что и как наблюдать на небе. — 6-е изд. — М.: Наука, 1984. — 304 с.
- ↑ 1 2 3 4 Белова Н. А. Курс сферической астрономии. — М.: Недра, 1971. — 183 с.
- ↑ 1 2 3 4 Воронцов-Вельяминов Б.А. Астрономия: Учеб. для 10 кл. сред. шк. — 17-е изд. — М.: Просвещение, 1987. — 159 с.
- ↑ Н.Александрович «Горизонтальная система координат» Архивная копия от 20 марта 2012 на Wayback Machine
- ↑ 1 2 Балк М. Б., Демин В. Г., Куницын А. Л. Сборник задач по небесной механике и космодинамике. — М.: Наука, 1972. — 336 с.
См. такжеПравить
- Система небесных координат
- Сферическая система координат
Система небесных координат
1 Основные положения небесной сферы
Для определения видимого положения небесных тел и изучения их движения в астрономии вводится понятие небесная сфера. Сфера имеет произвольные размеры и произвольный центр. В её центр в точке О помещён наблюдатель, а вращение сферы повторяет вращение небесного свода. Прямая ZOZ′ обозначает отвесную линию для наблюдателя, где бы он не находился. Верхняя точка над головой наблюдателя Z называется Зенит, а противоположная её точка Z′ – называется Надир. Большой круг SWNE перпендикулярен отвесной линии называется истинным горизонтом или математический горизонт. Математический горизонт делит сферу на две половины, видимую и невидимую для наблюдателя. Линия РР′ – называется ось мира, вокруг этой оси происходит вращение небесной сферы. Плоскость ЕQWQ′ перпендикулярна к оси мира называется небесный экватор. Он делит небесную сферу на два полушария – северное и южное. Большой круг небесной сферы PZQSP′Z′Q′N называется небесным меридианом. Небесный меридиан делит небесную сферу на Восточное и Западное полушарие. Линия NOS называется полуденной линией.

Положение основных элементов небесной сферы относительно друг друга зависит от географической широты места наблюдателя. Под углом к плоскости математического горизонта расположена ось мира РР′. Положения светил на небе определяется по отношению к основным плоскостям и связанным с ними линиями и точками небесной сферы и выражается количественно двумя величинами (центральными углами или дугами больших кругов) которые называются небесными координатами.
2 Горизонтальная система координат
Основной плоскостью горизонтальной системы координат является математический горизонт NWSE , а отчёт ведётся от Z зенита и от одной из точек математического горизонта. Одной координатной является зенитное расстояние z (Зенитное расстояние к югу zв = φ – δ; к северу zн = 180 – φ – δ) или высота светила над горизонтом h . Высотой h светила М называется высота вертикального круга mМ от математического горизонта до светила, или центральный угол mOM между плоскостью математического горизонта и направлением на светило М. Высоты отсчитываются от 0 до 90 к зениту и от 0 до -90 к надиру. Зенитным расстоянием светила называется дуга вертикального круга ZM от светила до зенита. z + h = 90 (1). Положение самого вертикального круга определяется дугой координатной – азимутом А. Азимутом А называется дуга математического горизонта Sm от точки юга S до вертикального круга, проходящего через светило. Азимуты отсчитывается в сторону вращения небесной сферы, т.е. к западу от точки юга, в пределах от 0 до 360. Система координат используется для непосредственных определений видимых положений светил с помощью угломерных инструментов.

3 Первая экваториальная система координат
Начало отсчёта – точка небесного экватора Q. Одной координатной является склонение. Склонением называется дуга mM часового круга PMmP′ от небесного экватора до светила. Отсчитываются от 0 до +90 к северному полюсу и от 0 до -90 к южному. p + = 90 . Положение часового круга определяется часовым углом t. Часовым углом светила М называется дуга небесного экватора Qm от верхней точки Q небесного экватора до часового круга PMmP′, проходящего через светило. Часовые углы отсчитываются в сторону суточного обращения небесной сферы, к западу от Q в пределах от 0 до360 или от 0 до 24 часов. Система координат используется в практической астрономии для определения точного времени и суточного вращения неба. Определяет Суточное движение Солнца, Луны и других светил.

4 Вторая экваториальная система координат
Одной координатной является склонение , другой прямое восхождение α. Прямое восхождение α светила М называется дуга небесного экватора ♈m от точки весеннего равноденствия ♈ до часового круга, проходящего через светило. Отсчитывается в сторону противоположную суточному вращению в пределах от 0 до до 360 или от 0 до 24 часов. Система используется для определения звёздных координат и составления каталогов. Определяет годичное движение Солнца и других светил.

5 Высота полюса мира над горизонтом, высота светила в меридиане
Высота полюса мира над горизонтом всегда равна астрономической широте места наблюдателя:
- Если склонение светила меньше географической широты, то оно кульминирует к югу от зенита на z = φ – δ или на высоте h = 90 – φ + δ
- Если склонение светила равно географической широте, то оно кульминирует в зените и z = 0, а h = + 90
- Если склонение светила больше географической широты, то оно кульминирует к северу от зенита на z = с – φ или на высоте h = 90 + φ – с

6 Условия для восхода и заката светил
Для наблюдателя на полюсах будут только незаходящие светила.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Если светило пересекает верхнюю часть меридиана – наступает верхняя кульминация, если нижнюю – нижняя кульминация.
Для наблюдателя на полюсах будут только незаходящие светила.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Если светило пересекает верхнюю часть меридиана – наступает верхняя кульминация, если нижнюю – нижняя кульминация.
