Как найти зенитное расстояние звезды

Высота светил: еще несколько задач

Рассмотрим еще несколько задач на определение высоты звезд на небесной сфере. Небесной сферой мы называем представление о небе как о пустом глобусе с нашей планетой в центре и небесными объектами на его внутренней поверхности. Оно пришло к нам из древности и остается удобным. Когда мы смотрим на звезды, можно вообразить, что мы находимся внутри такого глобуса, внутри небесной сферы. Высота звезды – угловое расстояние, отсчитываемое от истинного (математического) горизонта до звезды по небесному меридиану, или вертикалу.

Задача 1.

Определить высоту полюса мира и наклонение небесного экватора к истинному горизонту на земном экваторе, на северном тропике (), на северном полярном круге () и на северном географическом полюсе.

Если мы находимся на экваторе, то для нас полюс расположен под углом , то есть его высота – , а наклонение небесного экватора, совпадающего с земным,  – .

На северном тропике () полюс  будет иметь наклонение , а наклонение небесного экватора тогда равно . На северном полярном круге () полюс  будет иметь наклонение , а наклонение небесного экватора тогда равно . На северном географическом полюсе наклонение небесного экватора, совпадающего с земным,  – , а наклонение полюса .

Задача 2.

Склонение звезды Мицара ( Большой Медведицы) равно . На каком зенитном расстоянии и на какой высоте она бывает в верхней кульминации в Пулково () и Душанбе ()?

В Пулково , следовательно,

Зенитное расстояние равно

Теперь проведем расчет для Душанбе: .

Зенитное расстояние равно

Задача 3.

На каком наименьшем зенитном расстоянии и наибольшей высоте бывают в Евпатории () и Мурманске () звезды Алиот ( Большой Медведицы) и Антарес ( Скорпиона), склонение которых соответственно равно и ?

Для Мурманска: , следовательно,

Зенитное расстояние равно

, следовательно,

Зенитное расстояние равно

Для Евпатории: , следовательно,

Зенитное расстояние равно

, следовательно,

Зенитное расстояние равно

Ответ: Мурманск, Алиот: , ; Мурманск, Антарес: , (невидима); Евпатория, Алиот: , ; Евпатория, Антарес: , .

Задача 4.

В некотором месте наблюдения звезда со склонением поднимается над точкой юга на высоту в . Найти зенитное расстояние и высоту этой звезды в том же месте при азимуте, равном 180°.

Нас просят найти, по сути, высоту звезды в нижней кульминации. Высота дана над точкой юга, значит, :

Для нижней кульминации

Зенитное расстояние равно

Ответ: ,.

Задача 5.

Решить задачу для той же звезды при условии ее наименьшего зенитного расстояния к северу от зенита.

Если зенитное расстояние , следовательно, высота равна

Тогда, так как мы к северу от зенита, то и

Следовательно, речь идет о нижней кульминации.

Ее зенитное расстояние

Ответ: , .

Задача 6.

Какое склонение должны иметь звезды, чтобы в верхней кульминации проходить в зените, а в нижней кульминации — в надире, точке севера и точке юга места наблюдения? Чему равна географическая широта этих мест?

Чтобы звезда имела кульминации в зените и надире (это точка прямо под зенитом, «нижний зенит»), звезды должны иметь склонение, равное, во-первых, широте места, во-вторых, равное нулю (лежат на небесном экваторе):

Как видно из следующего рисунка, чтобы нижняя кульминация произошла в точке севера, высота полюса мира должна быть равна , а склонение будет таким же (из условия совпадения зенита и точки верхней кульминации). Соответственно, для того, чтобы нижняя кульминация была бы в точке юга, широта места должна быть равна , и таково же склонение звезды.

Задача 7.

Вычислить зенитное расстояние и  высоту в верхней и нижней кульминации звезды Лебедя (имеющей склонение ) на земном экваторе, на северном и южном тропике (), на географической широте (), на северном и южном полярных кругах () и географических полюсах.

Пусть в верхней кульминации высота светила , а в нижней – . Зенитное расстояние в верхней кульминации , в нижней – .

Сначала рассмотрим первую картинку – экватор.

При этом высота полюса – . Звезда в верхней кульминации находится на высоте ():

Нижняя кульминация:

Далее, северный тропик – тропик Рака.

Высота полюса – . Тогда ():

Нижняя кульминация:

Южный тропик – тропик Козерога.

Высота полюса – . Тогда ():

Нижняя кульминация:

На географической широте ситуация очень похожа на тропик Рака, поэтому рисунок тот же, а расчет другой:

Высота полюса – . Тогда ():

Итак, звезда в зените.

Нижняя кульминация:

На географической широте ситуация очень похожа на тропик Козерога, поэтому отдельный рисунок я не делала:

Высота полюса – . Тогда ():

Нижняя кульминация:

Логично, если на широте звезда была в верхней кульминации в зените, то на широте она должна быть в надире в своей нижней кульминации.

На широте : высота полюса – .

Тогда ():

Нижняя кульминация:

На широте : высота полюса – .

Тогда ():

Нижняя кульминация происходит над точкой юга, поэтому:

На северном полюсе , .

Звезда в обеих кульминациях находится на одинаковой высоте (), то есть можно сказать, что звезда не кульминирует:

На южном полюсе , , тоже совпадают высоты кульминаций:

Данные: Капелла   (α Возничего), δ=+45°58′;
северный тропик, φ=+23°27′; место с φ = +45°58′;
северный полярный круг, φ=+66°33′.
Решение: Склонение Капеллы δ = +45°58′>φ северного тропика, и поэтому следует воспользоваться формулами (6) и (3):
zв= δ-φ = +45°58′-23°27′ = 22°31’N, hв=90°—zв=90°—22°31’=+67°29’N;
следовательно, азимут Aв=180°, а часовой угол tв=0° = 0ч.
На географической широте φ=+45°58’=δ зенитное расстояние Капеллы zв=δ-φ=0°, т. е. в верхней кульминации она находится в зените, и ее высота hв=+90°, часовой угол tв=0°=0ч, а азимут AB неопределенный.
Те же величины для северного полярного круга вычисляются по формулам (4) и (3), так как склонение звезды δ<φ=+66°33′:
zв = φ—δ =+66°33’—45°58′ = 20°35’S, hв=90°—zв= +90°—20°35’= +69°25’S, а поэтому Aв=0° и tв = 0°=0ч,
Вычисления высоты hн и зенитного расстояния zн Капеллы в нижней кульминации проводятся по формулам (8) и (3): на северном тропике (φ=+23°27′)
hн=δ— (90°—φ) = + 45°58′-(90°—23°27′) = -20°35’N,
т. е. в нижней кульминации Капелла заходит за горизонт, и ее зенитное расстояние
zн=90°—hн=90°-(-20°35′) = 110°35′ N, азимут Aн=180° и часовой угол tн=180°=12ч,
На географической широте φ=+45°58′ у звезды hн=δ-(90°-φ) = +45°58′-(90°-45°58′) = + 1°56’N,
т. е. она уже незаходящая, и ее zн=90°—hн=90°-1°56’=88°04′ N, Aн=180° и tн=180°=12ч
На северном полярном круге (φ = +66°33′)
hн = δ—(90°—φ) = +45°58’— (90°—66°33′) = +22°31′ N, и zн = 90°—hн = 90°—22°31′ = 67°29′ N,
т. е. звезда тоже не заходит за горизонт.

Наименование разделов и тем	Содержание учебного материала, лабораторные  работы и практические занятия, самостоятельная работа обучающихся	Объем часов	Уровень освоения
Звезды и созвездия. Небесные координаты и  звездные карты.	Звезды и созвездия. Видимая звездная величина. Небесная сфера. Особые точки небесной сферы. Небесные координаты. Звездные карты. Видимое движение звезд на различных географических широтах. Связь видимого расположения объектов на небе и географических координат наблюдателя. Кульминация светил. Воспроизведение определений терминов и понятий (созвездие, высота и кульминация звезд). Объяснение наблюдаемых невооруженным глазом движения звезд на различных географических широтах.	2	2

Тема 2.1. Звезды и созвездия. Небесные координаты и  звездные карты.

2.1.1. Звезды и созвездия. Видимая звездная величина

Невооруженным глазом видно на небе большое количество звезд. Их так много, что, кажется, не сосчитать, однако звезд, которые видны невооруженным глазом, около трех тысяч. В общем случае на небе можно насчитать до 2500-3000 звезд (в зависимости от вашего зрения) – а всего видимых звезд около 6000.

Вероятно, еще на заре цивилизации люди, стремясь как-то разобраться во множестве звезд и запомнить их расположение, мысленно объединяли их в определенные фигуры. Тысячи лет назад люди глядели на небо, считали звезды и мысленно соединяли их в разнообразные фигуры (созвездия), называя их именами персонажей древних мифов и легенд, животных и предметов.

У разных народов имелись свои мифы и легенды о созвездиях, свои названия, разное их количество. Деления были чисто условны, рисунки созвездия редко соответствовали названной фигуре, однако это существенно облегчало ориентирование по небу. Даже босоногие мальчики в древней Халдее или Шумерах знали небо лучше любого из нас.

 Многие характерные «звездные фигуры» уже в глубокой древности получили имена героев греческих мифов и легенд, а также тех мифических существ, с которыми эти герои сражались. Так появились на небе Геркулес, Персей, Орион, Андромеда и т. д., а также Дракон, Телец, Кит и т. п. Некоторые из этих созвездий упоминаются в древнегреческих поэмах «Илиада» и «Одиссея». Их изображения можно видеть в старинных звездных атласах, на глобусах и картах звездного неба (рис. 2.1).

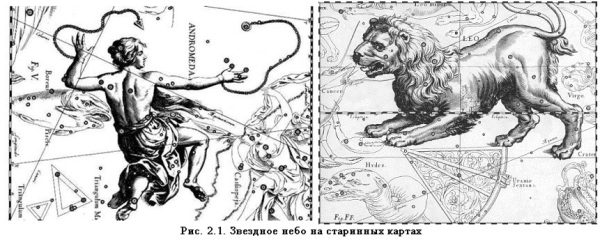
Созвездия – это определенные участки звездного неба, разделенные между собой строго установленными границами. Созвездия – область неба с характерной группой звезд и всеми звездами, находящимися внутри его границ. Соседство звезд, кажущиеся, в проекции на небесную сферу.

Старейшие по названиям считаются созвездия зодиакальные – пояс, вдоль которого происходит годичное движение Солнца, а также видимые пути Луны и планет. Так созвездия Телец – было известно > 4000 лет назад, так как в это время в этом созвездии находилась точка весеннего равноденствия.

У разных народов и в разное время был разный принцип деления звезд.

• 4 век до н.э. был список 809 звезд входящих в 122 созвездия.
• 18 век – Монголия – было 237 созвездий.
• 2 век – Птолемей (“Альмагеста”) – описано 48 созвездий.
• 15-16 век – период великих морских путешествий – описано 48 созвездий южного неба.
• В Русском звездном атласе Корнелия Рейссига, изданном в 1829г содержались 102 созвездия.

Были попытки переименовать установившиеся созвездия, но не одно название не прижилось у астрономов (так церковь в 1627г издала атлас созвездий «Христианское звездное небо», где им давались названия монархов – Георг, Карл, Людовик, Наполеон).

Многие звездные карты (атласы) 17-19 века содержали названия созвездий и рисунки фигур. Но прижился только один звездный атлас Яна Гевелия (1611-1687, Польша) изданный в 1690г и имеющий не только точное расположение звезд и впервые экваториальных координатах, но и прекрасные рисунки. (видеофильм «Звездный атлас Яна Гевелия»

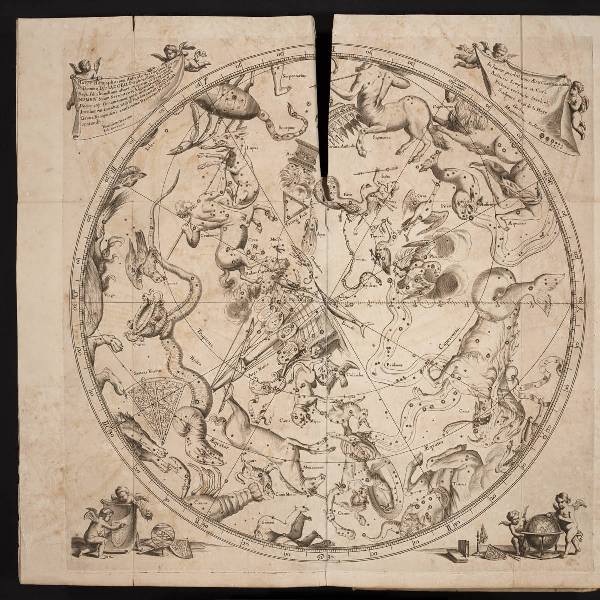
Созвездия Южного полушария автор Гевелий Ян, Уранография 1690 год

Атласы звёздного неба XVII века

Путаница с созвездиями прекращена в 1922г Международный астрономический союз разделил все небо на 88 созвездий, а границы окончательно установлены в 1928 году.

Среди всех 88 созвездий известное каждому Большая Медведица — одно из самых крупных.

Смотря на небо, нетрудно заметить, что звезды различны по яркости, или, как говорят астрономы, по блеску.

Видимые на небе невооруженным глазом звезды астрономы еще до нашей эры разделили на шесть величин. В 125г до НЭ Гиппарх (180-125, Греция) вводит деление звезд на небе по видимой яркости на звездные величины, обозначив самые яркие – первой звездной величины (1m), а еле видимые – 6m (т. е. разность в 5 звездных величин).

Звездная величина – видимая яркость (блеск) звезды. Звездная величина характеризует не размеры, а только блеск звезд. Чем слабее звезда, тем больше число, обозначающее ее звездную величину.

Когда ученые стали располагать приборами для измерения величины потока света, приходящего от звезд, оказалось, что от звезды первой величины света приходит в 2,5 раза больше, чем от звезды второй величины, от звезды второй величины в 2,5 раза больше, чем от звезды третьей величины, и т. д. Несколько звезд были отнесены к звездам нулевой величины, потому что от них света приходит в 2,5 раза больше, чем от звезд первой величины. А самая яркая звезда всего неба — Сириус (α Большого Пса) получила даже отрицательную звездную величину -1,5.

Было установлено, что поток энергии от звезды первой величины в 100 раз больше, чем от звезды шестой величины. К настоящему времени звездные величины определены для многих сотен тысяч звезд.

Звезды 1-й звездной величины – 1m, наиболее яркие назвали.

Звезды 2-й звездной величины – 2m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 1-й величины

Звезды 3-й звездной величины – 3m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 2-й величины

Звезды 4-й звездной величины – 4m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 3-й величины

Звезды 5-й звездной величины – 5m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 4-й величины

Звезды 6-й звездной величины – 6m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 5-й величины. Самые слабые по блеску из доступных невооруженному глазу Они слабее звезд 1-й звездной величины в 100 раз.

Всего на небе 22 звезды 1-й звездной величины, но блеск их не одинаков: одни из них несколько ярче 1-й величины, другие слабее. Так же обстоит дело со звездами 2-й, 3-й и последующих величин, поэтому для точного определения блеска той или иной пришлось ввести дробные числа. Измерения светового потока от звезд позволяют теперь определить их звездные величины с точностью до десятых и сотых долей.

Самая яркая звезда северного полушария неба Вега имеет блеск 0,14 звездной величины, а самая яркая звезда всего неба Сириус – минус 1,58 звездной величины, Солнце – минус 26,8.

Самые яркие звезды или наиболее интересные объекты из числа более слабых звезд получили собственные имена арабского и греческого происхождения (более 300 звезд имеют имена).

В 1603г Иоганн Байер (1572-1625, Германия) публикует каталог всех видимых звезд и впервые вводит их обозначение буквами греческого алфавита в порядке уменьшения блеска (наиболее яркие). Самые яркие – α, затем β, γ, δ, ε и т.д.

В каждом созвездии звезды обозначаются буквами греческого алфавита в порядке убывания их яркости. Наиболее яркая в этом созвездии звезда обозначается буквой α, вторая по яркости – β и т. д.

Поэтому звезды сейчас обозначаются: Вега (α Лиры), Сириус (α Большого Пса), Полярная (α М. Медведицы). Средняя звезда в ручке ковша Большой Медведицы называется Мицар, что по-арабски означает «конь». Эта звезда второй величины обозначается ζ Большой Медведицы. Рядом с Мицаром можно видеть более слабую звездочку четвертой величины, которую назвали Алькор – «всадник». По этой звезде проверяли качество зрения у арабских воинов несколько веков тому назад.

Звезды различаются не только по блеску, но и по цвету.

Они могут быть белыми, желтыми, красными. Чем краснее звезда, тем она холоднее. Солнце относится к желтым звездам.

С изобретением телескопа ученые получили возможность увидеть более слабые звезды, от которых приходит света гораздо меньше, чем от звезд шестой величины. Шкала звездных величин все дальше и дальше уходит в сторону их возрастания по мере того, как увеличиваются возможности телескопов. Так, например, хаббловский космический телескоп позволил получить изображение предельно слабых объектов – до тридцатой звездной величины.

2.1.2. Небесная сфера. Особые точки небесной сферы.

Люди в древности считали, что все звезды располагаются на небесной сфере, которая как единое целое вращается вокруг Земли. Уже более 2.000 лет тому назад астрономы стали применять способы, которые позволяли указать расположение любого светила на небесной сфере по отношению к другим космическим объектам или наземным ориентирам. Представлением о небесной сфере удобно пользоваться и теперь, хотя мы знаем, что этой сферы реально не существует.

Небесная сфера –  воображаемая шаровая поверхность произвольного радиуса, в центре которой находится глаз наблюдателя, и на которую мы проецируем положение небесных светил.

Понятием небесной сферы пользуются для угловых измерений на небе, для удобства рассуждений о простейших видимых небесных явлениях, для различных расчетов, например вычисления времени восхода и захода светил.

Построим небесную сферу и проведем из ее центра луч по направлению к звезде А (рис.1.1).

Там, где этот луч пересечет поверхность сферы, поместим точку А₁ изображающую эту звезду. Звезда В будет изображаться точкой В₁. Повторив подобную операцию для всех наблюдаемых звезд, мы получим на поверхности сферы изображение звездного неба – звездный глобус. Ясно, что если наблюдатель находится в центре этой воображаемой сферы, то для него направление на сами звезды и на их изображения на сфере будут совпадать.

• Что является центром небесной сферы? (Глаз наблюдателя)
• Каков радиус небесной сферы? (Произвольный)
• Чем отличаются небесные сферы двух соседей по парте? (Положением центра).

Для решения многих практических задач расстояния до небесных тел не играют роли, важно лишь их видимое расположение на небе. Угловые измерения не зависят от радиуса сферы. Поэтому, хотя в природе небесной сферы и не существует, но астрономы для изучения видимого расположение светил и явлений, которые можно наблюдать на небе в течении суток или многих месяцев, применяют понятие Небесная сфера. На такую сферу и проецируются звезды, Солнце, Луна, планеты и т.д, отвлекаясь от действительных расстояний до светил и рассматривая лишь угловые расстояние между ними. Расстояния между звездами на небесной сфере можно выражать только в угловой мере. Эти угловые расстояния измеряются величиной центрального угла между лучами, направленными на одну и другую звезду, или соответствующими им дугами на поверхности сферы.

Для приближенной оценки угловых расстояний на небе полезно запомнить такие данные: угловое расстояние между двумя крайними звездами ковша Большой Медведицы (α и β) составляет около 5° (рис. 1.2), а от α Большой Медведицы до α Малой Медведицы (Полярной звезды) – в 5 раз больше – примерно 25°.

Простейшие глазомерные оценки угловых расстояний можно провести также с помощью пальцев вытянутой руки.

Только два светила – Солнце и Луну – мы видим как диски. Угловые диаметры этих дисков почти одинаковы – около 30′ или 0,5°. Угловые размеры планет и звезд значительно меньше, поэтому мы их видим просто как светящиеся точки. Для невооруженного глаза объект не выглядит точкой в том случае, если его угловые размеры превышают 2–3′. Это означает, в частности, что наш глаз различает каждую по отдельности светящуюся точку (звезду) в том случае, если угловое расстояние между ними больше этой величины. Иначе говоря, мы видим объект не точечным лишь в том случае, если расстояние до него превышает его размеры не более чем в 1700 раз.

Отвесная линия Z,Z’, проходящая через глаз наблюдателя (точка С), находящегося в центре небесной сферы, пересекает небесную сферу в точках Z — зенит, Z’ — надир.

Зенит – эта наивысшая точка над головой наблюдателя.

Надир – противоположная зениту точка небесной сферы.

Плоскость, перпендикулярная отвесной линии, называется горизонтальной плоскостью (или плоскостью горизонта).

Математическим горизонтом называется линия пересечения небесной сферы с горизонтальной плоскостью, проходящей через центр небесной сферы.

Невооруженным глазом на всем небе можно видеть примерно 6000 звезд, но мы видим лишь половину из них, потому что другую половину звездного неба закрывает от нас Земля. Движутся ли звезды по небосводу? Оказывается, движутся все и притом одновременно. В этом легко убедиться, наблюдая звездное небо (ориентируясь по определенным предметам).

Вследствие ее вращения вид звездного неба меняется. Одни звезды только еще появляются из-за горизонта (восходят) в восточной его части, другие в это время находятся высоко над головой, а третьи уже скрываются за горизонтом в западной стороне (заходят). При этом нам кажется, что звездное небо вращается как единое целое. Теперь каждому хорошо известно, что вращение небосвода — явление кажущееся, вызванное вращением Земли.

Картину того, что в результате суточного вращения Земли происходит со звездным небом, позволяет запечатлеть фотоаппарат.

На полученном снимке каждая звезда оставила свой след в виде дуги окружности (рис. 2.3). Но есть и такая звезда, передвижение которой в течение всей ночи почти незаметно. Эту звезду назвали Полярной. Она в течение суток описывает окружность малого радиуса и всегда видна почти на одной и той же высоте над горизонтом в северной стороне неба. Общий центр всех концентрических следов звезд находится на небе неподалеку от Полярной звезды. Эта точка, в которую направлена ось вращения Земли, получила название северный полюс мира. Дуга, которую описала Полярная звезда, имеет наименьший радиус. Но и эта дуга, и все остальные — независимо от их радиуса и кривизны — составляют одну и ту же часть окружности. Если бы удалось сфотографировать пути звезд на небе за целые сутки, то на фотографии получились бы полные окружности – 360°. Ведь сутки – это период полного оборота Земли вокруг своей оси. За час Земля повернется на 1/24 часть окружности, т. е. на 15°. Следовательно, длина дуги, которую звезда опишет за это время, составит 15°, а за полчаса – 7,5°.

Звезды в течение суток описывают тем большие окружности, чем дальше от Полярной звезды они находятся.

Ось суточного вращения небесной сферы называют осью мира (РР’).

Точки пересечения небесной сферы с осью мира называют полюсами мира (точка Р — северный полюс мира, точка Р’ — южный полюс мира).

Полярная звезда расположена вблизи северного полюса мира. Когда мы смотрим на Полярную звезду, точнее, на неподвижную точку рядом с ней — северный полюс мира, направление нашего взгляда совпадает с осью мира. Южный полюс мира находится в южном полушарии небесной сферы.

Плоскость ЕАWQ, перпендикулярная оси мира РР’ и проходящая через центр небесной сферы, называется плоскостью небесного экватора, а линия пересечения ее с небесной сферой — небесным экватором.

Небесный экватор – линия окружности, полученная от пересечения небесной сферы с плоскостью проходящая через центр небесной сферы перпендикулярно к оси мира.

Небесный экватор делит небесную сферу на два полушария: северное и южное.

Ось мира, полюса мира и небесный экватор аналогичны оси, полюсам и экватору Земли, так как перечисленные названия связаны с видимым вращением небесной сферы, а оно является следствием действительного вращения земного шара.

Плоскость, проходящая через точку зенита Z, центр С небесной сферы и полюс Р мира, называют плоскостью небесного меридиана, а линия пересечения ее с небесной сферой образует линию небесного меридиана.

Небесный меридиан – большой круг небесной сферы, проходящий через зенит Z, полюс мира Р, южный полюс мира Р’, надир Z’

В любом месте Земли плоскость небесного меридиана совпадает с плоскостью географического меридиана этого места.

Полуденная линия NS — это линия пересечения плоскостей меридиана и горизонта. N – точка севера, S – точка юга

Она названа так потому, что в полдень тени от вертикальных предметов падают по этому направлению.

• Каков период вращения небесной сферы? (Равен периоду вращения Земли – 1 сутки).
• В каком направлении происходит видимое (кажущееся) вращение небесной сферы? (Противоположно направлению вращения Земли).
• Что можно сказать о взаимном расположении оси вращения небесной сферы и земной оси? (Ось небесной сферы и земная ось будут совпадать).
• Все ли точки небесной сферы участвуют в видимом вращении небесной сферы? (Точки, лежащие на оси, покоятся).

Земля движется по орбите вокруг Солнца. Ось вращения Земли наклонена к плоскости орбиты на угол 66,5°. Вследствие действия сил тяготения со стороны Луны и Солнца ось вращения Земли смещается, в то время как наклон оси к плоскости земной орбиты остается постоянным. Ось Земли как бы скользит по поверхности конуса. (то же происходит с осью у обыкновенного волчка в конце вращения).

Это явление было открыто еще в 125 г. до н. э. греческим астрономом Гиппархом и названо прецессией.

Один оборот земная ось совершает за 25 776 лет – этот период называется платоническим годом. Сейчас вблизи Р – северного полюса мира находится Полярная звезда – α Малой Медведицы. Полярной называется та звезда, которая на сегодняшний день находится вблизи Северного полюса мира. В наше время, примерно с 1100 года, такой звездой является альфа Малой Медведицы – Киносура. Раньше титул Полярной поочередно присваивался π, η и τ Геркулеса, звездам Тубан и Кохаб. Римляне вовсе не имели Полярной звезды, а Кохаб и Киносуру (α Малой Медведицы) называли Стражами.

На начало нашего летоисчисление – полюс мира был вблизи α Дракона – 2000 лет назад. В 2100 г полюс мира будет всего в 28′ от Полярной звезды – сейчас в 44′. В 3200г полярным станет созвездие Цефей. В 14000 г – полярной будет Вега (α Лиры).

Как найти в небе Полярную звезду?

Чтобы найти Полярную звезду, нужно через звезды Большой Медведицы (первые 2 звезды “ковша”) мысленно провести прямую линию и отсчитать по ней 5 расстояний между этими звездами. В этом месте рядом с прямой мы увидим звезду, почти одинаковую по яркости со звездами “ковша” – это и есть Полярная звезда.

В созвездии, которое нередко называют Малый Ковш, Полярная звезда является самой яркой. Но так же, как и большинство звезд ковша Большой Медведицы, Полярная — звезда второй величины.

А вот так выглядит звездное небо на 15 сентября, 21 час.

Летний (летне-осенний) треугольник = звезда Вега (α Лиры, 25,3 св. лет), звезда Денеб (α Лебедя, 3230 св. лет), звезда Альтаир (α Орла, 16,8 св. лет)

2.1.3. Небесные координаты и звездные карты

Чтобы отыскать на небе светило, надо указать, в какой стороне горизонта и как высоко над ним оно находится. С этой целью используется система горизонтальных координат – азимут и высота. Для наблюдателя, находящегося в любой точке Земли, нетрудно определить вертикальное и горизонтальное направления.

Первое из них определяется с помощью отвеса и изображается на чертеже (рис. 1.3) отвесной линией ZZ’, проходящей через центр сферы (точку О).

Точка Z, расположенная прямо над головой наблюдателя, называется зенитом.

Плоскость, которая проходит через центр сферы перпендикулярно отвесной линии, образует при пересечении со сферой окружность – истинный, или математический, горизонт.

Высота светила отсчитывается по окружности, проходящей через зенит и светило, и выражается длиной дуги этой окружности от горизонта до светила. Эту дугу и соответствующий ей угол принято обозначать буквой h.

Высота светила, которое находится в зените, равна 90°, на горизонте – 0°.

Положение светила относительно сторон горизонта указывает его вторая координата – азимут, обозначаемый буквой А. Азимут отсчитывается от точки юга в направлении движения часовой стрелки, так что азимут точки юга равен 0°, точки запада – 90° и т. д.

Горизонтальные координаты светил непрерывно меняются с течением времени и зависят от положения наблюдателя на Земле, потому что по отношению к мировому пространству плоскость горизонта в данном пункте Земли вращается вместе с ней.

Горизонтальные координаты светил измеряют для определения времени или географических координат различных пунктов на Земле. На практике, например в геодезии, высоту и азимут измеряют специальными угломерными оптическими приборами – теодолитами.

Чтобы создать звездную карту, изображающую созвездия на плоскости, надо знать координаты звезд. Для этого нужно выбрать такую систему координат, которая вращалась бы вместе со звездным небом. Для указания положения светил на небе используют систему координат, аналогичную той, которая используется в географии, – систему экваториальных координат.

Система экваториальных координат сходна с системой географических координат на земном шаре. Как известно, положение любого пункта на земном шаре можно указать с помощью географических координат – широты и долготы.

Географическая широта — это угловое расстояние пункта от земного экватора. Географическая широта (φ) отсчитывается по меридианам от экватора к полюсам Земли.

Долгота — угол между плоскостью меридиана данного пункта и плоскостью начального меридиана. Географическая долгота (λ) отсчитывается вдоль экватора от начального (Гринвичского) меридиана.

Так, например, Москва имеет следующие координаты: 37°30′ восточной долготы и 55°45′ северной широты.

Введем систему экваториальных координат, которая указывает положение светил на небесной сфере относительно друг друга.

Проведем через центр небесной сферы (рис. 2.4) линию, параллельную оси вращения Земли, – ось мира. Она пересечет небесную сферу в двух диаметрально противоположных точках, которые называются полюсами мира – Р и Р΄. Северным полюсом мира называют тот, вблизи которого находится Полярная звезда. Плоскость, проходящая через центр сферы параллельно плоскости экватора Земли, в сечении со сферой образует окружность, называемую небесным экватором. Небесный экватор (подобно земному) делит небесную сферу на два полушария: Северное и Южное. Угловое расстояние светила от небесного экватора называется склонением. Склонение отсчитывается по кругу, проведенному через светило и полюса мира, оно аналогично географической широте.

Склонение  – угловое расстояние светил от небесного экватора. Склонение обозначают буквой δ. В северном полушарии склонения считают положительными, в южном — отрицательными.

Вторая координата, которая указывает положение светила на небе, аналогична географической долготе. Эта координата называется прямым восхождением. Прямое восхождение отсчитывается по небесному экватору от точки весеннего равноденствия γ, в которой Солнце ежегодно бывает 21 марта (в день весеннего равноденствия). Оно отсчитывается от точки весеннего равноденствия γ против часовой стрелки, т. е. навстречу суточному вращению неба. Поэтому светила восходят (и заходят) в порядке возрастания их прямого восхождения.

Прямое восхождение — угол между плоскостью полукруга, проведенного из полюса мира через светило (круга склонения), и плоскостью полукруга, проведенного из полюса мира через лежащую на экваторе точку весеннего равноденствия (начального круга склонений). Прямое восхождение обозначается буквой α

Склонение и прямое восхождение (δ, α) называют экваториальными координатами.

Склонение и прямое восхождение удобно выражать не в градусах, а в единицах времени. Учитывая, что Земля делает один оборот за 24 ч, получаем:

360° — 24 ч,  1 ° — 4 мин;    

15° — 1 ч,  15′ —1 мин,  15″ — 1 с.

Следовательно, прямое восхождение, равное, например, 12 ч, составляет 180°, а 7 ч 40 мин соответствует 115°.

Если не нужна особая точность, то небесные координаты для звезд можно считать неизменными. При суточном вращении звездного неба вращается и точка весеннего равноденствия. Поэтому положения звезд относительно экватора и точки весеннего равноденствия не зависят ни от времени суток, ни от положения наблюдателя на Земле.

Экваториальная система координат изображена на подвижной карте звездного неба.

Принцип создания карты звездного неба весьма прост. Спроектируем сначала все звезды на глобус: там, где луч, направленный на звезду, пересечет поверхность глобуса, будет находиться изображение этой звезды. Обычно на звездном глобусе изображаются не только звезды, но и сетка экваториальных координат. По сути дела, звездным глобусом является модель небесной сферы, которая используется на уроках астрономии в школе. На этой модели нет изображений звезд, но зато представлены ось мира, небесный экватор и другие круги небесной сферы.

Пользоваться звездным глобусом не всегда удобно, поэтому в астрономии (как и в географии) широкое распространение получили карты и атласы.

Атлас звездного неба начинающего наблюдателя

Карту земной поверхности можно получить, если все точки глобуса Земли спроектировать на плоскость (поверхность цилиндра или конуса). Проведя ту же операцию со звездным глобусом, можно получить карту звездного неба.

Познакомимся с простейшей звездной картой, помещенной в Школьном астрономическом календаре.

Расположим плоскость, на которой мы хотим получить карту, так, чтобы она касалась поверхности глобуса в точке, где находится северный полюс мира. Теперь надо спроектировать все звезды и сетку координат с глобуса на эту плоскость. Получим карту, подобную географическим картам Арктики или Антарктики, на которых в центре располагается один из полюсов Земли. В центре нашей звездной карты будет располагаться северный полюс мира, рядом с ним Полярная звезда, чуть дальше остальные звезды Малой Медведицы, а также звезды Большой Медведицы и других созвездий, которые находятся неподалеку от полюса мира. Сетка экваториальных координат представлена на карте радиально расходящимися от центра лучами и концентрическими окружностями. На краю карты против каждого луча написаны числа, обозначающие прямое восхождение (от 0 до 23 ч). Луч, от которого начинается отсчет прямого восхождения, проходит через точку весеннего равноденствия, обозначенную γ. Склонение отсчитывается по этим лучам от окружности, которая изображает небесный экватор и имеет обозначение 0°. Остальные окружности также имеют оцифровку, которая показывает, какое склонение имеет объект, расположенный на этой окружности.

В зависимости от звездной величины звезды изображают на карте кружками различного диаметра. Те из них, которые образуют характерные фигуры созвездий, соединены сплошными линиями. Границы созвездий обозначены пунктиром.

2.1.4. Высота полюса мира над горизонтом

Рассмотрим, какова высота полюса мира над горизонтом по рисунку 2.5, где часть небесной сферы и земной шар изображены в проекции на плоскость небесного меридиана.

Пусть ОР — ось мира, параллельная оси Земли; OQ — проекция части небесного экватора, параллельного экватору Земли; OZ— отвесная линия. Тогда высота полюса мира над горизонтом h_P = PON, а географическая широта φ =Q₁O₁O. Очевидно, что эти углы (PON и Q₁O₁O)равны между собой, поскольку их стороны взаимно перпендикулярны (ОО₁ON, a OQOP). Отсюда следует, что высота полюса мира над горизонтом равна географической широте места наблюдения: h_P = φ. Таким образом, географическую широту пункта наблюдения можно определить, если измерить высоту полюса мира над горизонтом.

В зависимости от места наблюдателя на Земле меняется вид звездного неба и характер суточного движения звезд.

Проще всего разобраться в том, что и как происходит, на полюсах Земли. Полюс такое место на земном шаре, где ось мира совпадает с отвесной линией, а небесный экватор   с горизонтом (рис. 2.6).

Для наблюдателя, находящегося на Северном полюсе, Полярная звезда видна близ зенита. Здесь над горизонтом находятся только звезды Северного полушария небесной сферы (с положительным склонением). На Южном полюсе, наоборот, видны только звезды с отрицательным склонением. В обоих случаях, двигаясь вследствие вращения Земли параллельно небесному экватору, звезды остаются на неизменной высоте над горизонтом, не восходят и не заходят.

Отправимся с Северного полюса в привычные средние широты. Высота Полярной звезды над горизонтом будет постепенно уменьшаться, одновременно угол между плоскостями горизонта и небесного экватора будет увеличиваться.

Как видно из рисунка 2.7, в средних широтах (в отличие от Северного полюса) лишь часть звезд Северного полушария неба никогда не заходит. Все остальные звезды как Северного, так и Южного полушария восходят и заходят.

Продолжим наше воображаемое путешествие и отправимся из средних широт к экватору, географическая широта которого 0°.Здесь ось мира располагается в плоскости горизонта, а небесный экватор проходит через зенит. На экваторе в течение суток все светила побывают над горизонтом (рис. 2.9).

На полюсах Земли видна только половина небесной сферы. На экваторе Земли в течение года можно увидеть все созвездия. В средних широтах часть звезд является незаходящими, часть – невосходящими, остальные восходят и заходят каждые сутки.

2.1.5. Высота светила в кульминации

При своем суточном движении светило, вращаясь вокруг оси мира, за сутки дважды пересекает меридиан — над точками юга и севера. При этом оно один раз занимает самое высокое положение — верхняя кульминация, другой раз — самое низкое положение — нижняя кульминация.

В момент верхней кульминации над точкой юга светило достигает наибольшей высоты над горизонтом.

Кульминация — это явление  прохождения светила через меридиан, момент пересечения небесного меридиана.

Светило М в течение суток описывает суточную параллель – малый круг небесной сферы, плоскость которого перпендикулярна оси мира и проходит через глаз наблюдателя.

М₁ – верхняя кульминация (h max; А= 0^o), М2 – нижняя кульминация (h min; A =180^o), М₃ – точка восхода, М₄ – точка захода,

По суточному движению светила делятся на:

• невосходящие
• восходяще – заходящие (восходящие и заходящие в течении суток)
• незаходящие.
• К каким относится Солнце, Луна? (ко 2)

На рисунке 2.8 показано положение светила в момент верхней кульминации.

Как известно, высота полюса мира над горизонтом (угол PON): h_P = φ. Тогда угол между горизонтом (NS) и небесным экватором (QQ₁) будет равен 180° – φ – 90° = 90° – φ. Угол MOS, который выражает высоту светила М в кульминации, представляет собою сумму двух углов: Q₁OS  и MOQ₁. Величину первого из них мы только что определили, а второй является не чем иным, как склонением светила М, равным δ.

Таким образом, мы получаем следующую формулу, связывающую высоту светила в кульминации с его склонением и географической широтой места наблюдения:

h = 90° – φ + δ.

Зная склонение светила и определив из наблюдений его высоту в кульминации, можно узнать географическую широту места наблюдения.

На рисунке изображена небесная сфера. Рассчитаем зенитное расстояние светила в данном пункте в момент верхней кульминации, если его склонение известно.

Вместо высоты h часто употребляют зенитное расстояние Z, равное 90°—h.

Зенитное расстояние — угловое расстояние точки М от зенита.

Пусть в момент верхней кульминации светило находится в точке М, тогда дуга QМ есть склонение δ светила, так как AQ — небесный экватор, перпендикулярный оси мира РР’. Дуга QZ равна дуге NP и равна географиче­ской широте местности φ. Очевидно, зенитное расстояние, изображаемое дугой ZM, равно z = φ — δ.

Если бы светило кульминировало к северу от зенита Z (т. е. точка М оказалась бы между Z и P), то z = δ— φ. По этим формулам можно рассчитать зенитное расстояние светила с известным склонением в момент верхней кульминации в пункте с известной географической широтой φ.

Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.

Системы небесных координат отличаются друг от друга выбором основной плоскости и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.

Горизонтальная система координат

В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.

Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.

Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)

Первая экваториальная система координат

В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.

Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.

Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.

Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0^h до 24^h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0^h до +12^h) к западу и от 0° до −180° (от 0^h до −12^h) к востоку.

Вторая экваториальная система координат

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.

Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0^h до 24^h (в часовой мере).

RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.

Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.

• Объект на небесном экваторе имеет склонение 0°
• Склонение северного полюса небесной сферы равно +90°
• Склонение южного −90°

У склонения всегда указывается знак, даже если склонение положительно.

Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ < −90° + φ , то объект называется невосходящим, а значит он ненаблюдаем на широте φ.^[1]

Эклиптическая система координат

В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.

Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.

Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.

Галактическая система координат

В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.

Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.

Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.

Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.

Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).

Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:

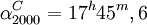
Изменения координат при вращении небесной сферы

Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.

История и применение

Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.

Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.

Использование различных систем координат

Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.

Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.

Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.

Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.

Примечания

См. также

• Небесная сфера