
Груз массой 45 кг с
помощью динамометра тянут равномерно по горизонтальной плоскости. Определите
деформацию пружины динамометра, если ее жесткость равна 7,8 кH/м, сила упругости направлена под углом 30 градусов к горизонту,
а коэффициент трения скольжения груза по поверхности равен 0,26.
Решение.
Деформация пружины x связана
с ее жесткостью l и модулем силы упругости F
соотношением F = kx (закон
Гука), откуда x = F/k. Силу F можно найти с помощью
второго закона Ньютона.
На груз действуют сила
тяжести mg, сила упругости пружины F,
сила нормальной реакции опоры N и сила трения Fтр . По второму закону
Ньютона получаем.
Запишем теперь его в
проекциях на координатные оси OX
и OY.
Кроме того, Fтр = mN. Решаем полученную систему уравнений и находим F.
Ответ: x = 15 мм.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | – |
| 200 | Нет | 200 | – |
| 300 | Есть, равномерное | – | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)

Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | – | – | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | – | – | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | – | – | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
Деревянную коробку массой 10 кг равномерно и прямолинейно тянут по горизонтальной доске с помощью горизонтально расположенной пружины. Коэффициент трения равен 0,4; удлинение пружины 0,2 м. Чему равна жёсткость пружины?
1) 200 Н/м
2) 100 Н/м
3) 50 Н/м
4) 20 Н/м
Спрятать решение
Решение.
Упругое растяжение пружины подчиняется закону Гука:
где F — приложенная сила, k — жесткость пружины, Δx — величина растяжения.
Поскольку известно, что коробку тянут равномерно и прямолинейно, ускорение коробки равно нулю. Сила тяги равна силе трения (третий закон Ньютона):
Сила трения равна силе реакции опоры (в данном случае она равна силе тяжести mg), умноженной на коэффициент трения μ:
Из закона Гука находим, что
Правильный ответ указан под номером 1.
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).

Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Мы уже познакомились с силами упругости и трения качественно, теперь рассмотрим их количественно, с привлечением формул.
Сила упругости возникает в любом теле, если менять его форму и/или размеры. Например, сжимая пластилин или глину, мы чувствуем их противодействие – это сила упругости. Она не зависит от того, насколько пластилин или глина уже сжаты. Иное дело, если мы возьмём резиновый шарик либо стальную пружину. Чем больше мы будем их сжимать или растягивать, тем большая сила упругости будет возникать (см. рисунок).

Продолжим опыт с гирями и динамометром, рассмотренный в предыдущем параграфе. С помощью линейки будем измерять удлинение пружины Δl, равное разности её конечной и начальной длины: l – l0. Мы обнаружим, что возникающая сила упругости прямо пропорциональна модулю изменения длины пружины:
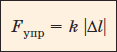 |
Fупр – сила упругости пружины, Н |Δl| – модуль удлинения пружины, м k – коэффициент жёсткости, Н/м |
Коэффициент k характеризует жёсткость пружины. Поясним его смысл. Пусть, например, мы растянули пружину динамометра на 5 см, и в ней возникла сила упругости 2 Н. Тогда жёсткость этой пружины равна: k = 2 Н : 0,05 м = 40 Н/м. Допустим теперь, что мы взяли пружину из более толстой проволки. Приложив к ней такую же силу 2 Н, мы заметим меньшее растяжение, например 1 см. Тогда жёсткость такой пружины будет больше: k = 2 Н : 0,01 м = 200 Н/м.
Более углублённо мы рассмотрим силу упругости в 9 классе.
Как вы уже знаете (см. § 3-б), сила трения бывает двух видов – трения скольжения и трения покоя. При участии жидкостей или газов сила трения покоя всегда равна нулю, а вместо термина «сила трения скольжения» чаще употребляют термин «сила сопротивления движению». Формулы, описывающие трение с участием жидкостей и газов, сложны, поэтому мы рассмотрим только формулу для силы трения скольжения твёрдого тела по поверхности другого твёрдого тела.
Проделаем опыт. Деревянный брусок весом 2 Н будем равномерно тянуть по горизонтальной доске, измеряя силу трения. Сверху на брусок будем ставить грузики по 1 Н, увеличивающие вес бруска. Результаты опыта занесём в таблицу:
| Количество грузиков, шт. | – | 1 | 2 | 3 |
| Вес бруска с грузиками | 2 Н | 3 Н | 4 Н | 5 Н |
| Сила трения скольжения | 0,6 Н | 0,9 Н | 1,2 Н | 1,5 Н |
Из сравнения нижних пар значений двух сил видно, что возникающая сила трения скольжения пропорциональна силе давления на опору (в нашем случае – действующему на доску весу бруска и грузиков). Эта закономерность выражается формулой:
 |
Fтр – сила трения скольжения, Н N – сила давления на опору, Н μ – коэффициент сухого трения |
Взяв любую пару значений сил, мы подсчитаем коэффициент трения скольжения деревянного бруска по деревянной доске в нашем опыте. Например, μ = 0,6 Н : 2 Н = 0,9 Н : 3 Н = 1,2 Н : 4 Н = 1,5 Н : 5 Н = 0,3. То есть μ = 0,3. Этот коэффициент показывает, что сила трения скольжения в нашем опыте составляет 3/10 от силы давления на опору.
Случаи негоризонтальных поверхностей мы рассмотрим в 9 классе.
