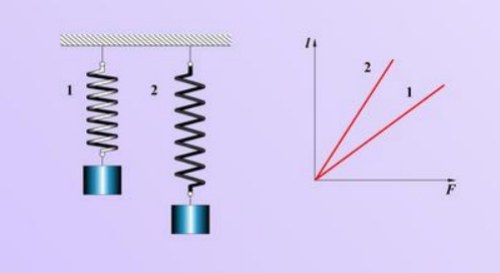
Как определить коэффициент жесткости
Коэффициент жесткости показывает, какую силу нужно приложить к телу, чтобы упруго деформировать его на единицу длины. Речь идет именно об упругой деформации, когда тело после воздействия на него снова принимает прежнюю форму. Для того чтобы найти эту величину, нужно деформировать тело, приложив к нему силу, или измерить потенциальную энергию его деформации.
Вам понадобится
- – калькулятор;
- – динамометр;
- – линейка.
Инструкция
Присоедините к телу динамометр и потяните за него, деформировав тело. Сила, которую покажет динамометр, будет по модулю равна силе упругости, действующей на тело. Найдите коэффициент жесткости, используя закон Гука, который говорит о том, что сила упругости прямо пропорциональна его удлинению и направлена в сторону, противоположную деформации. Рассчитайте коэффициент жесткости, поделив значение силы F на удлинение тела x, которое измерьте линейкой или рулеткой k=F/x. Чтобы найти удлинение деформированного тела вычтите длину деформированного тела от его первоначальной длины. Коэффициент жесткости измеряется в Н/м.
Если нет динамометра, подвесьте к деформируемому телу груз известной массы. Следите, чтобы тело деформировалось упруго и не разрушилось. В этом случае вес груза будет равен силе упругости, действующей на тело, коэффициент жесткости которого нужно найти, например, пружины. Рассчитайте коэффициент жесткости, поделив произведение массы m и ускорения свободного падения g≈9,81 м/с² на удлинение тела x, k=m•g/x. Удлинение измерьте по методике, предложенной в предыдущем пункте.
Пример. Под грузом 3 кг пружина длиной 20 см стала 26 см, определите ее жесткость. Сначала найдите удлинение пружины в метрах. Для этого от длины удлиненной пружины, вычтите ее длину в нормальном состоянии х=26-20=6 см=0,06 м. Вычислите жесткость, используя соответствующую формулу k=m•g/x=3•9,81/0,06≈500 Н/м.
В том случае, когда известна потенциальная энергия упруго деформированного тела, вычислите его жесткость. Для этого дополнительно измерьте его удлинение. Жесткость будет равна удвоенной потенциальной энергии Ер поделенной на квадрат удлинения тела х, k=2•Ep/x². Например, если мяч деформировался на 2 см и получил потенциальную энергию 4 Дж, то его жесткость k=2•4/0,02²=20000 Н/м.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Жесткость пружины, теория и онлайн калькуляторы
Жесткость пружины
При воздействии внешних сил тела способны приобретать ускорения или деформироваться. Деформацией называют изменение размеров и (или) формы тела. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Пусть на пружину на рис.1 действует растягивающая сила, направленная вертикально вниз.
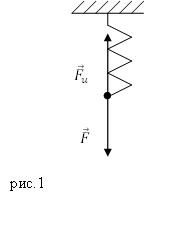
При воздействии деформирующей силы ($overline{F}$) длина пружины увеличивается. В пружине возникает сила упругости (${overline{F}}_u$), которая уравновешивает деформирующую силу. Если деформация небольшая и упругая, то удлинение пружины ($Delta l$) пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в качестве коэффициента пропорциональности выступает жесткость пружины $k$. Коэффициент $k$ называют также коэффициентом упругости, коэффициентом жесткости. Жесткость (как свойство) характеризует упругие свойства тела, подвергаемого деформации – это возможность тела оказывать противодействие внешней силе, сохранять свои геометрические параметры. Коэффициент жесткости является основной характеристикой жесткости.
Коэффициент жесткости пружины зависит от материала, из которого изготовлена пружина, ее геометрических характеристик. Так, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси вычисляется при помощи формулы:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ -модуль сдвига (величина зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.
Единицы измерения жесткости пружины
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Жесткость соединений пружин
При последовательном соединении $N$ пружин жесткость соединения вычисляется при помощи формулы:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(2right).}]
Если пружины соединены параллельно, то результирующая жесткость равна:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(3right).]
Примеры задач на жесткость пружин
Пример 1
Задание. Какова потенциальная энергия ($E_p$) деформации системы из двух параллельно соединенных пружин (рис.2), если их жесткости равны: $k_1=1000 frac{Н}{м}$; $k_2=4000 frac{Н}{м}$, а удлинение составляет $Delta l=0,01$ м.
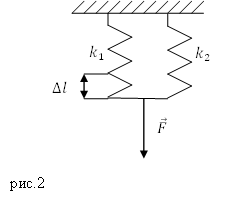
Решение. При параллельном соединении пружин жесткость системы вычислим как:
[k=k_1+k_2left(1.1right).]
Потенциальную энергию деформированной системы вычислим при помощи формулы:
[E_p=frac{k{left(Delta lright)}^2}{2}=frac{(k_1+k_2){left(Delta lright)}^2}{2}.]
Вычислим искомую потенциальную энергию:
[E_p=frac{left(1000+4000right){left({10}^{-2}right)}^2}{2}=0, 25 left(Джright).]
Ответ. $E_p=0, 25$ Дж
Пример 2
Задание. Чему равна работа ($A$) силы растягивающей систему из двух последовательно соединенных пружин, имеющих жесткости $k_1=1000 frac{Н}{м} и$ $k_2=2000 frac{Н}{м}$, если удлинение второй пружины составляет $Delta l_2=0, 1 м$?
Решение. Сделаем рисунок.
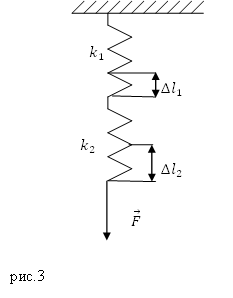
При последовательном соединении пружин на каждую из них действует одна и та же деформирующая сила ($overline{F}$), используя этот факт и закон Гука найдем удлинение первой пружины:
[F=k_1Delta l_1=k_2Delta l_2to Delta l_1=frac{k_2Delta l_2}{k_1}left(2.1right).]
Работа силы упругости при растяжении первой пружины, равна:
[A_1=frac{k_1{Delta l_1}^2}{2}left(2.2right).]
Учитывая полученное в (2.1) удлинение первой пружины имеем:
[A_1=frac{k_1{(frac{k_2Delta l_2}{k_1})}^2}{2}=frac{k^2_2{Delta l_2}^2}{2k_1}left(2.3right).]
Работа второй силы упругости:
[A_2=frac{k_2{Delta l_2}^2}{2}left(2.4right).]
Работа силы, которая растягивает систему пружин в целом, будет найдена как:
[A=A_1+A_2left(2.5right).]
Подставим правые части выражений (2.3) и (2.4) в формулу (2.5), получаем:
[A=frac{k^2_2{Delta l_2}^2}{2k_1}+frac{k_2{Delta l_2}^2}{2}=frac{k_2{Delta l_2}^2}{2k_1}left(k_2+k_1right).]
Вычислим работу:
[А=frac{2000cdot {({10}^{-1})}^2}{2cdot 1000}left(2000+1000right)=30 left(Джright).]
Ответ. $А$=30 Дж
Читать дальше: затухающие колебания.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Деформированное
упругое тело (например, растянутая или сжатая пружина) способно, возвращаясь в
недеформированное состояние, совершить работу над соприкасающимися с ним
телами. Следовательно, упруго деформированное тело обладает потенциальной
энергией. Она зависит от взаимного положения частей тела, например витков
пружины. Работа, которую может совершить растянутая пружина, зависит от
начального и конечного растяжений пружины. Найдем работу, которую может
совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е.
найдем потенциальную энергию растянутой пружины.
Пусть
растянутая пружина закреплена одним концом, а второй конец, перемещаясь,
совершает работу. Нужно учитывать, что сила, с которой действует пружина, не
остается постоянной, а изменяется пропорционально растяжению. Если
первоначальное растяжение пружины, считая от нерастянутого состояния, равнялось
![]() , то
, то
первоначальное значение силы упругости составляло ![]() , где
, где ![]() — коэффициент пропорциональности,
— коэффициент пропорциональности,
который называют жесткостью пружины. По мере сокращения пружины эта сила линейно
убывает от значения ![]() до нуля. Значит, среднее значение
до нуля. Значит, среднее значение
силы равно ![]() .
.
Можно показать, что работа ![]() равна этому среднему, умноженному
равна этому среднему, умноженному
на перемещение точки приложения силы:
![]() .
.
Таким
образом, потенциальная энергия растянутой пружины
![]() (98.1)
(98.1)
Такое
же выражение получается для сжатой пружины.
В
формуле (98.1) потенциальная энергия выражена через жесткость пружины и через
ее растяжение ![]() .
.
Заменив ![]() на
на
![]() , где
, где ![]() — упругая сила,
— упругая сила,
соответствующая растяжению (или сжатию) пружины ![]() , получим выражение
, получим выражение
![]() , (98.2)
, (98.2)
которое
определяет потенциальную энергию пружины, растянутой (или сжатой) силой ![]() . Из этой формулы
. Из этой формулы
видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им
различный запас потенциальной энергии: чем жестче пружина, т.е. чем больше ее
упругость, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем
больше энергия, которую она запасет при данной растягивающей, силе. Это можно уяснить
себе наглядно, если учесть, что при одинаковых действующих силах растяжение
мягкой пружины больше, чем жесткой, а потому больше и произведение силы на
перемещение точки приложения силы, т. е. работа.
Эта
закономерность имеет большое значение, например, при устройстве различных
рессор и амортизаторов: при посадке на землю самолета амортизатор шасси,
сжимаясь, должен произвести большую работу, гася вертикальную скорость
самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато
возникающие силы упругости будут меньше и самолет будет лучше предохранен от
повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки
ощущаются резче, чем при слабой накачке.
Задача №2
Условие
Необходимо рассчитать жесткость пружины, если известно, что при растяжении ее на 20 см пружина приобрела потенциальную энергию упругодеформированного тела 20 Дж.
Дано: х=20 см=0,2 м; Ер=20 Дж; k=?
Решение
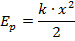
умножаем правую и левую часть на 2, для получения промежуточной формулы:
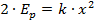
выражаем величину k:

проверим размерность величины, которую получили:
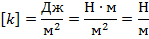
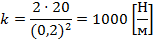
Ответ: жесткость пружины равна 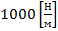 .
.
Задача №3
Условие
Спусковую пружину игрушечного пистолета сжали на 5 см, при вылете шарик массой 20 г приобрел скорость 2 м/с. Необходимо рассчитать, какова жесткость пружины.
Дано: х=5 см=0,05 м; m=20 г=0,02 кг; V=2 м/с; k=?
Решение
По закону сохранения энергии, потенциальная энергия упругодеформированной пружины перейдет в кинетическую энергию движения шарика:

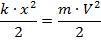
упрощаем данное выражение:
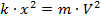
выражаем величину k:
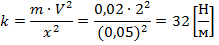
Ответ: жесткость пружины равна 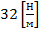 .
.
При решении задач на этом уроке мы применяли закон сохранения энергии, но не учитывали сопротивление среды, так как считали систему замкнутой. Вспомнили формулировку этого закона и формулы нахождения потенциальной и кинетической энергии.
Домашнее задание: Повторить §44, в рабочей тетради составить опорный конспект, выполнить расчётные задачи № 15, 41
