




5.5. РАСЧЕТ ВАЛОВ НА ЖЕСТКОСТЬ
За меру жесткости принимают относительный угол закручивания, то есть угол, приходящийся на единицу длины вала Условие жесткости: ≤ [θ] где [θ] имеет размерность рад/м. Чаще пользуются условием Допускаемое значение угла [θ°] закручивания зависит от назначения вала. Принимают [θ°] = (0,3–1,0) град/м. При расчете валов на прочность и жесткость часто задают мощность N, передаваемую валом и частоту его вращения n. Для вычисления крутящего момента по этим данным удобно воспользоваться таблицей Пример 5.1. Расчета вала на прочность и жесткость I. Определение внутренних усилий Значение ведущего момента Мвед определим из условия равновесия вала: Σ Мх = 0; Мвед – М1 – М2 – М3 = 0, откуда Мвед = М1 + М2 + М3 = 5 + 7 + 6 = 18 кН·м. Для расчетов на прочность и жесткость необходимо найти положение опасных сечений и величины крутящих моментов, действующих в этих сечениях вала (рис. 5.3, а). Воспользовавшись методом сечений определим внутренние усилия и построим эпюру крутящих моментов (рис. 5.3, б). Опасными являются все сечения на участке II, где действует Тmax = 12 кН·м. II. Проектный расчет валов сплошного и полого сечений Предварительно найдем допускаемое касательное напряжение, связанное с допускаемым нормальным напряжением. Принимаем по третьей теории прочности [τ] = 0,5 [σ] = 0,5·160 = 80 МПа. Из условия прочности и жесткости при кручении находим требуемые значения полярных момента сопротивления и момента инерции Из условия прочности и жесткости выполнить проектный расчет: определить диаметры валов в двух вариантах исполнения – сплошного и полого с коэффициентом пустотелости с = d/D = 0,8. Результаты округлить согласно ГОСТу. Построить эпюры углов закручивания вала. Валы сопоставить по металлоемкости и жесткости. Дано: М1 = 5 кН·м; a = 0,6 м; М2 = 7 кН·м; b = 0,8 м; М3 = 6 кН·м; с = 0,7 м; [σ] = 160 МПа; [θ] = 0,8 град/м. Рис. 5.3. Схема нагружения вала (а), эпюра крутящих моментов (б), эпюры углов закручивания сплошного (в) и полого (г) валов Результаты расчетов Форма сечения Сплошное Полое Момент сопротивления Углы закручивания характерных сечений вала сплошного и полого сечений Момент инерции принятый Жесткость сечения G·Ip = 80·109·1,19·10-5 = 0,955·106 Н·м2 G·Ip = 80·109·1,20·10-5 = 0,961·106 Н·м2. Углы закручивания участков вала Углы закручивания характерных сечений вала Строим эпюры углов закручивания сплошного и полого валов (рис. 5.3, в и г) III. Сопоставление металлоемкости валов двух вариантов Металлоемкость вала определяется его объемом, то есть произведением длины на площадь поперечного сечения. Поскольку длина вала неизменна, сопоставим площади поперечных сечений сплошного вала с полым Выводы: 1. Из условий прочности и жесткости найдены диаметры вала двух вариантов исполнения, сплошного и пустотелого: 105 и 120 мм соответственно. 2. Вычислены деформации валов на каждом из участков, построены эпюры углов закручивания валов сплошного и пустотелого. Жесткости валов практически одинаковы. 3. Сопоставлены металлоемкости валов двух вариантов исполнения. Расход металла для вала сплошного сечения вдвое больше, чем для вала пустотелого. Примечание. Полученный результат по сопоставлению металлоемкости валов ожидаем, поскольку достаточно большой объем материала, сосредоточенный около центра тяжести сечения, испытывает напряжения ниже допускаемого и вклад его в общую прочность конструкции невелик. Поэтому целесообразно убирать неработающий материал из этой области. Конструкции из полого сечения созданы природой: камыш, тростник, бамбук, злаковые культуры, трубчатые кости птиц и млекопитающих. В авиации и космонавтике используют полые валы, в строительстве – пустотные плиты перекрытий.
1.
Из условия равномерного вращения вала
определить диаметры зубчатых колес
![]() и
и![]() .
.
2.
Изобразить в масштабе схему нагружения
вала.
3.
Определить реакции опор вала во взаимно
перпендику
лярных
плоскостях, указанных на схеме нагружения
вала.
4.
Рассчитать изгибающие и крутящие моменты
в поперечных сечениях вала, построить
эпюры изгибающих и
крутящих
моментов.
5.
Рассчитать диаметры вала на прочность
по эквивалентным напряжениям (приведенному
моменту
![]() )
)
в
наиболее опасных сечениях вала. Опасным
сечением вала считать то, в котором
приведенный момент нагрузки на вал
максимален.
6.
Рассчитать вал на жесткость при кручении.
10.2. Расчет вала на прочность.
При
одновременном действии крутящего
![]() и изгибающего
и изгибающего![]() моментов расчет вала ведут по эквивалентному
моментов расчет вала ведут по эквивалентному
моменту в сечении (четвертая теория
прочности)
![]() =
=![]() ,
,
где![]() –
–
суммарный изгибающий момент в сечении
вала.
Опасным
сечением вала считать сечение, в котором
приведенный момент нагрузки на вал
максимален.
Диаметр
вала определяется по формуле
![]() ,
,
где
![]() = 50 МПа – допускаемое нормальное напряжение
= 50 МПа – допускаемое нормальное напряжение
материала вала.
Если
на вал или его участок действует только
крутящий момент
![]() ,
,
то его диаметр можно определить из
условия прочности на кручение:
![]() ,
,
где
![]() = 0,5
= 0,5![]() – допускаемое касательное напряжение
– допускаемое касательное напряжение
материала вала.
10.3. Расчет вала на жесткость
С
целью уменьшения упругого мертвого
хода в точных и силовых механизмах углы
закручивания сечений валов друг
относительно друга ограничиваются
допускаемым углом закручивания
![]() .
.
Условие жесткости вала при кручении
имеет вид
![]() ,
,
где
![]() – допустимая величина угла закручивания
– допустимая величина угла закручивания
вала на рабочей длине![]() (при расчете принять
(при расчете принять![]() =
=
20 угловых минут, то есть![]() рад).
рад).
Рабочая
длина вала
![]() определяется суммированием длин участков
определяется суммированием длин участков
вала, на которых крутящий момент вала
отличен от нуля.
Диаметр
вала на закручиваемом участке определяется
по формуле
![]() ,
,
где
![]() 8*104
8*104
МПа – модуль сдвига материала вала
(стали).
Если
при диаметре
![]() условие жесткости вала не выполнено,
условие жесткости вала не выполнено,
то есть![]() ,
,
то в качестве диаметра вала принимают
наибольший из диаметров![]() и
и![]() .
.
Полученный диаметр выражают в миллиметрах
и округляют до целого числа из
предпочтительного ряда размеров, в
котором числа заканчиваются цифрами
0, 2, 4, 5, 6, 8.
11. Задача №7
ОПРЕДЕЛЕНИЕ
ГЛАВНЫХ НАПРЯЖЕНИЙ И ГЛАВНЫХ ПЛОЩАДОК
Для
напряженного состояния в точке тела,
заданного компонентами тензора напряжений
определить главные напряжения и
полдожения главных площадок. Исходные
данные определить по табл. 7.1, где
напряжения заданы в Мпа.
Величины
компонентов тензора напряжений выбираются
из столбцов табл. 7.1 по цифрам
![]() .
.
Остальные компоненты тензора напряжений
определить на основании закона парности
касательных напряжений.
Таблица
7.1
|
Номер |
|
|
|
|
|
|
|
1 |
-20 |
36 |
44 |
-54 |
24 |
33 |
|
2 |
10 |
-20 |
30 |
20 |
30 |
40 |
|
3 |
-32 |
35 |
40 |
25 |
-15 |
-25 |
|
4 |
54 |
-16 |
-24 |
-18 |
-36 |
-24 |
|
5 |
39 |
42 |
27 |
33 |
39 |
36 |
|
6 |
-20 |
36 |
44 |
-54 |
24 |
33 |
|
7 |
10 |
-20 |
30 |
20 |
30 |
40 |
|
8 |
-32 |
35 |
40 |
25 |
-15 |
-25 |
|
9 |
54 |
-16 |
-24 |
-18 |
-36 |
-24 |
|
0 |
39 |
42 |
27 |
33 |
39 |
36 |
|
|
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
![]()
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.

Для обеспечения прочности и жесткости вала при кручении, напряжения и деформации от крутящих моментов не должны превышать соответствующих допустимых значений.
Кручением называется такой вид нагружения (деформации), при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – крутящий момент T (рис 5.1).
Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.
Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М1, М2, …, Мn или распределенными m по длине вала l.
Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.
Внутренний крутящий момент
При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.
Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T. Затем из условий равновесия остановленной части вала определяют крутящий момент:
T = Мк = ΣМi. (5.1)
Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.
Правило знаков внутреннего крутящего момента T.
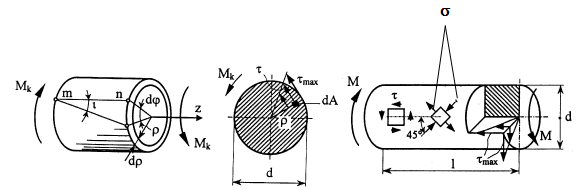
Рис. 5.1
Угол сдвига
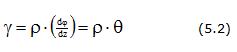
Напряжения при кручении
Распределение касательных напряжений
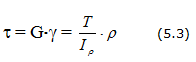
Максимальное касательное напряжение
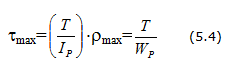
Геометрические характеристики круглых сплошных сечений вала
Полярный момент инерции
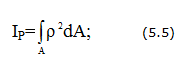
Полярный момент сопротивления
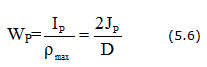
Деформации вала
Угол закручивания:
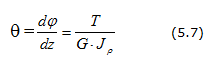
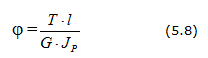
Условия прочности и жесткости вала
Расчет вала при кручении сводится к одновременному удовлетворению двух условий:
— условия прочности:
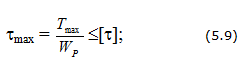
— и условия жесткости:
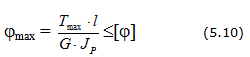
Примеры решения задач >
Поперечная сила и изгибающий момент >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Валы и оси
Конструкции машин содержат множество вращающихся деталей и узлов, работающих в различных условиях. Так, детали двигателей, редукторов, воздушные и корабельные винты, колеса автомобилей и шасси самолета движутся с большими угловыми скоростями, испытывая значительные динамические нагрузки и подвергаясь в некоторых случаях интенсивному нагреву.
Для поддержания вращающихся деталей и для передачи вращающего момента от одной детали к другой (в осевом направлении) в конструкциях используют детали, называемые валами (рис. 3.1, а – г).

Рис. 3.1. Эскизы валов и осей
В зависимости от вида испытываемой деформации условно различают:
– простые валы – работают в условиях кручения, изгиба, как, например, вал воздушного винта самолета, нагруженный силой веса винта и вращающим моментом, или вал привода агрегатов двигателя, несущий зубчатые колеса. Зубчатые колеса могут быть насажены на вал или изготовлены с ним как одно целое;
– торсионные валы – работают лишь в условиях кручения, т.е. передают только вращающий момент (валы приводов управления закрылками ВС);
– оси – поддерживающие невращающиеся валы, работающие лишь в условиях изгиба. Например, оси тормозных колес шасси, оси роликов тросовой системы управления, оси шарнирных соединений стоек шасси, элеронов, рулей, управляемых стабилизаторов не вращаются.
По геометрической форме валы бывают прямыми (рис. 3.1, б), коленчатыми (рис. 3.1, в) (в поршневых двигателях и компрессорах) гибкими (рис. 3.1, г), а оси только прямыми (рис. 3.1, а). Гибкие валы дают возможность передавать вращение с изменяющейся геометрией оси, их используют в переносных механизированных инструментах, в приборах и др.
В зависимости от расположения, быстроходности и назначения валы называют входными, промежуточными, выходными, тихо- или быстроходными, распределительными и т.п.
Конструктивные элементы.
Опорные части валов, воспринимающие радиальные нагрузки (рис. 3.2, а), называют цапфами, а воспринимающие осевые нагрузки (рис. 3.2, б) – пятами. Концевые цапфы называют шипами (в подшипниках скольжения), а промежуточные – шейками. Шипы чаще всего бывают цилиндрическими (рис. 3.2, а), а также коническими и сферическими (рис. 3.2, в, г).

Рис. 3.2. Опорные части валов
Прямой вал ступенчатой формы более удобен для монтажа деталей и по профилю приближается к брусу равного сопротивления. Переход от одной ступени к другой может осуществляться канавкой для выхода шлифовального круга (рис. 3.3, а), однако это приводит к повышению концентрации напряжений, галтелью (рис. 3.3, б, в) – плавным переходом по дуге с постоянным или переменным радиусом (в этом случае снижается концентрация напряжений и повышается прочность вала).

Рис. 3.3. Переходные участки вала
Закрепление деталей на валах от осевого перемещения осуществляют с помощью буртиков (рис. 3.4, а), гаек (рис. 3.4, б), посадки с натягом (рис. 3.4, в), пружинных колец (рис. 3.4, г). Передачу вращающего момента осуществляют за счет устройства шпоночных, шлицевых и других соединений валов.

Рис. 3.4. Крепление деталей на валах
Оси и валы авиационных конструкций – пустотелые. Канал уменьшает массу вала, кроме того, в ряде случаев через полый вал проходят детали системы смазки или управления.
Технические условия на изготовление валов зависят от требований к конструкции. Наиболее жесткие требования по точности и шероховатости поверхности предъявляются к шейкам валов, на которые устанавливают подшипники качения.
Материалы валов.
Для изготовления валов используют углеродистые стали марок 20, 30, 40, 45 и 50, легированные стали марок 20Х, 40Х, 40ХН, 18Х2Н4МА и др., титановые сплавы ВТ3-1, ВТ6 и ВТ9.
Выбор материала, термической и химико-термической обработки определяется конструкцией вала и опор, условиями эксплуатации.
Расчет валов и осей
Валы и оси рассчитывают на прочность, жесткость и колебания. Основной причиной выхода из строя валов является недостаточная их прочность при длительной работе, усталостное разрушение металла.
Нагрузки на валы создают силы и вращающие моменты, действующие в зубчатых, червячных, цепных и других передачах. Расчет ведут по наибольшей из длительно действующих нагрузок.
Проектирование вала включает три этапа: предварительное определение размеров, разработку конструкции и проверочный расчет.
При проектном расчете приближенно определяют из условия прочности при кручении диаметр вала и проводят его конструирование. Проверочный расчет ведут на статическую прочность вала и усталость материала, а при повышенных требованиях – на жесткость и колебания.
Расчет валов на прочность.
В предварительном (проектном) расчете при отсутствии данных об изгибающих моментах диаметр вала может быть найден по известному значению крутящего момента из условия прочности по сниженным допускаемым напряжениям:
 , (3.1)
, (3.1) где Т – крутящий момент в расчетном сечении вала;
[τK] – допускаемое напряжение на кручение, [τK] = 20…25 МПа под шкив, звездочку или муфту; для средних участков вала [τK] = 10…20 МПа;
Р – передаваемая мощность, кВт;
n – частота вращения вала, об./мин.
После определения расчетного диаметра вала определяют диаметры других ступеней, изменяя их на 2…5 мм. Независимо от результатов расчета диаметр выходного конца вала может быть принят равным 0,8…1,2 диаметра вала электродвигателя, с которым он будет соединен муфтой.
Наименьший диаметр промежуточного вала принимают обычно равным внутреннему диаметру подшипника.
Расчет валов на статическую прочность
Расчет ведут по наибольшей возможной кратковременной нагрузке, повторяемость которой мала и не может вызвать усталостного разрушения.
Валы работают в условиях изгиба и кручения, эквивалентное напряжение
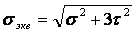 , (3.2)
, (3.2) где σ и τ – наибольшие напряжения от изгибающего момента Мх и крутящего момента Т
; ,
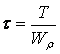 ,(3.3)
,(3.3)где WX и Wρ – соответственно осевой и полярный момент сопротивления сечения вала диаметром d, WX = 0,1d3; Wρ = 0,2d3, а т.к. Wρ = 2WX, то с учетом этих соотношений можно записать.
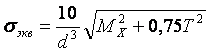 ,(3.4)
,(3.4)Запас прочности по пределу текучести.
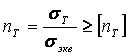 ,(3.5)
,(3.5) Обычно принимают допускаемый запас прочности [nT] = 1,2…1,8.
Полагают, что имеет место симметричный цикл напряжений при изгибе вала и отнулевой цикл напряжений при его кручении.
Сопротивление материала детали усталости может быть повышено за счет ее поверхностного упрочнения: поверхностной закалки, обкатки роликом, наклепом.
Жесткость валов
Расчет на прочность не всегда обеспечивает достаточную жесткость (изгибную и крутильную) валов, необходимую для нормальной работы подшипников, передач, обеспечения точности механизмов и др. При значительном прогибе вала происходит перекос зубчатых колес, возрастает неравномерность распределения нагрузки по длине зуба, возможно защемление тел качения в подшипниках.
При проектировании валов проверяют прогибы и углы поворота сечений. Их вычисляют, используя дифференциальное уравнение изогнутой оси балки, и другими методами.
