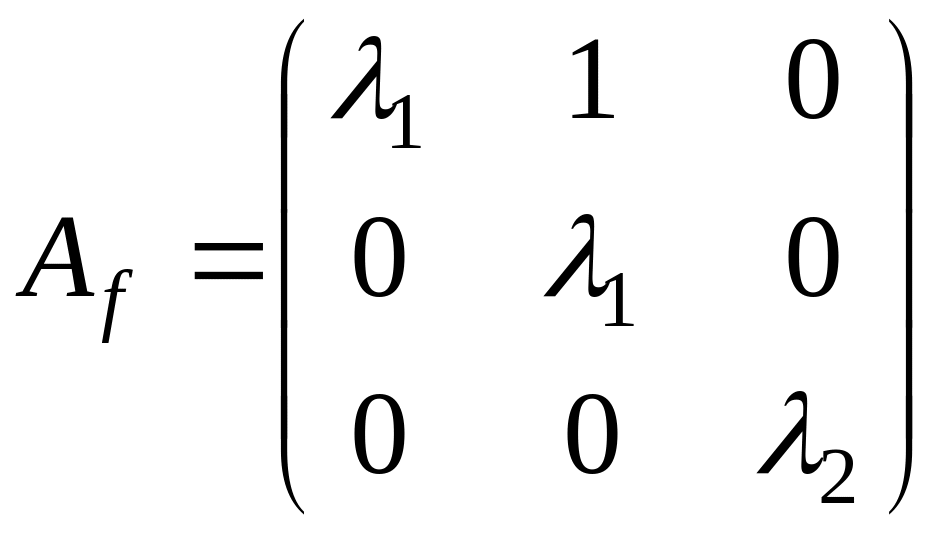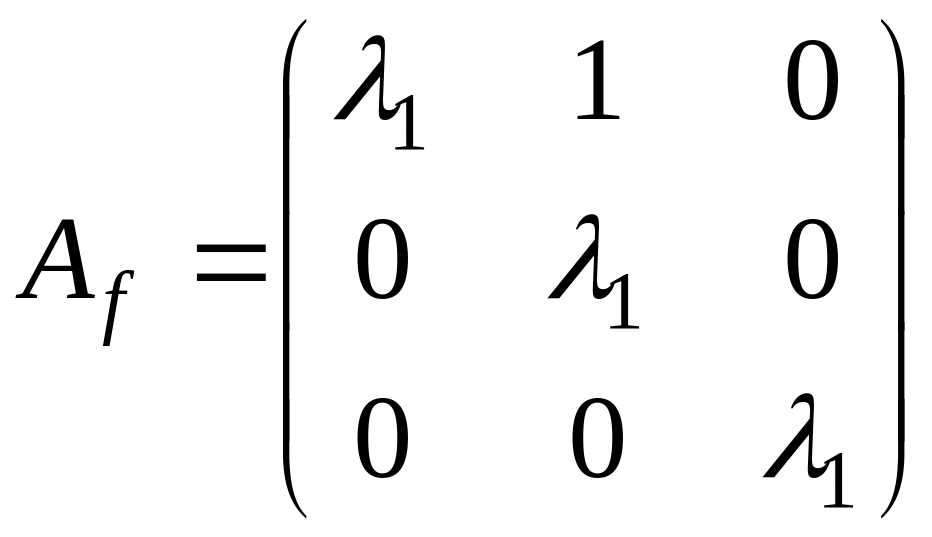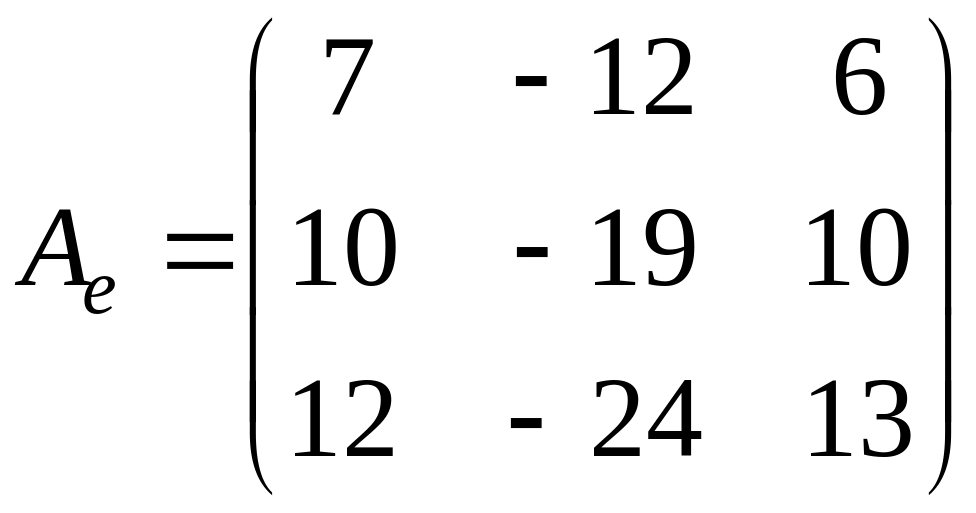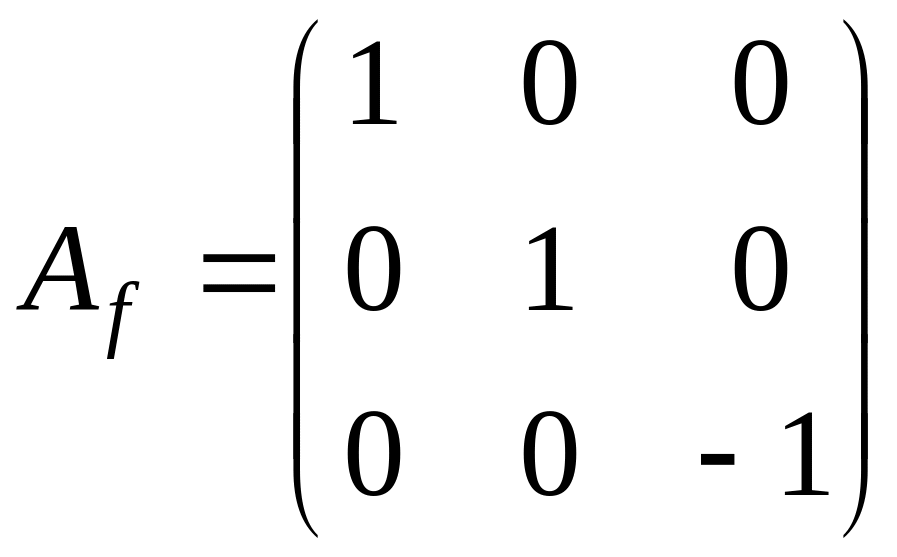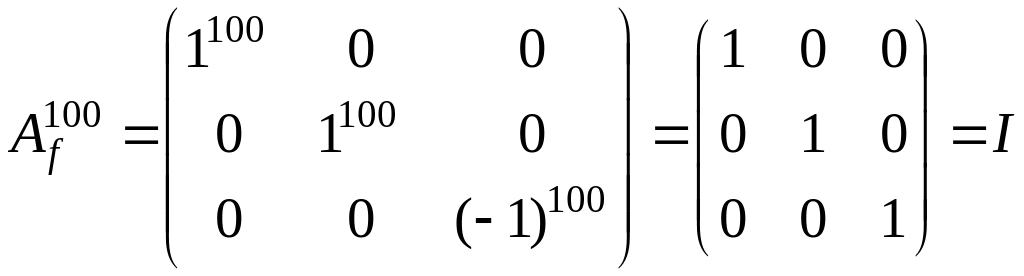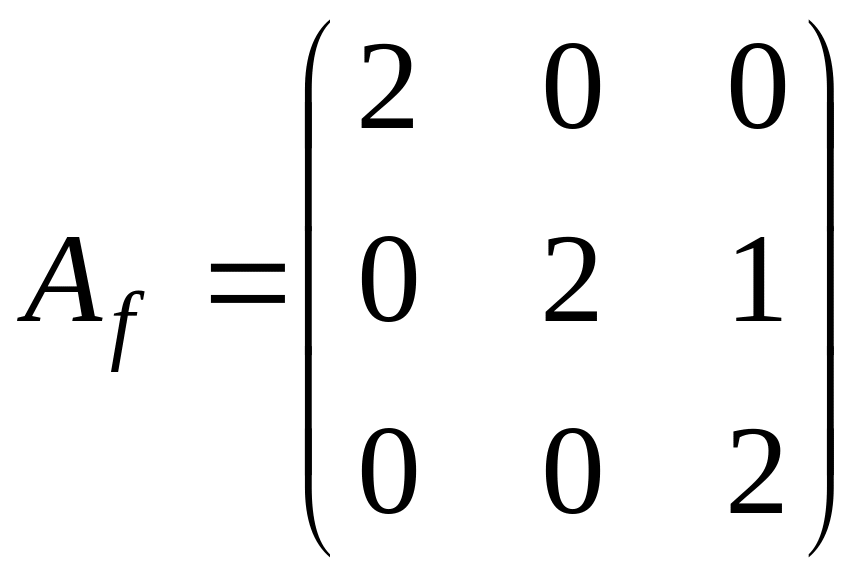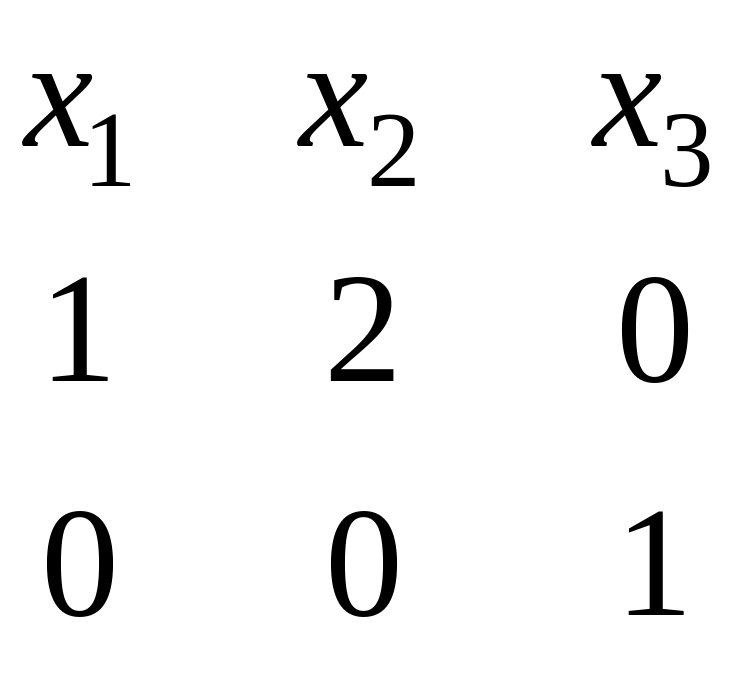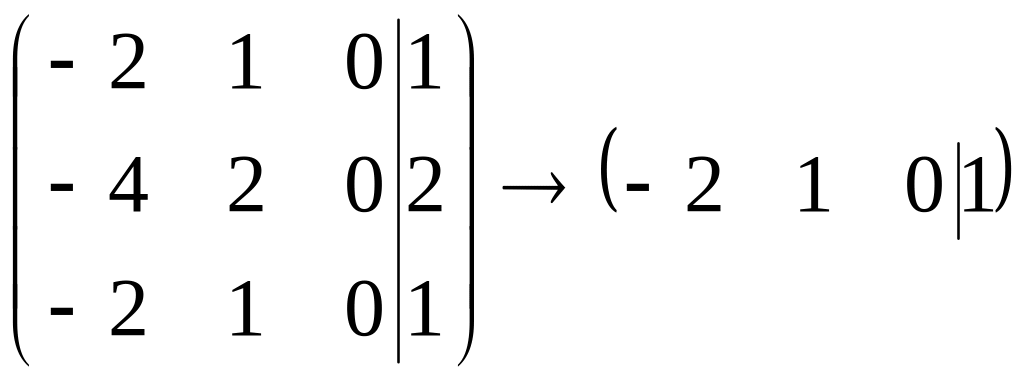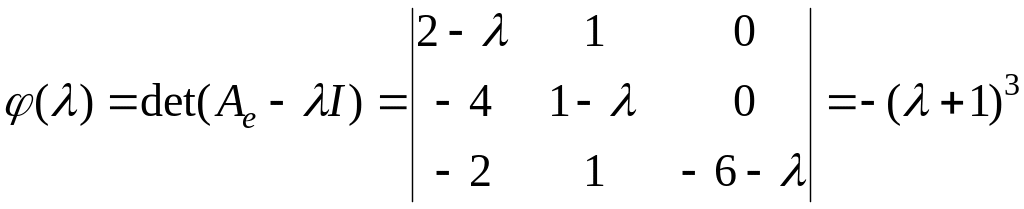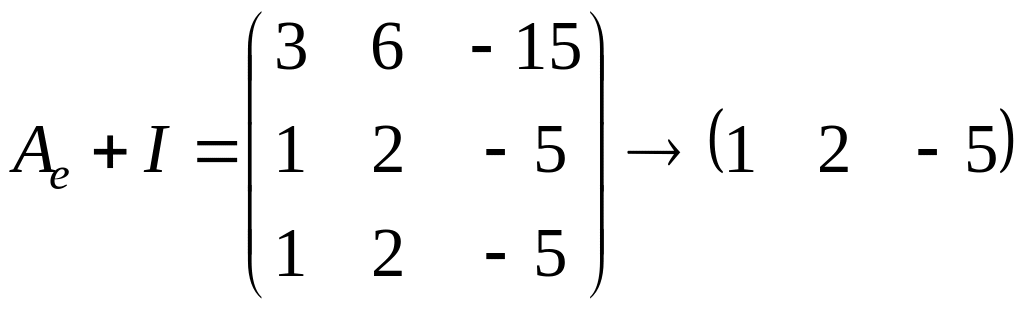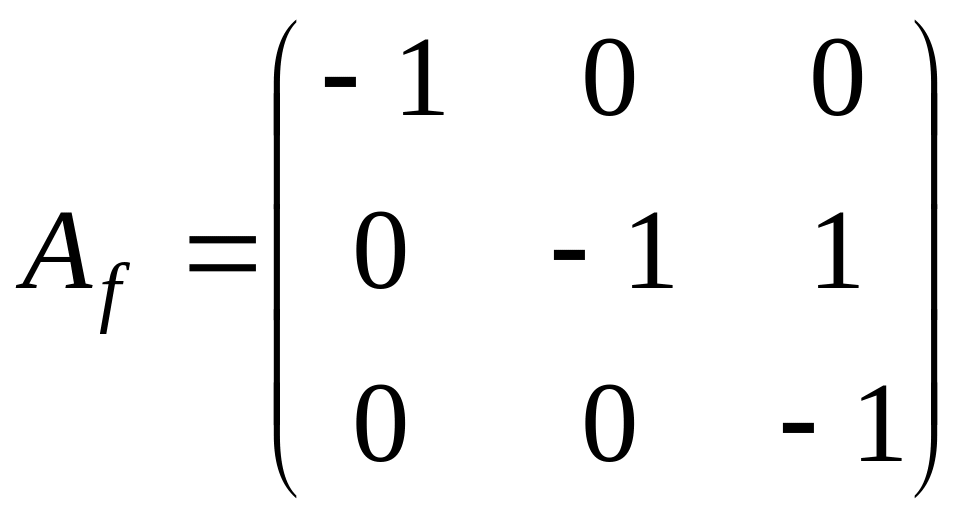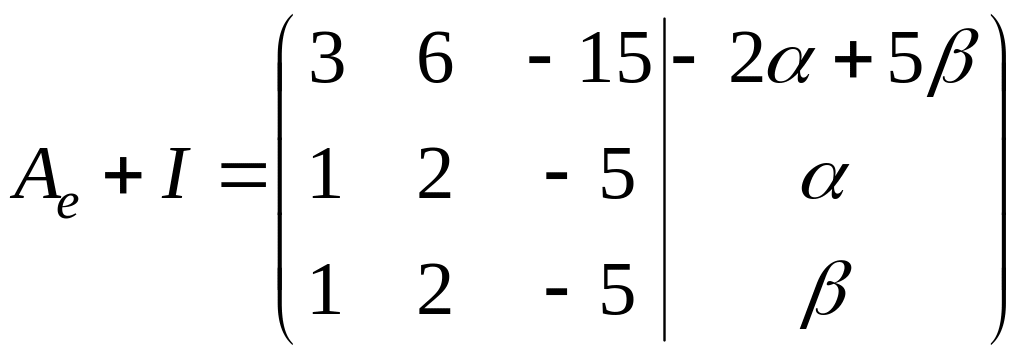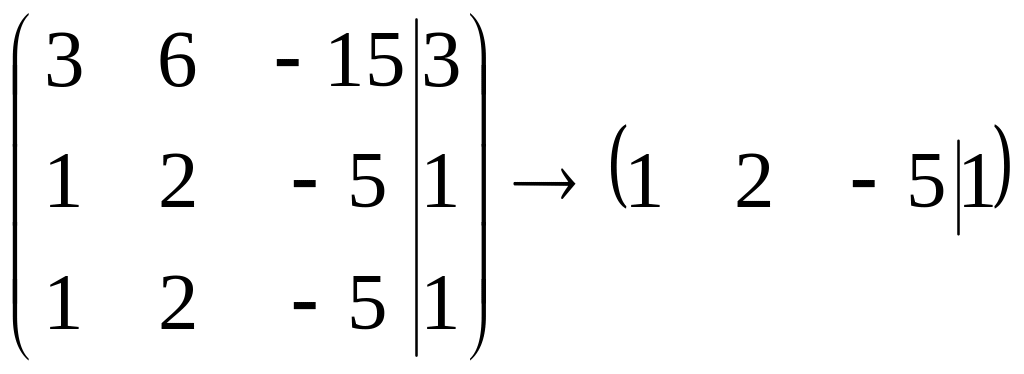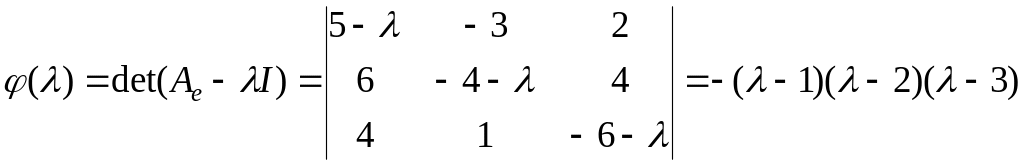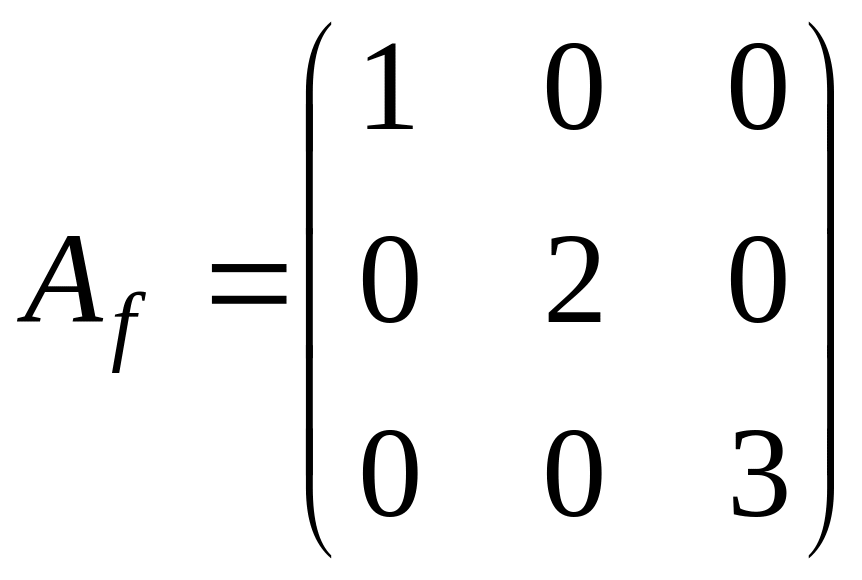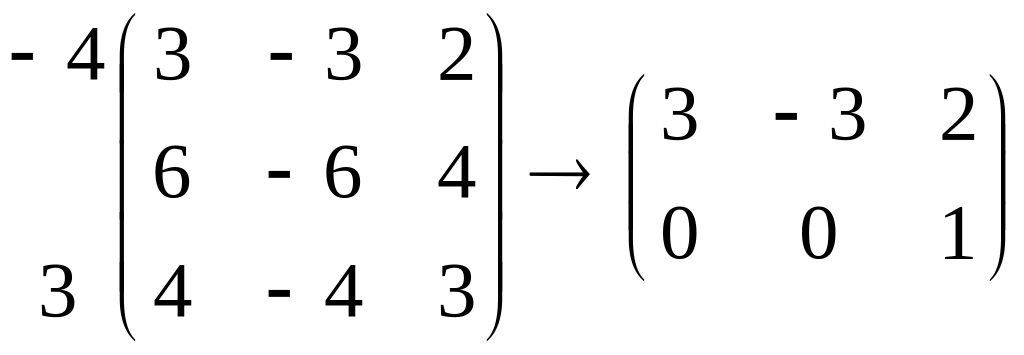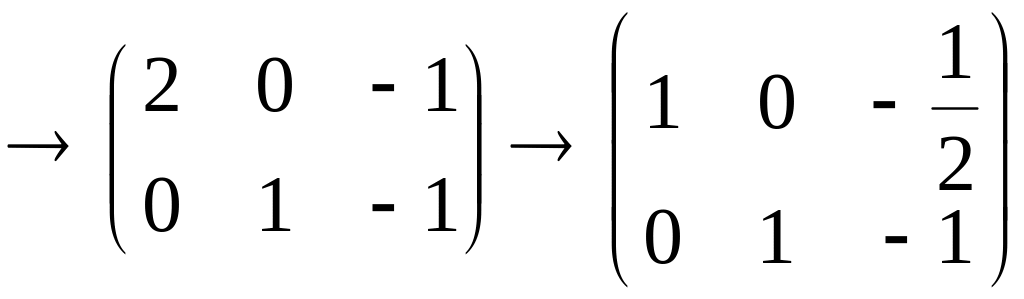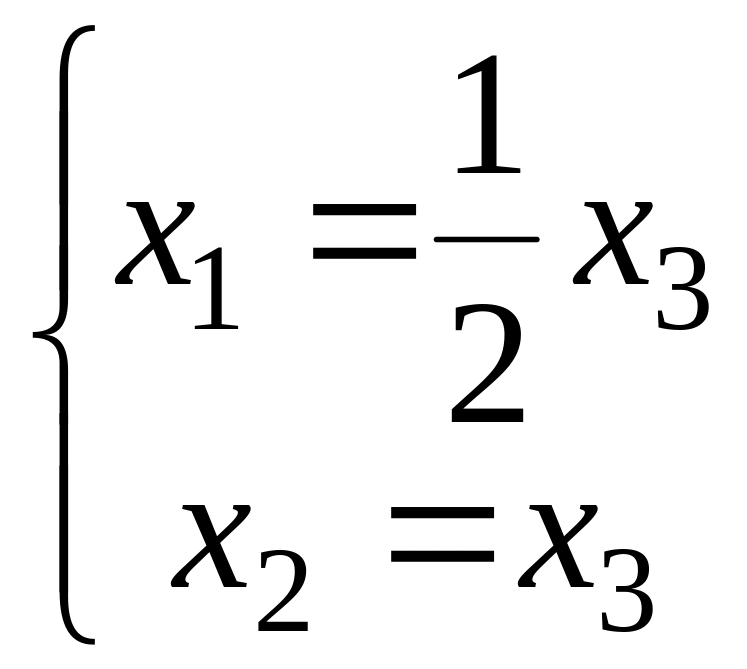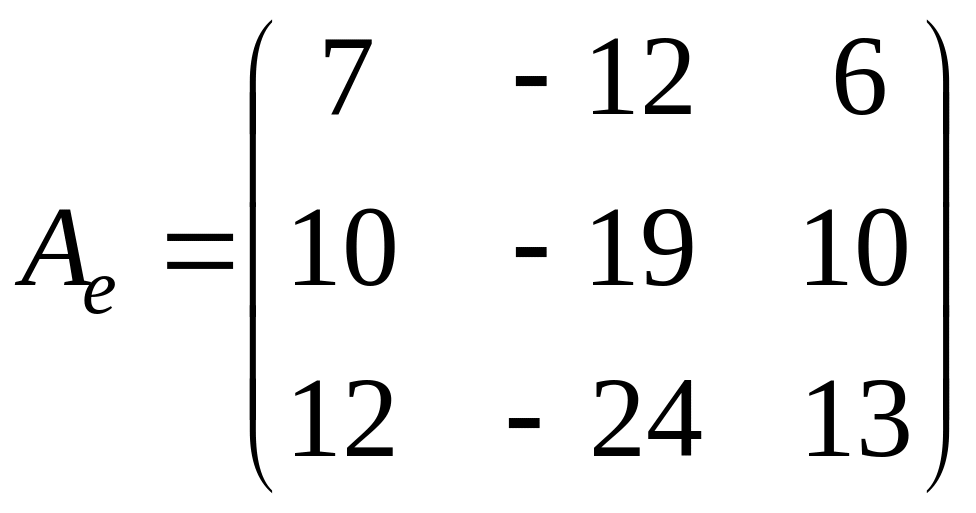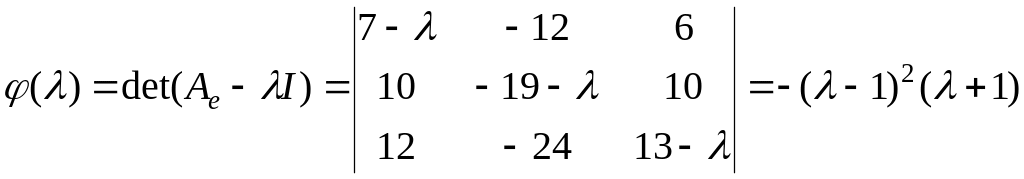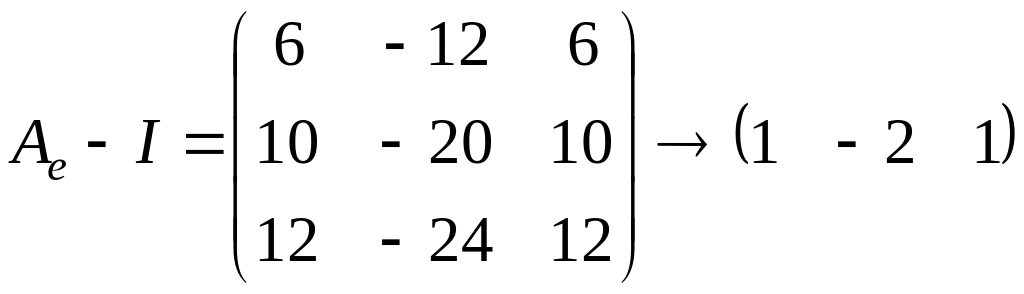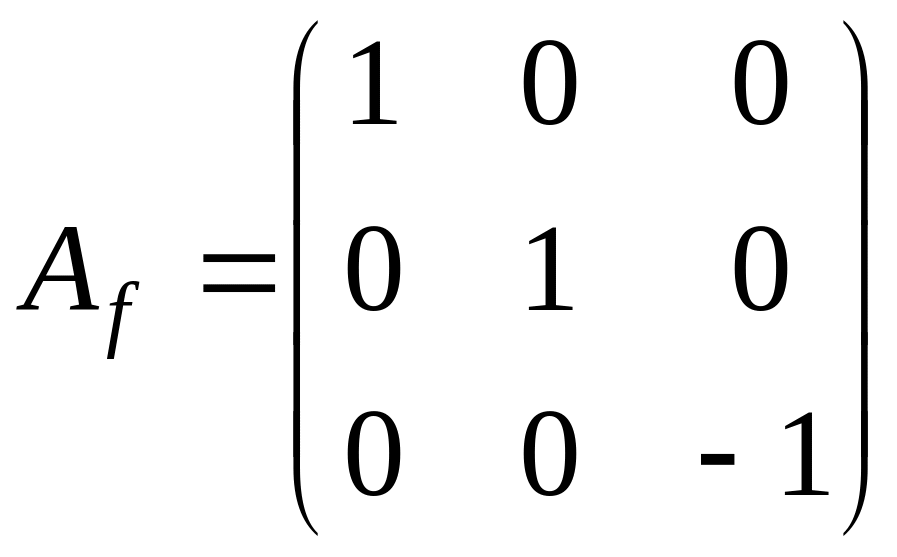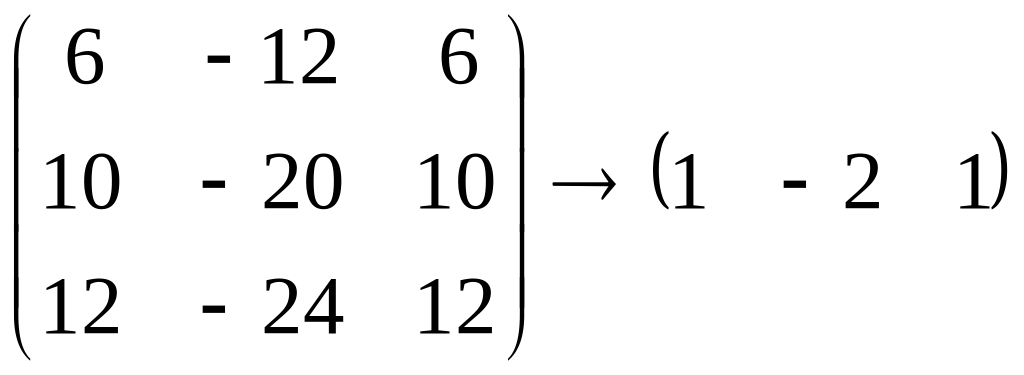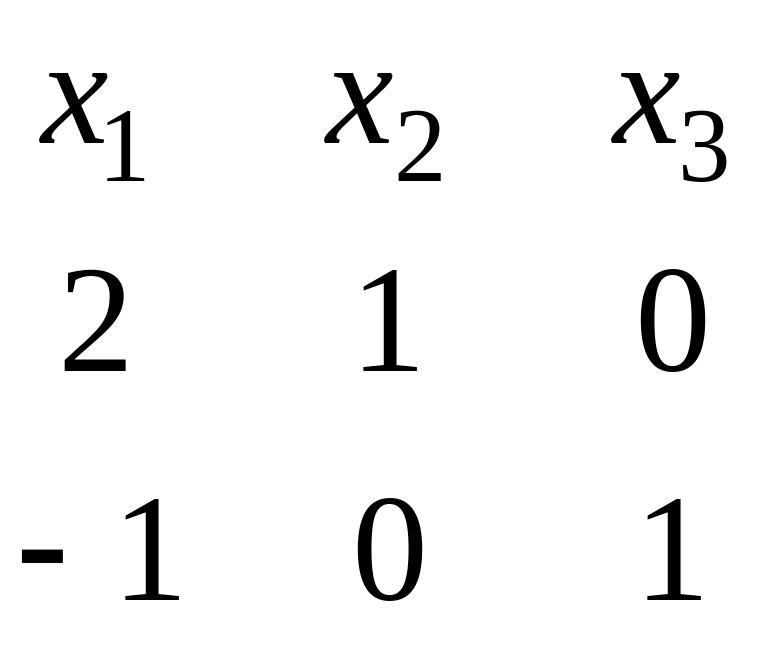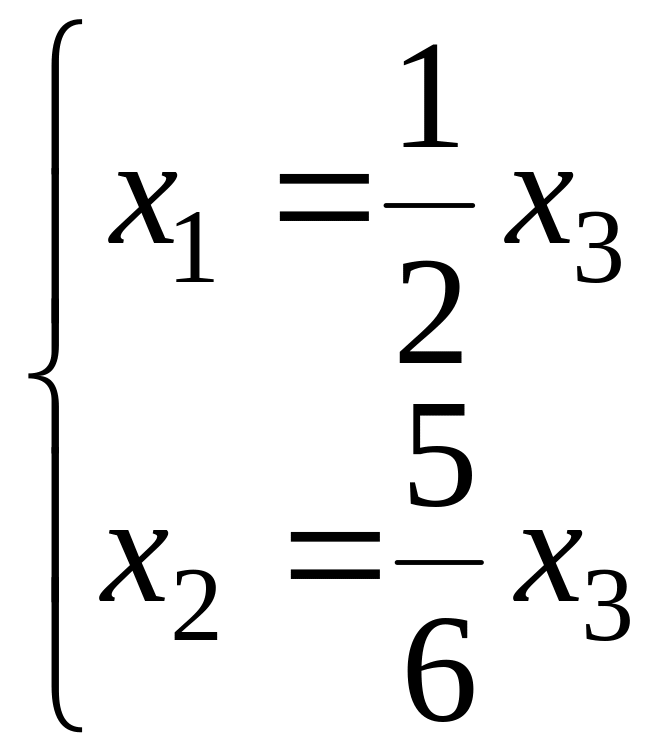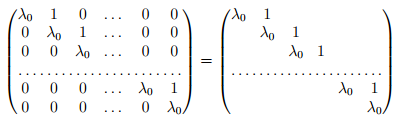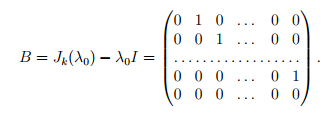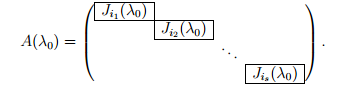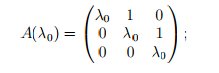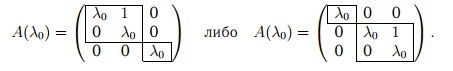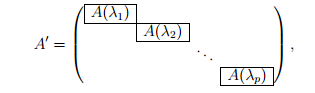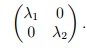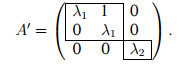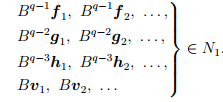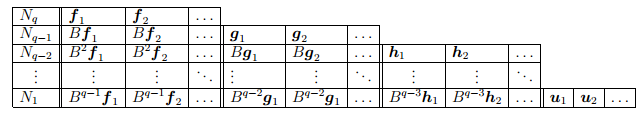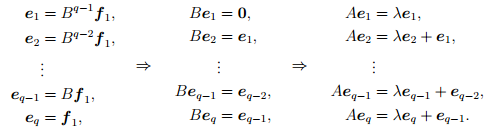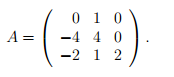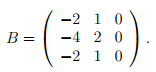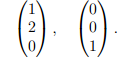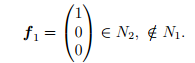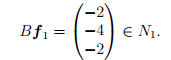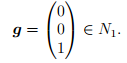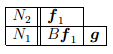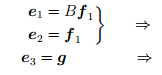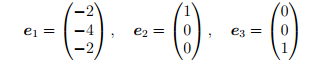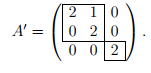Как найти жорданов базис онлайн

Пусть дана матрица
3-го порядка. Надо найти жорданову форму
и жорданов базис.

1. Пусть
   характеристический многочлен матрицы

   имеет вид

,
где

.

Тогда
жорданова форма матрицы имеет вид

.

1. Пусть
   характеристический многочлен матрицы

   имеет вид

,

где

.
Возможны два случая:

а)

,
поэтому

и, следовательно,

,
поэтому жорданова форма содержит две
жордановы клетки с собственным значением

:

;

б)

,
поэтому

и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением

:

.

1. Пусть
   характеристический многочлен матрицы

   имеет вид

.

Возможны два
случая:

а)

,
поэтому

и, следовательно, жорданова форма
содержит две жордановы клетки с
собственным значением

:

;

б)

,
поэтому

и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением

:

.

Задача.
Дана матрица

.
Найти

.

Р е ш е
н и е.

Найдем характеристический многочлен
матрицы:

.

Жорданова
форма матрицы

имеет вид

.

Найдем

.

Для
нахождения

воспользуемся формулой

,
где

– матрица перехода от базиса

к базису

.
Очевидно, что

,

поэтому

.

Пример
1. Найти жорданову форму и жорданов
базис матрицы оператора

.

Р е ш е
н и е.

Вычислим

,

следовательно,
собственное значение

,

.

Найдем
геометрическую кратность собственного
значения

.
Для этого посчитаем ранг матрицы

.

Следовательно,

,

поэтому
жорданова форма имеет вид

или

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он удовлетворяет условию

,

то
решим систему

.

Следовательно,
координаты собственного вектора

удовлетворяют уравнению

.

Заметим, что коэффициент при

равен 0, поэтому

может принимать любые значения.
Отбрасывать

нельзя !!!

Для
нахождения ФСР построим таблицу

.

Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается и,
следовательно, имеет вид

.
Так как

,

,
то должен быть один присоединенный
вектор, который будет являться решением
системы

.
Подберем коэффициенты

и

таким образом, чтобы система

была совместна. Так как

,

то для
совместности системы необходимо, чтобы
выполнялось условие

.
Возьмем

,
тогда

,
и координаты присоединенного вектора
являются решением системы

,

то есть
удовлетворяют уравнению

или

.

Возьмем

.

Таким образом, у нас есть собственный
вектор

,
присоединенный к нему

и нужен еще один собственный вектор,
отвечающий собственному значению

.
Можно взять или вектор

,
или

,
или любой другой, отличный от

,
отвечающий собственному значению

.
Эти три вектора и будут образовывать
жорданов базис.

Пример 2. Найти жорданову
форму и жорданов базис матрицы оператора

.

Р е ш е
н и е.

Вычислим

,

следовательно,
собственное значение

,

.

Найдем
геометрическую кратность собственного
значения

.
Для этого посчитаем ранг матрицы

.

Следовательно,

,

поэтому
жорданова форма имеет вид

или

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он удовлетворяет условию

,

то
решим систему

.

Очевидно,
что координаты собственного вектора

удовлетворяют уравнению

или

.

Для
нахождения ФСР построим таблицу

.

Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается
и, следовательно, имеет вид

.

Так как

,

,
то должен быть один присоединенный
вектор, который будет являться решением
системы

.
Подберем коэффициенты

и

таким образом, чтобы система

была совместна. Так как

,

то для
совместности системы необходимо, чтобы
выполнялось условие

.
Возьмем

,
тогда

и координаты присоединенного вектора
являются решением системы

,

то есть
удовлетворяют уравнению

или

.

Возьмем

.

Таким образом, у нас есть собственный
вектор

,
присоединенный к нему

и нужен еще один собственный вектор,
отвечающий собственному значению

.
Можно взять или вектор

,
или

,
или любой другой, отличный от

,
отвечающий собственному значению

.
Эти три вектора и будут образовывать
жорданов базис.

Пример 3. Найти жорданову
форму и жорданов базис матрицы оператора

.

Р е ш е
н и е.

Вычислим

.

Таким образом, получили три собственных
значения

,

,

.
Так как алгебраическая кратность каждого
из них равна 1, то жорданова форма имеет
следующий вид

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он является решением
уравнения

и, следовательно, его координаты
удовлетворяют системе

,

то есть

,
поэтому можем взять

.

Вычислим собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он удовлетворяет уравнению

,
а его координаты – системе

,

откуда
следует, что

,
поэтому можем взять

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он является решением уравнения

,
то его координаты удовлетворяют системе

,

и,
следовательно,

,
поэтому можем взять

.

Векторы

образуют жорданов базис матрицы.

Пример 4. Найти жорданову
форму и жорданов базис матрицы оператора

.

Р е ш е
н и е.

Вычислим

.

Таким образом, получили два собственных
значения

,

.
Так как алгебраическая кратность

равна 2, нужно вычислить геометрическую
кратность

собственного значения

.
Для этого посчитаем ранг матрицы

.

Очевидно, что

,
поэтому

и, следовательно, жорданова форма имеет
следующий вид

.

Найдем собственные векторы

,

,
соответствующие собственному значению

.
Очевидно, что они являются решением
уравнения

,
а их координаты

– решением системы

,

и,
следовательно, удовлетворяют уравнению

или

.

Для
нахождения ФСР построим таблицу

.

Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается и,
следовательно, имеет вид

.

Так
как

,
то нужно выбрать любые два линейно
независимых вектора из этой линейной
комбинации. Возьмем

,

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он удовлетворяет уравнению

,
а его координаты

– системе

,

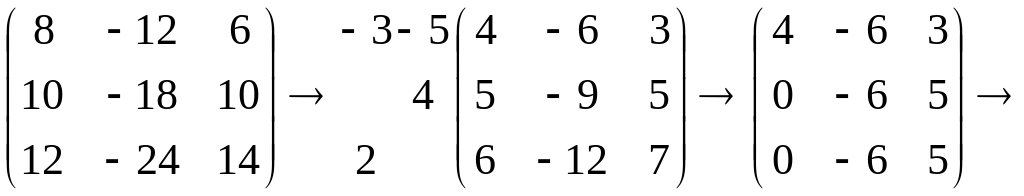
то есть

,
поэтому можем взять

.

Векторы

образуют жорданов базис матрицы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

NenSi писал(а):

Вычислим характеристический многочлен [math]varphi(lambda)[/math] матрицы [math]mathbf{A}[/math]:

[math]{varphi(lambda)=det(mathbf{A}-lambdamathbf{E})=,,vline!!begin{array}{*{20}{c}}{-1-lambda}&5&4\[3pt]4&{-6-lambda}&{-6}\[3pt]{-8}&{16}&{14-lambda}end{array}!vline,=12-16lambda+7lambda^2-lambda^3=-(lambda-2)^2(lambda-3)}[/math].

Таким образом, получили два собственных значения [math]lambda_1=2[/math] и [math]lambda_2=3[/math]. Так как алгебраическая кратность [math]lambda_1=2[/math] равна 2, нужно вычислить геометрическую кратность [math]k[/math] этого собственного значения. Для этого посчитаем ранг матрицы [math]mathbf{A}-lambda_1mathbf{E}[/math]:

[math]det(mathbf{A}-lambda_1mathbf{E})=,,vline!!begin{array}{*{20}{r}}{-3}&5&4\[3pt]4&{-8}&{-6}\[3pt]{-8}&{16}&{12}end{array}!vline,=0[/math] и [math]operatorname{M}_2(mathbf{A}-lambda_1mathbf{E})=,,vline!!begin{array}{*{20}{r}}{-3}&5\[3pt]4&{-8}end{array}!vline,=4ne0[/math], следовательно, [math]operatorname{rang}(mathbf{A}-lambda_1mathbf{E})=2[/math]

Таким образом, имеем [math]k=n-operatorname{rang}(mathbf{A}-2mathbf{E})=3-2=1,[/math] где [math]n[/math]-порядок матрицы [math]mathbf{A}[/math].

Итак, жорданова форма линейного оператора, заданного матрицей [math]mathbf{A}[/math] имеет вид

[math]{J!}_mathbf{A}=left(!!begin{array}{*{20}{c}}2&1&0\[3pt]0&2&0\[3pt]0&0&3end{array}!!right)[/math] или [math]{J!}_mathbf{A}=left(!!begin{array}{*{20}{c}}3&0&0\[3pt]0&2&1\[3pt]0&0&2end{array}!!right)[/math]

NenSi писал(а):

[math]{varphi(lambda)=det(mathbf{A}-lambdamathbf{E})=,,vline!!begin{array}{*{20}{c}}1-lambda&-1&1&-2\[3pt]0&1-lambda&-2&-2\[3pt]0&0&1-lambda&2\[3pt]0&0&0&{1-lambda}end{array}!vline,=(lambda-1)^4}[/math]

[math]operatorname{rang}(mathbf{A}-mathbf{E})=operatorname{rang}!left(!!begin{array}{*{20}{r}}0&-1&1&-2\[3pt]0&0&-2&-2\[3pt]0&0&0&2\[3pt]0&0&0&0end{array}!!right)=3[/math]

[math]k=4-operatorname{rang}(mathbf{A}-mathbf{E})=4-3=1[/math]

[math]{J!}_mathbf{A}=left(!!begin{array}{*{20}{c}}1&1&0&0\[3pt]0&1&1&0\[3pt]0&0&1&1\[3pt]0&0&0&1end{array}!!right)[/math]

Как найти жорданов базис, я ещё не въехал
Может быть, Prokop знает, как это сделать.

ДОКЛАД:

Жорданова нормальная форма матрицы оператора, жорданов базис.

1. Определения и основные понятия

Введем два основных понятия.

1.1 Жорданова клетка

Жордановой клеткой порядка k, относящейся к числу λ₀, называется матрица порядка k, 1≤k≤n, имеющая вид:

Также можем сказать, что на её главной диагонали стоит одно и то же число из поля P, а параллельные элементы, ближайшие к главной диагонали сверху, равны 1, все остальные элементы матрицы равны нулю.

Её характеристический многочлен (λ₀ − λ)^k имеет корень λ₀ кратности k.

Таким образом, данная матрица имеет собственное значение λ₀ алгебраической кратности k. Отвечающие ему собственные векторы — это ненулевые решения однородной системы линейных уравнений с матрицей

Так как rangB = k −1, так что размерность собственного подпространства равна 1, то существует лишь один линейно независимый собственный вектор. Таким образом, при k ≥ 2 не существует базиса, состоящего из собственных векторов этого оператора, то есть ни в одном базисе матрица оператора не может иметь диагонального вида. Матрица J_k(λ₀) называется жордановой клеткой порядка k, соответствующей собственному значению λ₀.

1.2 Жорданов блок

Жордановым блоком, отвечающим собственному значению λ₀, называется блочно-диагональная матрица, каждый блок которой представляет собой жорданову клетку вида:

На главной диагонали матрицы расположены s жордановых клеток J_i1(λ₀), J_i2(λ₀), . . . , J_is(λ0) порядков i₁, i₂ . . . , i_s, где s — геометрическая кратность собственного значения λ₀.

Сумма порядков этих клеток равна алгебраической кратности собственного значения λ₀, т.е. i₁ + i₂ + · · · + i_s = m.

Все элементы матрицы вне жордановых клеток равны нулю. Порядок расположения жордановых клеток в матрице A(λ₀) определен неоднозначно.

1.3 Примеры жордановых блоков

Рассмотрим простой случай, когда характеристический многочлен матрицы имеет вид f(λ) = (λ₀ − λ)^m и геометрическая кратность собственного значения λ₀ равна s.

Пример 1. Пусть m = 2, s = 1. Тогда

имеем одну жорданову клетку порядка 2.

Пример 2. Пусть m = 3, s = 1. Тогда

имеем одну жорданову клетку порядка 3.

Пример 3. Пусть m = 3, s = 2. Имеем жорданов блок, состоящий из двух жордановых клеток порядков 1 и 2:

1. Теорема о жордановой форме матрицы оператора

Пусть линейный оператор A действует в линейном пространстве над полем комплексных чисел размерности n и его характеристический многочлен имеет вид

f(λ) = (λ1 − λ)^m1(λ2 − λ)^m2. . .(λp − λ)^mp, где λ_j ≠ λ_k при j ≠ k,

m₁ + m₂ + · · · + m_p = n.

Тогда в этом пространстве существует базис, состоящий из собственных и присоединенных векторов оператора A, в котором матрица оператора имеет блочно-диагональную форму (она называется жордановой формой)

где A(λ_j ) — жорданов блок, соответствующий собственному значению λ_j. Указанный базис называется жордановым.

Сформулированная теорема верна и в случае, когда линейный оператор действует в линейном пространстве над произвольным числовым полем K, но все корни характеристического многочлена принадлежат полю K.

Рассмотрим примеры. Обозначаем через n размерность пространства, m_j и s_j — алгебраическую и геометрическую кратности собственного значения λ_j соответственно.

Пример 1. Пусть n = 2, λ₁ ≠ λ₂. Тогда матрица оператора может быть приведена к диагональному виду:

Пример 2. Пусть n = 3 и оператор имеет два различных собственных значения λ₁ (m₁ = 2, s₁ = 1) и λ₂ (m₂= s₂ = 1). Тогда матрица оператора может быть приведена к виду

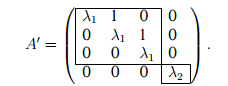
Пример 3. Пусть n = 4 и оператор имеет два различных собственных значения λ₁ (m₁ = 3, s₁ = 1) и λ₂ (m₂ = s₂ = 1). Тогда

3 Жорданов базис

Базис векторного пространства, в котором матрица оператора имеет вид одной сплошной ячейки, должен обладать свойством (“цикличность”), которое получим на основе правила “столбцы матрицы = образы базисных векторов”.

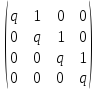
Итак, пусть матрица A линейного оператора в некотором базисе e₁,e₂,e₃,e₄   имеет вид одной ячейки: 

Здесь q обозначает некое, известное нам число.

Очевидно, векторы базиса e₁,e₂,e₃,e₄ можно записать в виде линейных комбинаций векторов этого же базиса. Так, например:

e₁ = 1e₁ + 0e₂+0e₃+ 0e₄ .

Это означает, что координаты вектора e₁ в этом базисе равны (1,0,0,0).

Если мы умножим нашу матрицу на столбец (1,0,0,0), то получим, очевидно, ее первый столбец, то есть (q,0,0,0). Это означает, что Ae₁= qe₁, то есть e₁– собственный вектор, q – собственное число.

Как нетрудно проверить, верно и обратное: если первый базисный вектор   является по совместительству собственным вектором оператора с собственным числом q, то первый столбец матрицы оператора в таком базисе равен (q,0,0,0).

Запишем равенство Ae₁= qe₁ в другом виде: (A- qE)e₁ = 0   или

Be₁ = 0 (где B = A – qE).

Теперь займемся вторым базисным вектором e₂. Его координаты равны (0,1,0,0). Умножив на столбец (0,1,0,0) нашу матрицу, мы получим в качестве результата ее второй столбец (1,q,0,0). Это означает, что

Ae₂= qe₂+ e₁        или      (A– qE) e₂ = e₁       или       Be₂ = e₁.

Точно так же получаются равенства

Be₃ = e₂    и    Be₄ = e₃.

В итоге мы приходим к выводу: если матрица оператора A в некотором базисе имеет вид Жордановой клетки (ячейки) с числом q на диагонали и с единичкам над ней, то векторы базиса превращаются друг в друга под воздействием оператора B=A-qE:

e₄ →e₃ →e₂ →e₁→0

В этой цепочке стрелки (слева направо) показывают, что из каждого базисного вектора получается под воздействием оператора B.

4 Построение жорданова базиса и жордановой формы матрицы

Пусть λ — собственное значение оператора, m и s — алгебраическая и геометрическая кратности числа λ. Опишем построение линейно независимой совокупности из m собственных и присоединенных векторов, отвечающих данному λ. Этой совокупности векторов в жордановой матрице A′ будет соответствовать жорданов блок A(λ).

Обозначим:

B = A − λI, B^k= (A − λI)^k, n_k = ker B^k, n_k = dim N_k, r_k = rang B^k.

Ясно, что n_k + r_k = n. Для удобства считаем, что B⁰ = I, так что r₀ = n, n₀ = 0.

Поскольку rang B^k+1 ≤ rang B^k, имеем n_k+1≥ n_k, так что

N₁ ⊂ N₂ ⊂ N₃ ⊂ . . . .

Теорема. Существует такое натуральное число q, что

N₁ ⊂ N₂ ⊂ · · · ⊂ N_q = N_q+1 = N_q+2 = . . . ,

т.е. все ядра с номером, большим, чем q, совпадают с ядром N_q. При этом

n₁ = s, n_q = m.

Построим часть жорданова базиса, соответствующую данному собственному значению λ, следующим образом.

1. Возводя матрицу B в последовательные натуральные степени, найдем показатель q, начиная с которого ранг степеней матрицы B перестает уменьшаться.

2. Рассмотрим ядра N_q и N_q-1. Пусть векторы f₁, f₂, · · · ∈ N_q достраивают произвольный базис пространства N_q-1 до базиса пространства N_q; их количество равно n_q –n_q-1. Эти векторы являются присоединенными векторами высоты q, и каждый из них порождает цепочку, состоящую из q векторов, которые войдут в состав жорданова базиса. Каждой такой цепочке будет соответствовать жорданова клетка порядка q; таким образом, в состав жордановой формы матрицы оператора A войдет n_q –n_q-1 жордановых клеток порядка q.

3. Рассмотрим ядра N_q-1 и N_q-2, а также векторы Bf₁, Bf₂ , · · · ; их количество равно

n_q –n_q-1 = (n – r_q) − (n – r_q-1) = r_q-1− r_q.

К этим векторам добавим векторы g₁, g₂, . . . из пространства N_q-1 так, чтобы система векторов

Bf₁, Bf₂, . . . , g₁, g₂, . . . ∈ N_q-1

дополняла произвольный базис ядра N_q-2 до базиса ядра N_q-1. Векторы g₁, g₂, . . являются присоединенными векторами высоты q −1, и каждому из них будет соответствовать, во-первых, цепочка векторов жорданова базиса, и во-вторых, жорданова клетка порядка q − 1. Количество добавляемых векторов g₁, g₂, . . равно

таким же будет количество жордановых клеток порядка q − 1.

4. Рассмотрим ядра N_q-2 и N_q-3 и векторы B²f₁, B²f₂, . . . , Bg₁, Bg₂, . . .К этим векторам (если их не хватает) добавим векторы h₁,h₂, . . . из пространства N_q–2 так, чтобы совокупность векторов

дополняла произвольный базис пространства N_q-3 до базиса пространства N_q-2. Количество добавляемых векторов h₁,h₂, . . . равно

таким же будет количество жордановых клеток порядка q − 2.

Процесс продолжаем аналогично. Наконец, рассмотрим ядро N₁ и векторы

Если эта система не образует базис пространства N₁, то добавим собственные векторы u₁, u₂, . . . так, чтобы пополненная система являлась базисом в N₁.

Итак, мы описали процесс построения жорданова базиса и выяснили, что количество жордановых клеток порядка k, входящих в состав жордановой формы матрицы оператора, может быть найдено по формуле

Построенную часть жорданова базиса, состоящую из m векторов, соответствующих данному λ (m — алгебраическая кратность этого собственного значения), запишем в таблицу («жорданова лестница»):

Все векторы таблицы линейно независимы, и их число равно m (алгебраической кратности собственного значения λ). Каждому столбцу этой таблицы соответствует одна жорданова клетка, порядок которой равен высоте столбца. Количество столбцов жордановой лестницы, т.е. полное количество жордановых клеток в блоке, соответствующем собственному значению λ, равно геометрической кратности s этого собственного значения.

Будем нумеровать векторы построенной части базиса по столбцам жордановой лестницы: внутри каждого столбца снизу вверх, а сами столбцы в произвольном порядке.

Например, пусть e₁, . . . , e_q — векторы первого столбца жордановой лестницы. Тогда

Этой группе векторов (собственный вектор e1 и присоединенные к нему векторы e₁, . . . , e_q) жорданова базиса соответствуют первые q столбцов матрицы A′, которые имеют вид

где J_q(λ) — жорданова клетка порядка q с числом λ на главной диагонали.

В следующих q столбцах матрицы A′, определенных векторами второго столбца жордановой лестницы, расположена жорданова клетка J_q(λ) так, что числа λ стоят на главной диагонали матрицы A′, а элементы вне клетки равны нулю. Подобным образом для данного λ получаем m столбцов матрицы A′. На этих m столбцах находится жорданов блок A(λ).

Для других собственных значений эта схема повторяется, в результате чего получим жорданову матрицу A′ и соответствующий жорданов базис.

4.1 Пример решения задач

Дана матрица A линейного оператора в некотором базисе. Требуется найти жорданов базис и жорданову форму матрицы оператора в этом жордановом базисе. Рассмотрим пример решения такой задачи методом построения жорданова базиса.

Характеристический многочлен

имеет корень λ = 2 кратности 3, т.е. m = 3. Матрица B = A − λI равна

Легко проверить, что

Собственные векторы находим, решив однородную систему линейных уравнений BX = O; фундаментальная совокупность решений состоит из двух векторов, например,

Количество этих векторов (т.е. геометрическая кратность собственного значения) равно двум, s = 2, так что для построения жорданова базиса требуется еще один присоединенный вектор.

Так как B² = O, то ядро N₂ оператора B² совпадает со всем пространством, т.е. n₂ = 3, и при этом q = 2.

Дополним базис ядра N₁, т.е. набор векторов (2), до базиса ядра N₂, например, вектором

Тогда

Дополним вектор Bf₁ до базиса пространства N₁ вектором

Построим жорданову лестницу:

Жорданов базис:

соответствует жорданова клетка порядка 2,

соответствует жорданова клетка порядка 1.

При этом Be₁ = 0, Be₂ = e­1, Be₃ = 0, т.е. e₁ — собственный вектор, e₂ — его присоединенный вектор, e₃ — собственный вектор.

В жордановом базисе

матрица оператора A′ имеет вид

Список использованной литературы:

1. В.В. Колыбасова, Н.Ч. Крутицкая, А.В. Овчинников «Жорданова форма матрицы оператора» (интернет ресурс).

2. В.И. Сушков «Строим Жорданову башню: снизу вверх и сверху вниз» (интернет ресурс).

3. А. Г. Курош «Курс Высшей Алгебры».

5

Пусть – линейный оператор, – все его собственные значения с кратностями равными соответственно , – соответствующие корневые подпространства, – индуцированнный нильпотентный оператор Ai на инвариантном корневом подпространстве Ri.

Определение 6: Жордановым базисом пространства V для оператора *** называется объединение жордановых базисов корневых подпространств Ri построенных для Ai.

Имеем: , где .

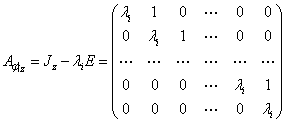
Фиксируем циклическое подпространство и рассмотрим индуцированный линейный оператор на инвариантном подпространстве Z. Так как , то φ(Z) < Z – инварантное подпространство. Найдем матрицу оператора в циклическом базисе Z: , это квадратичная матрица, ее порядок равен dim Z = H. Эта матрица называется жордановой клеткой порядка H для собственного значения λI. Если , то эту матрицу обозначим . Размер жордановой клетки . Так как , то матрица A линейного оператора φ в базисе подпространства Ri имеет вид: , тогда матрица линейного оператора φ в жордановом базисе V имет вид: (5).

Таким образом, доказано следующее утверждение.

Утверждение 2: матрица линейного оператора в жордановом базисе – клеточно-диагональная. На ее диагонали располагаются жордановы клетки размеров, равных размерам циклических подпространств, на которые распадаются корневые подпространства соответствующие собственным значениям оператора φ.

Определение 7: матрицу вида (5), описанную в Утверждении 2 называют жордановой матрицей. Нахождение матрицы линейного оператора φ в его жордановом базисе назвается приведением матрицы оператора φ к жордановой нормальной форме.

Теорема 3 (Жордана):

Для любого линейного оператора , имеющего собственные значения с кратностями существует базис, в котором матрица Aφ имеет жорданову нормальную формулу J. При этом жорданова нормальная форма J однозначно определена для оператора φ с точностью до порядка расположения диагональных клеток.

Доказательство: возьмем жорданов базис в пространстве V. По Утверждению 2 матрица Aφ оператора φ имеет в этом базисе жорданову нормальную форму. Докажем единственность J.Для построения J нужны корни характеристического уравнения с кратностями . Кроме того нужны размерности циклических подпространств. Характеристический многочлен – инвариант. Размерности циклических подпространств по Теореме 2 определяются однозначно. Следовательно J – единственно (с точностью до порядка расположения диагональных клеток). #

Построение жорданова базиса и жордановой нормальной формы J линейного оператора φ, заданного матрицей A.

1) находим корни характеристического ур-я и их кратности.

2) Для каждого составляем матрицу и вычисляем rang, если rang>, товычисляем , и т. д., пока не найдется минимальная степень такая, что rang=.

3) Рассмотрим столбцы, в которых расположен базисный минор матрицы . Их линейная оболочка очевидно есть Im. Найдем подпространство =Im∩Ker. В находим базис – это те с. в-ры, с которых начинаются жордановы цепочки максимальной длины, равной , если общее число в-в в этих цепочках равно , по процесс прекращается. Если же длина цепочек <, то рассматриваем = Im∩Ker и дополняем уже выбранные векторы (из ) до базиса . Вновь добавленные с. в-ры служат началом жорданновых цепочек максимальной длины . Если общая длина цепочек <, то продолжаем построение новых с. в-ор из (дадут цепочки длиной ). И так далее, пока общая длина цепочек не окажется равной .

4) Жорданов базис получается при объединении жордановых базисов корневых подпространств.

5) Жорданова нормальная форма J матрицы A имеет клеточно-диагональный вид и может быть выписана непосредственно или получена по формуле , где T– матрица перехода от исходного базиса (E) к жорданову базису. В столбцах матр. T Стоят коорд. базис. в-в жорданова базиса.

Замечание:

Последовательно присоединенные к векторы находятся, как решения сист. лин. ур-ий вида: , где .

< Предыдущая		Следующая >