Как найти жорданову форму матрицы онлайн - Сайт, где вы сможете решить свои вопросы

Пусть дана матрица
3-го порядка. Надо найти жорданову форму
и жорданов базис.

Пусть
характеристический многочлен матрицы

имеет вид

,
где

Тогда
жорданова форма матрицы имеет вид

.

Пусть
характеристический многочлен матрицы

имеет вид

где

.
Возможны два случая:

а)

,
поэтому

и, следовательно,

,
поэтому жорданова форма содержит две
жордановы клетки с собственным значением

;

б)

,
поэтому

и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением

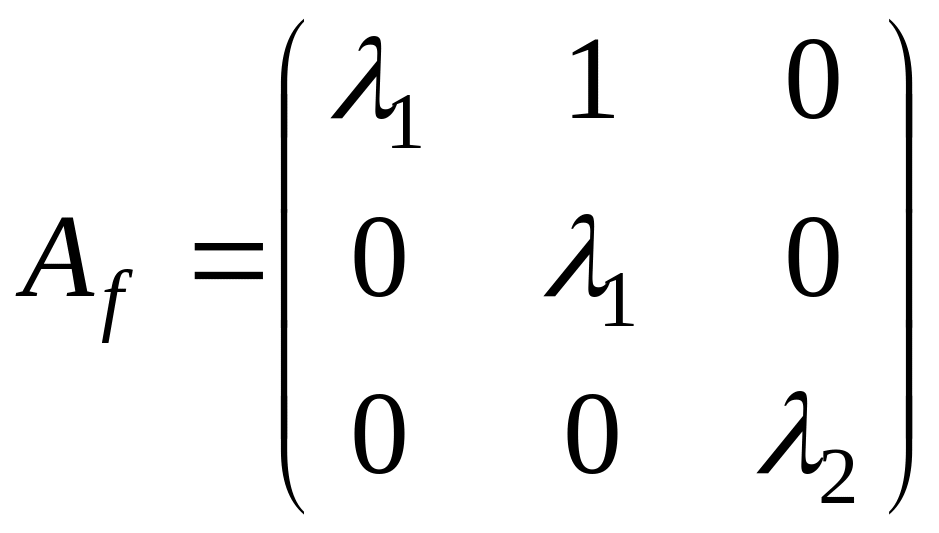
Пусть
характеристический многочлен матрицы

имеет вид

Возможны два
случая:

а)

,
поэтому

и, следовательно, жорданова форма
содержит две жордановы клетки с
собственным значением

;

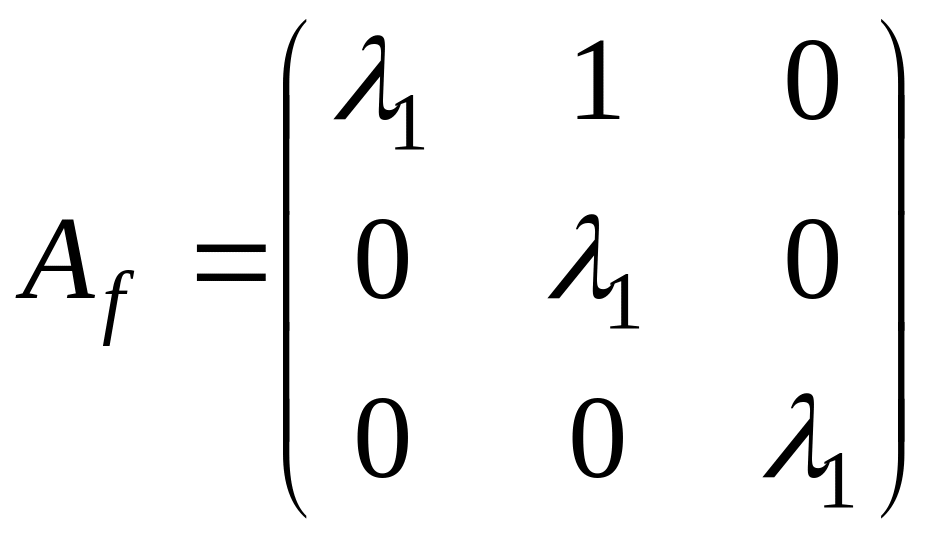
б)

,
поэтому

и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением

Задача.
Дана матрица

.
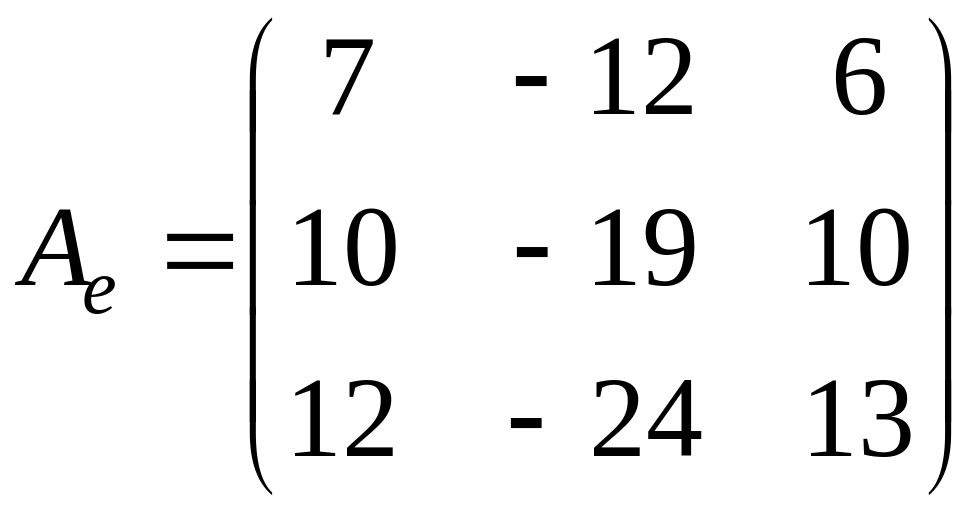
Найти

.

Р е ш е
н и е.

Найдем характеристический многочлен
матрицы:

Жорданова
форма матрицы

имеет вид

.

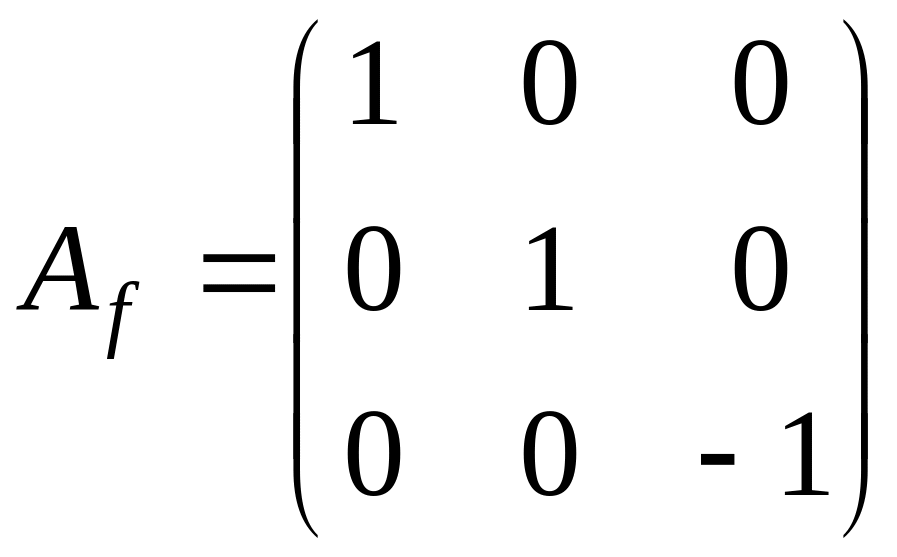
Найдем

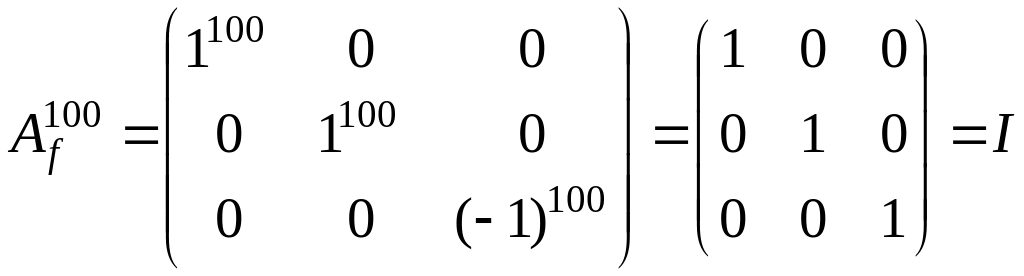
Для
нахождения

воспользуемся формулой

,
где

– матрица перехода от базиса

к базису

.
Очевидно, что

поэтому

Пример
1. Найти жорданову форму и жорданов
базис матрицы оператора

Р е ш е
н и е.

Вычислим

следовательно,
собственное значение

,

Найдем
геометрическую кратность собственного
значения

.
Для этого посчитаем ранг матрицы

Следовательно,

поэтому
жорданова форма имеет вид

или

.

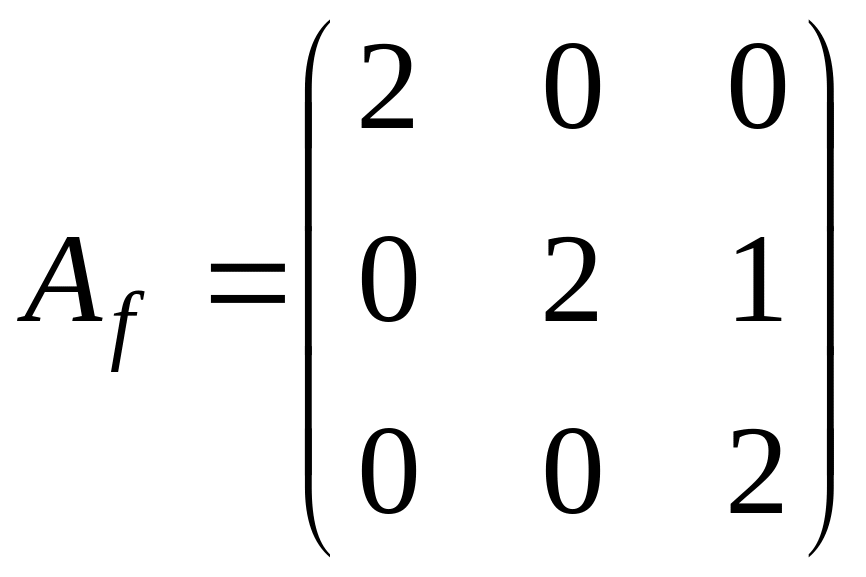
Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он удовлетворяет условию

то
решим систему

Следовательно,
координаты собственного вектора

удовлетворяют уравнению

Заметим, что коэффициент при

равен 0, поэтому

может принимать любые значения.
Отбрасывать

нельзя !!!

Для
нахождения ФСР построим таблицу

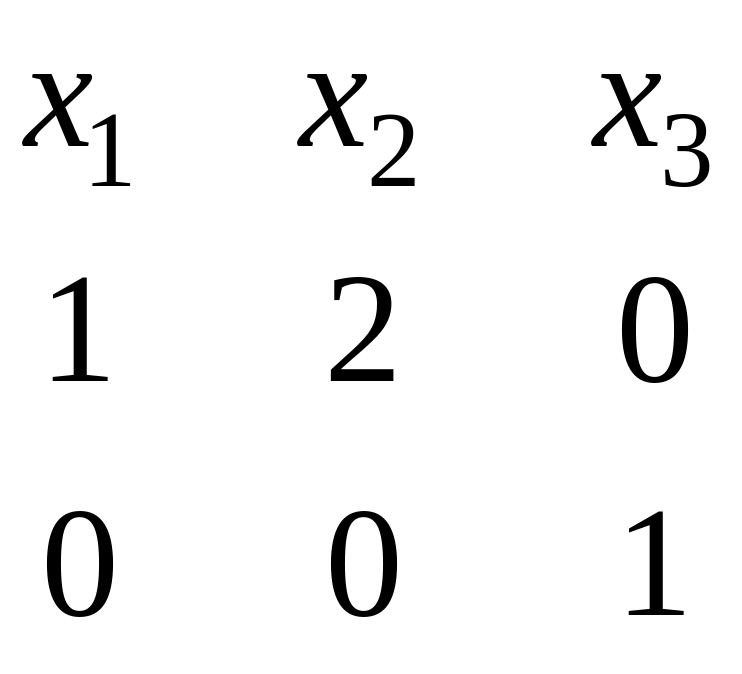
Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается и,
следовательно, имеет вид

.
Так как

,

,
то должен быть один присоединенный
вектор, который будет являться решением
системы

.
Подберем коэффициенты

таким образом, чтобы система

была совместна. Так как

то для
совместности системы необходимо, чтобы
выполнялось условие

.
Возьмем

,
тогда

,
и координаты присоединенного вектора
являются решением системы

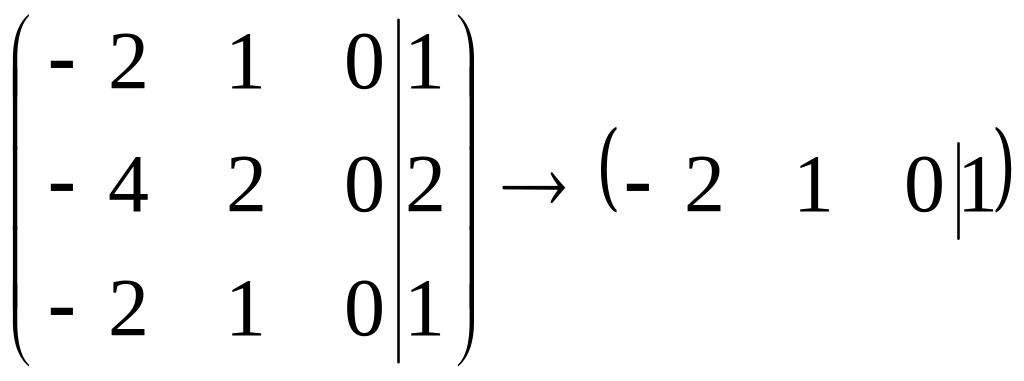
то есть
удовлетворяют уравнению

или

.

Возьмем

Таким образом, у нас есть собственный
вектор

,
присоединенный к нему

и нужен еще один собственный вектор,
отвечающий собственному значению

.
Можно взять или вектор

,
или

,
или любой другой, отличный от

,
отвечающий собственному значению

.
Эти три вектора и будут образовывать
жорданов базис.

Пример 2. Найти жорданову
форму и жорданов базис матрицы оператора

Р е ш е
н и е.

Вычислим

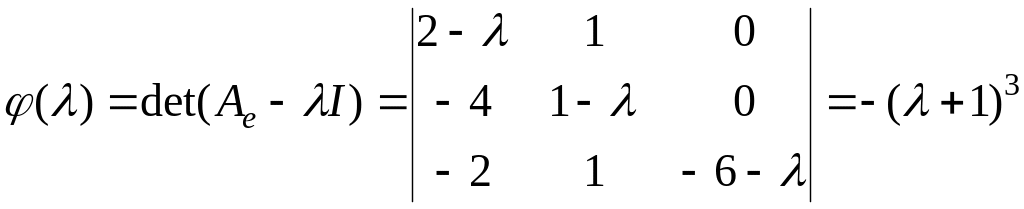
следовательно,
собственное значение

,

Найдем
геометрическую кратность собственного
значения

.
Для этого посчитаем ранг матрицы

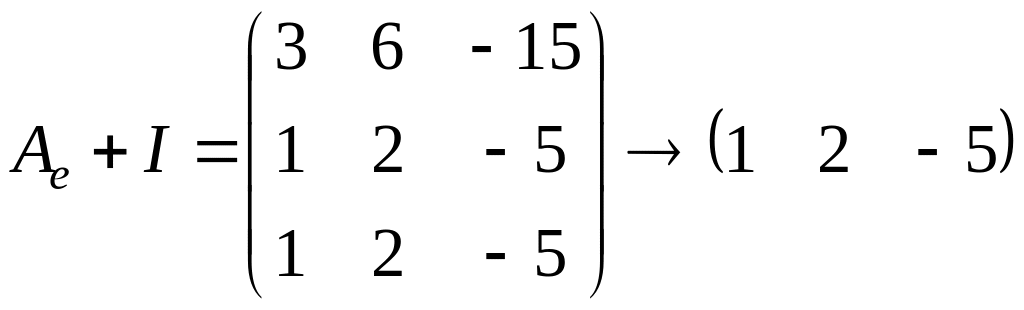
Следовательно,

поэтому
жорданова форма имеет вид

или

.

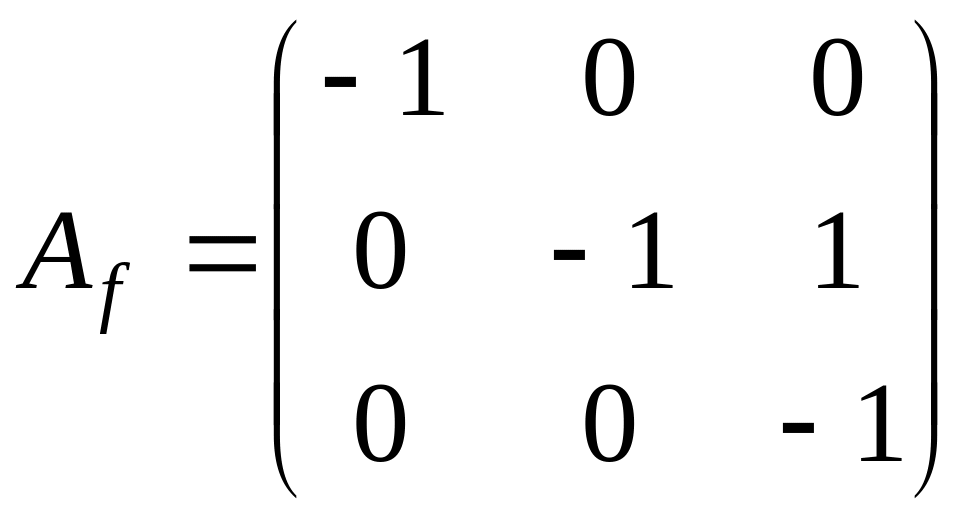
Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он удовлетворяет условию

то
решим систему

Очевидно,
что координаты собственного вектора

удовлетворяют уравнению

или

.

Для
нахождения ФСР построим таблицу

Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается
и, следовательно, имеет вид

Так как

,
то должен быть один присоединенный
вектор, который будет являться решением
системы

.
Подберем коэффициенты

таким образом, чтобы система

была совместна. Так как

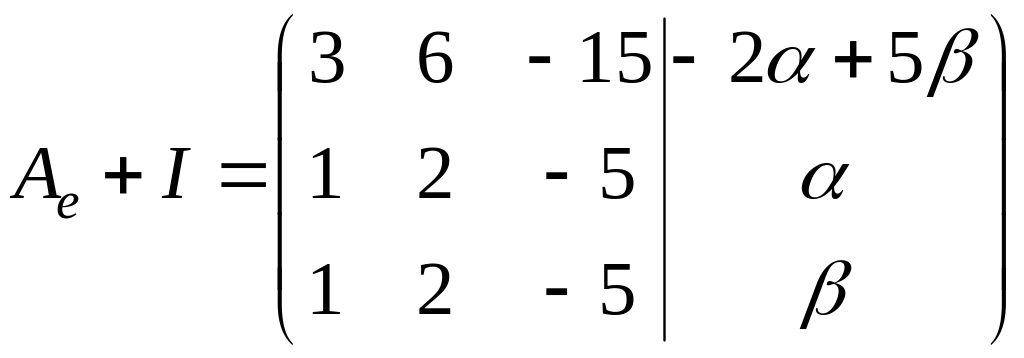
то для
совместности системы необходимо, чтобы
выполнялось условие

.
Возьмем

,
тогда

и координаты присоединенного вектора
являются решением системы

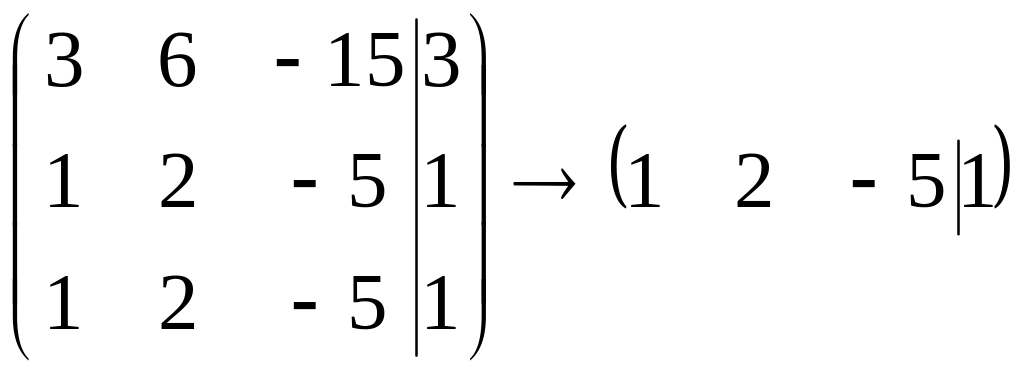
то есть
удовлетворяют уравнению

или

.

Возьмем

Таким образом, у нас есть собственный
вектор

,
присоединенный к нему

и нужен еще один собственный вектор,
отвечающий собственному значению

.
Можно взять или вектор

,
или

,
или любой другой, отличный от

,
отвечающий собственному значению

.
Эти три вектора и будут образовывать
жорданов базис.

Пример 3. Найти жорданову
форму и жорданов базис матрицы оператора

Р е ш е
н и е.

Вычислим

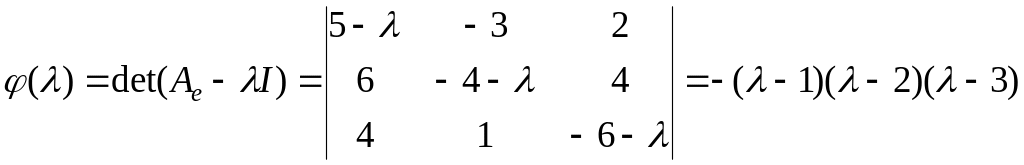
Таким образом, получили три собственных
значения

,

,

.
Так как алгебраическая кратность каждого
из них равна 1, то жорданова форма имеет
следующий вид

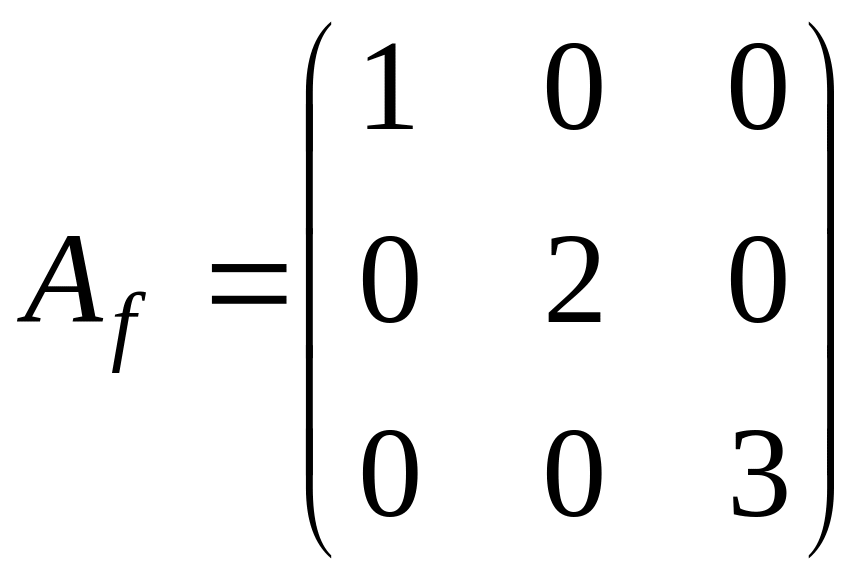
Найдем собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он является решением
уравнения

и, следовательно, его координаты
удовлетворяют системе

то есть

,
поэтому можем взять

.

Вычислим собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он удовлетворяет уравнению

,
а его координаты – системе

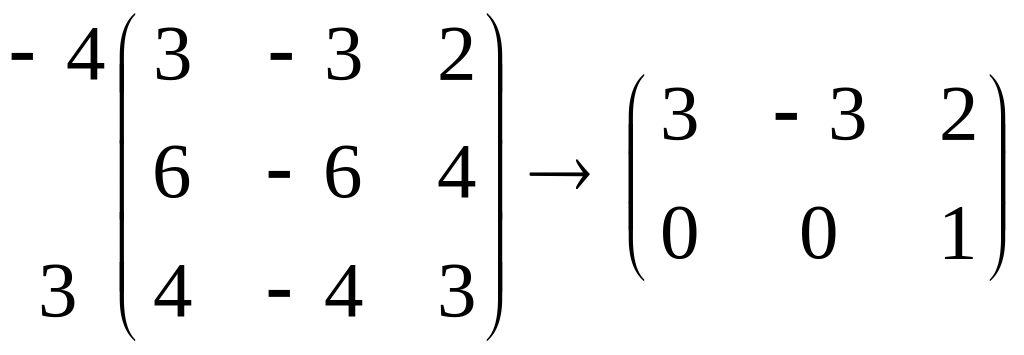
откуда
следует, что

,
поэтому можем взять

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он является решением уравнения

,
то его координаты удовлетворяют системе

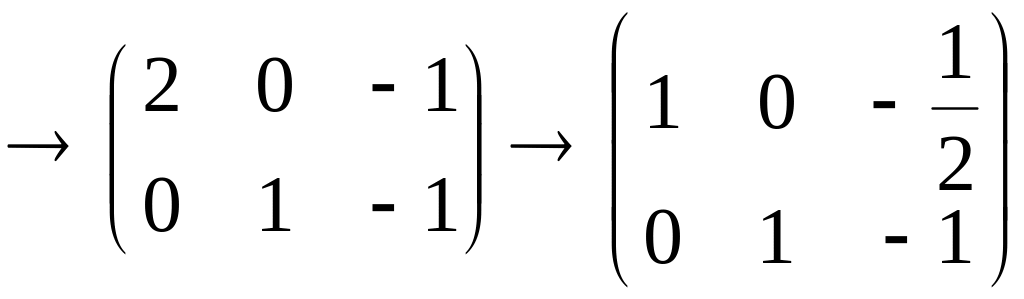
и,
следовательно,

,
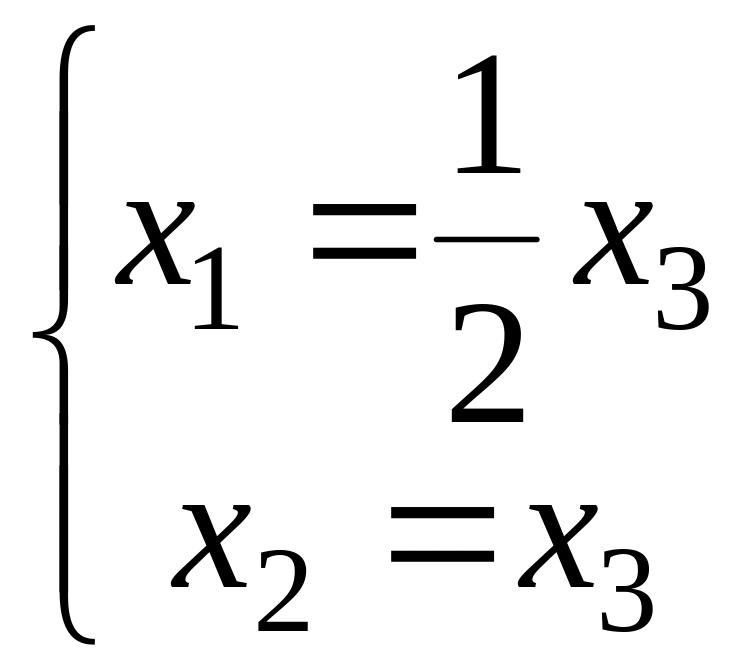
поэтому можем взять

.

Векторы

образуют жорданов базис матрицы.

Пример 4. Найти жорданову
форму и жорданов базис матрицы оператора

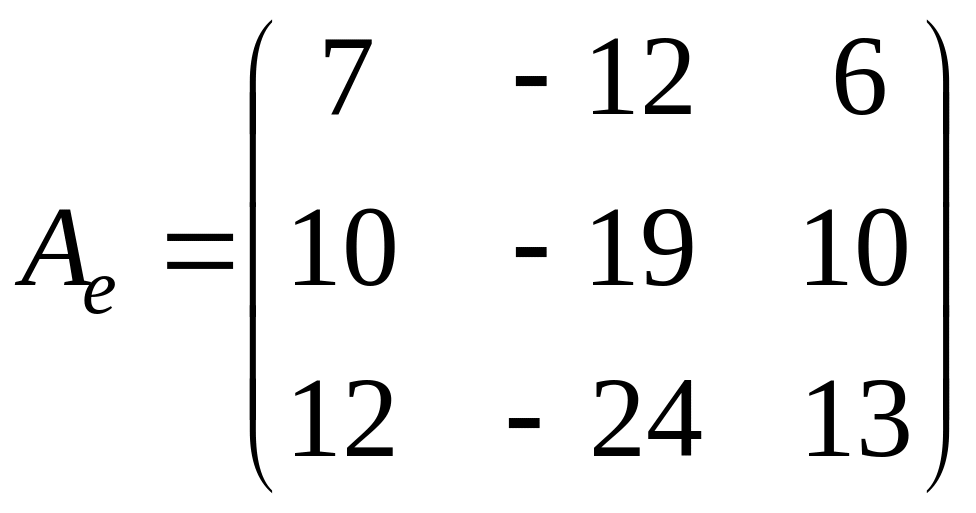
Р е ш е
н и е.

Вычислим

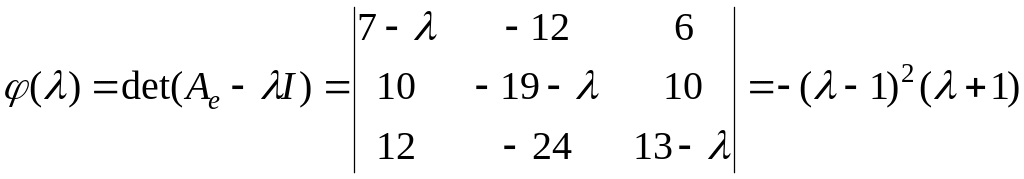
Таким образом, получили два собственных
значения

,

.
Так как алгебраическая кратность

равна 2, нужно вычислить геометрическую
кратность

собственного значения

.
Для этого посчитаем ранг матрицы

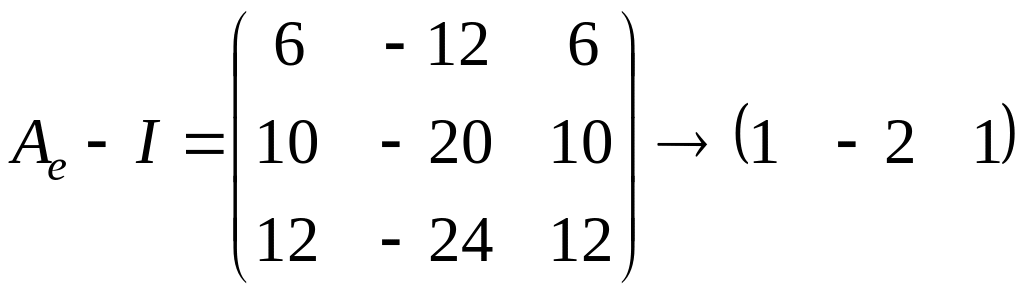
Очевидно, что

,
поэтому

и, следовательно, жорданова форма имеет
следующий вид

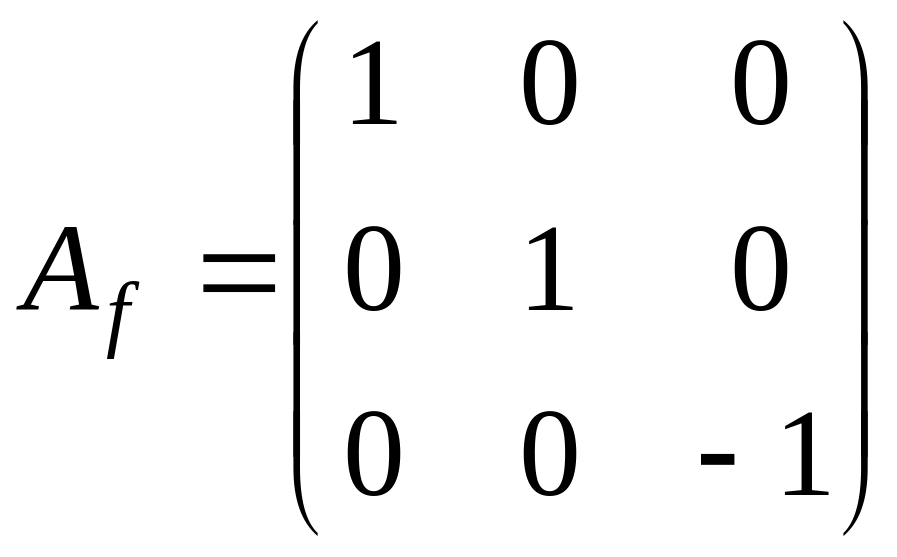
Найдем собственные векторы

,
соответствующие собственному значению

.
Очевидно, что они являются решением
уравнения

,
а их координаты

– решением системы

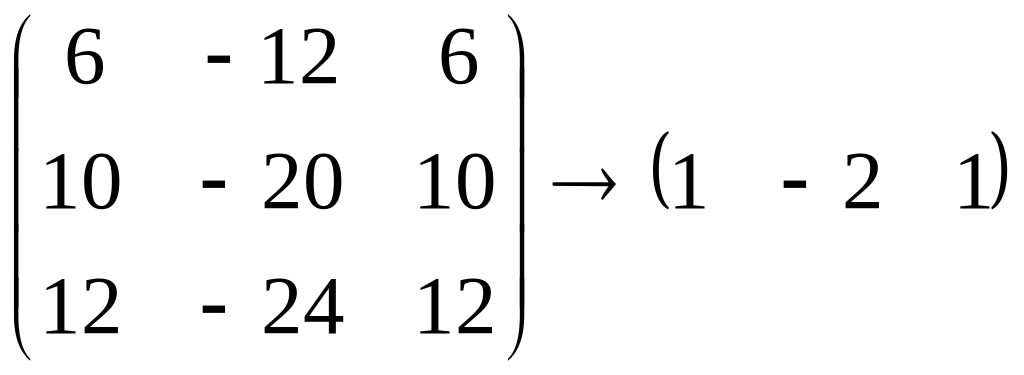
и,
следовательно, удовлетворяют уравнению

или

.

Для
нахождения ФСР построим таблицу

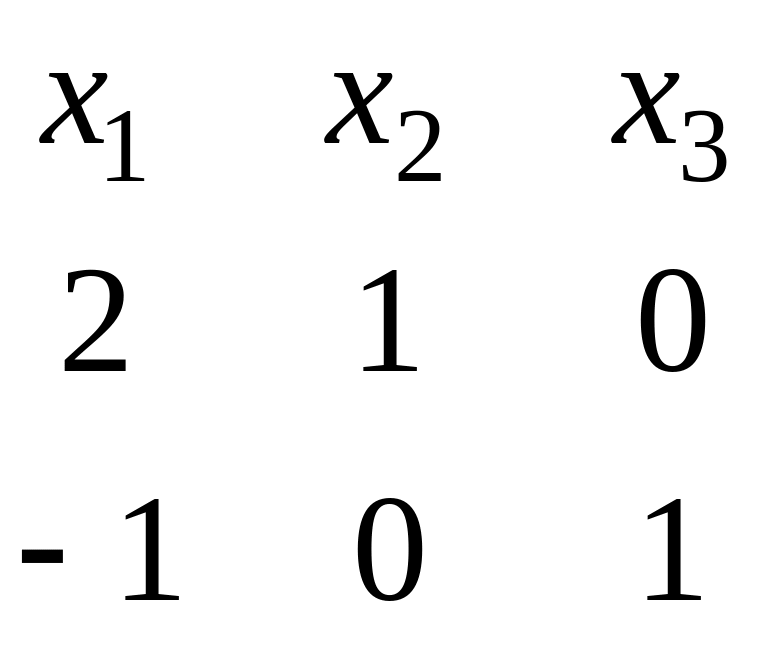
Векторы

образуют фундаментальную систему
решений в собственном подпространстве

Так
как

,
то нужно выбрать любые два линейно
независимых вектора из этой линейной
комбинации. Возьмем

,

Найдем собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он удовлетворяет уравнению

,
а его координаты

– системе

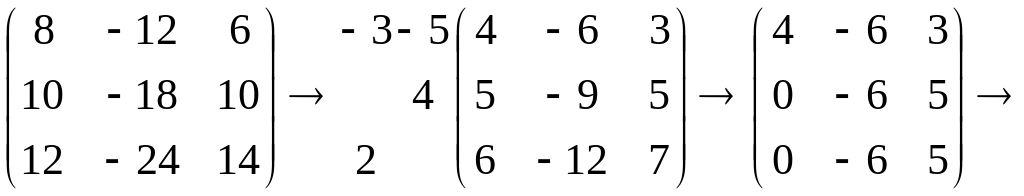
то есть

,
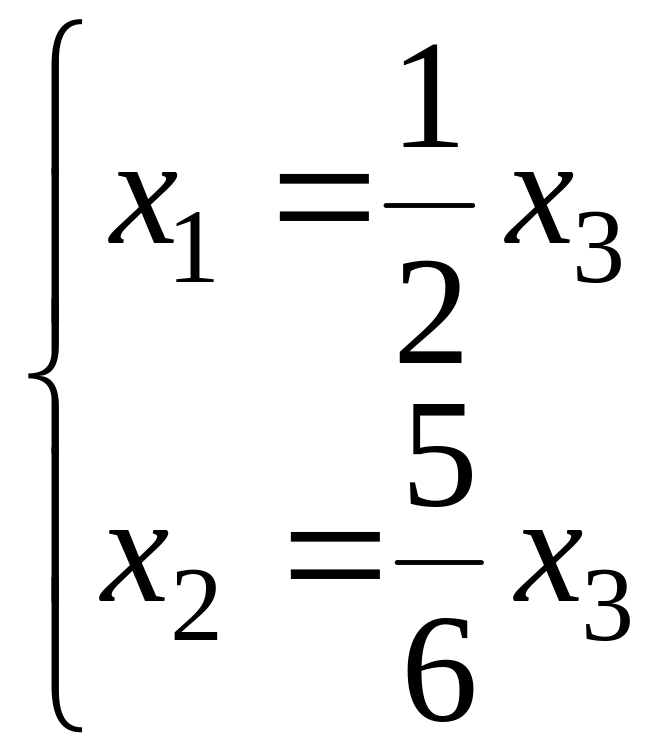
поэтому можем взять

.

Векторы

образуют жорданов базис матрицы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Radians}	mathrm{Degrees}	square!	(	)	%	mathrm{clear}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Subscribe to verify your answer

Number Line

Examples

gauss:jordan:begin{pmatrix}1 & 2 \3 & 4end{pmatrix}
gauss:jordan:begin{pmatrix}1 & 2 & 3 \4 & 5 & 6 \7 & 8 & 9end{pmatrix}
gauss:jordan:begin{pmatrix}1 & 3 & 5 & 9 \1 & 3 & 1 & 7 \4 & 3 & 9 & 7 \5 & 2 & 0 & 9end{pmatrix}

Description

Reduce matrix to Gauss Jordan (RREF) form step-by-step

matrix-gauss-jordan-calculator

Приведение матрицы к жордановой форме

Задача приведения матрицы к жордановой форме формулируется следующим образом. Требуется привести квадратную матрицу к жордановой форме J_A при помощи преобразования подобия: $J_A=S^{-1}AS$ , т.е.

найти жорданову форму J_A квадратной матрицы {первый этап);

найти преобразующую матрицу (второй этап), для которой

$J_A=S^{-1}cdot Acdot S.$

(7.39)

В некоторых прикладных и теоретических задачах достаточно определить только жорданову форму матрицы, т.е. ограничиться первым этапом. Однако чаще кроме жордановой формы J_A матрицы требуется также найти и преобразующую матрицу , т.е. выполнить оба этапа.

Нахождение жордановой формы матрицы

Для нахождения жордановой формы J_A квадратной матрицы нужно выполнить следующие действия (см. лекцию жордановой форме).

1. Составить характеристическую матрицу (A-lambda E) .

2. Найти ее инвариантные множители (7.33) одним из способов, рассмотренных в предыдущей лекции.

3. По инвариантным множителям (7.33) составить таблицу (7.34) элементарных делителей.

4. По элементарным делителям составить жорданову форму J_A .

Нахождение преобразующей матрицы

Рассмотрим два способа нахождения преобразующей матрицы.

Первый способ. Если жорданова форма J_A матрицы известна, то для нахождения преобразующей матрицы нужно выполнить следующие действия.

1. Составить матричное уравнение SJ_A=AS относительно неизвестной матрицы , которое равносильно однородной системе n^2 линейных уравнении с n^2 неизвестными элементами $s_{ij}$ матрицы .

2. Найти такое частное решение этой системы уравнений, для которого det{S}ne0 .

Второй способ. Для нахождения преобразующей матрицы можно использовать следствие теоремы 7.7.

1. Составить блочную λ-матрицу (A-lambda Emid E) , приписав к характеристической матрице (A-lambda E) единичную матрицу того же порядка. При помощи элементарных преобразований, выполняемых над строками и столбцами блочной матрицы, привести ее левый блок к нормальному диагональному виду (7.9). При этом блочная матрица преобразуется к виду $begin{pmatrix}Lambda(lambda)!!&vline!!&S_A(lambda)end{pmatrix}$ , где $Lambda(lambda)=operatorname{diag}(e_1(lambda),ldots,e_n(lambda))$ — матрица нормального диагонального вида, эквивалентная матрице (A-lambda E) , a — некоторая элементарная λ-матрица.

2. Составить блочную λ-матрицу (J_A-lambda Emid E) , приписав к характеристической матрице (J_A-lambda E) единичную матрицу того же порядка. При помощи элементарных преобразований, выполняемых над строками и столбцами блочной матрицы, привести ее левый блок к нормальному диагональному виду (7.9). При этом блочная матрица преобразуется к виду $begin{pmatrix}Lambda(lambda)!!&vline!!&S_J(lambda)end{pmatrix}$ , где $Lambda(lambda)=operatorname{diag}(e_1(lambda),ldots,e_n(lambda))$ -такая же матрица, что и в пункте 1, а — некоторая элементарная λ-матрица.

3. Найти λ-матрицу $S(lambda)=S_J^{-1}(lambda)cdot S_A(lambda)$ .

4. Вычислить левое значение $S_{text{left}}(J_A)$ при замене переменной lambda матрицей J_A .

5. Найти преобразующую матрицу , обращая матрицу $S_{text{left}}(J_A)colon~ S=[S_{text{left}}(J_A)]^{-1}$ .

Действительно, при помощи элементарных преобразований характеристические матрицы (A-lambda E) и (J_A-lambda E) приводятся к одному и тому же нормальному диагональному виду Lambda(lambda):

S_J(lambda)cdot (J_1-lambda E)cdot T_J(lambda)= Lambda(lambda)= S_A(lambda)cdot (A-lambda E)cdot T_A(lambda).

Отсюда $J_A-lambda E=S_J^{-1}(lambda)S_A(lambda)(A-lambda E)T_A(lambda)T_J^{-1}(lambda)$ , то есть

J_A-lambda E=S(lambda)cdot (A-lambda E)cdot T(lambda), где $S(lambda)=S_J^{-1}(lambda) S_A(lambda),~ T(lambda)=T_A(lambda)T_J^{-1}(lambda).$

Согласно следствию теоремы j? 7.6, преобразующая числовая матрица $S=[S_{text{left}}(J_A)]^{-1}$ , т.е. — это матрица, /Обратная к левому значению λ-матрицы $S_{text{left}}(J_A)$ при подстановке вместо lambda матрицы J_A .

Замечания 7.7.

1. Несмотря на простоту, первый способ мало пригоден из-за большого Объема вычислений. Количество решаемых уравнений n^2 .

2.Второй способ позволяет полностью решить задачу приведения матрицы к жордановой форме. Выполняя пункт 1, находим нормальный диагональный вид $Delta(lambda)= operatorname{diag}(e_1(lambda),ldots,e_n(lambda))$ характеристической матрицы (A-lambda E) , и, как следствие, ее инвариантные множители . Тогда выполняя пункты 3, 4 алгоритма нахождения жордановой формы, получим жорданову форму J_A матрицы . Далее выполняем пункты 2, 3 второго способа и находим преобразующую матрицу.

3. В пунктах 1,2 второго способа λ-матрицы, стоящие в левых блоках матриц (A-lambda Emid E) и (J_A-lambda Emid E) , приводятся к нормальному диагональному виду при помощи элементарных преобразований над строками и над столбцами. При этом правые блоки этих матриц “учитывают” только преобразования строк, в отличие от алгоритма, описанного в пункте 5 замечаний 7.4.

4. Преобразующая матрица в (7.39) определяется неоднозначно. В самом деле, если — преобразующая матрица, а — невырожденная матрица, перестановочная с (AM=MA) , то матрица T=MS будет также преобразующей. Действительно, матрица — обратимая и

$T^{-1}cdot Acdot T= S^{-1}cdot M^{-1}cdot Acdot Mcdot S= S^{-1}cdot M^{-1}cdot Mcdot Acdot S=S^{-1}cdot Acdot S=J_A.$

Первый способ нахождения преобразующей матрицы, вообще говоря, позволяет найти все такие матрицы, перебирая в пункте 2 подходящие частные решения однородной системы. Второй способ позволяет найти одну преобразующую матрицу из этого множества. Как правило, на практике достаточно найти хотя бы одну преобразующую матрицу.

5. Задачу приведения матрицы к диагональному виду можно считать частным случаем задачи приведения матрицы к жордановой форме. Если квадратная матрица n-го порядка имеет линейно независимых собственных векторов, то, как это следует из теоремы 7.5, ее жорданова форма J_A является диагональной матрицей (с собственными значениями на главной диагонали), а преобразующая матрица может быть составлена из линейно независимых собственных векторов матрицы .

Пример 7.15. Привести к жордановой форме следующие матрицы:

$A=begin{pmatrix}4&4\ -1&0 end{pmatrix}!;quad B=begin{pmatrix} 1&0&1\ 0&1&-1 end{pmatrix}!;quad C=begin{pmatrix} 1&1&1\ 1&1&1\ 1&1&1 end{pmatrix}!;quad D=begin{pmatrix} -2&5&-3\ -2&5&-3\ 1&-1&0 end{pmatrix}!.$

Решение для матрицы A

Первый этап — нахождение жордановой формы матрицы .

1. Составляем характеристическую матрицу $A-lambda E= begin{pmatrix}4-lambda&4\ -1&-lambdaend{pmatrix}$ .

2. Инвариантные множители будем искать по формуле (7.11). Записываем миноры 1-го порядка: $M_{{}_1}^{{}^1}=4-lambda,$ $M_{{}_2}^{{}^1}=4,$ $M_{{}_1}^{{}^2}=-1,$ $M_{{}_2}^{{}^2}=-lambda$ . Находим наибольший общий делитель этих многочленов: d_1(lambda)=1 . Минор второго порядка равен определителю характеристической матрицы $M_{{}_{1,2}}^{{}^{1,2}}= begin{vmatrix}4-lambda&4\ -1&-lambda end{vmatrix}=(lambda-2)^2$ . Следовательно, d_2(lambda)=(lambda-2)^2 . Таким образом, по формуле (7.11) получаем

$e_1(lambda)=d_1(lambda)=1,qquad e_2(lambda)=frac{d_2(lambda)}{d_1(lambda)}= (lambda-2)^2.$

3. По инвариантным множителям составляем таблицу (7.34) элемен тарных делителей. Так как собственное значение матрицы единственное (lambda_1=2) , то таблица (7.34) состоит из одной строки (и одного столбца): (lambda-2)^2 .

4. Единственному элементарному делителю (lambda-2)^2 соответствует од на жорданова клетка 2-го порядка, образующая жорданову форму матрицы $Acolon~ J_A= begin{pmatrix}2&1\0&2end{pmatrix}$ .

Второй этап — нахождение преобразующей матрицы. Воспользуемся первым способом.

1. Составляем матричное уравнение $SJ_A=AS~Rightarrow, begin{pmatrix}x&y\z&w end{pmatrix}!cdot! begin{pmatrix}2&1\0&2end{pmatrix}= begin{pmatrix}4&4\-1&0end{pmatrix} !cdot! begin{pmatrix}x&y\z&wend{pmatrix}$ . Перемножая матрицы, получаем однородную систему уравнений относительно элементов искомой матрицы $S=begin{pmatrix}x&y\ z&wend{pmatrix}colon$

$begin{cases} 2x=4x+4z,\ 2z=-x,\x+2y=4y+4w,\ z+2w=-y,end{cases}Leftrightarrowquad begin{cases} 2x+4z=0,\ x+2z=0,\ x-2y-4w=0,\ y+z+2w=0.end{cases}$

2. Решаем эту систему. Расширенную матрицу системы приводим к ступенчатому, а затем к упрощенному виду:

$begin{pmatrix}2&0&4&0!!&vline!!&0\ 1&0&2&0!!&vline!!&0\ 1&-2&0&-4!!&vline!!&0\ 0&1&1&2!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&0&2& 0!!&vline!!&0\ 0&0&0&0!!&vline!!&0\ 0&-2&-2&-4!!&vline!!&0\ 0&1&1& 2!!&vline!!&0 end{pmatrix}sim begin{pmatrix}1&0&2&0!!&vline!!&0\ 0&1&1&2!!& vline!!&0\ 0&0&0&0!!&vline!!&0\ 0&0&0&0!!&vline!!&0 end{pmatrix}sim begin{pmatrix} E_2!!&vline!!&A'!!&vline!!&o\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!,$

где $A'=begin{pmatrix}2&0\1&2end{pmatrix}$ . Находим фундаментальную матрицу Phi и общее решение:

$Phi=begin{pmatrix}dfrac{-A'}{E_2}end{pmatrix}=begin{pmatrix}-2&0\-1&-2\hline 1&0\0&1end{pmatrix}!,quad begin{pmatrix}x\y\z\wend{pmatrix}=C_1cdot! begin{pmatrix}-2\-1\1\0end{pmatrix}+ C_2cdot! begin{pmatrix}0\-2\0\1end{pmatrix}!,$ где C_1,,C_2 — произвольные постоянные.

Следовательно, любая преобразующая матрица имеет вид

$S=begin{pmatrix}x&y\z&wend{pmatrix}= begin{pmatrix}-2C_1&-C_1-2C_2\ C_1&C_2 end{pmatrix}!,$

где C_1,,C_2 — произвольные постоянные, но C_1ne0 , так как матрица невырожденная:

$det{S}=-2C_1cdot C_2+C_1^2+2C_1cdot C_2=C_1^2ne0.$

Например, при C_1=-1,~ C_2=0 получаем $S=begin{pmatrix}2&1\-1&0 end{pmatrix}$ .

Используем второй способ нахождения преобразующей матрицы.

Составляем блочную матрицу: $(A-lambda Emid E)= begin{pmatrix}4-lambda&4!!&vline!!&1&0\ -1&-lambda!!& vline!!&0&1end{pmatrix}$ . При помощи элементарных преобразований, выполняемых над строками и над столбцами этой блочной матрицы, приводим левый блок к нормальному диагональному виду. Меняем местами строки и умножаем первую строку на (-l). Выбрав ведущий элемент, равный единице, делаем равными нулю остальные элементы в первом столбце и в первой строке левого блока:

$begin{pmatrix}4-lambda&4!!&vline!!&1&0\ -1&-lambda!!& vline!!&0&1 end{pmatrix}sim begin{pmatrix}1&lambda !!&vline!!&0&-1\ 4-lambda&4!!& vline!!&1&0 end{pmatrix}sim begin{pmatrix}1&0 !!&vline!!&0&-1\ 0&(lambda-2)^2!!& vline!!&1&4-lambdaend{pmatrix}!.$ Следовательно, $S_{A}(lambda)=begin{pmatrix}0&-1\ 1&4-lambdaend{pmatrix}!.$

2. Составляем блочную матрицу и приводим левый блок этой матрицы к нормальному диагональному виду

$begin{pmatrix}J_A-lambda E!!&vline!!&Eend{pmatrix}!=! begin{pmatrix}2-lambda&1!!&vline!!&1&0\ 0&2-lambda!!& vline!!&0&1end{pmatrix}!sim! begin{pmatrix} 1&2-lambda!!&vline!!&1&0\ 2-lambda&0!!& vline!!&0&1end{pmatrix}!sim! begin{pmatrix} 1&lambda-2!!&vline!!&1&0\ 2-lambda&0!!& vline!!&0&1end{pmatrix}!sim! begin{pmatrix} 1&0!!&vline!!&1&0\ 0&(lambda-2)^2!!& vline!! lambda-20&1end{pmatrix}!.$

Следовательно, $S_J(lambda)=begin{pmatrix}1&0\ lambda-2&1end{pmatrix}$ .

3. Обращаем матрицу $S_J^{-1}(lambda)=frac{1}{det{S_J(lambda)}}cdot S_J^{+}(lambda)= frac{1}{1}cdot! begin{pmatrix}1&0\2-lambda&1end{pmatrix}$ . Находим λ-матрицу, которая оказалась не зависящей от lambda:

$S(lambda)=S_J^{-1}(lambda)cdot S_A(lambda)= begin{pmatrix}1&0\ 2-lambda&1 end{pmatrix}!cdot! begin{pmatrix}0&-1\1&4-lambda end{pmatrix}= begin{pmatrix}0&-1\1&2 end{pmatrix}!.$

4. Так как λ-матрица S(lambda) оказалась числовой, то $S_{text{left}}(J_A)=begin{pmatrix} 0&-1\1&2end{pmatrix}$ .

5. Находим преобразующую матрицу $S=[ S_{text{left}}(J_A)]^{-1}= begin{pmatrix}0&-1\1&2end{pmatrix}^{-1}= begin{pmatrix} 2&1\-1&0 end{pmatrix}$ . Такой же результат, как частный случай, был получен первым способом.

Решение для матрицы B

Будем искать преобразующую матрицу вторым способом. При этом попутно найдем и жорданову форму J_B матрицы (см. пункт 2 замечаний 7.7).

1. Составляем блочную матрицу: $(B-lambda Emid E)= begin{pmatrix} 1-lambda&0&1!!&vline!!&1&0&0\ 0&1-lambda&-1!!&vline!!&0&1&0\ -1&-1&1-lambda!!&vline!!&0&0&1 end{pmatrix}!.$

Выполняя элементарные преобразования над строками и над столбцами этой блочной матрицы, приводим левый блок к нормальному диагональному виду. Меняем местами первую и третью строки и умножаем первую строку на (-1). Выбрав ведущий элемент, равный единице, делаем равными нулю остальные элементы в первом столбце и в первой строке левого блока:

$begin{gathered}begin{pmatrix}1-lambda&0&1!!&vline!!&1&0&0\ 0&1-lambda&-1!!&vline!!&0&1&0\ -1&-1&1-lambda!!&vline!!&0&0&1end{pmatrix}sim begin{pmatrix}-1&-1&1-lambda!!&vline!!&0&0&1\ 0&1-lambda&-1!!&vline!!&0&1&0\ 1-lambda&0&1!!& vline!!&1&0&0end{pmatrix}sim\[2pt] simbegin{pmatrix} 1&1&lambda-1!!&vline!!&0&0&-1\ 0&1-lambda&-1!!&vline!!&0&1&0\ 1-lambda&0&1!!&vline!!&1&0&0end{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&0&0&-1\ 0&1-lambda&-1!!&vline!!&0&1&0\ 0&lambda-1&(lambda-1)^2+1!!&vline!!&1&0&1-lambdaend{pmatrix}!.end{gathered}$

Меняем местами второй и третий столбцы и умножаем вторую строку на (-1). Выбрав ведущий элемент, равный единице, делаем равными нулю остальные элементы во втором столбце и во второй строке левого блока:

$begin{gathered} begin{pmatrix} 1&0&0!!& vline!!&0&0&-1\ 0&1-lambda&-1!!& vline!!&0&1&0\ 0&lambda-1&(lambda-1)^2+1!!&vline!!&1&0&1-lambdaend{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&0&0&-1\ 0&-1&1-lambda!!&vline!!&0&1&0\ 0&(lambda-1)^2+1&lambda-1!!&vline!!&1&0&1-lambdaend{pmatrix}sim\[2pt] begin{pmatrix} 1&0&0!!& vline!!&0&0&-1\ 0&1&lambda-1!!&vline!!&0&-1&0\ 0&(lambda-1)^2+1&lambda-1!!&vline!!&1&0&1-lambdaend{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&0&0&-1\ 0&1&0!!&vline!!&0&-1&0\ 0&0&(lambda-1)^3!!&vline!!&1&(lambda-1)^2+1&1-lambdaend{pmatrix}!.end{gathered}$

Умножая третий столбец на (-1), получаем нормальную диагональную форму характеристической матрицы и матрицу S_B(lambda):

$B-lambda Esim begin{pmatrix}1&0&0\ 0&1&0\ 0&0&(lambda-1)^3end{pmatrix}= Lambda(lambda),quad S_B(lambda)=begin{pmatrix}0&0&-1\0&-1&0\ 1&lambda^2-2 lambda+2& 1-lambdaend{pmatrix}!.$

Находим жорданову форму J_B матрицы (см. пункт 2 замечаний 7.7). По инвариантным множителям e_1(lambda)=e_2(lambda)=1, e_3(lambda)= (lambda-1)^3 составляем таблицу элементарных делителей. Таблица состоит из одного делителя , которому соответствует одна жорданова клетка 3-го порядка (для собственного значения lambda_1=lambda_2=lambda_3 ):

$J_B=begin{pmatrix}1&1&0\0&1&1\0&0&1end{pmatrix}!.$

2. Составляем блочную матрицу

$(J_B-lambda Emid E)= begin{pmatrix}1-lambda&1&0!!&vline!!&1&0&0\ 0&1-lambda&1!!&vline!!&0&1&0\ 0&0&1-lambda!!&vline!!&0&0&1 end{pmatrix}!.$

Приводим левый блок этой матрицы к нормальному диагональному виду. Меняем местами столбцы левого блока

$begin{pmatrix}1-lambda&1&0!!&vline!!&1&0&0\ 0&1-lambda&1!!& vline!!& 0&1&0\ 0&0&1-lambda!!&vline!!&0&0&1 end{pmatrix}sim begin{pmatrix} 1&0&1-lambda!!& vline!!&1&0&0\ 1-lambda&1&0!!&vline!!&0&1&0\ 0&1-lambda&0!!&vline!!&0&0&1 end{pmatrix}!.$

Выбираем ведущий элемент, равный единице, в левом верхнем углу. Делаем в левом блоке равными нулю все элементы ведущей (первой) строки и ведущего (первого) столбца, за исключением ведущего элемента:

$begin{pmatrix} 1&0&1-lambda!!& vline!!&1&0&0\ 1-lambda&1&0!!&vline!!& 0&1&0\ 0&1-lambda&0!!&vline!!&0&0&1 end{pmatrix} sim begin{pmatrix} 1&0&0!!& vline!!&1&0&0\ 0&1&-(lambda-1)^2!!&vline!!&lambda-1&1&0\ 0&1-lambda& 0!!&vline!!& 0&0&1 end{pmatrix}!.$

Выбираем ведущий элемент, равный единице, на пересечении второго столбца и второй строки. К третьей строке прибавляем вторую, умноженную на (lambda-1) , а затем к третьему столбцу прибавляем второй, умноженный на (lambda-1)^2 , и, наконец, умножаем третий столбец на (-1). В результате получим

$begin{pmatrix} 1&0&0!!& vline!!&1&0&0\ 0&1&-(lambda-1)^2!!&vline!!& lambda-1&1&0\ 0&1-lambda&0!!&vline!!&0&0&1 end{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&1&0&0\ 0&1&0!!&vline!!&lambda-1&1&0\ 0&0&(lambda-1)^3!!&vline!!&(lambda-1)^2&lambda-1&1 end{pmatrix}!.$

Следовательно, $S_J(lambda)=begin{pmatrix}1&0&0\ lambda-1&1&0\ (lambda-1)^2&lambda-1&1 end{pmatrix}!,~ Lambda(lambda)= operatorname{diag}Bigl(1,1,(lambda-1)^3Bigr)$

3. Обращаем матрицу $S_J^{-1}(lambda)= frac{1}{det{S_J(lambda)}}cdot S_J^{+}(lambda)= begin{pmatrix}1&0&0\ 1-lambda&1&0\ 0&1-lambda&1end{pmatrix}$ .

Находим λ-матрицу $S(lambda)=S_J^{-1}(lambda)cdot S_B(lambda):$

$S(lambda)= begin{pmatrix}1&0&0\ 1-lambda&1&0\ 0&1-lambda&1 end{pmatrix}!cdot! begin{pmatrix}0&0&-1\ 0&-1&-1\ 1&(lambda-1)^2+1&1-lambda end{pmatrix}= begin{pmatrix}0&0&-1\ 0&-1&lambda-1\ 1&lambda^2-lambda+1&1-lambda end{pmatrix}!.$

Представляем λ-матрицу S(lambda) в виде многочлена с матричными коэффициентами, ставя переменную lambda перед коэффициентами:

$S(lambda)= lambda^2cdot! begin{pmatrix}0&0&0\ 0&0&0\ 0&1&0end{pmatrix}+ lambdacdot! begin{pmatrix}0&0&0\ 0&0&1\ 0&-1&-1end{pmatrix}+ begin{pmatrix}0&0&-1\ 0&-1&-1\ 1&1&1 end{pmatrix}!.$

Подставляем вместо аргумента lambda матрицу J_B:

$begin{aligned}S_{text{left}}(J_B)&= begin{pmatrix}1&1&0\ 0&1&1\ 0&0&1 end{pmatrix}^2!cdot! begin{pmatrix}0&0&0\ 0&0&0\ 0&1&0end{pmatrix}+ begin{pmatrix} 1&1&0\ 0&1&1\ 0&0&1end{pmatrix}!cdot! begin{pmatrix}0&0&0\0&0&1\0&-1&-1 end{pmatrix}+ begin{pmatrix}0&0&-1\0&-1&-1\1&1&1end{pmatrix}=\[2pt] &=begin{pmatrix} 1&2&1\ 0&1&2\ 0&0&1 end{pmatrix}!cdot! begin{pmatrix}0&0&0\ 0&0&0\ 0&1&0 end{pmatrix}+ begin{pmatrix}0&0&1\ 0&-1&0\ 0&-1&-1end{pmatrix}+ begin{pmatrix}0&0&-1\ 0&-1&-1\ 1&1&1 end{pmatrix}= begin{pmatrix}0&1&0\0&0&-1\ 1&1&0 end{pmatrix}!. end{aligned}$

5. Обращая полученную матрицу, находим преобразующую

$S=Bigl[S_{text{left}}(J_B)Bigr]^{-1}= begin{pmatrix}0&1&0\0&0&-1\ 1&1&0end{pmatrix}^{-1}= begin{pmatrix}-1&0&1\ 1&0&0\ 0&-1&0end{pmatrix}!.$

Сделаем проверку, сравнивая левую и правую части равенства SJ_B=BS:

$begin{aligned}Scdot J_B&= begin{pmatrix}-1&0&1\ 1&0&0\ 0&-1&0 end{pmatrix} !cdot! begin{pmatrix}1&1&0\ 0&1&1\ 0&0&1end{pmatrix}= begin{pmatrix}-1&-1&1\ 1&1&0\ 0&-1&-1 end{pmatrix}!;\[5pt] Bcdot S&= begin{pmatrix}1&0&1\ 0&1&-1\ -1&-1&1 end{pmatrix} !cdot! begin{pmatrix}-1&0&1\ 1&0&0\ 0&-1&0end{pmatrix}= begin{pmatrix}-1&-1&1\ 1&1&0\ 0&-1&-1 end{pmatrix}!. end{aligned}$

Следовательно, равенство верное.

Решение для матрицы C

Применяем второй способ нахождения преобразующей матрицы, попутно определяя жорданову форму J_C матрицы (см. пункт 2 замечаний 7.7).

1. Составляем блочную матрицу:

$(C-lambda Emid E)= begin{pmatrix}1-lambda&1&1!!&vline!!&1&0&0\ 1&1-lambda&1!!&vline!!&0&1&0\ 1&1&1-lambda!!&vline!!&0&0&1 end{pmatrix}!.$

Элементарными преобразованиями приводим левый ее блок к нормальному диагональному виду (см. пример 7.12). Меняем местами первый и третий столбцы, выбираем первую строку и первый столбец в качестве ведущих и делаем равными нулю все элементы выбранной строки (в пределах левого блока) и выбранного столбца, за исключением ведущего элемента:

$begin{pmatrix}1&1&1-lambda!!&vline!!&1&0&0\ 1&1-lambda&1!!& vline!!& 0&1&0\ 1-lambda&1&1!!&vline!!&0&0&1 end{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&1&0&0\ 0&-lambda&lambda!!& vline!!&-1&1&0\ 0&lambda&2 lambda-lambda^2!!& vline!!&lambda-1&0&1 end{pmatrix}!.$

Умножаем второй столбец на (-l), выбираем ведущими вторую строку и второй столбец, делаем равными нулю соответствующие элементы этой строки и столбца:

$begin{pmatrix} 1&0&0!!& vline!!&1&0&0\ 0&lambda&lambda!!& vline!!&-1&1&0\ 0&-lambda&2 lambda-lambda^2!!& vline!!&lambda-1&0&1 end{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&1&0&0\ 0&lambda&0!!& vline!!&-1&1&0\ 0&0&3 lambda-lambda^2!!& vline!!&lambda-2&1&1 end{pmatrix}!.$

Умножим третий столбец на (-1), чтобы старший коэффициент многочлена был равен единице. Итак, получили матрицу $S_C(lambda)= begin{pmatrix} 1&0&0\-1&1&0\ lambda-2&1&1 end{pmatrix}$ и нормальный диагональный вид характеристической матрицы (C-lambda E)sim operatorname{diag}(1,lambda,lambda(lambda-3)) . Составляем таблицу (7.33) инвариантных множителей:

e_1(lambda)=1;qquad e_2(lambda)=lambda;qquad e_3(lambda)=lambda(lambda-3).

Составляем таблицу (7.34) элементарных делителей: $begin{vmatrix}lambda,&quad lambda,\ lambda-3.&quad {}end{vmatrix}$ . Каждому из трех делителей соответствует жорданова клетка 1-го порядка (для собственных значений lambda_1=lambda_2=0, lambda_3=3 ), т.е. жорданова форма матрицы — диагональная матрица:

$J_C=operatorname{diag}Bigl(J_1(0),,J_1(0),,J_1(3)Bigr)= begin{pmatrix}0&0&0\ 0&0&0\ 0&0&3 end{pmatrix}!.$

2. Составляем блочную матрицу

$Bigl(J_C-lambda Emid EBigr)= begin{pmatrix} -lambda&0&0!!& vline!!&1&0&0\ 0&-lambda&0!!& vline!!&0&1&0\ 0&0&3-lambda!!& vline!!&0&0&1 end{pmatrix}!.$

Левый блок этой матрицы имеет диагональный вид, который не является нормальным, так как (3-lambda) не делится на (-lambda) . Прибавляем к первому столбцу третий, к третьей строке прибавляем первую, умноженную на (-1), меняем местами первую и третью строки:

$Bigl(J_C-lambda Emid EBigr)sim! begin{pmatrix} -lambda&0&0!!& vline!!&1&0&0\ 0&-lambda&0!!& vline!!&0&1&0\ 3-lambda&0&3-lambda!!& vline!!&0&0&1 end{pmatrix}!sim! begin{pmatrix} -lambda&0&0!!& vline!!&1&0&0\ 0&-lambda&0!!& vline!!&0&1&0\ 3&0&3-lambda!!& vline!!&-1&0&1 end{pmatrix}!sim! begin{pmatrix} 3&0&3-lambda!!& vline!!&-1&0&1\ 0&-lambda&0!!& vline!!&0&1&0\ -lambda&0&0!!& vline!!&1&0&0 end{pmatrix}!.$

Разделим первый столбец на 3, возьмем ведущий элемент, стоящий в левом верхнем углу, и сделаем равными нулю соответствующие элементы:

$begin{pmatrix} 1&0&3-lambda!!& vline!!&-1&0&1\ 0&-lambda&0!!& vline!!&0&1&0\ -lambda/3&0&0!!& vline!!&1&0&0 end{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&-1&0&1\ 0&-lambda&0!!& vline!!&0&1&0\ 0&0&lambda-lambda^2/3!!& vline!!&1-lambda/3&0&lambda/3 end{pmatrix}!.$

Умножив второй столбец на (-1), а третью строку на (-3), получим в левом блоке нормальный диагональный вид $Lambda(lambda)= operatorname{diag}(1,lambda,lambda^2-3 lambda)$ , а в правом блоке матрицу

$S_J(lambda)= begin{pmatrix} -1&0&1\0&1&0\ lambda-3&0&-lambdaend{pmatrix}!.$

3. Обращаем матрицу S_J(lambda):

$S_J^{+}(lambda)= frac{1}{det{S_J(lambda)}}cdot S_J^{+}(lambda)= frac{1}{3}cdot! begin{pmatrix}-lambda&0&-1\ 0&3&0\ 3-lambda&0&-1end{pmatrix}= begin{pmatrix} -lambda/3&0&-1/3\ 0&1&0\ 1-lambda/3&0&-1/3end{pmatrix}!.$

Находим λ-матрицу S(lambda)=S_J^{-1}(lambda)cdot S_C(lambda):

$S(lambda)= begin{pmatrix}-lambda/3&0&-1/3\ 0&1&0\ 1-lambda/3&0&-1/3 end{pmatrix}!cdot! begin{pmatrix}1&0&0\ -1&1&0\ lambda-2&1&1end{pmatrix}= begin{pmatrix}2/3-2 lambda/3&-1/3&-1/3\ -1&1&0\ 5/2-2 lambda/3&-1/3&-1/3 end{pmatrix}!.$

4. Представляем λ-матрицу S(lambda) в виде многочлена с матричными коэффициентами, помещая переменную перед коэффициентами:

$S(lambda)= lambdacdot! begin{pmatrix} -2/3&0&0\ 0&0&0\ -2/3&0&0end{pmatrix}+ begin{pmatrix}2/3&-1/3&-1/3\ -1&1&0\ 5/3&-1/3&-1/3end{pmatrix}!.$

Подставляем вместо аргумента lambda матрицу J_C:

$S_{text{left}}(J_C)= begin{pmatrix} 0&0&0\ 0&0&0\ 0&0&3 end{pmatrix}!cdot! begin{pmatrix}-2/3&0&0\ 0&0&0\ -2/3&0&0end{pmatrix}+ begin{pmatrix}2/3&-1/3&-1/3\ -1&1&0\ 5/3&-1/3&-1/3end{pmatrix}= begin{pmatrix}2/3&-1/3&-1/3\ -1&1&0\ -1/3&-1/3&-1/3 end{pmatrix}!.$

5. Обращая полученную матрицу, находим преобразующую

$S=begin{pmatrix}2/3&-1/3&-1/3\ -1&1&0\ -1/3&-1/3&-1/3end{pmatrix}^{-1}= begin{pmatrix}1&0&-1\ 1&1&-1\ -2&-1&-1 end{pmatrix}!.$

Сделаем проверку, вычислив матрицу $C=SJ_CS^{-1}:$

$begin{aligned}C&= begin{pmatrix}1&0&-1\ 1&1&-1\ -2&-1&-1end{pmatrix}!cdot! begin{pmatrix}0&0&0\ 0&0&0\ 0&0&3 end{pmatrix}!cdot! begin{pmatrix}2/3&-1/3&-1/3\ -1&1&0\ -1/3&-1/3&-1/3end{pmatrix}=\[2pt] &= begin{pmatrix}1&0&-1\ 1&1&-1\ -2&-1&-1 end{pmatrix}!cdot! begin{pmatrix}0&0&0\ 0&0&0\ -1&-1&-1 end{pmatrix}= begin{pmatrix} 1&1&1\1&1&1\1&1&1end{pmatrix}!.end{aligned}$

Заметим, что в примере 7.10 эта матрица была приведена к диагональному виду. Поэтому, согласно пункта 5 замечаний 7.7, ее жорданова форма является диагональной, а преобразующая матрица составляется из линейно независимых собственных векторов:

$J_C= begin{pmatrix}0&0&0\ 0&0&0\ 0&0&3end{pmatrix}!,qquad S=begin{pmatrix} 1&1&1\ 0&-1&1\ -1&0&1 end{pmatrix}!.$

Эта матрица отличается от найденной вторым способом. Но она тоже является преобразующей (проверка равенства $J_A=S^{-1}AS$ была фактически выполнена в примере 7.10).

Решение для матрицы D

Применяем второй способ нахождения преобразующей матрицы , попутно определяя жорданову форму J_D матрицы (см. пункт 2 замечаний 7.7).

1. Составляем блочную матрицу:

$bigl(D-lambda E~|~Ebigr)= left(!!begin{array}{ccc|ccc}-2-lambda&5&-3&1&0&0\-2&5-lambda&-3&0&1&0\1&-1&-lambda&0&0&1end{array}!!right)!.$

Элементарными преобразованиями приводим левый ее блок к нормальному диагональному виду. Взяв элемент, равный единице, в качестве ведущего, делаем равными нулю все элементы ведущего (первого) столбца и ведущей (третьей) строки (в пределах левого блока):

$bigl(D-lambda E~|~Ebigr)sim left(!! begin{array}{ccc|ccc}0&3-lambda&-3-2 lambda-lambda^2&1&0&lambda+2\ 0&3-lambda&-3-2 lambda&0&1&2\ 1&0&0&0&0&1end{array} !!right)!.$

К первой строке прибавляем вторую, умноженную на (-1) , затем к третьему столбцу прибавляем второй, умноженный на (-2)colon

$left(!! begin{array}{ccc|ccc}0&0&-lambda^2&1&-1&lambda\ 0&3-lambda&-3-2lambda&0&1&2\ 1&0&0&0&0&1 end{array} !!right)sim left(!! begin{array}{ccc|ccc}0&0&-lambda^2&1&-1&lambda\ 0&3-lambda&-9&0&1&2\ <br />1&0&0&0&0&1 end{array} !!right)!.$

Ко второму столбцу прибавляем третий, умноженный на $tfrac{3-lambda}{9}$ , а затем к первой строке прибавляем вторую, умноженную на (-lambda^2slash9)colon

$left(!! begin{array}{ccc|ccc}0&frac{lambda^2(lambda-3)}{9}&-lambda^2&1&-1&lambda\ 0&0&-9&0&1&2\ 1&0&0&0&0&1 end{array} !!right)sim left(!! begin{array}{ccc|ccc}0&frac{lambda^2(lambda-3)}{9}&0&1&-1-frac{lambda^2}{9}&lambda-frac{2lambda^2}{9}\ 0&0&-9&0&1&2\ 1&0&0&0&0&1 end{array} !!right)!.$

Меняем местами второй и третий столбцы, затем умножим первую строку на 9, второй столбец разделим на (-9):

$left(!! begin{array}{ccc|ccc}0&0&frac{lambda^2(lambda-3)}{9}&1&frac{-9-lambda^2}{9}&frac{9lambda-2lambda^2}{9}\ 0&-9&0&0&1&2\ 1&0&0&0&0&1 end{array} !!right)sim left(!! begin{array}{ccc|ccc}0&0&lambda^2(lambda-3)&9&-9-lambda^2&9lambda-2lambda^2\ 0&1&0&0&1&2\ 1&0&0&0&0&1 end{array} !!right)!.$

Меняем местами первую и третью строки, после чего получим в левом блоке нормальный диагональный вид характеристической матрицы (D-lambda E) , a в правом блоке – матрицу S_D(lambda)colon

$(D-lambda E)sim begin{pmatrix}1&0&0\0&1&0\0&0&lambda^2(lambda-3)end{pmatrix}!,quad S_D(lambda)= begin{pmatrix}0&0&1\0&1&2\9&-9-lambda^2&9 lambda-2 lambda^2end{pmatrix}!.$

Составляем таблицу (7.33) инвариантных множителей:

$begin{gathered}e_1(lambda)=1;\ e_2(lambda)=1;\ e_3(lambda)=lambda^2(lambda-3).end{gathered}$

Составляем таблицу (7.34) элементарных делителей:

$begin{gathered}lambda^2,\ lambda-3.end{gathered}$

Делителю lambda^2 соответствует жорданова клетка 2-го порядка, а делителю (lambda-3) – жорданова клетка 1-го порядка, т.е. жорданова форма матрицы имеет вид:

$J_D=operatorname{diag}bigl(J_2(0),J_1(3)bigr)= begin{pmatrix}0&1&0\0&0&0\0&0&3end{pmatrix}!.$

2. Составляем блочную матрицу:

$bigl(J_D-lambda E~|~Ebigr)=left(!! begin{array}{ccc|ccc}-lambda&1&0&1&0&0\ 0&-lambda&0&0&1&0\ 0&0&3-lambda&0&0&1 end{array} !!right)!.$

Приводим левый блок этой матрицы к нормальному диагональному виду. Выбираем единицу в качестве ведущего элемента и делаем равными нулю соответствующие элементы левого блока, а затем меняем местами первый и второй столбцы:

$bigl(J_D-lambda E~|~Ebigr)sim left(!! begin{array}{ccc|ccc}0&1&0&1&0&0\-lambda^2&0&0&lambda&1&0\ 0&0&3-lambda&0&0&1 end{array} !!right)sim left(!! begin{array}{ccc|ccc}1&0&0&1&0&0\ 0&-lambda^2&0&lambda&1&0\ 0&0&3-lambda&0&0&1 end{array} !!right)!.$

Полученный диагональный вид не является нормальным, так как (3-lambda) не делится на (-lambda^2) . Поэтому прибавляем ко второму столбцу третий, умноженный на (-1) , а затем ко второй строке прибавляем третью, умноженную на (lambda+3)colon

$left(!! begin{array}{ccc|ccc}1&0&0&1&0&0\ 0&-lambda^2&0&lambda&1&0\ 0&lambda-3&3-lambda&0&0&1 end{array} !!right)sim left(!! begin{array}{ccc|ccc}1&0&0&1&0&0\ 0&-9&9-lambda^2&lambda&1&lambda+3\ 0&lambda-3&3-lambda&0&0&1 end{array} !!right)!.$

Разделив второй столбец на (-9) , получим элемент, равный единице, который принимаем за ведущий, и делаем равными нулю соответствующие элементы второй строки и второго столбца:

$left(!! begin{array}{ccc|ccc}1&0&0&1&0&0\ 0&1&9-lambda^2&lambda&1&lambda+3\ 0&frac{3-lambda}{9}&3-lambda&0&0&1 end{array} !!right)sim left(!! begin{array}{ccc|ccc}1&0&0&1&0&0\ 0&1&0&lambda&1&lambda+3\ <br />0&0&frac{lambda^2(3-lambda)}{9}&frac{lambda(lambda-3)}{9}&frac{lambda-3}{9}&frac{lambda^2}{9}end{array} !!right)!.$

Умножив третью строку на (-9) , получим в левом блоке нормальный диагональный вид характеристической матрицы $(J_D-lambda E)sim operatorname{diag}bigl(1,1,lambda^2 (lambda-3)bigr)$ , а в правом блоке – матрицу

$S_J(lambda)=begin{pmatrix}1&0&0\ lambda&1&lambda+3\ 3 lambda-lambda^2&3-lambda&-lambda^2 end{pmatrix}!.$

3. Обращаем матрицу S_J(lambda)colon

$S_{J}^{-1}(lambda)= frac{1}{det S_{J}(lambda)}cdot S_{J}^{+}(lambda)= frac{1}{-9}! begin{pmatrix}-9&0&0\ 9 lambda&-lambda^2&-lambda-3\ 0&lambda-3&1 end{pmatrix}!.$

Находим λ-матрицу $S(lambda)=S_{J}^{-1}(lambda)cdot S_{D}(lambda)colon$

$begin{aligned}S(lambda)&=frac{1}{-9}cdot! begin{pmatrix}-9&0&0\ 9 lambda&-lambda^2&-lambda-3\ 0&lambda-3&1 end{pmatrix}!cdot! begin{pmatrix}0&0&1\0&1&2\ 9&-9-lambda^2&9lambda-2lambda^2end{pmatrix}=\ &=-frac{1}{9}cdot! begin{pmatrix}0&0&-9\-9lambda-27&lambda^3+2lambda^2+9lambda+27&2lambda^3-5lambda^2-18lambda\ 9&-lambda^2+lambda-12&-2lambda^2+11lambda-6end{pmatrix}!.end{aligned}$

4. Представляем λ-матрицу S(lambda) в виде многочлена с матричными коэффициентами, помещая переменную lambda перед коэффициентами:

$S(lambda)=-frac{lambda^3}{9}! begin{pmatrix}0&0&0\0&1&2\0&0&0 end{pmatrix}!-frac{lambda^2}{9}! begin{pmatrix}0&0&0\0&2&-5\0&-1&-2end{pmatrix}!-frac{lambda}{9}! begin{pmatrix}0&0&0\-9&9&-18\0&1&11end{pmatrix}!-frac{1}{9}! begin{pmatrix}0&0&-9\-27&27&0\9&-12&-6end{pmatrix}$

Подставляем вместо аргумента lambda матрицу J_D . Учитывая, что

$J_D=begin{pmatrix}0&1&0\0&0&0\0&0&3end{pmatrix}!,quad J_{D}^{2}=begin{pmatrix}0&0&0\0&0&0\0&0&9end{pmatrix}!,quad J_{D}^{3}=begin{pmatrix}0&0&0\0&0&0\0&0&27end{pmatrix}!,$

получаем

$S_{text{left}}(J_D)=frac{-1}{9}cdot left[!begin{pmatrix} 0&0&0\0&0&0\0&-9&-18 end{pmatrix}+begin{pmatrix}-9&9&-18\0&0&0\0&3&33 end{pmatrix}+begin{pmatrix} 0&0&-9\-27&27&0\9&-12&-6 end{pmatrix}!right]=begin{pmatrix}1&-1&3\3&-3&0\-1&2&-1end{pmatrix}!.$

5. Обращая полученную матрицу, находим преобразующую

$S={begin{pmatrix}1&-1&3\3&-3&0\-1&2&-1end{pmatrix}!!}^{-1}=frac{1}{9}cdot! begin{pmatrix}3&5&9\3&2&9\3&-1&0end{pmatrix}!.$

Сделаем проверку, вычислив матрицу $D=S,J_D,S^{-1}colon$

$begin{aligned}D&=frac{1}{9}cdot! begin{pmatrix}3&5&9\3&2&9\3&-1&0end{pmatrix}!cdot! begin{pmatrix}0&1&0\0&0&0\0&0&3end{pmatrix}!cdot! begin{pmatrix}1&-1&3\3&-3&0\-1&2&-1end{pmatrix}=\&=frac{1}{9}cdot! begin{pmatrix}0&3&27\0&3&27\0&3&0end{pmatrix}!cdot! begin{pmatrix}1&-1&3\3&-3&0\-1&2&-1end{pmatrix}=begin{pmatrix}-2&5&-3\-2&5&-3\1&-1&0end{pmatrix}!.<br />end{aligned}$

Получили заданную матрицу .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Number Line

Приведение матрицы к жордановой форме

Нахождение жордановой формы матрицы

Нахождение преобразующей матрицы

Вам также может понравиться

Как найти массу зная удельную теплоту сгорания

Что такое медиана ряда как ее найти

Как составить устное публичное выступление

Добавить комментарий Отменить ответ