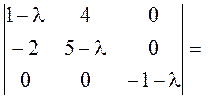Пусть дана матрица
3-го порядка. Надо найти жорданову форму
и жорданов базис.
-
Пусть
характеристический многочлен матрицыимеет вид
,
где
.
Тогда
жорданова форма матрицы имеет вид
.
-
Пусть
характеристический многочлен матрицыимеет вид
,
где
.
Возможны два случая:
а)
,
поэтому
и, следовательно,
,
поэтому жорданова форма содержит две
жордановы клетки с собственным значением
:
;
б)
,
поэтому
и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением
:
.
-
Пусть
характеристический многочлен матрицыимеет вид
.
Возможны два
случая:
а)
,
поэтому
и, следовательно, жорданова форма
содержит две жордановы клетки с
собственным значением
:
;
б)
,
поэтому
и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением
:
.
Задача.
Дана матрица
.
Найти
.
Р е ш е
н и е.
Найдем характеристический многочлен
матрицы:
.
Жорданова
форма матрицы
имеет вид
.
Найдем
.
Для
нахождения
воспользуемся формулой
,
где
– матрица перехода от базиса
к базису
.
Очевидно, что
,
поэтому
.
Пример
1. Найти жорданову форму и жорданов
базис матрицы оператора
.
Р е ш е
н и е.
Вычислим
,
следовательно,
собственное значение
,
.
Найдем
геометрическую кратность собственного
значения
.
Для этого посчитаем ранг матрицы
.
Следовательно,
,
поэтому
жорданова форма имеет вид
или
.
Найдем собственный вектор
,
соответствующий собственному значению
.
Так как он удовлетворяет условию
,
то
решим систему
.
Следовательно,
координаты собственного вектора
удовлетворяют уравнению
.
Заметим, что коэффициент при
равен 0, поэтому
может принимать любые значения.
Отбрасывать
нельзя !!!
Для
нахождения ФСР построим таблицу
.
Векторы
,
образуют фундаментальную систему
решений в собственном подпространстве
,
поэтому любой собственный вектор,
отвечающий собственному значению
,
линейно через них выражается и,
следовательно, имеет вид
.
Так как
,
,
то должен быть один присоединенный
вектор, который будет являться решением
системы
.
Подберем коэффициенты
и
таким образом, чтобы система
была совместна. Так как
,
то для
совместности системы необходимо, чтобы
выполнялось условие
.
Возьмем
,
тогда
,
и координаты присоединенного вектора
являются решением системы
,
то есть
удовлетворяют уравнению
или
.
Возьмем
.
Таким образом, у нас есть собственный
вектор
,
присоединенный к нему
и нужен еще один собственный вектор,
отвечающий собственному значению
.
Можно взять или вектор
,
или
,
или любой другой, отличный от
,
отвечающий собственному значению
.
Эти три вектора и будут образовывать
жорданов базис.
Пример 2. Найти жорданову
форму и жорданов базис матрицы оператора
.
Р е ш е
н и е.
Вычислим
,
следовательно,
собственное значение
,
.
Найдем
геометрическую кратность собственного
значения
.
Для этого посчитаем ранг матрицы
.
Следовательно,
,
поэтому
жорданова форма имеет вид
или
.
Найдем собственный вектор
,
соответствующий собственному значению
.
Так как он удовлетворяет условию
,
то
решим систему
.
Очевидно,
что координаты собственного вектора
удовлетворяют уравнению
или
.
Для
нахождения ФСР построим таблицу
.
Векторы
,
образуют фундаментальную систему
решений в собственном подпространстве
,
поэтому любой собственный вектор,
отвечающий собственному значению
,
линейно через них выражается
и, следовательно, имеет вид
.
Так как
,
,
то должен быть один присоединенный
вектор, который будет являться решением
системы
.
Подберем коэффициенты
и
таким образом, чтобы система
была совместна. Так как
,
то для
совместности системы необходимо, чтобы
выполнялось условие
.
Возьмем
,
тогда
и координаты присоединенного вектора
являются решением системы
,
то есть
удовлетворяют уравнению
или
.
Возьмем
.
Таким образом, у нас есть собственный
вектор
,
присоединенный к нему
и нужен еще один собственный вектор,
отвечающий собственному значению
.
Можно взять или вектор
,
или
,
или любой другой, отличный от
,
отвечающий собственному значению
.
Эти три вектора и будут образовывать
жорданов базис.
Пример 3. Найти жорданову
форму и жорданов базис матрицы оператора
.
Р е ш е
н и е.
Вычислим
.
Таким образом, получили три собственных
значения
,
,
.
Так как алгебраическая кратность каждого
из них равна 1, то жорданова форма имеет
следующий вид
.
Найдем собственный вектор
,
соответствующий собственному значению
.
Очевидно, что он является решением
уравнения
и, следовательно, его координаты
удовлетворяют системе
,
то есть
,
поэтому можем взять
.
Вычислим собственный вектор
,
соответствующий собственному значению
.
Очевидно, что он удовлетворяет уравнению
,
а его координаты – системе
,
откуда
следует, что
,
поэтому можем взять
.
Найдем собственный вектор
,
соответствующий собственному значению
.
Так как он является решением уравнения
,
то его координаты удовлетворяют системе
,
и,
следовательно,
,
поэтому можем взять
.
Векторы
образуют жорданов базис матрицы.
Пример 4. Найти жорданову
форму и жорданов базис матрицы оператора
.
Р е ш е
н и е.
Вычислим
.
Таким образом, получили два собственных
значения
,
.
Так как алгебраическая кратность
равна 2, нужно вычислить геометрическую
кратность
собственного значения
.
Для этого посчитаем ранг матрицы
.
Очевидно, что
,
поэтому
и, следовательно, жорданова форма имеет
следующий вид
.
Найдем собственные векторы
,
,
соответствующие собственному значению
.
Очевидно, что они являются решением
уравнения
,
а их координаты
– решением системы
,
и,
следовательно, удовлетворяют уравнению
или
.
Для
нахождения ФСР построим таблицу
.
Векторы
,
образуют фундаментальную систему
решений в собственном подпространстве
,
поэтому любой собственный вектор,
отвечающий собственному значению
,
линейно через них выражается и,
следовательно, имеет вид
.
Так
как
,
то нужно выбрать любые два линейно
независимых вектора из этой линейной
комбинации. Возьмем
,
.
Найдем собственный вектор
,
соответствующий собственному значению
.
Очевидно, что он удовлетворяет уравнению
,
а его координаты
– системе
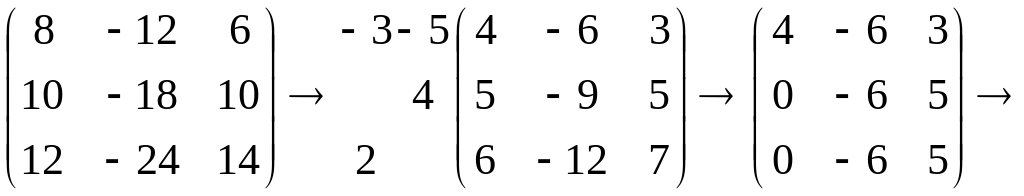
,
то есть
,
поэтому можем взять
.
Векторы
образуют жорданов базис матрицы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Жорданова матрица — квадратная блочно-диагональная матрица над полем 
Каждый блок 

Согласно теореме о жордановой нормальной форме, для произвольной квадратной матрицы 




является жордановой матрицей. При этом 




И наоборот, в силу эквивалентного соотношения
матрица 


Жорданова форма матрицы определена не однозначно, а с точностью до порядка жордановых клеток. Точнее, две жордановы матрицы подобны над 
случае, когда они составлены из одних и тех же жордановых клеток и отличаются друг от друга лишь расположением этих клеток на главной диагонали.
Свойства[править | править код]
- где
— единичная матрица того же порядка что и
, символ
обозначает ранг матрицы, а
, по определению, равен порядку
. Вышеприведённая формула следует из равенства
-
История[править | править код]
Одним из первых такую форму матрицы рассматривал Жордан.
Вариации и обобщения[править | править код]
- Помимо жордановой нормальной формы, рассматривают ряд других типов нормальных форм матрицы (например, фробениусова нормальная форма). К их рассмотрению прибегают, в частности, когда основное поле не содержит всех корней характеристического многочлена данной матрицы.
См. также[править | править код]
- Каноническая форма Вейра
Примечания[править | править код]
- ↑ Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
- ↑ Хорн Р. (Roger A. Horn), Джонсон Ч. (Charles C. Johnson) Матричный анализ. — М.: Мир, 1989 (ISBN 5-03-001042-4).
Литература[править | править код]
- Халмош П. Конечномерные векторные пространства. — М.: Физматгиз, 1963. — 264 с.
- Гантмахер Ф. Р. Теория матриц. — М.: Наука, 1966. — 576 с.
- Хорн Р. (Roger A. Horn), Джонсон Ч. (Charles C. Johnson). Матричный анализ. — М.: Мир, 1989, 655 с., ил. (ISBN 5-03-001042-4).
- Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
- Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.
- Ким, Г. Д. Линейная алгебра и аналитическая геометрия, Москва, 2005.
- В. В. Колыбасова, Н. Ч. Крутицкая, А. В. Овчинников. Жорданова форма матрицы оператора
- P. Aluffi. Algebra: Chapter 0 (Graduate Studies in Mathematics). — American Mathematical Society, 2009 — ISBN 0-8218-4781-3.
Жорданова форма матрицы
Рассматривается задача упрощения квадратной матрицы при помощи преобразования подобия. Наиболее простой вид квадратной матрицы — диагональный. Для диагональных матриц легко решаются многие типовые задачи линейной алгебры, например, обращение матриц, решение системы уравнений, нахождение многочлена от матрицы и т.п. Однако, как показано ранее, не всякая квадратная матрица подобна диагональной. Поэтому возникает необходимость приведения матрицы к такому виду, пусть даже не диагональному, чтобы при решении типовых задач линейной алгебры не возникало значительных трудностей.
Элементарные делители матрицы
Пусть — числовая квадратная матрица n-го порядка. Характеристическая матрица
приводится (элементарными преобразованиями) к нормальному диагональному виду
, где
— инвариантные множители матрицы
. Характеристический многочлен согласно свойству 2 можно представить в виде (7.25):
Разложим каждый из многочленов на линейные множители:
(7.33)
Здесь — различные собственные значения матрицы
; показатели степеней, удовлетворяют неравенствам
так как каждый последующий инвариантный множитель делится на предыдущий. Некоторые из множителей
в (7.33) могут иметь нулевую степень, т.е. быть равными единице. Исключение составляют множители
минимального многочлена (7.29) (
по свойству 6) , для которых согласно свойству 4 все показатели степеней больше или равны единицы
.
Учитывая, что характеристический многочлен (7.24) равен произведению инвариантных множителей (с коэффициентом ):
получаем, что и
, т.е. сумма степеней всех инвариантных множителей равна порядку квадратной матрицы
.
Каждый отличный от единицы многочлен вида , указанный в | разложениях (7.33) инвариантных множителей, называется элементарным делителем характеристической матрицы
(или просто элементарным делителем матрицы
).
По формулам (7.33) можно составить таблицу элементарных делителей:
(7.34)
Составление таблицы элементарных делителей по таблице инвариантных множителей
Для составления таблицы (7.34) элементарных делителей по таблице (7.33) инвариантных множителей нужно:
а) в первый столбец таблицы (7.34) записать элементарные делители последнего инвариантного множителя из таблицы (7.33);
б) во второй столбец (7.34) записать элементарные делители предпоследнего инвариантного множителя из таблицы (7.33) так, чтобы в i-й строке (7.34) были степени одного и того же двучлена
, и т.д. 18 последний столбец (7.34) записать элементарные делители первого инвариантного множителя
из таблицы (7.33) так, чтобы в i-й строке (7.34) были степени одного и того же двучлена
.
Элементы, тождественно равные единице, не являются элементарными делителями и в таблицу (7.34) не заносятся. Поэтому в каждой строке таблицы может быть разное количество элементарных делителей, точнее, в каждом последующем столбце количество делителей не больше, чем в предыдущем. В каждой строке таблицы (7.34) стоят делители , относящиеся к одному собственному значению
. Поскольку собственные значения
могут быть упорядочены по-разному, то и строки таблицы (7.34) можно переставлять. Это не будет в дальнейшем иметь существенного значения.
Составление таблицы инвариантных множителей по таблице элементарных делителей
По таблице (7.34) элементарных делителей можно восстановить таблицу (7.33) инвариантных множителей. Для этого нужно:
а) перемножая элементарные делители первого столбца таблицы (7.34), получить последний инвариантный множитель в таблице (7.33);
б) перемножая элементарные делители второго столбца таблицы (7.34), получить предпоследний инвариантный множитель в таблице (7.33) и т.д. Исчерпав столбцы таблицы (7.34), дописываем недостающие инвариантные множители, полагая их равными единице (количество инвариантных множителей равно сумме степеней всех элементарных делителей, т.е. порядку матрицы).
Заметим, что, составляя таблицу (7.33) по таблице (7.34), можно переставлять строки таблицы (7.34), так как это не приведет к изменению таблицы (7.33). Столбцы таблицы (7.34) переставлять нельзя.
Согласно теореме об инвариантных множителях, эквивалентные характеристические матрицы и
имеют одинаковые инвариантные множители (7.33). Тогда они имеют и одинаковые элементарные делители (7.34). Следовательно, критерий подобия числовых матриц можно сформулировать следующим образом.
Теорема 7.8 (критерий подобия матриц). Числовые матрицы подобны тогда и только тогда, когда они имеют одинаковые элементарные делители.
Таким образом, нахождение подобных матриц связано с умением составлять матрицы, элементарные делители которых совпадают с заданной таблицей (7.34).
Жордановы клетки и матрицы
Квадратную матрицу (r-го порядка) вида
(7.35)
называют жордановой клеткой r-го порядка, соответствующей собственному значению . Все элементы на главной диагонали этой верхней треугольной матрицы равны
, элементы над главной диагональю равны единице, а остальные элементы равны нулю.
Найдем элементарные делители жордановой клетки. Для этого составим характеристическую матрицу
и найдем наибольшие общие делители миноров i-го порядка. Среди ненулевых миноров первого порядка есть минор, равный единице
. Рассматривая его как многочлен нулевой степени, заключаем, что наибольший общий делитель миноров первого порядка должен быть также многочленом нулевой степени, т.е.
. Среди миноров второго порядка также имеется минор, равный единице:
, следовательно,
и т.д. Минор (r-l)-гo порядка
имеет нижний треугольный вид с единичными элементами на главной диагонали, т.е.
. Поэтому
. Минор r-го порядка, т.е. определитель характеристической матрицы, равен
, поэтому
. По формулам (7.11) находим инвариантные множители:
Следовательно, жорданова клетка (7.35) имеет всего один элементарный делитель . Поэтому характеристическая матрица приводится к нормальному диагональному виду (7.9):
(7.36)
Заметим, что характеристический многочлен имеет единственный корень
кратности
, т.е.
— собственное значение матрицы (7.35).
Рассмотрим теперь блочно-диагональную матрицу
(7.37)
где и
— жордановы клетки, а
— нулевые матрицы соответствующих размеров. Для определенности считаем, что
. Характеристическая матрица
также имеет блочно-диагональный вид. С помощью элементарных преобразований каждого блока матрица
, учитывая (7.36), приводится к диагональному виду
Если , то
.
Тогда .
Следовательно, матрица (7.37) имеет два элементарных делителя и
.
Если , то
.
Тогда .
Следовательно, матрица (7.37) имеет два элементарных делителя и
.
Таким образом, элементарные делители блочно-диагональной матрицы (7.37) получаются объединением элементарных делителей каждого блока.
Определение жордановой матрицы
Жордановой матрицей называют блочно-диагональную матрицу, на диагонали которой стоят жордановы клетки:
(7.38)
Здесь — нулевые матрицы соответствующих размеров. Среди собственных значений
могут быть равные, размеры
жордановых клеток (всех или некоторых) тоже могут совпадать. Жорданова матрица — почти диагональная. На ее главной диагонали стоят собственные значения, некоторые элементы над главной диагональю равны единице, остальные элементы нулевые. Про матрицу (7.38) говорят, что она имеет нормальную жорданову форму (или просто жорданову форму).
Элементарные делители жордановой матрицы (7.38) получаются в результате объединения элементарных делителей жордановых клеток.
Составление жордановой матрицы по таблице элементарных делителей
Чтобы составить по таблице (7.34) элементарных делителей соответствующую жорданову матрицу, нужно:
а) для первой строки элементарных делителей в (7.34) записать жордановы клетки
б) для второй строки элементарных делителей в (7.34) записать жордановы клетки
и т.д. Получив полный набор жордановых клеток (количество которых совпадает с количеством элементарных делителей в таблице (7.34)), составить из них блочно-диагональную матрицу вида (7.38). Порядок, в котором нужно располагать жордановы клетки на диагонали, строго не регламентирован. Поэтому для одной и той же таблицы (7.34) можно получить разные жордановы матрицы, отличающиеся только перестановкой жордановых клеток.
Составление таблицы элементарных делителей по жордановой матрице
Чтобы по жордановой матрице (7.38) составить таблицу (7.34) ее элементарных делителей, нужно:
а) выбрать в жордановой матрице все жордановы клетки, соответствующие собственному значению ; составить для каждой клетки элементарный делитель, а затем записать эти элементарные делители в порядке убывания степеней в первую строку таблицы (7.34), например, для жордановых клеток
, где
,
записать строку элементарных делителей;
б) выбрать в жордановой матрице все жордановы клетки, соответствующие собственному значению , составить для каждой клетки элементарный делитель, а затем записать эти элементарные делители в порядке убывания степеней во вторую строку таблицы (7.34) и т.д., пока не исчерпаются все собственные значения данной жордановой матрицы. Порядок, в котором выбираются собственные значения жордановой матрицы, точно не устанавливается. Поэтому для одной жордановой матрицы можно получить разные таблицы элементарных делителей, которые будут отличаться только перестановкой строк. Ранее отмечалось, что перестановка строк таблицы (7.34) не влияет на составление таблицы (7.33) инвариантных множителей.
Замечания 7.6
1. Диагональная матрица имеет жорданову форму, в которой все жордановы клетки первого порядка:
2. Хотя жорданова матрица в общем случае не диагональная, для нее достаточно просто решаются типовые задачи линейной алгебры. Например, для неоднородной системы уравнений с невырожденной матрицей
можно сразу записать решение:
3. Для решения тех или иных задач линейной алгебры используются различные простые виды квадратных матриц, которые обычно называют нормальными, или каноническими формами, например, первая и вторая естественные формы матрицы, вещественная жорданова форма. Матрицу (7.38) называют также канонической формой.
Пример 7.13. Найти элементарные делители и инвариантные множители жордановых матриц
Решение. Матрица состоит из трех жордановых клеток с разными собственными значениями
. Для каждого собственного значения запишем жорданову клетку и соответствующий элементарный делитель:
Получили таблицу элементарных делителей, которая состоит из одного столбца. По этой таблице составляем инвариантные множители (количество которых равно порядку матрицы ). Записываем последний инвариантный множитель
, перемножая элементарные делители первого столбца. Поскольку исчерпаны все элементарные делители (второго столбца в таблице нет), то остальные инвариантные множители полагаем равными единице:
.
Матрица состоит из трех жордановых клеток, соответствующих двум разным собственным значениям
.
Для каждого собственного значения записываем соответствующие жордановы клетки и элементарные делители:
Получили таблицу элементарных делителей, которая состоит из двух столбцов. По этой таблице составляем инвариантные множители (количество которых равно порядку матрицы ). Записываем последний инвариантный множитель
, перемножая элементарные делители первого столбца. Записываем предпоследний инвариантный множитель
по второму столбцу таблицы. Поскольку исчерпаны все элементарные делители (третьего столбца в таблице нет), то остальные инвариантные множители полагаем равными единице:
.
Матрица состоит из двух одинаковых жордановых клеток, соответствующих одному собственному значению
. Для этого собственного значения записываем жордановы клетки и соответствующие элементарные делители:
Получили таблицу элементарных делителей, которая состоит из двух столбцов. По этой таблице составляем инвариантные множители (количество которых равно порядку матрицы ). Записываем последний инвариантный множитель
по первому столбцу таблицы. Записываем предпоследний инвариантный множитель
по второму столбцу таблицы. Поскольку исчерпаны все элементарные делители (третьего столбца в таблице нет), то остальные инвариантные множители полагаем равными единице:
.
Пример 7.14. По инвариантным множителям найти жорданову матрицу:
а) матрица ;
б) матрица ;
в) матрица .
Решение. Для матрицы составляем таблицу (7.34) элементарных делителей. В первый столбец таблицы записываем элементарные делители последнего инвариантного множителя:
Остальные элементарные делители равны единице и в таблицу не заносятся. Составляем по таблице элементарных делителей жорданову матрицу. Для каждого элементарного делителя записываем соответствующую жорданову клетку:
. Располагая эти клетки на главной диагонали блочной матрицы, получаем искомую жорданову матрицу:
Для матрицы составляем таблицу (7.34) элементарных делителей. В первый столбец таблицы записываем единственный элементарный делитель последнего инвариантного множителя
, во второй столбец — предпоследнего инвариантного множителя
Инвариантные множители не содержат элементарных делителей, отличных от единицы, и поэтому в таблицу не записываются. Составляем по таблице элементарных делителей жорданову матрицу. Для каждого элементарного делителя записываем соответствующую жорданову клетку:
. Располагая эти клетки на главной диагонали блочной матрицы, получаем искомую жорданову матрицу:
Для матрицы составляем таблицу (7.34) элементарных делителей. В первый столбец таблицы записываем единственный элементарный делитель последнего инвариантного множителя
, второй столбец — предпоследнего инвариантного множителя
, в третий столбец —
Инвариантный множитель не содержит элементарных делителей, отличных от единицы, и поэтому в таблицу не записывается. Составляем по таблице элементарных делителей жорданову матрицу. Для каждого элементарного делителя записываем соответствующую жорданову клетку:
. Располагая эти клетки на главной диагонали блочной матрицы, получаем искомую жорданову матрицу:
Теорема 7.9 о приведении матрицы к нормальной жордановой форме. Любая квадратная матрица подобна жордановой матрице. Две жордановы матрицы подобны тогда и только тогда, когда они составлены из одинаковых жордановых клеток и отличаются друг от друга лишь расположением клеток на главной диагонали, другими словами, любую квадратную матрицу при помощи преобразования подобия можно привести к нормальной жордановой форме и притом единственной (с точностью до перестановок жордановых клеток).
В самом деле, для любой квадратной матрицы можно найти элементарные делители, т.е. составить таблицу (7.34). По элементарным делителям можно составить соответствующую жорданову матрицу
. При этом матрицы
и
будут иметь одинаковые элементарные делители, что является критерием их подобия. Значит, найдется невырожденная преобразующая матрица
такая, что
. Заметим, что жорданова форма
матрицы
определяется по ее элементарным делителям единственным образом с точностью до перестановок жордановых клеток.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Example of a matrix in Jordan normal form. All matrix entries not shown are zero. The outlined squares are known as “Jordan blocks”. Each Jordan block contains one number lambda on its main diagonal, and ones above the main diagonal. The lambdas are the eigenvalues of the matrix; they need not be distinct.
In linear algebra, a Jordan normal form, also known as a Jordan canonical form (JCF),[1][2]
is an upper triangular matrix of a particular form called a Jordan matrix representing a linear operator on a finite-dimensional vector space with respect to some basis. Such a matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them.
Let V be a vector space over a field K. Then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is algebraically closed (for instance, if it is the field of complex numbers). The diagonal entries of the normal form are the eigenvalues (of the operator), and the number of times each eigenvalue occurs is called the algebraic multiplicity of the eigenvalue.[3][4][5]
If the operator is originally given by a square matrix M, then its Jordan normal form is also called the Jordan normal form of M. Any square matrix has a Jordan normal form if the field of coefficients is extended to one containing all the eigenvalues of the matrix. In spite of its name, the normal form for a given M is not entirely unique, as it is a block diagonal matrix formed of Jordan blocks, the order of which is not fixed; it is conventional to group blocks for the same eigenvalue together, but no ordering is imposed among the eigenvalues, nor among the blocks for a given eigenvalue, although the latter could for instance be ordered by weakly decreasing size.[3][4][5]
The Jordan–Chevalley decomposition is particularly simple with respect to a basis for which the operator takes its Jordan normal form. The diagonal form for diagonalizable matrices, for instance normal matrices, is a special case of the Jordan normal form.[6][7][8]
The Jordan normal form is named after Camille Jordan, who first stated the Jordan decomposition theorem in 1870.[9]
Overview[edit]
Notation[edit]
Some textbooks have the ones on the subdiagonal; that is, immediately below the main diagonal instead of on the superdiagonal. The eigenvalues are still on the main diagonal.[10][11]
Motivation[edit]
An n × n matrix A is diagonalizable if and only if the sum of the dimensions of the eigenspaces is n. Or, equivalently, if and only if A has n linearly independent eigenvectors. Not all matrices are diagonalizable; matrices that are not diagonalizable are called defective matrices. Consider the following matrix:
Including multiplicity, the eigenvalues of A are λ = 1, 2, 4, 4. The dimension of the eigenspace corresponding to the eigenvalue 4 is 1 (and not 2), so A is not diagonalizable. However, there is an invertible matrix P such that J = P−1AP, where
The matrix 
Complex matrices[edit]
In general, a square complex matrix A is similar to a block diagonal matrix
where each block Ji is a square matrix of the form
So there exists an invertible matrix P such that P−1AP = J is such that the only non-zero entries of J are on the diagonal and the superdiagonal. J is called the Jordan normal form of A. Each Ji is called a Jordan block of A. In a given Jordan block, every entry on the superdiagonal is 1.
Assuming this result, we can deduce the following properties:
- Counting multiplicities, the eigenvalues of J, and therefore of A, are the diagonal entries.
- Given an eigenvalue λi, its geometric multiplicity is the dimension of ker(A − λi I), where I is the identity matrix, and it is the number of Jordan blocks corresponding to λi.[12]
- The sum of the sizes of all Jordan blocks corresponding to an eigenvalue λi is its algebraic multiplicity.[12]
- A is diagonalizable if and only if, for every eigenvalue λ of A, its geometric and algebraic multiplicities coincide. In particular, the Jordan blocks in this case are 1 × 1 matrices; that is, scalars.
- The Jordan block corresponding to λ is of the form λI + N, where N is a nilpotent matrix defined as Nij = δi,j−1 (where δ is the Kronecker delta). The nilpotency of N can be exploited when calculating f(A) where f is a complex analytic function. For example, in principle the Jordan form could give a closed-form expression for the exponential exp(A).
- The number of Jordan blocks corresponding to λ of size at least j is dim ker(A − λI)j − dim ker(A − λI)j−1. Thus, the number of Jordan blocks of size j is
- Given an eigenvalue λi, its multiplicity in the minimal polynomial is the size of its largest Jordan block.
Example[edit]
Consider the matrix 
that is,
Let 


We see that
For 






But 
Thus, 
Vectors such as 
Example: Obtaining the normal form[edit]
This example shows how to calculate the Jordan normal form of a given matrix.
Consider the matrix
which is mentioned in the beginning of the article.
The characteristic polynomial of A is
This shows that the eigenvalues are 1, 2, 4 and 4, according to algebraic multiplicity. The eigenspace corresponding to the eigenvalue 1 can be found by solving the equation Av = λv. It is spanned by the column vector v = (−1, 1, 0, 0)T. Similarly, the eigenspace corresponding to the eigenvalue 2 is spanned by w = (1, −1, 0, 1)T. Finally, the eigenspace corresponding to the eigenvalue 4 is also one-dimensional (even though this is a double eigenvalue) and is spanned by x = (1, 0, −1, 1)T. So, the geometric multiplicity (that is, the dimension of the eigenspace of the given eigenvalue) of each of the three eigenvalues is one. Therefore, the two eigenvalues equal to 4 correspond to a single Jordan block, and the Jordan normal form of the matrix A is the direct sum
There are three Jordan chains. Two have length one: {v} and {w}, corresponding to the eigenvalues 1 and 2, respectively. There is one chain of length two corresponding to the eigenvalue 4. To find this chain, calculate
where I is the 4 × 4 identity matrix. Pick a vector in the above span that is not in the kernel of A − 4I; for example, y = (1,0,0,0)T. Now, (A − 4I)y = x and (A − 4I)x = 0, so {y, x} is a chain of length two corresponding to the eigenvalue 4.
The transition matrix P such that P−1AP = J is formed by putting these vectors next to each other as follows
A computation shows that the equation P−1AP = J indeed holds.
If we had interchanged the order in which the chain vectors appeared, that is, changing the order of v, w and {x, y} together, the Jordan blocks would be interchanged. However, the Jordan forms are equivalent Jordan forms.
Generalized eigenvectors[edit]
Given an eigenvalue λ, every corresponding Jordan block gives rise to a Jordan chain of linearly independent vectors pi, i = 1, …, b, where b is the size of the Jordan block. The generator, or lead vector, pb of the chain is a generalized eigenvector such that (A − λI)bpb = 0. The vector p1 = (A − λI)b−1pb is an ordinary eigenvector corresponding to λ. In general, pi is a preimage of pi−1 under A − λI. So the lead vector generates the chain via multiplication by A − λI.[13][2] Therefore the statement that every square matrix A can be put in Jordan normal form is equivalent to the claim that the underlying vector space has a basis composed of Jordan chains.
A proof[edit]
We give a proof by induction that any complex-valued square matrix A may be put in Jordan normal form. Since the underlying vector space can be shown[14] to be the direct sum of invariant subspaces associated with the eigenvalues, A can be assumed to have just one eigenvalue λ. The 1 × 1 case is trivial. Let A be an n × n matrix. The range of A − λI, denoted by Ran(A − λI), is an invariant subspace of A. Also, since λ is an eigenvalue of A, the dimension of Ran(A − λI), r, is strictly less than n, so, by the inductive hypothesis, Ran(A − λI) has a basis {p1, …, pr} composed of Jordan chains.
Next consider the kernel, that is, the subspace ker(A − λI). If
the desired result follows immediately from the rank–nullity theorem. (This would be the case, for example, if A were Hermitian.)
Otherwise, if
let the dimension of Q be s ≤ r. Each vector in Q is an eigenvector, so Ran(A − λI) must contain s Jordan chains corresponding to s linearly independent eigenvectors. Therefore the basis {p1, …, pr} must contain s vectors, say {pr−s+1, …, pr}, that are lead vectors of these Jordan chains. We can “extend the chains” by taking the preimages of these lead vectors. (This is the key step.) Let qi be such that
The set {qi}, being preimages of the linearly independent set {pi} under A − λ I, is also linearly independent. Clearly no non-trivial linear combination of the qi can lie in ker(A − λI), for {pi}i=r−s+1, …, r is linearly independent. Furthermore, no non-trivial linear combination of the qi can belong to Ran(A − λ I) because it would then be a linear combination of the basic vectors p1, …, pr, and this linear combination would have a contribution of basic vectors not in ker(A − λI) because otherwise it would belong to ker(A − λI). The action of A − λI on both linear combinations would then produce an equality of a non-trivial linear combination of lead vectors and such a linear combination of non-lead vectors, which would contradict the linear independence of (p1, …, pr).
Finally, we can pick any linearly independent set {z1, …, zt} whose projection spans
Each zi forms a Jordan chain of length 1. By construction, the union of the three sets {p1, …, pr}, {qr−s +1, …, qr}, and {z1, …, zt} is linearly independent, and its members combine to form Jordan chains. Finally, by the rank–nullity theorem, the cardinality of the union is n. In other words, we have found a basis composed of Jordan chains, and this shows A can be put in Jordan normal form.
Uniqueness[edit]
It can be shown that the Jordan normal form of a given matrix A is unique up to the order of the Jordan blocks.
Knowing the algebraic and geometric multiplicities of the eigenvalues is not sufficient to determine the Jordan normal form of A. Assuming the algebraic multiplicity m(λ) of an eigenvalue λ is known, the structure of the Jordan form can be ascertained by analyzing the ranks of the powers (A − λI)m(λ). To see this, suppose an n × n matrix A has only one eigenvalue λ. So m(λ) = n. The smallest integer k1 such that
is the size of the largest Jordan block in the Jordan form of A. (This number k1 is also called the index of λ. See discussion in a following section.) The rank of
is the number of Jordan blocks of size k1. Similarly, the rank of
is twice the number of Jordan blocks of size k1 plus the number of Jordan blocks of size k1 − 1. The general case is similar.
This can be used to show the uniqueness of the Jordan form. Let J1 and J2 be two Jordan normal forms of A. Then J1 and J2 are similar and have the same spectrum, including algebraic multiplicities of the eigenvalues. The procedure outlined in the previous paragraph can be used to determine the structure of these matrices. Since the rank of a matrix is preserved by similarity transformation, there is a bijection between the Jordan blocks of J1 and J2. This proves the uniqueness part of the statement.
Real matrices[edit]
If A is a real matrix, its Jordan form can still be non-real. Instead of representing it with complex eigenvalues and ones on the superdiagonal, as discussed above, there exists a real invertible matrix P such that P−1AP = J is a real block diagonal matrix with each block being a real Jordan block.[15] A real Jordan block is either identical to a complex Jordan block (if the corresponding eigenvalue 

and describe multiplication by 
This real Jordan form is a consequence of the complex Jordan form. For a real matrix the nonreal eigenvectors and generalized eigenvectors can always be chosen to form complex conjugate pairs. Taking the real and imaginary part (linear combination of the vector and its conjugate), the matrix has this form with respect to the new basis.
Matrices with entries in a field[edit]
Jordan reduction can be extended to any square matrix M whose entries lie in a field K. The result states that any M can be written as a sum D + N where D is semisimple, N is nilpotent, and DN = ND. This is called the Jordan–Chevalley decomposition. Whenever K contains the eigenvalues of M, in particular when K is algebraically closed, the normal form can be expressed explicitly as the direct sum of Jordan blocks.
Similar to the case when K is the complex numbers, knowing the dimensions of the kernels of (M − λI)k for 1 ≤ k ≤ m, where m is the algebraic multiplicity of the eigenvalue λ, allows one to determine the Jordan form of M. We may view the underlying vector space V as a K[x]-module by regarding the action of x on V as application of M and extending by K-linearity. Then the polynomials (x − λ)k are the elementary divisors of M, and the Jordan normal form is concerned with representing M in terms of blocks associated to the elementary divisors.
The proof of the Jordan normal form is usually carried out as an application to the ring K[x] of the structure theorem for finitely generated modules over a principal ideal domain, of which it is a corollary.
Consequences[edit]
One can see that the Jordan normal form is essentially a classification result for square matrices, and as such several important results from linear algebra can be viewed as its consequences.
Spectral mapping theorem[edit]
Using the Jordan normal form, direct calculation gives a spectral mapping theorem for the polynomial functional calculus: Let A be an n × n matrix with eigenvalues λ1, …, λn, then for any polynomial p, p(A) has eigenvalues p(λ1), …, p(λn).
Characteristic polynomial[edit]
The characteristic polynomial of A is 
Therefore, 
where 


Cayley–Hamilton theorem[edit]
The Cayley–Hamilton theorem asserts that every matrix A satisfies its characteristic equation: if p is the characteristic polynomial of A, then 


then its Jordan block 

As the diagonal blocks do not affect each other, the ith diagonal block of 


The Jordan form can be assumed to exist over a field extending the base field of the matrix, for instance over the splitting field of p; this field extension does not change the matrix p(A) in any way.
Minimal polynomial[edit]
The minimal polynomial P of a square matrix A is the unique monic polynomial of least degree, m, such that P(A) = 0. Alternatively, the set of polynomials that annihilate a given A form an ideal I in C[x], the principal ideal domain of polynomials with complex coefficients. The monic element that generates I is precisely P.
Let λ1, …, λq be the distinct eigenvalues of A, and si be the size of the largest Jordan block corresponding to λi. It is clear from the Jordan normal form that the minimal polynomial of A has degree Σsi.
While the Jordan normal form determines the minimal polynomial, the converse is not true. This leads to the notion of elementary divisors. The elementary divisors of a square matrix A are the characteristic polynomials of its Jordan blocks. The factors of the minimal polynomial m are the elementary divisors of the largest degree corresponding to distinct eigenvalues.
The degree of an elementary divisor is the size of the corresponding Jordan block, therefore the dimension of the corresponding invariant subspace. If all elementary divisors are linear, A is diagonalizable.
Invariant subspace decompositions[edit]
The Jordan form of a n × n matrix A is block diagonal, and therefore gives a decomposition of the n dimensional Euclidean space into invariant subspaces of A. Every Jordan block Ji corresponds to an invariant subspace Xi. Symbolically, we put
where each Xi is the span of the corresponding Jordan chain, and k is the number of Jordan chains.
One can also obtain a slightly different decomposition via the Jordan form. Given an eigenvalue λi, the size of its largest corresponding Jordan block si is called the index of λi and denoted by v(λi). (Therefore, the degree of the minimal polynomial is the sum of all indices.) Define a subspace Yi by
This gives the decomposition
where l is the number of distinct eigenvalues of A. Intuitively, we glob together the Jordan block invariant subspaces corresponding to the same eigenvalue. In the extreme case where A is a multiple of the identity matrix we have k = n and l = 1.
The projection onto Yi and along all the other Yj ( j ≠ i ) is called the spectral projection of A at vi and is usually denoted by P(λi ; A). Spectral projections are mutually orthogonal in the sense that P(λi ; A) P(vj ; A) = 0 if i ≠ j. Also they commute with A and their sum is the identity matrix. Replacing every vi in the Jordan matrix J by one and zeroing all other entries gives P(vi ; J), moreover if U J U−1 is the similarity transformation such that A = U J U−1 then P(λi ; A) = U P(λi ; J) U−1. They are not confined to finite dimensions. See below for their application to compact operators, and in holomorphic functional calculus for a more general discussion.
Comparing the two decompositions, notice that, in general, l ≤ k. When A is normal, the subspaces Xi‘s in the first decomposition are one-dimensional and mutually orthogonal. This is the spectral theorem for normal operators. The second decomposition generalizes more easily for general compact operators on Banach spaces.
It might be of interest here to note some properties of the index, ν(λ). More generally, for a complex number λ, its index can be defined as the least non-negative integer ν(λ) such that
So ν(v) > 0 if and only if λ is an eigenvalue of A. In the finite-dimensional case, ν(v) ≤ the algebraic multiplicity of v.
Plane (flat) normal form[edit]
The Jordan form is used to find a normal form of matrices up to conjugacy such that normal matrices make up an algebraic variety of a low fixed degree in the ambient matrix space.
Sets of representatives of matrix conjugacy classes for Jordan normal form or rational canonical forms in general do not constitute linear or
affine subspaces in the ambient matrix spaces.
Vladimir Arnold posed[16] a problem:
Find a canonical form of matrices over a field for which the set of representatives of matrix conjugacy classes is a union of affine linear subspaces (flats). In other words, map the set of matrix conjugacy classes injectively back into the initial set of matrices so that the image of this embedding—the set of all normal matrices, has the lowest possible degree—it is a union of shifted linear subspaces.
It was solved for algebraically closed fields by Peteris Daugulis.[17]
The construction of a uniquely defined plane normal form of a matrix starts by considering its Jordan normal form.
Matrix functions[edit]
Iteration of the Jordan chain motivates various extensions to more abstract settings. For finite matrices, one gets matrix functions; this can be extended to compact operators and the holomorphic functional calculus, as described further below.
The Jordan normal form is the most convenient for computation of the matrix functions (though it may be not the best choice for computer computations). Let f(z) be an analytical function of a complex argument. Applying the function on a n×n Jordan block J with eigenvalue λ results in an upper triangular matrix:
so that the elements of the k-th superdiagonal of the resulting matrix are 
The following example shows the application to the power function f(z) = zn:
where the binomial coefficients are defined as 
of the coefficients. For negative n the identity 
Compact operators[edit]
A result analogous to the Jordan normal form holds for compact operators on a Banach space. One restricts to compact operators because every point x in the spectrum of a compact operator T is an eigenvalue; The only exception is when x is the limit point of the spectrum. This is not true for bounded operators in general. To give some idea of this generalization, we first reformulate the Jordan decomposition in the language of functional analysis.
Holomorphic functional calculus[edit]
Let X be a Banach space, L(X) be the bounded operators on X, and σ(T) denote the spectrum of T ∈ L(X). The holomorphic functional calculus is defined as follows:
Fix a bounded operator T. Consider the family Hol(T) of complex functions that is holomorphic on some open set G containing σ(T). Let Γ = {γi} be a finite collection of Jordan curves such that σ(T) lies in the inside of Γ, we define f(T) by
The open set G could vary with f and need not be connected. The integral is defined as the limit of the Riemann sums, as in the scalar case. Although the integral makes sense for continuous f, we restrict to holomorphic functions to apply the machinery from classical function theory (for example, the Cauchy integral formula). The assumption that σ(T) lie in the inside of Γ ensures f(T) is well defined; it does not depend on the choice of Γ. The functional calculus is the mapping Φ from Hol(T) to L(X) given by
We will require the following properties of this functional calculus:
- Φ extends the polynomial functional calculus.
- The spectral mapping theorem holds: σ(f(T)) = f(σ(T)).
- Φ is an algebra homomorphism.
The finite-dimensional case[edit]
In the finite-dimensional case, σ(T) = {λi} is a finite discrete set in the complex plane. Let ei be the function that is 1 in some open neighborhood of λi and 0 elsewhere. By property 3 of the functional calculus, the operator
is a projection. Moreover, let νi be the index of λi and
The spectral mapping theorem tells us
has spectrum {0}. By property 1, f(T) can be directly computed in the Jordan form, and by inspection, we see that the operator f(T)ei(T) is the zero matrix.
By property 3, f(T) ei(T) = ei(T) f(T). So ei(T) is precisely the projection onto the subspace
The relation
implies
where the index i runs through the distinct eigenvalues of T. This is the invariant subspace decomposition
given in a previous section. Each ei(T) is the projection onto the subspace spanned by the Jordan chains corresponding to λi and along the subspaces spanned by the Jordan chains corresponding to vj for j ≠ i. In other words, ei(T) = P(λi;T). This explicit identification of the operators ei(T) in turn gives an explicit form of holomorphic functional calculus for matrices:
- For all f ∈ Hol(T),
Notice that the expression of f(T) is a finite sum because, on each neighborhood of vi, we have chosen the Taylor series expansion of f centered at vi.
Poles of an operator[edit]
Let T be a bounded operator λ be an isolated point of σ(T). (As stated above, when T is compact, every point in its spectrum is an isolated point, except possibly the limit point 0.)
The point λ is called a pole of operator T with order ν if the resolvent function RT defined by
has a pole of order ν at λ.
We will show that, in the finite-dimensional case, the order of an eigenvalue coincides with its index. The result also holds for compact operators.
Consider the annular region A centered at the eigenvalue λ with sufficiently small radius ε such that the intersection of the open disc Bε(λ) and σ(T) is {λ}. The resolvent function RT is holomorphic on A.
Extending a result from classical function theory, RT has a Laurent series representation on A:
where
and C is a small circle centered at λ.
By the previous discussion on the functional calculus,
where
is 1 on
and 0 elsewhere.
But we have shown that the smallest positive integer m such that
and
is precisely the index of λ, ν(λ). In other words, the function RT has a pole of order ν(λ) at λ.
Numerical analysis[edit]
If the matrix A has multiple eigenvalues, or is close to a matrix with multiple eigenvalues, then its Jordan normal form is very sensitive to perturbations. Consider for instance the matrix
If ε = 0, then the Jordan normal form is simply
However, for ε ≠ 0, the Jordan normal form is
This ill conditioning makes it very hard to develop a robust numerical algorithm for the Jordan normal form, as the result depends critically on whether two eigenvalues are deemed to be equal. For this reason, the Jordan normal form is usually avoided in numerical analysis; the stable Schur decomposition[18] or pseudospectra[19] are better alternatives.
See also[edit]
- Canonical basis
- Canonical form
- Frobenius normal form
- Jordan matrix
- Jordan–Chevalley decomposition
- Matrix decomposition
- Modal matrix
- Weyr canonical form
Notes[edit]
- ^
Shilov defines the term Jordan canonical form and in a footnote says that Jordan normal form is synonymous.
These terms are sometimes shortened to Jordan form. (Shilov)
The term Classical canonical form is also sometimes used in the sense of this article. (James & James, 1976) - ^ a b Holt & Rumynin (2009, p. 9)
- ^ a b Beauregard & Fraleigh (1973, pp. 310–316)
- ^ a b Golub & Van Loan (1996, p. 355)
- ^ a b Nering (1970, pp. 118–127)
- ^ Beauregard & Fraleigh (1973, pp. 270–274)
- ^ Golub & Van Loan (1996, p. 353)
- ^ Nering (1970, pp. 113–118)
- ^ Brechenmacher, “Histoire du théorème de Jordan de la décomposition matricielle (1870-1930). Formes de représentation et méthodes de décomposition”, Thesis, 2007
- ^ Cullen (1966, p. 114)
- ^ Franklin (1968, p. 122)
- ^ a b Horn & Johnson (1985, §3.2.1)
- ^ Bronson (1970, pp. 189, 194)
- ^ Roe Goodman and Nolan R. Wallach, Representations and Invariants of Classical Groups, Cambridge UP 1998, Appendix B.1.
- ^ Horn & Johnson (1985, Theorem 3.4.5)
- ^ Arnold, Vladimir I, ed. (2004). Arnold’s problems. Springer-Verlag Berlin Heidelberg. p. 127. doi:10.1007/b138219. ISBN 978-3-540-20748-1.
- ^ Peteris Daugulis (2012). “A parametrization of matrix conjugacy orbit sets as unions of affine planes”. Linear Algebra and Its Applications. 436 (3): 709–721. arXiv:1110.0907. doi:10.1016/j.laa.2011.07.032. S2CID 119649768.
- ^ See Golub & Van Loan (2014), §7.6.5; or Golub & Wilkinson (1976) for details.
- ^ See Golub & Van Loan (2014), §7.9
References[edit]
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Dunford, N.; Schwartz, J. T. (1958), Linear Operators, Part I: General Theory, Interscience
- Finkbeiner II, Daniel T. (1978), Introduction to Matrices and Linear Transformations (3rd ed.), W. H. Freeman and Company
- Franklin, Joel N. (1968), Matrix Theory, Englewood Cliffs: Prentice-Hall, LCCN 68016345
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins University Press, ISBN 0-8018-5414-8
- Golub, Gene H.; Wilkinson, J. H. (1976). “Ill-conditioned eigensystems and the computation of the Jordan normal form”. SIAM Review. 18 (4): 578–619. doi:10.1137/1018113.
- Holt, Derek; Rumynin, Dmitriy (2009), Algebra I – Advanced Linear Algebra (MA251) Lecture Notes (PDF)
- Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
- James, Glenn; James, Robert C. (1976), Mathematics Dictionary (2nd ed.), Van Nostrand Reinhold
- MacLane, Saunders; Birkhoff, Garrett (1967), Algebra, Macmillan Publishers
- Michel, Anthony N.; Herget, Charles J. (1993), Applied Algebra and Functional Analysis, Dover Publications
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
- Shafarevich, I. R.; Remizov, A. O. (2012), Linear Algebra and Geometry, Springer, ISBN 978-3-642-30993-9
- Shilov, Georgi E. (1977), Linear Algebra, Dover Publications
- Jordan Canonical Form article at mathworld.wolfram.com
Жорданова нормальная форма матрицы. Характеристический многочлен жордановой клетки
Страницы работы
Содержание работы
§ 4. Жорданова нормальная
форма матрицы
Жордановой клеткой -го порядка
называется матрица -го порядка
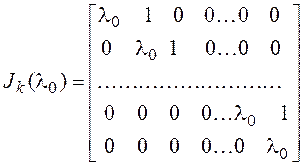
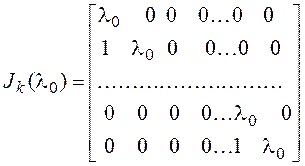
Ужордановой клетки все диагональные
элементы одинаковые, диагональ, параллельная главной и расположенная над ней или
под ней, состоит из единиц, а все остальные элементы равны нулю.
Характеристический многочлен жордановой клетки выглядит так:
. Таким образом, жорданова
клетка имеет единственное характеристическое
число , причем его кратность равна
порядку этой клетки. В дальнейшем мы будем использовать жордановы клетки только
первого вида. Примеры жордановых клеток:
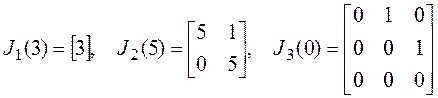
Пусть матрица линейного оператора в некотором базисе
пространства
совпадает с жордановой клеткой
первого вида. Тогда:
.
Отсюда видно, что первый вектор этого
базиса – собственный с собственным значением ,
а остальные – присоединенные к нему.
Жордановой
матрицей называется блочно
диагональная матрица , диагональными
блоками которой являются жордановы клетки: .
В этой матрице числа , также как и числа
могут совпадать или быть
различными. В частности, диагональная матрица является жордановой, все ее
клетки имеют первый порядок.
Для любой комплексной квадратной
матрицы А существует невырожденная матрица Т такая, что матрица – жорданова.
Матрица называется жордановой
нормальной формой матрицы А. Жорданова нормальная форма
матрицы определяется однозначно с точностью до порядка следования клеток.
Жорданова нормальная форма действительной матрицы А может оказаться
матрицей комплексной. Она будет действительной в том и только в том случае,
когда матрица имеет только действительные характеристические числа.
Свойства
жордановой матрицы. 1.
Характеристический многочлен жордановой матрицы равен произведению
характеристических многочленов составляющих ее жордановых клеток.
2. Диагональными элементами клеток, составляющих
жорданову нормальную форму матрицы А, являются ее характеристические
числа или собственные значения, что для комплексной матрицы одно и то же.
3. Сумма порядков всех клеток, соответствующих одному и
тому же собственному значению, равна кратности этого собственного значения.
4. Число клеток, соответствующих одному и тому же
собственному значению, равно количеству линейно независимых собственных
векторов с этим собственным значением.
5. Число клеток порядка выше ,
соответствующих данному собственному значению, равно количеству линейно
независимых собственных векторов с этим собственным значением, имеющих -е присоединенные векторы.
Пример 1. Записать жорданову
нормальную форму матрицы пятого порядка в том случае, когда она имеет одно собственное
значение кратности пять.
►Возможны следующие
принципиально различные случаи:
1) . Это значит, линейный оператор
имеет пять линейно независимых векторов, следовательно, жорданова форма имеет
пять клеток. Так как сумма их порядков равна пяти, то все они имеют первый
порядок, значит,
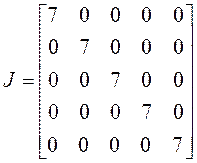
2) . Линейный оператор имеет
четыре линейно независимых вектора, жорданова форма имеет четыре клетки, сумма
их порядков равна пяти. Число пять можно разбить на четыре слагаемых только
одним способом: одна двойка и три единицы. Соответственно жорданова форма имеет
одну клетку второго порядка и три клетки первого порядка:
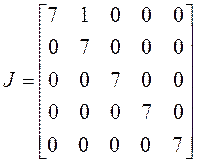
3) . Линейный оператор имеет три
линейно независимых вектора, жорданова форма имеет три клетки. На три слагаемых
число пять можно разбить двумя способами: а) тройка и две единицы, б) две
двойки и единица. Чтобы эти случаи различить, надо знать количество линейно
независимых собственных векторов, имеющих присоединенные. Если такой вектор
один, имеем случай а), если два – то б):
а) 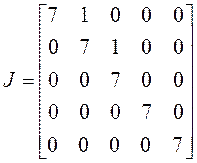
б) 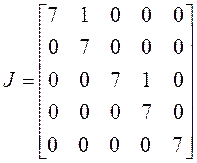
4) . Жорданова форма имеет две
клетки. Опять может быть два случая: а) по одной клетке четвертого и первого
порядка, б) по одной клетке третьего и второго порядка. Если только один из
собственных векторов имеет присоединенные, имеем случай а), если оба – то б):
а) 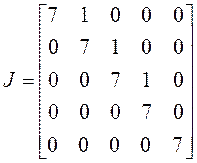
б) 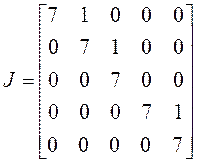
5) . Жорданова форма имеет только
одну клетку пятого порядка:
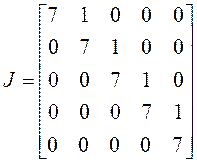
Для определения
числа клеток
го порядка, соответствующих
собственному значению в жордановой
нормальной форме матрицы, можно также воспользоваться следующей формулой:
.
Заметьте, что для определения числа клеток второго
порядка пришлось бы вычислять куб матрицы (пятого порядка!). Используя свойства
жордановой матрицы, мы прекрасно обошлись и без этой громоздкой формулы. Тем
более что в практических задачах, требующих приведения матрицы к жордановой нормальной форме,
используется и матрица , приводящая
к этой форме. Матрица
есть не что иное, как матрица
перехода от исходного базиса к базису из собственных и присоединенных векторов,
поэтому их все равно приходится находить.
В примерах 2 – 7 требуется найти жорданову нормальную
форму матрицы
и невырожденную матрицу
, приводящую
к жордановой нормальной форме.
Пример 2.
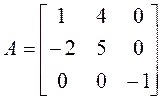
►Составляем характеристический многочлен и находим его
корни:
;
,
,
.
Все корни однократные,
поэтому все клетки будут иметь первый порядок, матрица имеет
диагональный вид:
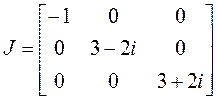
Находим собственные векторы:
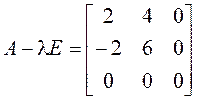
;
:
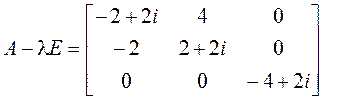
,
(используем
алгебраические дополнения к элементам первой строки);
:
(координаты
вектора – комплексно сопряженные числа
к координатам вектора , см. пример
§ ). Матрица , приводящая
к жордановой нормальной форме
– это матрица перехода от исходного базиса к базису из собственных векторов:
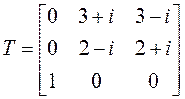
Пример 3.
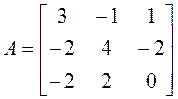
►1. Составляем характеристический многочлен и находим
его корни:
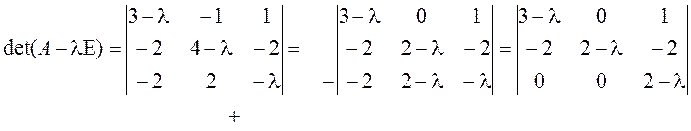
;
.
Один
из корней двукратный, ему может соответствовать одна или две клетки. Найдем для
этого корня собственные векторы:
:
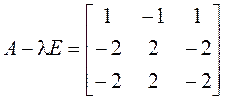
(14)
Так
как , то
, т.е. этому собственному значению
соответствуют два линейно независимых собственных вектора, а значит, жорданова
нормальная форма содержит две клетки с этим собственным значением. Сумма их порядков
равна двум (кратности корня), поэтому они обе имеют первый порядок. Таким
образом,
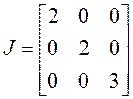
Похожие материалы
- Линейные операторы. Матрица линейного оператора. Линейный оператор, который переводит ненулевой вектор в нулевой
- Линейные пространства. Аксиома линейного пространства. Следствия из аксиом линейного пространства
- Линейный оператор. Правило Крамера. Матричный критерий. Ранг матрицы


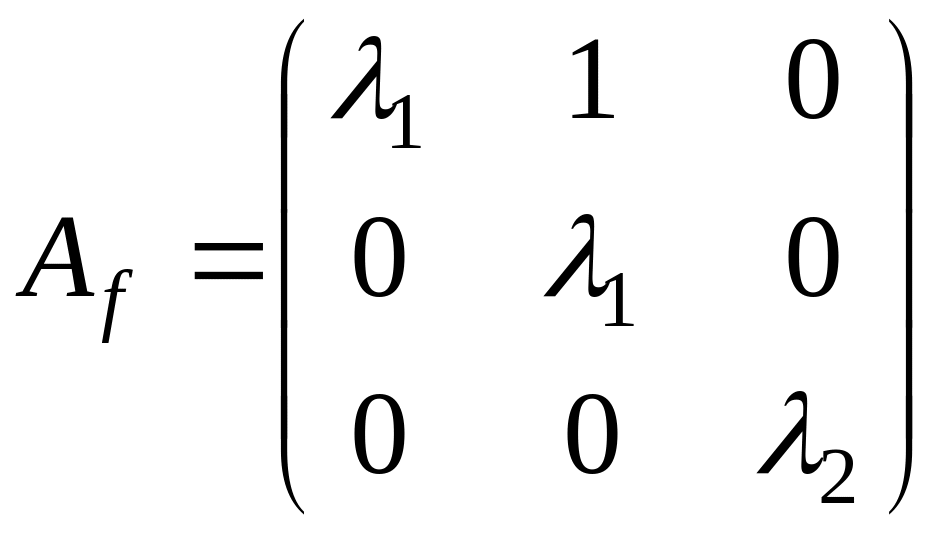
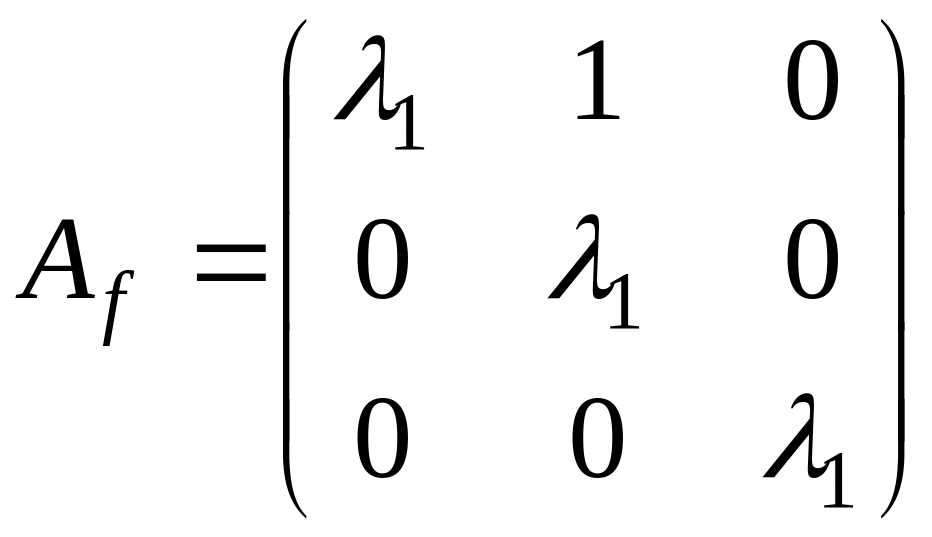

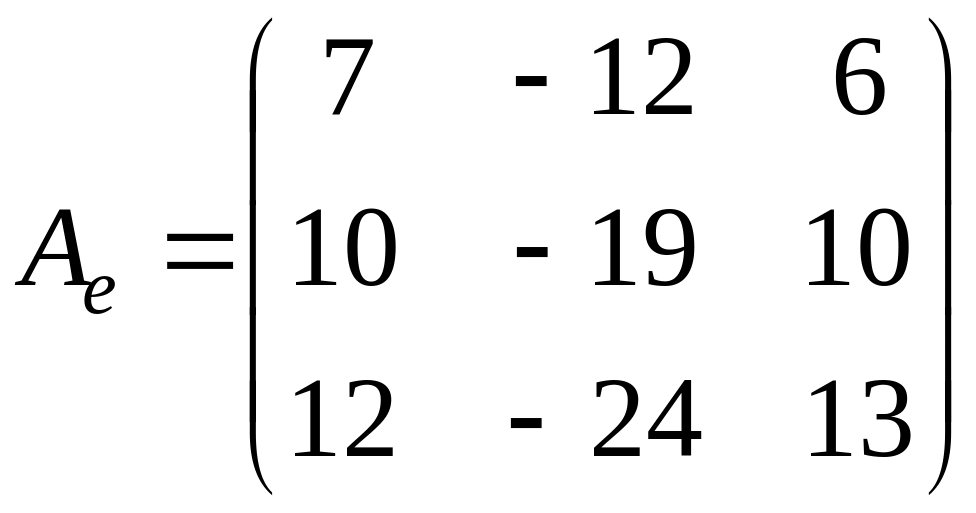
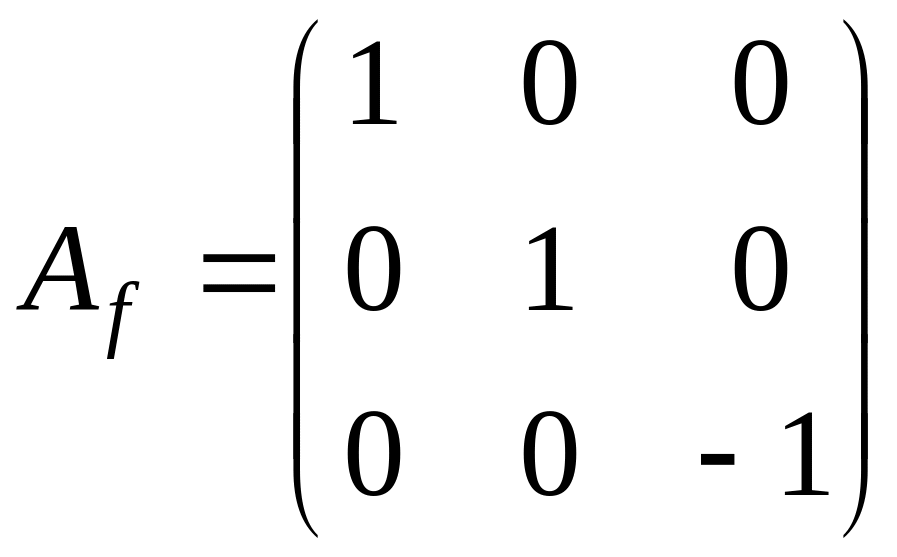
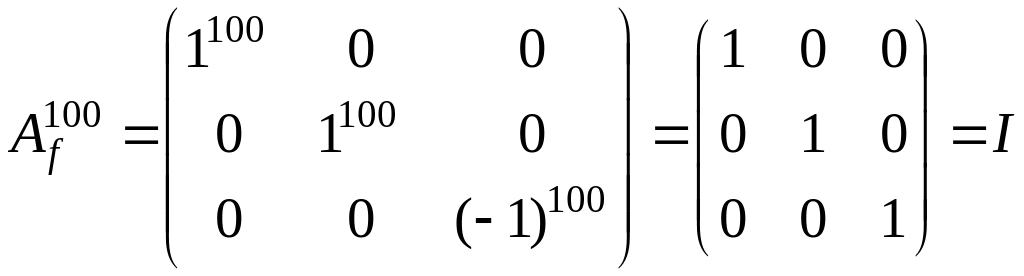




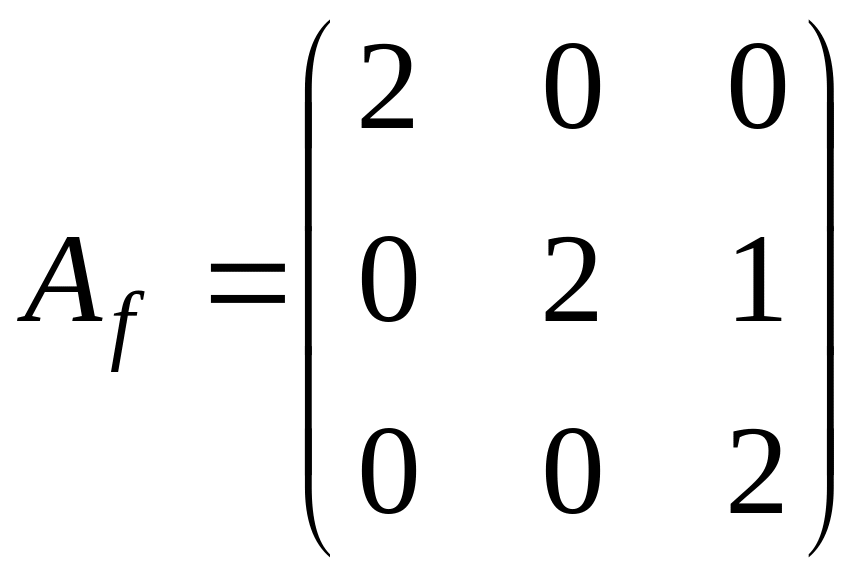

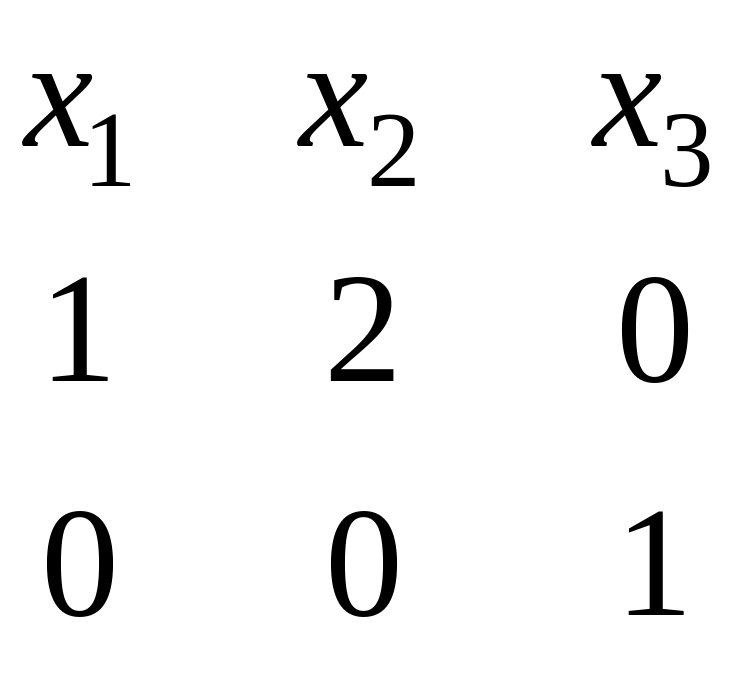

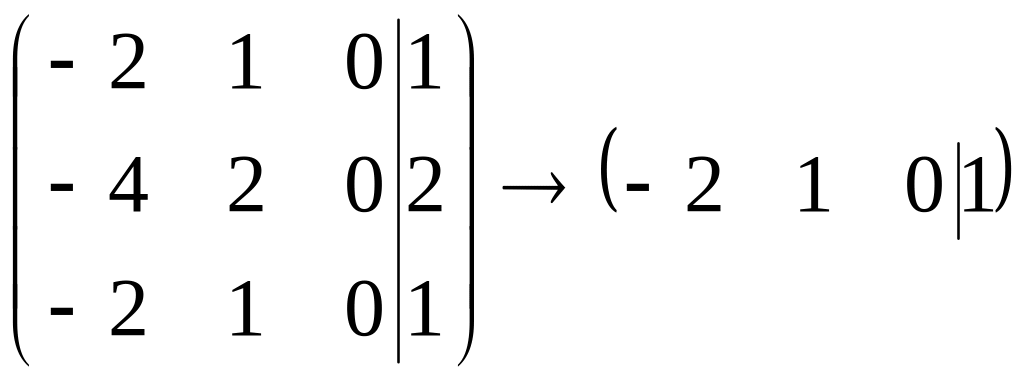

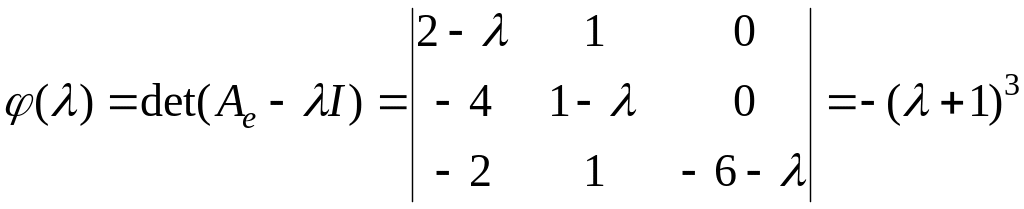
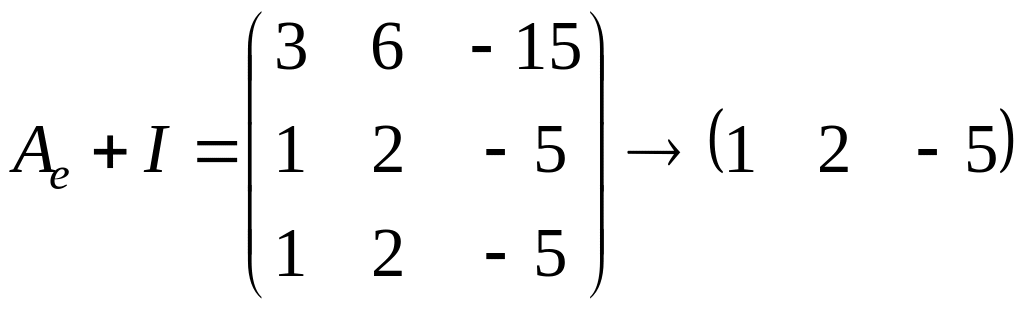

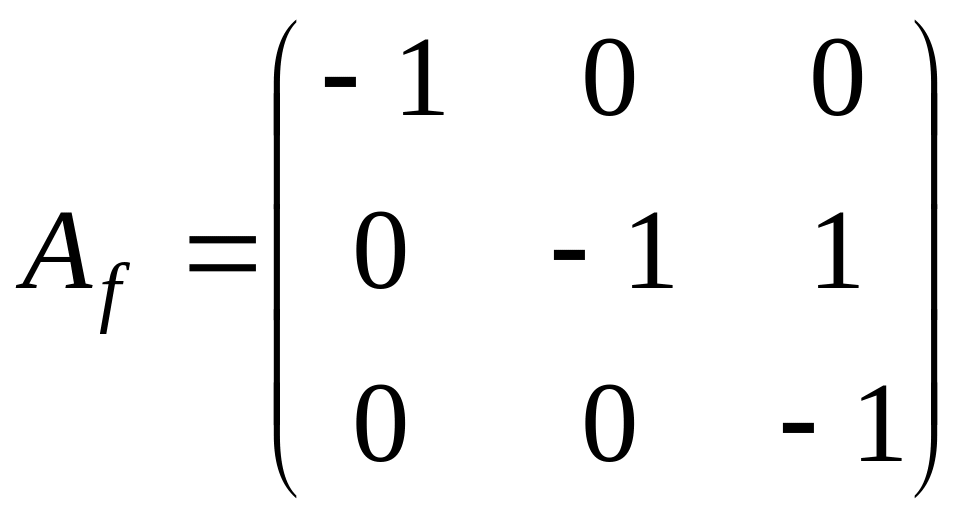


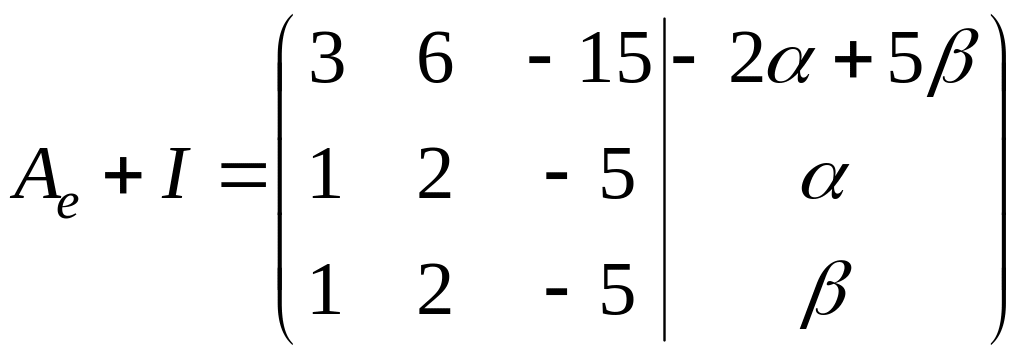
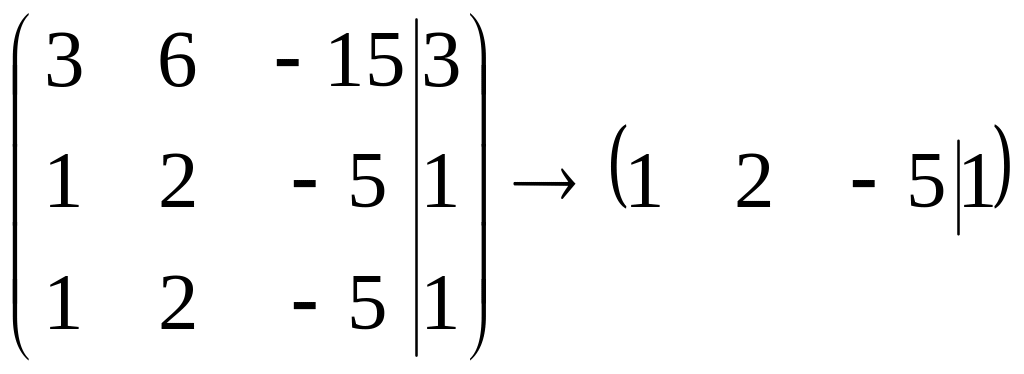

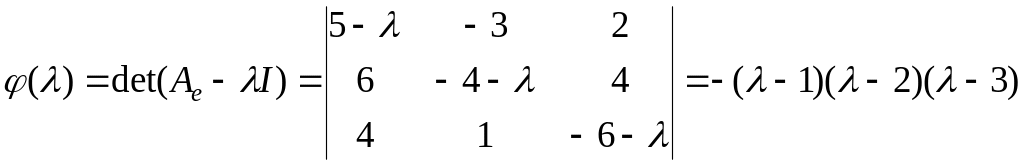
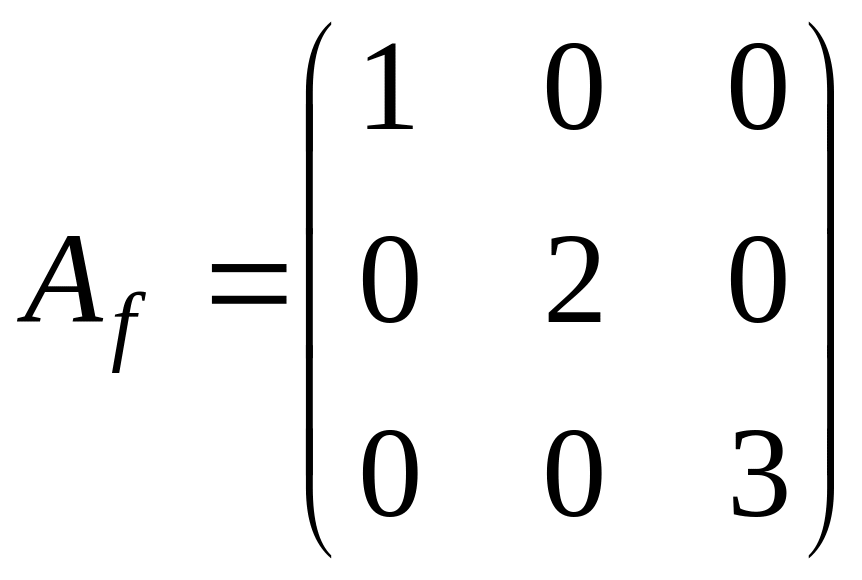
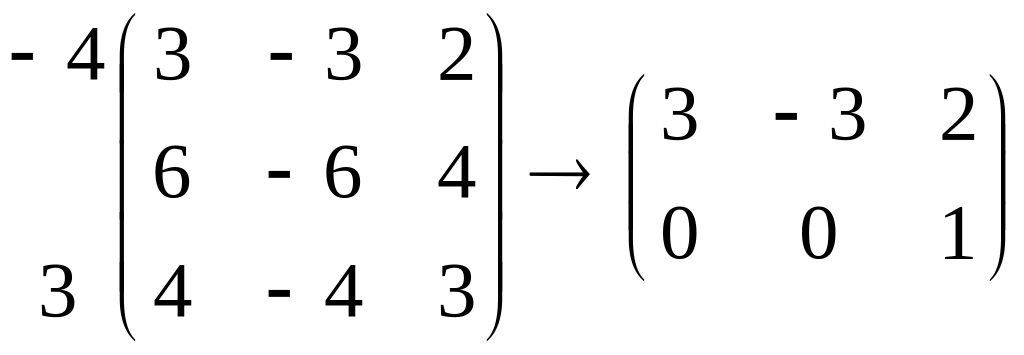
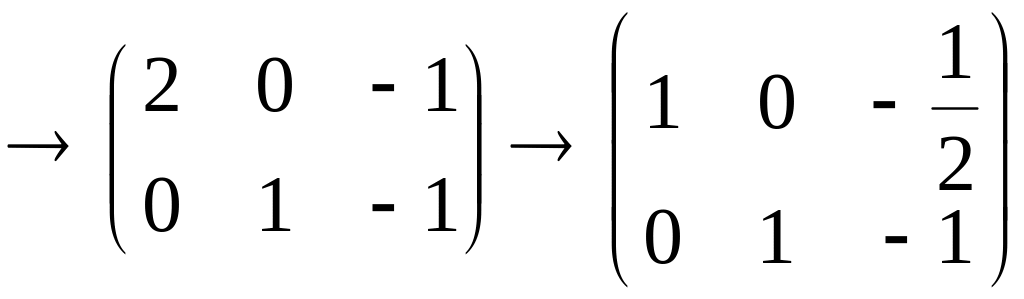
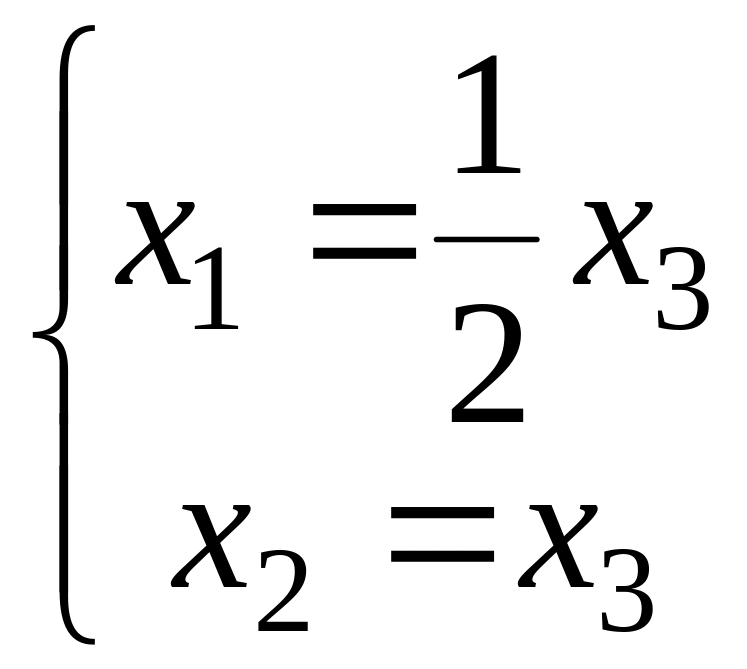
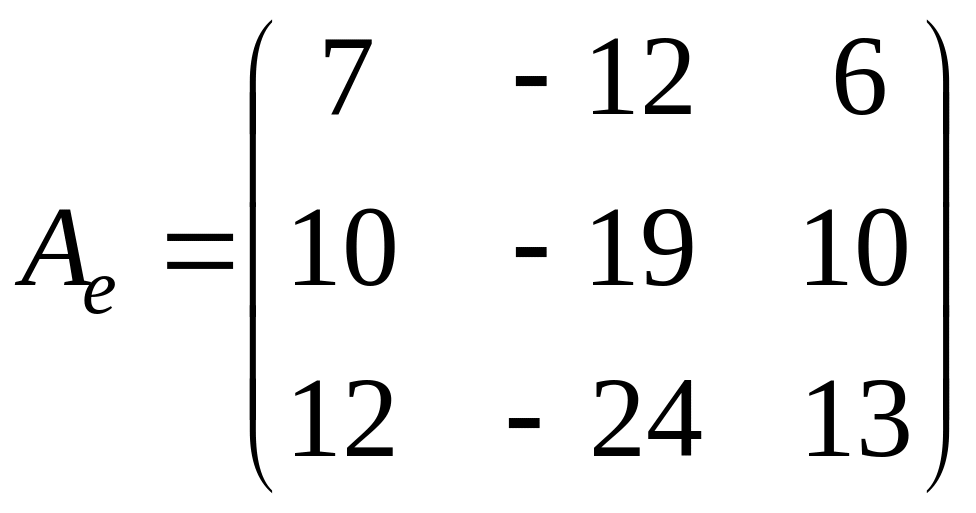
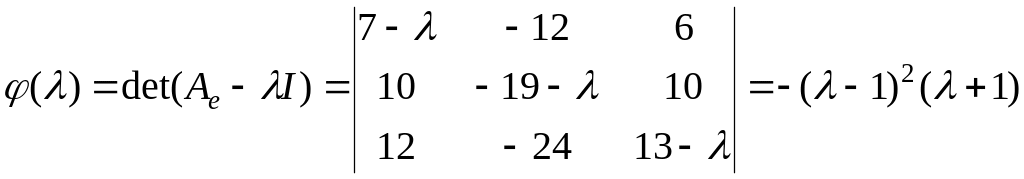
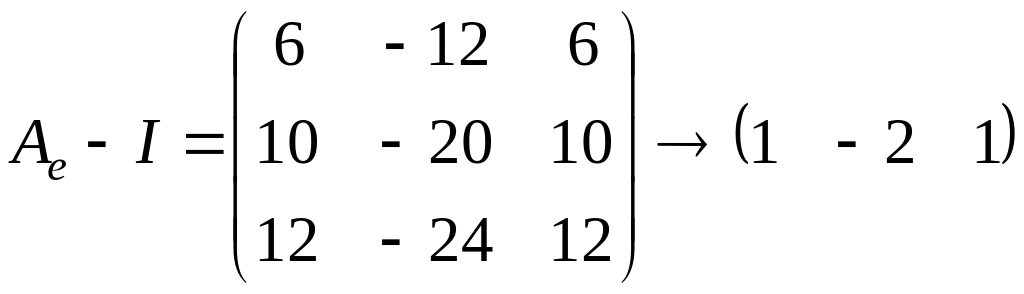
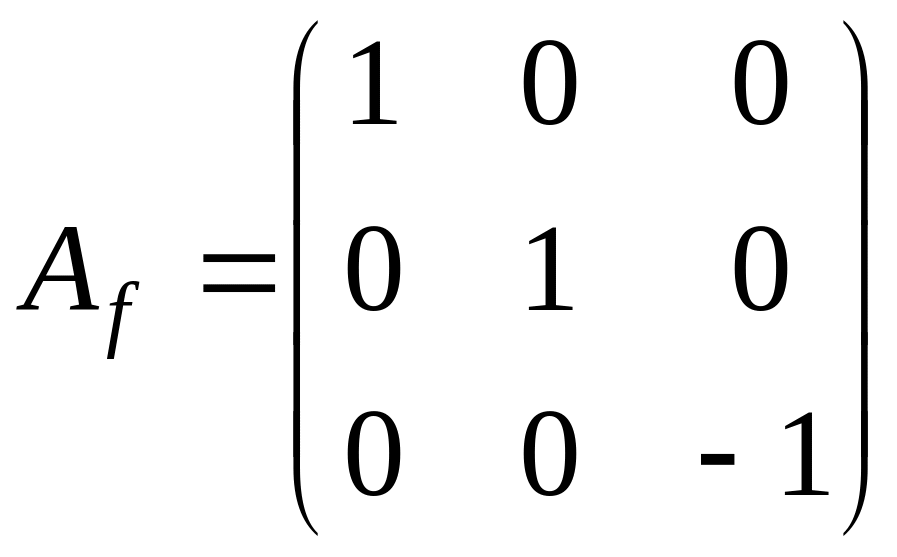
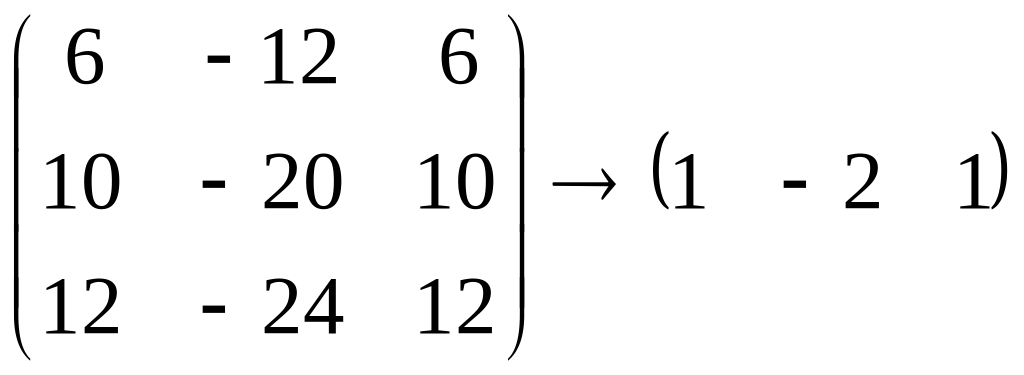
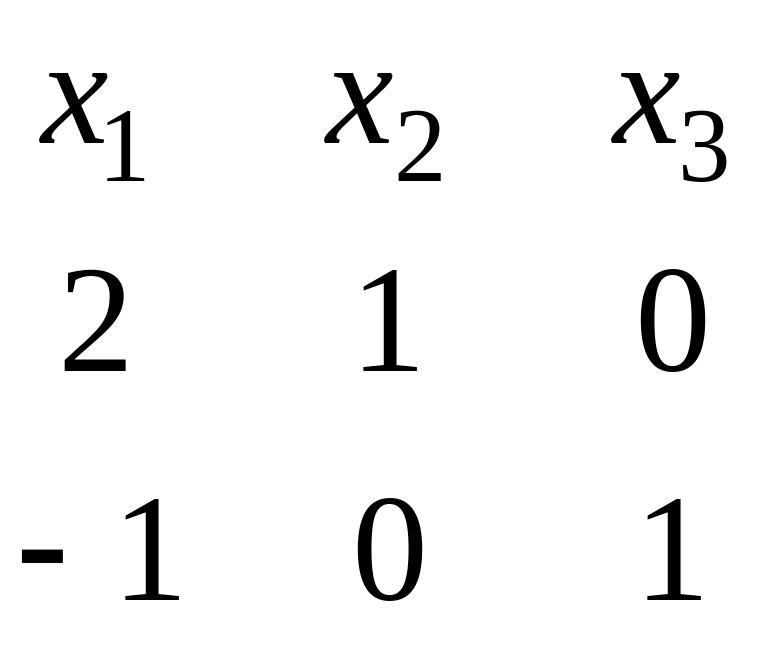

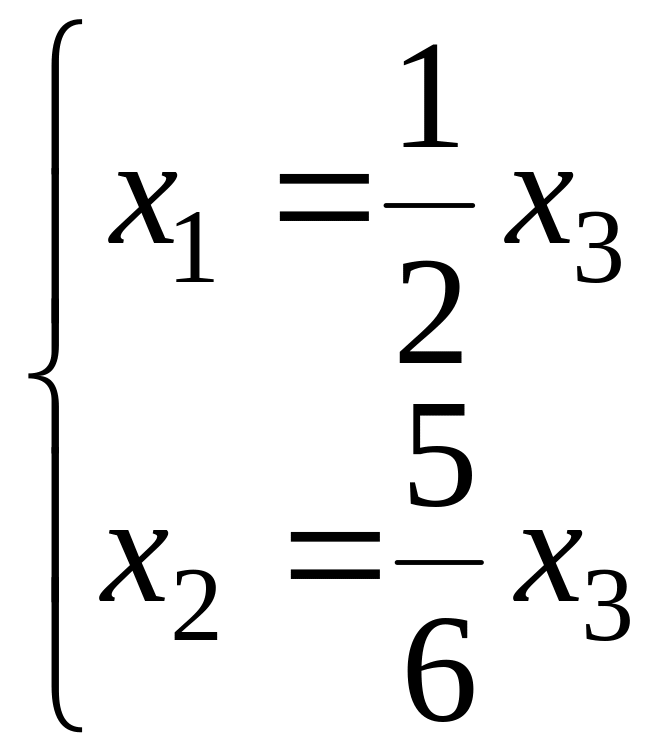









![{displaystyle A=left[{begin{array}{*{20}{r}}5&4&2&1\[2pt]0&1&-1&-1\[2pt]-1&-1&3&0\[2pt]1&1&-1&2end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/088ce7bbdb5151670fcab730b253ad4e5cf9c4c6)
![{displaystyle J={begin{bmatrix}1&0&0&0\[2pt]0&2&0&0\[2pt]0&0&4&1\[2pt]0&0&0&4end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6619a0fba90f217d06d070c5c83bd503575d2f04)











![{displaystyle A=left[{begin{array}{rrrr}5&4&2&1\0&1&-1&-1\-1&-1&3&0\1&1&-1&2end{array}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62067270065d03570c4683630978155bca215b77)


![{displaystyle ker(A-4I)^{2}=operatorname {span} ,left{{begin{bmatrix}1\0\0\0end{bmatrix}},left[{begin{array}{r}1\0\-1\1end{array}}right]right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bda4686073e56551fc5c6388f7b296357b246f8d)
![{displaystyle P=left[{begin{array}{c|c|c|c}v&w&x¥d{array}}right]=left[{begin{array}{rrrr}-1&1&1&1\1&-1&0&0\0&0&-1&0\0&1&1&0end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fbe8bda39f87aab54e3f7c68b6ef6ee4f727e78)








![{displaystyle C_{i}=left[{begin{array}{rr}a_{i}&-b_{i}\b_{i}&a_{i}\end{array}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd4b41c9734014e09f29e21864955dddd6be654f)