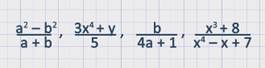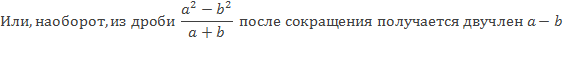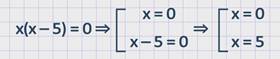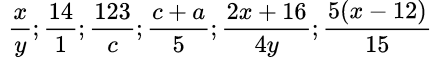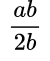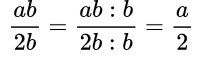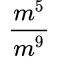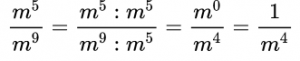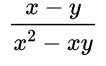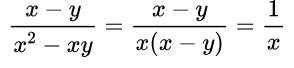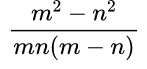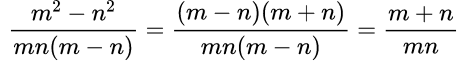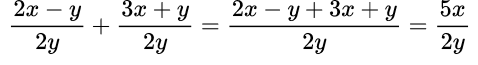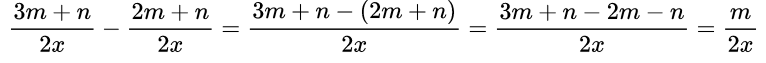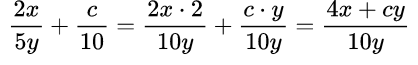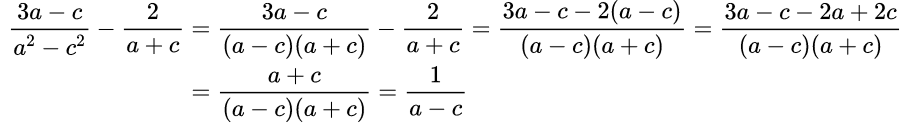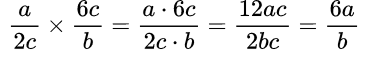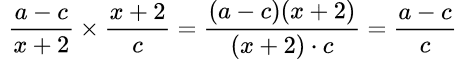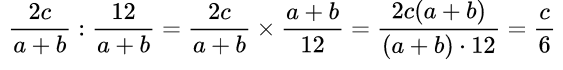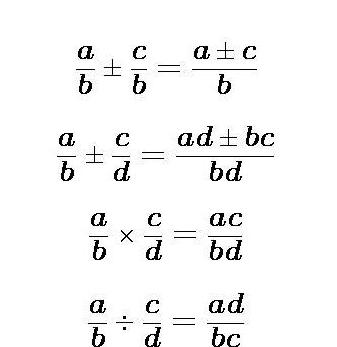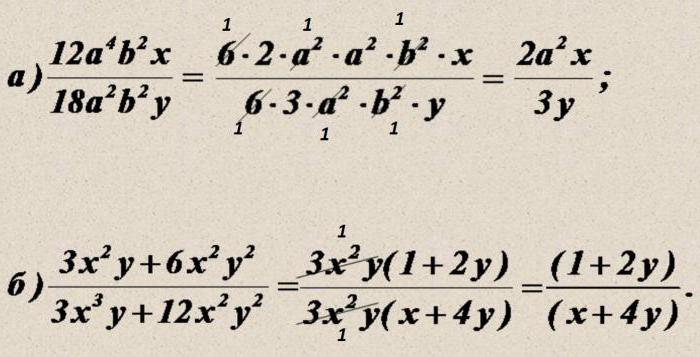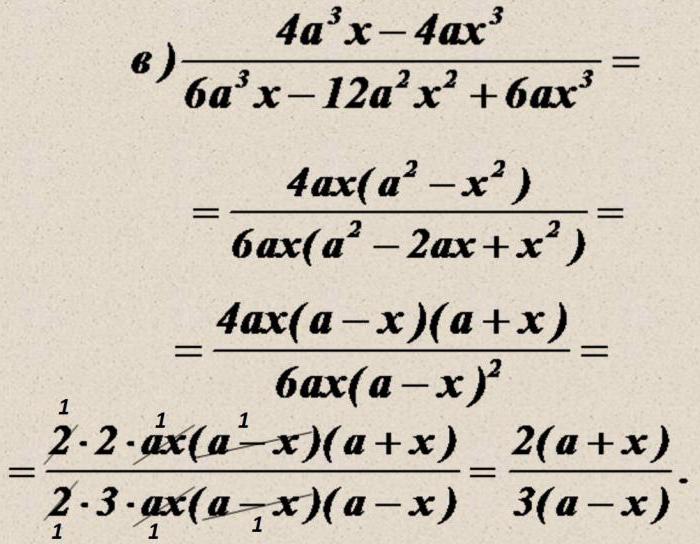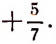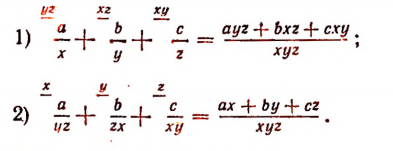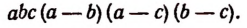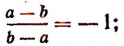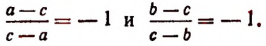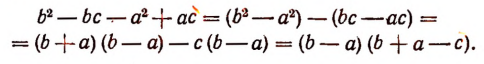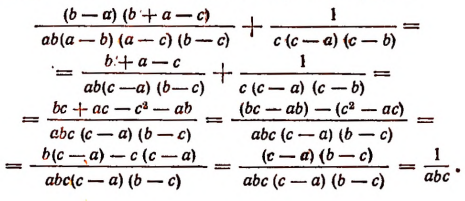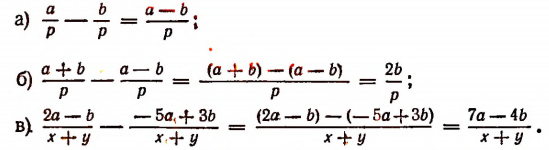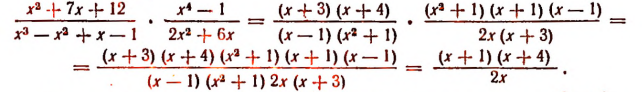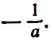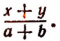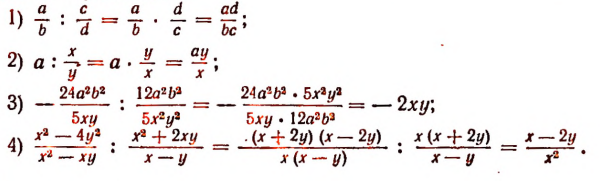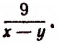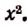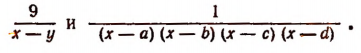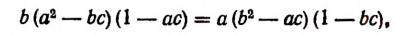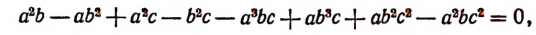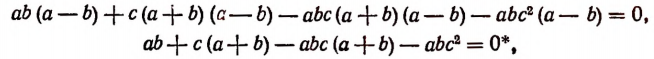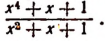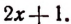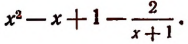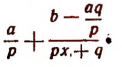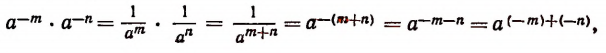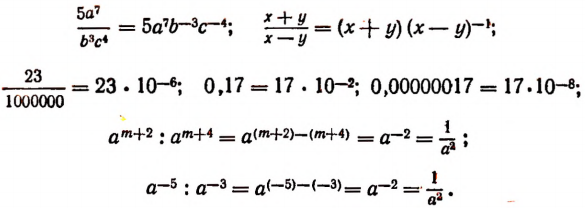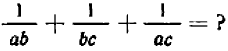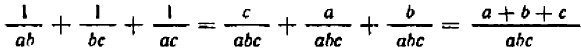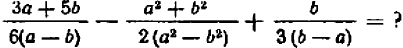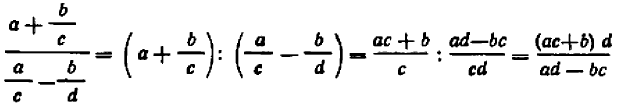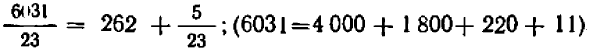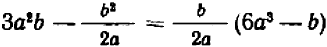Определение алгебраической дроби
Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).
Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).
Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.
Алгебраические (рациональные) дроби
Иррациональные дроби
$ frac{25+x^2}{x-4}$
$ frac{a^3-2sqrt3}{b^2-sqrt[3]13}$
$ frac{5+sqrt x}{4-x} $
$ frac{16a^frac{5}{3}+1}{4sqrt[3]a-1} $
Внимание!
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
Например: Дробь $frac{x+5}{x-4}$ существует при условии x≠4. Допустимые значения переменной ${x| x in Bbb R, x neq 4 } $.
Дробь $frac{y}{y^2-9}$ существует при условии y≠±3. Допустимые значения переменной $ { y| y in Bbb R, y neq pm 3 }$.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
$$ frac{a}{b} = frac{ma}{mb}, b neq 0, m neq 0 $$
Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:
$$ frac{2x+3y}{4x^2-9y^2} = frac{2x+3y}{(2x+3y)(2x-3y)} = frac{1}{2x-3y} $$
$$ frac{a^3-8}{a-2} = frac{(a-2)(a^2+2a+4)}{a-2} = a^2+2a+4 $$
Приведение алгебраических дробей к общему знаменателю
Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:
$$ frac{1^{(x+1)}}{x-1} – frac{1}{x^2-1} – frac{1^{(x-1)}}{x+1} = frac{x+1-1-(x-1)}{(x-1)(x+1)} = frac{1}{x^2-1} $$
Алгоритм приведения алгебраических дробей к общему знаменателю
- Разложить все знаменатели на множители (коэффициенты, степени переменных, двучлены, трехчлены, многочлены)
- Найти наименьшее общее кратное знаменателей – это будет общий знаменатель.
- Найти дополнительные множители для каждой из дробей.
- Умножить числитель каждой из дробей на её дополнительный множитель, записать результат с общим знаменателем.
Например: привести к общему знаменателю $frac{1}{xy^2}, frac{x}{y}, frac{-4}{x}$
Шаг 1. Наименьшее общее кратное: $xy^2$
Шаг 2. Дополнительные множители
$$ frac{1}{xy^2}, frac{x^{xy}}{y}, -frac{4^{y2}}{x}$$
Шаг 3. Результат:
$$ frac{1}{xy^2}, frac{x^2 y}{xy^2}, -frac{4y^2}{xy^2} $$
Перемена знака у члена дроби
Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:
$$ frac{x}{y} = frac{-x}{-y} $$
Дробь также не изменится, если провести следующие перемены знаков:
$$ frac{x}{y} = frac{-x}{y} = -frac{x}{-y} $$
Ещё несколько полезных формул, связанных с переменой знаков:
$$ frac{a-b}{b-a} = -1, frac{(a-b)^2}{(b-a)^2} = 1, frac{1}{a-b} = -frac{1}{b-a}, frac{1}{(a-b)^2} = frac{1}{(b-a)^2} $$
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
а)$ frac{5}{a^2-4}$
$ a^2-4 neq 0 iff (a-2)(a+2) neq 0 iff a neq pm 2$
${a| a in Bbb R, a neq pm 2}$ – все действительные числа, кроме $pm 2$
б)$ frac{7x+y}{3x-1}$
$ 3x-1 neq 0 iff x neq frac{1}{3}$
${x|x in Bbb R, x neq frac{1}{3}}$ – все действительные числа, кроме $frac{1}{3}$
в)$ frac{k^2-1}{k+1}$
$k+1 neq 0 iff k neq -1 $
${k|k in Bbb R, k neq -1}$ – все действительные числа, кроме -1
Обратите внимание: несмотря на то, что дробь сокращается $frac{k^2-1}{k+1} = frac{(k+1)(k-1)}{k+1} = k-1$ требование $k neq -1$ сохраняется.
г) $ frac{5}{x^2+6x+9}$
$x^2+6x+9 neq 0 iff (x+3)^2 neq 0 iff x neq -3 $
$ {x|x in Bbb R, x neq -3}$ – все действительные числа, кроме -3
д)*$ frac{1}{x-frac{4}{x}} $
$$ x- frac{4}{x} neq 0 iff frac{x^2-4}{x} neq 0 iff {left{ begin{array}{c} x^2-4 neq 0 \ x neq 0 end{array} right.} iff x neq {0; pm2}$$
${x|x in Bbb R, x neq {0;pm2}}$ – все действительные числа, кроме $0,pm2$
е)*$ frac{5}{y^2-3|y|} $
$ y^2-3|y| neq 0 iff |y|(|y|-3) neq 0 iff {left{ begin{array}{c} |y| neq 0 \ |y| neq 3 end{array} right.} iff y neq {0; pm3} $
${y|y in Bbb R, y neq {0; pm3} }$ – все действительные числа, кроме $0, pm3$
Пример 2. Сократите дроби:
а) $$ frac{a^2-9}{2a+6} = frac{(a-3)(a+3)}{2(a+3)} = frac{a-3}{2}$$
б)$$ frac{x^2+2x+1}{x^2-1} = frac{(x+1)^2}{(x+1)(x-1)} = frac{x+1}{x-1}$$
в) $$ frac{12x^2-8xy}{3xy-2y^2} = frac{4x(3x-2y)}{y(3x-2y)} = frac{4x}{y} $$
г) $$ frac{b+5}{b^3-125} = frac{b+5}{(b+5)(b^2-5b+25)} = frac{1}{b^2-5b+25} $$
Пример 3. Упростите выражение:
а) $$ frac{a-b}{(b-a)^2} = frac{a-b}{(a-b)^2} = frac{1}{a-b}$$
б) $$ frac{(-a-b)^2}{a+b} = frac{(-1)^2 (a+b)^2}{a+b} = a+b $$
в) $$ frac{(-a-b)^2}{(a+b)^2} = frac{(a+b)^2}{(a+b)^2} = 1 $$
г) $$ frac{(a-b)^2}{b-a} = frac{(b-a)^2}{b-a} = b-a $$
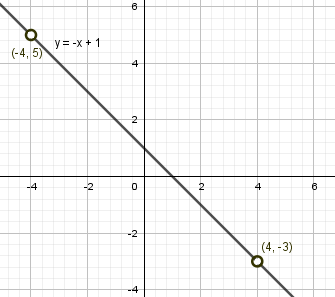
Пример 4. Постройте график функции:
(О графике линейной функции – см. §38 справочника для 7 класса)
$а) y(x) = frac{x^2-4}{2x+4}$
$$ y(x) = frac{(x-2)(x+2)}{2(x+2)} = {left{ begin{array}{c} frac{x-2}{2} \ x neq -2 end{array} right.} $$
График – прямая y(x) = 0,5x-1, кроме точки (-2;-2), т.к. $x neq -2$.
$б) y(x) = frac{x^3-16x}{x^2-16}-2x+1$
$$ y(x) = frac{x(x^2-16)}{x^2-16}-2x+1 = {left{ begin{array}{c} -x+1 \ x neq pm 4 end{array} right.} $$
График – прямая y(x) = -x+1, кроме точек (-4;5) и (4;-3), т.к. $x neq pm 4$.
Содержание:
- § 1 Понятие алгебраической дроби
- § 2 Допустимые значения переменных алгебраической дроби
§ 1 Понятие алгебраической дроби
Алгебраической дробью называют выражение
где Р и Q —многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
Любой многочлен – это частный случай алгебраической дроби, потому что любой многочлен можно записать в виде
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, вычислим значение дроби
1)
2)
В первом случае получаем:
Заметим, данную дробь можно сократить:
Таким образом, вычисление значения алгебраической дроби упрощается. Воспользуемся этим.
Во втором случае получим:
Как видно, с изменением значений переменных изменилось значение алгебраической дроби.
§ 2 Допустимые значения переменных алгебраической дроби
Рассмотрим алгебраическую дробь
Значение x = –1 является недопустимым для данной дроби, т.к. знаменатель дроби при таком значении х обращается в нуль. При этом значении переменной алгебраическая дробь не имеет смысла.
Таким образом, допустимыми значениями переменных алгебраической дроби являются такие значения переменных, при которых знаменатель дроби не обращается в нуль.
Решим несколько примеров.
Пример 1:
При каких значениях переменной не имеет смысла алгебраическая дробь:
Решение:
Для нахождения недопустимых значений переменных знаменатель дроби приравнивается к нулю, и находятся корни соответствующего уравнения.
Ответ:
Пример 2:
При каких значениях переменной равна нулю алгебраическая дробь:
Решение:
Дробь равна нулю, если числитель равен нулю. Приравняем к нулю числитель нашей дроби и найдем корни получившегося уравнения:
Далее следует найти недопустимые значения переменной х. Действуем как в предыдущем примере, приравниваем к нулю знаменатель алгебраической дроби и решаем получившееся уравнение:
Таким образом, при x = 0 и x= 3 данная алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Ответ:
Итак, на этом уроке Вы изучили основные понятия алгебраической дроби: числитель и знаменатель дроби, а также допустимые значения переменных алгебраической дроби.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений / А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2007. – 215 с.: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.2 Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – 8-е изд., – М.: Мнемозина, 2006 – 239с.
- Алгебра. 8 класс. Контрольные работы для учащихся образовательных учреждений Л.А. Александрова под ред. А.Г. Мордковича 2-е изд., стер. – М.: Мнемозина 2009. – 40с.
- Алгебра. 8 класс. Самостоятельные работы для учащихся образовательных учреждений: к учебнику А.Г. Мордковича, Л.А. Александрова под ред. А.Г. Мордковича. 9-е изд., стер. – М.: Мнемозина 2013. – 112с.
Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.
Примеры алгебраических дробей:
Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.
Сокращение алгебраической дроби
Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.
Пример №1. Сократим дробь:
В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:
Промежуточные действия можно не записывать, а выполнять устно.
Пример №2. Сократим дробь:
Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m5:
Пример №3. Сократим дробь:
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).
Пример №4. Сократим дробь:
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m2– n2=(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).
Сложение и вычитание алгебраических дробей с одинаковым знаменателем
При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).
Пример №5. Выполним сложение дробей:
Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.
Пример №6. Выполним вычитание дробей:
В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.
Сложение и вычитание алгебраических дробей с разными знаменателями
Алгоритм действий
Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:
- найти общий знаменатель, который может состоять из таких множителей, как числа, степени, многочлены и т.д.
- Найти дополнительный множитель к каждой дроби.
- Умножить каждый числитель на его дополнительный множитель.
- Выполнить сложение (вычитание) дробей с одинаковыми знаменателями.
- При необходимости сократить полученную дробь.
Пример №7. Выполнить сложение дробей:
Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.
Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.
Пример №8. Выполнить вычитание дробей:
Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а2 – с2=(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).
Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).
Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).
Умножение алгебраических дробей
Алгоритм действий
Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.
Пример №9. Выполнить умножение дробей:
Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.
Пример №10. Выполнить умножение дробей:
Здесь в числителях и знаменателях – многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.
Деление алгебраических дробей
Алгоритм действий
Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.
Пример №11. Выполнить деление дробей:
Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.
Задание OM1306o
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению:
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b):
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):
Подставим полученные значения в выражение и найдем конечный результат:
Ответ: 39
pазбирался: Даниил Романович | обсудить разбор
Задание OM1305o
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
pазбирался: Даниил Романович | обсудить разбор
Задание OM1304o
Найдите значение выражения
где a = 9, b = 36
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
9b² + 5a – 9b²
Приведем подобные слагаемые – это 9b² и – 9b², в числителе остается 5a. Запишем конечную дробь:
5a/b
Вычислим её значение, подставив числа из условия:
5•9/36 = 1,25
Ответ: 1,25
pазбирался: Даниил Романович | обсудить разбор
Задание OM1303o
Найдите значение выражения:
при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y
Подставим значение y = 0,5: – 1 / (5 • 0,5) = – 1 / 2,5 = – 0,4
Ответ: -0,4
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 8.2k
Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. Как решать алгебраические дроби? Вопрос, который будет мучить на протяжении всей школьной жизни.
Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.
Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.
Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.
Основное правило обыкновенных дробей
Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей.
Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами.
Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.
Математические операции с дробями
Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.
Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но! Нужно помнить, что при наличии знака «–» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как сокращение дробей. Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру.
Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов:
- Нахождение НОД для обеих частей дроби.
- Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предшествующей.
Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть.
Несколько примеров с решениями
С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал.
1. Преобразовать дроби и привести их к общему знаменателю.
2. Преобразовать дроби и привести их к общему знаменателю.
3. Сократить указанные выражения (с использованием изученного основного правила дроби и сокращения степеней)
4. Сократить многочлены. Подсказка: нужно обнаружить формулы сокращенного умножения, привести к подобающему виду, сократить одинаковые элементы.
Задание на закрепление материала
1. Какие действия нужно произвести, что найти скрытое число? Решите примеры.
2. Умножьте и поделите дроби, пользуясь основным правилом.
После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно.
Определение и основное свойство дроби:
Определение:
Частное (отношение) двух алгебраических выражений, записанное при помощи черты деления, называется алгебраической дробью. Например, выражения
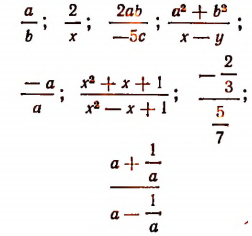
суть алгебраические дроби. При этом делимое называется числителем, а делитель — знаменателем. Например, алгебраическая дробь
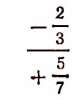
имеет числителем число 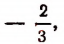
Основное свойство алгебраической дроби. Величина алгебраической дроби не изменится, если числитель и знаменатель умножить (или разделить) на одно и то же число, не равное нулю. Это свойство следует из того, что частное не меняется при умножении (или делении) делимого и делителя на одно и то же число, не равное нулю.
Основное свойство дроби записывается в виде формул:
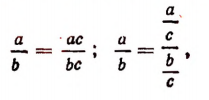
где
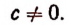
Несократимые и сократимые дроби
Если наибольший общий делитель числителя и знаменателя дроби равен единице, то дробь называется несократимой. Например: .
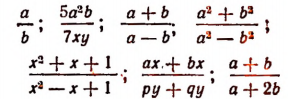
суть несократимые дроби.
Если же наибольший общий делитель числителя и знаменателя отличен от единицы, то дробь называется сократимой. Например:
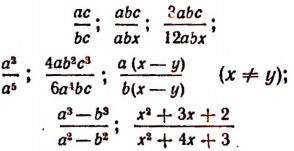
суть сократимые дроби.
Если числитель или знаменатель дроби отдельно или одновременно являются многочленами, то для решения вопроса о сократимости или несократимости этой дроби необходимо эти многочлены предварительно разложить на целые неприводимые множители, если это возможно. Например, дробь 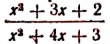
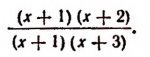
Если числитель и знаменатель дроби разделить на их наибольший общий делитель, то получится . несократимая дробь, тождественно равная данной дроби.
Примеры сокращения дробей:
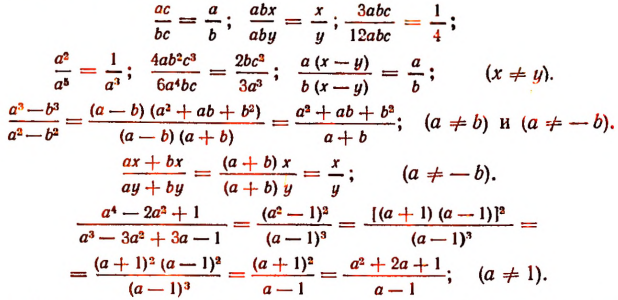
Сократить дробь — это значит разделить числитель и знаменатель этой дроби на какой-нибудь их общий множитель.
Полученная после этого новая дробь будет тождественно равна первоначальной дроби. Например,
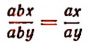
(Здесь дробь сокращена только на общий множитель b.)
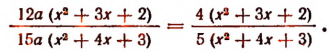
(Здесь дробь сокращена только на За.)
Примечание:
Выражение 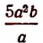
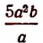
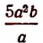
Перемена знаков у членов дроби
Если числитель и знаменатель дроби заменить величинами, им противоположными, то значение дроби не изменится, так как эта операция равносильна умножению числителя и знаменателя на одно и то же число —1. Например,
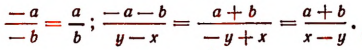
Если числитель дроби заменить величиной, ему противоположной, и при этом переменить знак, стоящий перед дробью, на противоположный, то получится выражение, равное первоначальному.
Например:
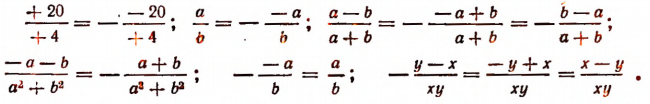
Если знаменатель дроби заменить величиной, ему противоположной, и при этом переменить знак, стоящий перед дробью, на противоположный, то получится выражение, равное первоначальному.
Например:
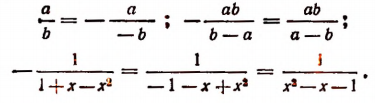
Примечание. Так как а — b и b — а являются величинами противоположными, то 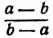
Если же а = b , то выражение обращается в 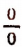
Наименьшее общее кратное
Из арифметики известно, что наименьшим общим кратным произведений
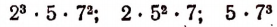
является произведение
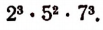
По аналогии с этим наименьшим общим кратным произведений
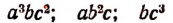
будет выражение
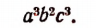
Наименьшим общим кратным произведений
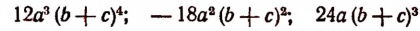
будет
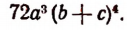
Наименьшим общим кратным произведений
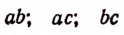
будет
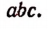
Чтобы составить наименьшее общее кратное нескольких многочленов, следует сначала эти многочлены разложить на неприводимые множители.
Примеры:
1. Найти наименьшее общее кратное многочленов
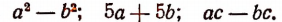
Очевидно, что
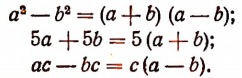
Искомым наименьшим кратным будет
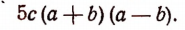
2. Найти наименьшее общее кратное многочленов

Очевидно, что
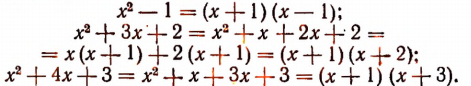
Искомым наименьшим кратным будет
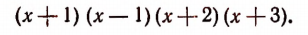
Сложение и вычитание дробей
Сложение дробей с одинаковыми знаменателями
Правило. Чтобы сложить дроби с. одинаковыми знаменателями, надо сложить их числители, оставив знаменатель без изменения.
Примеры:
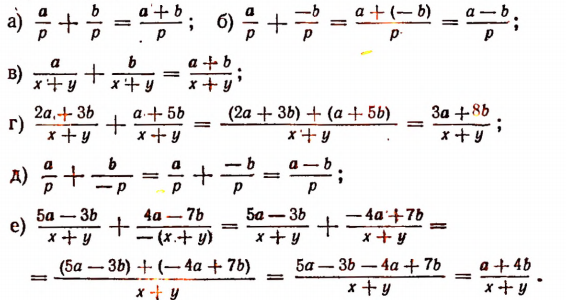
Сложение дробей с одночленными знаменателями
Правило. Чтобы сложить дроби с различными одночленными знаменателями, надо:
- Составить наименьшее кратное знаменателей всех дробей и принять его за общий знаменатель.
- Найти дополнительный множитель для каждой дроби.
- Сумму произведений дополнительных множителей на соответствующие числители разделить на общий знаменатель.
Примеры:
Рассмотрим еще такой пример:
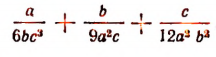
Здесь общий знаменатель
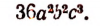
Дополнительный множитель для
Поэтому получим:
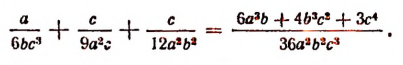
Сложение дробей, среди знаменателей которых встречаются многочлены
Чтобы сложить дроби, среди знаменателей которых встречаются многочлены, сначала эти многочлены следует разложить на неприводимые множители. Далее надо поступать, как и при сложении дробей с одночленными знаменателями.
Примеры:
Найти сумму трех дробей:
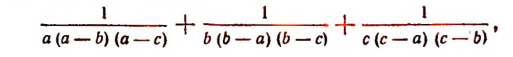
где а и b и с различные числа, отличные от нуля. Искомую сумму найдем двумя способами.
1-й способ. Общим знаменателем всех трех дробей будет произведение
Множитель (b—а) не следует включать в общий знаменатель, так как его абсолютная величина такая же, как и абсолютная величина множителя (а — b). По такой же причине не включается и множитель (с — b).
Дополнительными множителями будут:
для первой дроби 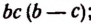
для второй 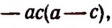
для третьей 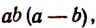
Поэтому
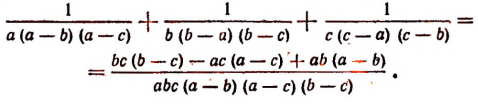
Преобразуем числитель последней дроби:
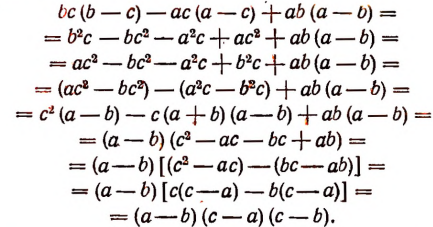
Таким образом, сумма данных трех дробей будет равна
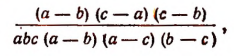
или 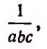
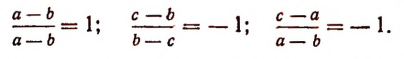
2-й способ. Найдем сперва сумму первых двух дробей:
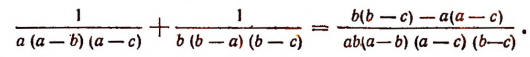
Преобразуем числитель этой дроби:
Теперь искомая сумма трех заданных дробей будет:
Вычитание дробей с одинаковыми знаменателями
Правило. Чтобы вычесть из одной дроби другую с тем же знаменателем, надо вычесть числитель второй дроби из числителя первой и подписать общий знаменатель.
Например:
Вычитание дробей в более сложных случаях выполняется аналогично тому, как и сложение.
Пример:
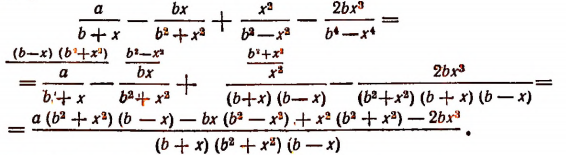
Преобразуем числитель полученной дроби:
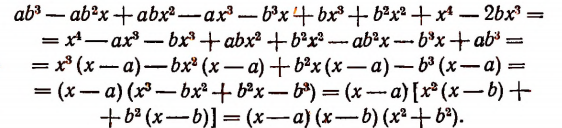
Таким образом, алгебраическая сумма данных четырех дробей будет равна дроби
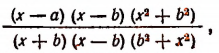
которая после сокращения примет вид
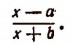
Умножение дробей
Чтобы перемножить дроби, надо произведение их числителей разделить на произведение знаменателей.
Например:
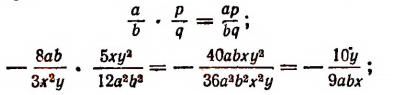
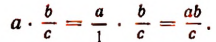
Если среди числителей и знаменателей дробей имеются многочлены, то эти многочлены целесообразно разложить на множители и лишь после этого совершать операцию умножения дробей.
Например:
Само собой разумеется, что при умножении дроби 
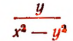
Взаимно обратные выражения
Определение. Два алгебраических выражения называются взаимно обратными, если их произведение равно единице. Например, выражения а и 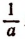
Если данное выражение 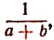
Если данное выражение — a, то ему обратным будет
Если данное выражение 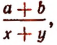
Если данноe число 1, то ему обратным будет тоже 1.
Нуль обратного себе числа не имеет.
Деление дробей
Чтобы разделить одну дробь на другую или одно выражение на другое, достаточно первую дробь или первое выражение умножить на величину, обратную второй дроби или второму выражению.
Таким образом, деление дробей или алгебраических выражений сводится к умножению.
Упрощение дроби, числитель и знаменатель которой являются алгебраическими суммами дробей
Пример:
Чтобы упростить лучшим способом дробь
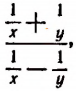
умножим ее числитель и знаменатель на ху. В результате получим 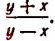
Чтобы упростить дробь
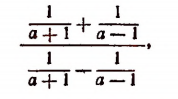
умножим ее числитель и знаменатель на выражение
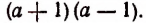
В результате получим:
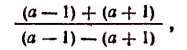
т. е. 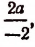
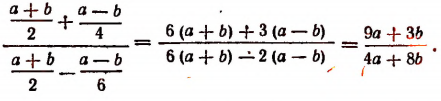
Общее преобразование рациональных выражений
Сколь бы сложным ни было даyное выражение, если оно рационально, т. е. содержит лишь действия сложения, вычитания, умножения и деления, то его всегда можно преобразовать так, что в результате получится либо целое выражение, либо несократимая дробь, числитель и знаменатель которой суть целые выражения. Например, выражение
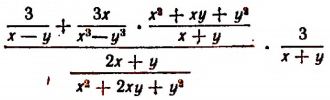
тождественно равно выражению
Выражение
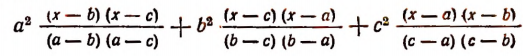
тождественно равно выражению
Выражение
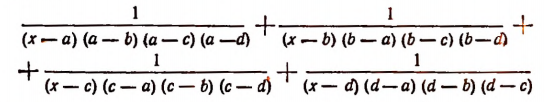
тождественно равно выражению
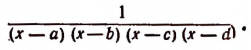
Во втором примере в результате преобразования получилось целое выражение
В качестве примера на применение общих преобразований рациональных выражений покажем, что из равенства
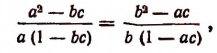
если а, b, c не равны между собой и отличны от нуля, вытекает равенство
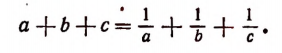
Решение:
Из данного равенства следует:
или после раскрытия скобок и переноса всех членов в левую часть:
или последовательно
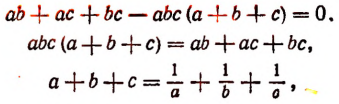
что и требовалось доказать.
Выделение целой части неправильной рациональной дроби
Выражение
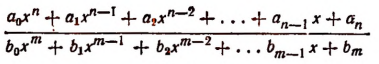
называется рациональной дробью.
Если 

Например, рациональные дроби
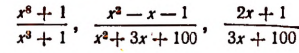
являются неправильными.
Рациональные дроби
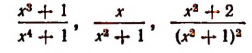
являются правильными.
Выделение целой части
Пусть требуется выделить целую часть неправильной рациональной дроби, например дроби
Разделим многочлен 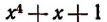
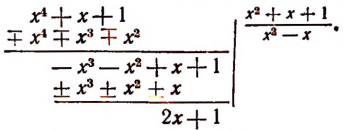
Получили частное 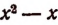
Делимое равно делителю, умноженному на частное плюс остаток. Поэтому
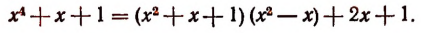
Разделив левую и правую части этого тождества на 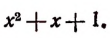
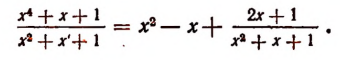
Выражение 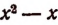
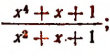
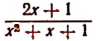
Таким образом, неправильная рациональная дробь
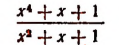
оказалась представленной в виде суммы многочлена 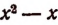
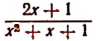
Изложенное преобразование применимо ко всякой неправильной рациональной дроби.
В курсе высшей математики встречаются задачи, для решения которых необходима операция выделения целой части неправильной рациональной дроби.
Примеры:
1. Выделить целую часть неправильной рациональной дроби
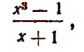
т. е. представить эту дробь в виде алгебраической суммы целого многочлена и правильной рациональной дроби.
Отв.
2. Выделить целую часть дроби
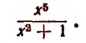
3. Выделить целую часть дроби
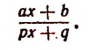
Отв.
О символах 
1. О символе
Символ 
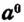
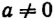
Итак, примем по определению, что 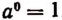
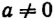
Тогда
Выражение же 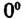
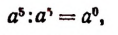
где 
2. О символе
Символ 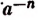
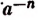
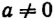
Итак, примем по определению, что 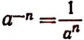
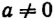
Тогда
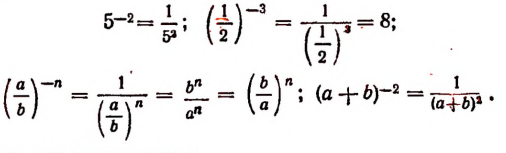
Теперь мы можем писать
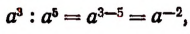
где 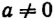
И эта запись будет вполне оправданной. В самом деле, левая часть есть 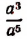
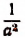
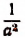
3. Действия над символами 
Хотя символы 
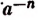
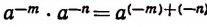
является верным.
что и требовалось доказать.
Также легко убедиться в справедливости и такого равенства
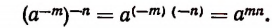
Действительно,
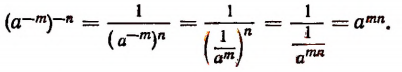
Все это позволяет нам символы 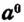
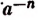
Символ 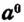
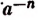
Теперь мы можем равенство
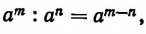
где 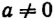
Примеры:
Очевидно, что
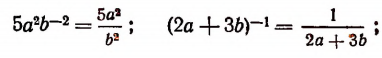
Алгебраические дроби и их решение
Если алгебраическое выражение, составленное из букв и чисел, содержит, кроме трех первых действий— сложения, вычитания и умножения, — также еще и деление (на буквенное выражение), то такое выражение называют дробным. Примером могут служить выражения: 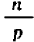
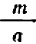
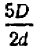
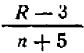
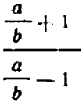
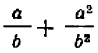
Если последнее действие, указываемое выражением, есть деление, то такое выражение называется просто «дробью (алгебраической дробью). При этом, если, кроме этого последнего действия, делений больше производить не нужно, дробь называется простой, в противном случае — сложной. Так, среди предыдущих примеров только последний нельзя назвать дробью (это сумма двух дробей); предпоследний есть сложная дробь, четыре предыдущих — простые дроби.
К сложным дробям мы обратимся несколько позднее; сначала же будем заниматься только простыми.
Простая алгебраическая дробь есть отношение двух целых алгебраических выражений, являющихся числителем и знаменателем дроби.
Мы знаем, что существует число, которое ни в коем случае не может быть знаменателем дроби: это — нуль; поэтому, если знаменатель про стой алгебраической дроби оказывается тождественное равным нулю, то сама дробь не имеет смысла ни при каких значениях входящих букв. Примером служит дробь
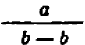
Иногда это отмечают и в явной форме: например, 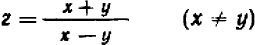
В дальнейшем, говоря о данной дроби, мы всегда будем подразумевать, что буквам даются лишь такие значения, которые не обращают знаменатель в нуль. Что касается числителя дроби, то исключать из рассмотрения те случаи, когда он обращается в нуль, излишне. Напомним, что если числитель дроби равен нулю, то и сама дробь равна нулю. Обратно, если дробь равна нулю, то непременно числитель равен нулю. Итак, простая алгебраическая дробь обращается в нуль при тех и только при тех значениях входящих букв, при которых ее числитель обращается в нуль.
Из арифметики отлично известно основное свойство дроби (частного); дробь (частное) не изменяется, если числитель (делимое) и знаменатель (делитель) умножить или разделить на одно и то же число 
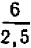
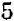
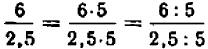
Число 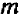
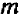
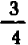
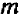
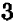
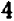
В виде формулы основное свойство дроби записывается следующим образом: 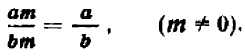
Основное свойство дроби можно выразить следующими словами; если некоторое выражение входит множителем в числитель и в знаменатель алгебраической дроби, то при условии, что оно не равно нулю, можно на него «сократить» данную дробь: значение дроби при этом не меняется. И, напротив, можно умножить числитель и знаменатель алгебраической дроби на произвольное выражение при условии, что оно не обращается в нуль.
Примечание:
Равенство (1), выражающее основное свойство дроби, считается тождеством, несмотря на то, что его левая часть теряет смысл при 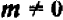

Вообще за равенством двух алгебраических выражений принято сохранять наименование тождества и в том случае, если одно из этих выражений или оба теряют смысл при некоторых исключительных значениях входящих букв. Такое расширенное понимание тождества, между прочим, позволяет относить сокращение дроби на буквенное выражение к числу тождественных преобразований.
Руководствуясь основным свойством дроби, можно сокращать алгебраическую дробь (как и арифметическую) на буквенные или числовые множители, входящие одновременно в ее числитель и в ее знаменатель.
Если таких множителей нет, дробь называют несократимой.
Например, дробь 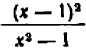

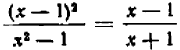
Левая и правая часть равенства тождественно равны (хотя левая теряет смысл при 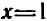
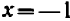
Мы переходим дальше к изучению действий над алгебраическими дробями — сложения, вычитания, умножения и деления. Выполнить одно из этих действий над данными простыми дробями — значит не только соединить эти дроби соответственным знаком, но также и произвести над полученным выражением тождественные преобразования, целью которых является представить это выражение в виде простой дроби (или целого выражения). Производя действия над дробями, стараются вместе с тем сокращать дробь на общие множители числителя и знаменателя.
При изучении действий над дробями мы начнем с более легких — умножения и деления, а затем перейдем к более трудным — сложению и вычитанию. Те случаи, когда какие-нибудь из данных выражений оказываются целыми, мы не будем рассматривать отдельно, так как всякое целое выражение можно представить в виде дробного, именно, подписывая под ним в качестве знаменателя единицу.
Умножение и деление дробей
Правило умножения арифметических дробей выражается формулой: 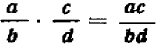
Написанная выше формула справедлива не только в том случае, если входящие буквы имеют целые положительные значения, но и в том случае, если эти значения — дробные; она справедлива также и в том случае, если некоторые из входящих букв имеют отрицательные значения. Значение нуль, конечно, исключено для знаменателей, но не исключено для числителей.
Но раз равенство (*) имеет место при всех значениях входящих букв (кроме тех исключительных, при которых знаменатели дробей обращаются в нуль), то оно является тождеством.
Таким образом, правило умножения алгебраических дробей выражается той же формулой и формулируется теми же словами, что и правило умножения арифметических дробей.
В алгебре вместо того, чтобы вычесть некоторое число, можно прибавить число, противоположное по знаку: 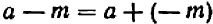
Таким же образом вместо того, чтобы разделить на некоторое число (не равное нулю), достаточно умножить на величину, обратную этому числу: 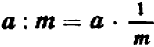
Действительно, следуя правилу умножения, мы получаем: 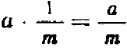
Так как величина, обратная дроби 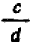
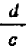
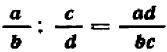
Чтобы разделить на дробь, достаточно умножить на величину, ей обратную («разделить на числитель и умножить на знаменатель).
Сложение и вычитание дробей
Сложить две алгебраические дроби означает — представить их сумму в виде одной алгебраической дроби; то же — для вычитания.
Если данные дроби имеют один и тот же знаменатель, то, чтобы сложить их — в алгебре, как и в арифметике, — достаточно составить дробь с тем же знаменателем и с числителем, равным сумме числителей: 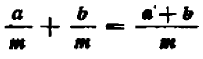
Это — распределительный закон деления, справедливый при любом 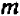
Если же складываемые дроби имеют различные знаменатели, то в алгебре, как и в арифметике, необходимо предварительно привести дроби к общему знаменателю. При этом пользуются основным свойством дроби — основным тождеством (*) , в котором мы теперь поменяем местами правую и левую части: 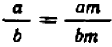
Желая сложить две дроби 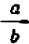
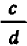
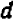
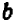
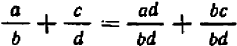
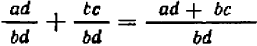
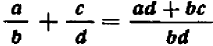
Подобным же образом, ссылаясь на распределительный закон деления и на основное свойство дроби, выведите общую формулу вычитания дробей: 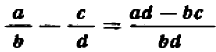
При действиях с дробями часто приходится пользоваться важным частным случаем основного свойства дроби (*) 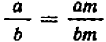
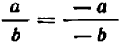
Таким образом, значение дроби не меняется при одновременном изменении знаков числителя и знаменателя.
Так как 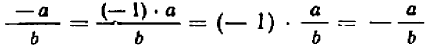
Отсюда следует: если мы меняем знак знаменателя, то, чтобы значение дроби не изменилось, достаточно еще изменить знак, или числителя или самой дроби; если мы меняем знак числителя, то, чтобы значение дроби не изменилось, достаточно еще изменить знак или знаменателя или самой дроби. Например,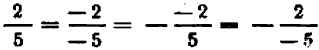
Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
В арифметике указывается правило для нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) нескольких целых чисел.
Пусть даны числа 
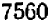
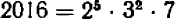
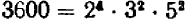
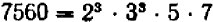
Составим новое число из данных чисел следующим образом: возьмем каждый встречающийся множитель в наименьшей из степеней, в которых он встречается, и затем перемножим: 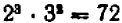
Полученное число 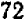
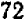
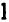
Составим другое число из данных чисел, отбирая каждый встречающийся множитель в наибольшей из степеней, в которых он встречается, и перемножая: 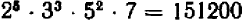
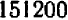
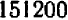
Таким же образом можно составлять НОД и НОК алгебраических одночленных выражений с целыми коэффициентами, обращаясь при этом с буквами как с целыми числами (хотя буквы могут иметь какие угодно, в том числе и дробные, значения). Так, если даны выражения 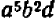
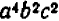
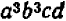
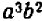
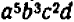
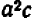
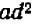
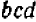
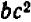
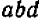
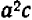
Наибольший общий делитель двух чисел может быть полезен в арифметике при сокращении дробей: найдя НОД числителя и знаменателя и сократив на него, мы сразу получаем несократимую дробь. При этом нахождение НОД стоит некоторого труда, так как не всегда очевидно с первого взгляда, каковы простые множите ли данного числа и в каких степенях они входят.
В алгебре же такого рода применение НОД излишне, так как буквенные множители выписываются явно.
Если, например, дана дробь 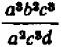
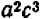
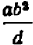
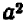
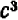
Зато в алгебре НОД приносит больше пользы при вынесении за скобку общих множителей много членных выражений. Пусть дано выражение 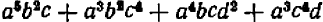
Мы видим сразу, что НОД всех членов равен 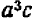
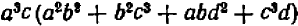
Что касается наименьшего общего кратного, то мы увидим дальше, что в алгебре, как и в арифметике, оно позволяет значительно упрощать записи при сложении и вычитании дробей.
Более сложные случаи сложения и вычитания дробей
При сложении и вычитании дробей удобно пользоваться приемом составления общего знаменателя посредством перемножения знаменателей данных дробей только в том случае, если каждые два, попарно взятые, знаменателя не имеют общих — ни буквенных, ни числовых — множителей. В других случаях употребление этого приема, хотя и дает верный результат, однако, ни коим образом не может быть рекомендовано, так как ведет к лишним записям и потере времени. Общее правило таково: в качестве общего знаменателя нескольких дробей следует брать НОК знаменателей всех данных дробей. Предварительно необходимо каждый знаменатель представить как про изведение отдельных множителей; в частности, если данный знаменатель — многочлен, нужно общие числовые и буквенные множители его членов выносить за скобку. Если встречаются многочленные множители, отличающиеся только знаком, то знак нужно менять, пользуясь уже известными приемами.
После того как общий знаменатель найден, необходимо выяснить, на какой один и тот же «дополнительный множитель» придется умножить знаменатель и числитель каждой дроби для того, чтобы ее знаменатель стал равным выбранному общему знаменателю.
Дальше, раз уже дроби приведены к общему знаменателю, сделать сложение или вычитание не представляет труда.
Пример:
Произведение знаменателей равно 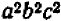
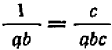
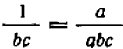
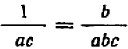
Итак,
Пример:
HOK знаменателей равно 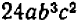
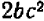
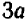
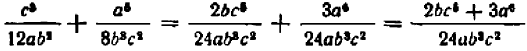
Пример:
Принимая во внимание, что 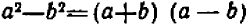
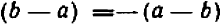
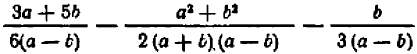
Теперь ясно, что наименьшее общее кратное знаменателей равно 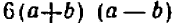
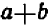
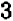
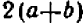
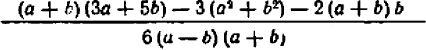
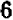
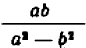
Сложные дроби
Если приходится выполнять деление над выражениями, уже содержащими дроби, то, записывая частное в виде дроби (с чертой), мы получаем сложную дробь. Для облегчения записи в таких случаях иногда пользуются знаком двоеточия, но смысл получаемого от этого, конечно, не изменяется. Например, если 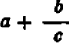
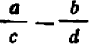
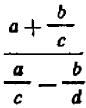
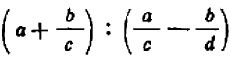
Сложную дробь всегда можно преобразовать в простую. Для этого достаточно выполнить все действия в том порядке, как они указаны: сначала числитель и знаменатель сложной дроби записать в виде простых дробей и затем разделить дробь на дробь, согласно правилу деления. Так, в нашем примере мы получим:
Однако такой способ преобразования сложной дроби в простую практически менее удобен, чем следующий. Пользуясь основным свойством дроби, умножим в нашем примере числитель и знаменатель на 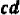
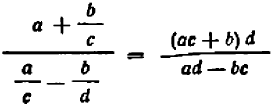
В качестве множителя, на который умножаются и числитель и знаменатель данной сложной дроби, следует, конечно, выбирать НОК знаменателей всех дробей, содержащихся в числителе и знаменателе данной дроби.
Всякое дробное алгебраическое выражение содержит лишь конечное число делений. Поэтому, сколько бы ни было «этажей» о сложной дроби, такую дробь всегда можно преобразовать в простую, постепенно уничтожая «этажи». Отсюда следует, что дробное алгебраическое выражение всегда может быте представлено в виде отношения двух целых алгебраических выражений.
Все действия с дробями. Расположенные многочлены в числителе и знаменателе дроби. Выделение целой части из неправильной дроби
Выполняя указанные действия над данными, простыми или сложными, алгебраическими дробями, мы получаем в результате простую алгебраическую дробь.
Если числители и знаменатели данных дробей — многочлены, расположенные по степеням одной и той же буквы, то числитель и знаменатель дроби, получающейся в результате выполнения действий, также представляются в виде многочленов, расположенных по степеням той же буквы.
После этого, если удастся в числителе и знамена теле обнаружить общие множители, на них следует сокращать полученную дробь.
Простая дробь, у которой числитель и знаменатель — многочлены, расположенные по степеням одной и той же буквы, называется: правильной, если степень числителя меньше, чем степень знаменателя; неправильной, если степень числителя больше или равна степени знаменателя.
Если дробь — неправильная, то ее всегда можно представить в виде суммы многочлена и правильной дроби. Это делается посредством деления числителя на знаменатель.
Неправильная дробь равна сумме: 1) частного, получающегося при делении числителя на знаменатель, и 2) правильной дроби, у которой числитель равен остатку при этом делении, а знаменатель — знаменателю данной дроби.
Например, деля многочлен 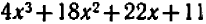
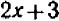
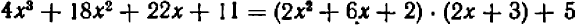
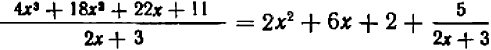
Описанное выше преобразование напоминает выделение целой части из неправильной арифметической дроби; сравните хотя бы с таким примером:
По указанной причине это преобразование называется выделением целой части из неправильной алгебраической дроби.
Вынесение за скобки каких угодно выражении
Заменяя в тождестве 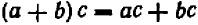
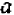
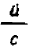
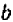
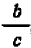
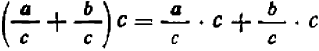
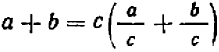
Оно говорит о следующем: любое отличное от нуля
число или алгебраическое выражение можно «вынести за скобки» из какой угодно алгебраической суммы. Вынося некоторое выражение из алгебраической суммы за скобки, нужно каждый член суммы разделить на это выражение.
Пример:
Вынести за скобки 
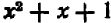
Мы получаем: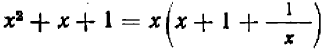
Пример:
Из выражения 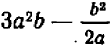
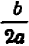
Мы получаем:
В многочленах, расположенных по степеням одной буквы, часто бывает полезно выносить за скобки или старший член или свободный член.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат