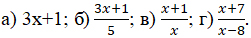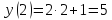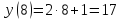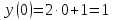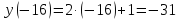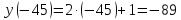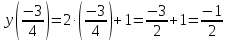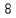Как найти значение аргумента функции 7 класс

Учитель
математики МБОУ СШ №5 

пгт. Яблоновский  Барчо Ф.Т. Урок. 7
класс

Тема:   Вычисление значений функции по формуле.

Цели:

§ 
изучить аналитический способ задания функции;

§ 
формировать умения и навыки находить значения аргумента и
значения функции.

Задачи:

 воспитательные:
воспитание интереса к математике и еѐ приложениям;      обучающие:

o   
вычисление значения функциипо заданному значению аргумента и
нахождение значения аргумента по заданному значению функции;

o   
совершенствование вычислительные навыки;              развивающие:

o   
формирование умений применять приѐмы наблюдения, сравнения,
анализа; o           развитие
общего и математического кругозора, мышления и речи.

Тип урока: урок
ознакомления с новым материалом.

Девиз урока:

Расскажи – и я забуду

Покажи – и я запомню Вовлеки – и я пойму.

Оборудование: учебник,
карточки, интернет ресурсы, проектор.

План урока:

1.      Организационный
момент

2.      Проверка
домашней работы

3.      Устный
опрос. (Актуализация опорных знаний)

4.      Изучение
нового материала (Введение в тему. Постановка учебных задач.)

5.      Закрепление
изученного материала

6.      Самостоятельная
работа

7.      Подведение
итогов урока

8.     
Сообщение домашнего задания, рефлексия. Ход урока

1. Организационный момент

(Обеспечить рабочую обстановку на
уроке. Учитель приветствует учащихся, проводит проверку готовности класса к
уроку).

–  
Здравствуйте, ребята, садитесь. Я рада видеть вас в хорошем
настроении.

Наш девиз сегодня:

Расскажи – и я забуду

Покажи – и я запомню Вовлеки – и я пойму.

Мы вместе активно включаемся в
учебный процесс. Будем внимательными, дружными и доброжелательными.

–   Откройте
рабочие тетради и запишите сегодняшнее число, классная работа.

2. Проверка домашней работы

– Проверка решения текстовой задачи
домашнего задания на доске (1 уч) (сверка с образцом)

Задача. В рамках акции
«Посади дерево» шестиклассники и семиклассники посадили вместе 210 саженцев.
Сколько саженцев посадили семиклассники, если известно, что они посадили на 10%
саженцев больше, чем шестиклассники?

Решение:

Пусть 6-классники посадили х
саженцев, то 7-классники посадили х+0,1х=1,1х саженцев.

х+1,1х=210 2,1х=210 х=210:2,1 х=100

1,1х=1,1*100=110(саж.) Ответ:
110 саженцев.

Дополнительные вопросы:

–  
При решении уравнения какими свойствами пользовались?

–  
Для чего проводятся такие акции?

–  
Чтобы сохранять природу

–  
Как связан с экологией 2017 год?

(- Каким годом был объявлен
2017-й год Президентом РФ Путиным В.В.?)

(2017-й год Президентом
РФ Путиным В.В.был объявлен Годом экологии.)

3. Устный опрос

1. Дайте определение функции.

– Функцией называют такую зависимость одной переменной
(зависимой) от другой (независимой), при которой каждому значению независимой
переменной соответствует единственное значение зависимой переменной.)

1.      Какая
переменная называется независимой переменной, а какая – зависимой? Что называют
аргументом?(Переменную а, значения которой выбираются произвольно, называют независимой
переменной. Переменную, значения которой определяются выбранными значениями а,
называют зависимой переменной. Независимую переменную иначе называют аргументом).

2.      Дана
функция y=2,7x – 15. Укажите независимую и зависимую переменные.

3.      Что
называется областью определения и областью значений функции?

4.      При
каких значениях переменной имеет смысл выражение:

 

4. Изучение нового материала

На прошлом уроке мы начали важную
тему для математики. Начиная с XVII века понятие функции – одно из основных в
математике. Оно играет большую роль в познании реального мира. На уроках
математики вы часто будете слышать это слово.

–  
Какие способы задания функции рассмотрели на прошлом уроке?

–   На предыдущем
уроке мы рассматривали различные способы задания функции: с помощью формулы,
графика, таблицы. 

Наиболее распространенным
способом является задание функции с помощью формулы (аналитический способ).
Формула позволяет для значения аргумента находить соответствующее значение
функции путем вычислений. (На примере функции y=2,7x – 15). Что же мы будем
сегодня изучать?

Сформулируйте тему урока. Запишем
тему в тетрадь.

А теперь поставим перед собой
цель сегодняшнего урока. Какой она будет?

Ответы детей:
научиться находить значение функции.

–  
Но и обратную задачу будем решать – находить значение аргумента.

Цель: научить для каждого
значения аргумента находить соответствующее значение функции и наоборот.

Пример 1. 

Пусть функция задана формулой у =
5х – 1, где -2< х<2.

Найдем значение функции, соответствующее целым значениям
аргумента х:

если х = -2, то у = 5*(-2)-1=-11; если
х = -1, то у = 5 * (-1) -1 = -6; если х = 0, то у = 5*0-1=-1; если х = 1, то у
= 5 * 1-1=4; если х = 2, то у = 5 * 2-1=9.

Результаты вычислений удобно записать в виде таблицы,
поместив в верхней строке значения аргумента, а в нижней строке –
соответствующие значения функции:

Класс делю на три группы

1группа	2группа	3группа
Нахождение значения функции по формуле при заданном значении аргумента.	Составление таблицы значений некоторой функции.	Нахождение области определения функции.
1.№267	1. №270	Найдите область определения функции, заданной формулой: а)у=3х-2; б)у=       ; в)у=х5+2х -3;  г)у= ;  д) у=   ;е)  у=
2.Вычислить значения следующих функций при  х равном  -2, -1,0, 1,2. а) у=3х; б) у= -2х; в) у=-х -3; г)у=20х +4	2.№271

Каждая группа представляет  своѐ решение (готовят ответы на
обратной стороне доски),работу каждого в группе оценивают  сами  и ставят
оценку в рабочую карточку.

Работа с учебником (пример 2 на стр.60). Разберем
решение.

На этой же странице видим портрет немецкого математика,
философа, физика и языковеда 17-18 вв. Лейбниц Готфрид Вильгельма. Именно им
был введен термин «Функция».

(Задание на дом одному уч. подготовить исследовательскую
работу о Лейбнице.)

 

Готфрид Вильгельм Лейбниц – немецкий
философ, математик, логик, физик, изобретатель, богослов, историк, юрист,
языковед, дипломат. В частности им введен термин «Функция».

– Сделаем вывод: Как найти
значение аргумента по заданному значению функции?

Физкультминутка

5.  Закрепление
изученного материала

а) Решение упражнений по
учебнику: №267, 269, 273, 272(а,в).

№267 – (1-й пример ученик на
доске, ост в тетрадях, затем обучающиеся решают с комментариями в тетрадях, без
записи на доске);

№269 – (обучающиеся решают устно,
заполняется таблица на слайде);

№273
(подробно на доске и в тетрадях обучающихся).

б) решение тренировочных упражнений из ЦОР (практика,
групповая работа)

6.  Самостоятельная
работа

(В тетрадях для СР, которые после
самопроверки через проектор собираются) B-I

1.  Функция
задана формулой у = 0,2х – 4.

Найдите значение функции,
соответствующее значению аргумента, равному 15.

2.  Функция
задана формулой у = 2х – 1.

При каком значении аргумента значение функции равно 8.

B-2

1.Функция задана формулой у =
0,5х + 3.

Найдите значение функции,
соответствующее значению аргумента, равному-12.

2.Функция задана формулой у = 4х
+ 12.

При каком значении аргумента значение функции равно 30

B-3

1.Функция задана формулой у = х +
3.

Найдите значение функции,
соответствующее значению аргумента, равному – 12.

2.Функция задана формулой у = х +
12.

При каком значении аргумента
значение функции равно 30.

Ответы

	1	2
I вариант	-1	4,5
II вариант	-3	4,5
III вариант	-9	18

7. Подведение итогов урока – Какую
тему мы сегодня изучили ?

– Чему вы научились?

8. Домашнее задание

№268, 270, 277.

Творческие задания 

1.  Объясните, почему
перечисленные формулы не задают функцию:

 

Как надо записать эти формулы,
чтобы они определили функцию?

2.  Вспомнить пословицы,
отражающие функциональную зависимость. (например: Чем дальше в лес, тем больше
дров. Кто не работает – тот не ест.)

9. Рефлексия

Предлагаю высказаться одним предложением, выбирая начало
фразы из предложенных (на доске).

•      
Было интересно… (узнать про Лейбниц)

•      
Теперь я могу… (вычислять значения функции)

•      
Я смог… (решить правильно СР)

•      
Мне захотелось… (еще больше узнать о функциях)

Во время урока я чувствовал себя:

•      
комфортно;            неуверенно;             превосходно.

Обновлено: 16.05.2023

Аргумент функции в алгебре это независимая перемена с помощью которой определяется значение функции. … Значение аргумента можно определить по значению функции. Для определения аргумента по функции y=f(x), надо заменить y заданным значением.

Что такое аргумент в алгебре х или у?

Аргумент — это независимая переменная. … Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто: y = f(x), где f (начальная буква слова function — функция) заменяет слово функция , y — это функция, а x — аргумент.

Что является аргументом в алгебре?

Аргумент в математике: Аргумент функции — независимая переменная, от значений которой зависят значения функции. Аргумент комплексного числа — одна из величин, связанных с комплексным числом. Аргумент максимизации, Аргумент минимизации

Что такое аргумент функции в алгебре 7 класс?

Что такое аргумент в линейной функции?

Где аргумент А где функция?

Если две величины связаны между собой так, что каждому допустимому значению одной соответствует определенное значение другой, то первая величина называется аргументом, а вторая — функцией этого аргумента.

Что из перечисленного может быть аргументом функции?

Аргументом функции может быть число, текст, логическое значение, массив, значение ошибки, ссылка на ячейку. В качестве аргументов используются также константы, формулы, или функции. … Оператором называют знак или символ, задающий тип вычисления в формуле.

Как найти значение аргумента в алгебре?

Это можно сделать с помощью формулы функции. Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.

Как найти значение функции при заданном аргументе?

Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.

Какие способы задания функции вы знаете?

Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.

Как задать функцию в Питоне?

Какие функции есть в алгебре?

• Понятие функции является одним из основных в математике. Оно вводится следующим образом. …
• Четная функция f(−x)=f(x)
• Нечетная функция f(−x)=−f(x)
• Периодическая функция f(x+kT)=f(x), …
• Обратная функция Пусть задана функция y=f(x). …
• Сложная функция …
• Линейная функция …
• Квадратичная функция

Что такое функция в алгебре 7 класс?

Как найти к в линейной функции?

Из формулы линейной функции y=kx получим, что k = y x . Чтобы определить коэффициент k, необходимо выбрать некоторую точку на прямой и вычислить частное ординаты и абсциссы заданной точки. Прямая проходит через точку M(4; 2), следовательно получим 2 4 = 0,5 .

Как написать формулу графика линейной функции?

1. Графиком функции является прямая, поэтому на рисунке изображен график линейной функции. …
2. Любую линейную функцию можно выразить формулой y=ax+b, где a и b — действительные числа.

Как найти значение х в функции?

Чтобы вычислить значение функции у(х) при х = а, надо в формулу, задающую функцию, подставить данное значение аргумента а и выполнить вычисления. Такое значение функции обозначают символом у(а).

Где производится зимняя резина Gislaved? Состоянием на 2021 год компания Гиславед является частью корпорации

Как работать с уайт спиритом? Компоненты уайт—спирита размягчают герметик до консистенции сливочного масла. Для

Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.

Функция — это зависимая переменная величина. Аргумент — это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.

Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:

y = f(x),

где f (начальная буква слова function — функция) заменяет слово функция , y — это функция, а x — аргумент.

Иногда, чтобы показать, что y зависит от x, пишут просто:

Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:

D(f) — область определения функции
(множество значений аргумента).

E(f) — множество значений функции.

f(x₀) — значение функции в точке x₀.

Пример. Возьмём формулу нахождения расстояния по скорости и времени:

S = vt,

где S — это расстояние, v — скорость, а t — время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:

t (ч)	1	1,5	2	2,5	3
S (км)	50	75	100	125	150

Следовательно, S является функцией от t — S(t) , область определения функции — D(S) ⩾ 0, так как время не может быть отрицательным, но при этом можно не затратить времени вообще, если не двигаться, в этом случае t = 0. Значение этой функции в точке t₀ можно обозначить в виде S(t₀), то есть записать таблицу со значениями в таком виде:

S(1) = 50, S(1,5) = 75, S(2) = 100, S(2,5) = 125, S(3) = 150.

Вокруг нас происходит множество событий или процессов, которые можно измерить. При этом величина одних зависит от величины каких-либо других.

Так, например, от того, сколько мы испишем страниц в тетради, зависит количество оставшихся в стержне чернил. Чем больше кружек наполнено компотом, тем меньше его останется в кастрюле. Чем больше мама оставит денег на обеды, тем больше можно на них купить мороженого. А чем сильнее велосипедист крутит педали, тем больше километров он проедет. Придумайте свои примеры?

В наших описанных выше примерах первые два имеют обратную зависимость, то есть при увеличении одной величины (количество страниц и кружек в наших случаях), уменьшается вторая (количество чернил и компота в кастрюле).

Примеры с велосипедистом и мороженым имеют прямую зависимость, то есть при увеличении одной величины (скорость движения педалями и количество оставленных мамой денег) увеличивается и другая (пройденное расстояние и количество мороженого).

Зависимость, которая показывает как одна величина связана с другой величиной, как раз и называется функцией.

Аргумент и функция

Если одна величина меняется независимо от другой (например, оставленные мамой деньги, исписанные страницы), то она называется независимой или аргументом и обозначается обычно $x$

Если же величина зависит от другой, то ее называют зависимой переменной или функцией и обычно обозначают как $y$ или $f(x)$. То есть $y=f(x)$.

Зависимые и независимые переменные могут обозначаться и любыми другими буквами (латинскими или греческими).

Примеры аргумента и функции

• Чем старше дерево, тем оно выше. Возраст дерева — аргумент, рост — функция
• Чем дольше машина едет с одной скоростью, тем большее расстояние она проедет. Время — аргумент, скорость — неизменяемая величина, расстояние — функция
• Чем меньше цена мороженого, тем больше можно купить за 100 рублей. Цена мороженого — аргумент, количество мороженого — функция, 100 рублей — неизменяемая величина
• Чем меньше мы вычтем из числа, тем больше результат. Вычитатель — аргумент, результат — функция

Запись функции

Посмотрим как можно записать функциональную зависимость купленного мороженого от оставленных денег на обед. Допустим мороженое стоит $20$ рублей. Тогда:

• если мама оставит $20$ рублей, мы купим только одно мороженое;
• если $40$ рублей – два мороженых;
• если $100$ рублей – целых пять мороженых.

Таким образом, количество порций мороженого обозначим $у$, а количество оставленных денег $x$. Функция будет выглядеть следующим образом:

Переменные могут принимать как положительные, так и отрицательные значения.

Один из разделов математики это алгебра, которая подразумевает выполнение различных операций с числами, так как сложение, умножение и т.д. Можно сказать, что алгебра это нечто вроде расширения арифметики до более высокого уровня. Понять, что такое алгебра и откуда она взялась, помогут исторические факты. Первые предпосылки алгебры появились в разных уголках мира, людям нужна была алгебра для того, чтобы решить определенные уравнения. Например, в Древней Греции впервые об уравнениях заговорил Диофант, это был 2-3 век нашей эры.

Когда начинают учить алгебру в школе?

Разделение математики на несколько областях определило для алгебры решение определенных уравнений, под названием алгебраические уравнения. Что такое алгебра как предмет можно узнать только в 7-ом классе. Именно тогда вместе привычной математики появляется два отдельных предмета: алгебра и геометрия. Изучение начинается с простых понятий, также как и в случае других учебных процессов, все строится от простого материала к сложному.

7 класс оптимальное время для того, чтобы узнать, что такое алгебра. Вместо обычных операций с числами осуществляется переход на переменные. Так проще понять общие законы арифметики, научиться работать с неизвестными и функциями. Алгебру можно разделить на 5 отдельных категорий:

Школьная программа подразумевает изучение исключительно элементарной категории. Элементарная алгебра занимается изучением операций с вещественными числами. Перемененные и постоянные обозначены в алгебре символами в виде букв. С их помощью происходит преображение уравнений и математических выражений на основе четких правил.

Функция в алгебре

Понимание алгебры как предмет требует знание определенных элементов, так как функция, аргумент и определение. Что такое функция в алгебре и чем она определена? Функция является одним из основных понятий и определяет зависимость между переменными с неодинаковой величиной.

Что такое функция?:

Функция в алгебре представляет собой сопоставимость между двумя множествами. Согласно этому каждый элемент множества соответствует по одному единственному элементу другого множества.

Функция задается различным образом:

– согласно словесной формулировке (описание словами)

– аналитическим образом (используя формулу).

Аргумент в алгебре

Что такое аргумент в алгебре? Это не что иное, как перемена х, от которой зависит у, то есть функция. Аргумент функции в алгебре это независимая перемена с помощью которой определяется значение функции.

Значение аргумента можно определить по значению функции. Для определения аргумента по функции y=f(x), надо заменить y заданным значением. Остается только решить уравнение относительно x для того, чтобы значение стало известным. Существует возможность определения данного параметра и по графику функции.

Определение алгебры и ее практическая польза

Определение, что такое алгебра, позволяет понять какая от нее практическая польза. Только понимая область деятельности этой части математики, появляется стремление ее изучать. Благодаря алгебре, можно шагать на более высокий уровень познания математики. Алгебра это та простая ступень, которая позволяет делать прогресс в процессе изучения современной математики. Благодаря ней, появилась возможность взглянуть иначе на множества.

Постепенно элементарные значения алгебры перешли в более сложные понятия. Так появилась универсальная алгебра, которая стала основой для развития топологии. Алгебра это ступень, которая позволяет ступать дальше, и без нее не быть некоторым явлений прогресса. Знания некоторых людей, может завершиться на элементарных основ дисциплины, но в определенных областях глубокое изучение обязательно.

Аргумент — это независимая переменная. … Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто: y = f(x), где f (начальная буква слова function — функция) заменяет слово функция , y — это функция, а x — аргумент.

Что является аргументом в алгебре?

argumentum — рассказ, довод, тема) — многозначный термин: … Аргумент в математике: Аргумент функции — независимая переменная, от значений которой зависят значения функции. Аргумент комплексного числа — одна из величин, связанных с комплексным числом.

Что такое функция в алгебре 7 класс?

Функция – это соответствие между двумя множествами такое, что каждому элементу одного множества ставится в соответствие единственный элемент другого множества . Первое множество называют областью определения функции, а второе – областью значений функции.

Что такое Х и У?

Что является аргументом?

Аргумент (лат. argumentum) — суждение (или совокупность взаимосвязанных суждений), посредством которого обосновывается истинность другого суждения (или теории).

Как найти значение аргумента в алгебре?

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции. Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.

Как найти значение функции при заданном аргументе?

Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию. Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.

Читайте также:

  

• Кто может стать президентом кратко

  

• Что такое рыночная площадь в средневековье кратко

  

• Что такое фи кратко

  

• Школа 1466 расписание внеурочной деятельности

  

• В каких случаях необходимо вызывать скорую помощь кратко

Цели:

• изучить аналитический способ задания функции;
• формировать умения и навыки находить значения аргумента и значения функции.

Задачи:

• воспитательные: воспитание интереса к математике и её приложениям;
• обучающие:
• вычисление значения функциипо заданному значению аргумента и нахождение значения аргумента по заданному значению функции;
• совершенствование вычислительные навыки;
• развивающие:
• формирование умений применять приёмы наблюдения, сравнения, анализа;
• развитие общего и математического кругозора, мышления и речи.

Тип урока: урок ознакомления с новым материалом.

Девиз урока:

Расскажи – и я забуду

Покажи – и я запомню

Вовлеки – и я пойму.

Оборудование: учебник, карточки, интернет ресурсы, проектор.

План урока:

1. Организационный момент
2. Проверка домашней работы
3. Устный опрос. (Актуализация опорных знаний)
4. Изучение нового материала (Введение в тему. Постановка учебных задач.)
5. Закрепление изученного материала
6. Самостоятельная работа
7. Подведение итогов урока
8. Сообщение домашнего задания, рефлексия.

Ход урока

1. Организационный момент

(Обеспечить рабочую обстановку на уроке. Учитель приветствует учащихся, проводит проверку готовности класса к уроку).

– Здравствуйте, ребята, садитесь. Я рада видеть вас в хорошем настроении.

Наш девиз сегодня:

Расскажи – и я забуду

Покажи – и я запомню

Вовлеки – и я пойму.

Мы вместе активно включаемся в учебный процесс. Будем внимательными, дружными и доброжелательными.

– Откройте рабочие тетради и запишите сегодняшнее число, классная работа.

2. Проверка домашней работы

– Проверка решения текстовой задачи домашнего задания на доске (1 уч) (сверка с образцом)

Задача. В рамках акции «Посади дерево» шестиклассники и семиклассники посадили вместе 210 саженцев. Сколько саженцев посадили семиклассники, если известно, что они посадили на 10% саженцев больше, чем шестиклассники?

Решение:

Пусть 6-классники посадили х саженцев, то 7-классники посадили

х+0,1х=1,1х саженцев.

х+1,1х=210

2,1х=210

х=210:2,1

х=100(саж.) 6-кл.

1,1х=1,1*100=110(саж.)

Ответ: 110 саженцев.

Дополнительные вопросы:

– При решении уравнения какими свойствами пользовались?

– Для чего проводятся такие акции?

– Чтобы сохранять природу

– Как связан с экологией 2017 год?

(- Каким годом был объявлен 2017-й год Президентом РФ Путиным В.В.?)

(2017-й год Президентом РФ Путиным В.В.был объявлен Годом экологии.)

3. Устный опрос

1. Дайте определение функции.

– Функцией называют такую зависимость одной переменной (зависимой) от другой (независимой), при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.)

1. Какая переменная называется независимой переменной, а какая – зависимой? Что называют аргументом?(Переменную а, значения которой выбираются произвольно, называют независимой переменной. Переменную, значения которой определяются выбранными значениями а, называют зависимой переменной. Независимую переменную иначе называют аргументом).
2. Дана функция y=2,7x – 15. Укажите независимую и зависимую переменные.
3. Что называется областью определения и областью значений функции?
4. При каких значениях переменной имеет смысл выражение:
   
   

4. Изучение нового материала

На прошлом уроке мы начали важную тему для математики. Начиная с XVII века понятие функции – одно из основных в математике. Оно играет большую роль в познании реального мира. На уроках математики вы часто будете слышать это слово.

– Какие способы задания функции рассмотрели на прошлом уроке?

– На предыдущем уроке мы рассматривали различные способы задания функции: с помощью формулы, графика, таблицы. (Показать на слайде)

Наиболее распространенным способом является задание функции с помощью формулы (аналитический способ). Формула позволяет для значения аргумента находить соответствующее значение функции путем вычислений. (На примере функции y=2,7x – 15). Что же мы будем сегодня изучать?

Сформулируйте тему урока. Запишем тему в тетрадь.

А теперь поставим перед собой цель сегодняшнего урока. Какой она будет?

Ответы детей: научиться находить значение функции.

– Но и обратную задачу будем решать – находить значение аргумента.

Цель: научиться вычислять значения функциипо заданному значению аргумента и находить значения аргумента по заданному значению функции.

Рассмотрим Пример 1. (На доске)

Пусть функция задана формулой у = 5х – 1, где -2< х<2.

Найдем значение функции, соответствующее целым значениям аргумента х:

• Если х = -2, то у = 5*(-2)-1=-11;
• если х = -1, то у = 5 * (-1) -1 = -6;
• если х = 0, то у = 5*0-1=-1;
• если х = 1, то у = 5 * 1-1=4;
• если х = 2, то у = 5 * 2-1=9.

Результаты вычислений удобно записать в виде таблицы, поместив в верхней строке значения аргумента, а в нижней строке – соответствующие значения функции:

х	-2	-1	0	1	2
у	-11	-6	-1	4	9

– Известна ли область определения этой функции по условию задачи?

Пример 2.

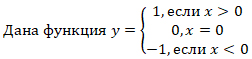
Найдем значение функции, соответствующее значению аргумента 5; -3;0.

• Если х=5,то у=1,
• Если х=-3,то у=-1,
• Если х=0,то у=0,

– Какая область определения этой функции по условию задачи?

Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

Часто приходится решать обратную задачу: нахождение значения аргумента по известным значениям функции.

Работа с учебником (пример 2 на стр.60). Разберем решение.

На этой же странице видим портрет немецкого математика, философа, физика и языковеда 17-18 вв. Лейбниц Готфрид Вильгельма. Именно им был введен термин «Функция». (Задание на дом одному уч. подготовить исследовательскую работу о Лейбнице.)

Готфрид Вильгельм Лейбниц – немецкий философ, математик, логик, физик, изобретатель, богослов, историк, юрист, языковед, дипломат. В частности им введен термин «Функция».

– Сделаем вывод: Как найти значение аргумента по заданному значению функции?

Физкультминутка

5. Закрепление изученного материала

а) Решение упражнений по учебнику: №267, 269, 273, 272(а,в).

№267 – (1-й пример ученик на доске, ост в тетрадях, затем обучающиеся решают с комментариями в тетрадях, без записи на доске);

№269 – (обучающиеся решают устно, заполняется таблица на слайде);

№269.

х	-6	-4	-3	2	5	6	12
у	-2	-3	-4	6	2,4	2	1

№273 (подробно на доске и в тетрадях обучающихся).

б) решение тренировочных упражнений из ЦОР (практика, групповая работа)

6. Самостоятельная работа

(В тетрадях для СР, которые после самопроверки через проектор собираются)

B-I

1. Функция задана формулой у = 0,2х – 4.

Найдите значение функции, соответствующее значению аргумента, равному 15.

2. Функция задана формулой у = 2х – 1.

При каком значении аргумента значение функции равно 8.

B-2

1.Функция задана формулой у = 0,5х + 3.

Найдите значение функции, соответствующее значению аргумента, равному-12.

2.Функция задана формулой у = 4х + 12.

При каком значении аргумента значение функции равно 30

B-3

1.Функция задана формулой у = х + 3.

Найдите значение функции, соответствующее значению аргумента, равному – 12.

2.Функция задана формулой у = х + 12.

При каком значении аргумента значение функции равно 30.

Ответы

	1	2
I вариант	-1	4,5
II вариант	-3	4,5
III вариант	-9	18

7. Подведение итогов урока

– Какую тему мы сегодня изучили ?

– Чему вы научились?

8. Домашнее задание

№268, 270, 277.

Творческие задания (на карточках)

1. Объясните, почему перечисленные формулы не задают функцию:

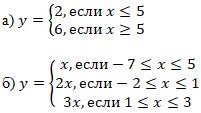
Как надо записать эти формулы, чтобы они определили функцию?

2. Вспомнить пословицы, отражающие функциональную зависимость. (например: Чем дальше в лес, тем больше дров. Кто не работает – тот не ест.)

9. Рефлексия

Предлагаю высказаться одним предложением, выбирая начало фразы из предложенных (на доске).

• Было интересно… (узнать про Лейбниц)
• Теперь я могу… (вычислять значения функции)
• Я смог… (решить правильно СР)
• Мне захотелось… (еще больше узнать о функциях)

Во время урока я чувствовал себя:

• комфортно;
• неуверенно;
• превосходно.

7 класс.

Вычисление значений функции по формуле.

Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь мы научимся находить значения функции по формуле, которой она задана, а также находить значения аргумента при известных значениях функции.

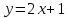
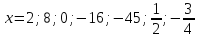
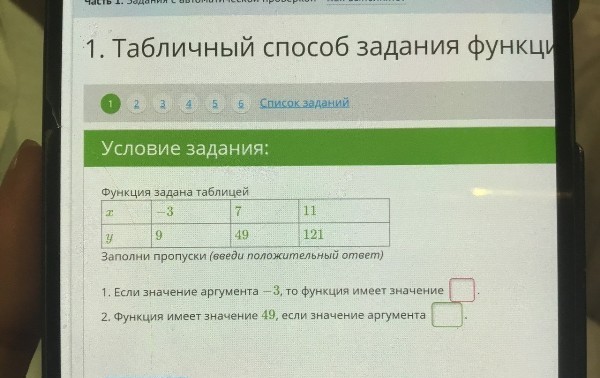
Рассмотрим пример функции: . Для того, чтобы найти значение функции, нужно знать значение аргумента. Эти значения могут быть заданы в условии задачи, а могут выбираться самостоятельно. Пусть заданы значения аргумента: . Для нахождения значений функции, необходимо подставить в формулу функции вместо х его значение (поочерёдно) и посчитать.

Для наглядности все значения удобно оформлять в таблице. В верхней строчке записываем значения х, а в нижней – значения у.

х
у

Если выбираем значения аргумента самостоятельно, то лучше это делать в порядке возрастания.

Чтобы найти значения аргумента при заданных значениях функции, сначала нужно выразить переменную х через переменную у из формулы, которой задана функция.

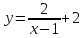
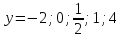
Например, дана функция . Нужно найти значения аргумента, если заданы значения функции: .

Решение. Сначала из формулы 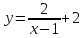выразим переменную х:

Теперь в эту формулу вместо у будем подставлять его значения:

Запишем все эти значения в таблицу.

х
у

1. Функция задана формулой . Найдите значения переменной у, если:

2. Функция задана формулой . Найдите значения переменной у, если:

3. Функция задана формулой . Найдите значения переменной у, если:

4. Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

1. Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

1. Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

1. Дана функция

Найдите: .

1. Дана функция

Найдите: .

1. Дана функция

Найдите: .

1. Функция задана формулой . Определите:

1. значение функции, если значение аргумента равно ;

2. значение аргумента, при котором значение функции равно .

1. Функция задана формулой . Определите:

1. значение функции, если значение аргумента равно ;

2. значение аргумента, при котором значение функции равно .

1. Дана функция . Найдите значение функции, если значение аргумента равно .

2. Дана функция . Найдите значение функции, если значение аргумента равно 1.

3. Дана функция . Найдите значение функции, если значение аргумента равно 3.

4. Дана функция . Найдите значение функции, если значение аргумента равно -3.

5. Найдите значение аргумента, при котором функция принимает значение .

6. Найдите значение аргумента, при котором функция принимает значение .

7. Найдите значение аргумента, при котором функция принимает значение .

8. Найдите значение аргумента, при котором функция принимает значение .

9. Дана функция . Найдите произведение значений функции

1. Дана функция . Найдите произведение значений функции

1. Дана функция . Найдите произведение значений функции .

2. Дана функция . Найдите произведение значений функции .

3. Для функции найдите значения и и сравните их.

4. Для функции найдите значения и и сравните их.

5. Для функции найдите значения и и сравните их.

6. Для функции найдите значения и и сравните их.

1. Функция задана формулой . Заполните таблицу:

х
у

1. Функция задана формулой . Заполните таблицу:

х
у

1. Длина (см) стального стержня при температуре изменяется по закону . На сколько миллиметров изменится длина стержня, если его температура повысится с до ?

2. Длина (см) медного стержня при температуре изменяется по закону . На сколько миллиметров изменится длина стержня, если его температура повысится с до ?

3. Составьте таблицу значений функции, заданной формулой , где , с шагом 1.

4. Составьте таблицу значений функции, заданной формулой , где , с шагом 1.

3