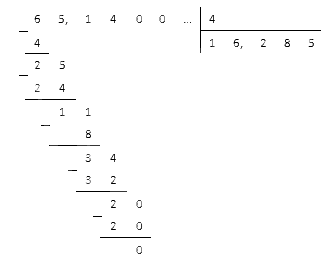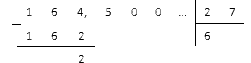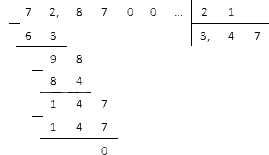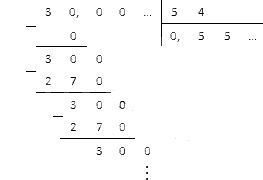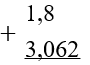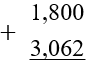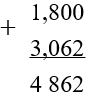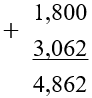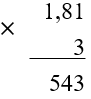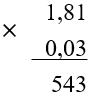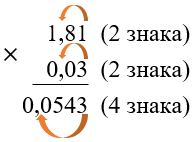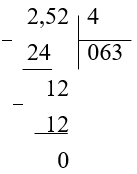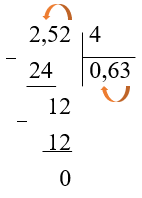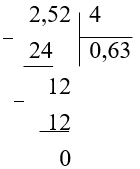Деление десятичных дробей
План урока
- Деление десятичной дроби на натуральное число
- Деление десятичной дроби на 10, 100, 1000 и т. д.
- Деление десятичной дроби на десятичную дробь
Цели урока
- Знать правила деления десятичной дроби на натуральное число; на 10, 100, 1000 и т. д.; на десятичную дробь
- Уметь делить десятичные дроби на натуральное число; на 10, 100, 1000 и т. д.; на десятичную дробь
- Уметь решать задачи на деление десятичных дробей
Разминка
- Как умножить десятичную дробь на 10, 100, 1000?
- Сформулируйте правило умножения десятичных дробей
- В чем отличие умножения десятичных дробей от умножения натуральных чисел?
Деление десятичной дроби на натуральное число
Вы знаете, что деление связано с умножением. Если нам известны компоненты деления, мы можем из них составить произведение, где делитель и частное будут множителями, а делимое — произведением.
Если 4 ∙ 0,6 = 2,4, значит 2,4 : 4 = 0,6.
Но не всегда можно устно подобрать множители. Давайте попробуем тот же пример посчитать другим способом.
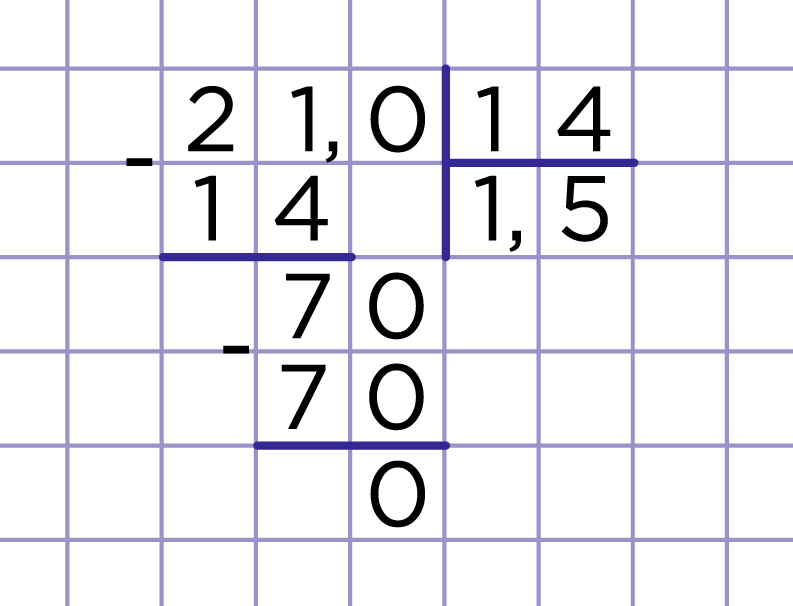
Если 2,4 в 10 меньше 24, то и частное должно быть в 10 раз меньше. Если 24 : 4 = 6, то 2,4 : 4 = 0,6. Другими словами, мы перенесли запятую в частном и в делимом на одинаковое количество знаков влево.
Рис. 1. Деление десятичной дроби на натуральное число, 1 случай
При делении десятичной дроби на натуральное число (см. рис. 1):
1) Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
2) Ставим в частном запятую, когда заканчивается деление целой части делимого.
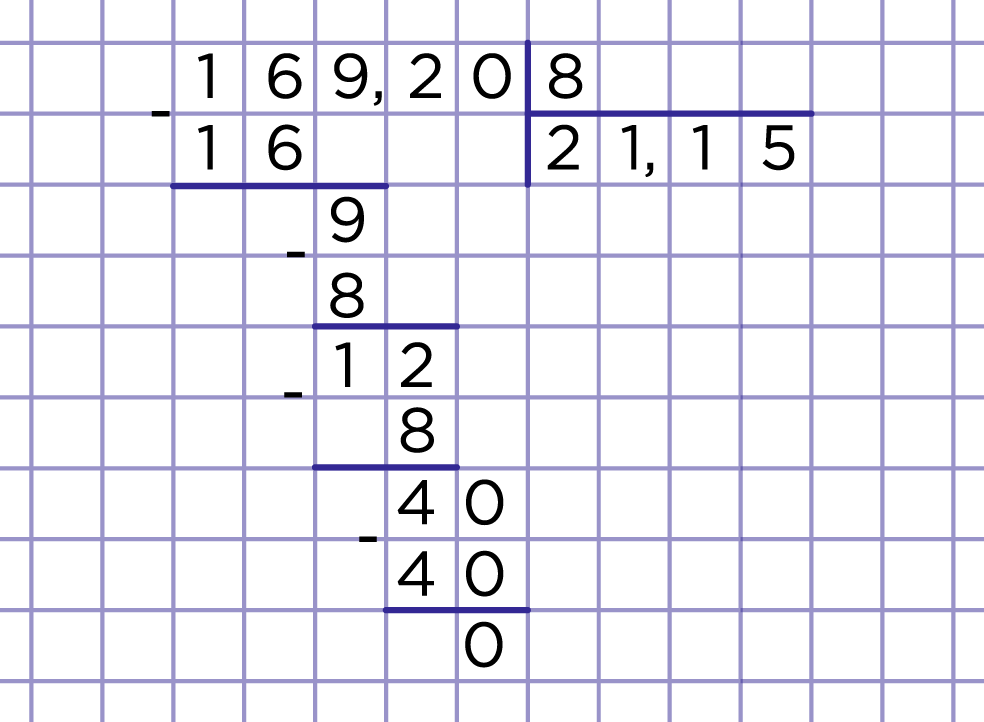
Рис. 2. Деление десятичной дроби на натуральное число, 2 случай
Рассмотрим деление 169,2 на 8. Если при делении, после использования последней цифры из дробной части делимого остается остаток, то после этой цифры сносится нуль (рис. 2), т.к. приписывание любого количества нулей в дробной части десятичной дроби не меняет её (169,2 = 169,20 = 169,200 = 169,200…).
После того, как мы сносим 2, 12 : 8 = 1 (ост. 4). Сносим 0 из дробной части (в дробной части после последней цифры. 40 : 8 = 5.
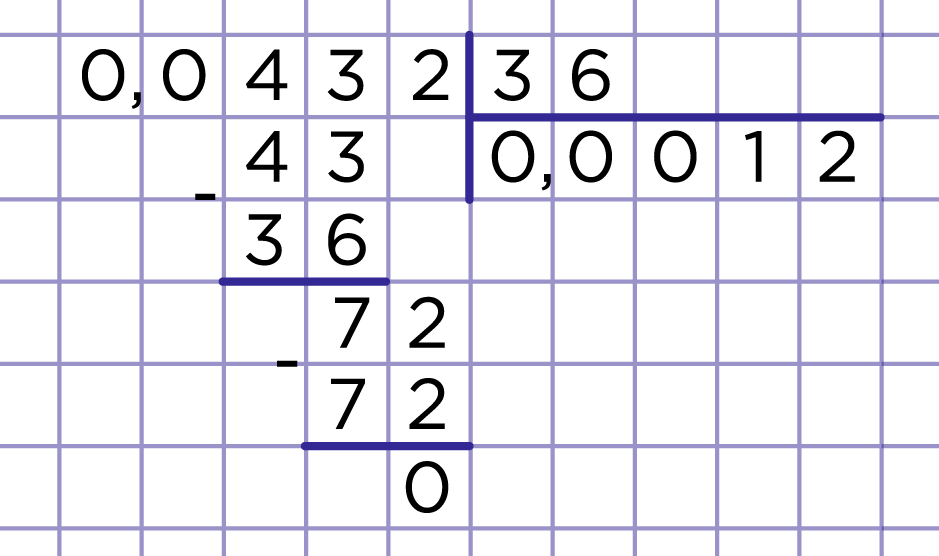
Если целая часть делимого меньше делителя, тогда в целой части частного ставится нуль (рис. 3).
Рис. 3. Деление десятичной дроби на натуральное число, 3 случай
Деление десятичной дроби на 10, 100, 1000 и т. д.
При изучении умножения десятичных дробей мы с вами говорили, что при переносе запятой вправо на 1, 2 или 3 знака, число увеличивается на 10, 100, 1000. Значит, при делении на 10, 100, 1000 должно происходить обратное действие, запятая должна переноситься влево на 1, 2 или 3 знака соответственно.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Используя это правило, найдем значение частного:
34,9:10=3,49; 746:100=7,46; 28,1:1000=0,0281
Деление на десятичную дробь
35км=600м; 3050км=600м; 300500км=600м.
Получается, что 35=3050=300500. Во второй дроби числитель и знаменатель исходной дроби умножили на 10, в третьей — на сто.
Если делимое и делитель увеличить одновременно в 10, 100 и т. д. раз, то частное не изменится.
Используя этот принцип, найдем значение частного 16,45 : 23,5. Так как мы уже умеем делить десятичную дробь на натуральное число, сделаем так, чтобы делитель стал натуральным числом. Для этого увеличим делимое и частное в 10 раз, получим 164,5 : 235 = 0,7, значит и 16,45 : 23,5 = 0,7.
Чтобы разделить десятичную дробь на десятичную, надо:
1) перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в
делителе
;
2) выполнить деление на натуральное число.
Оля собрала 36 кг яблок и слив, из них 0,3 составляли сливы. Сколько килограммов слив собрала Оля?
Решение
0,3=310.
1) 36 : 10=3,6 (кг) — 110 яблок и слив.
2) 3,6 · 3=10,8 (кг) — собрано слив.
Ответ: 10,8 кг
Сережа съел в обед 0,2 пакета огурцов. Сколько огурцов было в пакете, если Сережа съел 3 огурца?
Решение
0,2=210.
1) 3 : 2=1,5 — составляет 110 часть огурцов.
2) 1,5 · 10=15 огурцов.
Ответ: 15 огурцов.
1. Выполните деление:
1) 68,4 : 9;
2) 19,68 : 8;
3) 39,6 : 15;
4) 3,55 : 5;
5) 27 : 5;
6) 3 : 4.
7) 0,1547 : 17;
8) 16,32 : 16;
2. Чему равно частное:
1) 65,78 : 10;
2) 87 : 10;
3) 8 : 10;
4) 12,43 : 100;
5) 0,056 : 100;
6) 54 : 1 000?
3. Вычислите значение выражения:
1) (139 – 23,48) : 38 + 4,35 • 18;
2) 70,336 : 14 + 46,6 : 100 – 0,123.
4. Одно слагаемое равно 3,78, что составляет 0,45 суммы. Найдите второе слагаемое.
1. Сформулируйте правило деления десятичной дроби на натуральное число.
2. Какое число нужно записать в целую часть, если целая часть делимого меньше делителя?
3. Как разделить десятичную дробь на десятичную дробь?
4. Как изменится дробь, если ее числитель и знаменатель умножить на 10000?
Ответы
1. 1) 7,6; 2) 2,46; 3) 2,64; 4) 0,71; 5) 5,4; 6) 0,75; 7) 0,0091; 8) 1,02.
2. 1) 6,578; 2) 8,7; 3) 0,8; 4) 0,1243; 5) 0,00056; 6) 0,054.
3. 1) 81,34; 2) 5,367.
4. 4,62.
В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0,1, 0,01, 100, 10 и др.
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Разделите 1,2 на 0,48.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
1,2=1210=65
0,48=48100=1225.
Таким образом, нам надо разделить 65 на 1225. Считаем:
1,2:0,48=62:1225=65·2512=6·255·12=52
Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 212, а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 52=2,5. О том, как это сделать, мы уже писали ранее.
Ответ: 1,2:0,48=2,5.
Посчитайте, сколько будет 0,(504)0,56.
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
0,(504)=0,5041-0,001=0,5040,999=504999=56111
После этого конечную десятичную дробь также переведем в другой вид: 0,56=56100. Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:
0,(504):1,11=56111:56100=56111·10056=100111
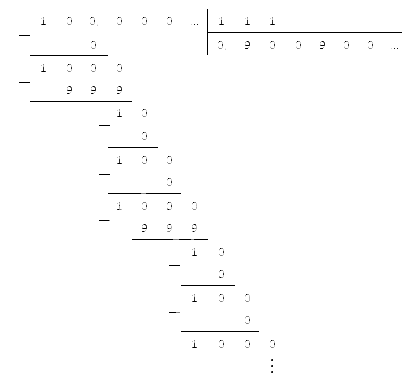
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Ответ: 0,(504):0,56=0,(900).
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Найдите, сколько будет 0,779…/1,5602.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
0,779…≈0,78
1,5602≈1,56
Можем продолжить подсчеты и получить примерный результат: 0,779…:1,5602≈0,78:1,56=78100:156100=78100·100156=78156=12=0,5.
Точность результата будет зависеть от степени округления.
Ответ: 0,779…:1,5602≈0,5.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Разделите 2,5 на 45.
Решение
Приведем 2,5 к виду обыкновенной дроби: 25510=512. Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:
25,5:45=512:45=512·145=1730
Если перевести результат в десятичную запись, то мы получим 0,5 (6).
Ответ: 25,5:45=0,5(6).
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Вычислите, сколько будет 65,144.
Решение
Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65,1400, которая будет равна исходной. Теперь пишем столбик для деления на 4:
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Ответ: 65,14:4=16,285.
Разделите 164,5 на 27.
Решение
Делим сначала дробную часть и получаем:
Отделяем полученную цифру запятой и продолжаем делить:
Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6,0(925).
Ответ: 164,5:27=6,0(925).
Как разделить столбиком одну десятичную дробь на другую
Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на 10, 100 и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:
a:b=(a·10):(b·10), a:b=(a·100):(b·100) и так далее.
Сформулируем правило:
Для деления одной конечной десятичной дроби на другую необходимо:
1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Разберем конкретную задачу.
Разделите 7,287 на 2,1.
Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби 72,87 на 21. Запишем полученные числа столбиком и вычислим
Ответ: 7,287:2,1=3,47
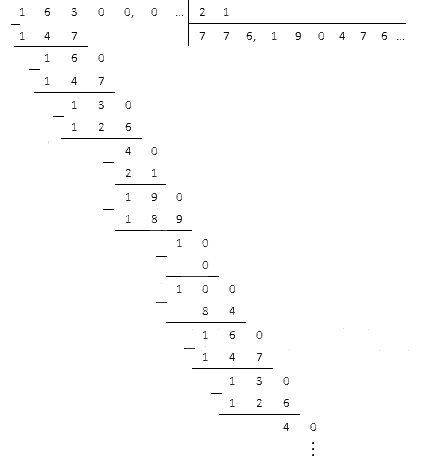
Вычислите 16,30,021.
Решение
Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:
Видим периодическое повторение остатков 4, 19, 1, 10, 16, 13. В частном повторяются 1, 9, 0, 4, 7 и 5. Тогда наш результат является периодической десятичной дробью 776,(190476).
Ответ: 16,3:0,021=776,(190476)
Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.
Подсчитайте, сколько будет 3 5,4.
Решение
Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению 30,0 на 54. Запишем данные столбиком и вычислим результат:
Повторение остатка дает нам в итоге число 0,(5), которое является периодической десятичной дробью.
Ответ: 3:5,4=0,(5).
Как разделить десятичные дроби на 1000, 100, 10 и др.
Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и др. Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.
Так, 56,21:10=5,621, а 0,32:100 000=0,0000032.
В случае с бесконечными десятичными дробями мы поступаем таким же образом.
Например, 3,(56):1 000=0,003(56) и 593,374…:100=5,93374….
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.
Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на 1000, 100, 10 соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.
К примеру, 5,739:0,1=57,39 и 0,21:0,00001=21 000.
Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.
Так, 7,5(716):0,01=757,(167), поскольку после того, как мы перенесли запятую в записи десятичной дроби 7,5716716716… на два знака вправо, у нас получилось 757,167167….
Если же у нас в примере непериодические дроби, то все обстоит проще: 394,38283…:0,001=394382,83….
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.
Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.
План урока:
Введение
Сложение и вычитание десятичных дробей
Умножение и деление десятичных дробей
Округление десятичных дробей
Интересные факты
Введение
Мы уже познакомились с дробями и их видами. Давайте вспомним, какие бывают дробные числа:
Сегодня рассмотрим новый вид дробных чисел – десятичные дроби. Очень часто возникает необходимость в использовании дробных чисел, знаменатели которых имеют числовые значения 10, 100, 1000, 10000. Что такое десятичная дробь, как правильно её записывать, выполнять математические действия, именно об этом мы сегодня и поговорим.
Рассмотрим такую ситуацию:
У Маши был День Рождения, пришли гости. Праздничный торт мама разрезала на 10 кусков по количеству гостей. Какая часть торта досталась каждому гостю?
Давайте разберемся: Торт разрезан на 10 кусков, значит, знаменатель дроби равен 10, каждому достался один кусок, значит, числителем записываем единицу. Записываем как 1/10. Это числовое выражение возможно представить и в другом виде – 0,1. Такой вид числаназывается десятичной дробью. Получается, каждому досталась одна десятая доля торта.
Сформулируем определение:
Десятичная дробь – это числовое выражение, имеющее знаменатель, кратный 10. Всегда пишется в строку. Во время написания после целой части указывают только числитель. Целую и дробную части разделяет запятая.
17/100=0,17 или 3/10=0,3
18+(11/100) =18,11 или 39+(7/10)=39,7
В случае, когда дробь правильная, то перед запятой, необходимо записывать 0.
9/10=0,9
Умение записывать десятичные дроби очень помогает в решении многих математических задач.
Теперь давайте разберемся, как же обозначать десятичные дроби на координатной прямой?
Рассмотрим ситуацию из жизни:
После окончания учебного года школьники пошли в поход. Длина маршрута составляет 10 километров. Первый привал только через 4 километра. Определите пройденную детьми часть маршрута до привала.
Чтобы ответить на главный вопрос необходимо выяснить:
- Из скольких одинаковых долей состоит весь маршрут;
- Определите числовое значение одной части всего маршрута;
- Найдите числовое значение 4 частей?
На рисунке видно, что весь маршрут разбит на 10 одинаковых частей. Одна часть пути равна 1/10 всего маршрута или 0,1. Теперь понятно, что привал будет через 4 такие части, через 4/10 или 0,4 всего пути.
А теперь давайте изобразим на координатном луче числовое выражение 4,5.
4,5 состоит из 4 целых единиц и 5 десятых доли. Значит, на координатном луче нужно отложить 4 единичных отрезка (это расстояние между началом луча и единицей), а один такой отрезок необходимо поделить на десять долей и отсчитать 5 таких частей – то есть половину.
Запомни! Всегда слева будут лежать меньшие, а справа большие числовые значения.
Сложение и вычитание десятичных дробей
В повседневной жизни у каждого из нас почти ежедневно возникает необходимость в выполнении математических действий над десятичными дробями. Разберем простую ситуацию.
Бабушка попросила внука сходить в магазин и купить продукты. Она написала список всего необходимого:
1.Сахар – 1,5кг.
2.Соль – 0,5 кг.
3.Картофель – 1,3кг.
Также бабушка сказала, чтобы внук посчитал общий вес продуктов и определился, сможет он донести покупку или нет!
Для нахождения общего веса необходимо суммировать вес всех компонентов, указанных в списке: 1,5+0,5+1,3. О том, как это сделать сейчас узнаем!
Для выполнения сложения десятичных дробей нужно:
- использовать способ сложения столбиком, необходимое условие – расположение запятой под запятой;
- сначала суммировать дробную, ипотом целую составляющую;
- в результат, вписать запятую в то место, в котором она находилась у слагаемых.
Приведем пример:
1,5
+
0,5
2,0
2,0
+
1,3
3,3
Суммарный вес покупки составил 3,3 кг. Ребенок сможет донести необходимые продукты!
Чтобы выполнить вычитание десятичных дробей необходимо придерживаться очень похожего алгоритма:
- при нахождении разности использовать способ вычисления в столбик, обязательное условие – расположение запятой под запятой;
- сначала найти разность дробной, а потом целой составляющей;
- в разность вписать запятую в то место, в котором она находилась у компонентов.
Приведем пример:
5,6
–
4,1
1,5
9,3
–
1,2
8,1
Умножение и деление десятичных дробей
Хомячку в день дают по половинке яблока. Сколько нужно взять яблок, чтобы накормить 10 хомячков?
Половинка яблока, это ½ = 0,5 яблока.Чтобы узнать количество яблок, долю одного зверька умножаем на количество животных. То есть 0,5×10. А как выполнить данное действие?
Для умножения десятичной дроби на числовые значения 10, 100, 1000, 10000, необходимо переместить запятую вправо на количество символов, равном количеству нулей в целом множителе.
Получается: 0,5×10=5. Чтобы накормить 10 хомячков нужно взять 5 яблок.
Но часто возникают ситуации, когда натуральное число нужно умножить на 0,1; 0,01; 0,0001.
Результат умножения натурального числа на десятичную дробь вида 0,1; 0,01; 0,0001 равен результату деления этого числа на 10, 100, 1000. Нужно в делимом перенести запятую на количество символов влево, равное количеству нулей, находящихся перед единицей в делителе.
7×0,1=0,715×0,01=0,1521×0,1=2,1
Переходим к следующему определению.
В школьную столовую, для изготовления булочек привезли 7 пакетов муки, расфасованную по 1,5 кг в один пакет. Какой общий вес муки, привезенной в столовую?
Чтобы ответить на главный вопрос, нужно перемножить массу одного пакета и количество таких пакетов: 1,5×7.
При умножении десятичной дроби на натуральное число или десятичную дробь, проводим вычисления, не учитывая запятую. Потом отсчитываем в левую сторону количество символов, равное количеству, находящемуся после запятой в двух компонентах.
1,5
х
7
10,5
В столовую привезли 10,5 кг. муки.
Действуем по такому же алгоритму, если нужно найти произведение двух десятичных дробей.
Приведем пример: 3,4×5,8
3,4
х
5,8
272
+
170
19,72
Сначала 34 умножаем на 8, получаем 272.Находим произведение привычным способом.
Записываем под чертой, при этом последняя цифра произведения должна записываться под множителем (8), на который умножали 34.
Далее 34 умножаем на 5, получаем 170. Записываем под первым произведением, сместив на одну клетку влево (последняя цифра произведения, должна записываться под множителем (5), на который умножали 34).
Суммируем. После, в полученном результате отделяем запятой два символа.
Переходим к делению десятичных дробей
Для изготовления 6 банок варенья понадобится 10,2 килограмма фруктов и ягод. Какое количество килограммов потребуется для изготовления одной банки варенья?
Все очень просто. Вычислим частное массы фруктов и количества банок, выходит: 10,2/6.
Чтобы найти частное десятичной дроби и натурального числа нужно:
- выполнять деление целой составляющей, не учитывая запятую;
- после вычисления целой составляющей, поставить запятую;
- окончить вычисление с дробной составляющей.
10,2 делим на 6.
Сначала берем единицу, она не делится на 6, значит берем 10.
Сколько раз в 10 может поместиться 6? Один раз.
Единицу пишем в результат и ставим запятую, так как действия с целой составляющей окончены, а произведение делителя(6) и целой составляющей частного(1) отнимаем от 10, 10 – 6 = 4.
4 записываем вниз и туда же сносим дробную составляющую – 2.
Получилось число 42. Сколько раз помещается в 42? Семь раз.
В результат записываем 7, а произведение делителя и дробной составляющей частного, отнимаем от 42. В результате получаем 0.
Деление без остатка окончено.
Выходит, что для приготовления одной банки варенья потребуется 1,7 кг фруктов.
Иногда встречаются задания в которых нужно выполнить деление десятичной дроби на десятичную дробь вида 0,1, 0,01, 0,001.
Для деления десятичных дробей на числовые выражения вида 0,1, 0,01, 0,001, необходимо в делимом, переместить запятую наколичество нулей в делителе.
Приведем пример:
4,99/0,1 = 49,937
48/0,01 = 3748
Алгоритм деления на десятичную дробь:
- Переместитьзапятую в обоих компонентах на число символов, находящихся после запятой в делителе, чтобы избавиться от запятой.
- Выполнить действие.
12,4/0,4 = 124/4 = 31124/0,4 = 1240/4 = 310
Ничего сложного нет! Главное – запомнить алгоритмы действий для каждого случая
В нашей жизни встречаются ситуации, когда необходимо округлить какое-то числовое значение. Как правильно это сделать мы сегодня узнаем.
Округление десятичных дробей
Округление – изменение числового значения на самое близкое. Знак равенства при округлении заменяется на специальный символ – ≈ (примерно).
Округлим 5,05 до целых. Необходимо, все цифры, стоящие после запятой отбросить, оставив только целую часть: 5,05≈5.
Если необходимо округлить число до указанного разряда, то цифры, стоящие после этого разряда заменяют нулями, а если они находятся после запятой, то их просто не учитывают.
Округлим до десятых число 3,124. Для этого все цифры после разряда десятых отбрасываем. Получаем: 3,124≈3,1.
Помни! В случае, когда первая отброшенная цифра 0,1,2,3,4, то разряд, до которого выполняется округление, оставляем без изменений.
Округлим число 12,344 до целых. Первой цифрой, которую мы не учитываем будет цифра 3, поэтому целое число оставляем без изменений. 12,344≈12.
Но если первой неучтенной цифрой будут цифры от 5 до 9, то тогда разряд до которого выполняется округление увеличивается на 1 единицу.
Округлим число 4,578 до сотых. Первой неучтенной цифрой станет цифра 8, поэтому число разряда десятков увеличивается на единицу. 4,578≈4,58
Интересные факты
Число 0,001 очень маленькое. Его невозможно даже представить! А насколько мала величина 0,001 секунды! Но именно за это время наша планета оборачивается на тридцать метров, при вращении вокруг солнца! Любой звук в воздухе перемещается на 33 метра за этот промежуток времени. За такое же время, вредный комар успевает махнуть крылышками!
А число 0,000001 в тысячу раз меньше предыдущего, но даже оно имеет свое название. При измерении длин его называют микрон, и оно в миллион раз меньше метра. В микронах измеряется размер красных кровяных телец, входящих в состав крови. Размер одного тельца составляет 7 микрон в длину, и 2 в толщину! За промежуток времени равный 0,000001 луч света преодолевает 300 метров.
Десятичные дроби и действия с ними
Десятичная дробь – это дробь, имеющая в знаменателе 10, 100, 1000 и т.д.
Такие дроби принято записывать в строчку, а не как обыкновенную дробь.
ЗАПИСЬ ДЕСЯТИЧНОЙ ДРОБИ:
-
Сначала выделяют целую часть, ставят запятую, а потом записывают числитель дробной части.
Например:
(7frac{38}{100} = 7,38)
-
Если дробь правильная, то целая часть равна 0:
Например:
(frac{6}{10} = 0,6)
-
После запятой должно стоять столько цифр, сколько нулей стоит после единицы в знаменателе дроби. Например, если в знаменателе 10, то после запятой будет одна цифра.
-
Если в знаменателе 1000, то после запятой должно быть три цифры. Если в числителе дроби цифр меньше, чем нулей в знаменателе, тогда после запятой ставят нужное количество нулей, а уже потом записывают числитель:
Например:
(frac{56}{1000})
в знаменателе три нуля, а в числителе только две цифры. Чтобы уравнять количество цифр и нулей, представим дробь как
(frac{056}{1000})
Ноль в начале числителя никак на него не влияет, но помогает нам записать дробь в виде десятичной. Получается, что:
(frac{56}{1000} = frac{056}{1000} = 0,056)
ЧТЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ:
-
Читают десятичные дроби в соответствии с количеством цифр после запятой. Если цифра одна, то знаменатель соответствует числу 10. Тогда мы говорим, что доля десятичная. Если цифры две, то знаменатель соответствует числу 100, доля такой дроби – сотая. Так же называют тысячную долю, десятитысячную, миллионную и так далее.
Например:
(19frac{32}{100} = 19,32) – девятнадцать целых, 32 сотых;
(2frac{9}{1000} = 2frac{009}{1000} = 2,009) – две целых, 9 тысячных;
(frac{3}{10} = 0,3) – три десятых.
-
Если приписать или убрать ноль в конце дроби, то она не изменится.
Например:
(0,80 = 0,8) (80 сотых = 8 десятых);
(0,0780 = 0,078) (780 десятитысячных = 78 тысячных).
СРАВНЕНИЕ ДСЯТИЧНЫХ ДРОБЕЙ:
Чтобы сравнить дроби, их нужно привести к одинаковому количеству знаков после запятой.
Например:
Сравним 0,07 и 0,5.
У первой дроби после запятой две цифры, у второй только одна. Значит второй дроби нужно ее добавить так, чтобы дробь не изменилась. Мы можем приписать ноль в конце дроби.
Получим 0,07 и 0,50. Теперь мы сравниваем две дроби со знаменателем 100. Становится понятно, что 7<50, значит 0,07<0,50, значит 0,07<0,5.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:
Сложим две десятичные дроби:
(1,8 + 3,062)
СПОСОБ 1:
-
Чтобы найти сумму или разность десятичных дробей, можно представить их как обыкновенные.
(1frac{8}{10} + 3frac{62}{1000})
-
Если дроби имеют разные знаменатели, приведем их к одному. Проще всего приписать к одной дроби (и к числителю, и к знаменателю) одинаковое количество недостающих нулей:
(1frac{800}{1000} + 3frac{62}{1000})
-
Теперь сложим дроби как смешанные:
(1frac{800}{1000} + 3frac{62}{1000} = 4frac{800 + 62}{1000} = 4frac{862}{1000})
-
Переведем дробь обратно в десятичную:
(4frac{862}{1000} = 4,862)
СПОСОБ 2:
-
Сумму или разность десятичных дробей можно найти столбиком. Запишем одно число под другим так, чтобы запятая одной дроби находилась по запятой другой:
-
Уравняем количество знаков (чисел) после запятой:
-
Сложим числа в столбик не обращая внимание на запятую.
-
Поставим запятую суммы под запятыми слагаемых:
СПОСОБ 3:
Можно воспользоваться тем фактом, что число состоит из целой и дробной частей и сложить сначала одно, потом другое.
-
Представим дроби в ином виде:
(1,8 = 1 + 0,8)
(3,062 = 3 + 0,062)
-
Сложим целые части:
(1 + 3 = 4)
-
Сложим дробные части:
(0,8 + 0,062 = 0,862)
-
Сложим полученные значения:
(4 + 0,862 = 4,862)
УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:
Умножение десятичной дроби на натуральное число:
Например:
(1,81 bullet 3)
1. Чтобы умножить десятичную дробь на число, нужно найти их произведение в столбик, не обращая внимания на запятую:
2. В полученном произведении отделить запятой столько знаков справа, сколько отделено у дроби:
Умножение десятичной дроби на десятичную дробь:
Например:
(1,81 bullet 0,03)
-
Чтобы умножить десятичную дробь на десятичную, нужно найти их произведение в столбик, не обращая внимания на запятую:
-
В полученном произведении отделить запятой столько знаков справа, сколько в сумме отделено у множителей:
Умножение десятичной дроби на 10, 100, 1000 и т.д.:
Чтобы умножить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков вправо, сколько нулей стоит в множителе после единицы.
Например:
(2,34 bullet 10 = 23,4)
(0,687 bullet 1000 = 687)
(7,095 bullet 100 = 709,5)
Умножение десятичной дроби на 0,1, 0,01, 0,001 и т.д.:
Чтобы умножить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков влево, сколько знаков отделяет запятая в множителе:
(183,7 bullet 0,01 = 1,837)
(0,22 bullet 0,1 = 0,022)
(619 bullet 0,001 = 0,619)
ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:
Деление десятичной дроби на число:
Например:
(2,52 : 4)
-
Найдем частное в столбик, не обращая внимание на запятую:
-
В полученном частном отделим запятой столько знаков справа, сколько отделяется в делимом:
Деление десятичной дроби на десятичную дробь:
Например:
(0,252 : 0,4)
-
В делителе и делимом перенести вправо запятую на столько знаков, сколько их после запятой в делителе.
(0,252 : 0,4 = 2,52 : 4)
-
Выполнить деление на натуральное число.
Деление десятичной дроби на 10, 100, 1000 и т.д.:
Чтобы разделить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков влево, сколько знаков отделяет запятая в множителе.
-
Разделить на 10 = умножить на 0,1
-
Разделить на 100 = умножить на 0,01
-
Разделить на 1000 = умножить на 0,001
Деление десятичной дроби на 0,1, 0,01, 0,001 и т.д.:
Чтобы разделить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков вправо, сколько нулей стоит в множителе после единицы.
-
Разделить на (0,1 =) умножить на 10
-
Разделить на( 0,01 =) умножить 100
-
Разделить на (0,001 = )умножить на 1000
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Все это здесь.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right)))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули ( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: ( 0,014330000=0,01433);
- Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: ( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз);
- Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: ( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, ( displaystyle frac{1}{3}, frac{1}{4},frac{5}{112}).
Наравне с приведенными выше дробями существуют дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
( displaystyle frac{8}{10}=0,8)
( displaystyle frac{13}{100}=0,13)
( displaystyle frac{49}{1000}=0,049)
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
- Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««( 46) целых»;
- Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».
А теперь прочитаем все вместе – «( 46) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат ( 10) на ( 10) и закрась какую-нибудь его часть равную:
- ( 0,05;)
- ( 0,4;)
- ( 0,27;)
- ( 0,245)
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат ( 10) на ( 10) состоит из ( 100) клеточек. Соответственно, ( 0.05) – ( 5) клеточек из ( 100); ( 0,4) – ( 40) клеточек из ( 100) и так далее.
Наверняка, наибольшее затруднение составило последнее число – ( -0,245). На картинке это необходимо отразить как 24,5 клетки.
В общем, смотри:
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Попробуй перевести:
- ( 0,136)
- ( 0,2436)
- ( 0,0456)
- ( 0,21)
Сравним ответы:
- ( displaystyle 0,136=frac{136}{1000})
- ( displaystyle 0,2436=frac{2436}{10000})
- ( displaystyle 0,0456=frac{456}{10000})
- ( displaystyle 0,21=frac{21}{100})
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
- ( displaystyle frac{2}{10})
- ( displaystyle frac{3}{100})
- ( displaystyle frac{4}{1000})
- ( displaystyle frac{4562}{100})
А вот и ответы:
- ( displaystyle frac{2}{10}=0,2)
- ( displaystyle frac{3}{100}=0,03)
- ( displaystyle frac{4}{1000}=0,004)
- ( displaystyle frac{4562}{100}=45frac{62}{100}=45,62)
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
- Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
- После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь ( displaystyle frac{4}{1000}) — ( 3) нуля в знаменателе, соответственно, мы как бы мысленно выделяем ( 3) ячейки.
- Затем записываем числитель – ( 4), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
- ( displaystyle frac{26}{10})
- ( displaystyle frac{43}{100})
- ( displaystyle frac{99}{1000})
- ( displaystyle frac{3562}{100})
А теперь ответы:
- ( displaystyle frac{26}{10}=2,6)
- ( displaystyle frac{43}{100}=0,43)
- ( displaystyle frac{99}{1000}=0,099)
- ( displaystyle frac{3562}{100}=35,62)
Виды десятичных дробей
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))).
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: ( displaystyle frac{1}{4})? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
( displaystyle frac{1}{4}=frac{1cdot 25}{4cdot 25}=frac{25}{100}=0,25)
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен ( 10), ( 100), ( 1000) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
- ( displaystyle frac{1}{5})
- ( displaystyle frac{1}{8})
- ( displaystyle frac{3}{5})
- ( displaystyle frac{1}{16})
Сравним наши ответы:
- ( displaystyle frac{1cdot 2}{5cdot 2}=frac{2}{10}=0,2)
- ( displaystyle frac{125}{1000}=0,125)
- ( displaystyle frac{3}{5}=frac{6}{10}=0,6)
- ( displaystyle frac{1}{16}=frac{625}{10000}=0,0625)
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели ( 1) на ( 17). Поделил? Ты получил ( 0,05882352941) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к ( {{10}^{n}}), с учетом, что ( n) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – ( nto +infty )
Таким образом:
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как ( displaystyle frac{1}{17}).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число ( pi ) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что ( pi =3,14), но это далеко не так. Число ( pi ) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа ( pi ). Мировой рекорд по запоминанию знаков числа ( pi ) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
( pi =3,1415926535text{ }8979323846text{ }2643383279text{ }5028841971)
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь ( displaystyle frac{1}{3}). Что у тебя получилось?
( displaystyle frac{1}{3}=0,333333333….)
Чтобы не повторять число ( 3) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
( displaystyle frac{1}{3}=0,underbrace{3}_{период}33333333….=0,left( 3 right))
( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))
Важно, что период не может начинаться слева от запятой:
( displaystyle frac{100}{7}=underbrace{14,2857}_{не период}1428571428571…=14,left( 285714 right)).
Свойства десятичных дробей
Существует четыре свойства десятичных дробей. Они очень простые, и ты 100% знаешь о всех них, но давай их перечислим и вспомним:
1. Десятичная дробь не меняется, если справа добавить нули
( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.
2. Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби:
( 0,014330000=0,01433)
ВНИМАНИЕ!!! Нельзя удалять нули, расположенные не в конце десятичной дроби!!!!
( 0,014330000ne 0,1433)
3. Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо:
( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз)
4. Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:
( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз)
Последние два свойства позволяют быстро умножать и делить десятичные дроби на ( 10), ( 100), ( 1000) и т.д. о чем подробнее мы поговорим чуть ниже.
Действия с десятичными дробями
Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.
Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене.
Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.
Как складывать десятичные дроби
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.
Разберемся на примере:
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при сложении в сумме мы получаем больше ( 10), то одна единица прибавляется к сумме при сложении цифр следующего разряда.
Решим наш пример, учтя все правила:
Разобрался? Посчитай в столбик самостоятельно:
- ( 0,0125+0,141)
- ( 2,4225+0,34)
- ( 122,4355+1,34)
- ( 2,435+12,3)
Сравним ответы:
- ( 0,0125+0,141=0,1535)
- ( 2,4225+0,34=2,7625)
- ( 122,4355+1,34=123,7755)
- ( 2,435+12,3=14,735)
Как вычитать десятичные дроби
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения.
Соответственно, запятые стоят четко друг под другом.
Вычитание происходит, как и вычитание натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в числах, с которыми мы работаем.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при вычитании получается, что мы из меньшего числа вычитаем большее, то мы как бы занимаем десяток у более высокого разряда (при вычитании сотых частей, берем десяток у десятых, при вычитании десятых – у единиц и так далее), не забывая уменьшить вычитаемое число у заимствованного разряда.
Посмотрим подробно на примере:
Думаю, с рисунком тебе стало все понятно. Попробуй посчитать в столбик следующие выражения:
- ( 0,0125-0,141)
- ( 2,4225-0,34)
- ( 122,4355-1,34)
- ( 12,435-12,3)
Сравним полученные ответы:
- ( 0,0125-0,141=-0,1285)
- ( 2,4225-0,34=2,0825)
- ( 122,4355-1,34=121,0955)
- ( 12,435-12,3=0,135)
Как умножать десятичные дроби
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
Мы начинаем запись числа, получающего при перемножении, под тем разрядом второго числа, на который умножаем. Далее мы суммируем полученные числа и только затем ставим запятую.
Чтобы определить, между какими числами должна стоять запятая, мы должны посмотреть, сколько чисел стоит после знака запятой у первого множителя, сколько у второго, сложить их и отсчитать справа данное количество чисел.
Непонятно? Смотри:
Как ты видишь, при перемножении мы будем складывать столько слагаемых, сколько разрядов содержится во втором множителе, поэтому удобней записывать числа так, чтобы первый множитель был по количеству чисел больше, чем второй.
Таким способом мы значительно снизим вероятность ошибок.
Не веришь? Смотри:
Если при умножении мы получаем число, которое больше ( 9), например ( 12), то единицу мы прибавляем к значению, полученному при умножении последующих чисел следующего десятка.
Соответственно, если получаем, например, ( 24), то прибавляем ( 2).
Проиллюстрируем данное правило:
Разобрался? Дорешай данный пример самостоятельно.
Сколько у тебя получилось? У меня ( 10,33911).
А теперь пора приступить к некоторым очень важным моментам, которые помогут сохранить время на экзамене.
Как делить десятичные дроби
Теперь ты знаешь о десятичных дробях почти все. Осталось только разобраться с тем, как их делить друг на друга.
Если ты отлично это представляешь, смело пропускай данный подраздел. Если нет – смотри инструкцию к применению.
Итак. Мы рассмотрим два вида деления:
- деление десятичной дроби на натуральное число;
- деление десятичной дроби на десятичную дробь.
Начнем с деления десятичной дроби на натуральное число.
Чтобы делить десятичную дробь на натуральное число, необходимо пользоваться следующими правилами:
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Важно!!!
Если целая часть делимого меньше делителя, то в частном ставим ( 0) целых. Логично, правда?
Рассмотрим на конкретном примере:
Усвоил? Раздели столбиком следующие числа:
- ( 135,2:5)
- ( 16,4:2)
- ( 158,14:4)
- ( 2,456:2)
- ( 0,626:2)
Сравним наши ответы:
- ( 135,2:5=27,04)
- ( 16,4:2=8,2)
- ( 158,14:4=39,535)
- ( 2,456:2=1,228)
- ( 0,626:2=0,313)
Вспомни теперь свойства десятичных дробей, описанные ранее: если нам необходимо разделить дробь на ( 10), ( 100), ( 1000) и так далее, нет необходимости делать это в столбик – мы можем просто перенести запятую на столько цифр влево, сколько нулей у нас в делителе.
Например: ( 135,2:10=13,52).
А теперь попробуй самостоятельно:
- ( 135,2:100)
- ( 16,4:10)
- ( 158,14:1000)
- ( 2,456:10)
Перенес? Смотри, что у меня получилось:
- ( 135,2:100=1,352)
- ( 16,4:10=1,64)
- ( 158,14:1000=0,15814)
- ( 2,456:10=0,2456)
Молодец! Переходим к делению десятичных дробей друг на друга.
Деление десятичных дробей друг на друга
Итак, для того чтобы это делать существует три правила:
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на ( 10), ( 100) или ( 1000) и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
- Делим числа как натуральные.
ВАЖНО!!! При умножении мы смотрим, в каком из чисел, участвующих в делении, присутствует наибольшее количество знаков после запятой? Ориентируясь именно на это число мы умножаем на ( 10), ( 100), ( 1000) и так далее.
Рассмотрим на примере ( 16,4:0,02)
В каком числе у нас стоит наибольшее количество знаков после запятой? Правильно, во втором, то есть в делителе: после нуля стоит два знака. Что из этого следует? Что мы умножаем и делимое и делитель на ( 100)!
Что дальше? Мы получаем следующий пример: ( 1640:2) Посчитай, сколько это будет самостоятельно. У меня получилось ( 820).
Рассмотрим примерчик посложнее: ( 5,31:0,3)
Самое большое количество знаков после запятой содержится в первом числе – их два, соответственно, умножаем оба числа, участвующего в делении на ( 100). Получаем: ( 531:30).
А теперь делим в столбик:
Ты видишь, что нацело разделить не получилось, мы «снесли» еще один ноль, и только тогда пришли к ответу, поэтому сразу после окончания деления нашего делимого, мы ставим запятую.
Теперь ты полностью готов совершать любые действия с десятичными дробями. Молодец! Рассмотрим только, как их сравнивать, хотя я думаю, ты уже и сам с этим справишься!
Как сравнивать десятичные дроби
Мы можем сравнивать десятичные дроби двумя способами.
Способ первый – поразрядно.
Допустим, нам необходимо сравнить ( 5,365 V 5,36)
1. Смотрим, одинаковое ли количество знаков после запятой стоит у каждой дроби? Нет? Значит дописываем справа необходимое количество нулей (ты же помнишь, что от дописывания нулей дробь неизменна, правда?)
Что у нас получилось? Верно: ( 5,365 V 5,360)
2. Начинаем сравнивать слева направо: целую часть с целой, десятые части с десятыми и так далее. Когда одна из частей дроби оказывается больше аналогичной части другой, эта дробь и больше.
Перейдем к нашему примеру: целые части у нас одинаковы – их значение ( 5). Десятые тоже – ( 3). Сотые – ( 6), а вот тысячные у первой дроби ( 5), а у второй ( 0). Что больше: ( 5) или ( 0)? Верно, ( 5), соответственно:
( 5,365 > 5,360)
Способ второй – с помощью умножения.
Внимательно смотрим на дроби. На сколько нам нужно умножить два числа, чтобы сравнивать целые числа? Смотрим на ту дробь, у которой знаков после запятой больше, то есть на первую. У нее после запятой ( 3) знака, соответственно, чтобы сделать из нее целое число, необходимо умножить на ( 1000) Умножаем обе дроби на это значение:
( 5,365cdot 1000 V 5,36cdot 1000)
( 5365 V 5360)
Эти числа ты сравнишь без проблем:
( 5365 > 5360)
Заметь, результат получился одинаковый. Теперь попробуй сравнить дроби самостоятельно любым наиболее удобным для тебя способом:
- ( 21,34 V 20,34)
- ( 0,34 V 0,341)
- ( 120,15 V 1210,16)
- ( 10,565 V 10,465)
Справился? Смотри что вышло:
- ( 21,34 > 20,34)
- ( 0,34 < 0,341)
- ( 120,15 < 1210,16)
- ( 10,565 > 10,465)
Вот теперь ты усвоил дроби полностью!
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».