Как найти значение числа в десятичном виде

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34,21, 0,35035044, 0,0001, 11 231 552,9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой (5.67, 6789.1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000, 100, 10 и др. или смешанное число. Например, вместо 610 мы можем указать 0,6, вместо 2510000 – 0, 0023, вместо 5123100 –  512,03.

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0,14, которой соответствует 14100, читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56,002, которой соответствует 5621000, мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Что такое разряды в десятичных дробях

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0,7 семерка – это десятые доли, в 0,0007 – десятитысячные, а в дроби 70 000,345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

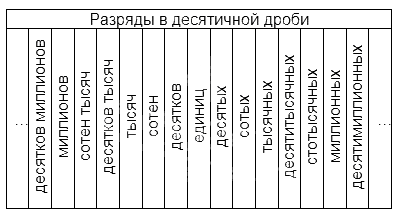
Разберем пример.

У нас есть десятичная дробь 43,098. У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9, тысячных – 8.

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10-тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56+0,0455, или 56,0055+0,4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0,367, 3,7, 55,102567958, 231 032,49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5,63 мы можем привести к виду 563100, а 0,2 соответствует 210 (или любая другая равная ей дробь, например, 420 или 15.)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 513 нельзя заменить на равную дробь с знаменателем 100, 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0,143346732…, 3,1415989032…, 153,0245005…, 2,66666666666…, 69,748768152…. и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3,444444…. периодом будет цифра 4, а для 76, 134134134134… – группа 134.

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3,444444…. правильно будет записать как 3,(4), а 76, 134134134134…– как 76,(134).

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0,677777 – это то же самое, что 0,6(7) и 0,6(77) и т.д. Также допустимы записи вида 0,67777(7), 0,67(7777) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0,6(7), а, например, в случае с дробью 8,9134343434 будем писать 8,91(34).

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2, то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45,32. В периодическом виде она будет выглядеть как 45,32(0). Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9, например, 4,89 (9), 31,6(9). Они являются альтернативной записью схожих дробей с периодом 0, поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0). Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8,31(9) можно заменить на соответствующую ей дробь 8,32(0). Или 4,(9)=5,(0)=5.

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9,03003000300003… на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Положение десятичных дробей на оси координат

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 1410 – это то же самое, что и 1,4, поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

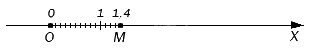
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15,4008, то мы предварительно представим это число в виде суммы 15+0,4+,0008. Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15,4008.

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2=1,41421…, и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M. Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1,4.

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Как перевести в десятичную систему

Система счисления – это метод представления чисел в математике. Для записи используется определенный набор символов, цифр и/или латинских букв. Чтобы перевести любое число в десятичную систему, нужно преобразовать его по определенным правилам.

Инструкция

Значение десятичного числа зависит от расположения его цифр. Этот способ записи называется позиционной системой. Таких систем множество, ведь за основание можно взять не только 10. Например, довольно распространены восьмеричная и шестнадцатеричная системы, а также двоичная, которую используют компьютеры для передачи, хранения и кодирования данных. Двоичный код числа представляет собой различные комбинации всего лишь двух символов: 0 и 1. Несмотря на удобство применения вычислительными машинами, такая система трудно воспринимается человеком.

Число в позиционной системе счисления можно представить в виде суммы элементов. Эти элементы являются произведениями цифр числа на основание, возведенное в соответствующую степень. Разряды чисел идут по убыванию, следовательно, удобнее начинать справа, т.е. с нулевой степени. Например, двоичное число 011101 равно 1•2^0 + 0•2¹ + 1•2² + 1•2³ + 1•2^4 + 0•2^5 = 29.

Таким образом, можно перевести в десятичную систему любое число. Попробуйте преобразовать семеричное число 743: 743_7 = 3•7^0 + 4•7¹ + 7•7² = 374_10. Несколько сложной, на первый взгляд, выглядит ситуация, когда основание больше 10, но это не так. В этом случае просто необходимо вспомнить, что когда заканчиваются цифры, в ход идет латинский алфавит. Применительно к шестнадцатеричной записи это значит, что в ней участвуют заглавные буквы A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Пример:
12FE_16 = 14•16^0 + 15•16¹ + 2•16² + 1•16³ = 4849.

Помимо позиционных систем счисления существуют также непозиционные, когда позиция символа в числе не влияет на его общее значение. Ярким примером такой записи является римская. В ней используется ограниченный набор заглавных латинских букв: I, V, Х, L, С, D и М. Для перевода таких чисел в десятичный вид необходимо знать значения этих символов:
I = 1; V = 5; Х = 10; L = 50; С = 100; D = 500; М = 1000

Кроме того, есть два основных принципа. Принцип сложения состоит в том, что если большая цифра занимает позицию перед меньшей, то они складываются. В обратном случае – меньшая вычитается из большей:
МСМLХХХI = 1 + 10 + 10 + 10 + 50 + 900[CM=1000–100] + 1000 = 1981;
ММХII = 2 + 10 + 1000 + 1000 = 2012.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

При решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует.

Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель.

Как перевести обыкновенную дробь в конечную десятичную дробь?

Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в столбик).

Пример №1. ½ = 0,5  так как 1:2=0,5

Пример №2. ¾ = 0,75 так как 3:4=0,75

Пример №3. Так как 18:25=0,72, то

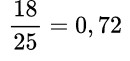
Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет.

Пример №4.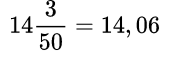

здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06.

Пример №5.

в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель – это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06.

Как перевести десятичную дробь (конечную) в обыкновенную?

Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь.

Пример №6.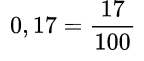

целая часть равна нулю, нуль перед обыкновенной дробью  не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля.

Пример №7.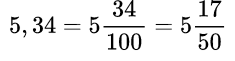

целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь

Задание 7OM21R

На координатной прямой отмечены точки А, В, С и D.

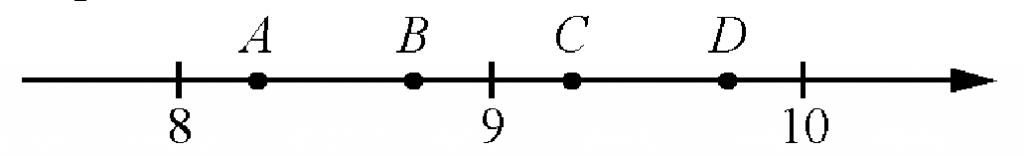
Одна из них соответствует числу 10713. Какая это точка?

1. точка А
2. точка В
3. точка С
4. точка D

---

Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А.

Ответ: 1

pазбирался: Даниил Романович | обсудить разбор

Задание OM0705o

Одно из чисел  отмечено на прямой точкой.

Какое это число?

---

Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.

Итак, выделяем целые части:

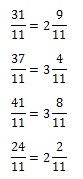
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.

Ответ: 31/11

pазбирался: Даниил Романович | обсудить разбор

Задание OM0704o

На координатной прямой отмечена точка А:

Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?

1. 181/16
2. √37
3. 0,6
4. 4

---

Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.

Оцениваем 181/16 – можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.

Оцениваем √37 – самое близкое значение, из которого вычисляется квадратный корень – это 36, значит  √37 – это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.

Посмотрим на вариант 0,6 – это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.

Вариант с ответом 4 также не подойдет по вышеуказанной причине.

Ответ: √37

pазбирался: Даниил Романович | обсудить разбор

Задание OM0701o

Какое из следующих чисел заключено между числами 8/3 и 11/4 ?

1. 2,7
2. 2,8
3. 2,9
4. 3

---

В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:

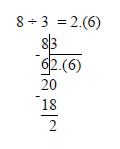
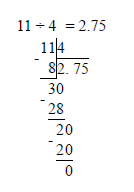
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.

Ответ: 2,7

pазбирался: Даниил Романович | обсудить разбор

Задание OM0604o

Найдите значение выражения:  ¼ + 0,07

---

К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.

Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:

0,25 + 0,07 = 0,32

Ответ: 0,32

pазбирался: Даниил Романович | обсудить разбор

Задание OM0601o

Найдите значение выражения:

---

Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.

Вычислим значение знаменателя:

4,5 • 2,5

Можно произвести вычисления в столбик, тогда получим:

4,5 • 2,5 = 11,25

Либо перевести дробь к простому виду:

4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4

Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:

9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )

9 и 45 можно сократить на 9:

( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8

Ответ: 0,8

pазбирался: Даниил Романович | обсудить разбор

Алла Василевская | Просмотров: 9k

Перевод чисел в различные системы счисления с решением

Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую. Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку “Получить запись”.

Также может быть интересно:

• Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
• Калькулятор комплексных чисел

Системы счисления

Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.

Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:

Число:	5	9	2	1
Позиция:	3	2	1	0

Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 = 5·103+9·102+2·101+1·100. Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.

Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:

Число:	1	2	3	4	5	6	7
Позиция:	3	2	1	0	-1	-2	-3

Число 1234.567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·103+2·102+3·101+4·100+5·10-1+6·10-2+7·10-3.

Перевод чисел из одной системы счисления в другую

Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:

1. Перевести число 1001101.11012 в десятичную систему счисления.
Решение: 1001101.11012 = 1·26+0·25+0·24+1·23+1·22+0·21+1·20+1·2-1+1·2-2+0·2-3+1·2-4 = 64+8++4+1+0.5+0.25+0.0625 = 77.812510
Ответ: 1001101.11012 = 77.812510

2. Перевести число E8F.2D16 в десятичную систему счисления.
Решение: E8F.2D16 = 14·162+8·161+15·160+2·16-1+13·16-2 = 3584+128+15+0.125+0.05078125 = 3727.1757812510
Ответ: E8F.2D16 = 3727.1757812510

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.

Перевод целой части числа из десятичной системы счисления в другую систему счисления

Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.

3. Перевести число 27310 в восьмиричную систему счисления.
Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421
Проверка: 4·82+2·81+1·80 = 256+16+1 = 273 = 273, результат совпал. Значит перевод выполнен правильно.
Ответ: 27310 = 4218

Рассмотрим перевод правильных десятичных дробей в различные системы счисления.

Перевод дробной части числа из десятичной системы счисления в другую систему счисления

Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.

4. Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 – целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 – вторая цифра результата), 0.5·2 = 1.0 (1 – третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
Ответ: 0.12510 = 0.0012

Оглавление:

• Целые числа
• Дробные числа
• Чтение десятичных чисел: примеры
• Операции с десятичными числами: сложение, вычитание, умножение и деление
• Дополнение
• Вычитание
• Умножение
• Деление
• Решенные упражнения

Розимар Гувейя, профессор математики и физики

В десятичных чисел являются рациональными числами (Q) не целые числа, выраженные запятыми и знаков после запятой, которые имеют, например, 1,54; 4.6; 8.9 и др. Они могут быть положительными или отрицательными.

Десятичные разряды отсчитываются от запятой, например, число 12 451 имеет три десятичных разряда, то есть три цифры после запятой.

Целые числа

В отличие от десятичных чисел, целые числа – это действительные числа (положительные или отрицательные), представленные буквой Z. У них нет запятой, например: 1; 2; -3; -4 и т. Д.

Дробные числа

Хотя они могут иметь соответствующее значение, дробные числа выражаются следующим образом:

• ½ (половина), что соответствует десятичной дроби 0,5
• ¾ (три четверти), соответствующие десятичной дроби 0,75
• ¼ (одна четверть), что соответствует 0,25

Следовательно, все десятичные числа можно выражать дробями.

Чтение десятичных чисел: примеры

Чтение десятичных чисел осуществляется путем соединения целой части числа (выраженного перед запятой) и количества десятичных знаков (после запятой), соответствующего дробной части: десятая, сотая, тысячная, десятая тысячная, сотая тысячная., миллионный и др.

Чтобы лучше понять, посмотрите несколько примеров ниже:

• 0,1: одна десятая
• 0,4: четыре десятых
• 0,01: одна сотая
• 0,35: тридцать пять сотых
• 0,125: сто двадцать пять тысячных
• 1.50: одна целая пятьдесят сотых
• 2.1: два целых числа и одна десятая
• 4.8: четыре целых числа и восемь десятых

Операции с десятичными числами: сложение, вычитание, умножение и деление

Чтобы выполнять операции с десятичными числами, мы должны выровнять числа в соответствии с запятой и имеющимися у них десятичными знаками.

Дополнение

Вычитание

Умножение

Деление

Подробнее о цифрах читайте в статьях:

Решенные упражнения

1. Укажите, какие десятичные числа выражаются следующими дробями:)

Б)

ç)

г)

а также)

Посмотреть ответ

а) 0,875

б) 0,66

в) 2,037

г) 13,14

д) 0,59

2. Добавьте десятичные числа ниже:

а) 0,34 + 057

б) 0,098 + 2,4

в) 7,9 + 8,56

г) 0,002 + 0,01

д) 97,9 + 52,54

Посмотреть ответ

а) 0,91

б) 2,488

в) 16,46

г) 0,012

д) 150,44

3. (Энем-2011) Владельцу автомастерской для ремонта автомобиля нужен поршень из деталей двигателя диаметром 68 мм. Чтобы получить его, хозяин идет на свалку и находит поршни диаметром 68,21 мм; 68,102 мм; 68.001 мм; 68,02 мм и 68,012 мм.

Чтобы поместить поршень в ремонтируемый двигатель, хозяину мастерской придется приобрести поршень с диаметром, наиболее близким к необходимому.

В таком состоянии владелец мастерской должен купить поршень диаметром

а) 68,21 мм.

б) 68.102 мм.

в) 68,02 мм.

г) 68.012 мм.

д) 68.001 мм.

Посмотреть ответ

Альтернативный вариант e) 68 001 мм.