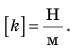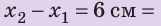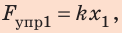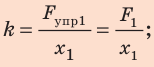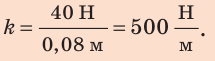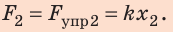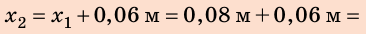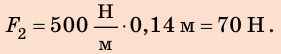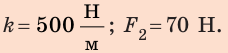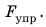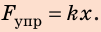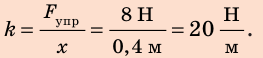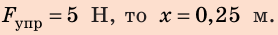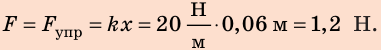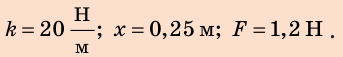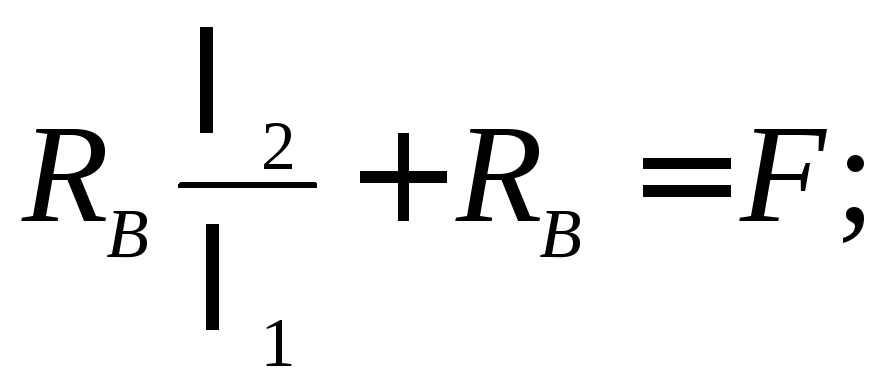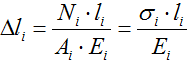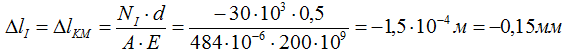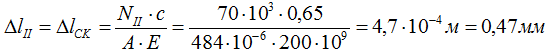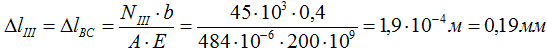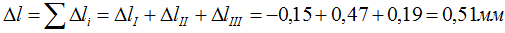Частицы, из которых состоят твердые тела (как аморфные, так и кристаллические) постоянно совершают тепловые колебания около положений равновесия. В таких положениях энергия их взаимодействия минимальная. Если расстояние между частицами уменьшается, начинают действовать силы отталкивания, а если увеличиваться – то силы притяжения. Именно этими двумя силами обусловлены все механические свойства, которыми обладают твердые тела.
Если твердое тело изменяется под воздействием внешних сил, то частицы, из которых оно состоит, меняют свое внутреннее положение. Такое изменение называется деформацией.
Виды деформации
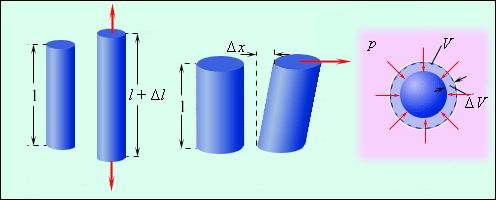
Различают деформации нескольких видов. На изображении показаны некоторые из них.
Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.
Первый вид – растяжение или сжатие – является наиболее простым видом деформации. В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δl, которое происходит под действием сил, обозначаемых F→. Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.
Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).
Обозначим этот показатель ε и запишем следующую формулу:
ε=∆ll.
Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.
Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.
Механическое напряжение
Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.
σ=FS.
Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.
Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y. На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.
Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.
В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.
Деформация, исчезающая при снятии напряжения, называется упругой.
Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.
Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.
На данном участке будет выполняться закон Гука:
ε=1Eσ.
В формуле содержится так называемый модуль Юнга, обозначенный буквой E.
Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.
Предел упругости
Предел упругости – максимальное напряжение, после снятия которого тело восстановит свою форму и размер.
После перехода этого предела восстановления первоначальных параметров тела уже не происходит. Когда мы снимаем напряжение, у тела остается так называемая остаточная (пластическая) деформация.
Обратите внимание на участок диаграммы bc, где напряжение практически не увеличивается, но деформация при этом продолжается. Это свойство называется текучестью материала.
Предел прочности
Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.
В точке e материал разрушается.
Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.
Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.
Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:
∆xl=1GFS
Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Н/м2, G=0,42·1011 Н/м2.
Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен 0.
При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
∆VV=1Bp
Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Н/м2, у стали B=1,6·1011Н/м2. В Тихом океане на глубине 4 км давление составляет 4·107 Н/м2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно 0,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.
От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.
Содержание:
Деформация тела:
Вспомните ненастный день: дует порывистый ветер, гнутся деревья. Чем сильнее ветер, тем больше гнутся деревья. А вот физики говорят, что деревья деформируются. Когда ветер стихает, деревья возвращаются в свое первоначальное положение — деформация исчезает. Но если ветер достаточно сильный, то ветви деревьев и даже их стволы могут сломаться.
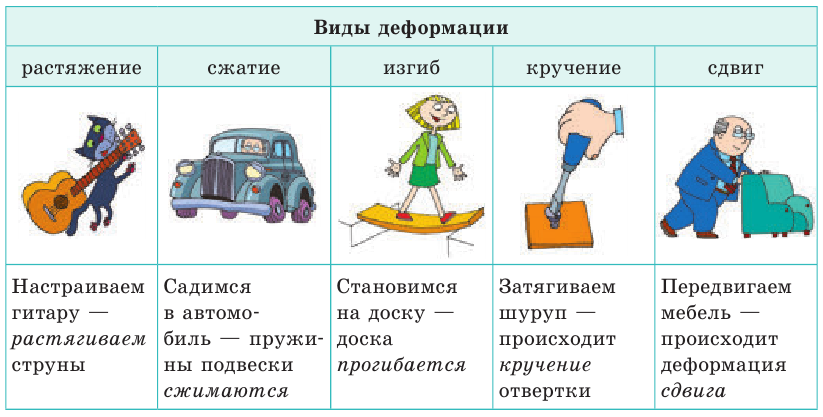
Виды деформации
Уже отмечалось, что результатом действия силы на тело может быть как изменение скорости движения тела, так и его деформация. Например, если толкнуть мячик, то он придет в движение, а некоторые его части при толчке сместятся относительно друг друга — мячик деформируется.
Деформация — изменение формы и (или) размеров тела. В зависимости от того, как именно части тела смещаются относительно друг друга, различают деформации растяжения, сжатия, изгиба, кручения, сдвига (см. таблицу).
Различия упругих и пластических деформаций
Возьмите эспандер (или ластик) и сожмите его — эспандер согнется. Но если прекратить сжимать эспандер, он полностью восстановит свою форму — деформация исчезнет (рис. 19.1). Деформации, которые полностью исчезают после прекращения действия на тело внешних сил, называют упругими.
Делая глиняную фигурку, мастер мнет руками комок глины, и глина сохранит форму, которую придаст ей мастер (рис. 19.2). Тяжелый пресс на монетном дворе чеканит монеты из металлических заготовок, — после прекращения действия пресса монета не восстановит свою прежнюю форму куска металла. И глина, и металл «не помнят» своей формы до деформации и не восстанавливают ее. Деформации, которые сохраняются после прекращения действия на тело внешних сил, называют пластическими. Попробуйте привести другие примеры упругих и пластических деформаций.
Определение силы упругости
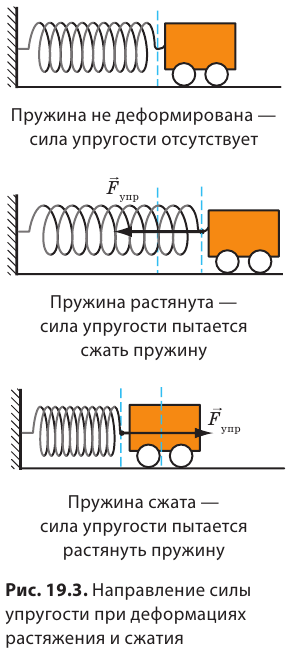
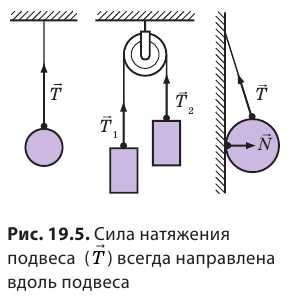
При деформации всегда возникает сила, стремящаяся восстановить то состояние тела, в котором оно находилось до деформации. Эту силу называют силой упругости (рис. 19.3).
Сила упругости — это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации. Обычно силу упругости обозначают символом 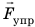
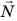
Если тело растягивает подвес (нить, жгут, шнур), то возникает сила упругости, направленная вдоль подвеса. Эту силу называют силой натяжения подвеса и обозначают символом 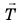
Закон Гука
Научное исследование процессов растяжения и сжатия тел начал Роберт Гук (рис. 19.6) в XVII в. Результатом работы ученого стал закон, который позже получил название закон Гука: При малых упругих деформациях растяжения или сжатия сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: 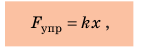
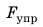
Удлинение — это физическая величина, которая характеризует деформации растяжения и сжатия и равна изменению длины тела в результате деформации. Удлинение х определяется по формуле: 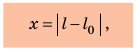
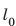
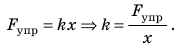
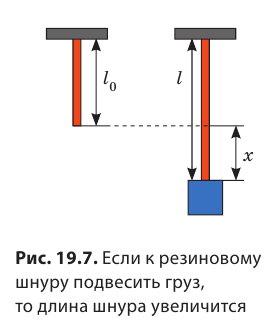
Жесткость — это характеристика тела, поэтому она не зависит ни от силы упругости, ни от удлинения. Жесткость зависит от формы и размеров тела, а также от материала, из которого тело изготовлено. Сила упругости прямо пропорциональна удлинению тела, поэтому график зависимости 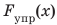
- Заказать решение задач по физике
Почему возникает сила упругости
Вы хорошо знаете, что все тела состоят из частиц (атомов, молекул, ионов). В твердых телах частицы колеблются около положений равновесия и взаимодействуют межмолекулярными силами притяжения и отталкивания. В положениях равновесия данные силы уравновешены. При деформации тела во взаимном расположении его частиц происходят изменения. Если расстояние между частицами увеличивается, то межмолекулярные силы притяжения становятся больше сил отталкивания. Если же частицы сближаются, то больше становятся межмолекулярные силы отталкивания. Другими словами: при деформации частицы «стремятся» вернуться в положение равновесия. Силы, возникающие при изменении положения одной частицы, очень малы. Но когда тело деформируется, изменяется взаимное расположение огромного количества частиц. В результате сложение сил дает заметную равнодействующую, которая противостоит деформации тела. Это и есть сила упругости. Итак, сила упругости — проявление действия межмолекулярных сил.
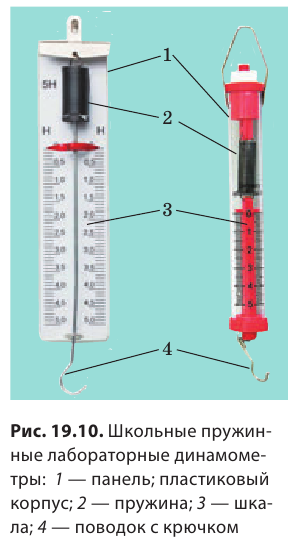
Приборы для измерения силы
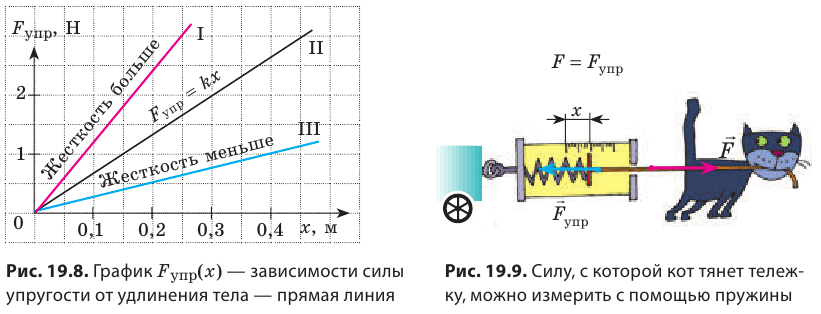
Сила — это физическая величина, поэтому ее можно измерить. Приборы для измерения силы называют динамометрами. Основная составляющая простейших динамометров — пружина. Рассмотрим принцип действия таких динамометров на простом примере. Чтобы с помощью пружины, жесткость k которой известна, измерить силу F, с которой кот тянет тележку (рис. 19.9), необходимо:
1) измерить удлинение x пружины; 2) воспользовавшись законом Гука, определить силу упругости 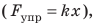
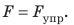
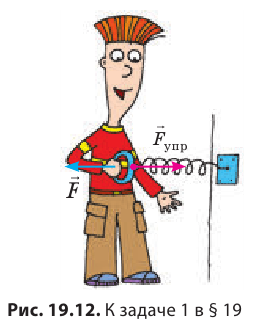
Пример №1
Действуя на пружину силой 40 Н, мальчик растянул ее на 8 см. Определите жесткость пружины. Какую силу нужно приложить мальчику, чтобы растянуть эту пружину еще на 6 см? Деформацию пружины считайте малой упругой. Анализ физической проблемы. Сила, которую прикладывает мальчик, по значению равна силе упругости, возникающей при растяжении пружины: F= уFпр (рис. 19.12). Деформация является малой упругой, поэтому воспользуемся законом Гука. Задачу будем решать в единицах СИ.
Дано:
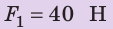
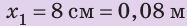
Найти:

Решение:
1. Вычислим жесткость пружины:
поэтому
2. Найдем силу, которую нужно приложить мальчику, чтобы дополнительно растянуть пружину:
По условию 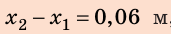
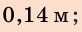
Анализ результатов. Для удлинения пружины на 8 см мальчик прикладывал силу 40 Н; для удлинения пружины еще на 6 см ему нужно увеличить силу на 30 Н — это правдоподобный результат.
Ответ:
Пример №2
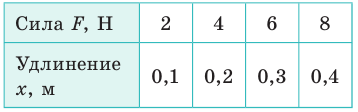
Выполняя экпериментальное задание, девочка увеличивала нагрузку на резиновый шнур. Каждый раз она измеряла силу, действующую на шнур, и соответствующее удлинение шнура. Воспользовавшись таблицей, составленной девочкой, постройте график уFпр(x). С помощью графика определите: 1) жесткость шнура; 2) удлинение шнура, когда к нему приложена сила 5 Н; 3) силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 6 см.
Анализ физической проблемы. При растяжении шнура возникает сила упругости, которая по значению равна силе, действующей на шнур: 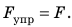
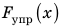
Решение:
Построив указанные в таблице точки (см. рисунок), увидим, что все они принадлежат одной прямой, значит, для любой точки графика имеем:
1) Выбрав точку А графика, найдем жесткость шнура:
2) Удлинение шнура в результате действия силы 5 Н найдем по графику: если
3) Силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 0,06 м, найдем по закону Гука:
Ответ:
Итоги:
Деформацией называют изменение формы и (или) размеров тела. Если после прекращения действия на тело внешних сил деформация полностью исчезает, то это упругая деформация; если деформация сохраняется, то это пластическая деформация.
Сила упругости 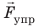
Сила упругости — проявление действия межмолекулярных сил. При малых упругих деформациях растяжения и сжатия выполняется закон Гука: сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: 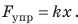
- Плотность вещества в физике
- Сила трения в физике
- Вес тела в физике
- Закон всемирного тяготения
- Сила в физике
- Силы в механике
- Сила тяжести в физике
- Сила упругости в физике и закон Гука
Для большинства
конструкционных материалов при нагружении
до определённых значений напряжений
справедлива следующая зависимость
между деформацией стержня и нормальным
напряжением:
(2.3)
где ε – относительное
удлинение стержня;;
– абсолютное
удлинение стержня;
–
длина образца до деформации;
–длина образца
после деформации (рис. 2.2).
Зависимость (2.3)
носит название закона Гука и формулируется
следующим образом: линейные деформации
прямо пропорциональны нормальным
напряжениям.
Коэффициент Е,
зависящий
от материала, называется модулем
продольной упругости, или модулем
упругости первого рода. Он характеризует
жёсткость материала, т.е. его способность
сопротивляться деформации. Поскольку
–
величина безразмерная, то единица
измерения модуля продольной упругостиЕ
та же, что и у напряжения
,
т.е. паскаль. В табл. 2.1 приведены значенияЕ
для некоторых материалов [1].
Таблица 2.1
|
Материал |
E, |
Материал |
E, |
|
Сталь |
|
Бронза |
|
|
Медь |
|
Титан |
|
|
Чугун |
|
Дерево |
|
|
Алюминий |
|
Стеклопластики |
|
Поскольку
и
,
из формулы (2.3) получаем выражение для
определения абсолютного удлинения или
укорочения стержня длиной:
(2.4)
Между продольной
и поперечной деформациями существует
зависимость
,
(2.5)
где
–
относительное поперечное сужение
стержня. Коэффициентназывается коэффициентом Пуассона или
коэффициентом поперечной деформации.
Значениедля различных материалов колеблется в
пределах от 0 до 0,5. Для всех марок сталей
можно принимать значение.
Поскольку,
то полное поперечное сужение (при
растяжении) или уширение (при сжатии)
определяется по формуле
,
где ∆b
– абсолютная поперечная деформация;
–
первоначальный поперечный размер;–
поперечный размер стержня после
деформации.
В практике часто
встречаются стержни переменного сечения,
в основном – ступенчатые. У таких
стержней полное изменение длины
определяется как алгебраическая сумма
деформаций его отдельных частей, в
пределах которых величины Е,
N
и A
постоянны:
В частности, для
приведённой на рис. 2.3 схемы полное
удлинение ступенчатого стержня
определится как сумма деформаций двух
участков:

Рис. 2.3
2.4. Статически неопределимые задачи при осевом растяжении или
сжатии
Определить реакции
и усилия в частях бруса
и
(рис. 2.4).
Сила F
растягивает верхнюю часть бруса и
сжимает нижнюю. Обозначим реакции
заделки
и
.
Рис. 2.4
Уравнение равновесия:
Рассмотрим
деформации. Поскольку концы бруса
защемлены, то удлинение верхней части
равно укорочению нижней, следовательно,
;
или
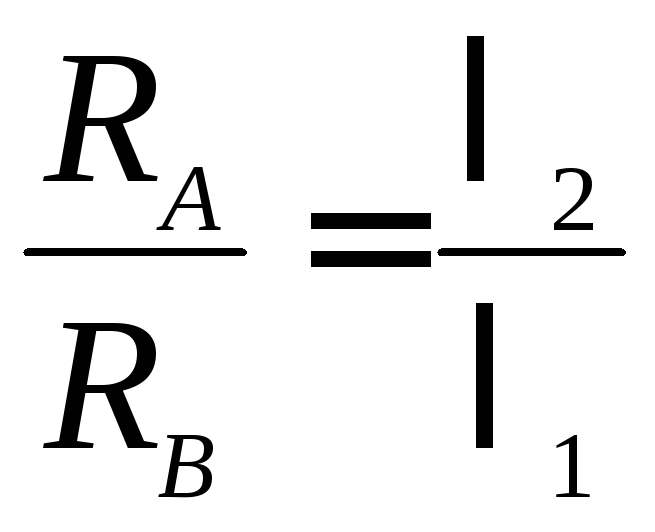
т.е. реакции обратно
пропорциональны длинам
и
.
Решаем это уравнение
совместно с уравнением статики.

3. МЕХАНИЧЕСКИЕ
ИСПЫТАНИЯ СВОЙСТВ МАТЕРИАЛОВ
3.1. Диаграмма растяжения
Для изучения
свойств материалов и установления
значений предельных напряжений проводят
испытания образцов материалов вплоть
до разрушения.
По виду деформации,
испытываемой образцом, различают
испытания на растяжение, сжатие, кручение
и изгиб. Реже проводят испытания на
сложное сопротивление.
Поскольку результаты
испытаний зависят от формы образца,
скорости его деформирования, температуры
и других факторов, то эксперимент
проводят в условиях, предусмотренных
ГОСТом. Испытания проводят на специальных
машинах. Наибольшее распространение
имеют испытания на растяжение статической
нагрузкой, т.к. они наиболее просты и в
то же время во многих случаях дают
возможность достаточно верно судить о
поведении материала при других видах
деформаций. Для испытаний на растяжение
применяют цилиндрические или плоские
образцы. В качестве основных используются
цилиндрические образцы диаметром
длиной
(короткие) либо
(длинные).
Целью испытаний
на растяжение является определение
механических характеристик материала.
При испытании автоматически изображается
диаграмма зависимости между растягивающим
усилием F
и удлинением образца
.
Для того чтобы
можно было сравнить результаты испытания
образцов различных размеров, изготовленных
из одинаковых материалов, полученную
диаграмму перестраивают в другой системе
координат. По оси ординат откладывают
не силы, а нормальные напряжения,
получаемые делением силы на первоначальную
площадь поперечного сечения образца
По оси абсцисс вместо абсолютных
откладывают относительные удлиненияТакую диаграмму называют условной
диаграммой растяжения, т.к. напряжения
и относительные деформации вычисляются
соответственно по отношению к
первоначальной площади сечения и длине
образца. Таким образом, диаграмма
устанавливает связь между напряжениями
и деформациями образца за всё время
испытаний.
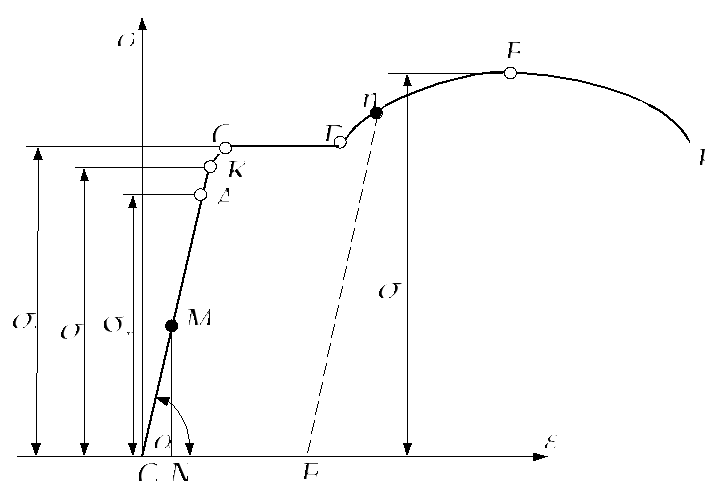
На рис. 3.1 изображена
условная диаграмма растяжения для
малоуглеродистой стали. Рассмотрим её
характерные точки.
Рис. 3.1
На участке ОА
до некоторого напряжения σпр
деформации растут пропорционально
напряжениям, следовательно, на этом
участке сохраняет силу закон Гука. Точка
А
соответствует напряжению, называемому
пределом пропорциональности σпр.
Предел пропорциональности – это
наибольшее напряжение, до которого
деформации в материале растут
пропорционально напряжениям. Если взять
какое-нибудь состояние образца в пределах
прямолинейного участка деформации,
например М,
то тангенс угла наклона линии ОА
к оси абсцисс можно представить в виде
(3.1)
Модуль упругости
первого рода может быть определён как
тангенс угла наклона прямолинейного
участка ОА
к оси абсцисс.
За точкой А
диаграмма становится криволинейной.
Однако если величина напряжений не
превысит некоторого значения
,
соответствующего точкеК,
то материал сохраняет свои упругие
свойства и при разгрузке образец
восстанавливает свою форму и размеры.
Это напряжение называется пределом
упругости. Разница между σпр
и
на практике невелика и обычно между
ними не делают различия. Например, для
стали Ст3 эти величины соответственно
равны 210 МПа и 220 МПа.
При дальнейшем
увеличении нагрузки за пределом
упругости, начиная с точки С,
деформации начинают расти без увеличения
напряжений. Это явление называется
текучестью материала. Горизонтальный
участок диаграммы CD
называется площадкой текучести.
Напряжение, при котором происходит рост
деформации без увеличения нагрузки,
называется пределом текучести и
обозначается
.
Для стали Ст3 предел текучести равен
230 МПа. Напряжения выше предела текучести
вызывают в деталях недопустимые
остаточные деформации. Если от какой-нибудь
точкиn
диаграммы
(см. рис. 3.1), лежащей
выше площадки текучести, произвести
разгрузку образца, то линия разгрузки
nF
будет прямой, параллельной ОА.
Отрезок OF
представляет величину пластической
деформации, которая останется в образце
после разгрузки.
Ряд материалов,
таких как легированные стали, не имеют
ярко выраженной площадки текучести, и
для них устанавливается так называемый
условный предел текучести. Напряжение,
при котором остаточная деформация равна
0,2 %, называется условным пределом
текучести и обозначается
.
После перехода
площадки текучести материал снова
приобретает способность сопротивляться
деформированию. Диаграмма за точкой D
вновь поднимается вверх, хотя и менее
интенсивно, чем в зоне упругих деформаций.
Точка В
диаграммы соответствует наибольшему
напряжению, которое называется пределом
прочности или временным сопротивлением.
Обозначается предел прочности
или
.
Для стали Ст3 σв
= 380 МПа. У высокопрочных легированных
сталей
достигает 1700
МПа.
После перехода
предела прочности на образце появляется
местное сужение – шейка. Площадь сечения
шейки быстро уменьшается, вследствие
чего деформация образца происходит при
уменьшающихся нагрузке и соответственно
напряжении. При напряжении,
соответствующем точке В,
образец разрывается.
Для изготовления
деталей и элементов конструкций применяют
пластичные и хрупкие материалы. Под
пластичностью понимают способность
материала получать большие остаточные
деформации без разрушения. В качестве
мер пластичности в технике используют
относительное остаточное удлинение
образца после разрыва
и относительное остаточное уменьшение
площади поперечного сечения в шейке
после разрыва:


где
–
длина образца после разрыва, составленного
из двух частей;– длина образца до испытания;
– площадь сечения в шейке;
– площадь поперечного сечения образца
до испытания.
Для стали Ст3
значение
составляет 50…60 %.
Хрупкостью
называется свойство материала разрушаться
без образования заметных остаточных
деформаций. Для таких материалов
удлинение при разрыве составляет менее
5 %. Это свойство противоположно
пластичности. Для сравнения на рис. 3.2
приведены условные диаграммы растяжения
для пластичного (малоуглеродистая
сталь) и хрупкого (чугун) материалов.
Рис. 3.2
Деление материалов
на пластичные и хрупкие является
условным, т.к. в зависимости от температуры,
скорости деформирования, напряжённого
состояния и других факторов пластичность
изменяется. При изготовлении деталей
в практике широко используется термическая
обработка, которая позволяет изменять
свойства материалов для улучшения
эксплуатационных характеристик деталей.
В частности, закалка резко повышает
прочность стали и одновременно снижает
её пластические свойства.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи на расчет деформаций участков и изменение общей длины стального стержня при его растяжении-сжатии.
Задача
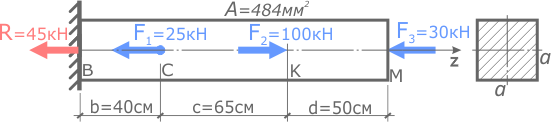
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Другие примеры решений >
Помощь с решением задач >
Модуль продольной упругости стали E=200ГПа.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций,
- Построение эпюр внутренних продольных сил,
- Подбор размеров поперечного сечения стержня,
- Построение эпюр нормальных напряжений.
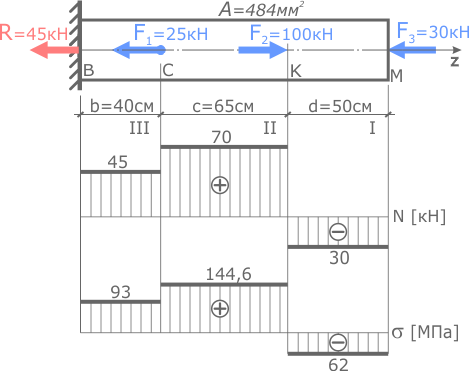
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.
Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).
По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Рассчитаем их:
Деформация I участка (KM)
II участок (CK)
Удлинение третьего участка BC
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
В результате деформации общая длина стержня увеличится на 0,51мм.
Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 декабря 2022 года; проверки требуют 4 правки.
Диаграмма деформирования твердого тела
| Причины отказа механики |
|---|
|
Деформа́ция (от лат. deformatio — «искажение») — изменение формы и размеров тел или объема, связанное с их перемещением друг относительно друга за счет приложения усилия, при котором тело искажает свои формы. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.
Виды деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Обратимые деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе обратимых деформаций лежит смещение атомов тела от положения равновесия, в основе необратимых — необратимые перемещения атомов на расстояния от исходных положений равновесия (после снятия нагрузки происходит переориентация в новое равновесное положение). Деформация определяется как отношение изменения длины деформированного объекта к его начальной длине. Деформация не имеет физической размерности. Виды деформации: сдвиг, сжатие, смятие, изгиб, кручение, срез.
Физико-механические основы деформации[править | править код]
Деформация представляет собой изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга за счет приложения усилия, при котором твёрдое тело искажает свои формы. Деформация является результатом изменения межатомных расстояний и перегруппировки блоков атомов[1]. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение[2].
Деформация твёрдого тела может явиться следствием:
- Фазовых превращений, связанных с изменением объёма;
- Теплового расширения;
- Намагничивания (магнитострикция);
- Появления электрического заряда (пьезоэлектрический эффект);
- Результатом действия внешних сил.
Деформация при растяжении-сжатии[править | править код]
Растяжение или сжатие твердого объекта можно описать выражением:
где:
— длина элемента после деформации;
— исходная длина этого элемента.
На практике чаще встречаются малые деформации — такие, что 
Физическая величина, равная модулю разности конечной и изначальной длины (изменения размера) деформированного тела, называется абсолютной деформацией[3]:
.
Средним напряжением — называют интенсивность распределения внутренних сил[4].
Виды деформации[править | править код]
Деформации разделяют на:
- Упругая деформация — обратимая деформация, описываемая законом Гука[5], при которой после окончания действия приложенных сил смещенные межатомные связи возвращаются в свое исходное положение.
- Пластическая деформация — необратимая деформация, при которой после окончания воздействия приложенных сил происходит необратимое смещение межатомных связей. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность. Природа пластической деформации может быть различной в зависимости от температуры, продолжительности действия нагрузки или скорости деформации. Одной из теорий, объясняющих механизм пластической деформации, является теория дислокаций в кристаллах. Все реальные твёрдые тела при деформации в большей или меньшей мере обладают пластическими свойствами. При некоторых условиях пластическими свойствами тел можно пренебречь, как это и делается в теории упругости. Твёрдое тело с достаточной точностью можно считать упругим, то есть не обнаруживающим заметных пластических деформаций, пока нагрузка не превысит предела упругости.
- Ползучесть материалов — необратимые деформации, происходящие с течением времени при неизменной нагрузке. С возрастанием температуры скорость ползучести увеличивается. Частными случаями ползучести являются релаксация и упругое последействие.
Виды деформации тела разделяют:
- растяжение-сжатие;
- сдвиг;
- изгиб;
- кручение.
В большинстве практических случаев наблюдаемая деформация представляет собой совмещение нескольких одновременных простых деформаций. В конечном счёте, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.
- Виды деформации
-
Сжатие
-
Растяжение
-
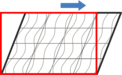
Сдвиг
-
Кручение
-
Изгиб
Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки (то есть тело возвращается к первоначальным размерам и форме), и пластической, если после снятия нагрузки деформация не исчезает (или исчезает не полностью).
Изучение деформации[править | править код]
Деформация физического тела определяется, если известен вектор перемещения каждой его точки.
Физика твёрдого тела — занимаются изучением деформации твёрдых тел в связи со структурными особенностями.
Теория упругости и пластичности — рассматривают перемещения и напряжения в деформируемых твёрдых телах. Тела рассматриваются как «Сплошные».
Механика деформируемого твердого тела — занимается изучением в реальных телах равновесных состояний и перемещений с учётом изменения расстояний между частицами в процессе перемещения. При этом реальные тела рассматриваются ка сплошные[4].
Сплошность — под сплошностью понимается материальные объекты тела которые сплошным образом занимают весь объем пространства, который ограничен непрерывными поверхностями[4]. Тело является сплошным, если удовлетворяет условиям сплошности[5]. Понятие сплошности относится также к элементарным объёмам, на которые можно мысленно разбить тело.
Закон Гука — описывает поведение деформируемого твердого тела в зоне упругости.
У жидкостей и газов, частицы которых легкоподвижны, исследование деформации заменяется изучением мгновенного распределения скоростей.
Изменение расстояния между центрами каждых двух смежных бесконечно малых объёмов у тела, не испытывающего разрывов, должно быть малым по сравнению с исходной величиной этого расстояния.
Измерение деформации[править | править код]
Измерение деформации производится либо в процессе испытания материалов с целью определения их механических свойств, либо при исследовании сооружения в натуре или на моделях для суждения о величинах напряжений.
Упругие деформации весьма малы, и их измерение требует высокой точности.
Измерение деформаций называется тензометрией.
Измерения деформации проводят с помощью:
- Тензометров;
- Тензометрических датчиков;
- Поляризационно-оптического метода исследования напряжения;
- Рентгеноструктурного анализа.
Для измерения локальных пластических деформациях применяют накатку на поверхности изделия сетки, в качестве материала используют легко растрескивающимся лак или хрупкие прокладки.
Литература[править | править код]
- Работнов Ю. Н. Сопротивление материалов. — М.: Физматгиз, 1962.
- Кузнецов В. Д. Физика твердого тела. — 2-е изд. — Томск, 1941—1947. — Т. 2—4.
- Седов Л. И. Введение в механику сплошной среды. — М.: Физматгиз, 1962.
- Деформация // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1972. — Т. VIII. — С. 175. — 592 с.
См. также[править | править код]
- Поляризованная световая модель — модель для изучения напряженных состояний конструкций и их элементов.
- Закон Гука
- Модуль Юнга
- Коэффициент Пуассона
- Постоянная Ламе
- Деформация сдвига
- Упругая деформация
- Ползучесть материалов
Ссылки[править | править код]
- Пластическая деформация металлов — Учебный фильм. Производство Союзвузфильм.
Примечания[править | править код]
- ↑ Гуляев А. П. Металловедение. Учебник для вузов. — 6-е. — М.: Металлургия, 1985. — С. 54—71. — 544 с.
- ↑ Большая советская энциклопедия. — 2-е. — Большая советская энциклопедия. — Т. 14. — С. 183—185.
- ↑ Твёрдые тела и их свойства (§ 4. Механические свойства твёрдых тел). Дата обращения: 2 марта 2016. Архивировано из оригинала 15 марта 2016 года.
- ↑ 1 2 3 Толоконников Л. А. Механика деформируемого твердого тела: учебное пособие для вузов. — М.: Высшая школа, 1979. — С. 318.
- ↑ 1 2 Кац А. М. Теория упругости. — 2-е. — СПб.: Лань, 2002. — С. 44. — 208 с. — ISBN 5-8114-0453-0.