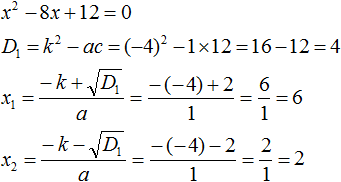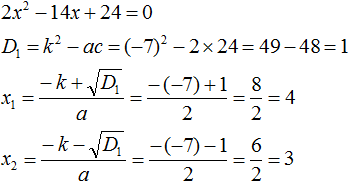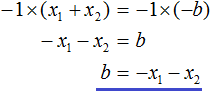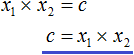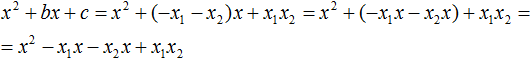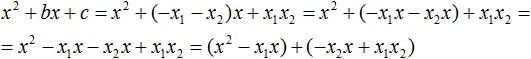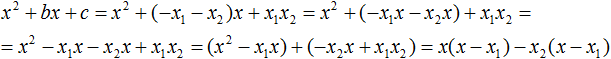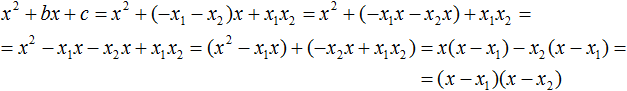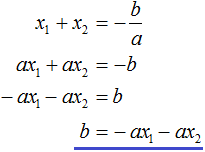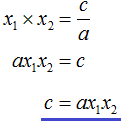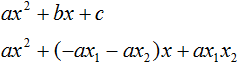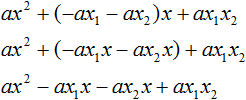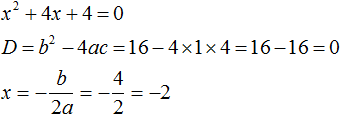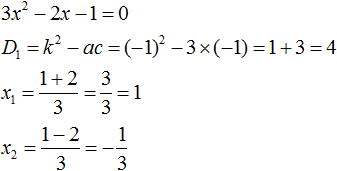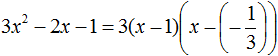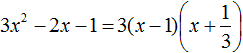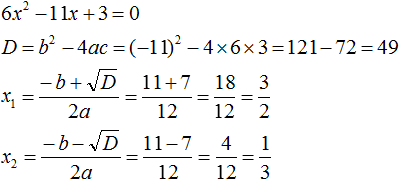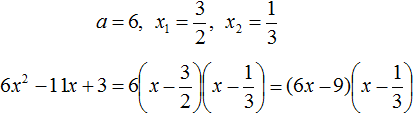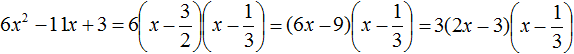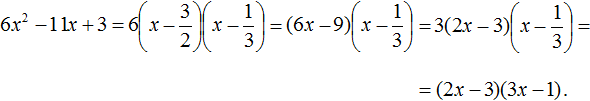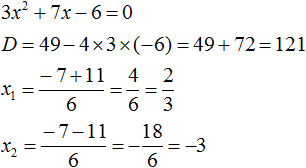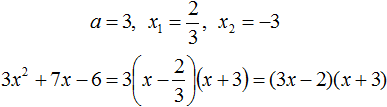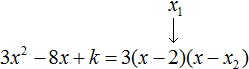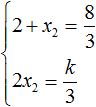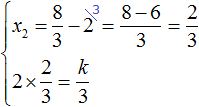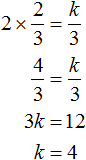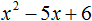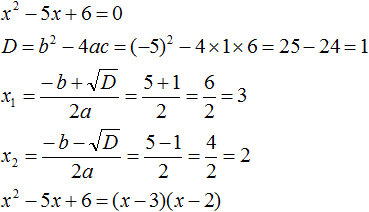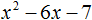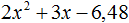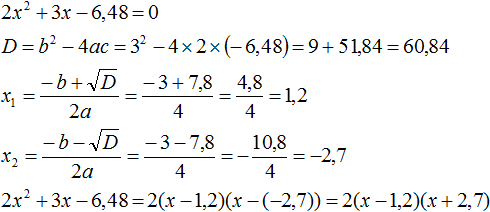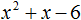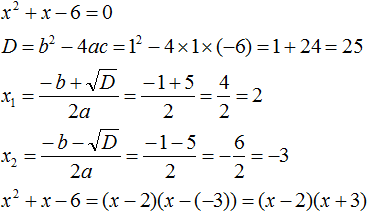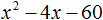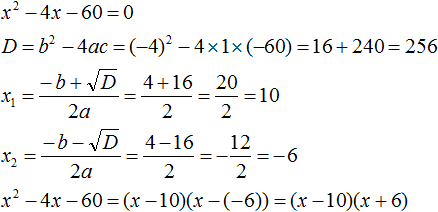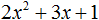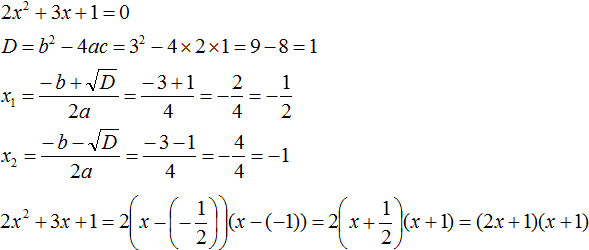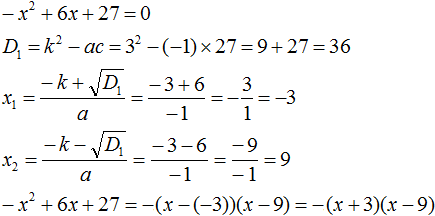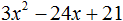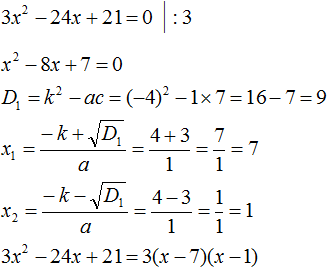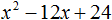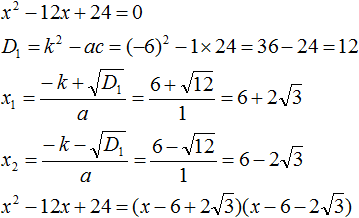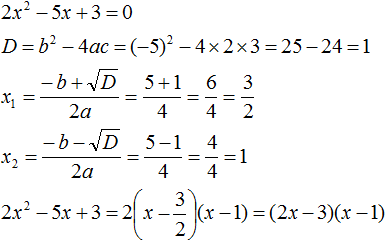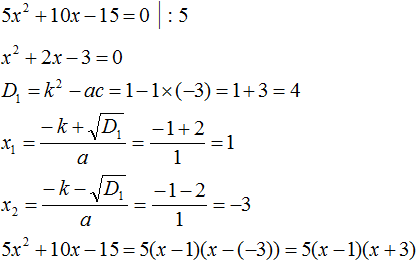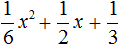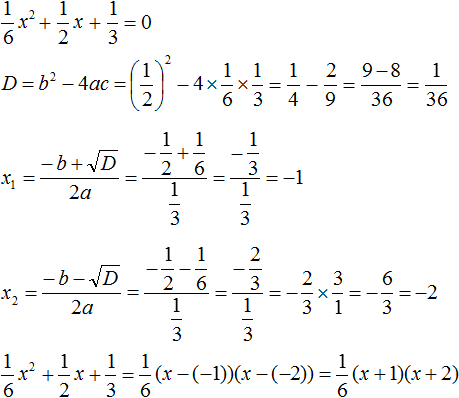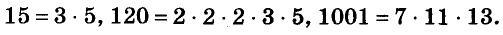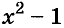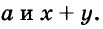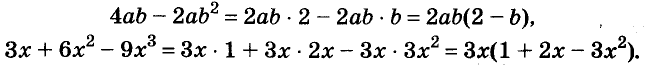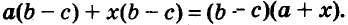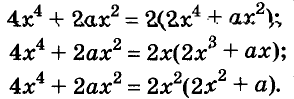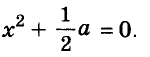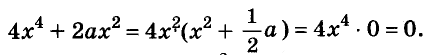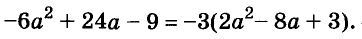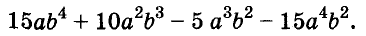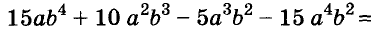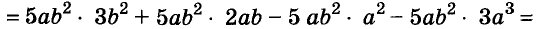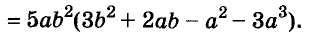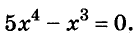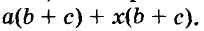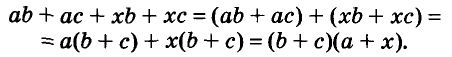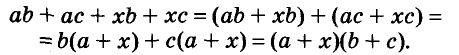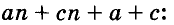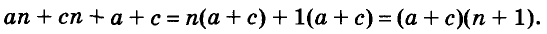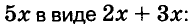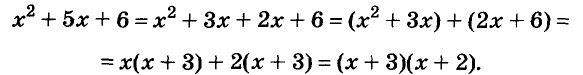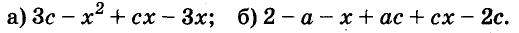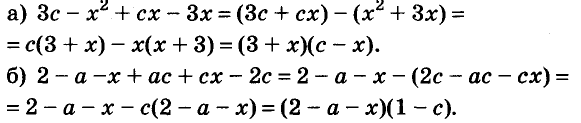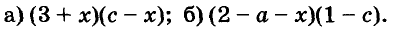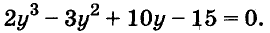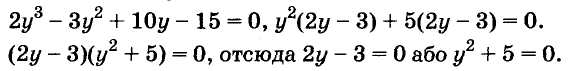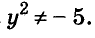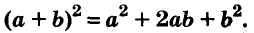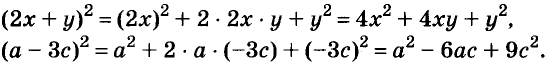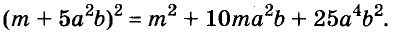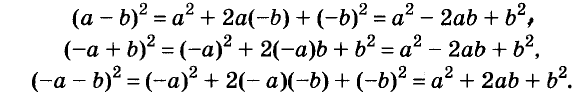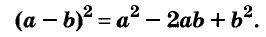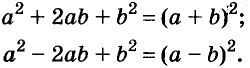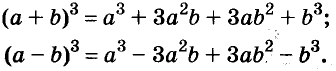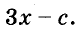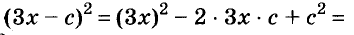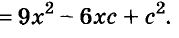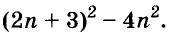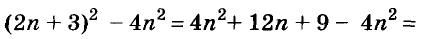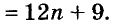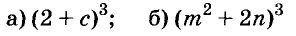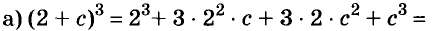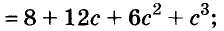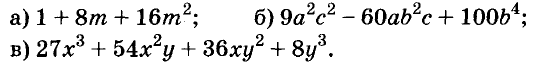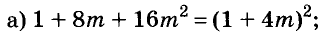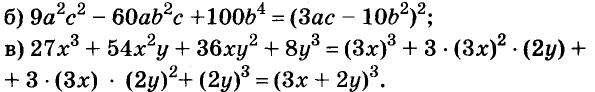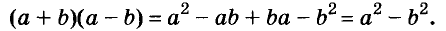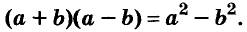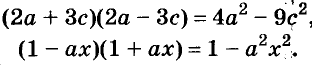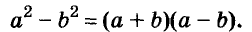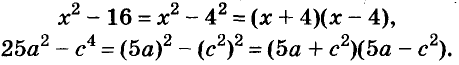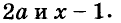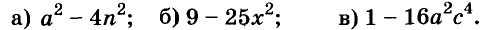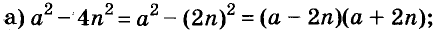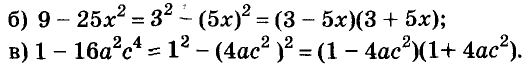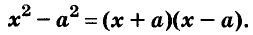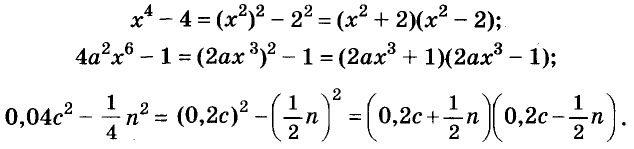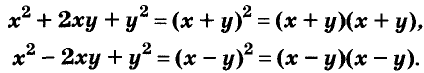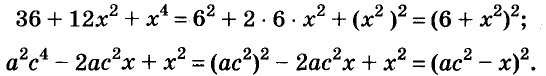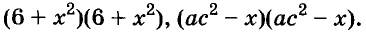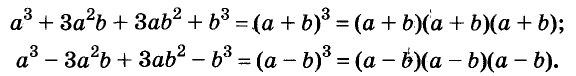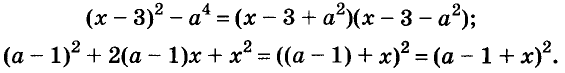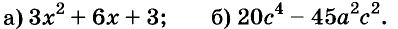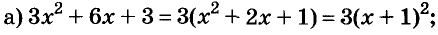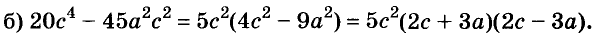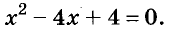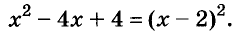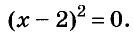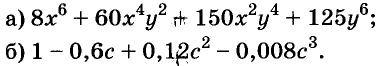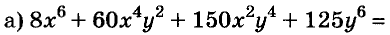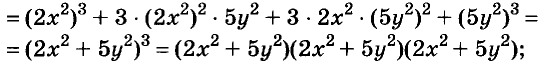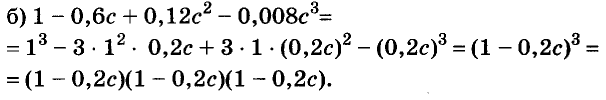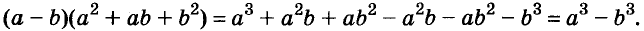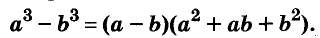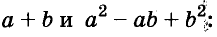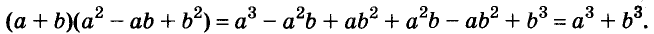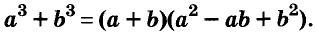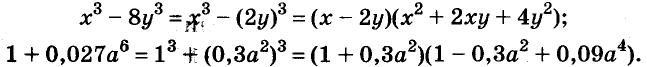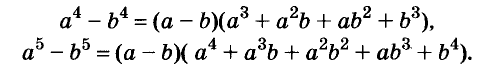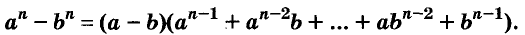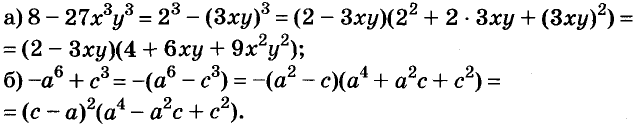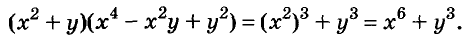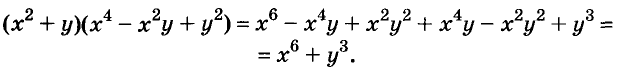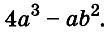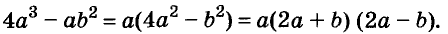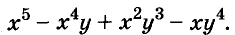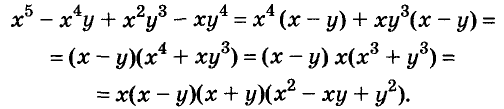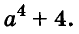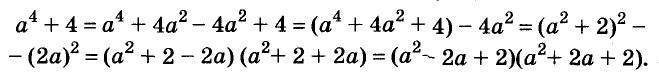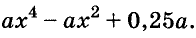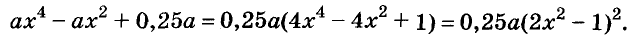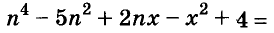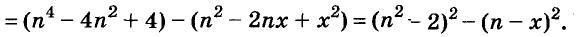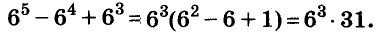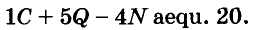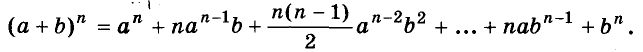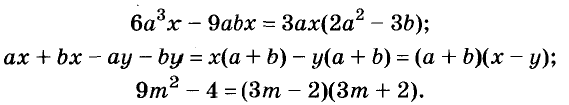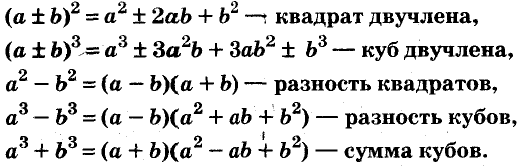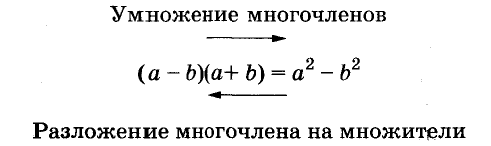Как найти корни квадратного уравнения
2 методика:Использование формулыНахождение корней через разложение на множители
Квадратное уравнение – это любое уравнение вида ax2 + bx + c = 0, где a ≠ 0. Нахождение корней квадратного уравнения – это то же самое, что и решение уравнения, то есть нахождение значений «х». Любое квадратное уравнение можно решить с помощью формулы x = (-b +/-√(b2 – 4ac))/2a. Кроме того, в зависимости от данного вам уравнения, вы можете воспользоваться некоторыми приемами, которые упростят нахождение корней.
Шаги
Метод 1 из 2: Использование формулы
-
1
Запишите данное вам уравнение в форме квадратного уравнения. Квадратное уравнение – это полином второго порядка с одной переменной «х» и а ≠ 0.[1] Другими словами, это уравнение с одной переменной (обычно «х»), самый высокий показатель степени которой равен 2: ax2 + bx + c = 0 - Чтобы записать данное вам уравнение в форме квадратного уравнения, перенесите все его члены на левую сторону, чтобы на правой стороне остался 0. Например, дано уравнение 2×2 + 8x = -5×2 – 11.
- 2×2 + 8x = -5×2 + 11
- 2×2 + 5×2 + 8x = + 11
- 2×2 + 5×2 + 8x – 11 = 0
- 7×2 + 8x – 11 = 0. Обратите внимание, что данное уравнение приняло вид ax2+ bx + c = 0.
-
2
Подставьте значения коэффициентов a, b, c в формулу x = (-b +/-√(b2 – 4ac))/2a, чтобы найти значения «х» (то есть решить уравнение или найти корни). Так как квадратное уравнения имеет вид ax2+ bx + c = 0, то число, стоящее перед x2, равно «а», перед «х» равно «b», а свободный член равен «с». - В нашем примере: 7×2 + 8x – 11 = 0, a = 7, b = 8, c = -11.
- Подставив эти значения в формулу, вы получите x = (-8 +/-√(82 – 4(7)(-11)))/2(7).
-
3
Найдите значения «х» (с положительным и отрицательным знаком), выполнив основные алгебраические операции. - В нашем примере:
- x = (-8 +/-√(82 – 4(7)(-11)))/2(7)
- x = (-8 +/-√(64 – (28)(-11)))/(14)
- x = (-8 +/-√(64 – (-308)))/(14)
- x = (-8 +/-√(372))/(14)
- x = (-8 +/- 19,29/(14)
-
4
Для получения двух значений «х» необходимо прибавить и вычесть некоторое значение. Это обусловлено тем, что при извлечении корня из числа вы получаете два значения, которые равны по модулю, но противоположны по знаку. - Прибавьте и получите:
- x = (-8 + 19,29)/(14)
- x = 11.29/14
- x = 0,81
- Вычтите и получите:
- x = (-8 – 19.29)/(14)
- x = (-27.29)/(14)
- x = -1,95 .
- Таким образом, х1 = 0,81 и х2 = -1,95.
-
5
Проверьте найденные корни, так как нахождение корней включает длинный ряд алгебраических операций и поэтому здесь легко допустить ошибку. - Быстрый и простой способ проверить корни уравнения – это подставить значения постоянных a, b, с в онлайн калькулятор квадратных уравнений, например, сюда.[2]
-
6
Также вы можете проверить ответ вручную. Для этого подставьте найденные значения «х» в исходное уравнение. Если соблюдается равенство, то корни верные (из-за округлений чисел равенство может соблюдаться приблизительно). - Подставьте найденные значения «х» в исходное уравнение 7×2 + 8x – 11 = 0:
- 7(-1,95)2 + 8(-1,95) – 11
- 26,62 – 15,6 – 11
- 26,62 – 26,5 = 0,02; 0,02 примерно равно 0, то есть равенство соблюдено и х1 – это корень данного уравнения.
- 7(0,81)2 + 8(0,81) – 11
- 4,59 + 6,48 – 11 = 0,07; 0,07 примерно равно 0, то есть равенство соблюдено и х2 – это корень данного уравнения.
Метод 2 из 2: Нахождение корней через разложение на множители
Разложение на множители при а = 1
-
1
Запишите данное вам уравнение в форме квадратного уравнения. Вы можете найти корни уравнения и без использования формулы, например, некоторые квадратные уравнения можно переписать так, что найти корни будет очень легко. Но сначала запишите данное вам уравнение в форме квадратного уравнения: ax2 + bx + c = 0. - В этом разделе мы будем рассматривать только те квадратные уравнения, у которых а = 1 (уравнения с а ≠ 1 рассмотрены в следующем разделе). Например: x2 + 7x + 12 = 0.
-
2
Запишите уравнение в виде (х + _)(х + _) = 0. Разложение квадратного уравнения на множители – это нахождение двух двучленов, при перемножении которых получается исходное уравнение. Так как x2 = х * х, то каждый двучлен начинается с «х»: (х + _) (х + _) = 0. - Обратите внимание на пробелы (обозначены символом подчеркивания; далее мы объясним, как найти числа, которые подставляются в эти пробелы).
-
3
Разложите на множители коэффициент «с». То есть надо найти пары чисел, при перемножении которых получится значение «с». - В нашем уравнении с = 12. Множителями 12 являются пары чисел 1 и 12, 2 и 6, 3 и 4.
-
4
Найдите такую пару множителей «с», которая при суммировании дает значение коэффициента «b» (не перепутайте – искать множители «b» не нужно). - В нашем уравнении b = 7. Множителями «с» являются пары чисел 1 и 12, 2 и 6, 3 и 4. Выбираем пару чисел 3 и 4, так как 3 + 4 = 7 (и b = 7).
- Если нет такой пары множителей «с», которая при суммировании дает значение коэффициента «b», то уравнение разложить на множители описанным способом нельзя.[3] В этом случае воспользуйтесь другим методом нахождения корней квадратного уравнения.
-
5
Теперь вместо пробелов в двух двучленах (см. выше) подставьте найденные числа (то есть подходящую пару множителей коэффициента «с»). Таким образом, вы разложите исходное уравнение на множители. - В нашем примере: (х + 3)(х + 4) = 0.
-
6
Найдите два значения «х». Для этого приравняйте каждый из двучленов к 0 и решите их (это верно, так как даже если один из двучленов равен 0, то произведение двух двучленов равно 0). - В нашем примере: (х + 3) = 0 и (х + 4) = 0.
- x + 3 = 0: x = -3
- x + 4 = 0: x = -4
- Обратите внимание, что эти ответы могут быть проверены теми же способами, которые описаны в предыдущем разделе.
Разложение на множители при а ≠ 1
-
1
Разложите коэффициент «а» на множители. Так как «а» стоит перед x2, то каждый множитель будет включать переменную «х». - Например: 2×2 + 14x + 12 = 0. Здесь а = 2 и раскладывается на одну пару множителей 2 и 1. То есть первый член уравнения 2×2 = 2х * х.
- Обратите внимание, что бывают случаи, когда у коэффициента «а» несколько пар множителей. Например, член 8×2 можно разложить на следующие множители: 8x * х и 2x * 4x. В этом случае необходимо проверить, какая пара множителей подходит для разложения данного уравнения.
-
2
Запишите уравнение в виде ((множитель1) + _) ((множитель2) + _). Мы не начинаем двучлены с «х», как в предыдущем разделе, так как здесь перед «х» могут стоять некоторые коэффициенты.[4] - В нашем примере запишите уравнение в виде (2x + _)(х + _).
-
3
Разложите на множители коэффициент «с». То есть надо найти пары чисел, при перемножении которых получится значение «с». - В нашем примере с = 12; множителями 12 являются пары чисел 1 и 12, 2 и 6, 3 и 4.
-
4
Вместо пробелов в произведении двух двучленов (см. выше) подставьте пары множителей «с» и найдите такую пару, которая при перемножении и суммировании членов двучленов даст значение «b». Помните, что здесь двучлены начинаются не с «х», а с некоторых членов, содержащих коэффициент и переменную «х». - В нашем примере b = 14, а второй член уравнения равен 14х. Это означает, что мы хотим найти два числа (пару множителей «с»), одно из которых умножим на 2х, другое на х, а затем сложим результаты произведения; полученная сумма должна равняться 14x.
- Рассмотрим пару множителей 3 и 4: 3 * 2x = 6х; 4 * х = 4x; 4x + 6x = 10x. Не подходит. Поменяем местами числа: 4 * 2x = 8х; 3 * х = 3x; 8x + 3x = 11x. Не подходит.
- Рассмотрим пару множителей 6 и 2: 6 * 2x = 12х; 2 * х = 2x; 12x + 2x = 14x. Подходит! Вместо пробелов подставьте числа 6 и 2.
-
5
Теперь вместо пробелов в двух двучленах (см. выше) подставьте найденные числа (то есть подходящую пару множителей коэффициента «с»). Таким образом, вы разложите исходное уравнение на множители. Имейте в виду, что каждое число нужно ставить на свое место (не перепутайте!), чтобы в итоге получить правильный коэффициент «b». После этого приравняйте каждый из двучленов к 0 и решите их. - В нашем примере: (2x + 2)(х + 6) = 0.
- 2x + 2 = 0
- 2x = -2: x = -1
- x + 6 = 0: x = -6
Советы
- Помните, что квадратный корень может быть как положительным, так и отрицательным. Поэтому у квадратного уравнения всегда два корня.
- Обратите внимание, что корни некоторых квадратных уравнений можно найти, дополнив уравнение до полного квадрата.
- Разложение на множители и дополнение до полного квадрата – это два обходных пути решения квадратного уравнения при помощи формулы. Если вам интересно, прочитайте статью о том, как вывести формулу для корней квадратного уравнения.
Калькулятор онлайн.
Выделение квадрата двучлена и разложение на множители квадратного трехчлена.
Эта математическая программа выделяет квадрат двучлена из квадратного трехчлена, т.е. делает преобразование вида:
( ax^2+bx+c rightarrow a(x+p)^2+q )
и раскладывает на множители квадратный трехчлен:
( ax^2+bx+c rightarrow a(x+n)(x+m) )
Т.е. задачи сводятся к нахождению чисел ( p, q ) и ( n, m )
Программа не только даёт ответ задачи, но и отображает процесс решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода квадратного трехчлена, рекомендуем с ними ознакомиться.
Правила ввода квадратного многочлена
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x – 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 – 5&6/5x +1/7x^2
Результат: ( 3frac{1}{3} – 5frac{6}{5} x + frac{1}{7}x^2 )
При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)
Пример подробного решения
Выделение квадрата двучлена.
$$ ax^2+bx+c rightarrow a(x+p)^2+q $$
$$2x^2+2x-4 = $$
$$2x^2 +2 cdot 2 cdotleft( frac{1}{2} right)cdot x+2 cdot left( frac{1}{2} right)^2-frac{9}{2} = $$
$$2left( x^2 + 2 cdotleft( frac{1}{2} right)cdot x + left( frac{1}{2} right)^2 right)-frac{9}{2} = $$
$$2left( x+frac{1}{2} right)^2-frac{9}{2} $$
Ответ: $$2x^2+2x-4 = 2left( x+frac{1}{2} right)^2-frac{9}{2} $$
Разложение на множители.
$$ ax^2+bx+c rightarrow a(x+n)(x+m) $$
$$2x^2+2x-4 = $$
$$ 2left( x^2+x-2 right) = $$
$$ 2 left( x^2+2x-1x-1 cdot 2 right) = $$
$$ 2 left( x left( x +2 right) -1 left( x +2 right) right) = $$
$$ 2 left( x -1 right) left( x +2 right) $$
Ответ: $$2x^2+2x-4 = 2 left( x -1 right) left( x +2 right) $$
Наши игры, головоломки, эмуляторы:
Немного теории.
Выделение квадрата двучлена из квадратного трехчлена
Если квадратный трехчлен aх2+bx+c представлен в виде a(х+p)2+q, где p и q — действительные числа, то
говорят, что из квадратного трехчлена выделен квадрат двучлена.
Покажем на примере как это преобразование делается.
Выделим из трехчлена 2x2+12x+14 квадрат двучлена.
Вынесем за скобки коэффициент a, т.е. 2:
( 2x^2+12x+14 = 2(x^2+6x+7) )
Преобразуем выражение в скобках.
Для этого представим 6х в виде произведения 2*3*х, а затем прибавим и вычтем 32. Получим:
$$ 2(x^2+2 cdot 3 cdot x + 3^2-3^2+7) = 2((x+3)^2-3^2+7) = $$
$$ = 2((x+3)^2-2) = 2(x+3)^2-4 $$
Т.о. мы выделили квадрат двучлена из квадратного трехчлена, и показоли, что:
$$ 2x^2+12x+14 = 2(x+3)^2-4 $$
Разложение на множители квадратного трехчлена
Если квадратный трехчлен aх2+bx+c представлен в виде a(х+n)(x+m), где n и m — действительные числа, то
говорят, что выполнена операция разложения на множители квадратного трехчлена.
Покажем на примере как это преобразование делается.
Разложим квадратный трехчлен 2x2+4x-6 на множители.
Вынесем за скобки коэффициент a, т.е. 2:
( 2x^2+4x-6 = 2(x^2+2x-3) )
Преобразуем выражение в скобках.
Для этого представим 2х в виде разности 3x-1x, а -3 в виде -1*3. Получим:
$$ = 2(x^2+3 cdot x -1 cdot x -1 cdot 3 ) = 2(x(x+3)-1 cdot (x+3) ) = $$
$$ = 2(x-1)(x+3) $$
Т.о. мы разложили на множители квадратный трехчлен, и показоли, что:
$$ 2x^2+4x-6 = 2(x-1)(x+3) $$
Заметим, что разложение на множители квадратного трехчлена возможно только тогда, когда, квадратное уравнение, соответсвующее этому
трехчлену имеет корни.
Т.е. в нашем случае разложить на множители трехчлен 2x2+4x-6 возможно, если квадратное уравнение 2x2+4x-6 =0
имеет корни. В процессе разложения на множители мы установили, что уравнение 2x2+4x-6 =0 имеет два корня 1 и -3,
т.к. при этих значениях уравнение 2(x-1)(x+3)=0 обращается в верное равенство.
Как разложить на множители квадратный трёхчлен
Квадратный трёхчлен — это многочлен вида ax2 + bx + c.
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
ax2 + bx + c = 0
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
a(x − x1)(x − x2)
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
ax2 + bx + c = a(x − x1)(x − x2)
Где левая часть — исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
x2 − 8x + 12
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
x2 − 8x + 12 = 0
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Итак, x1 = 6, x2 = 2. Теперь воспользуемся формулой ax2 + bx + c = a(x − x1)(x − x2). В левой части вместо выражения ax2 + bx + c напишем свой квадратный трёхчлен x2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x1 = 6, x2 = 2
x2 − 8x + 12 = 1(x − 6)(x − 2) = (x − 6)(x − 2)
Если a равно единице (как в данном примере), то решение можно записать покороче:
x2 − 8x + 12 = (x − 6)(x − 2)
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2). Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x2 − 8x + 12
(x − 6)(x − 2) = x2 − 6x − 2x + 12 = x2 − 8x + 12
Пример 2. Разложить на множители следующий квадратный трёхчлен:
2x2 − 14x + 24
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
2x2 − 14x + 24 = 0
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Итак, x1 = 4, x2 = 3. Приравняем квадратный трехчлен 2x2 − 14x + 24 к выражению a(x − x1)(x − x2), где вместо переменных a, x1 и x2 подстáвим соответствующие значения. В данном случае a = 2
2x2 − 14x + 24 = 2(x − 4)(x − 3)
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x2 − 14x + 24
2(x − 4)(x − 3) = 2(x2 − 4x −3x + 12) = 2(x2 − 7x + 12) = 2x2 − 14x + 24
Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
x2 + bx + c
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Тогда приведённый квадратный трехчлен x2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x1 + x2 = −b. Для этого можно умножить обе его части на −1
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Из первых скобок вынесем общий множитель x, из вторых скобок — общий множитель −x2
Далее замечаем, что выражение (x − x1) является общим множителем. Вынесем его за скобки:
Мы пришли к тому, что выражение x2 + bx + c стало равно (x − x1)(x − x2)
x2 + bx + c = (x − x1)(x − x2)
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
ax2 + bx + c = a(x − x1)(x − x2)
Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax2 + bx + c = 0, то теорема Виета принимает следующий вид:
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 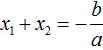
Для начала выразим b и c. В первом равенстве умножим обе части на a. Затем обе части получившегося равенства умножим на −1
Теперь из второго равенства выразим c. Для этого умножим обе его части на a
Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax2 + bx + c. Для наглядности каждое преобразование будем выполнять на новой строчке:
Здесь вместо переменных b и c были подставлены выражения −ax1 − ax2 и ax1x2, которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Теперь из первых скобок вынесем общий множитель ax, а из вторых — общий множитель −ax2
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Вторые скобки содержат общий множитель a. Вынесем его за скобки. Его можно расположить в самом начале выражения:
Мы пришли к тому, что выражение ax2 + bx + c стало равно a(x − x1)(x − x2)
ax2 + bx + c = a(x − x1)(x − x2)
Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x1)(x − x2) вместо переменных x1 и x2.
Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x1 и x2. Например, квадратный трёхчлен x2 + 4x + 4 имеет только один корень −2
Тогда значение −2 в процессе разложения на множители будет подставлено вместо x1 и x2. А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2)2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
3x2 − 2x − 1
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x2 − 2x − 1, а в правой части — его разложение в виде a(x − x1)(x − x2), где вместо a, x1 и x2 подстáвим соответствующие значения:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен:
3 − 11x + 6x2
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:
6x2 − 11x + 3
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен:
3x2 + 7x − 6
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Пример 4. Найдите значение k, при котором разложение на множители трёхчлена 3x2 − 8x + k содержит множитель (x − 2)
Если разложение содержит множитель (x − 2), то один из корней квадратного трёхчлена равен 2. Пусть корень 2 это значение переменной x1
Чтобы найти значение k, нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Теперь из второго равенства выразим k. Так мы найдём его значение.
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится
. То есть коэффициент a станет равным
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Задания для самостоятельного решения
Задание 1. Разложить на множители квадратный трёхчлен:
Решение:
Задание 2. Разложить на множители квадратный трёхчлен:
Решение:
Задание 3. Разложить на множители квадратный трёхчлен:
Решение:
Задание 4. Разложить на множители квадратный трёхчлен:
Решение:
Задание 5. Разложить на множители квадратный трёхчлен:
Решение:
Задание 6. Разложить на множители квадратный трёхчлен:
Решение:
Задание 7. Разложить на множители квадратный трёхчлен:
Решение:
Задание 8. Разложить на множители квадратный трёхчлен:
Решение:
Задание 9. Разложить на множители квадратный трёхчлен:
Решение:
Задание 10. Разложить на множители квадратный трёхчлен:
Решение:
Задание 11. Разложить на множители квадратный трёхчлен:
Решение:
Задание 12. Разложить на множители квадратный трёхчлен:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Как выделить квадрат двучлена из квадратного трехчлена
Метод выделения полного квадрата двучлена из квадратного трехчлена является основой алгоритма решения уравнений второй степени, а также применяется при упрощении громоздких алгебраических выражений.
Инструкция
Метод выделения полного квадрата применяется как для упрощения выражений, так и при решении квадратного уравнения, которое, по сути, является трехчленом второй степени от одной переменной. В основе метода лежат некоторые формулы сокращенного умножения многочленов, а именно частные случаи Бинома Ньютона – квадрат суммы и квадрат разности:(а ∓ b)² = а² ∓ 2•а•b + b².
Рассмотрим применение метода для решения квадратного уравнения вида а•х² + b•х + с = 0. Чтобы выделить квадрат двучлена из квадратного трехчлена, разделите обе части уравнения на коэффициент при наибольшей степени, т.е. при х²:а•х² + b•х + с = 0 /а → х² + (b/а)•х + с/а = 0.
Представьте полученное выражение в виде:(х² + 2•(b/2а)•х + (b/2а)²) – (b/2а)² + с/а = 0, где одночлен (b/а)•х преобразован в удвоенное произведение элементов b/2а и х.
Сверните первую скобку в квадрат суммы:(х + b/2а)² – ((b/2а)² – с/а) = 0.
Теперь возможны две ситуации нахождения решения: если (b/2а)² = с/а, то уравнение имеет единственный корень, а именно х = -b/2а. Во втором случае, когда (b/2а)² = с/а, решений будет следующим:(х + b/2а)² = ((b/2а)² – с/а) → х = -b/2а + √((b/2а)² – с/а) = (-b + √(b² – 4•а•с))/(2•а).
Двойственность решения вытекает из свойства квадратного корня, результат вычисления которого может быть как положительным, так и отрицательным, в то время как модуль остается неизменным. Таким образом, получается два значения переменной:х1,2 = (-b ± √(b² – 4•а•с))/(2•а).
Так, используя метод выделения полного квадрата, мы пришли к понятию дискриминанта. Очевидно, что он может быть либо нулем, либо положительным числом. При отрицательном дискриминанте уравнение не имеет решений.
Пример: выделить квадрат двучлена в выражении х² – 16•х + 72.
РешениеПерепишите трехчлен в виде х² – 2•8•х + 72, откуда следует, что составляющими полного квадрата двучлена являются 8 и х. Следовательно, для его завершения нужно еще число 8² = 64, которое можно вычесть из третьего члена 72: 72 – 64 = 8. Тогда исходное выражение преобразуется в:х² – 16•х + 72 → (х – 8)² + 8.
Попробуйте решить это уравнение:(х-8)² = -8
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
Разложение многочленов на множители
Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:
- вынесении общего множителя за скобки;
- способе группировки;
- формулах сокращённого умножения;
- применении разных способов разложения многочленов на множители.
Вынесение общего множителя за скобки
Вы уже умеете раскладывать на множители натуральные числа. Например,
На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен
Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.
Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 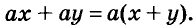
Другие примеры:
Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.
Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 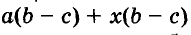
Один и тот же многочлен можно разложить на множители по-разному. Например,
Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.
Пусть, например, надо найти значение выражения 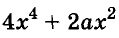
Чтобы использовать условие, это упражнение можно решить так:
Здесь вынесено за скобки не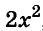
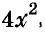
Пример:
Разложите на множители многочлен
Решение:
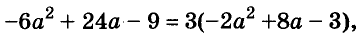
Пример:
Разложите на множители многочлен
Решение:
Пример:
Докажите, что число 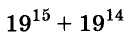
Доказательство:
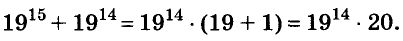
Пример:
Решите уравнение
Решение:
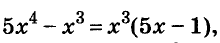
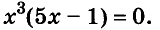
Значит, 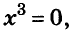
Ответ. Уравнение имеет два корня: 0 и 0,2.
Способ группировки
Разложим на множители многочлен 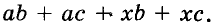
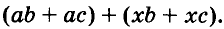
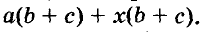
Указанные преобразования можно записать цепочкой:
Такой способ разложения многочленов на множители называют способом группировки.
Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:
Получили такой же результат.
Разложим на множители многочлен
Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.
Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 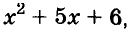
Подобные преобразования также можно выполнять, используя тождества.
Пример:
Разложите на множители многочлен:
Решение:
Ответ.
Пример:
Решите уравнение:
Решение:
Разложим левую часть уравнения на множители:
Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как
Ответ. у = 1,5.
Квадрат двучлена
Решая различные задачи, часто приходится умножать двучлены вида 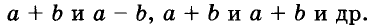
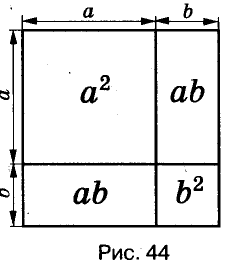
Умножим двучлен
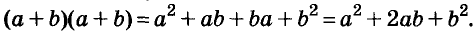
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.
Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:
Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:
По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе
Запомните формулу
Формулы квадрата двучлена используют и в «обратном направлении»:
Формулу 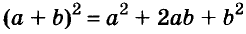
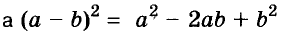
Для положительных чисел а и b формулу
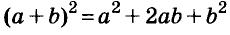
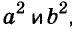
Существуют и другие формулы сокращённого умножения:
Пример:
Возведите в квадрат двучлен
Решение:
Пример:
Упростите выражение
Решение:
Пример:
Представьте в виде многочлена выражение:
Решение:
Пример:
Представьте выражение в виде степени двучлена:
Решение:
- Заказать решение задач по высшей математике
Разность квадратов
Умножим сумму переменных а и b на их разность.
Значит,
Это равенство — тождество. Словами его читают так:
Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.
Пользуясь доказанной формулой, можно сразу записать:
Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:
Разность квадратов двух выражений равна произведению их суммы и разности.
Пример:
Формула разности квадратов очень удобна для разложения многочленов на множители.
Для положительных чисел а и b формулу 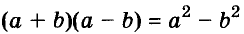
Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.
Пример:
Напишите разность квадратов и квадрат разности выражений
Решение:
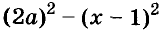
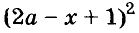
Пример:
Запишите в виде произведения двух двучленов выражение:
Решение:
Пример:
Представьте в виде двучлена выражение:
Решение:
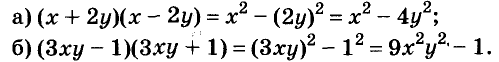
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.
Использование формул сокращённого умножения
С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 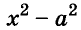
Примеры:
Трёхчлены 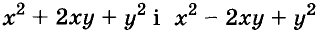
Примеры:
Полученные, выражения можно разложить на множители и записать так:
Многочлен 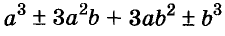
Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.
Например, 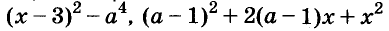
Пример:
Разложите на множители многочлен:
Решение:
Пример:
Решите уравнение
Решение:
Значит, данное уравнение равносильно такому:
Квадрат числа равен нулю только тогда, когда это число равно 0. А х – 2 = 0, когда х = 2.
Ответ. х = 2.
Пример:
Разложите на множители многочлен:
Решение:
Разность и сумма кубов
Выполним умножение многочленов 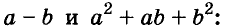
Следовательно, при любых значениях а и b
Трёхчлен 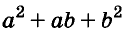
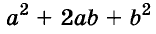
разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Выполним умножение многочленов
Следовательно,
Трёхчлен 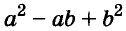
сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.
Примеры:
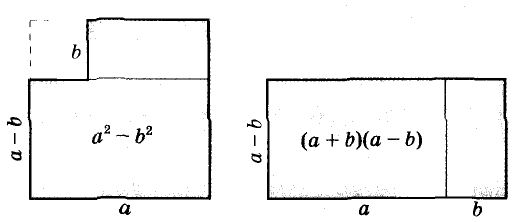
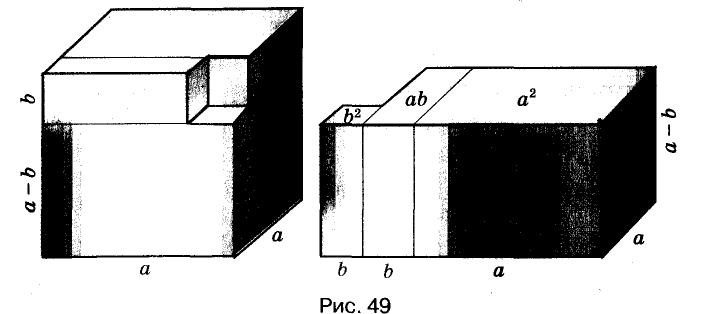
Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.
Можно доказать, что для каждого натурального значения n истинна формула:
Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.
Пример:
Разложите на множители двучлен:
Решение:
Пример:
Найдите произведение многочленов: 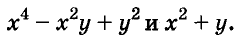
Решение:
Первый способ. По формуле суммы кубов:
Второй способ. По правилу умножения многочленов:
Применение разных способов разложения многочленов на множители
Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.
Пример:
Разложите на множители многочлен
Решение:
Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.
Пример:
Разложите на множители выражение
Решение:
Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.
Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.
В этом случае можно использовать такое правило-ориентир:
- Вынести общий множитель (если он есть) за скобки.
- Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
- Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
- Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.
Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.
Пример:
Разложите на множители двучлен
Решение:
Прибавим к данному двучлену выражение
Пример:
Разложите на множители выражение
Решение:
Пример:
Представьте многочлен 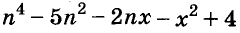
Решение:
Пример:
Докажите, что число 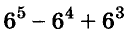
Доказательство:
Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.
Исторические сведения:
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо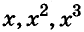
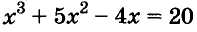
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать 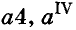
Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 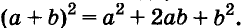
В учебнике рассмотрены простейшие формулы сокращённого умножения.
Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:
Напомню:
Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.
Простейшие способы разложения многочленов на множители:
- вынесение общего множителя за скобки;
- способ группировки;
- использование формул сокращённого умножения.
Примеры:
Формулы сокращённого умножения
Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
- Квадратные корни
- Квадратные уравнения
- Целые выражения
- Одночлены
- Многочлены
- Формулы сокращенного умножения