Как найти функцию, если известна производная функции?
Happy Smile
Ученик
(67),
на голосовании
11 лет назад
Пожалуйста помогите, не могу понять как найти саму функцию, если известна производная функции и также известно что предел функции при х стремящимся к 1 равен 0.
Само задание такое:
если g'(x)=1/(1+x)^2, lim g(x)=0 при x стремящимся к нулю. показать что g(x)=(x-1)/2(x+1)
Дополнен 11 лет назад
с помощью первообразной не получается. тут надо использовать скорее всего лимит, вот только как не знаю
Голосование за лучший ответ
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Как найти функцию еси известны производные
|
|
21/12/05 |
|
|
|
|
|
LynxGAV |
|
||
28/10/05 |
|||
|
|
|||
|
LynxGAV |
|
||
28/10/05 |
Вобщем, вот у Вас есть одна частная производная, при интегрировании Вы должны добавить функцию от двух других переменных… (для проверки возьмите частную производную после интегрирования).
Это Вы группы перестановок узучали?
|
||
|
|
|||
|
Dolopihtis |
|
|
17/01/06 |
LynxGAV писал(а): Интегрирование, но для Вас не особо простое. Ведь Может лучше так?
|
|
|
|
|
Someone |
|
||
23/07/05 |
Можно и так:
В таком варианте интегралы берутся по трёхзвенной ломаной, соединяющей начальную Кроме того, должны выполняться некоторые условия, которые в учебной литературе формулируются под названием “условия независимости криволинейного интеграла от пути интегрирования”.
|
||
|
|
|||
|
LynxGAV |
|
||
28/10/05 |
“Diko” izvinyayus´, mojet Java i budet proshe, no lichno mne ne kajetsya, chto “tak luchshe”.
|
||
|
|
|||
|
вв |
то есть найти функцию по градиенту.
|
|
02/08/05 |
Зельдович, Мышкис. Элементы математической физики.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
На этой странице вы узнаете
- Кто всегда протянет руку помощи в определении производной?
- Что такое сложная функция и зачем тут матрешка?
- Как никогда не ошибаться при решении задач с производными?
Теория теорией, а дифференцировать хочется всегда. Эта статья посвящена практике нахождения производных.
Производные основных функций
Должно быть, вы уже слышали о производной и даже пробовали взять её мозговым штурмом. При отрицательном ответе вам обязательно нужно прокатиться на американских горках в нашей статье «Производная». В ней рассмотрели основные понятия производной.
Главный вопрос этой статьи: как ее находить? Для этого существуют свои формулы и правила, которых необходимо придерживаться для правильного решения заданий.
Ниже приведена таблица с формулами для нахождения производных основных функций. Применяя эти формулы, можно найти производную почти любой функции.
Не пугайтесь, если вам покажется, что их много: это основные формулы, с помощью которых можно решить большинство задач.
| 1 | C’ = 0, C = const |
| 2 | ((x^n)’ = n * x^{n — 1}, x > 0) |
| 3 | ((a^x)’ = a^x * ln(a), a > 0, a neq 1) |
| 4 | ((e^x)’ = e^x) |
| 5 | ((log_{a}x)’ = frac{1}{x * ln(a)}, x > 0, a > 0, a neq 1) |
| 6 | ((ln(x))’ = frac{1}{x}, x > 0) |
| 7 | ((sqrt{x})’ = frac{1}{2sqrt{x}}, x > 0) |
| 8 | (sin(x))’ = cos(x) |
| 9 | (cos(x))’ = -sin(x) |
| 10 | ((tg(x))’ = frac{1}{cos^{2}x}, x neq frac{pi}{2} + pi n, n in Z) |
| 11 | ((ctg(x))’ = -frac{1}{sin^{2}x}, x neq pi n, n in Z) |
Смотреть на формулы и учить их — это круто, прямо ощущаем себя великими учеными. Что может быть круче этого? Только применять их на практике. Рассмотрим несколько примеров нахождения производной.
Пример 1. Найдите производную функции f(x) = 5.
Решение: 5 — это число, то есть константа. Тогда, пользуясь первой формулой в таблице, получаем:
f'(x) = 5′ = 0.
Ответ: 0
Пример 2. Найдите производную функции (f(x) = x^4)
Решение: В этом случае необходимо воспользоваться второй формулой из таблицы.
(f'(x) = (x^4)’ = 4 * x^{4-1} = 4 * x^3)
Ответ: (4x^3)
Пример 3. Найдите производную функции (f(x) = e^x)
Решение: В этом случае необходимо воспользоваться четвертой формулой из таблицы.
(f'(x) = (e^x)’ = e^x)
Ответ: (e^x)
Правила дифференцирования
С полной уверенностью можем сказать, что вам встречались сложные функции. Даже намного сложнее, чем те, которые приведены в таблицах. Там и сумма, и произведение, и формула в формуле. Одним словом: ужас! Как брать производную, если перед функцией стоит коэффициент, или в функцию включено несколько разных выражений? На этот случай существуют правила дифференцирования.
В сложных функциях невозможно пользоваться только формулами для нахождения производной.
Если функция
— усложнена коэффициентом,
— представлена в виде суммы, произведения или частного
— или является сложной функцией,
то для выбора правильной производной необходимо воспользоваться правилами дифференцирования. Они играют роль супергероев от мира производных. Рассмотрим их внимательнее.
1. Коэффициент можно вынести за знак производной.
(k * f(x))’ = k * (f(x))’
Например, необходимо взять производную у функции f(x) = 6sin(x). Тогда, пользуясь правилом дифференцирования и таблицей, получаем ответ 6cos(x).
2. Производная суммы (разности) равняется сумме (разности) производных.
((f(x) pm g(x))’ = f'(x) pm g'(x))
Найдем производную (f(x) = 4x^5 — sqrt{x} + cos(x)).
(f'(x) = (4x^5 — sqrt{x} + cos(x))’ = (4x^5)’ — (sqrt{x})’ + (cos(x))’ = 4 * 5 * x^{5 — 1} — frac{1}{2sqrt{x}} — sin(x))
(f'(x) = 20x^4 — frac{1}{2sqrt{x}} — sin(x). )
3. Производная произведения.
(f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x)
Для примера возьмем производную функции f(x) = x2 * ln(x)
f'(x) = (x2 * ln(x))’ = (x2)’ * ln(x) + x2 * (ln(x))’
(f'(x) = 2x * ln(x) + x^2 * frac{1}{x} = 2x * ln(x) + x)
4. Производная частного.
((frac{f(x)}{g(x)})’ = frac{f'(x) * g(x) — f(x) * g'(x)}{g^{2}(x)})
Возьмем производную функции (f(x) = frac{e^x}{3x})
(f'(x) = frac{(e^x)’ * 3x — ex * (3x)’}{(3x)^2} = frac{e^x * 3x — e^x * 3}{9x^2} = frac{3e^x * (x-1)}{9x^2} = frac{e^x * (x-1)}{3x^2})
5. Производная сложной функции.
Сложная функция — это функция, внутри которой есть другая функция.
Давайте представим матрешку: в одну большую куклу складывается куколка поменьше, а в нее еще меньше и так далее. Точно так же и с функцией: “внутри” одной функции может лежать другая функция.
Например, у нас есть две функции: (sqrt{x}) и cos(x). А теперь попробуем поместить корень в функцию с косинусом, и получим (cos(sqrt{x})). Это и будет сложная функция.

Чтобы найти производную сложной функции, необходимо найти производную “внутренней” функции и умножить ее на производную “внешней” функции.
(f(g(x))’ = g'(x) * f'(g(x))
Найдем производную уже рассмотренной функции (f(x) = cos(sqrt{x})).
(f'(x) = (cos(sqrt{x}))’ = (sqrt{x})’ * (cos(sqrt{x}))’ = frac{1}{2sqrt{x}} * (-sin(sqrt{x})) = -frac{sin(sqrt{x})}{2sqrt{x}})
Исследование функции с помощью производной
В задании нам может быть дана только функция без ее графика. Что делать в таком случае, если нам нужно найти, например, отрезки возрастания, точки экстремума, наибольшее или наименьшее значение функции? Не во всех случаях получится построить график, да и это займет достаточно большое количество времени, которое и без того ограничено на экзамене.
В этом случае мы можем проанализировать поведение функции с помощью производной.
Исследуем функцию f(x) = (x — 4)2(x + 11) + 4.
Cначала возьмем производную от этой функции:
f'(x) = ((x — 4)2(x + 11))‘ + 4′ = ((x — 4)2(x + 11))’ = ((x — 4)2)'(x + 11) + (x — 4)2(x + 11)’
f'(x) = 2(x — 4)(x + 11) + (x — 4)2 * 1 = (x — 4)(2(x + 11) + (x — 4)) = (x — 4)(3x + 18)
Любое исследование функции с помощью производной начинается именно с дифференцирования функции.
Теперь рассмотрим алгоритм нахождения точек минимума и максимума:
2 шаг. Найденную производную необходимо приравнять к 0 и решить полученное уравнение.
3 шаг. Расставить корни полученного уравнения на числовой прямой.
4 шаг. Определяем знаки производной на промежутках. Для этого необходимо подставить любое значение с выбранного промежутка в производную функции.
5 шаг. Определить, какие точки будут точками минимума (в них знак меняется с минуса на плюс), а какие — точками максимума (знак меняется с плюса на минус).
Найдем точки минимума и максимума в нашей функции. Поскольку производную мы уже взяли, можно сразу перейти ко второму шагу:
(x — 4)(3x + 18) = 0
x = 4, x = -6.
Полученные значения х расставляем на числовой прямой:

Теперь определим знаки на промежутках слева направо.
1. Возьмем точку -10 и подставим ее в производную функции:
(-10 — 4)(3 * (-10) + 18) = (-14) * (-12) = 168. Производная на этом промежутке будет положительной.
2. Возьмем точку 0 и подставим ее в производную функции:
(0 — 4)(3 * 0 + 18) = (-4) * 18 = -72. Производная на этом промежутке будет отрицательной.
3. Возьмем точку 5 и подставим ее в производную функции:
(5 — 4)(3 * 5 + 18) = 33. Производная на этом промежутке будет положительной.
Расставим полученные знаки на прямой:
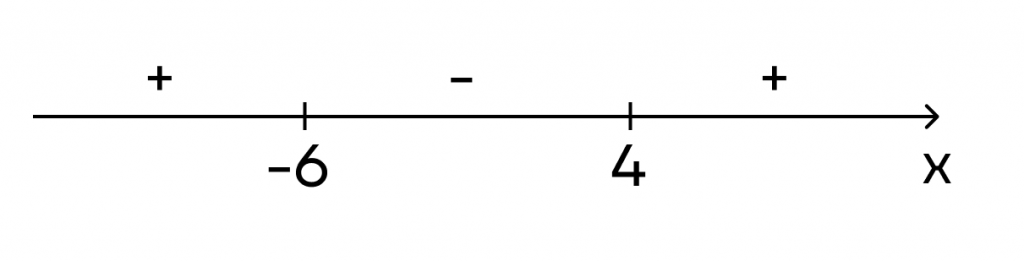
Остался последний пятый шаг. В точке -6 производная меняет знак с плюса на минус, значит, это точка максимума. В точке 4 производная меняет знак с минуса на плюс, значит, это точка минимума.
Важно!
Если в задании встречается формулировка “Найдите точку минимума (максимума) функции”, то необходимо пользоваться именно этим алгоритмом.
Но это не все выводы, которые уже можно сделать о функции. Вспомним, что функция возрастает, когда производная положительна, а убывает, когда производная отрицательна. Поскольку мы уже определили знаки производной, то смело можем сделать вывод, что на промежутках до -6 и после 4 функция будет возрастать, а на промежутке от -6 до 4 — убывать.
Однако могут встретиться задания, в которых необходимо найти наибольшее или наименьшее значение функции на определенном интервале.
Для выполнения таких заданий существует следующий алгоритм нахождения наибольшего и наименьшего значения функции.
Шаг 2. Найти точки минимума и максимума функции.
Шаг 3. Определить, какие из точек минимума и максимума принадлежат заданному интервалу.
Шаг 4. Найти значение функции в отобранных в предыдущем шаге точках, а также в точках, которые являются границами заданного интервала. Для этого необходимо подставить точки в функцию (не в производную от функции).
Для примера найдем наибольшее значение функции f(x) = (x — 4)2(x + 11) + 4 на отрезке [-10; 0].
Первые два шага мы уже выполнили, когда рассматривали алгоритм нахождения точек минимума и максимума. Из них отрезку [-10; 0] принадлежит х = -6 — точка максимума.
Теперь определим значение функции в трех точках:
f(-10) = (-10 — 4)2(-10 + 11) + 4 = 196 + 4 = 200
f(-6) = (-6 — 4)2(-6 + 11) + 4 = 500 + 4 = 504
f(0) = (0 — 4)2(0 + 11) + 4 = 176 + 4 = 180
Наибольшее из полученных значений — это 504. Это и будет ответ.
Может возникнуть вопрос, почему важно проверять значение функции и на границах отрезка? В заданиях ЕГЭ очень часто встречаются случаи, когда нужно найти наибольшее значение, и в интервале лежит точка максимума, или когда нужно найти наименьшее значение функции и в интервале лежит точка минимума. Логично будет проверить только экстремумы, поскольку в них, скорее всего, достигается наибольшее или наименьшее значение.
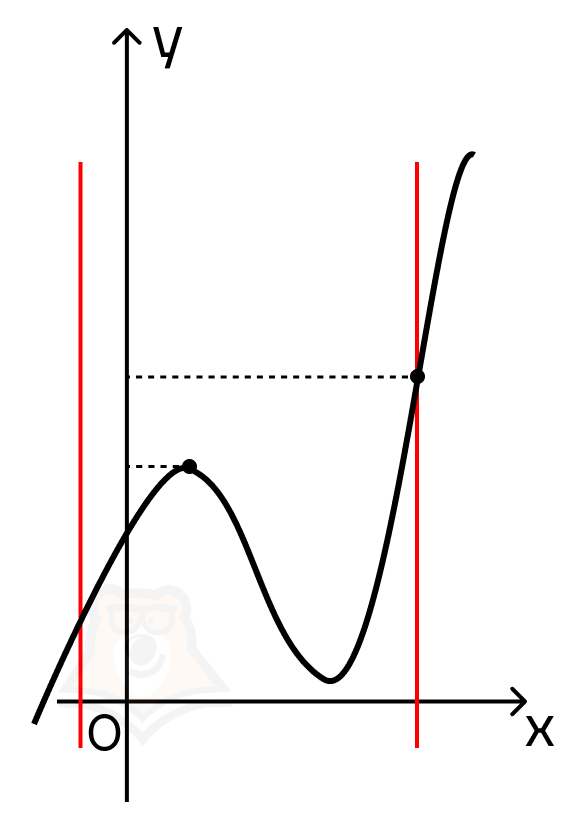
Однако стоит вспомнить, что мы не видим график функции и не можем с точностью определить, что в экстремуме достигается нужное нам значение. С помощью экстремумов мы можем описать поведение функции: где она возрастает, а где убывает. Но можно столкнуться с графиком, на котором граничная точка будет лежать выше или ниже точки экстремума. Тогда наибольшее или наименьшее значение будет достигаться именно в ней. Пример на картинке (красными линиями обозначены границы отрезка).
Подведем итог.
Как можно исследовать функцию с помощью производной?
С помощью производной можно с точностью сказать, на каких участках функция будет возрастать и убывать, сколько точек максимума и минимума у нее есть, какое наибольшее или наименьшее значение принимает функция на заданном участке.
Фактчек
- Для нахождения производной необходимо пользоваться специальными формулами для производной. С их помощью можно найти производную любой из основных функций.
- Если функция усложнена коэффициентом, является сложной или представлена в виде суммы, произведения или частного, то необходимо пользоваться правилами дифференцирования. Они помогут правильно найти производную.
- Сложная функция — это функция, внутри которой есть другая функция.
- С помощью производной можно исследовать функцию, а именно найти точки минимума и максимума, определить, на каких участках функция возрастает и убывает, найти наибольшее и наименьшее значение функции на заданном отрезке.
Проверь себя
Задание 1.
Чему будет равна производная f(x) = 3?
- 3;
- 1;
- 0;
- Производную этой функции невозможно найти.
Задание 2.
Чему будет равна производная f(x) = 5x2?
- 10x;
- 10x2;
- 5x2;
- 2x.
Задание 3.
Чему будет равна производная f(x) = 13x + 5 + x3?
- 18 + 3x2;
- 13 + 3x2;
- 18;
- 3x2.
Задание 4.
Чему будет равна производная f(x) = ln(x)?
- x
- (frac{1}{x})
- (frac{1}{2sqrt{x}})
- ex
Задание 5.
Чему будет равна производная f(x) = tg(x)?
- (frac{1}{cos^{2}(x)})
- (-frac{1}{sin^{2}(x)})
- (-frac{1}{cos^{2}(x)})
- (frac{1}{sin^{2}(x)})
Ответы: 1. — 3 2. — 1 3. — 2 4. — 2 5. — 1
Как использовать Калькулятор Функции от производных
1
Шаг 1
Введите свою производную задачу в поле ввода.
2
Шаг 2
Нажмите Enter на клавиатуре или на стрелку справа от поля ввода.
3
Шаг 3
Во всплывающем окне выберите «Найти функцию из производной». Вы также можете воспользоваться поиском.

Что такое функция от производной
Как мы знаем, функция, обратная функции, делает противоположное тому, что делает исходная функция, и в порядке, обратном тому, что она делает в обратном порядке. Вы используете интеграцию. В конце концов, теоремы фундаментального исчисления утверждают, что в определенном свободном смысле слова производная и интеграл обратны друг другу.
Производная и интеграл — проще некуда
Время на прочтение
12 мин
Количество просмотров 57K
19 декабря 2020 г. на Хабре вышла статья «Интуитивное объяснение интеграла».
В комментариях к ней некоторые пользователи указали, что объяснение получилось не очень интуитивным, например:
“Тема сама по себе интересная, недавно снова повторял курс, но должен сказать, что на мой взгляд, в материале нет изюминки. Автор прав, что в современных изданиях часто даются темы без описания их прикладного применения, из-за чего непонятен смысл их изучения.
Но конкретно интегралы это такая тема, которую надо описать или короче, чем у вас, или намного дольше.
Иначе и школьник не поймет, и те, кто знает, ничего нового не откроют.”
Я попробую изложить материал максимально коротко и просто. Так, чтобы школьники, наконец, поняли, пусть и с помощью родителей. Итак:
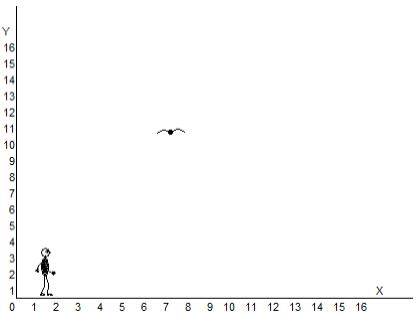
Я живу на плоскости, и мой мир выглядит так:
Все мои перемещения ограничиваются прямой линией, которую я называю «ось абсцисс» и обозначаю ее латинской буквой х. Таким образом, я могу гулять от точки, обозначенной цифрой ноль (там находится мой дом), вправо до бесконечности и назад, до нуля. Цифры на оси абсцисс позволяют мне понять, как далеко я от дома. Сейчас я нахожусь в 10 делениях от него.
Да, я слышал, что есть миры, в которых можно перемещаться и влево от нуля, и там расстояния обозначаются отрицательными числами: -1, -2 и т. д., до бесконечности. Кроме того, в тех мирах можно опуститься ниже оси абсцисс, но мой мир максимально прост.
Как-то раз, летящие птицы навели меня на мысль, что по нашему миру можно перемещаться не только влево или вправо, но и «вверх». Потом я узнал, что есть некие люди, умеющие строить дороги, ведущие в наши плоские небеса. Было бы неплохо бы с ними переговорить. И вот я общаюсь со специалистом (С), по строительству таких дорог:
Я: Здравствуйте, вы занимаетесь строительством дорог в небо?
С: Добрый день, да.
Я: А какие дороги вы умеете строить?
С: Самые простые варианты — прямые дороги различной крутизны.
Я: А что такое «крутизна»? Я всегда жил на горизонтальной прямой, и понятия не имею, что это слово может значить.
С: «Крутизна» показывает то, насколько трудно будет вам подниматься (или опускаться) по данной дороге. Чем круче дорога, тем тяжелее подъем или спуск. Давайте нарисуем на нашей плоскости еще одну ось — вертикальную. Мы назовем ее осью ординат, и обозначим латинской буквой у. На этой оси есть цифры, обозначающие «высоту» – расстояние до оси х.
Чтобы нам было проще ориентироваться в нашем двухмерном мире, нанесем на его плоскость линии, идущие от цифр, расположенных на осях х и у:
Теперь любое место (точку) на плоскости мы можем обозначить двумя цифрами. Первая цифра будет обозначать расстояние от нуля до проекции этой точки на ось х…
Я: Простите, а что такое «проекция»?
С: Видите внизу, на оси абсцисс, тень от летящей птицы? Она находится в точке, обозначенной цифрой 6 на оси х. Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее.
Мы можем обозначить положение птицы двумя цифрами (6, 8). Первая цифра — проекция на ось х, вторая — проекция на ось у. Эти две цифры мы называем координатами птицы.
Вместо запятой между целой и дробной частями чисел, я буду ставить точку (т.е., не 13,5 а 13.5) для того, чтобы не путать с запятыми между соседними числами.
Я: Отлично, что дальше?
С: Дальше мы отгоним птицу и нарисуем дорогу:
Вы можете заметить, что эта дорога поднимается на одну клеточку вверх, при перемещении проекции на ось х на одну клеточку вправо.
Когда человек перемещается из точки с координатами (4, 4) в точку с координатами (10, 10), его проекция на ось х меняется на 6 цифр. То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц.
Изменение какого-либо параметра (например, проекции на ось х или у), мы обозначаем буквой d (дельта). Изменение высоты мы запишем как dy, а изменение проекции на ось х — как dx. То есть, в данном случае, dу = 6, и dx также = 6.
Разделив изменение высоты на изменение положение тени человека при его перемещении (dy/dx), мы узнаём крутизну данного участка дороги: 6 / 6 = 1.
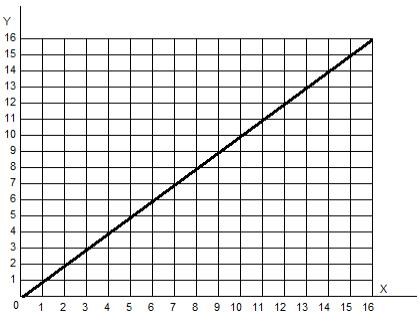
В нашей проектной документации мы используем очень краткое описание маршрута прокладываемой дороги. В данном случае оно будет выглядеть как математическая формула у = 1*х.
Это значит, что у всегда равен х, и это справедливо для любой точки дороги. Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой.
Разумеется, можно было просто указать крутизну дороги одно цифрой, в данном случае, единицей, но проблема в том, что во-первых, дороги не всегда начинаются у вашего дома – в точке с координатами (0, 0). Во-вторых, существуют дороги, крутизна которых не постоянна. Но о них позже. А пока давайте нарисуем еще пару прямых дорог:
Мы видим, что верхняя дорога поднимается круче, чем та, которую мы рассмотрели ранее. А нижняя дорога – наоборот, более пологая. Высота (проекция на ось у), на которой находится человек, идущий по верхней дороге, равна 10. То есть, перемещаясь от начала координат до точки, в которой он находится сейчас, он изменил свою проекцию на ось у на 10 единиц. В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно?
Я: Да, я понял это еще на первом примере. А если мы разделим проекцию перемещения человека, идущего по нижней дороге на ось у, на перемещение его тени по оси х, (5/10), мы получим цифру 0.5, или 1/2. Это и есть показатель крутизны нижней дороги?
С: Совершенно верно! Между каждой из дорог и осью х (горизонталью) есть некоторый угол. Чем больше этот угол, тем круче поднимается дорога. Соотношение координаты любой точки дороги (если дорога прямая) по оси у и координаты этой же точки по оси х, называют тангенсом этого угла. Для каждого угла — свой тангенс. Тангенс угла верхней дороги равен 2, тангенс угла нижней, более пологой дороги, равен 0.5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х.
Эти формулы мы называем функциями. Мы говорим, что у – функция от х, где х независимая переменная (мы ее задаём), а у – зависимая переменная, так как мы ее вычисляем, исходя из заданного значения х. И она жестко зависит от значения х. Например, задав х = 12 для дороги, описываемой формулой у = 0.5х, мы, подставляя цифру 12 вместо х, узнаём, что у в этой точке равен 6.
В математике функции обозначают, например, так: f(x) = x. Эта функция справедлива для дороги, рассмотренной нами в самом первом примере. Для второй и третьей дорог, функции будут выглядеть соответственно, как f(x) = 2x и f(x) = 0.5x. Не очень сложно, да?
Я: Не очень. Что еще мне нужно знать о дорогах?
С: Мы делаем не только прямые дороги. Например, мы можем построить дорогу, которая описывается формулой (функцией) у = x2, или f(x) = x2. Крутизна этой дороги будет увеличиваться, по мере ее удаления от оси у.
Чтобы построить рисунок этой дороги, мы найдем (вычислим) координаты нескольких ее точек. Для этого мы подставим в формулу у = x2 вместо х сначала 1, потом 2, затем 3 и т.д. И рассчитаем значение у для всех этих точек. Сначала подставим 1:
y = х2 = 12 = 1.
Это значит, что для точки, с координатой по х равной 1, ее координата по у также равна 1. Нанесем эту точку на график:
Теперь рассчитаем координату по у для точки, с координатой по х равной 2:
y = x2 = 22 = 4.
Таким образом, наша вторая точка будет иметь координаты (2, 4). Рассчитав у для точек с координатами по х 3 и 4, получим их полные координаты (3, 9) и (4, 16) соответственно. Нанесем эти точки на график:
Теперь соединим все точки линией, обозначающей дорогу:
Для любой точки этой дороги справедлива формула y = x2. Например, для точки, с координатой по х = 1,5, мы получим ее координату по у, возведя 1,5 в квадрат. То есть, ее координаты (1.5, 2.25). Таким образом, мы можем узнать высоту любой точки дороги, задавая ее абсциссу (положение ее тени на оси х).
Но возникает проблема: мы не можем посчитать крутизну какой-либо точки дороги, так как она меняется постоянно. Не получится просто взять две точки дороги сверху и снизу от исследуемой и посмотреть, насколько изменится высота при прохождении пути между ними, разделив перемещение проекции на ось у на перемещение тени по оси х. Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:
Допустим, мы хотим узнать крутизну нашей кривой дороги на участке от начала координат (точки с координатами (0, 0)), до точки с координатами (3, 9). На этом участке дорога поднимается на 9 единиц, в то время, как удаление от начала координат по х составляет 3 единицы. Считаем крутизну так же, как мы считали ее для прямой дороги: 9 / 3 = 3. То есть, крутизна на этому участке, вроде бы, равна 3. Но если мы проведем прямую с крутизной, равной 3, то увидим, что на самом деле дорога в самом низу идет гораздо более полого, чем прямая, а в точке пересечения прямой и дороги, крутизна дороги уже больше крутизны прямой! Крутизна кривой в центре между этими точками также не совпадает с крутизной прямой. Засада. Что же делать? Как нам узнать крутизну каждой точки в ситуации, когда первая постоянно меняется, и нет ни единого прямого участка? Вот для таких случаев господин Ньютон и придумал дифференцирование.
Дифференцирование преобразует нашу функцию в другую функцию, которая как раз-таки позволяет точно вычислить крутизну дороги в данной точке. Мы не будем вдаваться в то, как он пришел к своему решению, а просто воспользуемся результатом его работы — таблицей дифференциалов. Я не буду ее приводить, в Сети такого добра навалом. Можно просто ввести в строку поиска формулу, которую нужно дифференцировать.
Для нашей функции f(x) = x2 дифференцирование будет выглядеть таким образом: нам нужно перенести двойку из показателя степени влево, перед х, и уменьшить степень х на единицу. То есть, в данном случае степень х станет равна 1: f ‘(x) = 2x.
Обратите внимание на штрих после буквы f: f ‘(x) — так обозначается функция, которая произошла от нашей оригинальной функции. Поэтому ее называют производной функцией.
Но что нам теперь делать с этой производной? Как с ее помощью найти крутизну какой-либо точки оригинальной функции f(x) = x2? Очень просто. Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение:
f ‘(x) = 2x = 2*1 = 2.
Эта двойка и показывает нам крутизну дороги над точкой 1 по оси х.
А какова крутизна дороги в точке с абсциссой 4 (проекцией на ось х = 4)? Подставляем эту четверку в производную функцию f ‘(x) = 2x = 2*4 и получаем цифру 8.
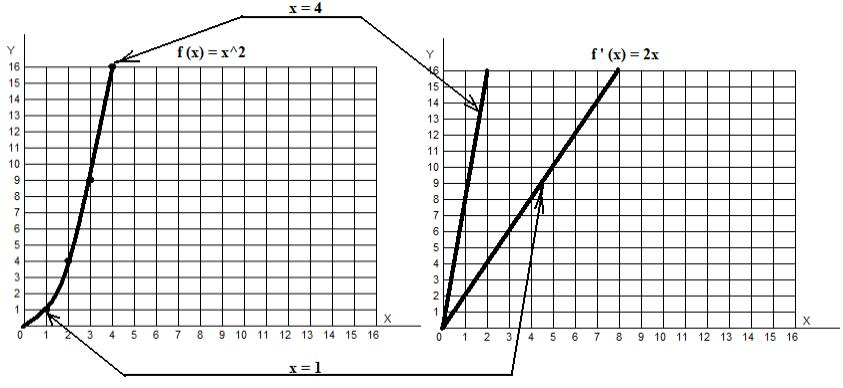
Эта восьмерка означает, что крутизна дороги в точке с абсциссой 4 равна 8. То есть, в этой точке дорога поднимается так же круто, как верхняя прямая на правом графике. Вот и весь смысл дифференцирования (нахождения производной).
Слева — график самой дороги, а справа — прямые, крутизна которых соответствует крутизне дороги в указанных точках. То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».
Давайте найдем производную нашей самой первой функции f (x) = x.
Мы проделаем такой же трюк: перенесем степень переменной вперед, перед х (это ничего не изменит, так как степень х была равна 1). Кроме того, мы уменьшим степень х на единицу. При этом степень станет равна нулю, и х превратится в единицу (потому, что любое число (кроме нуля) в нулевой степени равно 1).
Мы получили производную функции f(x) = x. Она выглядит так: f ‘(x) = 1. Что это значит? Это значит, что крутизна данной дороги на любом ее участке равна 1. То есть, при изменении абсциссы на dx, dy изменится ровно на такую же величину. В принципе, мы это знали и раньше, но теперь мы вычислили крутизну дороги через производную.
В учебниках пишут, что производная постоянной (некоторого числа) равна нулю. Почему это так?
Давайте построим дорогу, которая описывается функцией f(x) = 5. Это означает, что высота (проекция на ось у) любой точки данной дороги всегда равна 5, следовательно, dy (изменение высоты) равно нулю.
Поэтому эта дорога идет параллельно оси абсцисс, то есть, никакого изменения высоты не будет, на сколько бы мы не перемещались вправо. А раз крутизна дороги равна нулю, то и производная данной функции равна нулю (dy/dx = 0/dx = 0).
Повторим: производная отображает крутизну функции (графика, дороги), а в данном случае никакой крутизны нет. Что и имеется ввиду, когда говорят, что производная постоянной равна нулю.
Я: Хорошо, я все понял: по оригинальной функции я могу вычислить высоту дороги в любой ее точке, а по производной — крутизну в любой ее точке. Но дорога не может висеть в воздухе, она же должна опираться на ось х?
С: Совершенно правильный вопрос. Под дорогой нам придется сделать насыпь. И чем больше материала (клеточек) мы потратим на данный участок дороги, тем больше вам придется заплатить.
Я: А как вы посчитаете, сколько клеточек вам понадобится? Для участка прямой дороги, параллельной оси абсцисс f(x) = 5, все просто:
У нас получается прямоугольник, высота которого равна постоянной 5, а длину мы можем посчитать, вычитая координату по х левой стороны прямоугольника из координаты его правой стороны: 10 – 3 = 7. То есть, ширина прямоугольника равна 7, соответственно, его площадь равна 5 * 7 = 35 клеточек. Я буду вам должен за 35 клеточек.
Нет проблем и с дорогой, которая поднимается (или опускается) по прямой.
Как и в предыдущем случае, ширину основания мы узнаём, вычитая координаты границ по оси х друг из друга: 9 – 3 = 6.
Высоту найти немного сложнее: нам придется вычислить ее среднее значение. Для этого мы берем высоту (проекцию на ось у) левой верхней точки закрашенной фигуры, прибавляем к ней высоту правой верхней точки и делим пополам:
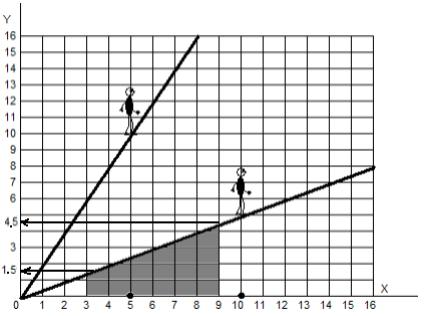
(1.5 + 4.5) : 2 = 3. Эта тройка — средняя высота фигуры. Мы умножаем ее на ширину фигуры и получаем цифру 18. То есть, на данный участок дороги потрачено 18 клеток, верно? Но как узнать, сколько клеток потребует участок дороги типа y = x2?
С протяженностью участка дороги слева направо разобраться легко, она равна 4 – 1 = 3 клетки, но как быть с высотой? Ведь мы не можем в данном случае сложить 1 и 16, затем разделить пополам и получить среднюю высоту фигуры? Как нам посчитать площадь этой насыпи?
С: Господин Ньютон предусмотрел и это. Метод подсчета площади криволинейных фигур называется «интегрирование». Нам придется вспомнить то, как мы находили производную функции f (x) = x2 Она выглядит так: f ‘(x) = 2x.
Эту, как и многие другие математические операции, можно производить и в обратную сторону. Если нам известна производная функции, мы можем восстановить эту изначальную функцию, называемую первообразной. То есть, имея функцию, показывающую изменение крутизны дороги, мы можем восстановить функцию, показывающую саму дорогу — высоту любой ее точки.
Если для нахождения производной мы переносили вперед показатель степени переменной (двойку), и уменьшали степень переменной х на единицу
f(x) = x2 => f ‘(x) = 2x,
то теперь нам следует поступить ровно наоборот: двойку, стоящую перед х следует перенести наверх, в степень: f ‘(x) = 2x => f(x) = x2 .Так мы получаем первообразную функцию. То есть, ту функцию, от которой производная произошла.
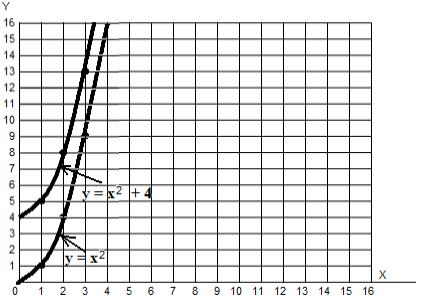
Но не все так просто, давайте рассмотрим дорогу, описываемую функцией
f (x) = x2 + 4:
Она выглядит точно так же, как дорога f (x) = x2 , но располагается выше. Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2 ! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.
Я: Почему?
С: Потому, что она не влияет на крутизну графика. Вы же помните, что производная описывает крутизну оригинального (первообразного) графика на каждом его участке? А теперь посмотрите на точки обоих графиков, расположенные, к примеру над цифрой 3 на оси х. Крутизна верхнего и нижнего графиков в этих точках одинакова! То же самое касается любых двух точек этих графиков, расположенных друг под другом. Эти две дороги идут параллельно друг другу, поэтому, их крутизна везде совпадает. Отличается только высота.
Но производная — это не про высоту, а про крутизну дороги. Потому и получается, что обе функции f (x) = x2 и f (x) = x2 + 4 приводят к одной и той же производной f ‘(x) = 2x.
Я: Погодите, но тогда получается, что функции, к примеру, f (x) = x2 + 5 или f (x) = x2 + 1.3 и даже f (x) = x2 – 2 также приводят к одной и той же производной? Ведь они все параллельны друг другу, и их крутизна в точках, расположенных друг под другом, совпадает?
С: Да, наша производная имеет бесконечный набор первообразных. Поэтому первообразную функции f (x) = 2x записывают как F (x) = x2 + C, где буква С может быть любым числом. От этого числа зависит только высота, на которой проходит дорога. Точнее, разница высот между данной дорогой, и дорогой, у которой С = 0. Если Вы снова посмотрите на графики выше, то увидите, что любая точка верхнего графика ровно на 4 клетки выше аналогичной точки нижнего графика.
Обратите внимание также на то, что буква F в первообразной — заглавная (большая), Первообразная является «матерью» производной, поэтому мы относимся к ней с уважением, и пишем ее имя заглавной буквой.
Все множество функций, описываемых формулой F (x) = x2 + C, называется неопределенным интегралом. Самая распространенная формула для нахождения неопределенного интеграла выглядит так:
По этой формуле мы можем найти неопределенный интеграл нашей функции f (x) = x2. Для этого мы увеличиваем степень переменной на единицу, а в знаменатель просто ставим получившуюся степень переменной. Степень нашей переменной была 2, увеличив ее на единицу, получаем x3. Эту же тройку мы ставим в знаменатель (под дробную черту). Получается выражение F (x) = x3/3 + С.
Теперь вернемся к нашей криволинейной фигуре.
Чтобы узнать ее площадь, в полученный нами неопределенный интеграл нужно подставить абсциссу ее правой границы — цифру 4 (при этом постоянная С отбрасывается):
F (x) = x3/3 = 43/3 = 21 1/3 (двадцать одна целая и одна треть)
То же самое проделаем с левой границей фигуры:
F (x) = x3/3 = 13/3 = 1/3 (одна треть)
Теперь нам остается вычесть из первого числа второе: 21 1/3 – 1/3 = 21
Искомая площадь равна 21 клетке. Для проверки вы можете примерно посчитать закрашенные клетки на картинке.
Давайте подытожим все вышесказанное. Итак, у нас есть некоторая формула (функция) f(x), описывающая некую линию на графике.
Чтобы найти крутизну этой линии (функции) в какой-либо ее точке, мы находим производную данной функции f ‘(x), затем подставляем в полученную производную проекцию на ось х интересующей нас точки оригинальной функции, и вычисляем искомый параметр. Полученная цифра будет показывать тангенс угла наклона прямой, которая поднимается (или опускается) так же круто, как исходный график в исследуемой точке.
А чтобы найти площадь под участком графика исходной функции, следует найти ее первообразную F, затем, в эту первообразную по очереди подставить координаты по х правой и левой границы фигуры, площадь которой мы хотим найти, а затем вычесть два полученных числа друг из друга. Результат вычитания и есть искомая площадь.
Я: А почему вы отбросили постоянную С? Разве это не приведет к тому, что площадь под участками кривых f (x) = x2 и f (x) = x2 + 4, находящимися друг под другом, будут одинаковыми?
С: Не беспокойтесь, при нахождении интеграла второй функции, постоянная 4 в ее первообразной превратится в 4х, поэтому, к площади под ней добавится прямоугольник высотой 4 клеточки и ошибки не будет. Ну так что, какую дорогу Вы выбираете?


 .
.

 и конечную
и конечную  точки; звенья ломаной параллельны осям координат. Естественно, форма области, в которой задана функция, должна допускать такую ломаную.
точки; звенья ломаной параллельны осям координат. Естественно, форма области, в которой задана функция, должна допускать такую ломаную.