Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
![]()
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
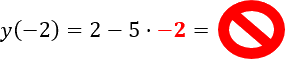
Правильно
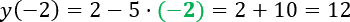
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
![]()
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
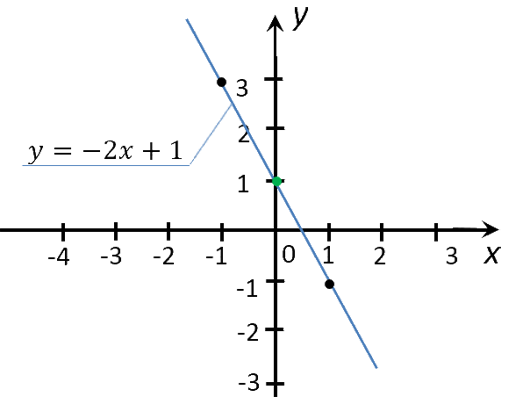
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
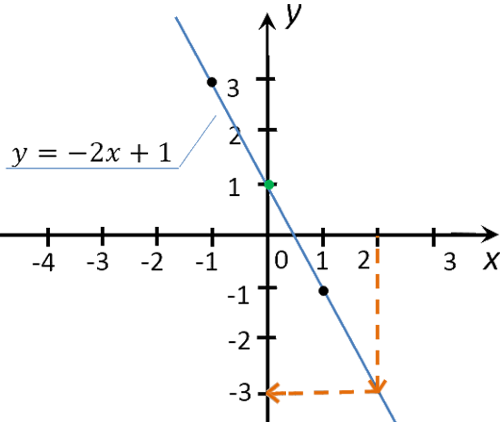
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры

Профиль
Благодарили: 0
Сообщений: 1

Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= – x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov

Профиль
Благодарили: 0
Сообщений: 1

Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов

Профиль
Благодарили: 0
Сообщений: 1

Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
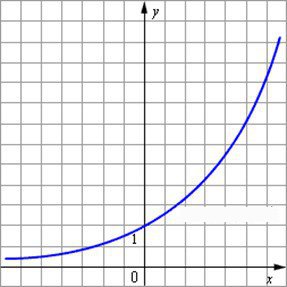 определите вид графика
определите вид графика
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов

Профиль
Благодарили: 0
Сообщений: 3

Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова

Профиль
Благодарили: 0
Сообщений: 11

Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
Вопросы
занятия:
·
показать, что способ задания функции с помощью формулы является более
распространенным и позволяет для любого значения аргументы путем вычисления
найти соответствующее значение функции.
Материал
урока
На
предыдущем уроке мы рассматривали функции, которые были заданы с помощью
формулы, с помощью графика, а также с помощью таблицы. Мы отмечали, что более
распространённым способом является задание функции с помощью формулы.
Прежде,
чем приступить к изучению новой темы вспомним, что
Способ задания функции с помощью формулы позволяет для любого
значения аргумента найти соответствующее значение функции путем вычислений.
Давайте рассмотрим это на примере.
Пусть функция задана формулой:
Такие вычисления удобно записывать в виде таблицы следующим
образом:
Обратите внимание, что каждое выбранное нами значение аргумента х
на 0,5 больше предыдущего. А поэтому можем сказать, что таблица значений
данной функции составлена с шагом 0,5.
Все выбранные нами значения независимой переменной составляют область
определения рассматриваемой функции.
Если же область определения функции не указана, то считается, что
она состоит из всех значений аргумента, при которых формула имеет смысл.
Например,
А вот область определения функции:
Решим несколько упражнений.
Пример.
Следующее упражнение звучит так.
Пример.
И выполним ещё одно упражнение.
Пример.
Цели:
- изучить аналитический способ задания функции;
- формировать умения и навыки находить значения аргумента и значения функции.
Задачи:
- воспитательные: воспитание интереса к математике и её приложениям;
- обучающие:
- вычисление значения функциипо заданному значению аргумента и нахождение значения аргумента по заданному значению функции;
- совершенствование вычислительные навыки;
- развивающие:
- формирование умений применять приёмы наблюдения, сравнения, анализа;
- развитие общего и математического кругозора, мышления и речи.
Тип урока: урок ознакомления с новым материалом.
Девиз урока:
Расскажи – и я забуду
Покажи – и я запомню
Вовлеки – и я пойму.
Оборудование: учебник, карточки, интернет ресурсы, проектор.
План урока:
- Организационный момент
- Проверка домашней работы
- Устный опрос. (Актуализация опорных знаний)
- Изучение нового материала (Введение в тему. Постановка учебных задач.)
- Закрепление изученного материала
- Самостоятельная работа
- Подведение итогов урока
- Сообщение домашнего задания, рефлексия.
Ход урока
1. Организационный момент
(Обеспечить рабочую обстановку на уроке. Учитель приветствует учащихся, проводит проверку готовности класса к уроку).
– Здравствуйте, ребята, садитесь. Я рада видеть вас в хорошем настроении.
Наш девиз сегодня:
Расскажи – и я забуду
Покажи – и я запомню
Вовлеки – и я пойму.
Мы вместе активно включаемся в учебный процесс. Будем внимательными, дружными и доброжелательными.
– Откройте рабочие тетради и запишите сегодняшнее число, классная работа.
2. Проверка домашней работы
– Проверка решения текстовой задачи домашнего задания на доске (1 уч) (сверка с образцом)
Задача. В рамках акции «Посади дерево» шестиклассники и семиклассники посадили вместе 210 саженцев. Сколько саженцев посадили семиклассники, если известно, что они посадили на 10% саженцев больше, чем шестиклассники?
Решение:
Пусть 6-классники посадили х саженцев, то 7-классники посадили
х+0,1х=1,1х саженцев.
х+1,1х=210
2,1х=210
х=210:2,1
х=100(саж.) 6-кл.
1,1х=1,1*100=110(саж.)
Ответ: 110 саженцев.
Дополнительные вопросы:
– При решении уравнения какими свойствами пользовались?
– Для чего проводятся такие акции?
– Чтобы сохранять природу
– Как связан с экологией 2017 год?
(- Каким годом был объявлен 2017-й год Президентом РФ Путиным В.В.?)
(2017-й год Президентом РФ Путиным В.В.был объявлен Годом экологии.)
3. Устный опрос
1. Дайте определение функции.
– Функцией называют такую зависимость одной переменной (зависимой) от другой (независимой), при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.)
- Какая переменная называется независимой переменной, а какая – зависимой? Что называют аргументом?(Переменную а, значения которой выбираются произвольно, называют независимой переменной. Переменную, значения которой определяются выбранными значениями а, называют зависимой переменной. Независимую переменную иначе называют аргументом).
- Дана функция y=2,7x – 15. Укажите независимую и зависимую переменные.
- Что называется областью определения и областью значений функции?
- При каких значениях переменной имеет смысл выражение:
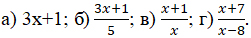
4. Изучение нового материала
На прошлом уроке мы начали важную тему для математики. Начиная с XVII века понятие функции – одно из основных в математике. Оно играет большую роль в познании реального мира. На уроках математики вы часто будете слышать это слово.
– Какие способы задания функции рассмотрели на прошлом уроке?
– На предыдущем уроке мы рассматривали различные способы задания функции: с помощью формулы, графика, таблицы. (Показать на слайде)
Наиболее распространенным способом является задание функции с помощью формулы (аналитический способ). Формула позволяет для значения аргумента находить соответствующее значение функции путем вычислений. (На примере функции y=2,7x – 15). Что же мы будем сегодня изучать?
Сформулируйте тему урока. Запишем тему в тетрадь.
А теперь поставим перед собой цель сегодняшнего урока. Какой она будет?
Ответы детей: научиться находить значение функции.
– Но и обратную задачу будем решать – находить значение аргумента.
Цель: научиться вычислять значения функциипо заданному значению аргумента и находить значения аргумента по заданному значению функции.
Рассмотрим Пример 1. (На доске)
Пусть функция задана формулой у = 5х – 1, где -2< х<2.
Найдем значение функции, соответствующее целым значениям аргумента х:
- Если х = -2, то у = 5*(-2)-1=-11;
- если х = -1, то у = 5 * (-1) -1 = -6;
- если х = 0, то у = 5*0-1=-1;
- если х = 1, то у = 5 * 1-1=4;
- если х = 2, то у = 5 * 2-1=9.
Результаты вычислений удобно записать в виде таблицы, поместив в верхней строке значения аргумента, а в нижней строке – соответствующие значения функции:
| х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
-11 |
-6 |
-1 |
4 |
9 |
– Известна ли область определения этой функции по условию задачи?
Пример 2.
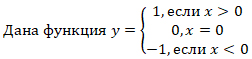
Найдем значение функции, соответствующее значению аргумента 5; -3;0.
- Если х=5,то у=1,
- Если х=-3,то у=-1,
- Если х=0,то у=0,
– Какая область определения этой функции по условию задачи?
Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
Часто приходится решать обратную задачу: нахождение значения аргумента по известным значениям функции.
Работа с учебником (пример 2 на стр.60). Разберем решение.
На этой же странице видим портрет немецкого математика, философа, физика и языковеда 17-18 вв. Лейбниц Готфрид Вильгельма. Именно им был введен термин «Функция». (Задание на дом одному уч. подготовить исследовательскую работу о Лейбнице.)

Готфрид Вильгельм Лейбниц – немецкий философ, математик, логик, физик, изобретатель, богослов, историк, юрист, языковед, дипломат. В частности им введен термин «Функция».
– Сделаем вывод: Как найти значение аргумента по заданному значению функции?
Физкультминутка
5. Закрепление изученного материала
а) Решение упражнений по учебнику: №267, 269, 273, 272(а,в).
№267 – (1-й пример ученик на доске, ост в тетрадях, затем обучающиеся решают с комментариями в тетрадях, без записи на доске);
№269 – (обучающиеся решают устно, заполняется таблица на слайде);
№269. ![]()
|
х |
-6 |
-4 |
-3 |
2 |
5 |
6 |
12 |
|
у |
-2 |
-3 |
-4 |
6 |
2,4 |
2 |
1 |
№273 (подробно на доске и в тетрадях обучающихся).
б) решение тренировочных упражнений из ЦОР (практика, групповая работа)
6. Самостоятельная работа
(В тетрадях для СР, которые после самопроверки через проектор собираются)
B-I
1. Функция задана формулой у = 0,2х – 4.
Найдите значение функции, соответствующее значению аргумента, равному 15.
2. Функция задана формулой у = 2х – 1.
При каком значении аргумента значение функции равно 8.
B-2
1.Функция задана формулой у = 0,5х + 3.
Найдите значение функции, соответствующее значению аргумента, равному-12.
2.Функция задана формулой у = 4х + 12.
При каком значении аргумента значение функции равно 30
B-3
1.Функция задана формулой у = х + 3.
Найдите значение функции, соответствующее значению аргумента, равному – 12.
2.Функция задана формулой у = х + 12.
При каком значении аргумента значение функции равно 30.
Ответы
|
1 |
2 |
|
|
I вариант |
-1 |
4,5 |
|
II вариант |
-3 |
4,5 |
|
III вариант |
-9 |
18 |
7. Подведение итогов урока
– Какую тему мы сегодня изучили ?
– Чему вы научились?
8. Домашнее задание
№268, 270, 277.
Творческие задания (на карточках)
1. Объясните, почему перечисленные формулы не задают функцию:
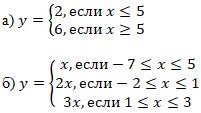
Как надо записать эти формулы, чтобы они определили функцию?
2. Вспомнить пословицы, отражающие функциональную зависимость. (например: Чем дальше в лес, тем больше дров. Кто не работает – тот не ест.)
9. Рефлексия
Предлагаю высказаться одним предложением, выбирая начало фразы из предложенных (на доске).
- Было интересно… (узнать про Лейбниц)
- Теперь я могу… (вычислять значения функции)
- Я смог… (решить правильно СР)
- Мне захотелось… (еще больше узнать о функциях)
Во время урока я чувствовал себя:
- комфортно;
- неуверенно;
- превосходно.
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x – 2.
Графическое решение уравнений
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На этом видеоуроке к изучению предлагается тема «Функция y=x 2 . Графическое решение уравнений». В ходе этого занятия учащиеся смогут познакомиться с новым способом решения уравнений – графическим, который основан на знании свойств графиков функций. Учитель покажет, как можно решить графическим способом функцию y=x 2 .
Учим алгебра 7 класс. Как решать уравнения алгебра 7 класс, примеры, дроби, функции, степени, модули
В 7 классе ученикам предстоит научиться решать уравнения, дроби, строить функции, разбираться в модулях. Для этого следует познакомиться с основными понятиями в темах, рассмотреть алгоритм решения и пошагово учиться находить ответы. Главное правило — начать с простых примеров, постепенно переходя на более сложные. Большинство задач можно решать несколькими методами (это касается и примеров), следует выбрать самый простой и удобный для себя.
Как решать уравнения алгебра 7 класс
Начнем с решения линейных уравнений (на рисунке показано, по какому принципу они устроены). Чтобы найти ответ в таких уравнениях, нужно совершать действия: раскрытие скобок, поиск подобных слагаемых, умножение/деление частей на одно и тоже число, перенос слагаемых из одной части уравнения в другую. Всё зависит от конкретного примера.

Рассмотрим несколько примеров пошагового решения линейных уравнений.
Пример 1.
6x + 24 = 0
Поскольку части уравнения (левая и правая) равны, то можно отнять из каждой одинаковое число. Равенство не изменится, а пример станет значительно проще. В представленном уравнении отняли 24 и слева, и справа. В левой части 24 сократилось, а в правой (0 — 24) получилось -24 (не забываем ставить знак минуса).
Получилось: 6x = -24. Теперь можем сократить 6 и -24 на число 6 (или рассуждаем так: чтобы найти множитель, нужно произведение разделить на другой множитель). В ответе будет -4. Не забудьте в самом конце подставить полученное число вместо х. Совпал ответ — значит, все правильно.

Можно рассуждать проще: чтобы упростить уравнение, нужно из левой части отправить в правую число 24, поменяв его знак. Равенство сохранится (на рисунке ниже).

Пример 2.
9 + 16x = 41 + 14x

Это уравнение более сложное. Здесь важно запомнить несколько моментов:
- числа без х переносятся в левую часть, а с х — в правую;
- при переносе знаки меняют.
Пример 3.
7(10 — 4x) + 5x = 12 — 3(5x + 2)

- Раскрыть скобки, выполнив умножение: 7 умножаем на каждое число в скобках (в правой части -3 на каждое). При выполнении действия не забывайте сохранять знаки.
- Записываем уравнение, получившееся после раскрытия скобок. Ещё раз сверяем знаки.
- Числа с х отправляются в левую часть, без х — в правую. Знаки чисел, которые переходят в другую часть, меняем.
- Подсчитываем результат с обеих сторон.
- Делим -64 на -8 и получаем ответ. Не забываем, что минус на минус при делении и умножении дают плюс.
В рассмотренных уравнениях корень точно определён. Так получается не всегда.
Пример 4.

Обратите внимание, в ответе получилось 0x = 0. Это значит, что x может быть любым числом, потому что при умножение хоть какого числа на 0 получится 0.

В этом примере корней нет, так как любое число, которое умножают на 0, будет равно 0 (21 никак не получится).
Как решать систему уравнений алгебра 7 класс
Системой называют несколько уравнений, в которых нужно найти такие значения неизвестных, чтобы равенство сохранилось. Разберемся на примерах, как выглядят системы и какие методы их решения существуют.
метод подстановки
Из самого названия следует, что алгоритм требует что-то подставлять. Ниже представлена система, где нужно найти значения x и y.
Суть метода подстановки: переменную в одном из уравнений выражают через другую переменную. Затем подставляют полученное выражение в другое уравнение.
Смотрим на систему. Видим, что удобнее будет выразить x во втором уравнении (так как он один). Выражаем путем переноса за знак «равно» 12y. Получилось: x = 11 — 12y (не забываем менять знак при переносе числа).
В первое уравнение вместо «x» записываем получившееся выражение. Меняем только x, остальное сохраняется в прежнем виде.

Далее преобразуем уравнение, в которое поместили выражение. Раскрываем скобки (перемножаем 5 на каждое значение). y оставляем в левой части, числа переносим в правую, знаки меняем. Таким образом нашли значение y (y = 1).

Теперь подставляем полученную единицу во второе уравнение (x = 11 — 12y).

Убедиться в правильном решение можно так: подставьте полученные значения в систему. Если равенства сохранятся, значит, решено верно.
метод сложения
Чтобы решить систему методом сложения, нужно из двух уравнений сделать одно. Просто складываем первое и второе. Здесь «y» просто сократились, и получилось простое уравнение. Как только нашли значение «х», нужно подставить его в любой пример (здесь поставили во второе уравнение). В ответе пишется так: (4; 3) — первым всегда пишется х, затем у.

графический метод
У нас есть система, где y = 5x и y = -2x + 7. Рассмотрим алгоритм решения системы уравнений:
- Подбираем 2 числа для х. Мы взяли 0 и 1, подставляем в первое уравнение: y = 5 * 0 = 0; у = 5 * 1 = 5. Значит первая прямая имеет координаты: (0; 0) и (1; 5).
- Для второго уравнения подбираем значения х. Взяли 3 и 2, подставляем и находим у: -2 * 3 + 7 = 1; -2 * 2 + 7 = 3. Значит прямая имеет координаты (3; 1) и (2; 3).
- Отмечаем на графике соответствующие прямые, подписываем их название.
- на месте пересечения получившихся прямых ставим точку — это будет решение.
- Точка имеет координаты (1; 5).

На заметку! Старайтесь подбирать такие значения х, чтобы у был небольшим. Так отмечать будет проще.
Выбирайте самый удобный способ решения. Третий метод — графический, считают самым неточным.
Как решать дроби 7 класс
Дроби можно разделить на 2 основных вида:
Они различаются в способе написания (смотрите рисунок ниже). В свою очередь и те, и другие делятся еще на несколько видов.

Для начала рассмотрим решение примеров с десятичными дробями.

Особое внимание при решении стоит уделить запятым. При сложении и вычитании запятые стоят строго друг под другом, при умножении это не имеет значения.
 Примеры решения обыкновенных дробей.
Примеры решения обыкновенных дробей.

- при сложении и вычитании нужно привести дроби к общему знаменателю, найти дополнительные множители. Так, для чисел 6 и 4 общим знаменателем стало число 24. Дополнительные множители считали так: 24 : 6 = 4 (для первой дроби) и 24 : 4 = 6 (для второй). Потом умножили доп. множители на числители и полученные числа сложили. Если в ответе получилась неправильная дробь, то выделяем целую часть, при необходимости сокращаем дроби.
- при умножении пишем дроби под одной чертой, сокращаем.
- при делении нужно вторую дробь перевернуть, поставить знак умножения и сократить дроби.
Если пример состоит из простой и десятичной дроби, то следует привести их к одному виду (к которому проще или удобнее считать).
Примеры 7 класс как решать
Теперь закрепим решение дробей на примерах.
Решение примера, представленного ниже:
- Видим, что присутствует как обыкновенная дробь, так и десятичные. Нужно привести к одному виду. Так как десятичных больше, и превратить 1/4 в этот вид проще, то делим 1 на 4, а целую часть сохраняем. Вышло 5,25.
- Далее умножаем — 3 на каждое число в скобках, внимательно следим за знаками.
- Остается от 10,4 отнять 9,3. В итоге вышло 1,1.
Но можно было решить проще. Первое действие всегда в скобках. Поэтому от 5,25 отнимаем 2,15. Получится 3,1. Умножаем ее на 3 — вышло 9,3. И отнимаем: 10,4 — 9,3 = 1,1. Этот способ даже проще, потому что не нужно следить за знаками при раскрытии скобок.

Чтобы верно решить следующий пример, нужно:
- точно проставить порядок действий (умножение и деление делаем в первую очередь, затем складываем);
- Умножить десятичные дроби столбиком, не забыть поставить запятую;
- деление здесь простое: переставили запятую на один знак вправо, поделили, получили -2.
- сложили числа.

Как решать задачи алгебра 7 класс
Задачи решаются путем составления уравнений.

Другие примеры задач с подробными решениями в видео-материалах.
Как решать функции алгебра 7 клас с
Функцией принято считать зависимость y от x. При этом x является переменной (или аргументом), а у — это значение функции (зависимая переменная).
- y(x) = 8x
- y(x) = −3x — 62
- y(x) = x−1 + 18
Чтобы найти значение у, которое бы соответствовало определенному значению х, нужно просто это значение х подставить в функцию.


Как решать степени алгебра 7 класс
Если требуется взять какое-либо число несколько раз, то проще записать его в степени. Например, нужно двойку взять три раза, т. е.: 2 * 2 * 2. Получается длинная запись. Поэтому придумали писать так: 2³ (читается: два в третьей степени).
Чтобы число возвести в степень (она указывается справа от числа вверху), нужно его умножать на самого себя столько раз, какая цифра указана. Рассмотрим подробнее на примерах.

Не всегда получается возвести число в степень «в уме». Иногда посчитать сложно. Например, возвести 6 в 5 степень, быстро получится не у каждого. Чтобы всякий раз не считать столбиком, лучше выучить основные степени. Они представлены в таблице.

При возведении любого числа в степень 1, получится это же число. Если возводить число в нулевую степень, в ответе будет 1.
Рассмотрим несколько примеров со степенями.

Отдельное внимание обращаем на возведение в степень отрицательного числа. Если такое число возводить в четную степень (2; 4; 6 и т.д.), то получится положительный ответ, если в нечетную, то ответ со знаком минус.
Алгебра модули как решать
Модулем числа называют это же число, только без знака минус. Например: | − 9 | = 9. При этом если число изначально неотрицательное, то оно остается прежним.

Перейдем к простым примерам.
Логично предположить, что под модулем будет число 4. Также подойдет число -4, ведь из-под модуля все равно выйдет положительное. Так, корнями уравнения будут: x = 4 и x = − 4.

Из-под модуля не может выйти отрицательное число. Поэтому, если видим что-то похожее: Ι-8 + хΙ = -8, значит, корней не будет, так как уравнение заведомо нерешаемо.
Другие примеры описаны в видео.
Об Авторе

Смотрите также
Сочинение рассуждение на тему патриотизм, патриотизм сочинение ЕГЭ: ложный и истинный патриотизм, народный патриотизм роман Война и мир, примеры сочинений

Урок патриотизма в школе. Тема урока патриотизм: урок литературы патриотизм, патриотическое воспитание на уроках истории, урок мужества патриотизм. Дети герои Великой Отечественной войны Валя Котик, Валерий Волков, Марат Казей, Надя Богданова, Люся Герасименко, Вашкевич Лида, Валя Зенкина, Костя Кравчук, Вася Коробко, Витя Хоменко, Саша Ковалёв: краткая биография

Современный сценарий выпускного в школе: сценарий выпускного современный прикольный веселый, красивые платья на выпускной 11 класс, современные песни текст на выпускной
2 комментария

Спасибо большое очень помогли.

Огромное спасибо!А то учитель неможет нормально тему объяснить
[spoiler title=”источники:”]
http://interneturok.ru/lesson/algebra/7-klass/funkciya-yx2/graficheskoe-reshenie-uravneniy
[/spoiler]
