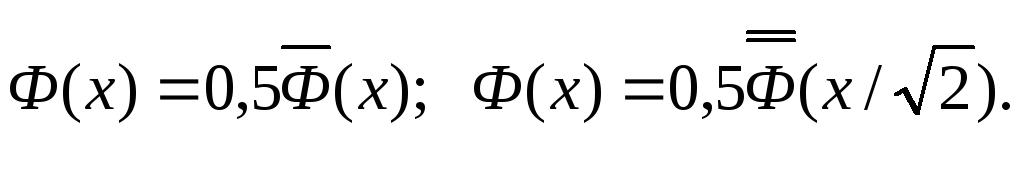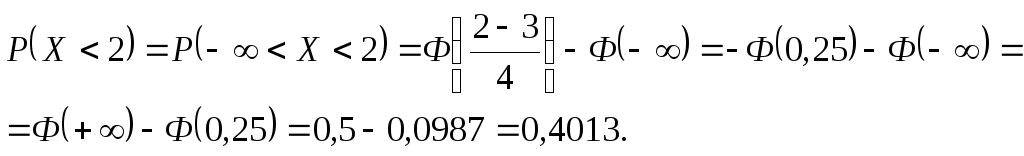Таблица значений функции Лапласа
В таблице даны значения функции
для положительных значений
и для
;
для
пользуются той же таблицей, так как функция
нечетна, то есть
.
В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
Таблица значений функции Лапласа в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
-
Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
-
Интегральная теорема Муавра – Лапласа
-
Доверительные интервалы для среднего и дисперсии
-
Проверка гипотезы о равенстве средних
Цветом в таблице подсвечены аргументы функции Лапласа, рядом, в соседнем столбце – значения функции Лапласа.
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Продолжение таблицы
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | -2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |
Пример решения задачи
Задача
Вероятность того, что
желание, загаданное на Новый год, сбудется, равна 0,7. Найти вероятность того,
что из 100 загаданных желаний сбудется от 60 до 85 желаний.
Решение
Вероятность того, что
событие
появится в
независимых
испытаниях от
до
раз:
В нашем случае
По таблице функции
Лапласа:
Искомая вероятность:
Содержание:
- Объяснение
- Таблица значений функции Лапласа
Таблица значений функции Лапласа – это вероятность того, что случайная величина примет значение,
принадлежащее заданному интервалу. При решении задач по
теории вероятности, как правило, требуется найти значение функции Лапласа по известному значению аргумента
или, наоборот, по известному значению функции Лапласа требуется найти значение аргумента. Для этого пользуются
таблицей значений функции Лапласа.
Таблица значений функции Лапласа незаменима при изучении теории вероятности, так как
решать интеграл (функцию Лапласа) сложно, а запомнить таблицу значений функции Лапласа просто невозможно.
Функцию Лапласа и данную таблицу чаще всего изучают на втором курсе университета, при изучении
математики и теории вероятности, если Вам в данной теме,
что-то не понятно, то Вы всегда можете задать вопрос на нашем
форуме, мы будем рады вам помочь. Пользуйтесь нашим сайтом и таблицей на здоровье.
Функция Лапласа
$$F(t)=frac{2}{sqrt{2 pi}} int_{0}^{t} e^{-frac{t^{2}}{2}} d t=frac{1}{sqrt{2 pi}} int_{-t}^{+infty} e^{-frac{t^{2}}{2}} d t$$
При разных значениях t; F(–t) = –F(t) (функция нормального распределения).
Таблица значений функции Лапласа
|
|
|
|

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
-
Функция лапласа. Ее свойства
2.1.
Функция (интеграл вероятностей) Лапласа
имеет вид:
График функции
Лапласа приведен на рис.5.
Функция Ф(х)
табулирована (см. табл. 1 приложений).
Для применения этой таблицы нужно знать
свойства
функции Лапласа:
1)
Функция Ф(х)
нечетная:
Ф(-х)=
–Ф(х).
2)
Функция Ф(х)
монотонно возрастающая.
3)
Ф(0)=0.
4)
Ф(+)=0,5;
Ф(–)=-0,5.
На практике можно считать, что при х5
функция Ф(х)=0,5;
при х-5
функция Ф(х)=-0,5.
2.2.
Существует другие формы функции Лапласа:
и
В отличие от
этих форм функция Ф(х)
называется стандартной или нормированной
функцией Лапласа. Она связана с другими
формами соотношениями:
ПРИМЕР 2.
Непрерывная случайная величина Х
имеет нормальный закон распределения
с параметрами: m=3,
=4.
Найти вероятность того, что в результате
испытания случайная величина Х:
а) примет значение, заключенное в
интервале (2; 6); б) примет значение, меньше
2; в) примет значение, больше 10; г) отклонится
от математического ожидания на величину,
не превышающую 2. Проиллюстрировать
решение задачи графически.
Решение. а)
Вероятность того, что нормальная
случайная величина Х
попадет в заданный интервал (,),
где =2
и =6,
равна:

Значения функции
Лапласа Ф(х)
определяют по таблице, приведенной в
приложении, учитывая, что Ф(–х)=
–Ф(х).
б) Вероятность
того, что нормальная случайная величина
Х
примет значение меньше 2, равна:
в) Вероятность
того, что нормальная случайная величина
Х
примет значение больше 10, равна:
г) Вероятность
того, что нормальная случайная величина
Х
отклонится от математического ожидания
на величину, меньшую =2,
равна:
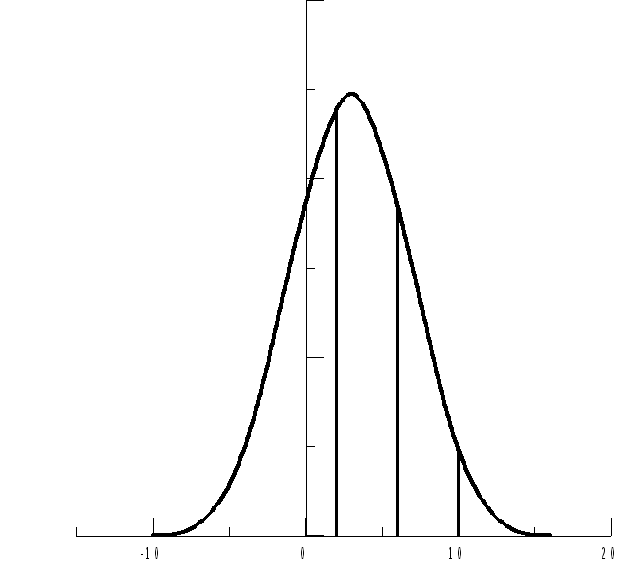
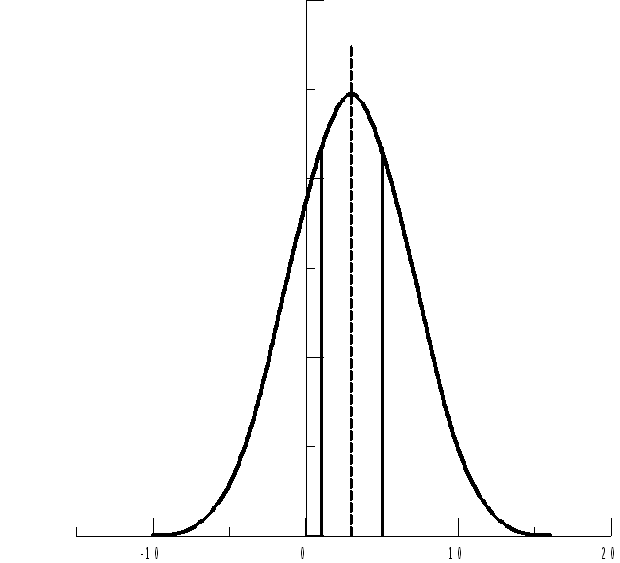
С
геометрической точки зрения, вычисленные
вероятности численно равны заштрихованным
площадям под нормальной кривой (см.
рис.6).
2
6
1
5
Рис. 6. Нормальная кривая для случайной
величины Х~N(3;4)
ПРИМЕР 3.
Производится
измерение диаметра вала без систематических
(одного знака) ошибок. Случайные ошибки
измерения подчинены нормальному закону
распределения со средним квадратическим
отклонением 10 мм. Найти вероятность
того, что измерение будет произведено
с ошибкой, не превышающей по абсолютной
величине 15 мм.
Решение.
Математическое
ожидание случайных ошибок равно нулю
m=0.
Тогда вероятность того, что нормальная
случайная величина Х
отклонится от математического ожидания
на величину, меньшую =15,
равна:
ПРИМЕР 4.
Автомат изготовляет шарики. Шарик
считается годным, если отклонение Х
диаметра шарика от проектного размера
по абсолютной величине меньше 0,7 мм.
Считая, что случайная величина Х
распределена нормально со средним
квадратическим отклонением 0,4 мм, найти,
сколько в среднем будет годных шариков
среди 100 изготовленных.
Решение.
Случайная величина Х
– отклонение диаметра шарика от проектного
размера. Математическое ожидание
отклонения равно нулю, т.е. М(Х)=m=0.
Тогда вероятность того, что нормальная
случайная величина Х
отклонится от математического ожидания
на величину, меньшую =0,7,
равна:
Отсюда
следует, что примерно 92 шарика из 100
окажутся годными.
ПРИМЕР 5.
Доказать правило «3».
Решение.
Вероятность того, что нормальная
случайная величина Х
отклонится от математического ожидания
на величину, меньшую =3,
равна:
ПРИМЕР 6.
Случайная величина Х
распределена нормально с математическим
ожиданием m=10.
Вероятность попадания Х
в интервал (10, 20) равна 0,3. Чему равна
вероятность попадания Х
в интервал (0, 10)?
Решение.
Нормальная кривая симметрична относительно
прямой х=m=10,
поэтому площади, ограниченные сверху
нормальной кривой и снизу интервалами
(0, 10) и (10, 20), равны между собой. Так как
площади численно равны вероятностям
попадания Х
в соответствующий интервал, то:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Функция Лапласа
- Оператор НОРМ.СТ.РАСП
- Решение задачи
- Вопросы и ответы
Одной из самых известных неэлементарных функций, которая применяется в математике, в теории дифференциальных уравнений, в статистике и в теории вероятностей является функция Лапласа. Решение задач с ней требует существенной подготовки. Давайте выясним, как можно с помощью инструментов Excel произвести вычисление данного показателя.
Функция Лапласа
Функция Лапласа имеет широкое прикладное и теоретическое применение. Например, она довольно часто используется для решения дифференциальных уравнений. У этого термина существует ещё одно равнозначное название – интеграл вероятности. В некоторых случаях основой для решения является построение таблицы значений.
Оператор НОРМ.СТ.РАСП
В Экселе указанная задача решается с помощью оператора НОРМ.СТ.РАСП. Его название является сокращением от термина «нормальное стандартное распределение». Так как его главной задачей является возврат в выделенную ячейку стандартного нормального интегрального распределения. Данный оператор относится к статистической категории стандартных функций Excel.
В Excel 2007 и в более ранних версиях программы этот оператор назывался НОРМСТРАСП. Он в целях совместимости оставлен и в современных версиях приложений. Но все-таки в них рекомендуется использование более продвинутого аналога – НОРМ.СТ.РАСП.
Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:
=НОРМ.СТ.РАСП(z;интегральная)
Устаревший оператор НОРМСТРАСП записывается так:
=НОРМСТРАСП(z)
Как видим, в новом варианте к существующему аргументу «Z» добавлен аргумент «Интегральная». Нужно заметить, что каждый аргумент является обязательным.
Аргумент «Z» указывает числовое значение, для которого производится построение распределения.
Аргумент «Интегральная» представляет собой логическое значение, которое может иметь представление «ИСТИНА» («1») или «ЛОЖЬ» («0»). В первом случае в указанную ячейку возвращается интегральная функция распределения, а во втором – весовая функция распределения.
Решение задачи
Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:
=НОРМ.СТ.РАСП(z;интегральная(1))-0,5
Теперь давайте на конкретном примере рассмотрим использование оператора НОРМ.СТ.РАСП для решения конкретной задачи.
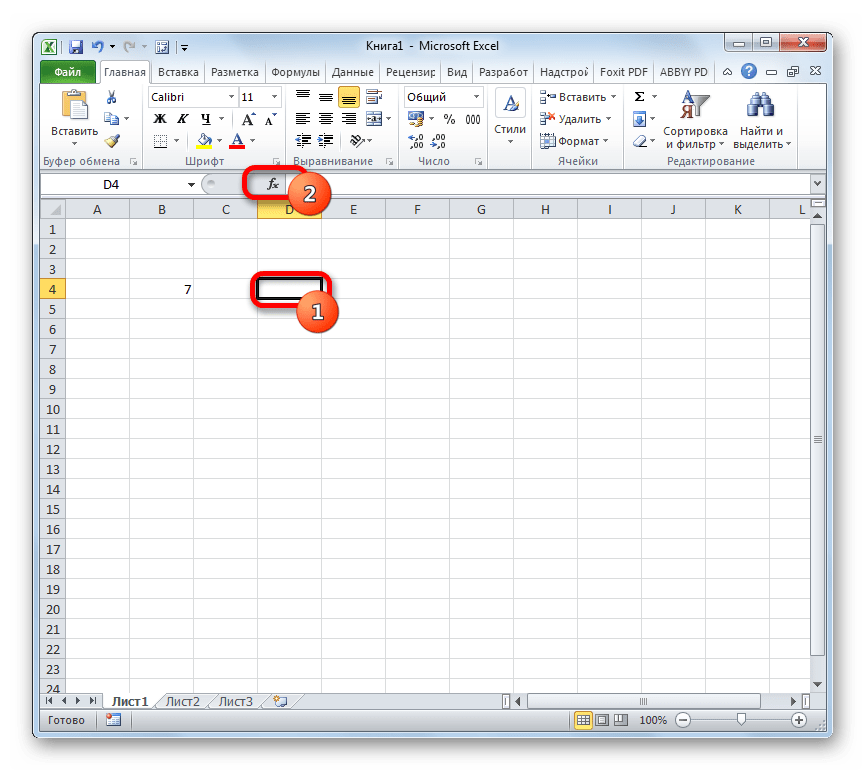
- Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.
- После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».
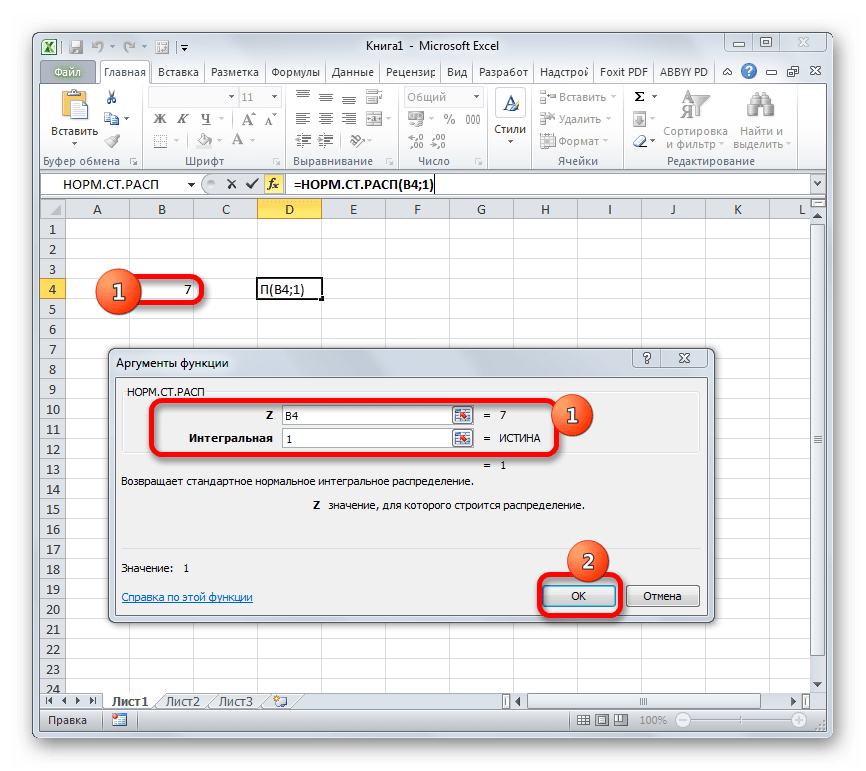
- Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».
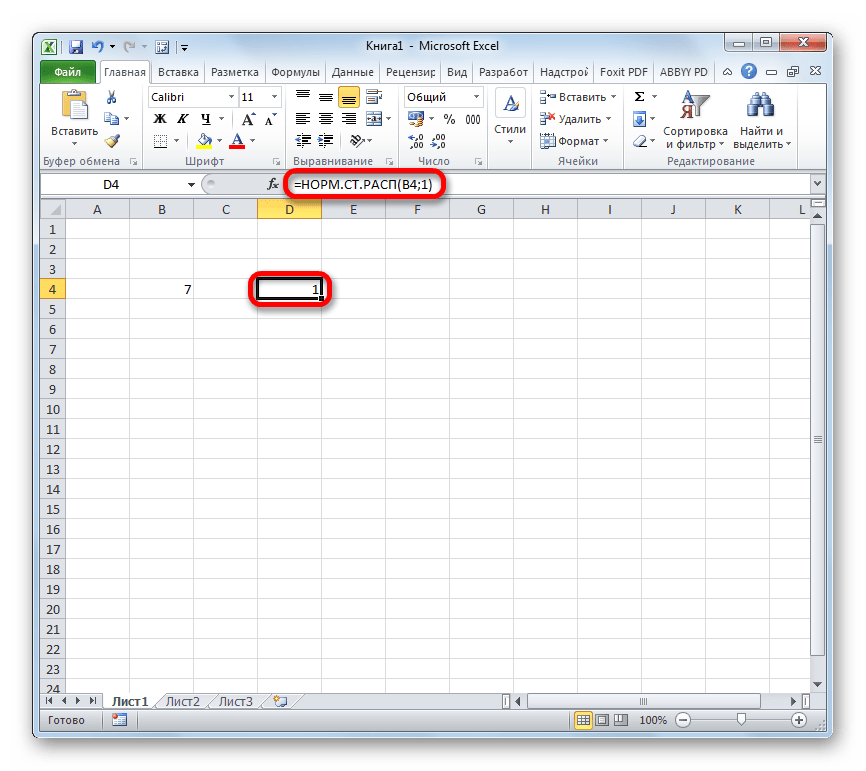
- После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.
- Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.
- Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.
Как видим, вычислить функцию Лапласа для конкретного заданного числового значения в программе Excel не составляет особенного труда. Для этих целей применяется стандартный оператор НОРМ.СТ.РАСП.
Еще статьи по данной теме:
Помогла ли Вам статья?
Таблица значений функции лапласа как пользоваться
Хотите получить точное значение функции Лапласа с большей точностью?
Например, Вам нужно найти Ф(x) при x=0.1234.
Тогда введите laplace(0.1234) в форму:
Вы получите результат:
Получается, что таблица нужна была раньше, когда не было калькулятора значений функции Лапласа.
Если всё же нужна таблица, то воспользуйтесь таблицей из excel ниже:
Таблица значений функции лапласа как пользоваться
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит ровно k раз (последовательность не важна), приближенно равна (при этом чем больше n, тем точнее вероятность):
Значения функции находятся в таблице для функции ф (х).
Важно помнить, что функция ф (х) — четная
=> ф (-х) = ф (х).
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна:
Для нахождения значений используют таблицу функции Лапласа для х:
0 , если же х>5, то автоматически Ф(х) = 0,5.
Функции Лапласа нечетная, т.е. Ф (-х) = — Ф(х).
Задача 1. Найдите вероятность того, что число зачисленных абитуриентов в институт психологии равно 86 из 250, подавших заявления. если вероятность зачисления для каждого абитуриента равна 0,35.
Решение
По условию задачи: р = 0.35; q = 0,65; n = 250;k = 86. В связи с тем, что n = 250 достаточно большое число, то целесообразней воспользоваться локальной теоремой Лапласа:
По таблице № 1 значений функции Лапласа найдем значение при х = 0,2, т.е. ф (х) = 0,391.
Тогда вероятность зачисления 86 абитуриентов в институт психологии равна
Ответ: 0,052.
Задача 2. Известно, что вероятность появления в семье мальчика равна 40 %. Сколько семей необходимо опросить, чтобы с вероятностью 0,75 утверждать, что в этих семьях родились мальчики, если всего в опросе участвовало 150 детей?
Решение
По условию задачи: n = 150; р = 0,4; q = 0,6.
Тогда, пусть было опрошено а– семей. Чтобы найти неизвестное а, при условии, что n p q > 10, воспользуемся интегральной теоремой Лапласа:
В результате, получаем неравенство:
Из таблицы № 2 для функции Лапласа получаем соответствующие значения, при Ф(х) > 0,25, то х > 0,67. Тогда неравенство принимает вид:
Следовательно, необходимо будет опросить 62 семьи, чтобы с вероятностью 0,75 утверждать, что в каждой из них ребенок – мальчик.
Ответ: 62.
Задача 3. Вероятность встретить на улице в солнечный день человека с зонтом равна 0,01. Чему равна вероятность того, что из 1 000 встречных мимо вас пройдет не более 4 человек с зонтами.
Решение
Так как события А0; А1;А2;А3;А4 несовместны, то соответственно вероятность события. А есть:
Ответ: 0,777.
Пользоваться таблицей несложно: вначале смотрим на столбец, а потом на строку, например, Ф(0,22) = 0,3894; Ф(2,99) = 0,0046.
Таблица значений функции Лапласа
Таблица значений функции Лапласа используется в теории вероятности довольно часто. В данном разделе описываюся случаи, в которых необходимо использовать значения таблицы. Разбираются примеры и прикладывается сама таблица значений.
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0 | 0 | 0,5 | 0,19146 | 1 | 0,34134 | 1,5 | 0,43319 | 2 | 0,47725 | 3 | 0,49865 |
| 0,01 | 0,00399 | 0,51 | 0,19497 | 1,01 | 0,34375 | 1,51 | 0,43448 | 2,02 | 0,47831 | 3,05 | 0,49886 |
| 0,02 | 0,00798 | 0,52 | 0,19847 | 1,02 | 0,34614 | 1,52 | 0,43574 | 2,04 | 0,47932 | 3,1 | 0,49903 |
| 0,03 | 0,01197 | 0,53 | 0,20194 | 1,03 | 0,34849 | 1,53 | 0,43699 | 2,06 | 0,4803 | 3,15 | 0,49918 |
| 0,04 | 0,01595 | 0,54 | 0,2054 | 1,04 | 0,35083 | 1,54 | 0,43822 | 2,08 | 0,48124 | 3,2 | 0,49931 |
| 0,05 | 0,01994 | 0,55 | 0,20884 | 1,05 | 0,35314 | 1,55 | 0,43943 | 2,1 | 0,48214 | 3,25 | 0,49942 |
| 0,06 | 0,02392 | 0,56 | 0,21226 | 1,06 | 0,35543 | 1,56 | 0,44062 | 2,12 | 0,483 | 3,3 | 0,49952 |
| 0,07 | 0,0279 | 0,57 | 0,21566 | 1,07 | 0,35769 | 1,57 | 0,44179 | 2,14 | 0,48382 | 3,35 | 0,4996 |
| 0,08 | 0,03188 | 0,58 | 0,21904 | 1,08 | 0,35993 | 1,58 | 0,44295 | 2,16 | 0,48461 | 3,4 | 0,49966 |
| 0,09 | 0,03586 | 0,59 | 0,2224 | 1,09 | 0,36214 | 1,59 | 0,44408 | 2,18 | 0,48537 | 3,45 | 0,49972 |
| 0,1 | 0,03983 | 0,6 | 0,22575 | 1,1 | 0,36433 | 1,6 | 0,4452 | 2,2 | 0,4861 | 3,5 | 0,49977 |
| 0,11 | 0,0438 | 0,61 | 0,22907 | 1,11 | 0,3665 | 1,61 | 0,4463 | 2,22 | 0,48679 | 3,55 | 0,49981 |
| 0,12 | 0,04776 | 0,62 | 0,23237 | 1,12 | 0,36864 | 1,62 | 0,44738 | 2,24 | 0,48745 | 3,6 | 0,49984 |
| 0,13 | 0,05172 | 0,63 | 0,23565 | 1,13 | 0,37076 | 1,63 | 0,44845 | 2,26 | 0,48809 | 3,65 | 0,49987 |
| 0,14 | 0,05567 | 0,64 | 0,23891 | 1,14 | 0,37286 | 1,64 | 0,4495 | 2,28 | 0,4887 | 3,7 | 0,49989 |
| 0,15 | 0,05962 | 0,65 | 0,24215 | 1,15 | 0,37493 | 1,65 | 0,45053 | 2,3 | 0,48928 | 3,75 | 0,49991 |
| 0,16 | 0,06356 | 0,66 | 0,24537 | 1,16 | 0,37698 | 1,66 | 0,45154 | 2,32 | 0,48983 | 3,8 | 0,49993 |
| 0,17 | 0,06749 | 0,67 | 0,24857 | 1,17 | 0,379 | 1,67 | 0,45254 | 2,34 | 0,49036 | 3,85 | 0,49994 |
| 0,18 | 0,07142 | 0,68 | 0,25175 | 1,18 | 0,381 | 1,68 | 0,45352 | 2,36 | 0,49086 | 3,9 | 0,49995 |
| 0,19 | 0,07535 | 0,69 | 0,2549 | 1,19 | 0,38298 | 1,69 | 0,45449 | 2,38 | 0,49134 | 3,95 | 0,49996 |
| 0,2 | 0,07926 | 0,7 | 0,25804 | 1,2 | 0,38493 | 1,7 | 0,45543 | 2,4 | 0,4918 | 4 | 0,49997 |
| 0,21 | 0,08317 | 0,71 | 0,26115 | 1,21 | 0,38686 | 1,71 | 0,45637 | 2,42 | 0,49224 | 4,05 | 0,49997 |
| 0,22 | 0,08706 | 0,72 | 0,26424 | 1,22 | 0,38877 | 1,72 | 0,45728 | 2,44 | 0,49266 | 4,1 | 0,49998 |
| 0,23 | 0,09095 | 0,73 | 0,2673 | 1,23 | 0,39065 | 1,73 | 0,45818 | 2,46 | 0,49305 | 4,15 | 0,49998 |
| 0,24 | 0,09483 | 0,74 | 0,27035 | 1,24 | 0,39251 | 1,74 | 0,45907 | 2,48 | 0,49343 | 4,2 | 0,49999 |
| 0,25 | 0,09871 | 0,75 | 0,27337 | 1,25 | 0,39435 | 1,75 | 0,45994 | 2,5 | 0,49379 | 4,25 | 0,49999 |
| 0,26 | 0,10257 | 0,76 | 0,27637 | 1,26 | 0,39617 | 1,76 | 0,4608 | 2,52 | 0,49413 | 4,3 | 0,49999 |
| 0,27 | 0,10642 | 0,77 | 0,27935 | 1,27 | 0,39796 | 1,77 | 0,46164 | 2,54 | 0,49446 | 4,35 | 0,49999 |
| 0,28 | 0,11026 | 0,78 | 0,2823 | 1,28 | 0,39973 | 1,78 | 0,46246 | 2,56 | 0,49477 | 4,4 | 0,49999 |
| 0,29 | 0,11409 | 0,79 | 0,28524 | 1,29 | 0,40147 | 1,79 | 0,46327 | 2,58 | 0,49506 | 4,45 | 0,5 |
| 0,3 | 0,11791 | 0,8 | 0,28814 | 1,3 | 0,4032 | 1,8 | 0,46407 | 2,6 | 0,49534 | 4,5 | 0,5 |
| 0,31 | 0,12172 | 0,81 | 0,29103 | 1,31 | 0,4049 | 1,81 | 0,46485 | 2,62 | 0,4956 | 4,55 | 0,5 |
| 0,32 | 0,12552 | 0,82 | 0,29389 | 1,32 | 0,40658 | 1,82 | 0,46562 | 2,64 | 0,49585 | 4,6 | 0,5 |
| 0,33 | 0,1293 | 0,83 | 0,29673 | 1,33 | 0,40824 | 1,83 | 0,46638 | 2,66 | 0,49609 | 4,65 | 0,5 |
| 0,34 | 0,13307 | 0,84 | 0,29955 | 1,34 | 0,40988 | 1,84 | 0,46712 | 2,68 | 0,49632 | 4,7 | 0,5 |
| 0,35 | 0,13683 | 0,85 | 0,30234 | 1,35 | 0,41149 | 1,85 | 0,46784 | 2,7 | 0,49653 | 4,75 | 0,5 |
| 0,36 | 0,14058 | 0,86 | 0,30511 | 1,36 | 0,41309 | 1,86 | 0,46856 | 2,72 | 0,49674 | 4,8 | 0,5 |
| 0,37 | 0,14431 | 0,87 | 0,30785 | 1,37 | 0,41466 | 1,87 | 0,46926 | 2,74 | 0,49693 | 4,85 | 0,5 |
| 0,38 | 0,14803 | 0,88 | 0,31057 | 1,38 | 0,41621 | 1,88 | 0,46995 | 2,76 | 0,49711 | 4,9 | 0,5 |
| 0,39 | 0,15173 | 0,89 | 0,31327 | 1,39 | 0,41774 | 1,89 | 0,47062 | 2,78 | 0,49728 | 4,95 | 0,5 |
| 0,4 | 0,15542 | 0,9 | 0,31594 | 1,4 | 0,41924 | 1,9 | 0,47128 | 2,8 | 0,49744 | 5 | 0,5 |
| 0,41 | 0,1591 | 0,91 | 0,31859 | 1,41 | 0,42073 | 1,91 | 0,47193 | 2,82 | 0,4976 | ||
| 0,42 | 0,16276 | 0,92 | 0,32121 | 1,42 | 0,4222 | 1,92 | 0,47257 | 2,84 | 0,49774 | ||
| 0,43 | 0,1664 | 0,93 | 0,32381 | 1,43 | 0,42364 | 1,93 | 0,4732 | 2,86 | 0,49788 | ||
| 0,44 | 0,17003 | 0,94 | 0,32639 | 1,44 | 0,42507 | 1,94 | 0,47381 | 2,88 | 0,49801 | ||
| 0,45 | 0,17364 | 0,95 | 0,32894 | 1,45 | 0,42647 | 1,95 | 0,47441 | 2,9 | 0,49813 | ||
| 0,46 | 0,17724 | 0,96 | 0,33147 | 1,46 | 0,42785 | 1,96 | 0,475 | 2,92 | 0,49825 | ||
| 0,47 | 0,18082 | 0,97 | 0,33398 | 1,47 | 0,42922 | 1,97 | 0,47558 | 2,94 | 0,49836 | ||
| 0,48 | 0,18439 | 0,98 | 0,33646 | 1,48 | 0,43056 | 1,98 | 0,47615 | 2,96 | 0,49846 | ||
| 0,49 | 0,18793 | 0,99 | 0,33891 | 1,49 | 0,43189 | 1,99 | 0,4767 | 2,98 | 0,49856 |
Рассмотрим примеры применения данной таблицы на конкретных примерах: