Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 – 3x^2 – 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 – 3x^2 – 4)’ = 6x^2 – 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 – 6x = 0 $$ $$ 6x(x – 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 – 3 cdot 0^2 – 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 – 3 cdot 1^2 – 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 – 3 cdot 2^2 – 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
![]()
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
![]()
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.

В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: – 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.

В точке производная равна нулю и меняет знак с “+” на “-“. Значит, x = – 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.

Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
![]() и
и ![]() Значит, наименьшее значение функции на отрезке
Значит, наименьшее значение функции на отрезке достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если ![]() то
то ![]() Если
Если ![]() , то
, то ![]()
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
![]()
![]()

При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
![]()
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
![]() При
При знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
![]()
![]()
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. ![]() — нет решений.
— нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
![]() для всех
для всех , и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции 
 , то функция
, то функция  возрастает на этом промежутке.
возрастает на этом промежутке.
Если на промежутке I производная функции 
 , то функция
, то функция  убывает на этом промежутке.
убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с “+” на “-“.
В точке минимума функции производная меняет знак с “-” на “+”.
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию  . График этой функции выглядит так:
. График этой функции выглядит так:
 В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;0}{]} {x}{in}delim{[}{-1;0}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_8d4ac2719ab1423f162f9779293da981.png)
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка:  , а наименьшее – в левом:
, а наименьшее – в левом:  .
.
2. Рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;1}{]} {x}{in}delim{[}{-1;1}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_fbae2bb0d6eaada0859d11280c8d6a23.png)
Очевидно, что наибольшее значение функция принимает в точке максимума  , а наименьшее – в одном из концов отрезка, то есть надо найти значения
, а наименьшее – в одном из концов отрезка, то есть надо найти значения  и
и  и выбрать из них наименьшее.
и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;2}{]} {x}{in}delim{[}{-1;2}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_3bae536560f42bd0f0875793dd5a92e2.png) , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть
, то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть  и
и  .
.
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть  и
и  .
.
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции  – множество действительных чисел.
– множество действительных чисел.
2. 
3.  , если
, если  или
или 
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание – убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1. Задание B15 (№ 26695)
Найдите наибольшее значение функции  на отрезке
на отрезке ![[-{pi}/2;0] [-{pi}/2;0]](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_9a7375f1961203c68e53ad122ab84a77.png) .
.
1. Функция  определена при всех действительных значениях х
определена при всех действительных значениях х
2. 
3. 
 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции  на отрезке [
на отрезке [ ].
].
1. ОДЗ функции 

2. 
Производная равна нулю при  , однако, в этих точках она не меняет знак:
, однако, в этих точках она не меняет знак:

 , следовательно,
, следовательно, 
 , значит,
, значит, 
 , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция
, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, при
возрастает и принимает наибольшее значение в правом конце промежутка, при  .
.
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Найдите наименьшее значение функции  на отрезке [
на отрезке [ ].
].
1. ОДЗ функции  :
: 

2. 
3. 
 ,
, 
Расположим корни этого уравнения на тригонометрической окружности.

Промежутку ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png) принадлежат два числа:
принадлежат два числа:  и
и 
Расставим знаки. Для этого определим знак производной в точке х=0: 
 . При переходе через точки
. При переходе через точки  и
и  производная меняет знак.
производная меняет знак.

Изобразим смену знаков производной функции  на координатной прямой:
на координатной прямой:

Очевидно, что точка  является точкой минимума ( в ней производная меняет знак с “-” на “+”), и чтобы найти наименьшее значение функции
является точкой минимума ( в ней производная меняет знак с “-” на “+”), и чтобы найти наименьшее значение функции  на отрезке
на отрезке ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png) , нужно сравнить значения функции в точке минимума и в левом конце отрезка,
, нужно сравнить значения функции в точке минимума и в левом конце отрезка,  .
.
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а  таковым на является, следовательно подставим в уравнение функции
таковым на является, следовательно подставим в уравнение функции 

Ответ: -1
Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.



Нахождение наибольшего и наименьшего значений функции, непрерывной на отрезке
П усть
усть
![]()
– функция, непрерывная на некотором
отрезке
![]()
оси ох
(рис. 5)
Ставится задача:
указать схему нахождения тех точек
отрезка
![]()
оси ох,
в которых функция
![]()
достигает своего наибольшего значения
![]()
и своего наименьшего значения
![]() ,
,
и найти эти
![]()
и
![]() .
.
Сразу отметим, что
такие точки на отрезке
![]()
заведомо существуют (это доказано). А
вот на интервале
![]()
их может и не быть. То есть на интервале
функция своих наибольшего и наименьшего
значений может и не иметь. Например,
функция
![]()
на отрезке
![]()
свое наименьшее значение
![]()
достигает в точке
![]() ,
,
а свое наибольшее значение
![]()
достигает в точке
![]() .
.
А вот на интервале
![]()
своих наибольшего и наименьшего значений
функция
![]() ,
,
очевидно, не имеет (не достигает).
Вернемся к рис. 5,
на котором изображена произвольная
непрерывная на отрезке
![]()
функция
![]() .
.
Здесь
![]()
достигается функцией на конце a
отрезка
![]() ,
,
а
![]() –
–
в точке x1,
являющейся одной из точек минимума
функции. И вообще, очевидно, что и при
любой другой форме графика непрерывной
функции наибольшее и наименьшее значения
достигаются ею на отрезке
![]()
или в её точках экстремума, содержащихся
на этом отрезке, или на концах отрезка.
Отсюда вытекает следующая
схема нахождения
![]()
и
![]()
функции
![]()
на отрезке
![]() :
:
-
Находим производную
 .
. -
Находим принадлежащие
отрезку

точки, подозрительные на экстремум. -
Не исследуя этих
точек, вычисляем значение функции
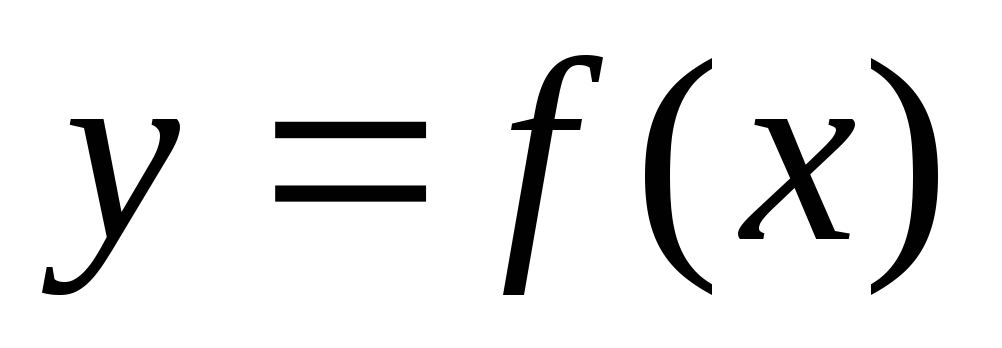
во всех найденных подозрительных
точках, а также на концах a
и b
отрезка
 .
.
Из всех найденных значений y
выбираем

и
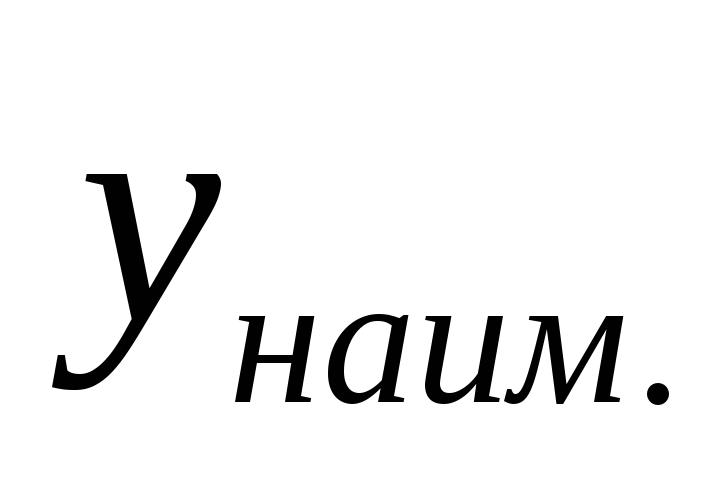 .
.
А заодно и устанавливаем, в каких точках
отрезка

эти

и

достигаются.
Пример 3.
На отрезке
![]()
найти наибольшее
![]()
и наименьшее
![]()
значения функции
![]() .
.
Решение.
Реализуем изложенную выше схему.
-
Найдем
 :
:
![]() .
.
-
Найдем на отрезке
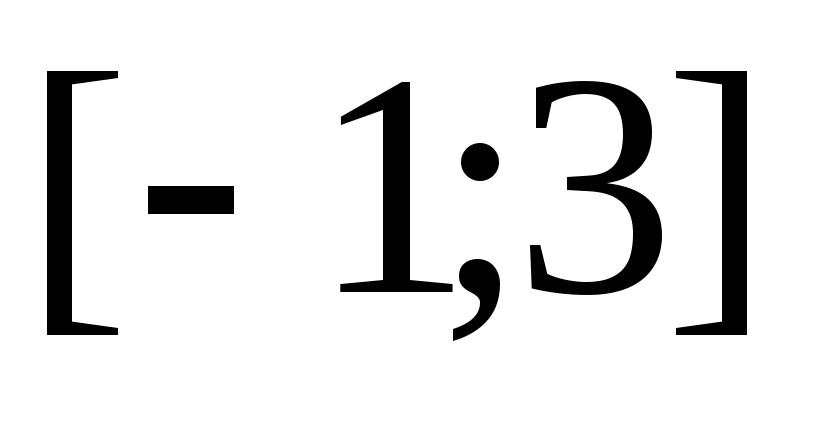
точки (значения x),
подозрительные на экстремум:
а)
![]() .
.
б)
![]()
не существует
таких x
нет.
На отрезке
![]()
содержатся лишь две подозрительные на
экстремум точки: это
![]()
и
![]() .
.
-
Вычисляем значении
функции

в обеих найденных подозрительных
точках, а также на концах отрезка, и
выберем из найденных значений функции
наибольшее и наименьшее:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Ответ:
![]() ;
;
![]() .
.
Выпуклость и вогнутость функции. Точки перегиба
Направление
выпуклости кривой является важной
характеристикой ее формы.
Понятие о выпуклости,
вогнутости и точках перегиба функции
![]()
дадим, исходя из рис. 6. На этом рисунке
изображен график функции, выпуклой на
интервале
![]() ,
,
вогнутой на интервале
![]() ,
,
и y
которой точка x0,
разделяющая интервалы выпуклости и
вогнутости, есть точка
перегиба функции.
Кстати, точка M0
называется точкой
перегиба графика функции
(не путать точку перегиба функции x0
и точку
перегиба её графика M0).
Интервалы выпуклости, вогнутости и
точки перегиба функции – важные
характеристики любой функции, поэтому
полезно уметь их находить.
Рассмотрим подробнее
функцию
![]()
на ее интервале выпуклости
![]()
(рис. 7 (а)) и на ее интервале вогнутости
(рис. 7 (б)).

Для выпуклой
функции (рис. 7 (а)) касательная к ее
графику в любой его точке расположена
выше графика, причем с увеличением
абсциссы x
точки касания эта касательная
поворачивается по часовой стрелке. Это
значит, что с увеличением x
угол
![]() наклона
наклона
касательной к оси ох
уменьшается. Но тогда уменьшается и
угловой коэффициент касательной
![]() .
.
А значит, с увеличением x
уменьшается (убывает) равная ему
производная функции
![]() .
.
Но если некая функция убывает, то, как
мы знаем, ее производная отрицательна.
Значит,
![]()
на всем интервале
![]()
выпуклости функции
![]() .
.
Аналогичное
рассуждение приводит к выводу, что если
функция
![]()
вогнута на некотором интервале
![]()
(см. рис. 7 (б)), то для любого x
из этого интервала
![]()
(проведите это рассуждение самостоятельно).
Верно, естественно,
и обратное: если на некотором интервале
оси ох
вторая производная функции положительна,
то функция вогнута на этом интервале.
А если эта производная отрицательна –
то функция выпукла на указанном интервале.
Определение 3.
Кривая обращена выпуклостью
вверх на
интервале
![]() ,
,
если все точки кривой лежат ниже любой
ее касательной на этом интервале.
Определение 4.
Кривая обращена выпуклостью
вниз на
интервале![]() ,
,
если все точки кривой лежат выше любой
ее касательной на этом интервале.
Кривая, обращенная
выпуклостью вверх, будет называть
выпуклой,
а обращенную выпуклостью вниз – вогнутой.
Теорема 5: Если
во всех точках интервала
![]()
вторая производная f(x)
отрицательна, т.е.
![]() ,
,
то кривая y=f(x)
на этом интервале обращена выпуклостью
вверх ( кривая выпукла )
Доказательство.
Возьмем в интервале
![]()
произвольную точку х=х0
и проведем касательную к кривой в точке
с абсциссой х=х0.Теорема
будет доказана, если мы установим, что
все точки кривой на интервале
![]()
лежат ниже этой касательной, т.е. что
ордината любой точки кривой y=f(x)
меньше
ординаты y
касательной при одном и том же значении
х.
Уравнение кривой
имеет вид
y=f(x).
Уравнение касательной
к кривой в точке х=х0
имеет вид
![]()
Откуда следует,
что разность ординат кривой и касательной
при одном и том же значении х
равна
![]()
Применяя теорему
Лагранжа к разности
![]() ,
,
получим:
![]() ,
,
( где с
лежит между
х0
и х
). К выражению, стоящему в квадратных
скобках, снова применим теорему Лагранжа,
тогда
![]() .
.
( где с1
лежит между
х0
и с
).
Рассмотрим два
случая:
-
Пусть х>x0.
Тогда x0<c1<c<x,
поскольку
 .
.
Учитывая этот факт и условие
 ,
,
получим
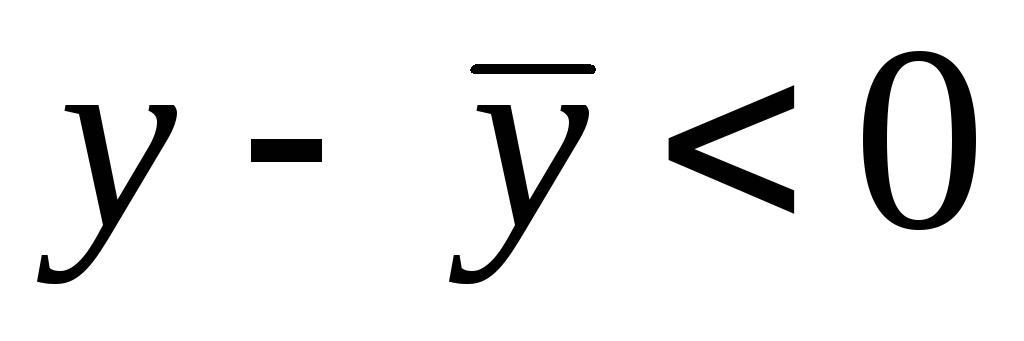 .
. -
Пусть х<x0.
Тогда x<c<c1<x0,
поскольку
 .
.
Учитывая этот факт и условие
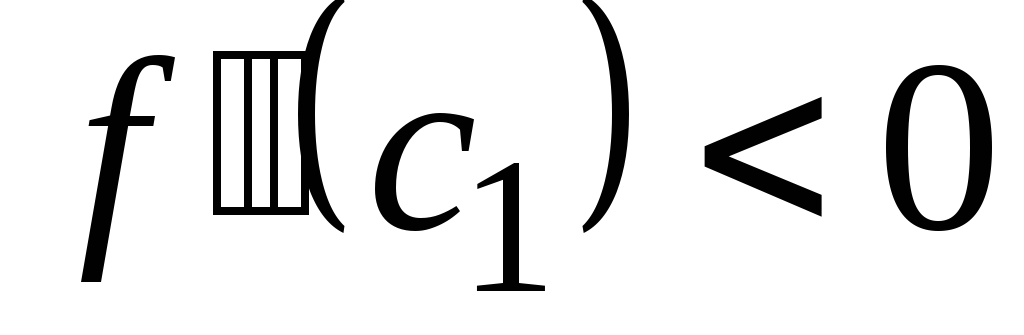 ,
,
получим
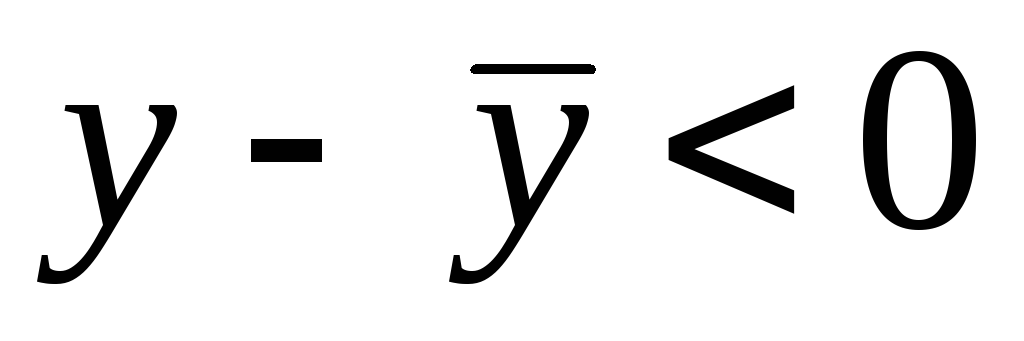 .
.
Таким образом, мы
доказали, что любая точка кривой лежит
ниже касательной к кривой, каковы бы ни
были значения х
и х0
на интервале
![]() .
.
Что и означает, что кривая выпукла.
Теорема доказана.
Аналогично
доказывается теорема для случая вогнутой
функции.
Теорема 6: Если
во всех точках интервала
![]()
вторая производная f(x)
положительна, т.е.
![]() ,
,
то кривая y=f(x)
на этом интервале обращена выпуклостью
вниз ( кривая вогнута )
Теперь перейдем
к точкам перегиба функции. Так как эти
точки разграничивают интервалы выпуклости
и вогнутости и, следовательно, не
принадлежат ни тем, ни другим, то в точках
перегиба вторая производная функции
не может быть ни положительной, ни
отрицательной. А значит, в этих точках
она или равна нулю, или не существует.
Но не все точки x,
в которых
![]()
или
![]()
не существует, непременно должны быть
точками перегиба. Точками перегиба
будут лишь те из них, в которых вторая
производная
![]()
меняет знак (с (+) на (–) или с (–) на (+)).
Таким образом, точки оси ох,
в которых
![]()
или
![]()
не существует, являются лишь подозрительными
на перегиб.
Окончательное выяснение сути этих точек
производится после исследования знака
второй производной слева и справа от
каждой из них. Справедлива следующая
Теорема 7. Пусть
кривая определяется уравнением
y=f(x).
Если
![]()
или
![]()
не существует и при переходе через
значение x=a
производная
![]()
меняет знак, то точка кривой с абсциссой
x=a
есть точка перегиба.
Из всего сказанного
вытекает
схема исследования
функции
![]()
на выпуклость-вогнутость
и точки
перегиба:
-
Находим область
определения функции, а заодно устанавливаем
интервалы ее непрерывности и точки
разрыва (стандартное начало любого
исследования функции). -
Находим вторую
производную
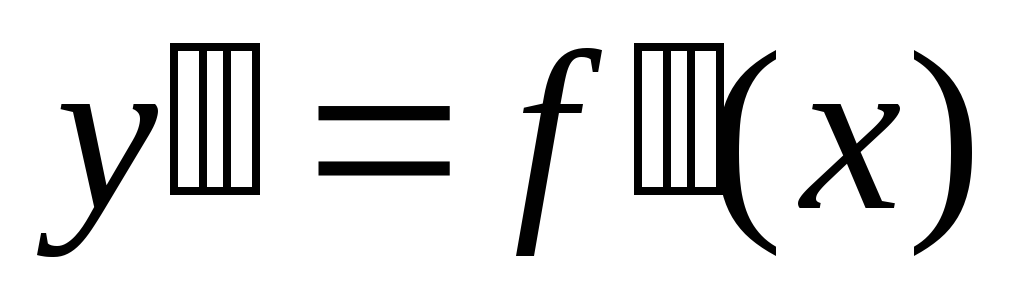 .
. -
Находим точки
(значения x),
подозрительные на перегиб. То есть
находим те точки (значения x),
в которых вторая производная функции
или равна нулю, или не существует:
а)
![]()
б)
![]()
не существует
![]()
-
Наносим все
найденные подозрительные на перегиб
точки на область определения функции
(на ось ох)
и отмечаем (например, дугами) интервалы,
на которые разобьется этими дугами
область определения функции. В каждом
из этих интервалов выясняем знак второй
производной
 .
.
По установленным знакам этой производной
отмечаем интервалы выпуклости и
вогнутости функции ((–) – выпуклость,
(+) – вогнутость), а также точки перегиба
функции. -
Вычисляем значения
функции

во всех найденных точках ее перегиба
и находим тем самым точки перегиба
графика функции.
Пример 4.
Исследовать на выпуклость-вогнутость
и точки перегиба функцию
![]()
(в примере 2 она уже исследовалась на
возрастание-убывание и точки экстремума).
Решение.
Реализуем изложенную выше схему.
-
Функция

определена, а следовательно и непрерывна
для любых x
от

до
 .
. -
Найдем
 :
:
![]() .
.
-
Найдем точки
(значения x),
подозрительные на перегиб:
а)
![]() .
.
б)
![]()
не существует
таких x
нет.
-
Нанесем на ось ох
найденную подозрительную на перегиб
точку
 .
.
Ось ох
(область определения функции) разобьется
этой точкой на два интервала:

Определяем знаки
второй производной
![]()
в этих интервалах (они отмечены на рис.
выше). Тем самым устанавливаем интервалы
выпуклости (знак
![]() )
)
и вогнутости (знак
![]() )
)
, а также устанавливаем, что
![]()
– точка перегиба функции.
-
Вычисляем значение
функции

в точке ее перегиба

и тем самым определим точку

перегиба графика функции (она указана
на рис. 4).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Наибольшее и наименьшее значения функции с примерами решения
От максимумов и минимумов функции следует отличать её наибольшее и наименьшее значения на промежутке. Функция может иметь несколько максимумов (минимумов) на некотором промежутке (рис. 91), но не более одного наибольшего (наименьшего) значения. Функция может не иметь максимума (минимума) на промежутке, но иметь наибольшее (наименьшее) значение.
Например функция, график которой изображён на рисунке 91, наибольшее значение имеет в точке 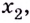
Наибольшее и наименьшее значения функции тесно связаны с её областью значений. Если область значений непрерывной функции — промежуток 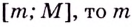 наименьшее значение данной функции,
наименьшее значение данной функции, 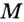 — наибольшее её значение.
— наибольшее её значение.
Поскольку непрерывная функция наибольшее и наименьшее значения может иметь только в точках экстремума или на концах отрезка, то для нахождения этих значений пользуются таким правилом.
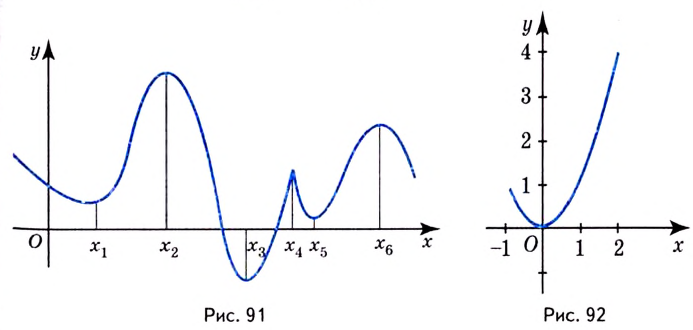
Чтобы найти наибольшее и наименьшее значения непрерывной функции 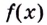 на промежутке
на промежутке 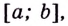 нужно вычислить её значения
нужно вычислить её значения 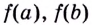 на концах данного промежутка и в критических точках, принадлежащих этому промежутку, а потом выбрать из них наибольшее и наименьшее.
на концах данного промежутка и в критических точках, принадлежащих этому промежутку, а потом выбрать из них наибольшее и наименьшее.
Записывают так: 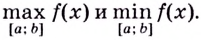
Пример №1
Найдите наибольшее и наименьшее значения функции 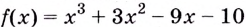 на промежутке
на промежутке 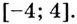
Решение:
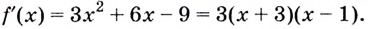 Критические точки:
Критические точки: 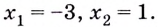
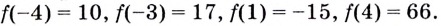
Из этих четырёх значений функции наименьшим является -15, а наибольшим — 66.
Ответ, 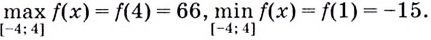
Пример №2
Найдите наибольшее и наименьшее значения функции 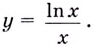
Решение:
Областью определения функции является промежуток 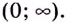
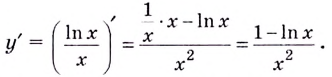
Если 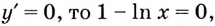 отсюда
отсюда 
Если 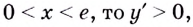 а если
а если 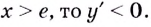 Следовательно,
Следовательно,  — точка максимума.
— точка максимума.
Поскольку на промежутке 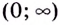 функция имеет только одну критическую точку
функция имеет только одну критическую точку 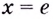 и эта точка является точкой максимума, то наибольшее значение функция принимает именно в этой точке и оно равно
и эта точка является точкой максимума, то наибольшее значение функция принимает именно в этой точке и оно равно 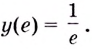 Наименьшего значения функция не имеет.
Наименьшего значения функция не имеет.
Ответ, 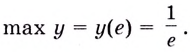 Наименьшего значения функция не имеет.
Наименьшего значения функция не имеет.
К нахождению наибольшего или наименьшего значений функции сводится решение многих прикладных задач.
Пример №3
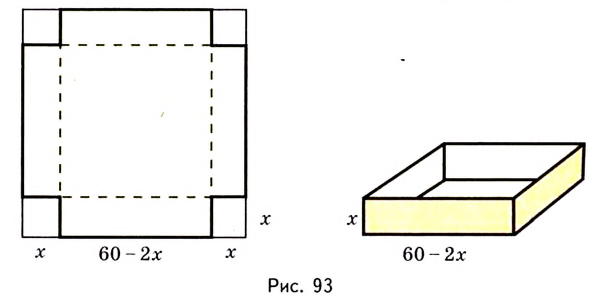
Есть квадратный лист жести со стороной 60 см. Найдите размеры квадратов, которые надо вырезать в углах данного листа, чтобы из полученной заготовки сделать коробку наибольшего объёма {рис. 93).
Решение:
Чтобы получить коробку (в форме прямоугольного параллелепипеда), надо вырезать равные квадраты в углах листа. Пусть 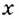 — длина стороны такого квадрата. Тогда высота коробки равна
— длина стороны такого квадрата. Тогда высота коробки равна 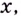 а сторона основания
а сторона основания 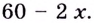 Объём коробки
Объём коробки 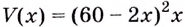 — функция от
— функция от 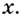
Надо исследовать математическую модель задачи: при каком значении 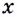 : функция
: функция 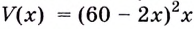 на промежутке
на промежутке 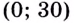 принимает наибольшее значение.
принимает наибольшее значение.
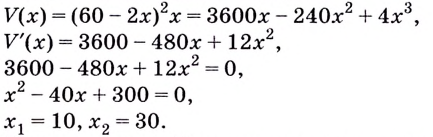
Значение  не принадлежит промежутку
не принадлежит промежутку 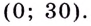 Поэтому
Поэтому 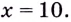
Поскольку при 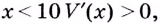 а при
а при 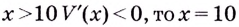 — точка максимума. Итак, в этой точке функция
— точка максимума. Итак, в этой точке функция 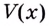 принимает наибольшее значение.
принимает наибольшее значение.
Ответ. Надо вырезать квадраты, стороны которых равны 10 см.
- Заказать решение задач по высшей математике
Пример №4
Найдите область значений функции 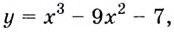 если
если 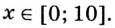
Решение:
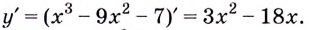 Найдём критические точки:
Найдём критические точки: 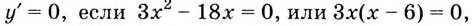 отсюда
отсюда 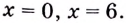
Найдём значение функции на концах промежутка 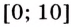 и в критических точках:
и в критических точках: 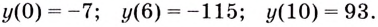
Заданная функция непрерывна, её наибольшее значение 93, а наименьшее -115, значит, область её значений — отрезок 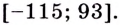
Ответ. 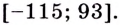
Пример №5
Найдите кратчайшее расстояние от точки 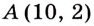 до графика функции
до графика функции 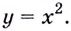
Решение:
Пусть ближайшая к 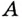 точка
точка 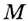 графика функции имеет абсциссу
графика функции имеет абсциссу 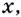 её ордината равна
её ордината равна 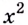 (рис. 94). Найдём квадрат расстояния между точками
(рис. 94). Найдём квадрат расстояния между точками 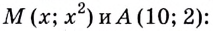
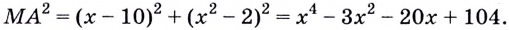 Длина расстояния
Длина расстояния 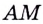 наименьшая, когда её квадрат наименьший. Итак, найдём наименьшее значение функции
наименьшая, когда её квадрат наименьший. Итак, найдём наименьшее значение функции 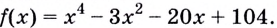
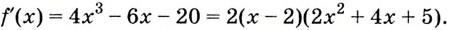
Уравнение 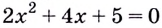 действительных корней не имеет, поэтому функция
действительных корней не имеет, поэтому функция 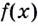 имеет одну критическую точку
имеет одну критическую точку 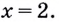 Если
Если 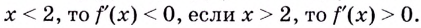 Следовательно,
Следовательно, 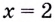 — точка минимума. В этой точке функция
— точка минимума. В этой точке функция 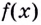 принимает наименьшее значение.
принимает наименьшее значение.
Наименьшее значение квадрата расстояния
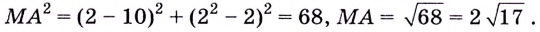
Ответ. 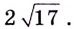
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Рациональная дробь
- Функция в математике
- Правило Лопиталя
- Вычисления в Mathematica с примерами

