ГЛАВА 10
ФУНКЦИИ ОТ МАТРИЦ
§ 10.1. ВЫЧИСЛЕНИЕ
ЗНАЧЕНИЙ ФУНКЦИЙ ОТ МАТРИЦ РАЗЛИЧНЫМИ
СПОСОБАМИ
Пусть
![]()
– минимальный многочлен матрицы А
степени
![]() .
.
Здесь
![]()
– кратность
![]()
как корня минимального многочлена
![]() .
.
Если
для функции f(λ)
существуют (т.е. имеют смысл) значения
![]()
![]() (10.1.1)
(10.1.1)
то
говорят, что функция
f(λ)
определена на спектре матрицы А,
и совокупность m
чисел (10.1.1) называют значениями
функции f(λ)
на спектре матрицы А.
Среди
всех многочленов, принимающих те же
значения на спектре матрицы А,
что и f(λ),
существует один и только один многочлен
r(λ),
имеющий степень, меньшую степени
минимального многочлена матрицы А.
Этот многочлен однозначно определяется
интерполяционными условиями
![]()
![]() (10.1.2)
(10.1.2)
и
называется интерполяционным
многочленом Лагранжа – Сильвестра
для функции f(λ)
на спектре матрицы А.
Его значение от матрицы А
по определению принимается за значение
функции f(λ)
от этой матрицы: f(A)
= r(A).
Заметим,
что если минимальный многочлен
![]()
матрицы А
не имеет кратных корней
![]() ,
,
то для того, чтобы f(A)
имело смысл, достаточно, чтобы функция
f(λ)
была определена в характеристических
точках
![]() .
.
Если же
![]()
имеет кратные корни, то в некоторых
характеристических точках должны быть
определены и производные от f(λ)
до известного порядка [см. соотношение
(10.1.2)].
Если
![]() ,
,
то минимальным многочленом матрицы А
будет
![]() .
.
Интерполяционный многочлен Лагранжа
– Сильвестра r(λ)
для функции f(λ)
в предположении существования значений
![]() ,
,
![]() ,…,
,…,![]()
определится равенством
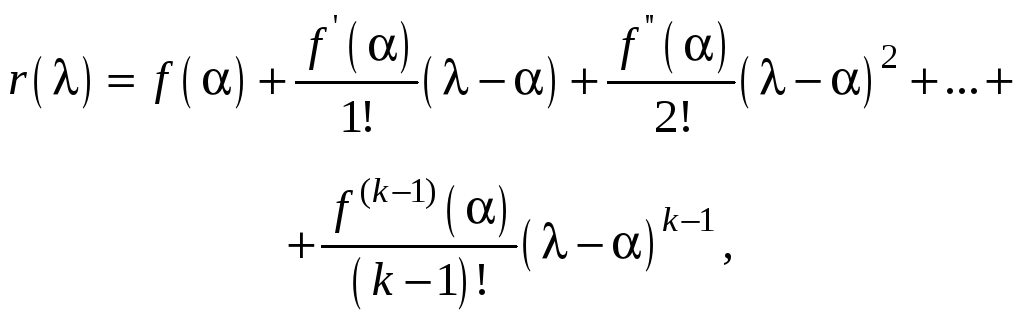
что
позволяет найти значение
![]() :
:
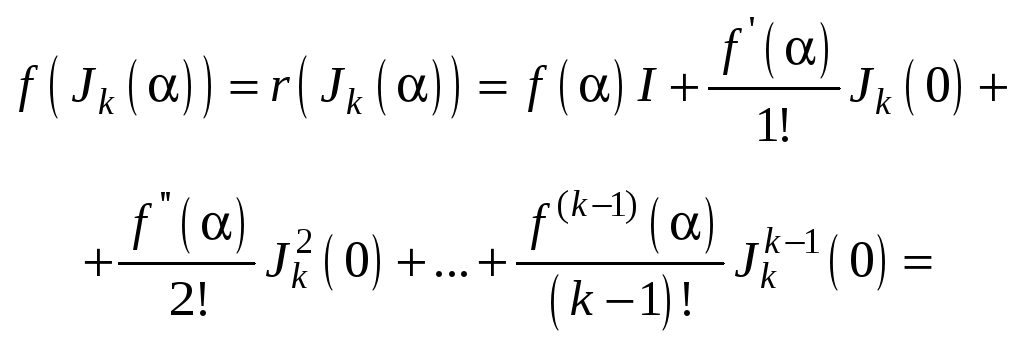
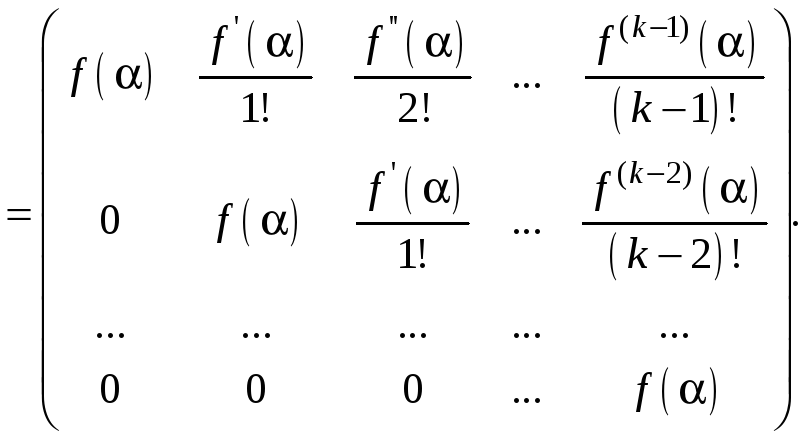 (10.1.3)
(10.1.3)
Подчеркнем
два важных для решения задач свойства
функций от матриц:
10.
Если две матрицы А
и В
подобны, причем
![]() ,
,
и для функции f(λ)
матрица f(А)
существует, то и матрица f(В)
существует и подобна f(А),
причем
![]() .
.
20.
Если
![]()
и функция f(λ)
определена на спектре матрицы А,
то
![]() .
.
Свойства
10,
20
наряду с результатом (10.1.3) используются
для вычисления значений функций от
матриц через жорданову нормальную
форму.
Пусть
функция f(λ)
определена на спектре матрицы А.
Тогда определена матрица f(А)
и, следовательно, существует интерполяционный
многочлен Лагранжа – Сильвестра r(λ).
Если
![]()
– минимальный многочлен матрицы А
и корни
![]()
различны между собой, то
![]()
![]()
(10.1.4)
где
![]() ,
,
(10.1.5)
а
коэффициенты
![]()
определяются из равенств
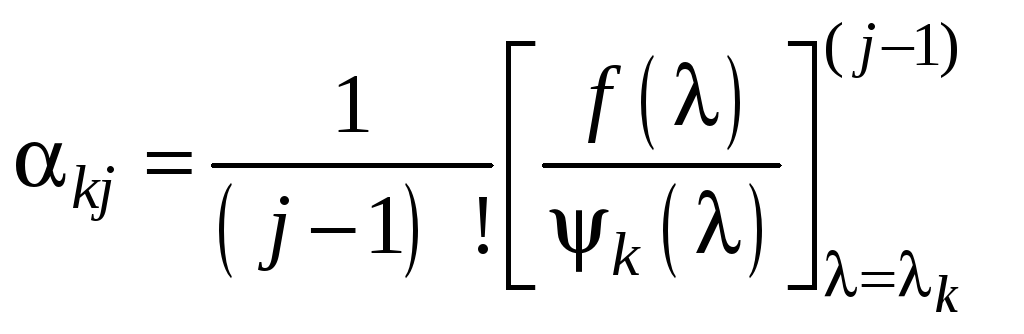
![]()
(10.1.6)
Заметим,
что выражение в квадратных скобках в
формуле (10.1.4) равно сумме первых
![]()
членов разложения в ряд Тейлора по
степеням разности
![]()
для функции
![]() .
.
Если
в формулу (10.1.4) для r(λ)
подставить выражения (10.1.6) для коэффициентов
![]() ,
,
раскрыть скобки и объединить члены,
содержащие
![]()
![]() ,
,
то ее можно записать в виде
![]()
![]() (10.1.7)
(10.1.7)
Из
равенства (10.1.7) следует основная
формула для f(A):
![]()
![]()
(10.1.8)
где
![]() .
.
(10.1.9)
Матрицы
![]() ,
,
называемые компонентами
матрицы А,
вполне определяются заданием матрицы
А
и не зависят от выбора функции f(λ).
В правой части формулы (10.1.8) функция
f(λ)
представлена только своими значениями
на спектре матрицы А.
Формула
(10.1.8) для f(А)
особенно удобна, когда требуется
вычислить несколько функций от одной
и той же матрицы. На практике компоненты
![]()
матрицы А
проще находить не по формуле (10.1.9), а из
системы, которая получится в результате
последовательной подстановки в (10.1.8)
вместо f(λ)
простейших линейно независимых
многочленов столько раз, сколько
содержится в (10.1.8) компонент
![]() .
.
Пример.
Вычислите
![]()
при помощи жордановой нормальной формы
матрицы А,
интерполяционного многочлена Лагранжа
– Сильвестра и основной формулы, если
![]() .
.
Решение.
Начнем с построения жордановой нормальной
формы J
матрицы А
и приводящей к ней матрицы Р.
Поскольку
![]() ,
,
матрица
А
имеет одно собственное значение
![]() .
.
Его алгебраическая кратность
![]() .
.
![]() .
.
(10.1.10)
Геометрическая
кратность
![]()
равна
![]() .
.
Следовательно, жорданов базис будут
составлять собственный вектор
![]()
и присоединенный к нему вектор первого
порядка
![]() ,
,
удовлетворяющие системам алгебраических
уравнений
![]()
и
![]() .
.
Общим решением однородной системы с
матрицей (10.1.10) является
![]() .
.
Поскольку
![]() ,
,
(10.1.11)
общим
решением неоднородной системы уравнений
(10.1.11) является
![]() .
.
Выбирая
![]() ,
,
![]() ,
,
получаем жорданов базис, состоящий из
векторов
![]() ,
,
![]() ,
,
позволяющий выписать матрицу
![]() ,
,
приводящую матрицу А
к матрице
![]() .
.
Учитывая,
что
![]()
и, следовательно,
![]() ,
,
по свойству 10
функций от матриц имеем
![]() .
.
Воспользовавшись соотношением (10.1.3)
для
![]() с
с![]() ,
,
окончательно получаем:
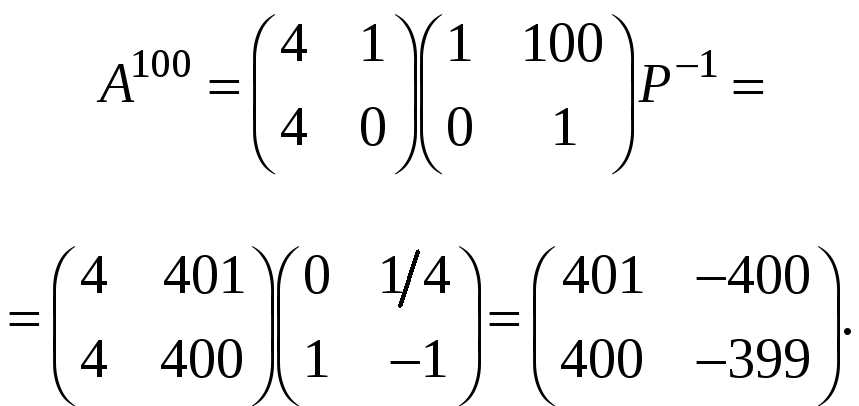
Перейдем
к интерполяционному многочлену Лагранжа
– Сильвестра. Поскольку жорданова
нормальная форма матрицы А
равна
![]() ,
,
инвариантные множители λ-матрицы
![]()
таковы:
![]() ,
,
![]() .
.
Поэтому минимальный многочлен матрицы
А
![]() ,
,
![]()
и
соотношение (10.1.4) принимает вид
![]() .
.
(10.1.12)
Коэффициенты
![]()
и
![]()
вычислим по формуле (10.1.6):
![]() ;
;
![]() .
.
Подставляя
найденные значения
![]()
и
![]() в
в
равенство (10.1.12), получаем:
![]() ,
,
что
позволяет определить
![]() :
:
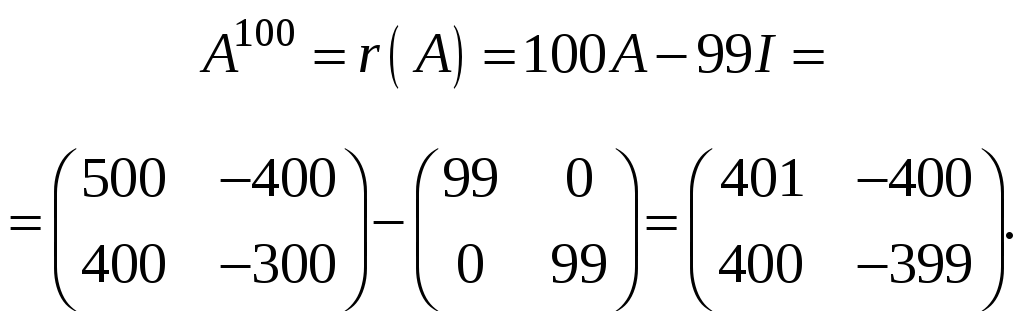
Воспользуемся
теперь основной формулой (10.1.8), которая
для рассматриваемого случая принимает
следующий вид
![]() .
.
(10.1.13)
Заменяя
в (10.1.13) f(λ)
на 1, а затем на
![]() ,
,
находим, что
![]()
и
![]() .
.
Следовательно,
![]() .
.
Полагая
![]() ,
,
находим
![]() .
.
10.1.1
Пусть
![]()
– минимальный многочлен матрицы А
и для функции f(λ)
существуют значения
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Запишите выражение для интерполяционного
многочлена Лагранжа – Сильвестра r(λ)
и вычислите коэффициенты
![]() ,
,
определенные соотношением (10.1.4).
10.1.2.
Найдите компоненты матрицы А
с минимальным многочленом ψ(λ), определенным
в задаче 10.1.1.
10.1.3.
Вычислите следующие значения функций
от матриц, пользуясь жордановой нормальной
формой, интерполяционным многочленом
Лагранжа – Сильвестра и основной
формулой:
а)
![]() ,
,
где
![]() ;
;
б)
![]() ,
,
где
![]() ;
;
в)
![]() ,
,
где
![]() ;
;
г)
![]() ,
,
где
![]() ;
;
д)
![]() ,
,
где
![]() ;
;
е)
![]() ,
,
где
![]() ;
;
ж)
![]() ,
,
где
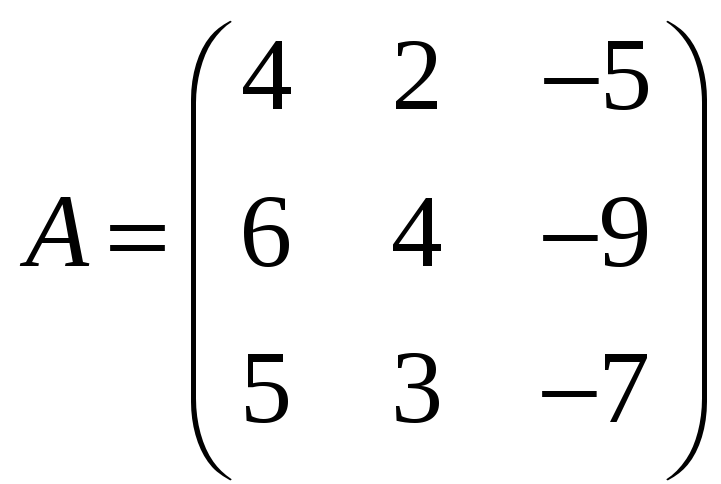 ;
;
з)
![]() ,
,
где
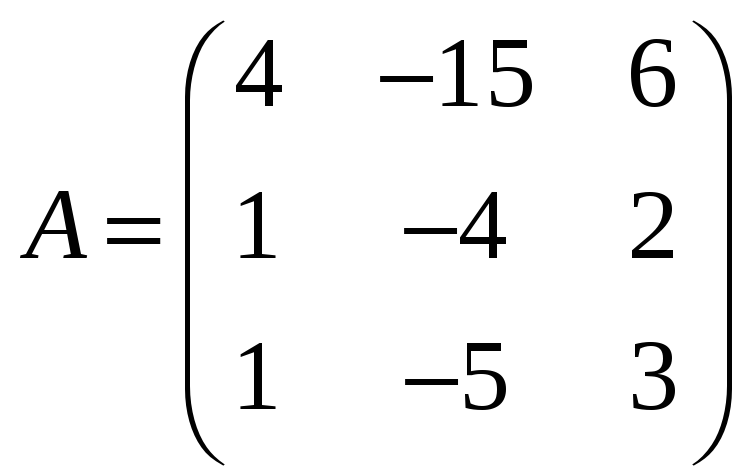 ;
;
и)
![]() ,
,
где
![]() ;
;
к)
![]() ,
,
где
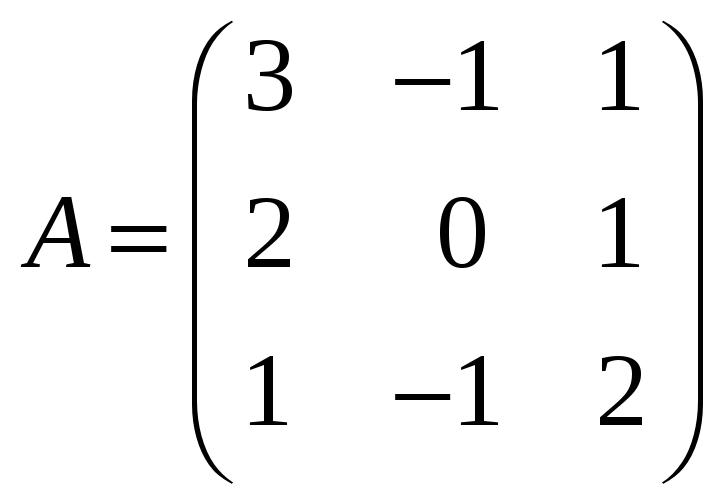 ;
;
л)
![]() ,
,
где
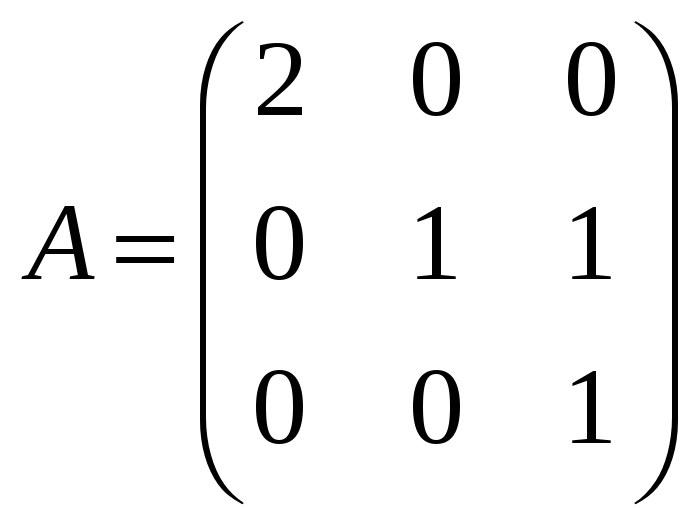 ;
;
м)
![]() ,
,
где
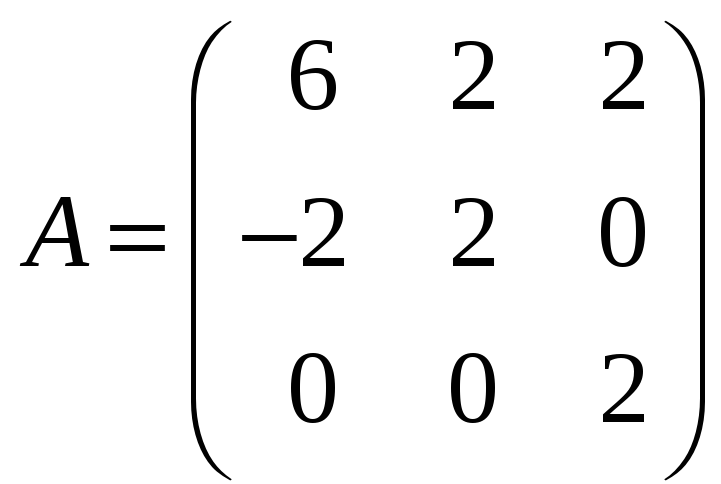 ;
;
89
Соседние файлы в папке сборник
- #
- #
- #
- #
- #
- #
- #
Содержание
Функция от матрицы
В настоящем разделе матрица $ A_{} $ считается квадратной порядка $ n_{} $.
Полином от матрицы
Сначала оптимизируем вычисление степени матрицы.
П
Пример 1. Вычислить
$$
A^{100} quad npu quad
A=left(
begin{array}{rrrr}
1 &2 &1 &0 \
1 & 1 & 0 &-1 \
-2& 0 & 1 & 2 \
0 & 2 & 1 & 1
end{array}
right)^{100} .
$$
Решение. Можно организовать вычисление $ A^{100} $ по алгоритму квадрирования-умножения, заимствованному из раздела “MОДУЛЯРНАЯ АРИФМЕТИКА”:
$$ A^{100}=left( left( left( left( left( left( A right)^2 A right)^2 right)^2 right)^2 Aright)^2 right)^2 . $$
Имеем: $ underline{100}_{_{10}}=underline{1100100}_{_2} $
$$
begin{array}{|c|c|c|c|c|}
hline
j & 1 & 2 & 3 & 4 \
hline
{mathfrak b}_j & 1 & 1 & 0 & 0 \
hline
& A & A^2 A & left(A^3 right)^2 & left(A^6 right)^2 \
&
left(
begin{array}{rrrr}
1 &2 &1 &0 \
1 & 1 & 0 &-1 \
-2& 0 & 1 & 2 \
0 & 2 & 1 & 1
end{array}
right)
&
left(
begin{array}{rrrr}
1 &6 & 3 &0 \
3& 1 & 0 &-3 \
-6& 0 & 1 & 6 \
0 & 6 & 3 & 1
end{array}
right)
&
left(
begin{array}{rrrr}
1 & 12 & 6 &0 \
6 & 1 & 0 &-6 \
-12& 0 & 1 & 12 \
0 & 12 & 6 & 1
end{array}
right)
&
left(
begin{array}{rrrr}
1 & 24 & 12 &0 \
12 & 1 & 0 &-12 \
-24& 0 & 1 & 24 \
0 & 24 & 12 & 1
end{array}
right)
\
hline
end{array}
$$
$$
begin{array}{|c|c|c|}
hline
5 &6 &7 \
hline
1 &0 & 0 \
hline
left(A^{12} right)^2 A &
left(A^{25} right)^2&
left(A^{50} right)^2 \
left(
begin{array}{rrrr}
1 & 50 & 25 &0 \
25 & 1 & 0 &-25 \
-50& 0 & 1 & 50 \
0 & 50 & 25 & 1
end{array}
right)
&
left(
begin{array}{rrrr}
1 & 100 & 50 &0 \
50 & 1 & 0 &-50 \
-100& 0 & 1 & 100 \
0 & 100 & 50 & 1
end{array}
right)
&
left(
begin{array}{rrrr}
1 & 200 & 100 &0 \
100 & 1 & 0 &-100 \
-200& 0 & 1 & 200 \
0 & 200 & 100 & 1
end{array}
right)
\
hline
end{array}
$$
♦
Рассмотрим далее произвольный полином $ g(x)=b_0x^m+b_1x^{m-1}+dots+b_m in mathbb C[x] $.
Вычисление его значения от матрицы $ A_{} $, т.е.
$$ g(A)=b_0A^m +b_1A^{m-1}+dots+b_m E , $$
где $ E_{} $ — единичная матрица того же порядка, что и $ A_{} $, может быть произведено с помощью
схемы Хорнера — чтобы сэкономить на операции умножения матриц.
П
Пример 2. Вычислить $ g(A)_{} $ для
$$ g(x)= 3,x^4-x^3+2,x^2-4,x-1 quad u quad
A=left( begin{array}{rrr}
1 & -3 & 4 \
3& 1 &8 \
-4 & -8 & 1
end{array}
right) .
$$
Решение. Схему Хорнера организуем по тому же принципу, что и для вычисления значения полинома в точке:
$$
g(A)=(((3,A-E)A+2,E)A-4,E)A-E .
$$
$$
B_1 = 3A-E =
left( begin{array}{rrr}
2 & -9 & 12 \
9& 2 & 24 \
-12 & -24 & 2
end{array}
right) ;
$$
$$
B_2=B_1A+2E=
left( begin{array}{rrr}
-71 & -111 & -52 \
-81& -215 & 76 \
-92 & -4 & -236
end{array}
right) ;
$$
$$
B_3=B_2A-4E=
left( begin{array}{rrr}
-200 & 518 & -1224 \
-1030& -584 & -1968 \
840 & 2160 & -640
end{array}
right) ;
$$
$$
g(A)=B_4=B_3A-E=
left( begin{array}{rrr}
6249 & 10910 & 2120 \
5090& 18249 & -10760 \
9880 & 4760 & 19999
end{array}
right)
$$
♦
Применение теоремы Гамильтона-Кэли
Дальнейшие упрощения возможны в случае, когда $ deg g ge n $, т.е. когда степень полинома становится больше или равной порядка матрицы. Предположим, что мы в состоянии вычислить характеристический полином матрицы $ A_{} $:
$$ f(x)=det (A-x E) , . $$
Т
Теорема 1. Обозначим $ g_1(x) $ остаток от деления $ g_{}(x) $ на характеристический полином $ f(x)=det (A – x E) $. Тогда
$$ g(A)= g_1(A) .$$
Доказательство. Действительно, указанное равенство последует из теоремы Гамильтона-Кэли при подстановке матрицы $ A_{} $ в
формулу
$$
g(x)equiv f(x)q(x)+g_1(x) , deg g_1 < n
$$
здесь $ q_{}(x) $ означает частное от деления $ g(x_{}) $ на $ f(x_{}) $.
♦
Эта теорема позволяет свести вычисление $ g({mathbf A}) $ к случаю полинома степени меньшей порядка матрицы. Это соображение существенно упрощает поставленную задачу, но при этом возникает другая: как вычислить остаток от деления если делимое существенно превосходит делитель по степени? Посмотрим, как этот подход будет выглядеть для примера 1.
П
Пример 3. Вычислить
$$
A^{100} quad npu quad
A=left(
begin{array}{rrrr}
1 &2 &1 &0 \
1 & 1 & 0 &-1 \
-2& 0 & 1 & 2 \
0 & 2 & 1 & 1
end{array}
right)^{100} .
$$
Решение. Здесь
$$det (A- x E) = x^4-4,x^3+6, x^2 – 4, x +1 . $$
Деление полинома $ g(x)equiv x^{100} $ на характеристический полином, организованное традиционным способом (т.е. “в столбик” ) дает в остатке полином
$$ g_1(x)=161700,x^3-480150,x^2+475300,x-156849 ; $$
при этом частное $ q_{}(x) $ является полиномом $ 96 $-й степени. Для вычислений обоих полиномов приходится использовать специализированный пакет компьютерной алгебры. Вычисление $ g_1(A) $ уже может быть произведено «вручную», например, с использованием схемы Хорнера.
♦
Заметим, что собственно частное от деления полинома $ g_{}(x) $ на характеристический полином не участвует в последующих вычислениях полинома от матрицы — для этого нужны только коэффициенты остатка. Можно ли изобрести обходной способ вычисления остатка, который не требует промежуточного вычисления частного? — Оказывается, можно.
Предположим, что мы в состоянии найти корни характеристического полинома $ f(x)=det (A-x E) $, т.е. собственные числа матрицы $ A_{} $. Предположим сначала, что все эти корни $ lambda_1,dots,lambda_n $ различны. Подставим их в тождество для определения частного и остатка:
$$
g(x)equiv f(x)q(x)+g_1(x) , .
$$
Поскольку $ f(lambda_j)=0 $ при $ jin {1,dots,n} $, получаем равенства
$$ {g(lambda_j) = g_1(lambda_j)}_{j=1}^n , . $$
Полином $ g_1(x) $ имеет степень меньшую $ n_{} $, а его значения совпадают со значениями полинома $ g(x) $ в $ n_{} $ точках. Такой полином определяется однозначно — как интерполяционный полином, построенный по таблице значений
$$
begin{array}{c|ccccc}
x & lambda_1 & lambda_2 & dots & lambda_n \ hline
y & g(lambda_1) & g(lambda_2) &dots & g(lambda_n)
end{array}
$$
Для его вычислений можно использовать любой из методов, изложенных в разделе “ИНТЕРПОЛЯЦИЯ”. Предпочтение отдается методу Лагранжа:
$$
g_1(x) equiv
sum_{k=1}^n frac{g(lambda_k)}{f_k(lambda_k)}f_k(x)
= sum_{k=1}^n frac{g(lambda_k)}{f'(lambda_k)}f_k(x)
$$
где $ f_{k}(x) $ означает частное от деления характеристического полинома на его линейный множитель:
$$
f_k(x)equiv frac{f(x)}{x-lambda_k}
equiv (x-lambda_1)times dots times (x-lambda_{k-1})
(x-lambda_{k+1})times dots times (x-lambda_{n})
, .
$$
Т
Теорема 2. Если все собственные числа $ lambda_{1},dots,lambda_n $
матрицы $ A_{} $ различны, то
$$
g(A)= sum_{k=1}^n frac{g(lambda_k)}{f_k(lambda_k)}f_k(A)
= sum_{k=1}^n frac{g(lambda_k)}{f'(lambda_k)}f_k(A)
$$
где $ f_k(x) $ означает частное от деления $ f_{}(x) $ на $ x- lambda_k $.
Каждое из суммируемых выражений в формуле можно представить в виде двух
сомножителей:
один из них зависит от полинома $ g_{}(x) $, а второй — не зависит. Таким образом,
при изменении полинома происходит лишь пересчет значений
$ g(lambda_1),dots, g(lambda_n) $, а их матричные сомножители не меняются.
Структура этих последних уже была нами установлена в пункте
☞
СОБСТВЕННЫЙ ВЕКТОР: каждая
матрица $ f_k(A) $ — ранга $ 1 $, т.е. имеет свои столбцы пропорциональными (и равными собственным векторам, принадлежащим $ lambda_{k} $).
П
Пример 4. Выписать формулу $ g(A)_{} $ для произвольного
$ g(x)in mathbb C[x] $ и
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right) .
$$
Решение. $ det (A-x E)=-(x-3) (x+2)(x+1) $.
Пренебрегая знаком – , имеем:
$$
begin{matrix}
f_1(x)=x^2+3x+2 & u & f_1(A)=
left( begin{array}{rrr}
40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20
end{array}
right) , f_1(3)=20 ; \
f_2(x)=x^2-2x-3 & u & f_2(A)=
left( begin{array}{rrr}
-10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0
end{array}
right) , f_2(-2)=5 ; \
f_3(x)=x^2-x-6 & u & f_3(A)=
left( begin{array}{rrr}
-4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8
end{array}
right), f_3(-1)=-4 .
end{matrix}
$$
$$
g(A)=g(3)
left(
begin{array}{rrr}
2 & 4 & -1 \ 0 &0 & 0 \ 2 & 4 & -1
end{array}
right) + g(-2)
left( begin{array}{rrr}
-2 & -6 & 2 \ 1 &3 & -1 \ 0 & 0 & 0
end{array}
right)
+ g(-1)
left( begin{array}{rrr}
1 & 2 & -1 \ -1 & -2 & 1 \ -2 & -4 & 2
end{array}
right) .
$$
♦
В случае, когда характеристический полином матрицы $ A_{} $ имеет кратные корни, для вычисления полинома $ g_1(x) $ из теоремы $ 1 $ приходится привлекать обобщение понятия классического интерполяционного полинома в виде интерполяционного полинома Эрмита. Действительно, полином $ g_1(x) $ определялся в теореме $ 1 $ как остаток от деления $ g_{}(x) $ на характеристический полином $ f(x)=det (A- xE) $:
$$
g(x)equiv f(x)q(x)+g_1(x) ;
$$
При этом $ deg g_1 < n $, и, следовательно, полином $ g_1(x) $ вполне определялся произвольным набором $ n_{} $ своих значений — мы брали их равными $ g(lambda_1),dots,g(lambda_n) $ в случае, когда все корни $ f_{}(x) $ были различными (простыми).
Если же теперь среди корней имеются кратные и разложение характеристического полинома на линейные множители имеет вид
$$
f(x)equiv (-1)^n(x – lambda_1)^{{mathfrak m}_1} times
dots times (x – lambda_{{mathfrak r}})^{ {mathfrak m}_{{mathfrak r}}} quad ; quad
{mathfrak m}_1+dots+{mathfrak m}_{{mathfrak r}}=n, lambda_k ne
lambda_{ell} npu k ne ell, exists {mathfrak m}_j > 1,
$$
то для нахождения полинома $ g_1(x) $ не хватает значений $ g(lambda_1),dots, g(lambda_{{mathfrak r}}) $. Для получения дополнительных условий, можно продифференцировать тождество $ g(x)equiv f(x)q(x)+g_1(x) $ по $ x_{} $ и подставить в получившееся значения всех кратных корней полинома $ f_{}(x) $:
$$ g^{prime}(lambda_j) = f^{prime}(lambda_j) q(lambda_j)+f(lambda_j) q^{prime}(lambda_j)+g_1(lambda_j) . $$
Поскольку для любого кратного корня $ lambda_{j} $ будет выполнено условие
(см.
☞
ЗДЕСЬ ): $ f^{prime}(lambda_j)=0 $, то результатом подстановки будет равенство $ g^{prime}(lambda_j)=g_1^{prime}(lambda_j) $. Получаем дополнительные условия для определения полинома $ g_{1}(x) $. Итак, для нахождения полинома $ g_1(x) $ нам следует дополнительно к значениям $ g_{}(x) $ на всех корнях характеристического полинома (т.е. на собственных числах) матрицы $ A_{} $ вычислить еще и значения производной этой функции на всех кратных корнях. Может, однако, так случиться, что и этих дополнительных условий будет недостаточно для нахождения полинома $ g_1(x) $. Тогда следует продолжить процесс вычисления производных — для тех значений $ lambda_{j} $, кратность которых $ {mathfrak m}_j $ больше $ 2_{} $. Окончательно, для определения полинома $ g_1(x) $ мы имеем значения полинома $ g(x) $
и его производных
$$
begin{matrix}
g(lambda_1),dots, g^{({mathfrak m}_{_1}-1)}(lambda_1), \
g(lambda_2),dots, g^{({mathfrak m}_{_2}-1)}(lambda_1), \
dots, \
g(lambda_{mathfrak r}),dots, g^{({mathfrak m}_{_{mathfrak r}}-1)}(lambda_{mathfrak r}) ;
end{matrix}
$$
при этом количество значений в каждой строке равно (алгебраической) кратности соответствующего собственного числа. По этим значениям полином степени меньшей $ n_{} $ восстанавливается однозначно.
Заметим, что данный метод не чувствителен к геометрической кратности каждого из собственных чисел (т.е. к структуре
жордановой нормальной формы матрицы $ A_{} $ вне ее главной диагонали); для его работы достаточно информации об алгебраической кратности.
П
Пример 5. Вычислить $ A^{100} $ для
$$
A=
left(
begin{array}{rrrr}
1 &2 &1 &0 \
1 & 1 & 0 &-1 \
-2& 0 & 1 & 2 \
0 & 2 & 1 & 1
end{array}
right) ;
A=
left(
begin{array}{rrrr}
1 &0 &0 &0 \
1 & 2 & 0 &1 \
2& 3 & 1 & 2 \
-1 & -1 & 0 & 0
end{array}
right) ;
A=
left(
begin{array}{rrrr}
1 &1 & 2 &-1 \
1 & -1 & -4 &2 \
0& 1 & 3 & -1 \
0 & 0 & 1 & 1
end{array}
right) .
$$
Решение. У всех трех матриц одинаковый характеристический полином: $ det (A- x E) = (x-1)^4 $. Остаток от деления $ x^{100} $ на $ (x-1)^4 $ совпадает с отрезком ряда Тейлора функции $ x^{100} $ при разложении ее по степеням $ x-1 $, т.е. с
$$
begin{matrix}
g_1(x)&=&1+100,(x-1)+frac{100cdot99}{2}(x-1)^2+frac{100cdot 99 cdot 98}{6}(x-1)^3= \
&= & -156849+475300,x-480150,x^2+161700,x^3 .
end{matrix}
$$
Для всех трех матриц формула вычисления $ A^{100} $ одна и та же:
$$
A^{100} =
-156849, E+475300,A-480150,A^2+161700,A^3 .
$$
Несмотря на то обстоятельство, что жордановы нормальные формы у этих матриц различны.
♦
В приведенном способе нахождения остатка от деления полинома $ g(x) $ на характеристический полином матрицы $ A_{} $ имеется один нюанс, требующий пояснений.
Предположим, что элементы матрицы $ A_{} $ целочислены: $ {a_{jk} in mathbb Z}_{j,k=1}^n $. Тогда и характеристический полином $ f(x)=det (A-x E) $ является полиномом
с целочисленными коэффициентами $ f(x) in mathbb Z[x] $. Поскольку старший коэффициент $ f_{}(x) $ равен $ 1_{} $ по абсолютной величине, то и остаток от деления
$ g_{} (x) $ на $ f_{}(x) $ будет иметь только целые коэффициенты (см.
☞
ЗДЕСЬ ): $ g_1(x) in mathbb Z[x] $. Между тем, вычисление этого полинома через посредство корней характеристического полинома, в общем случае, приводит к иррациональным выражениям: корни полинома, как правило, не выражаются в радикалах через его коэффициенты.
П
Пример 6. Вычислить $ g(A) $ для
$$ g(x)= x^{10}-6,x^8+11,x^7-x^3+4,x^2- 1 $$
и
$$
A=
left(
begin{array}{rrrrr}
6 &1 &5 &2 & -1 \
-5 & -1 & -4 & -2 & 1 \
-5 & -1 & -5 & -1 & 1 \
-5 & -1 & -5 & -2 & 2 \
-5 & 0 & -7 & -2 & 2
end{array}
right) , .
$$
Решение. Характеристический полином $ f(x)= det (A-x E)=-(x^5-4,x-2) $ имеет корни, не выражающиеся в радикалах.
Попробуем применить теорему 2 для приближенных значений корней:
$$ lambda_1 approx -1.243596, lambda_2 approx -0.508499, lambda_3 approx 1.518512, lambda_{4,5} approx 0.116792 pm {mathbf i}, 1.438448,, . $$
Для нахождения частных от деления $ f_{}(x) $ на линейные множители $ (x-lambda_j) $ воспользуемся следующим приемом. Частное от деления произвольного полинома
$$ f(x)=a_0x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5 $$
на линейный полином $ x – lambda $ находится по формуле
$$
q(x,lambda)=a_0x^4+(a_0lambda + a_1)x^3+(a_0lambda^2+a_1lambda+a_2)x^2+(a_0lambda^3+a_1lambda^2+a_2lambda+a_3)x+
$$
$$
+(a_0lambda^4+a_1lambda^3+a_2lambda^2+a_3 lambda+a_4) , ,
$$
которая является развернутым вариантом схемы Хорнера. Подставляя сюда значения коэффициентов характеристического полинома $ f_{}(x) $ и приближенные значения его корней, получаем приближения полиномов $ f_j(x) $:
$$
begin{array}{ccl}
f_1(x) &approx & -x^4+1.243596,x^3-1.546532,x^2+1.923266,x+1.608239 , , \
f_2(x) & approx &-x^4+0.508499,x^3-0.258572,x^2+0.131483,x+3.933141, , \
f_3(x) & approx & dots \
f_{4,5}(x) & approx & -x^4+(-0.116792mp 1.438448, mathbf i),x^3+(2.055491mp 0.335998, mathbf i),x^2+ dots
end{array}
$$
Вычисляем значения этих полиномов на матрице $ A_{} $:
$$
f_1(A) approx
left(
begin{array}{rrrrr}
1.844873 & 0.503518 & 3.247794 & -1.280266 & 0.201656 \
0.383692& 0.104720 & 0.675468 & -0.266266 & 0.041940 \
-4.616308& -1.259922 & -8.126748 & 3.203527 &-0.504592 \
1.601674 & 0.437142 & 2.819656 &-1.111496 & 0.175073 \
-6.130986 & -1.673321 & -10.793252 & 4.254651 & -0.670156
end{array}
right)
$$
$$
f_2(A) approx
left(
begin{array}{rrrrr}
-6.028030 & -5.334374 & -3.876435 & 0.470253 & 0.893870 \
9.342582 & 8.267515 & 6.007919& -0.728825 & -1.385371\
4.342582 & 3.842873 & 2.792577 & -0.338769 & -0.643943\
6.885079 & 6.092801 & 4.427577 & -0.537112 & -1.020959\
5.592221 & 4.948714 & 3.596180 &-0.436255 & -0.829246
end{array}
right)
$$
$$
f_3(A) approx dots
$$
$$
f_{4,5}(A) approx
left(
begin{array}{rrr}
-4.833170pm 17.111687 , mathbf i & -10.621186 pm 0.712576 , mathbf i & dots \
6.383099 mp 14.587375 , mathbf i & 9.509036 pm 0.668706 , mathbf i & dots \
1.383099 mp 14.587376 , mathbf i & 8.504395mp 2.151023 , mathbf i & dots \
0.799140 mp 21.779614 , mathbf i & 12.443094mp 3.925469 , mathbf i & dots \
11.076597 mp 23.459604 , mathbf i & 15.455549pm 1.532904 , mathbf i & dots
end{array}
right) , .
$$
Несмотря на кажущуюся хаотичность формирования элементов этих матриц, столбцы каждой из них пропорциональны (впрочем, равно как и строки).
Составляем матрицу из теоремы $ 2 $:
$$
sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)}f_k(A) =
sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)} q(A,lambda_k) approx
$$
$$
approx
left(
begin{array}{rrrrr}
-94.999999 & -173.999999 & -237.999999 & 143.999999 & 198.999999 \
159.999999 & 149.999999& 301.999999&-101.999999&-191.999999\
39.999999&156.999999&79.999999&-127.999999&-125.999999\
194.999999 &277.999999&229.999999&-239.999999&-140.999999\
404.999999&273.999999&435.999999&-67.999999&-278.999999
end{array}
right)
$$
(при уменьшении точности вычислений возможно появление ненулевых мнимых частей). Полученный ответ можно интерпретировать как приближение истинного, а именно, целочисленного:
$$
left(
begin{array}{rrrrr}
-95&-174&-238&144&199\
160&150&302&-102&-192\
40&157&80&-128&-126\
195&278&230&-240&-141\
405&274&436&-68&-279
end{array}
right) , .
$$
Возникает вопрос: можно ли было получить этот ответ, не прибегая к численным методам (и использованию мнимых чисел)? Где именно «заложена» принципиальная целочисленность ответа? Для ответа посмотрим на выражение
$$
sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)}f_k(A) = sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)}f_k(A) =
$$
$$
sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)} left(a_0A^4+(a_0lambda_k + a_1)A^3 + (a_0lambda_k^2+a_1lambda_k+a_2)A^2 dots right)=
$$
$$
= left(a_0sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)} right)A^4 +
left( a_0 sum_{k=1}^5 frac{g(lambda_k)lambda_k}{f_k(lambda_k)}+a_1 sum_{k=1}^5 frac{g(lambda_k)}{f_k(lambda_k)} right) A^3+ dots , ,
$$
здесь $ a_0=(-1)^n,a_1, a_2,dots $ обозначают коэффициенты полинома $ f_{}(x) $. Выражения в круглых скобках представляют собой симметрические рациональные функции от корней этого полинома. Согласно теореме Гаусса, эти функции допускают представление в виде рациональных функций от коэффициентов $ a_0,a_1, a_2,dots $ (а, на самом деле, полиномов от этих коэффициентов). Так что ответ в задаче действительно должен быть целочисленным. Другое дело, что для его практического поиска мы привлекли численные методы поскольку явное представление симметрических рациональных функций через коэффициенты полинома — задача весьма сложная.
♦
Анализ с помощью жордановой нормальной формы
Все применения ЖНФ основаны на формулах подобия матрицы и ее ЖНФ:
$$C^{-1}{mathbf A}C ={mathbf A}_{_{mathfrak J}} quad iff quad {mathbf A}=
C{mathbf A}_{_{mathfrak J}}C^{-1} . $$
Оказывается, что любая мыслимая операция над
матрицей $ {mathbf A} $ может быть сведена к этой же операции над формой Жордана:
$$g({mathbf A})= Cg({mathbf A}_{_{mathfrak J}})C^{-1} .$$
В самом деле, имеем, например:
$$
{mathbf A}^2 =(C{mathbf A}_{_{mathfrak J}}C^{-1})^2=C{mathbf A}_{_{mathfrak J}}C^{-1}C{mathbf A}_{_{mathfrak J}}C^{-1}=C{mathbf A}_{_{mathfrak J}}^2C^{-1} .
$$
По индукции можно показать справедливость равенства
$$
{mathbf A}^N=C{mathbf A}_{_{mathfrak J}}^NC^{-1} quad npu quad forall N in mathbb N .
$$
Далее, справедливость равенства $ {mathbf A}^0=E=C{mathbf A}_{_{mathfrak J}}^0C^{-1} $
очевидна.
Но тогда можно доказать и справедливость равенства
$$ g({mathbf A}) = Cg({mathbf A}_{_{mathfrak J}})C^{-1} $$
для любого полинома $ g(x)=b_0x^m+dots+b_m in mathbb C[x] $. Отсюда — прямая дорога к аналитическим функциям от матрицы… Этот переход обсудим НИЖЕ,
а пока остановимся и проведем анализ структуры полинома от ЖНФ.
Мы будем рассматривать матрицы и их ЖНФ над полем $ mathbb C_{} $. Пусть характеристический полином матрицы $ mathbf A_{} $
имеет следующее разложение на линейные множители над полем $ mathbb C_{} $:
$$
f(lambda)= det (mathbf A – lambda E) equiv (-1)^n(lambda – lambda_1)^{{mathfrak m}_1} times
dots times (lambda – lambda_{{mathfrak r}})^{ {mathfrak m}_{{mathfrak r}}} quad ; quad
{mathfrak m}_1+dots+{mathfrak m}_{{mathfrak r}}=n, lambda_k ne
lambda_{ell} npu k ne ell.
$$
ЖНФ матрицы $ mathbf A_{} $ имеет вид блочно-диагональной матрицы
$$
{mathbf A}_{_{mathfrak J}}=left(
begin{array}{cccc}
mathbf A_1 & mathbb O & dots & mathbb O \
mathbb O & mathbf A_2 & dots & mathbb O \
vdots & & ddots & vdots\
mathbb O & mathbb O & dots & mathbf A_{{mathfrak r}}
end{array}
right) quad , quad mbox{ здесь } mathbf A_j – mbox{ матрица порядка }
{mathfrak m}_jtimes {mathfrak m}_j .
$$
В свою очередь, каждая из составляющих матриц
$ mathbf A_j $ имеет снова блочно-диагональный вид
$$
mathbf A_j=
left(
begin{array}{cccc}
{mathbf A}_{j1} & mathbb O & dots & mathbb O \
mathbb O & {mathbf A}_{j2} & dots & mathbb O \
vdots & & ddots & vdots\
mathbb O & mathbb O & dots & {mathbf A}_{j ell_j}
end{array}
right)
$$
где на диагонали стоят клетки Жордана, т.е. матрицы вида
$$
{mathfrak J}_k (lambda_j) =
left(
begin{array}{cccccc}
lambda_j & & & & & \
1 & lambda_j & & & & \
0 & 1 & lambda_j & & mathbb O & \
vdots & & ddots & ddots& & \
0 & 0 & 0 & dots & lambda_j & \
0 & 0 & 0 & dots & 1 & lambda_j
end{array}
right)_{k times k} .
$$
Теперь наша задача — свести вычисление произвольного полинома от $ {mathbf A}_{_{mathfrak J}} $ к вычислению этого же полинома от клеток Жордана: $ g({mathbf A}_{_{mathfrak J}}) $ — к $ g({mathfrak J}_k (lambda_j)) $.
Структура степенной функции
Т
Теорема 3. Если матрица $ {mathbf D} $ — блочно-диагональная, то и $ {mathbf D}^N $ —
блочно-диагональная:
$$
left(
begin{array}{cccc}
{mathbf D}_1 & mathbb O & dots & mathbb O \
mathbb O & {mathbf D}_2 & dots & mathbb O \
vdots & & ddots & vdots \
mathbb O & mathbb O & dots & {mathbf D}_r
end{array}
right)^N=
left(
begin{array}{cccc}
{mathbf D}_1^N & mathbb O & dots & mathbb O \
mathbb O & {mathbf D}_2^N & dots & mathbb O \
& & ddots & \
mathbb O & mathbb O & dots & {mathbf D}_r^N
end{array}
right) .
$$
Здесь $ {mathbf D}_1, dots, {mathbf D}_r $ — квадратные матрицы1).
Т
Теорема 4. Если матрица $ L_{} $ — нижнетреугольная, то и $ L^N $ — нижнетреугольная.
Теоремы $ 3 $ и $ 4 $ сводят вычисление степени матрицы $ {mathbf A} $ к вычислению степени ее клеток Жордана $ {mathfrak J}_k (lambda_j) $.
Т
Теорема 5. Имеет место равенство:
$$
left(
begin{array}{rrrrrr}
lambda & & & & & \
1 & lambda & &mathbb O & & \
0& 1 & lambda & & & \
vdots & & ddots & ddots & & \
0 & 0 & dots & 1 & lambda & \
0 & 0 & dots & 0 & 1 &lambda
end{array}
right)_{ktimes k}^N=
left(
begin{array}{ccrlcc}
lambda^N & & & & & \
C_N^1 lambda^{N-1} & lambda^N & &mathbb O & & \
C_N^2 lambda^{N-2} & C_N^1 lambda^{N-1} & lambda^N & & & \
dots & & ddots & ddots & & \
C_N^{k-2} lambda^{N-k} & dots & & C_N^1 lambda^{N-1} &lambda^N & \
C_N^{k-1} lambda^{N-k+1} & dots & & C_N^2 lambda^{N-2} & C_N^1 lambda^{N-1} &lambda^N
end{array}
right)
$$
(считаем здесь элементы с отрицательными показателями $ lambda $ равными нулю).
Более корректная запись матрицы в правой части возможна с помощью матрицы
$$H_j = begin{array}{rl}
begin{array}{c}
{scriptstyle 0 to} \ {scriptstyle 1 to} \ vdots \ {scriptstyle j to}
\ vdots \ {scriptstyle k-1 to}
end{array}
left(begin{array}{llllll}
0 & & & & &\
0 & & & mathbb O & &\
vdots & & & & &\
1 & & & & \
vdots & ddots & & &\
0 & & 1 & dots & 0 & 0
end{array}
right)
end{array}
=left[
begin{array}{ll}
mathbb O_{jtimes (k-j)} & mathbb O_{jtimes j} \
E_{(k-j) times (k-j)} & mathbb O_{(k-j)times j}
end{array}
right]_{ktimes k}
$$
(единицами заполнена $ j_{} $-я диагональ, считая от нулевой — главной):
$$
left[{mathfrak J}_k (lambda) right]^N =
$$
$$
=lambda^N E +
C_N^1 lambda^{N-1} H_1 + C_N^2 lambda^{N-2} H_2 +
dots +left{ begin{array}{ccc}
C_N^N H_N & npu & N<k, \
C_N^{k-1}lambda^{N-k+1} H_{k-1} & npu & N ge k.
end{array}
right.
$$
П
Пример. Вычислить
$$
{mathbf A}=left(
begin{array}{rrrr}
1 &2 &1 &0 \
1 & 1 & 0 &-1 \
-2& 0 & 1 & 2 \
0 & 2 & 1 & 1
end{array}
right)^{100} .
$$
Решение. Найдем ЖНФ для матрицы $ {mathbf A} $ и матрицу $ C_{} $.
$$det ({mathbf A}- lambda E) = (lambda-1)^4 . $$
Ищем корневые векторы, принадлежащие $ lambda_1=1 $:
$$
{mathbf B}={mathbf A}- E=
left(
begin{array}{rrrr}
0 & 2 & 1 & 0 \
1 & 0 & 0 &-1 \
-2 & 0 & 0 & 2 \
0 & 2 & 1 & 0
end{array}
right)
quad
rightarrow
quad
left(
begin{array}{rrrr}
0 &2 &1 &0 \
1 & 0 & 0 &-1 \
0& 0 & 0 & 0 \
0 & 0 & 0 & 0
end{array}
right)
$$
Имеем: $ mathbb Q_1=mathcal L left(
left[ 0 , -1 , 2 , 0 right]^{^{top}},
left[ 1 , 0 , 0 , 1 right]^{^{top}}
right) $; следовательно геометрическая кратность собственного числа не равна его алгебраической кратности и матрица $ {mathbf A} $ недиагонализуема.
$$
{mathbf B}^2=mathbb O_{4times 4} quad
Longrightarrow quad mathbb Q_2=
mathcal L left(
left[ 0 , -1 , 2 , 0 right]^{^{top}},
left[ 1 , 0 , 0 , 1 right]^{^{top}},left[ 1 , 0 , 0 , 0 right]^{^{top}},
left[ 0 , 1 , 0 , 0 right]^{^{top}}
right) .
$$

В ЖНФ имеются $ 2_{} $ клетки $ 2 times 2 $. Для построения
канонического базиса берем векторы из относительного базиса $ mathbb Q_2 $ над
$ mathbb Q_1 $ и домножаем их на $ {mathbf B} $ (заполняем башни сверху вниз). Получаем
$$
C=
left(
begin{array}{rrrr}
1 & 0 & 0 & 2 \
0 & 1 & 1 & 0 \
0 & -2 & 0 & 0 \
0 & 0 & 0 & 2
end{array}
right) quad ,
{mathbf A}_{_mathfrak J}=
left(
begin{array}{rrrr}
1 & & & \
1 & 1 & & \
& & 1 & \
& & 1 & 1
end{array}
right)
$$
Теперь воспользуемся формулой $ {mathbf A}^{100}=C {mathbf A}_{_{mathfrak J}}^{100} C^{-1} $ и теоремами 1-3:
$$
{mathbf A}^{100}=C left(
begin{array}{rrrr}
1 & & & \
1 & 1 & & \
& & 1 & \
& & 1 & 1
end{array}
right)^{100}C^{-1}=
$$
$$=
left(
begin{array}{rrrr}
1 & 0 & 0 & 2 \
0 & 1 & 1 & 0 \
0 & -2 & 0 & 0 \
0 & 0 & 0 & 2
end{array}
right)
left(
begin{array}{llll}
1 & & & \
100 & 1 & & \
& & 1 & \
& & 100 & 1
end{array}
right)
left(
begin{array}{rrrr}
1 & 0 & 0 & -1 \
0 & 0 & -1/2 & 0 \
0 & 1 & 1/2 & 0 \
0 & 0 & 0 & 1/2
end{array}
right)
=
$$
$$
= left(
{begin{array}{rrrr}
1 & 200 & 100 & 0 \
100 & 1 & 0 & -100 \
-200 & 0 & 1 & 200 \
0 & 200 & 100 & 1
end{array}}
right) .
$$
♦
Решение линейного разностного уравнения
§
Настоящий пункт тесно связан с разделом ЛИНЕЙНОЕ РАЗНОСТНОЕ УРАВНЕНИЕ.
Пусть рекуррентная последовательность задается уравнением
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K
$$
и начальными данными $ x_0,x_1,dots,x_{n-1} $.
Введем в рассмотрение столбцы, состоящие из $ n_{} $ последовательных элементов этой последовательности, обозначив
$$
X_0=left( begin{array}{l}
x_0 \ x_1 \ vdots \ x_{n-1}
end{array}
right), X_1=left( begin{array}{l}
x_1 \ x_2 \ vdots \ x_{n}
end{array}
right), X_2=left( begin{array}{l}
x_2 \ x_3 \ vdots \ x_{n+1}
end{array}
right), dots,
X_K=left( begin{array}{l}
x_K \ x_{K+1} \ vdots \ x_{K+n-1}
end{array}
right),dots ;
$$
а также следующую матрицу, известную как матрица Фробениуса:
$$
{mathfrak F}=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n} .
$$
Используя правило умножения матриц, а также соотношение между элементами последовательности, получаем:
$$
X_1={mathfrak F}X_0, X_2={mathfrak F}X_1,dots, X_K={mathfrak F}X_{K-1},dots,
$$
откуда имеем:
$$
X_K={mathfrak F}^KX_0 quad npu quad Kin mathbb N .
$$
Искомое выражение для $ x_{K} $ получится умножением первой строки матрицы
$ {mathfrak F}^K $ на столбец начальных данных $ X_{0} $. Таким образом, задача решения разностного уравнения сводится к задаче возведения в степень матрицы $ {mathfrak F} $.
Для нахождения $ {mathfrak F}^{K} $ воспользуемся результатами предыдущего пункта. Найдя
жорданову нормальную форму (ЖНФ) $ {mathfrak F}_{mathfrak J} $ и соответствующую матрицу
преобразования базиса $ C_{} $, получим
$$
{mathfrak F}_{mathfrak J} =C^{-1} mathfrak F C Longrightarrow
{mathfrak F}^{K}=C {mathfrak F}_{_{mathfrak J}}^{K} C^{-1} , .
$$
Характеристический полином матрицы Фробениуса:
$$det ({mathfrak F}- lambda E)=
(-1)^n(lambda^n-a_1 lambda^{n-1}-dots-a_n) .
$$
с точностью до знака совпадает с характеристическим полиномом последовательности.
Обозначим его корни $ lambda_1,dots,lambda_n $. Если они различны, то жорданова нормальная форма $ {mathfrak F}_{_{mathfrak J}} $ диагональна. Если же среди этих корней имеются кратные, то установление структуры ЖНФ потребует усилий; однако же можно заранее утверждать, что эта форма диагональной не будет.
Т
Теорема 6. Если все корни характеристического полинома различны, то решение разностного уравнения получается в виде
$$ x_{K}= C_1lambda_1^K + dots+ C_n lambda_n^K , $$
числа $ C_{1},dots,C_n $ не зависят от $ K_{} $ и определяются с помощью начальных условий из системы линейных уравнений:
$$
left{begin{array}{rrrrcl}
C_1 &+C_2 &+dots &+ C_n &=& x_0 \
lambda_1 C_1 &+ lambda_2C_2&+dots & + lambda_n C_n & = & x_1 \
lambda_1^2 C_1 &+ lambda_2^2C_2&+dots & + lambda_n^2 C_n & = & x_2 \
dots &&&&& dots \
lambda_1^{n-1}C_1 &+ lambda_2^{n-1}C_2&+dots & + lambda_n^{n-1} C_n & = & x_{n-1}.
end{array}
right.
$$
Доказательство теоремы и ее обобщение на случай наличия кратных корней характеристического полинома
☞
ЗДЕСЬ.
Асимптотика степенной функции
Задача. Выяснить как себя ведет $ mathbf A^N $ при $ Nto +infty $.
Пример предыдущего пункта показывает, что существуют матрицы $ mathbf A_{} $, для которых некоторые элементы $ mathbf A^N $ неограниченно возрастают при $ Nto +infty $.
Т
Теорема 7. Если все собственные числа матрицы $ mathbf A_{} $ меньше $ 1 $ по абсолютной величине, т.е. $ {|lambda_j|<1}_{j=1}^n $, то
$$ lim_{Nto +infty} mathbf A^N = mathbb O_{ntimes n} , . $$
Если существует хотя бы одно собственное число $ lambda_j $ такое, что $ |lambda_j|>1 $, то существует хотя бы один элемент матрицы $ mathbf A^N $ неограниченно возрастающий при
$ Nto +infty $.
Условия теоремы можно переформулировать в виде соответствующих неравенств на спектральный радиус матрицы. Проверка этих условий возможна без непосредственного вычисления собственных чисел матрицы $ mathbf A_{} $. Достаточно построить характеристический полином матрицы и применить к нему критерий Шура-Кона.
Cлучай существования единичного по модулю собственного числа матрицы $ mathbf A $ кажется исключительным, маловероятным. Вероятность попадания случайно брошенной комплексной точки на окружность $ |z|=1 $ равна $ 0 $. И тем не менее,
реальный мир играет вероятностями — см.
☞
ЦЕПИ МАРКОВА.
Вычисление полинома от матрицы
Теперь проведем анализ структуры матрицы $ g(mathbb A) $ с помощью жордановой нормальной формы.
Способ вычисления матричной степени распространяется и на полином от матрицы:
$$g({mathbf A})= Cg({mathbf A}_{_{mathfrak J}})C^{-1}$$
и аналоги теорем $ 3 $ и $ 4 $ сводят вычисление $ g({mathbf A}) $ к вычислению $ g(x_{}) $ от клеток Жордана.
Поскольку
$$gleft( {mathfrak J}_k (lambda) right)=
b_0left[{mathfrak J}_k (lambda)right]^m+b_1left[{mathfrak J}_k (lambda)right]^{m-1}+dots+b_mE_{mtimes m}
$$
то на основании теоремы $ 5 $ получаем следующий результат
Т
Теорема 8. Имеет место равенство
$$
gleft(left[
begin{array}{rrrrr}
lambda & & & & \
1 & lambda & & mathbb O & \
0& 1 & lambda & & \
vdots & & ddots & ddots & \
0 & 0 & dots & 1 &lambda
end{array}
right]_{ktimes k}right)=
left[
begin{array}{ccccc}
g(lambda) & & & & \
g'(lambda) & g(lambda) & & mathbb O & \
frac{g”(lambda)}{2!}& g'(lambda) & g(lambda) & & \
vdots & & ddots & ddots & \
frac{g^{(k-1)}(lambda)}{(k-1)!} & frac{g^{(k-2)}(lambda)}{(k-2)!} & dots & g'(lambda) & g(lambda)
end{array}
right]=
$$
$$
=g(lambda)E+ g'(lambda) H_1 + frac{g”(lambda)}{2!}H_2+dots+
frac{g^{(k-1)}(lambda)}{(k-1)!} H_{k-1}
$$
?
Можно ли утверждать, что геометрическая кратность собственного числа $ g(lambda_j) $ матрицы $ g({mathbf A}) $ совпадает с геометрической кратностью собственного числа $ lambda_j $ матрицы $ {mathbf A} $ (т.е. что порядки соответствующих клеток Жордана одинаковы)?
Аналитическая функция от матрицы
Норма матрицы. Матричный ряд
Нормой произвольной (не обязательно квадратной) матрицы $ A in mathbb C^{mtimes n} $ называется неотрицательное число $ | A | $, удовлетворяющее условиям (аксиомам):
1.
$ | A |=0 $ тогда и только тогда, когда $ A=mathbb O_{mtimes n} $;
2.
для $ forall alphain mathbb C $ справедливо $ | alpha A |=|alpha |cdot | A | $;
3.
для любых матриц $ A, B $ из $ mathbb C^{mtimes n} $ справедливо $ | A + B | le | A |+| B | $;
Три эти аксиомы являются универсальными аксиомами нормы в произвольном линейном векторном пространстве. Для матриц можно ввести дополнительную операцию — операцию умножения. В этом случае норму подчиняют еще одной аксиоме.
4.
для любых матриц $ A_{} $ и $ B_{} $, допускающих умножение $ A cdot B $,
справедливо $ | A cdot B | le | A | cdot | B | $.
Здесь следует отметить, что матрицы $ A, B $ и $ Acdot B $ принадлежат, вообще говоря, разным линейным пространствам. В каждом из этих пространств норма может быть задана по различным формулам. Более подробное изложение материала с особенностями введения нормы в произвольном линейном векторном пространстве
☞
ЗДЕСЬ. В настоящем и последующем пунктах мы ограничимся только рассмотрением норм векторов и норм квадратных матриц.
Норму можно вводить разными способами.
П
Пример.
Для матриц с комплексными элементами евклидова норма (или норма Фробениуса) вводится формулой:
$$| A | = sqrt{sum_{j,k} |a_{jk}|^2} ;$$
эту формулу для матриц с вещественными элементами можно переписать в виде
$$
| A | = sqrt{ operatorname{Sp}_{}, (A cdot A^{^{top}})} , .
$$
Выполнение для нее аксиом
1
и
2
очевидно. Справедливость
3
следует из неравенства треугольника: $ |a_{jk}+b_{jk}|^2le |a_{jk}|^2 +|b_{jk}|^2 $, а
4
следует из неравенства Коши-Буняковского:
$$|a_{j1}b_{1k}+dots+ a_{jn}b_{nk}|^2 le
left(|a_{j1}|^2+dots+|a_{jn}|^2 right)
left(|a_{1k}|^2+dots+|a_{nk}|^2 right) , .$$
Эту норму можно рассматривать как обобщение понятия длины вектора в $ mathbb R^{n} $:
$ | X_{ntimes 1} | = sqrt{ x_1^2+dots+x_n^2}=|X| $.
Вообще, любая формула, задающая скалярное произведение в евклидовом пространстве матриц, порождает и норму матрицы:
$ | A |= sqrt{langle A,A rangle} $. Только что введенная норма соответствует стандартному скалярному произведению.
Т
Теорема 9. Евклидова норма вещественной матрицы не меняется при умножении этой матрицы на произвольную ортогональную.
Доказательство
☞
ЗДЕСЬ.
П
Пример.
$ displaystyle | A | = max_j sum_k |a_{jk}| $. Тогда
$ | X_{ntimes 1} | =displaystyle{ max_{j=1,dots,n} |x_j|} $.
П
Пример. $ displaystyle | A | = max_k sum_j |a_{jk}| $. Тогда
$ | X_{ntimes 1} | =displaystyle{ sum_{j=1}^n |x_j|} $.
Введение понятия нормы позволяет упростить рассуждения о сходимости матричной последовательности $ { A_N }_{N=1}^{infty} $. В предыдущих пунктах эта сходимость понималась в смысле существования пределов у
последовательностей элементов $ a_{jk}^{(N)} $ одновременно для всех индексов $ j_{} $ и $ k_{} $.
Норма позволяет объединить исследование этих последовательностей на сходимость в изучение одной.
Т
Теорема 10. Последовательность $ { A_N }_{N=1}^{infty} $ сходится при $ N to infty $ к матрице $ A_{} $ тогда и только тогда, когда
$$lim_{Nto infty} | A_N – A |=0 , .$$
Матричный ряд
$$
sum_{j=1}^{infty} A_j = A_1 + dots + A_N+ dots
$$
называется сходящимся если существует конечный предел последовательности
$$left{ S_N = sum_{j=1}^{N} A_j= A_1 + dots + A_N right}_{N=1}^{infty}$$
его частичных сумм. Тогда величина этого предела называется суммой матричного ряда:
$$ S= sum_{j=1}^{infty} A_j = lim_{Nto infty} S_N , .$$
Матричный ряд называется расходящимся если хотя бы для
одной пары индексов $ j_{} $ и $ k_{} $ последовательность $ s_{jk}^{(N)} $ расходится.
Матричный ряд называется абсолютно сходящимся если сходится числовой ряд его норм:
$ displaystyle sum_{j=1}^{infty} | A_j | $.
Т
Теорема 11. Если матричный ряд сходится абсолютно, то он сходится и в обычном смысле.
Т
Теорема 12 [признак сравнения]. Если ряд $ displaystyle sum_{j=1}^{infty} A_j $
абсолютно сходится и $ | A_j |ge | B_j | $ для
$ forall jin mathbb N $, то и ряд
$ displaystyle sum_{j=1}^{infty} B_j $ сходится абсолютно.
Матричный степенной ряд
Рассмотрим теперь степенной ряд
$$
sum_{j=0}^{infty}b_j z^j=b_0+b_1z+b_2z^2+dots
$$
переменную в котором предполагаем комплексной: $ z in mathbb C $.
Пусть $ R $ — радиус сходимости этого ряда, т.е. ряд сходится
при $ |z|<R $ и расходится при $ |z|>R $. Известно, что
$$R=overline{lim_{nto infty}}left| frac{b_n}{b_{n+1}} right|=
overline{lim_{nto infty}} frac{1}{sqrt[n]{|b_{n}|}} , .$$
Рассмотрим теперь соответствующий матричный степенной ряд
$$
sum_{j=0}^{infty} b_j Z^j =b_0E+b_1 Z +b_2 Z^2+dots
$$
при $ Z in mathbb C^{ntimes n} $.
Т
Теорема 13. Матричный степенной ряд сходится абсолютно
для любой матрицы $ Z $ такой, что $ | Z|<R $.
Доказательство. Имеем
$$ sum_{j=0}^{infty}| b_j Z^j | le sum_{j=0}^{infty}| b_j|, | Z |^j , .$$
Числовой ряд в правой части сходится при $ | Z|<R $. На основании теорем $ 11 $ и $ 12 $
сходится и ряд $ sum_{j=0}^{infty} b_j Z^j $.
П
Пример. Ряд
$$sum_{j=0}^{infty}z^j=1+z+z^2+dots+z^j+dots $$
сходится при $ |z|<1 $ к функции $ 1/(1-z) $. На основании теоремы $ 13 $
можно утверждать, что матричный ряд
$$
sum_{j=0}^{infty}Z^j=E+Z+Z^2+dots+Z^j+dots
$$
сходится абсолютно для любой матрицы $ Z $ такой, что $ | Z|<1 $.
=>
Если ряд $ sum_{j=0}^{infty}b_j z^j $ сходится при $ forall z in mathbb C $,
то и ряд $ sum_{j=0}^{infty}b_j Z^j $ сходится при любой матрице $ Zin mathbb C^{n times n} $.
Сумма сходящегося степенного ряда $ sum_{j=0}^{infty}b_j Z^j $ будет
функцией переменной матрицы $ Z $. Такая функция называется аналитической функцией матрицы.
Если обозначить сумму ряда $ sum_{j=0}^{infty}Z^j $ через $ F(Z) $, то
легко проверяется
свойство: $ F(Z)(E-Z)=E $. Таким образом, ряд сходится к матрице $ (E-Z)^{-1} $ при $ |Z |<1 $.
Т
Теорема 14. Если матрицы $ A $ и $ B $ подобны, а $ F $ — аналитическая функция, определенная для $ A $, то тогда она будет
определена и для $ B $, и матрицы $ F(A) $ и $ F(B) $ также подобны:
$$ A doteq B quad Rightarrow quad F(A) doteq F(B) , . $$
Доказательство. По условию $ B=C^{-1} AC $ при некоторой неособенной матрице
$ Cin mathbb C^{ntimes n} $. Рассмотрим $ N $-ю частичную сумму ряда:
$$ F_N(Z)= sum_{j=0}^{N} a_j Z^j, . $$
В
☝
ПУНКТЕ было доказано, что
$$F_N(B)=C^{-1}F_N(A) C , .$$
Переходя к пределу, получаем
$$lim_{N rightarrow infty} F_N(B)=
C^{-1}left( lim_{N rightarrow infty} F_N(A) right) C =C^{-1}F(A)C , .$$
Таким образом, функция $ F $ определена и для $ B $ и $ F(B)=C^{-1}F(A)C $.
♦
Т
Теорема 15. Ряд $ sum_{j=0}^{infty} b_j Z^j $ сходится для любой матрицы $ A $ чей спектр лежит внутри круга сходимости:
$$ {|lambda_j|<R}_{j=1}^n $$
и расходится если хотя бы одно число оказывается за пределами этого круга:
$$ exists j in {1,dots,n} quad mbox{ такое, что } quad |lambda_j|>R , . $$
Доказательство
☞
ЗДЕСЬ.
=>
Если $ {|lambda_j|<R}_{j=1}^n $, то спектр матрицы $ F(A) $ равен $ { F(lambda_j) }_{j=1}^n $.
П
Пример. Вычислить сумму ряда
$$sum_{j=1}^{infty}frac{1}{j} A^j quad npu quad
A=left( begin{array}{rrr}
-3/2& 0& -4 \
-7& 1/2 & -14\
1 & 0 & 5/2
end{array}
right)
,
.$$
Решение. Соответствующий степенной ряд сходится при $ |z|<1 $ и
имеет суммой $ (- ln (1-z)) $.
$$ det (A-lambda E)=-(lambda-1/2)^3 , . $$
По теореме $ 15 $ матричный ряд сходится. Для применения
формулы ?? нам потребуется ЖНФ матрицы $ A $. Опуская промежуточные вычисления, получим
$$
A=
underbrace{
left( begin{array}{rrr}
-2& -1& -2 \
0& 0 & -7\
1 & 1 & 1
end{array}
right)}_{C}
underbrace{
left( begin{array}{rrr}
1/2& 0& 0 \
0& 1/2 & 0\
0 & 1 & 1/2
end{array}
right)
}_{A_{_{mathfrak J}}}
underbrace{
left( begin{array}{rrr}
-1& 1/7& -1 \
1 & 0 & 2 \
0 & -1/7 & 0
end{array}
right)
}_{C^{-1}}
$$
$$
– ln (E-A)=
left( begin{array}{rrr}
-2& -1& -2 \
0& 0 & -7\
1 & 1 & 1
end{array}
right)
left( begin{array}{rrr}
ln 2& 0& 0 \
0 & ln 2 & 0\
0 & 2 & ln 2
end{array}
right)
left( begin{array}{rrr}
-1& 1/7& -1 \
1 & 0 & 2 \
0 & -1/7 & 0
end{array}
right)
$$
Ответ.
$$
left( begin{array}{ccc}
ln 2-4 & 0 & -8 \
-14 & ln 2 & -28 \
2 & 0 & ln 2+4
end{array}
right) , .
$$
Формула
$$
F(Z)=CF(Z_{_{mathfrak J}})C^{-1} quad npu quad
Fleft( {mathfrak J}_k (lambda) right)=left[
begin{array}{ccccc}
F(lambda) & & & & \
F'(lambda) & F(lambda) & & mathbb O & \
frac{F”(lambda)}{2!}& F'(lambda) & F(lambda) & & \
vdots & & ddots & ddots & \
frac{F^{(k-1)}(lambda)}{(k-1)!} & frac{F^{(k-2)}(lambda)}{(k-2)!} &
dots & F'(lambda) & F(lambda)
end{array}
right]
$$
может быть использована и для доопределения функции от матрицы для случая тех
матриц, которые не удовлетворяют условиям теорем $ 13 $ или $ 15 $. Действительно, если ряд
$ sum_{j=1}^{infty} z^j/j $ представляет функцию
$ (-ln (1-z)) $ только при $ |z|<1 $, то сама функция существует и для $ z le -1 $.
Если договориться положить последнюю формулу в качестве определения функции
от матрицы $ Z $, то эта формула будет вычислять $ F(Z) $ для
всех тех матриц, на спектрах которых определены значения функции $ F(z) $
и ее производных до порядков, соответствующих порядкам клеток Жордана.
С использованием этой договоренности возможно и дальнейшее упрощение вычислений $ F(A) $, основанное на теореме Гамильтона-Кэли. В самом деле,
поскольку степени матрицы $ A^{n}, A^{n+1},dots $ линейно
выражаются через степени
$$ E=A^0, A, A^{2},dots, A^{n-1} , $$
то бесконечный ряд $ sum_{j=0}^{infty} b_j A^j $ может быть свернут в матричный полином
степени не выше $ n-1 $. Нахождение этого полинома производится обобщением
теоремы $ 2 $.
Т
Теорема 16. Если $ {lambda_1,dots,lambda_n} subset mathbb C $ — различные
корни аналитической функции $ Phi(z) $, лежащие внутри ее круга сходимости, то
существует единственное представление функции в виде:
$$
Phi(z) equiv (z-lambda_1)times dots times (z-lambda_n)Q(z) ,
$$
где $ Q(z) $ — аналитическая функция с тем же радиусом сходимости.
Т
Теорема 17. Если все собственные числа
$ lambda_1,dots,lambda_n $ матрицы $ A $ различны, то
$$F(A)=g(A) , ,$$
где $ g(x) $ — интерполяционный полином, построенный по таблице
$$
begin{array}{c|ccc}
x & lambda_1 & dots & lambda_n \ hline
y & F(lambda_1) & dots & F(lambda_n)
end{array}
, .
$$
Доказательство. Рассмотрим функцию $ Phi(z)= F(z)-g(z) $.
Поскольку $ g(lambda_j)=F(lambda_j) $, то $ Phi(lambda_j)=0 $ для всех
$ jin {1,dots,n} $. Тогда для $ Phi(z) $ будет выполнено тождество из теоремы $ 16 $.
Подставим матрицу $ A $ в это тождество:
$$Phi(A) equiv underbrace{(A-lambda_1E)times dots
times (A-lambda_nE)}_{=mathbb O}Q(A)
$$
Отсюда и следует равенство $ F(A)=g(A) $.
Дифференцирование матрицы
Рассмотрим (не обязательно квадратную) матрицу, элементами которой являются
функции, зависящие от переменной $ tin ]a,b[ subset mathbb R $:
$ A(t)=left[a_{jk}(t) right]_{j,k} $.
Производной матрицы $ A(t) $ по $ t $ будем называть матрицу
$$frac{ d, A(t)}{ d, t}= A^{prime} (t)=
left[frac{ d, a_{jk}(t)}{ d, t} right]_{j,k} $$
в предположении, что все производные в правой части существуют.
Таким образом, дифференцирование матрицы определается как ее поэлементное
дифференцирование. Поэтому свойства дифференцирования матриц легко выводятся
из соответствующих свойств производных скалярных функций.
Т
Теорема 18. Если соответствующие матричные действия имеют смысл, то
справедливы следующие соотношения
$$frac{ d, C}{ d, t}=mathbb O $$
при постоянной матрице $ C $ (элементы которой не зависят от $ t $);
$$frac{ d,left( A(t)+B(t) right)}{ d, t}=
frac{ d, A(t)}{ d, t}+frac{ d, B(t)}{ d, t} , ;$$
$$frac{ d, C A(t)}{ d, t}=
Cfrac{ d, A(t)}{ d, t} , quad
frac{ d, A(t)C}{ d, t}=frac{ d, A(t)}{ d, t} {bf C}
, ;$$
$$frac{ d, left(A(t)B(t) right)}{ d, t}=
frac{ d, A(t)}{ d, t}
B (t)+A (t)frac{ d, B(t)}{ d, t}
, .
$$
Для квадратной матрицы $ A(t) $ и $ Kin mathbb N $:
$$frac{ d, A^K(t)}{ d, t}
=A^{prime} (t)A^{K-1}(t)+A(t)A^{prime} (t)A^{K-2}(t)
+dots+A^{K-1}(t)A^{prime} (t) , ,$$
а если она коммутирует со своей производной, т.е. $ A(t)A^{prime} (t)=
A^{prime}(t)A(t) $, то
$$frac{ d, A^K(t)}{ d, t}=K A^{prime} (t)A^{K-1}(t)
, . $$
Для матрицы $ A(t) $, неособенной при любых рассматриваемых значениях $ t $, справедливо:
$$frac{ d, A^{-1} (t)}{ d, t} =-A^{-1} (t)
frac{ d,A(t)}{ d, t} A^{-1} (t) , . $$
Матричная экспонента
Матричной экспонентой или экспоненциалом называется матричный ряд
$$
exp ( Z )=e^{ Z } = sum_{j=0}^{infty} frac{Z^j}{j!}=E+Z+frac{1}{2}Z^2+frac{1}{3!}Z^3+dots
, .
$$
На основании следствия к теореме $ 13 $ этот ряд сходится и притом абсолютно для любой матрицы $ Z in mathbb C^{ntimes n} $ .
В настоящем пункте мы ограничимся рассмотрением вещественной матрицы $ Z $.
Т
Теорема 19. Если матрицы $ A $ и $ B $ коммутируют, то коммутируют и $ e^{A} $ и $ e^{ B} $:
$$
e^{A} e^{B} =e^{B} e^{A}= e^{A+B} , .
$$
Доказательство
☞
ЗДЕСЬ.
=>
Для любой матрицы $ A $ матрица $ e^{A} $ обратима и $ left( e^{A} right)^{-1}=e^{-A} $ .
Особое прикладное значение имеет матрица
$$
e^{tA}= sum_{j=0}^{infty} frac{t^j}{j!} A^j , ,
$$
зависящая от параметра $ tin mathbb C $. Если продифференцировать ряд по этому параметру, то на основании теоремы ?? получим:
$$
frac{ d, e^{t A}}{ d, t}=sum_{j=1}^{infty}
frac{jt^{j-1}}{j!}A^j=A
sum_{j=1}^{infty} frac{t^{j-1}}{(j-1)!}A^{j-1}=Ae^{tA} , .
$$
Таким образом, $ e^{t A} $ является решением матричного дифференциального уравнения2)
$$
frac{ d, X}{ d, t}= A X , .
$$
Обычно это уравнение рассматривают не относительно квадратной матрицы $ X $,
а относительно вектора-столбца $ X_{ntimes 1} $, т.е. последнее уравнение представляет матричную запись системы обыкновенных
дифференциальных уравнений:
$$
left{
begin{array}{cccccc}
d, x_1/d, t &=&a_{11}x_1+&a_{12}x_2+&dots+&a_{1n}x_n , , \
d, x_2/d, t &=&a_{21}x_1+&a_{22}x_2+&dots+&a_{2n}x_n , ,\
dots & & & &dots & \
d, x_n/d, t &=&a_{n1}x_1+&a_{n2}x_2+&dots+&a_{nn}x_n , .
end{array}
right.
$$
При задании начальных условий
$$
x_1(t_0)=x_{10},x_2(t_0)=x_{20},dots , x_n(t_0)=x_{n0} quad iff
quad X(t_0)=X_0
$$
решение уравнения $ d, X big/ d, t= A X $
представляет естественное обобщение одномерного (скалярного) случая:
$$
X(t)=e^{(t-t_0)A}X_0 , .
$$
В пункте ?? указаны два способа вычисления аналитической функции матрицы. Применим их для нахождения $ e^{t A} $.
$$
e^{t A}=Ce^{t A_{mathfrak J}}C^{-1}
$$
и вычисление $ e^{t, x} $ от клетки Жордана производится по формуле
$$
exp left( t cdot left[
begin{array}{rrrrr}
lambda & & & & \
1 & lambda & &mathbb O & \
0& 1 & lambda & & \
vdots & & ddots & ddots & \
0 & 0 & dots & 1 &lambda
end{array}
right]_{ktimes k}right)=
left[
begin{array}{ccccc}
e^{lambda t} & & & & \
te^{lambda t} & e^{lambda t} & &mathbb O & \
frac{t^2}{2!}e^{lambda t}& te^{lambda t} & e^{lambda t} & & \
vdots & & ddots & ddots & \
frac{t^{k-1}}{(k-1)!}e^{lambda t} & frac{t^{k-2}}{(k-2)!}e^{lambda t}
& dots & te^{lambda t} &
e^{lambda t}
end{array}
right]=
$$
$$
=e^{lambda t} left( E+ t H_1 + frac{t^2}{2!}H_2+dots+
frac{t^{k-1}}{(k-1)!} H_{k-1} right) , .
$$
Матрицы $ {H_j} $ определяются в
☝
ПУНКТЕ.
?
Доказать справедливость равенства: $ det( e^A ) = e^{operatorname{Sp} (A )} $.
П
Пример. Для системы дифференциальных уравнений
$$
left{
begin{array}{ccccc}
d, x_1 / d, t &=&&x_2&+x_3, \
d, x_2 / d, t &=&x_1&+x_2&-x_3, \
d, x_3 / d, t &=&&x_2&+x_3
end{array}
right.
$$
а) найти решение при $ x_1(0)=1,x_2(0)=1,x_3(0)=1 $;
б) найти все начальные условия
$$ x_1(0)=x_{10},x_2(0)=x_{20},x_3(0)=x_{30}, , $$
для которых решения будут ограниченными при $ tto +infty $.
Решение. Здесь $ t_0=0 $, $ det (A – lambda E) = – lambda (lambda -1)^2 $.
$$
A=
underbrace{
left( begin{array}{rrr}
2& -1& 1 \
-1& 1 & 0\
1 & -1 & 1
end{array}
right)}_{C}
underbrace{
left( begin{array}{rrr}
0& 0& 0 \
0& 1 & 0\
0 & 1 & 1
end{array}
right)
}_{{bf A}_{mathfrak J}}
underbrace{
left( begin{array}{rrr}
1& 0& -1 \
1 & 1 & -1 \
0 & 1 & 1
end{array}
right)
}_{C^{-1}}
$$
$$
e^{t A}=
left( begin{array}{rrr}
2& -1& 1 \
-1& 1 & 0\
1 & -1 & 1
end{array}
right)
left( begin{array}{rrr}
1& 0& 0 \
0& e^{t} & 0\
0 & te^{t} & e^{t}
end{array}
right)
left( begin{array}{rrr}
1& 0& -1 \
1 & 1 & -1 \
0 & 1 & 1
end{array}
right)=
$$
$$
=left( begin{array}{rrr}
2-e^{t}+te^t & t, e^t & -2+ 2, e^t-t, e^t \
-1 +e^t & e^t & 1-e^t \
1 -e^t+t, e^t& t, e^t & -1+2, e^t-t, e^t
end{array}
right) , .
$$
Домножая эту матрицу справа на столбец $ [1,1,1]^{^{top}} $, получаем
$$x_1(t)=e^t(1+t),, x_2(t)=e^t,, x_3(t)=e^t(1+t) , . $$
Для решения б) домножим последнюю матрицу справа на столбец
$ [x_{10},x_{20},x_{30}]^{^{top}} $. Получившийся столбец можно представить в виде
линейной комбинации трех:
$$
left( begin{array}{c}
2x_{10}-2x_{30} \ -x_{10}+x_{30} \ x_{10} – x_{30}
end{array}
right)
+e^t
left( begin{array}{c}
-x_{10}+2,x_{30} \ x_{10}+x_{20}-x_{30} \ -x_{10} +2, x_{30}
end{array}
right)
+t, e^t
left( begin{array}{c}
x_{10}+x_{20}-x_{30} \ 0 \ x_{10}+x_{20}-x_{30}
end{array}
right)
$$
Решение может быть ограниченным лишь при условии, когда столбцы при $ e^t $
и $ t, e^t $ будут нулевыми. Решаем получившуюся систему линейных
однородных уравнений относительно $ x_{10},x_{20} $ и $ x_{30} $, получаем, что
при любом $ x_{30} $ решение, проходящее через точку $ [2, x_{30},-x_{30},x_{30}]^{^{top}} $
будет ограниченным; более того, оно будет стационарным, т.е. не покинет
этой точки при изменении $ t $.
♦
П
Пример. Найти решение системы дифференциальных уравнений
$$
left{
begin{array}{ccrrrr}
d, x_1 / d, t &=&-9,x_1&+12,x_2&-7,x_3 &-7, x_4, \
d, x_2 / d, t &=&-25,x_1&+35,x_2&-20,x_3&-22, x_4 , \
d, x_3 / d, t &=&-16,x_1&+24,x_2&-14,x_3&-15, x_4, \
d, x_4 / d, t &=&-17,x_1&+22,x_2&-12,x_3&-14, x_4,
end{array}
right.
$$
при $ x_1(0)=1,x_2(0)=0,x_3(0)=1,x_4(0)=0 $.
Решение. Имеем:
$$ f(lambda)=det (A-lambda E) = lambda^4+2lambda^3+6lambda^2+2lambda+5 , .$$
Спектр матрицы $ { -1 pm 2 mathbf i, pm mathbf i } $ состоит из мнимых чисел. Для вычисления $ e^{At} $ можно воспользоваться интерполяционной формулой из пункта ??. Вычисления частных при делении $ f(lambda) $ на линейные полиномы $ lambda- lambda_{ast} $ и
$ lambda- overline{lambda_{ast}} $ упрощаются соображениями комплексной сопряженности:
$$
f_1(lambda)equiv frac{f(lambda)}{lambda-(-1+2 mathbf i))}equiv lambda^3+(1+2 mathbf i)lambda^2+lambda+(1+2 mathbf i),
$$
$$
f_2(lambda)equiv frac{f(lambda)}{lambda-(-1-2 mathbf i))}equiv overline{f_1(lambda)} equiv lambda^3+(1-2 mathbf i)lambda^2+lambda+(1-2 mathbf i),
$$
$$
f_3(lambda)equiv frac{f(lambda)}{lambda-mathbf i}equiv
lambda^3+(2+mathbf i)lambda^2+(5+2mathbf i)lambda+5 mathbf i , ,
$$
$$
f_4(lambda)equiv frac{f(lambda)}{lambda+mathbf i}equiv overline{f_3(lambda)} equiv
lambda^3+(2-mathbf i)lambda^2+(5-2mathbf i)lambda-5 mathbf i , .
$$
Аналогичное упрощение возникает и при вычислениях полиномов от матрицы, т.е. $ {f_j(A)} $:
$$
f_1(A)=
left(
begin{array}{rrrr}
32+26 mathbf i & -40-20 mathbf i & 20+10 mathbf i & 28+4 mathbf i \
73+88 mathbf i & -98-76 mathbf i & 49+38 mathbf i & 74+26 mathbf i\
54+46 mathbf i & -68-36 mathbf i & 34+18 mathbf i & 48+8 mathbf i\
42+66 mathbf i & -60-60 mathbf i & 30+30 mathbf i & 48+24 mathbf i
end{array}
right), , f_2(A)=overline{f_1(A)} ,
$$
$$
f_3(A)=
left(
begin{array}{rrrr}
7-mathbf i & -2+14 mathbf i & -3-9 mathbf i & 2-12 mathbf i\
17-6 mathbf i &2+36 mathbf i &-12-21 mathbf i & -1-31 mathbf i \
13-9 mathbf i & 10+30 mathbf i & -15-15 mathbf i & -8-26 mathbf i \
7-mathbf i &-2+14 mathbf i & -3-9 mathbf i & 2-12 mathbf i
end{array}
right), , f_4(A)=overline{f_3(A)} .
$$
Формулы решения системы дифференциальных уравнений по формуле
$$
left(sum_{j=1}^4 e^{lambda_j t} frac{f_j(A)}{f_j(lambda_j)}right) left( begin{array}{c} 1 \ 0 \ 1 \ 0 end{array} right) , .
$$
приводим к вещественному виду с использованием
формулы Эйлера
представления экспонент от мнимых чисел:
$$ e^{lambda_j t} = e^{t mathfrak{R}mathbf{e} (lambda_j) } left{cos ( t mathfrak{I}mathbf{m}(lambda_j)) + mathbf i sin ( t mathfrak{I}mathbf{m}(lambda_j)) right} , .
$$
Ответ.
$$
x_1(t)=frac{1}{5}( 17 e^{-t} cos (2t)-31 e^{-t} sin (2t) -2 cos t – sin t ), ,
$$
$$
x_2(t)=frac{1}{10}( 59 e^{-t} cos (2t)-187 e^{-t} sin (2t) -59 cos t – 17sin t ), ,
$$
$$
x_3(t)=frac{1}{5}( 28 e^{-t} cos (2t)-54 e^{-t} sin (2t) -23 cos t – 14sin t ), ,
$$
$$
x_4(t)=frac{1}{10}( 12 e^{-t} cos (2t)-66 e^{-t} sin (2t) -12 cos t – sin t ), .
$$
Если при любых начальных условиях решение уравнения
$$
frac{ d, X}{ d, t}= A X , .
$$
ограничено при $ t to +infty $, то будем называть это уравнение устойчивым по Ляпунову.
Устойчивое уравнение называется асимптотически устойчивым по Ляпунову если
все решения стремятся к $ mathbb O_{ntimes 1} $ при $ t to +infty $.
Уравнение называется неустойчивым по Ляпунову, если существует хотя бы один набор начальных условий, для которого соответствующее решение $ X(t) $ неограничено при $ t to +infty $.
В дальнейшем будем говорить просто об устойчивости, имея в виду устойчивость по Ляпунову.
Представление решения уравнения формулой
$$
X(t)=e^{(t-t_0)A}X_0
$$
позволяет свести исследование устойчивость этого уравнения к анализу спектра матрицы $ A $, либо же — в случае наличия кратных собственных чисел матрицы — к анализу ее жордановой нормальной формы $ A_{mathfrak J} $.
Т
Теорема 20. Уравнение $ d, X big/ d, t= A X $
а) устойчиво тогда и только тогда, когда
$$ mathfrak{R}mathbf{e} (lambda_j) le 0 quad npu j in {1,dots,n} , ,$$
и клетки Жордана в ЖНФ $ A_{mathfrak J} $, соответствующие собственным числам с $ mathfrak{R}mathbf{e} (lambda_j) = 0 $, имеют порядок $ 1 $;
б) асимптотически устойчиво тогда и только тогда, когда
$$ mathfrak{R}mathbf{e} (lambda_j) < 0 quad npu j in {1,dots,n} $$
(т.е. спектр матрицы $ A $ лежит в левой полуплоскости комплексной плоскости).
Конструктивная проверка последнего условия возможна чисто алгебраическими методами. Действительно, это условие
означает устойчивость характеристического полинома $ f(lambda)=det (A-lambda E) $
и может быть проверено с помощью критериев Рауса или Льенара-Шипара за конечное
число элементарных операций над коэффициентами.
=>
Уравнение $ d, X big/ d, t= A X $ с симметричной матрицей $ A $
а) устойчиво тогда и только тогда, когда матрица отрицательно полуопределена;
б) асимптотически устойчиво тогда и только тогда, когда матрица отрицательно определена.
Возникает сильное желание обобщить предлагаемый подход на систему уравнений
$$
frac{ d, X}{ d, t}= A(t) X
$$
с матрицей, зависящей от $ t $. Например, в случае, когда $ A(t) $ является матричным полиномом
$$
A(t)=A_0t^K+A_1t^{K-1} + dots + A_K quad npu {A_0,A_1,dots,A_K} subset mathbb R^{ntimes n}
$$
соблазнительно записать решение в виде
$$ X(t)=e^{int_{t_0}^t A(tau) d tau} X_0 $$
при
$$
int_{t_0}^t A(tau) d tau= A_0 frac{(t^{K+1}-t_0^{K+1})}{(K+1)!}+A_1 frac{(t^{K}-t_0^{K})}{K!} + dots + A_K (t-t_0) , .
$$
К сожалению, в общем случае, этот подход не сработает. Причины этого объясняются
☞
ЗДЕСЬ.
Матричные синус и косинус
Решение дифференциального уравнения второго порядка, описывающего, например, закон Гука
$$frac{ d,^2 x}{ d, t^2}= a, x , { x,a,t} subset mathbb R, x(t_0)=x_0,
frac{ d, x(t)}{ d, t}Bigg|_{t=t_0}= x_0^{prime}
$$
представимо в виде
$$
x(t)=left{ begin{array}{ccc}
displaystyle
frac{sqrt{a}x_0+x_0^{prime}}{2sqrt{a}} e^{sqrt{a}(t-t_0)} +
frac{x_0-x_0^{prime}}{2sqrt{a}} e^{-sqrt{a}(t-t_0)}
& npu & a>0, \
displaystyle
x_0 cos left( sqrt{|a|}(t-t_0) right) +
frac{x_0^{prime}}{sqrt{|a|}}
sin left( sqrt{|a|}(t-t_0) right)
& npu & a<0, \
x_0+x_0^{prime}(t-t_0) & npu & a=0 , .
end{array}
right.
$$
По аналогии поставим задачу поиска решения для системы уравнений
$$
frac{ d^2 X}{ d, t^2}=AX
$$
при матрице $ A in mathbb R^{ntimes n} $. Желательно найти такие матричные
аналоги для используемых операций, чтобы формулы для решения сохранили тот же вид.
Аналогами тригонометрических функций являются матричные синус и косинус:
$$
sin Z = sum_{j=1}^{infty} (-1)^{j-1}frac{Z^{2j-1}}{(2j-1)!}=
Z- frac{Z^3}{3!}+frac{Z^5}{5!}-dots
$$
$$
cos Z = sum_{j=0}^{infty} (-1)^{j}frac{Z^{2j}}{(2j)!}=
E- frac{Z^2}{2!}+frac{Z^4}{4!}-dots
$$
На основании следствия к теореме $ 13 $ оба ряда сходятся при
любой матрице $ Z in mathbb C^{ntimes n} $.
П
Пример. Вычислить $ cos $ и $ sin $ от матрицы
$$
A=left(
begin{array}{rr}
0 & 1 \
-1 & 0
end{array}
right) , .
$$
Решение проведем двумя способами. Сначала следуем формальному определению.
$$
A^2=
left(
begin{array}{rr}
-1 & 0 \
0 & -1
end{array}
right),
A^3=
left(
begin{array}{rr}
0 & -1 \
1 & 0
end{array}
right),
A^4=
left(
begin{array}{rr}
1 & 0 \
0 & 1
end{array}
right),
A^5=
left(
begin{array}{rr}
0 & 1 \
-1 & 0
end{array}
right) = A,
A^6=
left(
begin{array}{rr}
-1 & 0 \
0 & -1
end{array}
right)=A^2,dots
$$
Очевидна цикличность получающейся матричной последовательности.
$$
cos A=
left(
begin{array}{rr}
1 & 0 \
0 & 1
end{array}
right)-frac{1}{2}
left(
begin{array}{rr}
-1 & 0 \
0 & -1
end{array}
right) + frac{1}{4!} left(
begin{array}{rr}
1 & 0 \
0 & 1
end{array}
right) – dots =
$$
$$
=
left(
begin{array}{cc}
1+1/2+1/4!+dots & 0 \
0 & 1+1/2+1/4!+dots
end{array}
right) =
left(
begin{array}{cc}
(e+e^{-1})/2 & 0 \
0 & (e+e^{-1})/2
end{array}
right) , .
$$
Аналогично:
$$
sin A=
left(
begin{array}{cc}
0 & (e-e^{-1})/2 \
-(e-e^{-1})/2 & 0
end{array}
right) , .
$$
А теперь проверим с помощью интерполяционного представления. Вычислим характеристический полином:
$$ det (A-lambda E) = lambda^2 +1 equiv (lambda- mathbf i)(lambda+ mathbf i) , . $$
Тогда
$$
cos A = frac{cos mathbf i}{2mathbf i} (A+mathbf i E) + frac{cos (-mathbf i)}{-2mathbf i} (A-mathbf i E)=E cos mathbf i , .
$$
Хотя и трудно поверить, но можно формально проверить справедливость равенства
$$ cos mathbf i = frac{e+e^{-1}}{2} , . $$
То есть косинус чисто мнимого числа равен числу вещественному (да еще и большему $ 1 $)! Но это действительно следует из формального определения косинуса как суммы степенного ряда.
♦
Т
Теорема 21. Справедливо основное тригонометрическое тождество
$$ cos^2 Z + sin^2 Z equiv E_{ntimes n} , . $$
Квадратный корень из матрицы
Сложности возникают при определении $ sqrt{ A} $. Формально, корнем
квадратным из матрицы $ {mathbf A} $ называется решение матричного уравнения
$$
X^2=A
$$
Уже для матриц второго порядка это уравнение не всегда разрешимо:
например, не существует решения при
$$A = left(
begin{array}{cc}
0 & 0 \
1 & 0
end{array}
right) .
$$
С другой стороны, при
$$A = left(
begin{array}{rr}
-1 & 0 \
0 & -1
end{array}
right)
$$
существует бесконечное множество решений
$$
X=
left(
begin{array}{cc}
alpha & -(alpha^2+1)/beta \
beta & -alpha
end{array}
right) ,
$$
задаваемое двумя параметрами $ alpha $ и $ beta ne 0 $.
Т
Теорема 22. Решение уравнения
$$
X^2=A
$$
а) всегда существует при $ det A ne 0 $;
б) всегда существует среди вещественных симметричных матриц,
если $ A $ — симметричная и положительно полуопределенная.
Доказательство проведем только для б). Симметричная матрица $ A $
приводится к диагональному виду с помощью ортогональной матрицы:
$$
P^{^{top}}{mathbf A}P=
left( begin{array}{cccc}
lambda_1 & & & mathbb O \
& lambda_2 & & \
&& ddots & \
mathbb O && & lambda_n
end{array}
right) quad npu quad P^{^{top}}=P^{-1} .
$$
Легко видеть, что матрица
$$
X= P left( begin{array}{cccc}
sqrt{lambda_1} & & & mathbb O \
& sqrt{lambda_2} & & \
&& ddots & \
mathbb O&& & sqrt{lambda_n}
end{array}
right)P^{^{top}}
$$
является решением уравнения $ X^2=A $. Здесь под $ sqrt {.} $
понимается произвольное значение квадратного корня. Это значение будет
вещественным при $ lambda_jge 0 $. Если матрица $ A $ положительно
полуопределена, то все $ lambda_j $ неотрицательны.
Таким образом, последняя формула определяет вещественное решение; матрица $ X $
будет симметричной и может быть выбрана положительно полуопределенной.
♦
П
Пример. Вычислить
$$sqrt{
left( begin{array}{rrr}
24 & 6 & -12 \
6 &33 & 6\
-12 & 6 & 24
end{array}
right)
}
.
$$
Решение. $ det (A – lambda E) = – (lambda-9) (lambda -36)^2 $.
Поскольку матрица $ A $ симметрична, то привести ее к диагональному
виду можно с помощью ортогональной матрицы $ C $. Мы, однако же, используем
общий алгоритм диагонализации чтобы получить возможно
большее число ответов:
$$
{mathbf A}=
underbrace{
left( begin{array}{rrr}
1& 0& 2 \
2& 2 & -1\
0 & 1 & 2
end{array}
right)}_{C}
underbrace{
left( begin{array}{rrr}
36& 0& 0 \
0& 36 & 0\
0 & 0 & 9
end{array}
right)
}_{{mathbf A}_{mathfrak J}}
underbrace{
left( begin{array}{rrr}
5/9& 2/9& -4/9 \
-4/9 & 2/9 & 5/9 \
2/9 & -1/9 & 2/9
end{array}
right)}_{C^{-1}}
$$
$$
sqrt{{mathbf A}}=
underbrace{
left( begin{array}{rrr}
1& 0& 2 \
2& 2 & -1\
0 & 1 & 2
end{array}
right)}_{C}
underbrace{
left( begin{array}{rrr}
pm 6& 0& 0 \
0& pm 6 & 0\
0 & 0 & pm 3
end{array}
right)
}_{sqrt{{mathbf A}_{mathfrak J}}}
underbrace{
left( begin{array}{rrr}
5/9& 2/9& -4/9 \
-4/9 & 2/9 & 5/9 \
2/9 & -1/9 & 2/9
end{array}
right)
}_{C^{-1}}
$$
Ответ. $ sqrt{A}= $
$$
pmunderbrace{ frac{1}{3}left( begin{array}{rrr}
14& 2& -4 \
2 & 17 & 2 \
-4 & 2 & 14
end{array}
right)}_{+++ sqrt{A_{mathfrak J}}} ;
pmunderbrace{ frac{1}{3}left( begin{array}{rrr}
14& 2& -4 \
34 & 1 & -38 \
12 & -6 & -6
end{array}
right)}_{+-+ sqrt{A_{mathfrak J}}} ;
pmunderbrace{ left( begin{array}{rrr}
-2& -2& 4 \
-2 & -5 & -2 \
4 & -2 & -2
end{array}
right)}_{–+ sqrt{A_{mathfrak J}}} ;
$$
$$
pmunderbrace{ frac{1}{3}left( begin{array}{rrr}
6& 6& -12 \
38 & -1 & -34 \
4 & -2 & -14
end{array}
right)}_{+– sqrt{A_{mathfrak J}}} .
$$
Т
Теорема 23. Если $ A $ —симметричная матрица такая, что
-
она положительно определена;
-
матрица $ E-A $ положительно определена;
то рекуррентная матричная последовательность
$$ X_0=mathbb O, left{ X_{j}=X_{j-1}+frac{1}{2}(A-X_{j-1}^2) right}_{j=1}^{infty} $$
сходится к положительно определенному квадратному корню из $ A $.
Условия на матрицу $ A $ эквивалентны тому, что ее спектр целиком лежит в интервале $ [0,1] $ (следствие
☞
теоремы Коши ).
П
Пример. Для
$$
A=left(begin{array}{rrr}
0.541667 & 0.205342 & -0.372008 \
0.205342 & 0.811004 & 0.166667 \
-0.372008 & 0.166667 & 0.522329
end{array}
right)
$$
имеем (все матрицы — симметричные)
$$
X_0=mathbb O_{3times 3}, X_1=left(begin{array}{rrr}
0.2708335 & 0.102671 & -0.186004\
ast & 0.405502 & 0.083333\
ast & ast & 0.261164
end{array}
right), dots,
$$
$$
X_{12}=left(begin{array}{rrr}
0.640657 & 0.167720& -0.315098\
ast & 0.871895 & 0.147379\
ast & ast & 0.630487
end{array}
right)
$$
и
$$
X_{12}^2-A approx
left(begin{array}{rrr}
-0.004 & 0.0019 & -0.0038\
ast & -0.0009& 0.0019\
ast & ast & -0.0038
end{array}
right) , .
$$
Задачи
Источники
Демидович Б.П. Лекции по математической теории устойчивости. М.: Изд-во МГУ: ЧеРо, 1998
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Функция от матрицы
В настоящем разделе матрица $ A_<> $ считается квадратной порядка $ n_<> $.
Полином от матрицы
Сначала оптимизируем вычисление степени матрицы.
Пример 1. Вычислить
$$ A^ <100>quad npu quad A=left( begin 1 &2 &1 &0 \ 1 & 1 & 0 &-1 \ -2& 0 & 1 & 2 \ 0 & 2 & 1 & 1 end right)^ <100> . $$
Решение. Можно организовать вычисление $ A^ <100>$ по алгоритму квадрирования-умножения, заимствованному из раздела “MОДУЛЯРНАЯ АРИФМЕТИКА”: $$ A^<100>=left( left( left( left( left( left( A right)^2 A right)^2 right)^2 right)^2 Aright)^2 right)^2 . $$ Имеем: $ underline<100>_<_<10>>=underline<1100100>_ <_2>$ $$ begin <|c|c|c|c|c|c|c|c|>hline j & 1 & 2 & 3 & 4 & 5 &6 &7 \ hline <mathfrak b>_j & 1 & 1 & 0 & 0 & 1 &0 & 0 \ hline & A & A^2 A & left(A^3 right)^2 & left(A^6 right)^2 & left(A^ <12>right)^2 A & left(A^ <25>right)^2& left(A^ <50>right)^2 \ & left( begin 1 &2 &1 &0 \ 1 & 1 & 0 &-1 \ -2& 0 & 1 & 2 \ 0 & 2 & 1 & 1 end right) & left( begin 1 &6 & 3 &0 \ 3& 1 & 0 &-3 \ -6& 0 & 1 & 6 \ 0 & 6 & 3 & 1 end right) & left( begin 1 & 12 & 6 &0 \ 6 & 1 & 0 &-6 \ -12& 0 & 1 & 12 \ 0 & 12 & 6 & 1 end right) & left( begin 1 & 24 & 12 &0 \ 12 & 1 & 0 &-12 \ -24& 0 & 1 & 24 \ 0 & 24 & 12 & 1 end right) & left( begin 1 & 50 & 25 &0 \ 25 & 1 & 0 &-25 \ -50& 0 & 1 & 50 \ 0 & 50 & 25 & 1 end right) & left( begin 1 & 100 & 50 &0 \ 50 & 1 & 0 &-50 \ -100& 0 & 1 & 100 \ 0 & 100 & 50 & 1 end right) & left( begin 1 & 200 & 100 &0 \ 100 & 1 & 0 &-100 \ -200& 0 & 1 & 200 \ 0 & 200 & 100 & 1 end right) \ hline end $$ ♦
Рассмотрим далее произвольный полином $ g(x)=b_0x^m+b_1x^+dots+b_m in mathbb C[x] $. Вычисление его значения от матрицы $ A_<> $, т.е. $$ g(A)=b_0A^m +b_1A^+dots+b_m E , $$ где $ E_<> $ — единичная матрица того же порядка, что и $ A_<> $, может быть произведено с помощью схемы Хорнера — чтобы сэкономить на операции умножения матриц.
Пример 2. Вычислить $ g(A)_<> $ для
Применение теоремы Гамильтона-Кэли
Дальнейшие упрощения возможны в случае, когда $ deg g ge n $, т.е. когда степень полинома становится больше или равной порядка матрицы. Предположим, что мы в состоянии вычислить характеристический полином матрицы $ A_<> $: $$ f(x)=det (A-x E) , . $$
Теорема 1. Обозначим $ g_1(x) $ остаток от деления $ g_<>(x) $ на характеристический полином $ f(x)=det (A – x E) $. Тогда
Доказательство. Действительно, указанное равенство последует из теоремы Гамильтона-Кэли при подстановке матрицы $ A_<> $ в формулу $$ g(x)equiv f(x)q(x)+g_1(x) , deg g_1 ♦
Эта теорема позволяет свести вычисление $ g(<mathbf A>) $ к случаю полинома степени меньшей порядка матрицы. Это соображение существенно упрощает поставленную задачу, но при этом возникает другая: как вычислить остаток от деления если делимое существенно превосходит делитель по степени? Посмотрим, как этот подход будет выглядеть для примера 1.
Пример 3. Вычислить
$$ A^ <100>quad npu quad A=left( begin 1 &2 &1 &0 \ 1 & 1 & 0 &-1 \ -2& 0 & 1 & 2 \ 0 & 2 & 1 & 1 end right)^ <100> . $$
Решение. Здесь $$det (A- x E) = x^4-4,x^3+6, x^2 – 4, x +1 . $$ Деление полинома $ g(x)equiv x^ <100>$ на характеристический полином, организованное традиционным способом (т.е. “в столбик” ) дает в остатке полином $$ g_1(x)=161700,x^3-480150,x^2+475300,x-156849 ; $$ при этом частное $ q_<>(x) $ является полиномом $ 96 $-й степени. Для вычислений обоих полиномов приходится использовать специализированный пакет компьютерной алгебры. Вычисление $ g_1(A) $ уже может быть произведено «вручную», например, с использованием схемы Хорнера. ♦
Заметим, что собственно частное от деления полинома $ g_<>(x) $ на характеристический полином не участвует в последующих вычислениях полинома от матрицы — для этого нужны только коэффициенты остатка. Можно ли изобрести обходной способ вычисления остатка, который не требует промежуточного вычисления частного? — Оказывается, можно.
Предположим, что мы в состоянии найти корни характеристического полинома $ f(x)=det (A-x E) $, т.е. собственные числа матрицы $ A_<> $. Предположим сначала, что все эти корни $ lambda_1,dots,lambda_n $ различны. Подставим их в тождество для определения частного и остатка: $$ g(x)equiv f(x)q(x)+g_1(x) , . $$ Поскольку $ f(lambda_j)=0 $ при $ jin <1,dots,n>$, получаем равенства $$ _^n , . $$ Полином $ g_1(x) $ имеет степень меньшую $ n_<> $, а его значения совпадают со значениями полинома $ g(x) $ в $ n_<> $ точках. Такой полином определяется однозначно — как интерполяционный полином, построенный по таблице значений $$ begin x & lambda_1 & lambda_2 & dots & lambda_n \ hline y & g(lambda_1) & g(lambda_2) &dots & g(lambda_n) end $$ Для его вычислений можно использовать любой из методов, изложенных в разделе “ИНТЕРПОЛЯЦИЯ”. Предпочтение отдается методу Лагранжа: $$ g_1(x) equiv sum_^n fracf_k(x) = sum_^n fracf_k(x) $$ где $ f_(x) $ означает частное от деления характеристического полинома на его линейный множитель: $$ f_k(x)equiv frac equiv (x-lambda_1)times dots times (x-lambda_) (x-lambda_)times dots times (x-lambda_) , . $$
Теорема 2. Если все собственные числа $ lambda_<1>,dots,lambda_n $ матрицы $ A_<> $ различны, то
Каждое из суммируемых выражений в формуле можно представить в виде двух сомножителей: один из них зависит от полинома $ g_<>(x) $, а второй — не зависит. Таким образом, при изменении полинома происходит лишь пересчет значений $ g(lambda_1),dots, g(lambda_n) $, а их матричные сомножители не меняются. Структура этих последних уже была нами установлена в пункте ☞ СОБСТВЕННЫЙ ВЕКТОР: каждая матрица $ f_k(A) $ — ранга $ 1 $, т.е. имеет свои столбцы пропорциональными (и равными собственным векторам, принадлежащим $ lambda_ $).
Пример 4. Выписать формулу $ g(A)_<> $ для произвольного $ g(x)in mathbb C[x] $ и
$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) . $$
Решение. $ det (A-x E)=-(x-3) (x+2)(x+1) $. Пренебрегая знаком – , имеем: $$ begin f_1(x)=x^2+3x+2 & u & f_1(A)= left( begin 40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20 end right) , f_1(3)=20 ; \ f_2(x)=x^2-2x-3 & u & f_2(A)= left( begin -10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0 end right) , f_2(-2)=5 ; \ f_3(x)=x^2-x-6 & u & f_3(A)= left( begin -4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8 end right), f_3(-1)=-4 . end $$ $$ g(A)=g(3) left( begin 2 & 4 & -1 \ 0 &0 & 0 \ 2 & 4 & -1 end right) + g(-2) left( begin -2 & -6 & 2 \ 1 &3 & -1 \ 0 & 0 & 0 end right) + g(-1) left( begin 1 & 2 & -1 \ -1 & -2 & 1 \ -2 & -4 & 2 end right) . $$ ♦
В случае, когда характеристический полином матрицы $ A_<> $ имеет кратные корни, для вычисления полинома $ g_1(x) $ из теоремы $ 1 $ приходится привлекать обобщение понятия классического интерполяционного полинома в виде интерполяционного полинома Эрмита. Действительно, полином $ g_1(x) $ определялся в теореме $ 1 $ как остаток от деления $ g_<>(x) $ на характеристический полином $ f(x)=det (A- xE) $: $$ g(x)equiv f(x)q(x)+g_1(x) ; $$ При этом $ deg g_1 1, $$ то для нахождения полинома $ g_1(x) $ не хватает значений $ g(lambda_1),dots, g(lambda_<<mathfrak r>>) $. Для получения дополнительных условий, можно продифференцировать тождество $ g(x)equiv f(x)q(x)+g_1(x) $ по $ x_<> $ и подставить в получившееся значения всех кратных корней полинома $ f_<>(x) $: $$ g^<prime>(lambda_j) = f^<prime>(lambda_j) q(lambda_j)+f(lambda_j) q^<prime>(lambda_j)+g_1(lambda_j) . $$ Поскольку для любого кратного корня $ lambda_ $ будет выполнено условие (см. ☞ ЗДЕСЬ ): $ f^<prime>(lambda_j)=0 $, то результатом подстановки будет равенство $ g^<prime>(lambda_j)=g_1^<prime>(lambda_j) $. Получаем дополнительные условия для определения полинома $ g_<1>(x) $. Итак, для нахождения полинома $ g_1(x) $ нам следует дополнительно к значениям $ g_<>(x) $ на всех корнях характеристического полинома (т.е. на собственных числах) матрицы $ A_<> $ вычислить еще и значения производной этой функции на всех кратных корнях. Может, однако, так случиться, что и этих дополнительных условий будет недостаточно для нахождения полинома $ g_1(x) $. Тогда следует продолжить процесс вычисления производных — для тех значений $ lambda_ $, кратность которых $ <mathfrak m>_j $ больше $ 2_<> $. Окончательно, для определения полинома $ g_1(x) $ мы имеем значения полинома $ g(x) $ и его производных $$ begin g(lambda_1),dots, g^<(<mathfrak m>_<_1>-1)>(lambda_1), \ g(lambda_2),dots, g^<(<mathfrak m>_<_2>-1)>(lambda_1), \ dots, \ g(lambda_<mathfrak r>),dots, g^<(<mathfrak m>_<_<mathfrak r>>-1)>(lambda_<mathfrak r>) ; end $$ при этом количество значений в каждой строке равно (алгебраической) кратности соответствующего собственного числа. По этим значениям полином степени меньшей $ n_<> $ восстанавливается однозначно.
Заметим, что данный метод не чувствителен к геометрической кратности каждого из собственных чисел (т.е. к структуре жордановой нормальной формы матрицы $ A_<> $ вне ее главной диагонали); для его работы достаточно информации об алгебраической кратности.
Пример 5. Вычислить $ A^ <100>$ для
Решение. У всех трех матриц одинаковый характеристический полином: $ det (A- x E) = (x-1)^4 $. Остаток от деления $ x^ <100>$ на $ (x-1)^4 $ совпадает с отрезком ряда Тейлора функции $ x^ <100>$ при разложении ее по степеням $ x-1 $, т.е. с $$ begin g_1(x)&=&1+100,(x-1)+frac<100cdot99><2>(x-1)^2+frac<100cdot 99 cdot 98><6>(x-1)^3= \ &= & -156849+475300,x-480150,x^2+161700,x^3 . end $$ Для всех трех матриц формула вычисления $ A^ <100>$ одна и та же: $$ A^ <100>= -156849, E+475300,A-480150,A^2+161700,A^3 . $$ Несмотря на то обстоятельство, что жордановы нормальные формы у этих матриц различны. ♦
В приведенном способе нахождения остатка от деления полинома $ g(x) $ на характеристический полином матрицы $ A_<> $ имеется один нюанс, требующий пояснений. Предположим, что элементы матрицы $ A_<> $ целочислены: $ in mathbb Z>_^n $. Тогда и характеристический полином $ f(x)=det (A-x E) $ является полиномом с целочисленными коэффициентами $ f(x) in mathbb Z[x] $. Поскольку старший коэффициент $ f_<>(x) $ равен $ 1_<> $ по абсолютной величине, то и остаток от деления $ g_<> (x) $ на $ f_<>(x) $ будет иметь только целые коэффициенты (см. ☞ ЗДЕСЬ ): $ g_1(x) in mathbb Z[x] $. Между тем, вычисление этого полинома через посредство корней характеристического полинома, в общем случае, приводит к иррациональным выражениям: корни полинома, как правило, не выражаются в радикалах через его коэффициенты.
Пример 6. Вычислить $ g(A) $ для
$$ g(x)= x^<10>-6,x^8+11,x^7-x^3+4,x^2- 1 $$ и $$ A= left( begin 6 &1 &5 &2 & -1 \ -5 & -1 & -4 & -2 & 1 \ -5 & -1 & -5 & -1 & 1 \ -5 & -1 & -5 & -2 & 2 \ -5 & 0 & -7 & -2 & 2 end right) , . $$
Решение. Характеристический полином $ f(x)= det (A-x E)=-(x^5-4,x-2) $ имеет корни, не выражающиеся в радикалах. Попробуем применить теорему 2 для приближенных значений корней: $$ lambda_1 approx -1.243596, lambda_2 approx -0.508499, lambda_3 approx 1.518512, lambda_ <4,5>approx 0.116792 pm <mathbf i>, 1.438448,, . $$ Для нахождения частных от деления $ f_<>(x) $ на линейные множители $ (x-lambda_j) $ воспользуемся следующим приемом. Частное от деления произвольного полинома $$ f(x)=a_0x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5 $$ на линейный полином $ x – lambda $ находится по формуле $$ q(x,lambda)=a_0x^4+(a_0lambda + a_1)x^3+(a_0lambda^2+a_1lambda+a_2)x^2+(a_0lambda^3+a_1lambda^2+a_2lambda+a_3)x+ $$ $$ +(a_0lambda^4+a_1lambda^3+a_2lambda^2+a_3 lambda+a_4) , , $$ которая является развернутым вариантом схемы Хорнера. Подставляя сюда значения коэффициентов характеристического полинома $ f_<>(x) $ и приближенные значения его корней, получаем приближения полиномов $ f_j(x) $: $$ begin f_1(x) &approx & -x^4+1.243596,x^3-1.546532,x^2+1.923266,x+1.608239 , , \ f_2(x) & approx &-x^4+0.508499,x^3-0.258572,x^2+0.131483,x+3.933141, , \ f_3(x) & approx & dots \ f_<4,5>(x) & approx & -x^4+(-0.116792mp 1.438448, mathbf i),x^3+(2.055491mp 0.335998, mathbf i),x^2+ dots end $$ Вычисляем значения этих полиномов на матрице $ A_<> $: $$ f_1(A) approx left( begin 1.844873 & 0.503518 & 3.247794 & -1.280266 & 0.201656 \ 0.383692& 0.104720 & 0.675468 & -0.266266 & 0.041940 \ -4.616308& -1.259922 & -8.126748 & 3.203527 &-0.504592 \ 1.601674 & 0.437142 & 2.819656 &-1.111496 & 0.175073 \ -6.130986 & -1.673321 & -10.793252 & 4.254651 & -0.670156 end right) $$ $$ f_2(A) approx left( begin -6.028030 & -5.334374 & -3.876435 & 0.470253 & 0.893870 \ 9.342582 & 8.267515 & 6.007919& -0.728825 & -1.385371\ 4.342582 & 3.842873 & 2.792577 & -0.338769 & -0.643943\ 6.885079 & 6.092801 & 4.427577 & -0.537112 & -1.020959\ 5.592221 & 4.948714 & 3.596180 &-0.436255 & -0.829246 end right) $$ $$ f_3(A) approx dots $$ $$ f_<4,5>(A) approx left( begin -4.833170pm 17.111687 , mathbf i & -10.621186 pm 0.712576 , mathbf i & dots \ 6.383099 mp 14.587375 , mathbf i & 9.509036 pm 0.668706 , mathbf i & dots \ 1.383099 mp 14.587376 , mathbf i & 8.504395mp 2.151023 , mathbf i & dots \ 0.799140 mp 21.779614 , mathbf i & 12.443094mp 3.925469 , mathbf i & dots \ 11.076597 mp 23.459604 , mathbf i & 15.455549pm 1.532904 , mathbf i & dots end right) , . $$ Несмотря на кажущуюся хаотичность формирования элементов этих матриц, столбцы каждой из них пропорциональны (впрочем, равно как и строки). Составляем матрицу из теоремы $ 2 $: $$ sum_^5 fracf_k(A) = sum_^5 frac q(A,lambda_k) approx $$ $$ approx left( begin -94.999999 & -173.999999 & -237.999999 & 143.999999 & 198.999999 \ 159.999999 & 149.999999& 301.999999&-101.999999&-191.999999\ 39.999999&156.999999&79.999999&-127.999999&-125.999999\ 194.999999 &277.999999&229.999999&-239.999999&-140.999999\ 404.999999&273.999999&435.999999&-67.999999&-278.999999 end right) $$ (при уменьшении точности вычислений возможно появление ненулевых мнимых частей). Полученный ответ можно интерпретировать как приближение истинного, а именно, целочисленного: $$ left( begin -95&-174&-238&144&199\ 160&150&302&-102&-192\ 40&157&80&-128&-126\ 195&278&230&-240&-141\ 405&274&436&-68&-279 end right) , . $$ Возникает вопрос: можно ли было получить этот ответ, не прибегая к численным методам (и использованию мнимых чисел)? Где именно «заложена» принципиальная целочисленность ответа? Для ответа посмотрим на выражение $$ sum_^5 fracf_k(A) = sum_^5 fracf_k(A) = $$ $$ sum_^5 frac left(a_0A^4+(a_0lambda_k + a_1)A^3 + (a_0lambda_k^2+a_1lambda_k+a_2)A^2 dots right)= $$ $$ = left(a_0sum_^5 frac right)A^4 + left( a_0 sum_^5 frac+a_1 sum_^5 frac right) A^3+ dots , , $$ здесь $ a_0=(-1)^n,a_1, a_2,dots $ обозначают коэффициенты полинома $ f_<>(x) $. Выражения в круглых скобках представляют собой симметрические рациональные функции от корней этого полинома. Согласно теореме Гаусса, эти функции допускают представление в виде рациональных функций от коэффициентов $ a_0,a_1, a_2,dots $ (а, на самом деле, полиномов от этих коэффициентов). Так что ответ в задаче действительно должен быть целочисленным. Другое дело, что для его практического поиска мы привлекли численные методы поскольку явное представление симметрических рациональных функций через коэффициенты полинома — задача весьма сложная. ♦
Анализ с помощью жордановой нормальной формы
Все применения ЖНФ основаны на формулах подобия матрицы и ее ЖНФ: $$C^<-1><mathbf A>C =<mathbf A>_<_<mathfrak J>> quad iff quad <mathbf A>= C<mathbf A>_<_<mathfrak J>>C^ <-1> . $$
Оказывается, что любая мыслимая операция над матрицей $ <mathbf A>$ может быть сведена к этой же операции над формой Жордана: $$g(<mathbf A>)= Cg(<mathbf A>_<_<mathfrak J>>)C^ <-1> .$$ В самом деле, имеем, например: $$ <mathbf A>^2 =(C<mathbf A>_<_<mathfrak J>>C^<-1>)^2=C<mathbf A>_<_<mathfrak J>>C^<-1>C<mathbf A>_<_<mathfrak J>>C^<-1>=C<mathbf A>_<_<mathfrak J>>^2C^ <-1> . $$ По индукции можно показать справедливость равенства $$ <mathbf A>^N=C<mathbf A>_<_<mathfrak J>>^NC^ <-1>quad npu quad forall N in mathbb N . $$ Далее, справедливость равенства $ <mathbf A>^0=E=C<mathbf A>_<_<mathfrak J>>^0C^ <-1>$ очевидна. Но тогда можно доказать и справедливость равенства $$ g(<mathbf A>) = Cg(<mathbf A>_<_<mathfrak J>>)C^ <-1>$$ для любого полинома $ g(x)=b_0x^m+dots+b_m in mathbb C[x] $. Отсюда — прямая дорога к аналитическим функциям от матрицы… Этот переход обсудим НИЖЕ, а пока остановимся и проведем анализ структуры полинома от ЖНФ.
Мы будем рассматривать матрицы и их ЖНФ над полем $ mathbb C_<> $. Пусть характеристический полином матрицы $ mathbf A_<> $ имеет следующее разложение на линейные множители над полем $ mathbb C_<> $: $$ f(lambda)= det (mathbf A – lambda E) equiv (-1)^n(lambda – lambda_1)^<<mathfrak m>_1> times dots times (lambda – lambda_<<mathfrak r>>)^< <mathfrak m>_<<mathfrak r>>> quad ; quad <mathfrak m>_1+dots+<mathfrak m>_<<mathfrak r>>=n, lambda_k ne lambda_ <ell> npu k ne ell. $$ ЖНФ матрицы $ mathbf A_<> $ имеет вид блочно-диагональной матрицы $$ <mathbf A>_<_<mathfrak J>>=left( begin mathbf A_1 & mathbb O & dots & mathbb O \ mathbb O & mathbf A_2 & dots & mathbb O \ vdots & & ddots & vdots\ mathbb O & mathbb O & dots & mathbf A_<<mathfrak r>> end right) quad , quad mbox < здесь > mathbf A_j – mbox< матрица порядка > <mathfrak m>_jtimes <mathfrak m>_j . $$ В свою очередь, каждая из составляющих матриц $ mathbf A_j $ имеет снова блочно-диагональный вид $$ mathbf A_j= left( begin <mathbf A>_ & mathbb O & dots & mathbb O \ mathbb O & <mathbf A>_ & dots & mathbb O \ vdots & & ddots & vdots\ mathbb O & mathbb O & dots & <mathbf A>_ end right) $$ где на диагонали стоят клетки Жордана, т.е. матрицы вида $$ <mathfrak J>_k (lambda_j) = left( begin lambda_j & & & & & \ 1 & lambda_j & & & & \ 0 & 1 & lambda_j & & mathbb O & \ vdots & & ddots & ddots& & \ 0 & 0 & 0 & dots & lambda_j & \ 0 & 0 & 0 & dots & 1 & lambda_j end right)_ . $$ Теперь наша задача — свести вычисление произвольного полинома от $ <mathbf A>_<_<mathfrak J>> $ к вычислению этого же полинома от клеток Жордана: $ g(<mathbf A>_<_<mathfrak J>>) $ — к $ g(<mathfrak J>_k (lambda_j)) $.
Структура степенной функции
Теорема 3. Если матрица $ <mathbf D>$ — блочно-диагональная, то и $ <mathbf D>^N $ — блочно-диагональная:
$$ left( begin <mathbf D>_1 & mathbb O & dots & mathbb O \ mathbb O & <mathbf D>_2 & dots & mathbb O \ vdots & & ddots & vdots \ mathbb O & mathbb O & dots & <mathbf D>_r end right)^N= left( begin <mathbf D>_1^N & mathbb O & dots & mathbb O \ mathbb O & <mathbf D>_2^N & dots & mathbb O \ & & ddots & \ mathbb O & mathbb O & dots & <mathbf D>_r^N end right) . $$ Здесь $ <mathbf D>_1, dots, <mathbf D>_r $ — квадратные матрицы 1) .
Теорема 4. Если матрица $ L_<> $ — нижнетреугольная, то и $ L^N $ — нижнетреугольная.
Теоремы $ 3 $ и $ 4 $ сводят вычисление степени матрицы $ <mathbf A>$ к вычислению степени ее клеток Жордана $ <mathfrak J>_k (lambda_j) $.
Теорема 5. Имеет место равенство:
$$ left( begin lambda & & & & & \ 1 & lambda & &mathbb O & & \ 0& 1 & lambda & & & \ vdots & & ddots & ddots & & \ 0 & 0 & dots & 1 & lambda & \ 0 & 0 & dots & 0 & 1 &lambda end right)_^N= left( begin lambda^N & & & & & \ C_N^1 lambda^ & lambda^N & &mathbb O & & \ C_N^2 lambda^ & C_N^1 lambda^ & lambda^N & & & \ dots & & ddots & ddots & & \ C_N^ lambda^ & dots & & C_N^1 lambda^ &lambda^N & \ C_N^ lambda^ & dots & & C_N^2 lambda^ & C_N^1 lambda^ &lambda^N end right) $$ (считаем здесь элементы с отрицательными показателями $ lambda $ равными нулю). Более корректная запись матрицы в правой части возможна с помощью матрицы $$H_j = begin begin <scriptstyle 0 to>\ <scriptstyle 1 to>\ vdots \ <scriptstyle j to>\ vdots \ <scriptstyle k-1 to>end left(begin 0 & & & & &\ 0 & & & mathbb O & &\ vdots & & & & &\ 1 & & & & \ vdots & ddots & & &\ 0 & & 1 & dots & 0 & 0 end right) end =left[ begin mathbb O_ & mathbb O_ \ E_ <(k-j) times (k-j)>& mathbb O_ <(k-j)times j>end right]_ $$ (единицами заполнена $ j_<> $-я диагональ, считая от нулевой — главной): $$ left[<mathfrak J>_k (lambda) right]^N = $$ $$ =lambda^N E + C_N^1 lambda^ H_1 + C_N^2 lambda^ H_2 + dots +left< begin C_N^N H_N & npu & N ♦
Решение линейного разностного уравнения
Настоящий пункт тесно связан с разделом ЛИНЕЙНОЕ РАЗНОСТНОЕ УРАВНЕНИЕ.
Пусть рекуррентная последовательность задается уравнением $$ x_=a_1 x_+ dots+ a_n x_K $$ и начальными данными $ x_0,x_1,dots,x_ $.
Введем в рассмотрение столбцы, состоящие из $ n_<> $ последовательных элементов этой последовательности, обозначив $$ X_0=left( begin x_0 \ x_1 \ vdots \ x_ end right), X_1=left( begin x_1 \ x_2 \ vdots \ x_ end right), X_2=left( begin x_2 \ x_3 \ vdots \ x_ end right), dots, X_K=left( begin x_K \ x_ \ vdots \ x_ end right),dots ; $$ а также следующую матрицу, известную как матрица Фробениуса: $$ <mathfrak F>= left( begin 0 & 1 & 0 & 0 & dots & 0 & 0 \ 0 & 0 & 1 & 0 & dots & 0 & 0 \ 0 & 0 & 0 & 1 & dots & 0 & 0 \ vdots& &&&ddots & & vdots \ 0 & 0 & 0 & 0 & dots & 0 & 1 \ a_n & a_ & a_ & & dots & a_2 & a_1 end right)_ . $$ Используя правило умножения матриц, а также соотношение между элементами последовательности, получаем: $$ X_1=<mathfrak F>X_0, X_2=<mathfrak F>X_1,dots, X_K=<mathfrak F>X_,dots, $$ откуда имеем: $$ X_K=<mathfrak F>^KX_0 quad npu quad Kin mathbb N . $$ Искомое выражение для $ x_ $ получится умножением первой строки матрицы $ <mathfrak F>^K $ на столбец начальных данных $ X_ <0>$. Таким образом, задача решения разностного уравнения сводится к задаче возведения в степень матрицы $ <mathfrak F>$.
Для нахождения $ <mathfrak F>^ $ воспользуемся результатами предыдущего пункта . Найдя жорданову нормальную форму (ЖНФ) $ <mathfrak F>_ <mathfrak J>$ и соответствующую матрицу преобразования базиса $ C_<> $, получим $$ <mathfrak F>_ <mathfrak J>=C^ <-1>mathfrak F C Longrightarrow <mathfrak F>^=C <mathfrak F>_<_<mathfrak J>>^ C^ <-1>, . $$ Характеристический полином матрицы Фробениуса: $$det (<mathfrak F>- lambda E)= (-1)^n(lambda^n-a_1 lambda^-dots-a_n) . $$ с точностью до знака совпадает с характеристическим полиномом последовательности. Обозначим его корни $ lambda_1,dots,lambda_n $. Если они различны, то жорданова нормальная форма $ <mathfrak F>_<_<mathfrak J>> $ диагональна. Если же среди этих корней имеются кратные, то установление структуры ЖНФ потребует усилий; однако же можно заранее утверждать, что эта форма диагональной не будет.
Теорема 6. Если все корни характеристического полинома различны, то решение разностного уравнения получается в виде
$$ x_= C_1lambda_1^K + dots+ C_n lambda_n^K , $$ числа $ C_<1>,dots,C_n $ не зависят от $ K_<> $ и определяются с помощью начальных условий из системы линейных уравнений: $$ left<begin C_1 &+C_2 &+dots &+ C_n &=& x_0 \ lambda_1 C_1 &+ lambda_2C_2&+dots & + lambda_n C_n & = & x_1 \ lambda_1^2 C_1 &+ lambda_2^2C_2&+dots & + lambda_n^2 C_n & = & x_2 \ dots &&&&& dots \ lambda_1^C_1 &+ lambda_2^C_2&+dots & + lambda_n^ C_n & = & x_. end right. $$
Доказательство теоремы и ее обобщение на случай наличия кратных корней характеристического полинома ☞ ЗДЕСЬ.
Асимптотика степенной функции
Задача. Выяснить как себя ведет $ mathbf A^N $ при $ Nto +infty $.
Пример предыдущего пункта показывает, что существуют матрицы $ mathbf A_<> $, для которых некоторые элементы $ mathbf A^N $ неограниченно возрастают при $ Nto +infty $.
Теорема 7. Если все собственные числа матрицы $ mathbf A_<> $ меньше $ 1 $ по абсолютной величине, т.е. $ <|lambda_j| 1 $, то существует хотя бы один элемент матрицы $ mathbf A^N $ неограниченно возрастающий при $ Nto +infty $.
Вычисление полинома от матрицы
Теперь проведем анализ структуры матрицы $ g(mathbb A) $ с помощью жордановой нормальной формы. Способ вычисления матричной степени распространяется и на полином от матрицы: $$g(<mathbf A>)= Cg(<mathbf A>_<_<mathfrak J>>)C^<-1>$$ и аналоги теорем $ 3 $ и $ 4 $ сводят вычисление $ g(<mathbf A>) $ к вычислению $ g(x_<>) $ от клеток Жордана. Поскольку $$gleft( <mathfrak J>_k (lambda) right)= b_0left[<mathfrak J>_k (lambda)right]^m+b_1left[<mathfrak J>_k (lambda)right]^+dots+b_mE_ $$ то на основании теоремы $ 5 $ получаем следующий результат
Теорема 8. Имеет место равенство
$$ gleft(left[ begin lambda & & & & \ 1 & lambda & & mathbb O & \ 0& 1 & lambda & & \ vdots & & ddots & ddots & \ 0 & 0 & dots & 1 &lambda end right]_right)= left[ begin g(lambda) & & & & \ g'(lambda) & g(lambda) & & mathbb O & \ frac<2!>& g'(lambda) & g(lambda) & & \ vdots & & ddots & ddots & \ frac(lambda)> <(k-1)!>& frac(lambda)> <(k-2)!>& dots & g'(lambda) & g(lambda) end right]= $$ $$ =g(lambda)E+ g'(lambda) H_1 + frac<2!>H_2+dots+ frac(lambda)> <(k-1)!>H_ $$
Можно ли утверждать, что геометрическая кратность собственного числа $ g(lambda_j) $ матрицы $ g(<mathbf A>) $ такая же, как и геометрическая кратность собственного числа $ lambda_j $ матрицы $ <mathbf A>$ (т.е. что порядки соответствующих клеток Жордана одинаковы)?
Аналитическая функция от матрицы
Норма матрицы. Матричный ряд
Нормой произвольной (не обязательно квадратной) матрицы $ A in mathbb C^ $ называется неотрицательное число $ | A | $, удовлетворяющее условиям (аксиомам):
1. $ | A |=0 $ тогда и только тогда, когда $ A=mathbb O_ $;
2. для $ forall alphain mathbb C $ справедливо $ | alpha A |=|alpha |cdot | A | $;
3. для любых матриц $ A, B $ из $ mathbb C^ $ справедливо $ | A + B | le | A |+| B | $;
Три эти аксиомы являются универсальными аксиомами нормы в произвольном линейном векторном пространстве. Для матриц можно ввести дополнительную операцию — операцию умножения. В этом случае норму подчиняют еще одной аксиоме.
4. для любых матриц $ A_<> $ и $ B_<> $, допускающих умножение $ A cdot B $, справедливо $ | A cdot B | le | A | cdot | B | $.
Норму можно вводить разными способами.
Пример. Для матриц с комплексными элементами евклидова норма (или норма Фробениуса) вводится формулой:
$$| A | = sqrt <sum_|a_|^2> ;$$ эту формулу для матриц с вещественными элементами можно переписать в виде $$ | A | = sqrt< operatorname_<>, (A cdot A^<^<top>>)> , . $$ Выполнение для нее аксиом 1 и 2 очевидно. Справедливость 3 следует из неравенства треугольника: $ |a_+b_|^2le |a_|^2 +|b_|^2 $, а 4 следует из неравенства Коши-Буняковского: $$|a_b_<1k>+dots+ a_b_|^2 le left(|a_|^2+dots+|a_|^2 right) left(|a_<1k>|^2+dots+|a_|^2 right) , .$$ Эту норму можно рассматривать как обобщение понятия длины вектора в $ mathbb R^ $: $ | X_ | = sqrt< x_1^2+dots+x_n^2>=|X| $. Вообще, любая формула, задающая скалярное произведение в евклидовом пространстве матриц, порождает и норму матрицы: $ | A |= sqrt <langle A,A rangle>$. Только что введенная норма соответствует стандартному скалярному произведению.
Теорема 9. Евклидова норма вещественной матрицы не меняется при умножении этой матрицы на произвольную ортогональную.
Доказательство ☞ ЗДЕСЬ.
Пример. $ displaystyle | A | = max_j sum_k |a_| $. Тогда $ | X_ | =displaystyle < max_|x_j|> $.
Пример. $ displaystyle | A | = max_k sum_j |a_| $. Тогда $ | X_ | =displaystyle< sum_^n |x_j|> $.
Введение понятия нормы позволяет упростить рассуждения о сходимости матричной последовательности $ < A_N >_^ <infty>$. В предыдущих пунктах эта сходимость понималась в смысле существования пределов у последовательностей элементов $ a_^ <(N)>$ одновременно для всех индексов $ j_<> $ и $ k_<> $. Норма позволяет объединить исследование этих последовательностей на сходимость в изучение одной.
Теорема 10. Последовательность $ < A_N >_^ <infty>$ сходится при $ N to infty $ к матрице $ A_<> $ тогда и только тогда, когда $$lim_ | A_N – A |=0 , .$$
Матричный ряд $$ sum_^ <infty>A_j = A_1 + dots + A_N+ dots $$ называется сходящимся если существует конечный предел последовательности $$left< S_N = sum_^ A_j= A_1 + dots + A_N right>_^<infty>$$ его частичных сумм. Тогда величина этого предела называется суммой матричного ряда: $$ S= sum_^ <infty>A_j = lim_ S_N , .$$ Матричный ряд называется расходящимся если хотя бы для одной пары индексов $ j_<> $ и $ k_<> $ последовательность $ s_^ <(N)>$ расходится. Матричный ряд называется абсолютно сходящимся если сходится числовой ряд его норм: $ displaystyle sum_^ <infty>| A_j | $.
Теорема 11. Если матричный ряд сходится абсолютно, то он сходится и в обычном смысле.
Теорема 12 [признак сравнения]. Если ряд $ displaystyle sum_^ <infty>A_j $ абсолютно сходится и $ | A_j |ge | B_j | $ для $ forall jin mathbb N $, то и ряд $ displaystyle sum_^ <infty>B_j $ сходится абсолютно.
Матричный степенной ряд
Рассмотрим теперь степенной ряд $$ sum_^<infty>b_j z^j=b_0+b_1z+b_2z^2+dots $$ переменную в котором предполагаем комплексной: $ z in mathbb C $. Пусть $ R $ — радиус сходимости этого ряда, т.е. ряд сходится при $ |z| R $. Известно, что $$R=overline<lim_>left| frac> right|= overline<lim_> frac<1><sqrt[n]<|b_|>> , .$$
Рассмотрим теперь соответствующий матричный степенной ряд $$ sum_^ <infty>b_j Z^j =b_0E+b_1 Z +b_2 Z^2+dots $$ при $ Z in mathbb C^ $.
Теорема 13. Матричный степенной ряд сходится абсолютно для любой матрицы $ Z $ такой, что $ | Z|
Если ряд $ sum_^<infty>b_j z^j $ сходится при $ forall z in mathbb C $, то и ряд $ sum_^<infty>b_j Z^j $ сходится при любой матрице $ Zin mathbb C^ $.
Сумма сходящегося степенного ряда $ sum_^<infty>b_j Z^j $ будет функцией переменной матрицы $ Z $. Такая функция называется аналитической функцией матрицы.
Если обозначить сумму ряда $ sum_^<infty>Z^j $ через $ F(Z) $, то легко проверяется свойство: $ F(Z)(E-Z)=E $. Таким образом, ряд сходится к матрице $ (E-Z)^ <-1>$ при $ |Z | ☝ ПУНКТЕ было доказано, что $$F_N(B)=C^<-1>F_N(A) C , .$$ Переходя к пределу, получаем $$lim_ F_N(B)= C^<-1>left( lim_ F_N(A) right) C =C^<-1>F(A)C , .$$ Таким образом, функция $ F $ определена и для $ B $ и $ F(B)=C^<-1>F(A)C $. ♦
Теорема 15. Ряд $ sum_^ <infty>b_j Z^j $ сходится для любой матрицы $ A $ чей спектр лежит внутри круга сходимости: $$ <|lambda_j| R , . $$
Доказательство ☞ ЗДЕСЬ.
Особое прикладное значение имеет матрица $$ e^= sum_^ <infty>frac A^j , , $$ зависящая от параметра $ tin mathbb C $. Если продифференцировать ряд по этому параметру, то на основании теоремы ?? получим: $$ frac< d, e^>< d, t>=sum_^ <infty>frac>A^j=A sum_^ <infty>frac><(j-1)!>A^=Ae^ , . $$ Таким образом, $ e^ $ является решением матричного дифференциального уравнения 2) $$ frac< d, X>< d, t>= A X , . $$ Обычно это уравнение рассматривают не относительно квадратной матрицы $ X $, а относительно вектора-столбца $ X_ $, т.е. последнее уравнение представляет матричную запись системы обыкновенных дифференциальных уравнений: $$ left< begin d, x_1/d, t &=&a_<11>x_1+&a_<12>x_2+&dots+&a_<1n>x_n , , \ d, x_2/d, t &=&a_<21>x_1+&a_<22>x_2+&dots+&a_<2n>x_n , ,\ dots & & & &dots & \ d, x_n/d, t &=&a_x_1+&a_x_2+&dots+&a_x_n , . end right. $$ При задании начальных условий $$ x_1(t_0)=x_<10>,x_2(t_0)=x_<20>,dots , x_n(t_0)=x_ quad iff quad X(t_0)=X_0 $$ решение уравнения $ d, X big/ d, t= A X $ представляет естественное обобщение одномерного (скалярного) случая: $$ X(t)=e^<(t-t_0)A>X_0 , . $$
В пункте ?? указаны два способа вычисления аналитической функции матрицы. Применим их для нахождения $ e^ $. $$ e^=Ce^>C^ <-1>$$ и вычисление $ e^ $ от клетки Жордана производится по формуле $$ exp left( t cdot left[ begin lambda & & & & \ 1 & lambda & &mathbb O & \ 0& 1 & lambda & & \ vdots & & ddots & ddots & \ 0 & 0 & dots & 1 &lambda end right]_right)= left[ begin e^ <lambda t>& & & & \ te^ <lambda t>& e^ <lambda t>& &mathbb O & \ frac<2!>e^<lambda t>& te^ <lambda t>& e^ <lambda t>& & \ vdots & & ddots & ddots & \ frac><(k-1)!>e^ <lambda t>& frac><(k-2)!>e^ <lambda t>& dots & te^ <lambda t>& e^ <lambda t>end right]= $$ $$ =e^ <lambda t>left( E+ t H_1 + frac<2!>H_2+dots+ frac> <(k-1)!>H_ right) , . $$ Матрицы $ $ определяются в ☝ ПУНКТЕ.
Доказать справедливость равенства: $ det( e^A ) = e^ <operatorname(A )> $.
Пример. Для системы дифференциальных уравнений
$$ left< begin d, x_1 / d, t &=&&x_2&+x_3, \ d, x_2 / d, t &=&x_1&+x_2&-x_3, \ d, x_3 / d, t &=&&x_2&+x_3 end right. $$
а) найти решение при $ x_1(0)=1,x_2(0)=1,x_3(0)=1 $;
б) найти все начальные условия $$ x_1(0)=x_<10>,x_2(0)=x_<20>,x_3(0)=x_<30>, , $$ для которых решения будут ограниченными при $ tto +infty $.
Решение. Здесь $ t_0=0 $, $ det (A – lambda E) = – lambda (lambda -1)^2 $. $$ A= underbrace< left( begin 2& -1& 1 \ -1& 1 & 0\ 1 & -1 & 1 end right)>_ underbrace< left( begin 0& 0& 0 \ 0& 1 & 0\ 0 & 1 & 1 end right) >_<<bf A>_<mathfrak J>> underbrace< left( begin 1& 0& -1 \ 1 & 1 & -1 \ 0 & 1 & 1 end right) >_> $$ $$ e^= left( begin 2& -1& 1 \ -1& 1 & 0\ 1 & -1 & 1 end right) left( begin 1& 0& 0 \ 0& e^ & 0\ 0 & te^ & e^ end right) left( begin 1& 0& -1 \ 1 & 1 & -1 \ 0 & 1 & 1 end right)= $$ $$ =left( begin 2-e^+te^t & t, e^t & -2+ 2, e^t-t, e^t \ -1 +e^t & e^t & 1-e^t \ 1 -e^t+t, e^t& t, e^t & -1+2, e^t-t, e^t end right) , . $$ Домножая эту матрицу справа на столбец $ [1,1,1]^<^<top>> $, получаем $$x_1(t)=e^t(1+t),, x_2(t)=e^t,, x_3(t)=e^t(1+t) , . $$
Для решения б) домножим последнюю матрицу справа на столбец $ [x_<10>,x_<20>,x_<30>]^<^<top>> $. Получившийся столбец можно представить в виде линейной комбинации трех: $$ left( begin 2x_<10>-2x_ <30>\ -x_<10>+x_ <30>\ x_ <10>- x_ <30>end right) +e^t left( begin -x_<10>+2,x_ <30>\ x_<10>+x_<20>-x_ <30>\ -x_ <10>+2, x_ <30>end right) +t, e^t left( begin x_<10>+x_<20>-x_ <30>\ 0 \ x_<10>+x_<20>-x_ <30>end right) $$ Решение может быть ограниченным лишь при условии, когда столбцы при $ e^t $ и $ t, e^t $ будут нулевыми. Решаем получившуюся систему линейных однородных уравнений относительно $ x_<10>,x_ <20>$ и $ x_ <30>$, получаем, что при любом $ x_ <30>$ решение, проходящее через точку $ [2, x_<30>,-x_<30>,x_<30>]^<^<top>> $ будет ограниченным; более того, оно будет стационарным, т.е. не покинет этой точки при изменении $ t $. ♦
Пример. Найти решение системы дифференциальных уравнений
$$ left< begin d, x_1 / d, t &=&-9,x_1&+12,x_2&-7,x_3 &-7, x_4, \ d, x_2 / d, t &=&-25,x_1&+35,x_2&-20,x_3&-22, x_4 , \ d, x_3 / d, t &=&-16,x_1&+24,x_2&-14,x_3&-15, x_4, \ d, x_4 / d, t &=&-17,x_1&+22,x_2&-12,x_3&-14, x_4, end right. $$ при $ x_1(0)=1,x_2(0)=0,x_3(0)=1,x_4(0)=0 $.
Решение. Имеем: $$ f(lambda)=det (A-lambda E) = lambda^4+2lambda^3+6lambda^2+2lambda+5 , .$$ Спектр матрицы $ < -1 pm 2 mathbf i, pm mathbf i >$ состоит из мнимых чисел. Для вычисления $ e^ $ можно воспользоваться интерполяционной формулой из пункта . Вычисления частных при делении $ f(lambda) $ на линейные полиномы $ lambda- lambda_ <ast>$ и $ lambda- overline<lambda_<ast>> $ упрощаются соображениями комплексной сопряженности: $$ f_1(lambda)equiv frac<lambda-(-1+2 mathbf i))>equiv lambda^3+(1+2 mathbf i)lambda^2+lambda+(1+2 mathbf i), $$ $$ f_2(lambda)equiv frac<lambda-(-1-2 mathbf i))>equiv overline equiv lambda^3+(1-2 mathbf i)lambda^2+lambda+(1-2 mathbf i), $$ $$ f_3(lambda)equiv frac<lambda-mathbf i>equiv lambda^3+(2+mathbf i)lambda^2+(5+2mathbf i)lambda+5 mathbf i , , $$ $$ f_4(lambda)equiv frac<lambda+mathbf i>equiv overline equiv lambda^3+(2-mathbf i)lambda^2+(5-2mathbf i)lambda-5 mathbf i , . $$ Аналогичное упрощение возникает и при вычислениях полиномов от матрицы, т.е. $ $: $$ f_1(A)= left( begin 32+26 mathbf i & -40-20 mathbf i & 20+10 mathbf i & 28+4 mathbf i \ 73+88 mathbf i & -98-76 mathbf i & 49+38 mathbf i & 74+26 mathbf i\ 54+46 mathbf i & -68-36 mathbf i & 34+18 mathbf i & 48+8 mathbf i\ 42+66 mathbf i & -60-60 mathbf i & 30+30 mathbf i & 48+24 mathbf i end right), , f_2(A)=overline , $$ $$ f_3(A)= left( begin 7-mathbf i & -2+14 mathbf i & -3-9 mathbf i & 2-12 mathbf i\ 17-6 mathbf i &2+36 mathbf i &-12-21 mathbf i & -1-31 mathbf i \ 13-9 mathbf i & 10+30 mathbf i & -15-15 mathbf i & -8-26 mathbf i \ 7-mathbf i &-2+14 mathbf i & -3-9 mathbf i & 2-12 mathbf i end right), , f_4(A)=overline . $$ Формулы решения системы дифференциальных уравнений по формуле $$ left(sum_^4 e^ <lambda_j t>fracright) left( begin 1 \ 0 \ 1 \ 0 end right) , . $$ приводим к вещественному виду с использованием формулы Эйлера представления экспонент от мнимых чисел: $$ e^ <lambda_j t>= e^mathbf (lambda_j) > left<cos ( t mathfrakmathbf(lambda_j)) + mathbf i sin ( t mathfrakmathbf(lambda_j)) right> , . $$
Ответ. $$ x_1(t)=frac<1><5>( 17 e^ <-t>cos (2t)-31 e^ <-t>sin (2t) -2 cos t – sin t ), , $$ $$ x_2(t)=frac<1><10>( 59 e^ <-t>cos (2t)-187 e^ <-t>sin (2t) -59 cos t – 17sin t ), , $$ $$ x_3(t)=frac<1><5>( 28 e^ <-t>cos (2t)-54 e^ <-t>sin (2t) -23 cos t – 14sin t ), , $$ $$ x_4(t)=frac<1><10>( 12 e^ <-t>cos (2t)-66 e^ <-t>sin (2t) -12 cos t – sin t ), . $$
Если при любых начальных условиях решение уравнения $$ frac< d, X>< d, t>= A X , . $$ ограничено при $ t to +infty $, то будем называть это уравнение устойчивым по Ляпунову. Устойчивое уравнение называется асимптотически устойчивым по Ляпунову если все решения стремятся к $ mathbb O_ $ при $ t to +infty $. Уравнение называется неустойчивым по Ляпунову, если существует хотя бы один набор начальных условий, для которого соответствующее решение $ X(t) $ неограничено при $ t to +infty $.
В дальнейшем будем говорить просто об устойчивости, имея в виду устойчивость по Ляпунову.
Представление решения уравнения формулой $$ X(t)=e^<(t-t_0)A>X_0 $$ позволяет свести исследование устойчивость этого уравнения к анализу спектра матрицы $ A $, либо же — в случае наличия кратных собственных чисел матрицы — к анализу ее жордановой нормальной формы $ A_ <mathfrak J>$.
Теорема 20. Уравнение $ d, X big/ d, t= A X $
а) устойчиво тогда и только тогда, когда $$ mathfrakmathbf (lambda_j) le 0 quad npu j in <1,dots,n>, ,$$ и клетки Жордана в ЖНФ $ A_ <mathfrak J>$, соответствующие собственным числам с $ mathfrakmathbf (lambda_j) = 0 $, имеют порядок $ 1 $;
б) асимптотически устойчиво тогда и только тогда, когда $$ mathfrakmathbf (lambda_j)
Уравнение $ d, X big/ d, t= A X $ с симметричной матрицей $ A $
а) устойчиво тогда и только тогда, когда матрица отрицательно полуопределена;
б) асимптотически устойчиво тогда и только тогда, когда матрица отрицательно определена.
Матричные синус и косинус
Теорема 21. Справедливо основное тригонометрическое тождество
Квадратный корень из матрицы
Сложности возникают при определении $ sqrt < A>$. Формально, корнем квадратным из матрицы $ <mathbf A>$ называется решение матричного уравнения $$ X^2=A $$ Уже для матриц второго порядка это уравнение не всегда разрешимо: например, не существует решения при $$A = left( begin 0 & 0 \ 1 & 0 end right) . $$ С другой стороны, при $$A = left( begin -1 & 0 \ 0 & -1 end right) $$ существует бесконечное множество решений $$ X= left( begin alpha & -(alpha^2+1)/beta \ beta & -alpha end right) , $$ задаваемое двумя параметрами $ alpha $ и $ beta ne 0 $.
Теорема 22. Решение уравнения
а) всегда существует при $ det A ne 0 $;
б) всегда существует среди вещественных симметричных матриц, если $ A $ — симметричная и положительно полуопределенная.
Пример. Вычислить
Решение. $ det (A – lambda E) = – (lambda-9) (lambda -36)^2 $. Поскольку матрица $ A $ симметрична, то привести ее к диагональному виду можно с помощью ортогональной матрицы $ C $. Мы, однако же, используем общий алгоритм диагонализации чтобы получить возможно большее число ответов: $$ <mathbf A>= underbrace< left( begin 1& 0& 2 \ 2& 2 & -1\ 0 & 1 & 2 end right)>_ underbrace< left( begin 36& 0& 0 \ 0& 36 & 0\ 0 & 0 & 9 end right) >_<<mathbf A>_<mathfrak J>> underbrace< left( begin 5/9& 2/9& -4/9 \ -4/9 & 2/9 & 5/9 \ 2/9 & -1/9 & 2/9 end right)>_> $$ $$ sqrt<<mathbf A>>= underbrace< left( begin 1& 0& 2 \ 2& 2 & -1\ 0 & 1 & 2 end right)>_ underbrace< left( begin pm 6& 0& 0 \ 0& pm 6 & 0\ 0 & 0 & pm 3 end right) >_<sqrt<<mathbf A>_<mathfrak J>>> underbrace< left( begin 5/9& 2/9& -4/9 \ -4/9 & 2/9 & 5/9 \ 2/9 & -1/9 & 2/9 end right) >_> $$
Теорема 23. Если $ A $ —симметричная матрица такая, что
то рекуррентная матричная последовательность $$ X_0=mathbb O, left< X_=X_+frac<1><2>(A-X_^2) right>_^ <infty>$$ сходится к положительно определенному квадратному корню из $ A $.
Условия на матрицу $ A $ эквивалентны тому, что ее спектр целиком лежит в интервале $ [0,1] $ (следствие ☞ теоремы Коши ).
Пример. Для
$$ A=left(begin 0.541667 & 0.205342 & -0.372008 \ 0.205342 & 0.811004 & 0.166667 \ -0.372008 & 0.166667 & 0.522329 end right) $$ имеем (все матрицы — симметричные) $$ X_0=mathbb O_<3times 3>, X_1=left(begin 0.2708335 & 0.102671 & -0.186004\ ast & 0.405502 & 0.083333\ ast & ast & 0.261164 end right), dots, $$ $$ X_<12>=left(begin 0.640657 & 0.167720& -0.315098\ ast & 0.871895 & 0.147379\ ast & ast & 0.630487 end right) $$ и $$ X_<12>^2-A approx left(begin -0.004 & 0.0019 & -0.0038\ ast & -0.0009& 0.0019\ ast & ast & -0.0038 end right) , . $$
Задачи
Источники
Демидович Б.П. Лекции по математической теории устойчивости. М.: Изд-во МГУ: ЧеРо, 1998
Часть 2: Функции от матриц
ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ № 1.
Часть1 : МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
Выполнил Образцов С.П
Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 03
Часть 1.(K – поле вещественных чисел)
1.01. Построение заданного матричного многочлена . . . . . . . . . . 03
1.02. Определение ранга матрицы B . . . . . . . . . . . . . . . . . . 04
1.03. Определение собственных векторов и собственных значений . . 04
1.04. Построение матрицы, союзной матрице B. . . . . . . . . . . . . . 07
1.05. Решение уравнения  . . . . . . . . . . . . . . . . . . . . . . 08
. . . . . . . . . . . . . . . . . . . . . . 08
Часть 2.(K – поле вычетов по модулю 11)
2.01.Построение заданного матричного многочлена . . . . . . . . . . 08
2.02.Определение ранга матрицы B . . . . . . . . . . . . . . . . . . 09
2.03.Определение собственных векторов и собственных значений . . 09
2.04. Построение матрицы, союзной матрице B . . . . . . . . . . . . . 11
2.05.Решение уравнения  . . . . . . . . . . . . . . . . . . . . . . 13
. . . . . . . . . . . . . . . . . . . . . . 13
Литература.
01. Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1967. –575 стр., с илл.
02. Проскуряков И.В. Сборник задач по линейной алгебре. Изд-во “Наука”. – М., 1967 г.,-384 стр.
Постановка задачи. Дана матрица  и числа p = 3 , q = 1.
и числа p = 3 , q = 1.
1. Построить матрицу  .
.
2. Определить ранг матрицы B.
3. Найти собственные векторы и собственные значения матрицы B.
4. Построить матрицу, союзную к матрице B.
5. Найти все решения уравнения 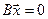 . Определить ранг этого множества.
. Определить ранг этого множества.
Задание выполнить для двух вариантов числового поля:
a) K – поле вещественных чисел,
b) K – поле вычетов по модулю 11.
Часть 1. (К – поле вещественных чисел)
1.01. Построение заданного матричного многочлена.
Определим матричный многочлен  . Пусть
. Пусть  ,
,
тогда  ;
;
Определим матрицу  :
:
 ;
;
1.02. Определение ранга матрицы B .
Для определения ранга матрицы B приведем ее к усеченно треугольному виду путем элементарных преобразований. Для этого выполним цепочку действий над строками:
 ;
;
Таким образом, rg(B) = 4.
1.03. Определение собственных векторов и собственных значений.
Построим характеристический многочлен.
 .
.
Выполним эквивалентные преобразования определителя:
 ;
;
 ;
;
 ;
;
Таким образом,  .
.
Определим собственные векторы.

Решаем систему уравнений  . Используя преобразования матрицы, приведем матрицу
. Используя преобразования матрицы, приведем матрицу  к усеченно-диагональному виду.
к усеченно-диагональному виду.
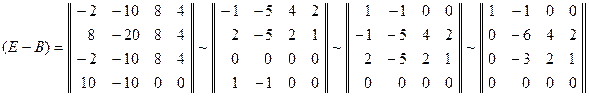 ;
;
Столбцы 2 и 4 меняем местами.
 .
.
Учитывая перестановку столбцов, получим равенства с двумя степенями свободы:

Дадим свободным переменным сначала значения  , а затем
, а затем  . Получим два линейно независимых собственных вектора :
. Получим два линейно независимых собственных вектора :  ;
;  .
.
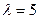
Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу
. Используя элементарные преобразования, приведем матрицу  к усеченно-диагональному виду.
к усеченно-диагональному виду.
 ;
;
 .
.
Таким образом,  Полагая
Полагая  , получим
, получим  .
.

Решаем систему уравнений 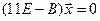 . Используя элементарные преобразования, приведем матрицу (11E – B) к усеченно-диагональному виду.
. Используя элементарные преобразования, приведем матрицу (11E – B) к усеченно-диагональному виду.
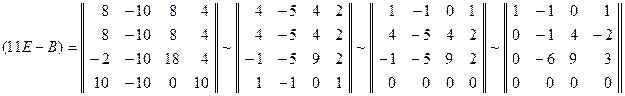 ;
;
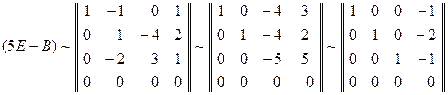 .
.
Тогда  . Полагая
. Полагая  , получим
, получим  .
.
Таким образом, матрица B имеет простую структуру и неособенным
преобразованием  приводится к диагональному виду:
приводится к диагональному виду:
 .
.
Матрица B имеет отличный от нуля определитель:
 .
.
1.04. Построение союзной матрицы.
Из не вырожденности матрицы B следует равенство:  . Тогда союзная матрица может быть найдена методом эквивалентных преобразований
. Тогда союзная матрица может быть найдена методом эквивалентных преобразований  . Построив блочную матрицу, выполним эти преобразования.
. Построив блочную матрицу, выполним эти преобразования.


 .
.
Таким образом,  .
.
1.05. Решение уравнения  .
.
Так как определитель матрицы B отличен от нуля, то уравнение 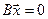 имеет только нулевое (тривиальное) решение. Ранг множества всех решений этого уравнения равен нулю.
имеет только нулевое (тривиальное) решение. Ранг множества всех решений этого уравнения равен нулю.
Часть 2. (K – поле вычетов по модулю 11)
2.01.Построение заданного матричного многочлена.
Для построения матричного многочлена  , где
, где  , приведем элементы матрицы A к числам поля K:
, приведем элементы матрицы A к числам поля K:
 .
.
Возведем матрицу в квадрат:
 ;
;
Вычисление элементов матрицы H:
Определим матрицу  :
:
 ;
;
2.02.Определение ранга матрицы B.
Для определения ранга матрицы B приведем ее к усеченно-треугольному виду путем элементарных преобразований. Для этого выполним цепочку действий над строками :
 ;
;
Таким образом, rg(B) = 3.
6. Найти собственные векторы и собственные значения матрицы B.
Рассмотрим характеристический многочлен матрицы B.
 .
.
Выполним эквивалентные преобразования определителя:
1-й этап. Преобразование 1-й строки : – .
2-й этап. Преобразование 3-го столбца <2>+ <1>и понижение порядка определителя.
3-й этап. Еще раз понижение порядка определителя.
 ;
;
4-й этап. – и понижение порядка определителя.
 ;
;
Таким образом,  .
.
Определим собственные векторы.

Решаем систему уравнений 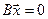 . Используя элементарные преобразования, приведем матрицу B к усеченно-диагональному виду.
. Используя элементарные преобразования, приведем матрицу B к усеченно-диагональному виду.
1-й этап. * 4, * 4, * 6.
2-й этап. Меняем местами 2-ю и 4-ю строки. Далее – , – , – .
3-й этап. * 4, + 4* , + 2* .
4-й этап. *3, + 4* , + 4* .
 ;
;
Получаем систему равенств с одной степенью свободы:

Полагая 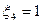 , получим
, получим  .
.

Решаем систему уравнений 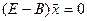 . Используя элементарные преобразования, приведем матрицу (E – B) к усеченно-диагональному виду.
. Используя элементарные преобразования, приведем матрицу (E – B) к усеченно-диагональному виду.
 ;
;
Таким образом, система уравнений имеет две степени свободы:

Полагая первый раз  , получим
, получим  . Во втором случае положим
. Во втором случае положим  . Тогда
. Тогда  .
.
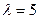
Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу (5E – B) к усеченно-диагональному виду.
. Используя элементарные преобразования, приведем матрицу (5E – B) к усеченно-диагональному виду.
1-й этап. *6, *7, *5, *10.
3-й этап. – , *4, + , + 7* .
 ;
;
Таким образом,  Полагая
Полагая  , получим
, получим  .
.
Матрица, составленная из собственных векторов, имеет вид:  .
.
2.04.Построение союзной матрицы.
Определитель матрицы B равен нулю, поэтому нельзя применить способ вычисления союзной матрицы, основанный на обращении матрицы B . Воспользуемся простой структурой матрицы B. Пусть  , тогда
, тогда  . Матрица D имеет диагональный вид, где диагональными элементами являются собственные значения матрицы B , взятые в том же порядке, что и собственные векторы:
. Матрица D имеет диагональный вид, где диагональными элементами являются собственные значения матрицы B , взятые в том же порядке, что и собственные векторы:
 .
.
Определим матрицу  , вычисляя алгебраические дополнения каждого ее элемента.
, вычисляя алгебраические дополнения каждого ее элемента.
 .
.
Найдем обратную матрицу форм.



 .
.
2.05.Решение уравнения  .
.
Так как определитель матрицы B равен нулю, то уравнение  имеет и решения, отличные от нулевого. Такими решениями являются собственные векторы матрицы B, соответствующие нулевому собственному значению. Множество всех решений заданного уравнения образует линейное подпространство, размерность которого зависит от кратности нулевого собственного значения. В нашем случае нулевое собственное значение является простым, поэтому размерность подпространства равна 1. Это подпространство можно представить как линейную оболочку, натянутую на собственный вектор
имеет и решения, отличные от нулевого. Такими решениями являются собственные векторы матрицы B, соответствующие нулевому собственному значению. Множество всех решений заданного уравнения образует линейное подпространство, размерность которого зависит от кратности нулевого собственного значения. В нашем случае нулевое собственное значение является простым, поэтому размерность подпространства равна 1. Это подпространство можно представить как линейную оболочку, натянутую на собственный вектор  .
.
В настоящей работе проведено исследование матричного многочлена  , где матрица
, где матрица  – задана. Выполнены вычисления элементов матрицы
– задана. Выполнены вычисления элементов матрицы  , определены её ранг, собственные векторы и собственные значения. Найдена матрица, союзная к матрице
, определены её ранг, собственные векторы и собственные значения. Найдена матрица, союзная к матрице  . Исследована однородная система уравнений
. Исследована однородная система уравнений 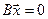 . Работа выполнена в двух вариантах:
. Работа выполнена в двух вариантах:
1. Вычисления проведены над полем вещественных чисел;
2. Вычисления проведены над полем вычетов по модулю 11.
Часть 2: Функции от матриц
Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 03
Часть 1. Исследование спектральных свойств матрицы A.
1.06. Определение собственных значений и собственных векторов . . 03
1.07. Построение минимального многочлена матрицы. . . . . . . . . . 05
1.08. Построение интерполяционного многочлена . . . . . . . . . . . . 05
1.09. Вычисление функции от матрицы  . . . . . . . . . . . . 05
. . . . . . . . . . . . 05
Часть 2. Исследование спектральных свойств матрицы B.
2.01.Определение собственных значений и собственных векторов . . 06
2.02.Сравнительный анализ матриц  и
и  . . . . . . . . . . . . . 08
. . . . . . . . . . . . . 08
Литература.
03. Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1967. –575 стр., с илл.
04. Проскуряков И.В. Сборник задач по линейной алгебре. Изд-во “Наука”. – М., 1967 г. -384 стр.
Постановка задачи. Дана матрица  и функция
и функция 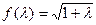 .
.
1. Найти собственные векторы и собственные значения матрицы A.
2. Найти минимальный многочлен  матрицы A .
матрицы A .
3. Построить интерполяционный многочлен  , совпадающий с заданной функцией
, совпадающий с заданной функцией  на спектре матрицы A .
на спектре матрицы A .
4. Вычислить  , используя соотношение:
, используя соотношение:  .
.
5. Найти собственные векторы и собственные значения матрицы B .
6. Установить зависимость собственных значений матрицы B от собственных значений матрицы A .
Часть 1. Исследование спектральных свойств матрицы A.
1.01. Определение собственных значений и собственных векторов.
Построим характеристический многочлен.
 .
.
Выполним эквивалентные преобразования определителя:


Таким образом,  . Определим собственные векторы.
. Определим собственные векторы.

Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу A к усеченно-диагональному виду.
. Используя элементарные преобразования, приведем матрицу A к усеченно-диагональному виду.
 .
.
Получаем два линейно независимых собственных вектора:
 ,
,  .
.
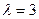
Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу
. Используя элементарные преобразования, приведем матрицу  к усеченно-диагональному виду.
к усеченно-диагональному виду.
 .
.
Получаем собственный вектор:  .
.

Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу
. Используя элементарные преобразования, приведем матрицу  к усеченно-диагональному виду.
к усеченно-диагональному виду.

 .
.
Получаем собственный вектор:  .
.
Таким образом, матрица A имеет простую структуру.
1.02. Построение минимального многочлена матрицы.
Матрица A имеет простую структуру, поэтому минимальный многочлен не имеет кратных корней:  . Таким образом,
. Таким образом,  .
.
1.03. Построение интерполяционного многочлена.
Так как корни минимального многочлена простые, то строим интерполяционный многочлен Лагранжа.
 ;
;
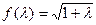 ,
,  .
.
Тогда  .
.
Выполнив преобразования, получим:
 .
.
1.04. Вычисление функции от матрицы  ,
,
Используя равенство  , получим
, получим  . Определим
. Определим  .
.  . Далее
. Далее


Часть 2. Исследование спектральных свойств матрицы B.
2.01.Определение собственных значений и собственных векторов.
Построим характеристический многочлен матрицы B:
 .
.
Выполним следующие эквивалентные преобразования определителя:

 .
.
Таким образом,  .
.
Определим собственные векторы.

Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу системы уравнений к усеченно-диагональному виду.
. Используя элементарные преобразования, приведем матрицу системы уравнений к усеченно-диагональному виду.
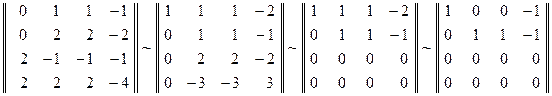
 .
.
Получаем два линейно независимых собственных вектора:  ,
,  .
.

Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу
. Используя элементарные преобразования, приведем матрицу  к усеченно-диагональному виду.
к усеченно-диагональному виду.
 .
.
Получаем собственный вектор:  .
.

Решаем систему уравнений  . Используя элементарные преобразования, приведем матрицу
. Используя элементарные преобразования, приведем матрицу  к усеченно-диагональному виду.
к усеченно-диагональному виду.
 .
.
Получаем собственный вектор:  .
.
2.02.Сравнительный анализ матриц  и
и  .
.
a). Матрица B имеет простую структуру,
b). Собственные векторы матрицы B являются собственными векторами матрицы A,
c).  .
.
d).  ,
,
Работа посвящена вычислению функции от заданной матрицы при помощи интерполяционного многочлена. 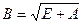 . Выполнен сравнительный анализ структуры, собственных векторов и собственных значений исходной матрицы и её функции.
. Выполнен сравнительный анализ структуры, собственных векторов и собственных значений исходной матрицы и её функции.
Матричные функции
Матричные ряды
Краткая запись произведения матриц А А-. А может быть сделана в форме А*, где к – число множителей, входящих в произведение. Как и возведение в степень скаляров, умножение степеней матриц подчиняется обычным
правилам: А а ‘А ш = А* + “’, (а а ) =A to ”,A°=En где Еп – единичная матрица порядка п.
Эти же правила справедливы и при возведении матрицы в отрицательную степень при условии, что матрица неособенная, т. е. существует обратная матрица.
Можно возводить матрицы и в дробную степень. Так, если А”‘ =В, где А – квадратная матрица, то А является корнем т-й степени из В: А = л/в = В 1/ “‘.
В отличие от скаляров, у которых имеется ровно т корней т-й степени, не существует общего правила определения, каким количеством корней т-й степени обладает матрица В. Это число корней зависит от конкретного вида матрицы.
Возьмем произвольный многочлен m-го порядка от скалярной переменной х:
Заменив в этом выражении х на квадратную матрицу А порядка п, получим соответствующий матричный многочлен:
Многочлен (5.31) можно, как известно, представить в виде произведения:
где Xt (i = 1,2- корни многочлена, которые предполагаются различными. Подобным же образом можно представить и матричный многочлен:
Обобщением ряда (5.31) будет бесконечный степенной ряд:
Заменив переменную х в последнем выражении на квадратную матрицу А, получим бесконечный ряд по А:
Вопросы сходимости матричных рядов затрагивать не будем, достаточно знать только, что ряд (5.34) сходится, если сходятся соответствующие скалярные ряды (i = 1,2. и), где Я,. – собственные значения матрицы А.
Функции от матриц
Разложение известных скалярных функций в степенные ряды дает основание для определения этих функций от матриц.
Ряды (5.35) сходятся равномерно и абсолютно. Поскольку произведение матриц в общем случае некоммутативно, равенство е А е в – е в е А – е А+в выполняется, только если матрицы А и В коммутативны АВ = ВА. Последнее условие выполняется, если В = А или В = – А. В частности, при В = – А имеем
откуда ясно, что матрица е
А является обратной к матрице е А .
Если А не зависит от времени, то матричная экспонента е ы определяется подобно уравнению (5.35) в форме бесконечного ряда:
Этот ряд сходится равномерно и абсолютно для всех значений времени t. Производная по t от матричной экспоненты е ы находится почленным дифференцированием ряда (5.36):
Обобщая соотношение (5.37) для ?-й производной с учетом обозначения d
Если N(p) – многочлен от оператора дифференцированияр, то
Интеграл от матричной экспоненты е* можно найти путем интегрирования бесконечного ряда (5.36)
Из последнего соотношения, предполагая, что матрица А – неособенная, получим:
Матричная комплексная экспонента в формулах (5.41) и (5.42) определяется уравнением (5.35) при замене А на /А:
Как легко видеть, формулы (5.41)-(5.43) являются матричными аналогами формул Эйлера.
Матричный гиперболический синус:
Матричный гиперболический косинус:
Матричные тригонометрические тождества имеют соответствующие аналоги скалярных тригонометрических тождеств и выводятся с помощью вышеприведенных матричных соотношений.
[spoiler title=”источники:”]
http://megapredmet.ru/1-53869.html
http://bstudy.net/829119/tehnika/matrichnye_funktsii
[/spoiler]
