В этой статье мы разберём нахождение наибольшего и наименьшего значения функции на отрезке, интервале, в
бесконечности, а также повторим основные свойства функции и связанные термины.
Что такое функция
Наш мир — это огромная коллекция взаимосвязей, которые порой явно, а порой невидимо влияют на всех, кто в них
участвует. Ваше настроение может влиять на успеваемость в школе, питание — на спортивные достижения, навыки — на
возможность поступить в университет. В физическом мире температура влияет на скорость протекания процесса,
плотность тела — на его способность к плаванию в воде, угол падения лучей — на то, каким образом они будут преломляться, пройдя
через прозрачную призму.
Некоторые из этих взаимоотношений можно описать математически: обозначить участников буквами латинского алфавита и
описать их взаимосвязь через математические действия и знаки.
Функция — это правило, формула или выражение, которое описывает взаимосвязь двух величин.
Как описать зависимость пройденного пути от времени?
Есть ли правило, которое описывает отношение ускорения тела и силы, приложенной к нему? Да:
А что, если нужно вычислить зависимость остатка денег от количества купленных товаров? Пожалуйста:
, где
— остаток денег,
— исходная сумма,
— количество товара,
— стоимость товара за одну единицу.
В каждом из этих выражений есть зависимая и независимая переменные. Зависимая переменная — это и есть функция, а
независимая — аргумент. Так, в нашем последнем примере стоимость товара за одну его единицу
является независимой переменной (цену назначил продавец, и мы на это повлиять никак не можем). Зато остаток в
кошельке поддаётся изменениям — чем меньше мы купим товара, тем больше останется денег. И так в любой зависимости!
Обратите внимание
Зависимая переменная стоит слева от знака «равно» и определяется через выражение, содержащее аргумент.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Графическое задание функции
Представьте, что для школьной научной конференции вы готовите доклад о загрязнении окружающей среды. Как вы
думаете, что произведёт больший эффект на аудиторию:
-
перечисление статистических данных об увеличении количества мусора за последний год;
-
наглядная демонстрация роста загрязнений в виде графика?
Верно — иллюстрации, фотографии, графики и диаграммы говорят порой громче любых слов! 📈
Для наглядного отображения зависимости одной переменной от другой мы введём систему координат, в которой построим график.
График — это прямая, кривая или ломаная линия, которая была построена чётко по уравнению
(функции).
Как мы уже говорили, функция состоит из зависимой и независимой переменной. В декартовой системе координат
независимая переменная отображается с помощью оси
зависимая — с помощью оси
В зависимости от типа функции график может выглядеть, например, так:
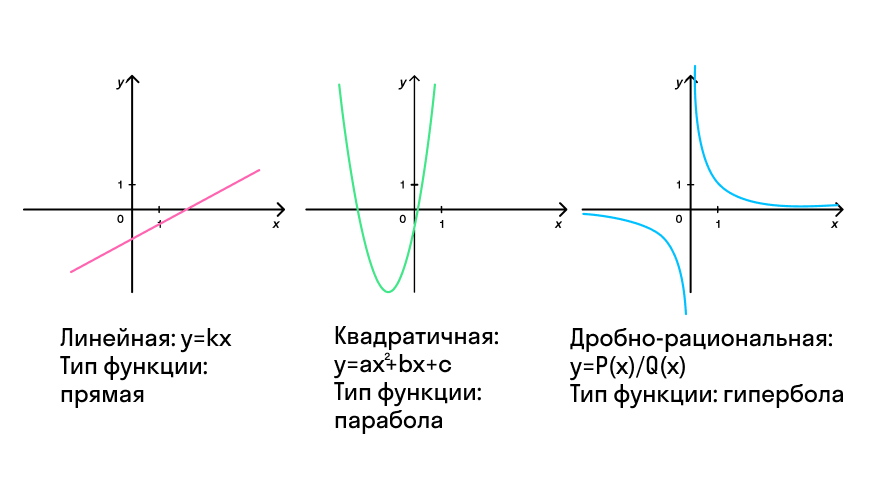
Наибольшее и наименьшее значение функции
На уроках алгебры учитель просит определить наибольшее и наименьшее значение функции. Что он имеет в виду?
Чтобы найти наименьшее или наибольшее значение функции, необходимо понять, какое наименьшее или наибольшее
численное значение принимает
— зависимая переменная.
Наибольшее значение функции
на некотором промежутке
— это значение
которое при любом значении
делает справедливым неравенство
Теперь расшифровка! 😅 Если на данном интервале значение
больше, чем значение
в окрестностях точки
то такой
будет считаться наибольшим значением на данном промежутке.
Наименьшее значение функции
на некотором промежутке
— это значение
которое при любом значении
делает справедливым неравенство
Если на данном интервале значение
меньше, чем значение
в окрестностях точки
то такой
будет считаться наименьшим значением на данном промежутке.
Наибольшее и наименьшее значение функции на графиках
Самый простой способ определить
и
— рассмотреть график.
Если заданный интервал представлен прямой:
-
при возрастающей функции: наименьшее значение функция примет при наименьшем аргументе и наоборот, наибольшее
значение функции будет соответствовать наибольшему значению аргумента; -
при убывающей функции: наименьшее значение функция примет при наибольшем аргументе и наоборот, наибольшее
значение функции будет соответствовать наименьшему значению аргумента.
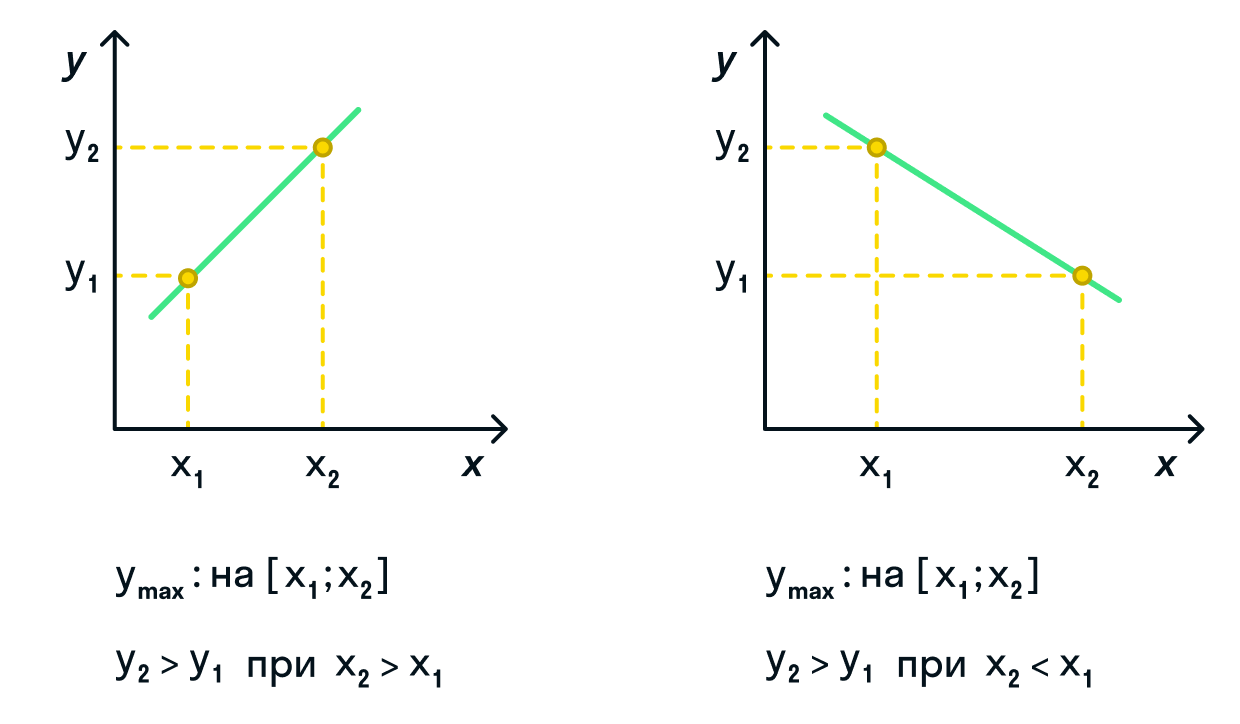
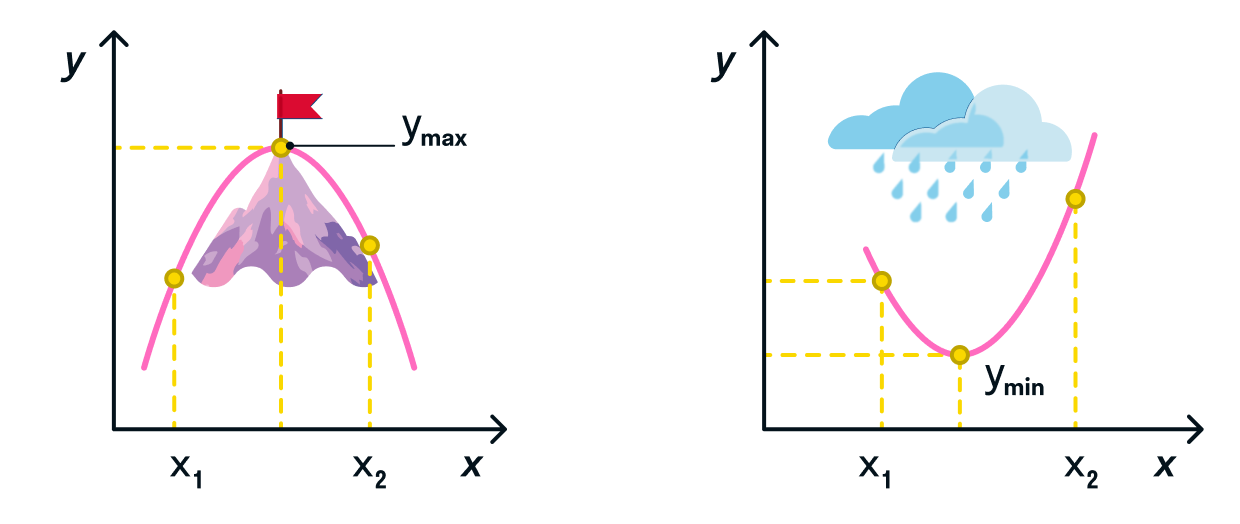
Если заданный интервал представлен кривой:
-
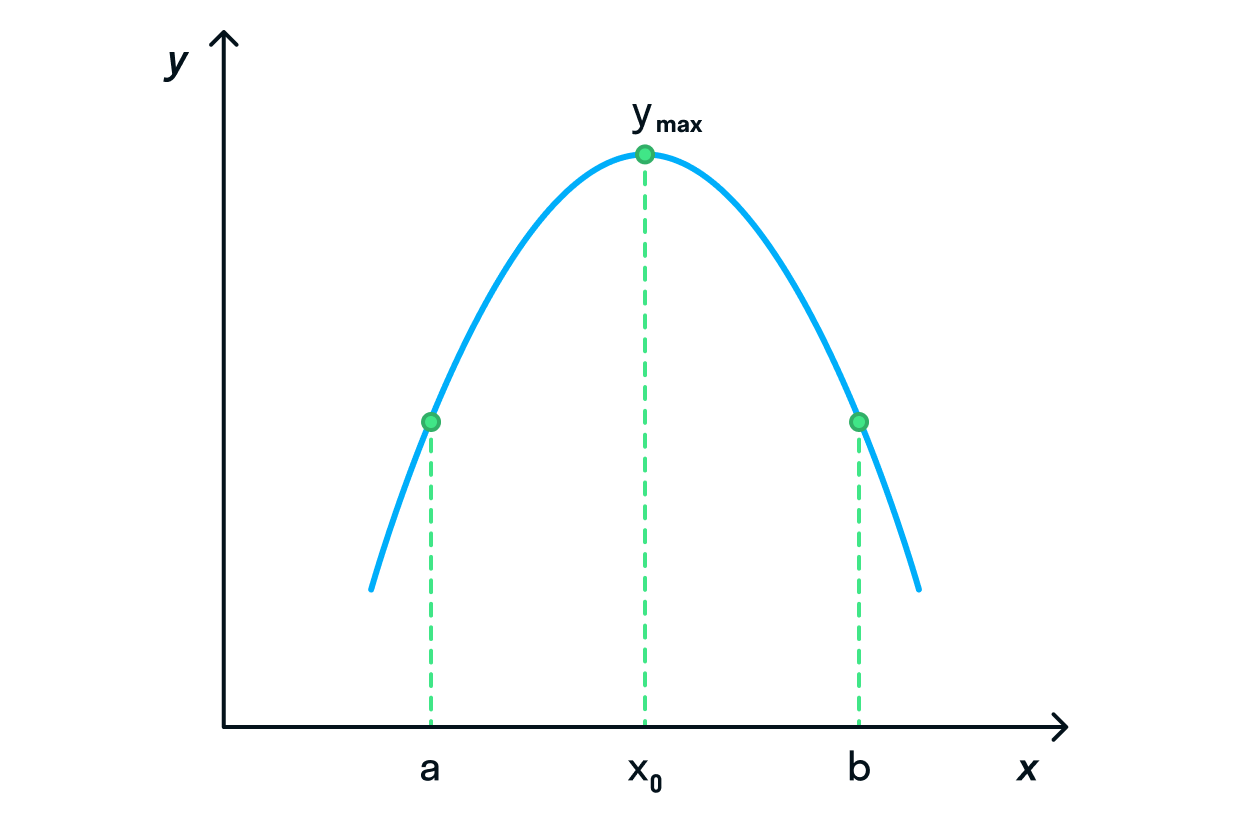
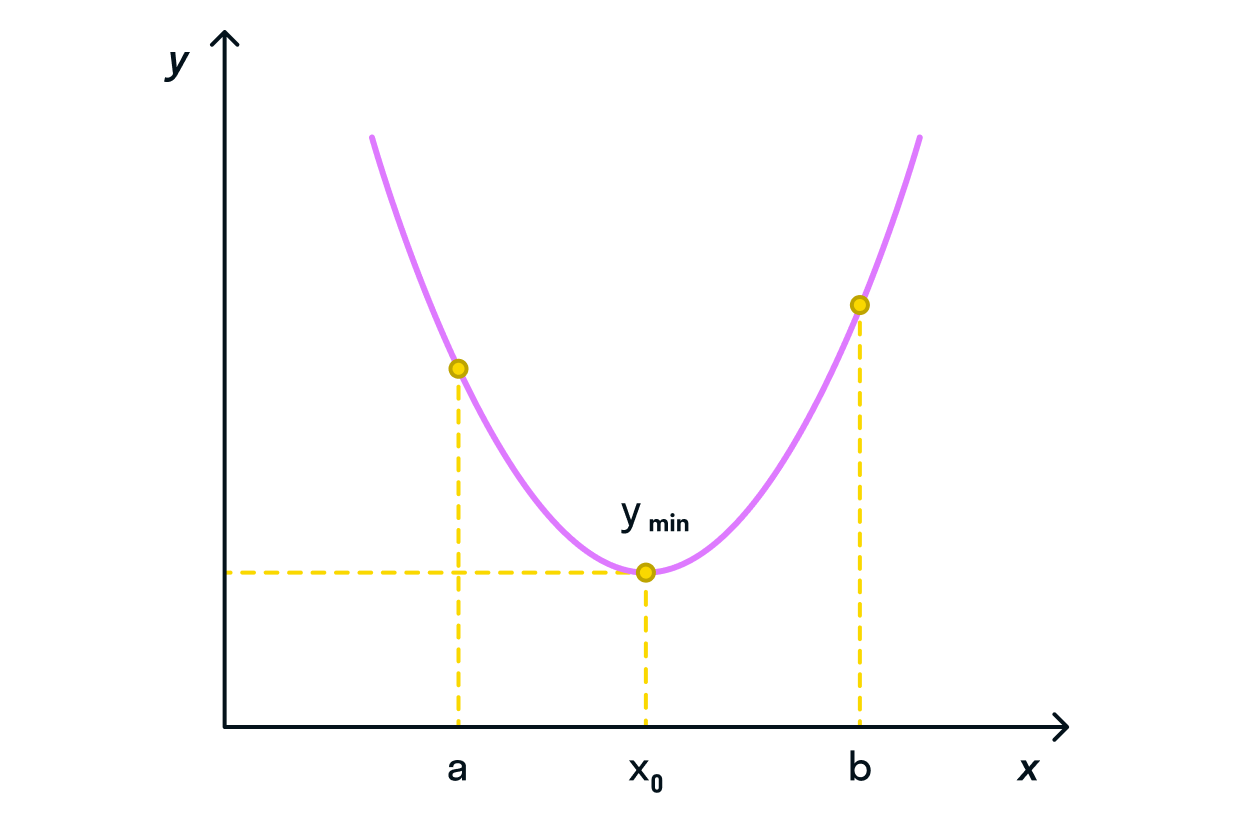
максимальное значение функции выглядит как вершина горы, возвышенности, тогда как минимальное значение мы
можем определить как самую низкую точку относительно этого пика; -
минимальное значение функции выглядит как дно низины, оврага, тогда как максимальное значение мы можем
определить как самую высокую точку относительно этого пика.
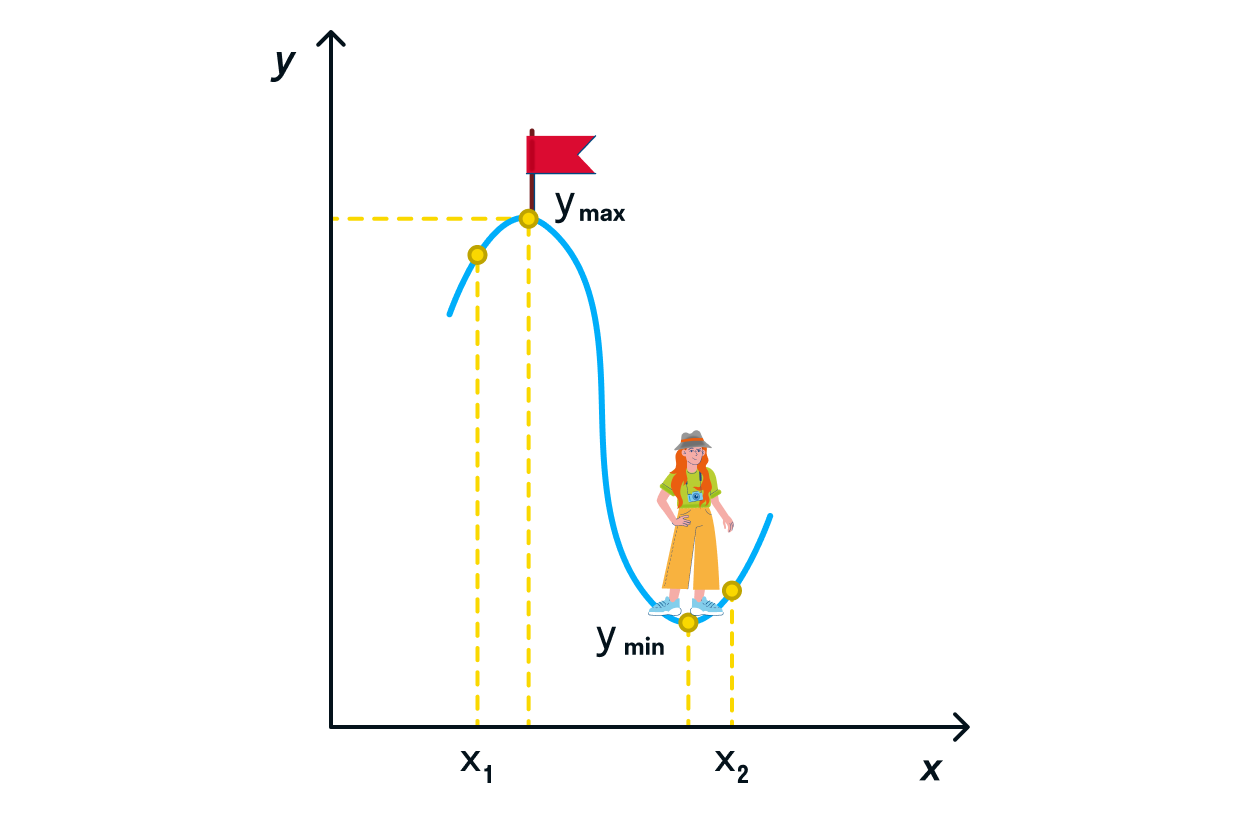
Возможен и такой вариант, когда горы и овраги встречаются на одном промежутке — тогда мы просто объединяем оба
пункта для нахождения
и
Помним главное правило: максимальное значение функции всегда представлено самой
высокой точкой относительно оси
минимальное значение функции — самой низкой точкой.
Определение наименьшего и наибольшего значения через производную
Удобен ли способ нахождения
и
через график? Определённо!
Всегда ли его можно использовать? К сожалению, нет.
Дело в том, что большинство заданий в алгебре на эту тему даются не через график, а через уравнение функции.
Зачастую эти функции сложные, и построение их графиков займёт время. Ошибётесь в построении — допустите ошибку и в
нахождении максимального и минимального значения, а нам это не нужно.
Способ, который не уступает первому в простоте и лаконичности, заключается в определении производной функции и
поиске стационарных точек. Кажется, нам встретились два новых термина — давайте их разберём.
Производная функции — это отношение приращения функции к приращению аргумента при бесконечно
малом приращении аргумента.
Производная функции показывает, как быстро увеличивается функция
при бесконечно малом увеличении
По сути, найти производную означает провести определённые действия с помощью таблицы производных
функций. Обязательно загляните в нашу статью об этом и изучите материал, а мы пока пойдём дальше.
Стационарная точка — точка, в которой значение аргумента производной функции равно нулю.
Дело в том, что по теореме Ферма в стационарных точках определяется экстремум функции, поэтому можно сделать
вывод, что на некотором промежутке в них можно определить и наибольшее/наименьшее значение функции.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке
Как определить наибольшее и наименьшее значения функции на отрезке?
-
Найдём область определения данной функции и проверим, входит ли в неё заданный отрезок.
-
Найдём производную данной функции.
-
Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).
-
Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
них. -
Возьмём точки начала и конца отрезка и найдём значение функции в них.
-
Сделаем вывод о наибольшем и наименьшем значении функции.
Разберём пару примеров.
Задача 1
Найдите наибольшее и наименьшее значение функции
на отрезке
Решение:
-
ОДЗ:
-
не попадает в промежуток
Найдём значение функции только в крайних точках:
-
Тогда
является наименьшим значением на данном отрезке, а
наибольшим.
Задача 2
Найдите наибольшее и наименьшее значение функции
на отрезке
Решение:
-
ОДЗ:
-
, но в таком случае знаменатель равен нулю, что невозможно. А значит, производная
не обращается в нуль, стационарных точек нет. -
Найдём значение функции в крайних точках отрезка:
— точка максимума на промежутке;
— точка минимума на промежутке.
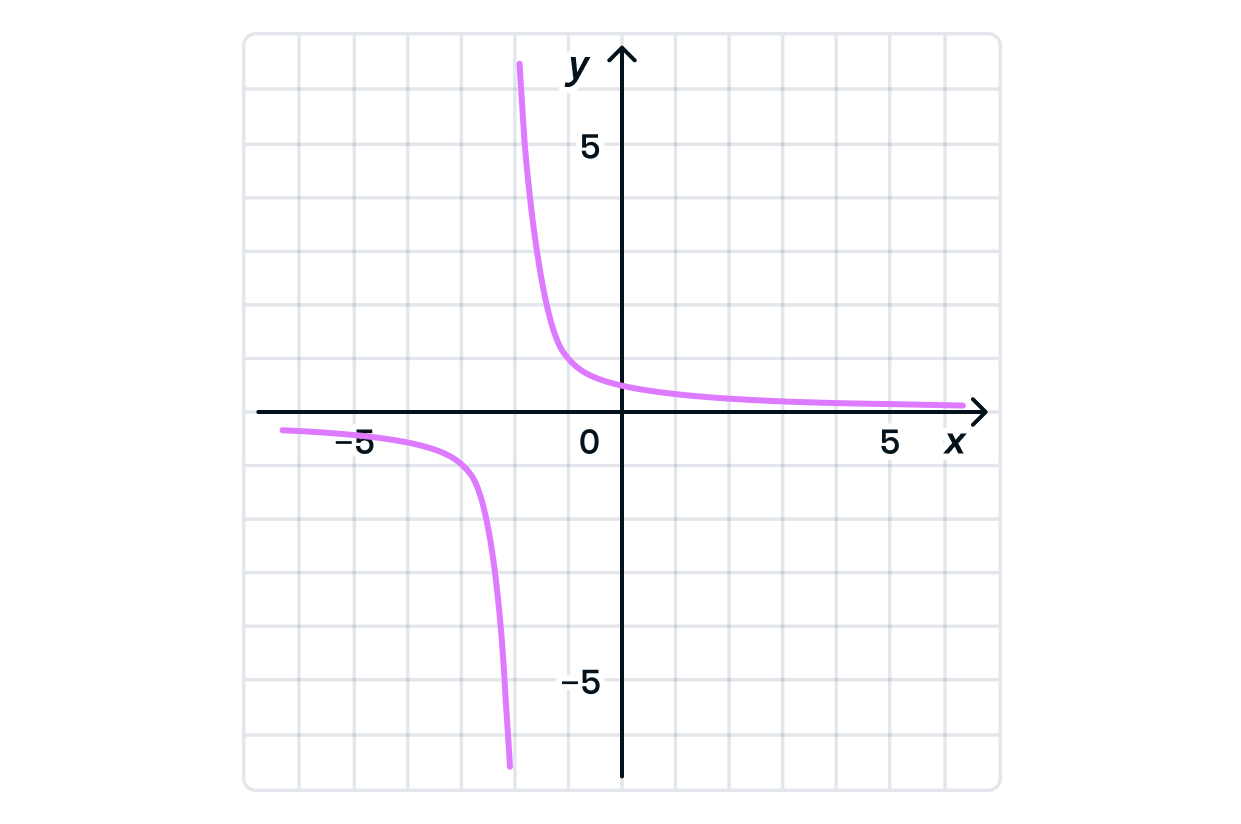
Наименьшее и наибольшее значение функции на открытом или бесконечном интервале
В чём отличие отрезка от интервала? В отрезке определены крайние точки, в интервале же крайние точки могут не
существовать (например
), или значение функции в них мы рассматривать не будем (на интервале
мы рассмотрим значение функции в окрестностях этих точек, но не в них самих).
Вариантов задания интервала может быть множество, но каждый из них сведёт определение
и
к поиску производной и вычислению пределов в крайних точках, например
и
Вернёмся на пару шагов назад. А что такое предел функции?
Если говорить коротко, то предел функции — это такое число
, к которому функция стремится, в то время как аргумент стремится достичь числа
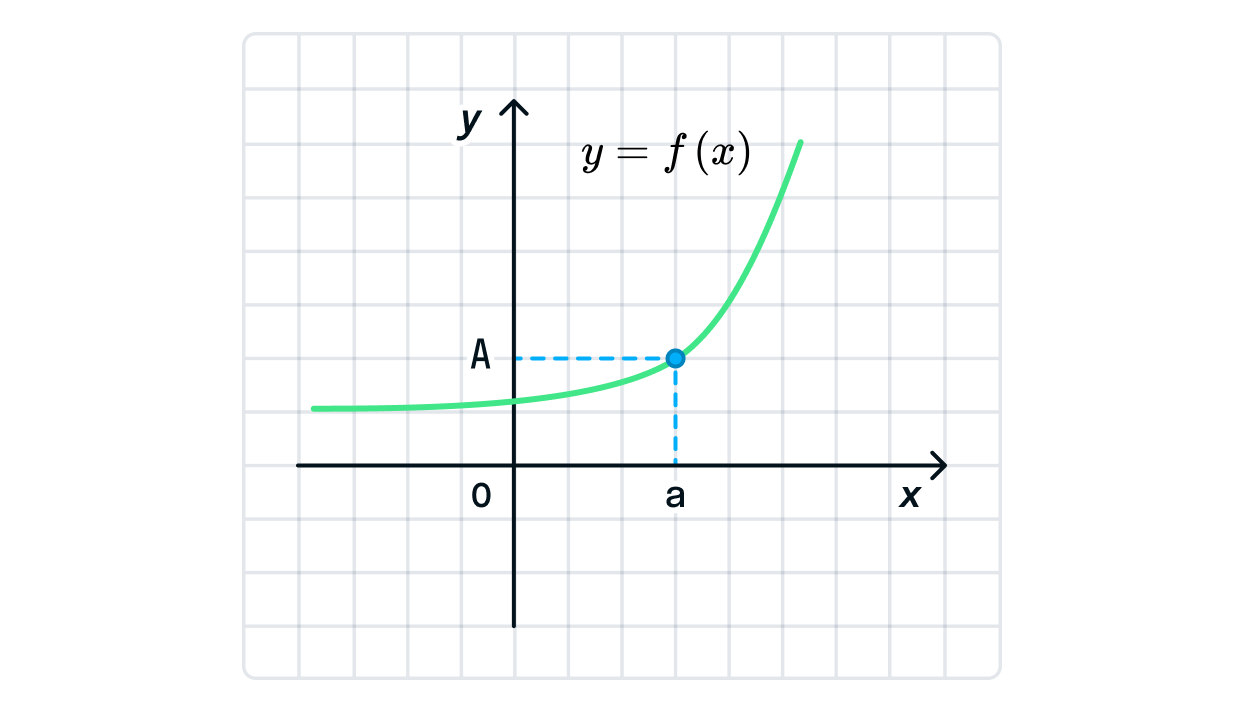
Предположим, наша функция представлена уравнением
Найдём предел функции при
подставив это значение вместо
в уравнение:
Это означает, что функция стремится приблизиться к числу
в то время как аргумент тоже приближается к этому значению. В отрыве от настоящего
уравнения мы могли бы представить это так:
Функция может стремиться не только к рациональному
числу, но также и к бесконечности. В таком случае при подстановке бесконечности в функцию возникает
неопределённость, которую необходимо решить разными методами.
В рамках этой статьи мы не можем посвятить этому много времени, поэтому ждём Вас на курсах математики в онлайн-школе
Skysmart — там ни один предел не останется незамеченным. 😉
Вернёмся к функции! Итак, как же определить наибольшее и наименьшее значение на интервале?
-
Найдём область определения данной функции и проверим, входит ли в неё заданный интервал.
-
Найдём производную данной функции.
-
Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).
-
Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
них. -
Возьмём крайние точки интервала и вычислим значение предела в этих точках (согласно типу интервала).
-
Сделаем вывод о наибольшем и наименьшем значении функции.
Для вычисления предела вам поможет сводная таблица, которая учитывает вид интервала:
Если при вычислении одностороннего предела вы получаете бесконечность, то вычислить наибольшее/наименьшее
значение невозможно.
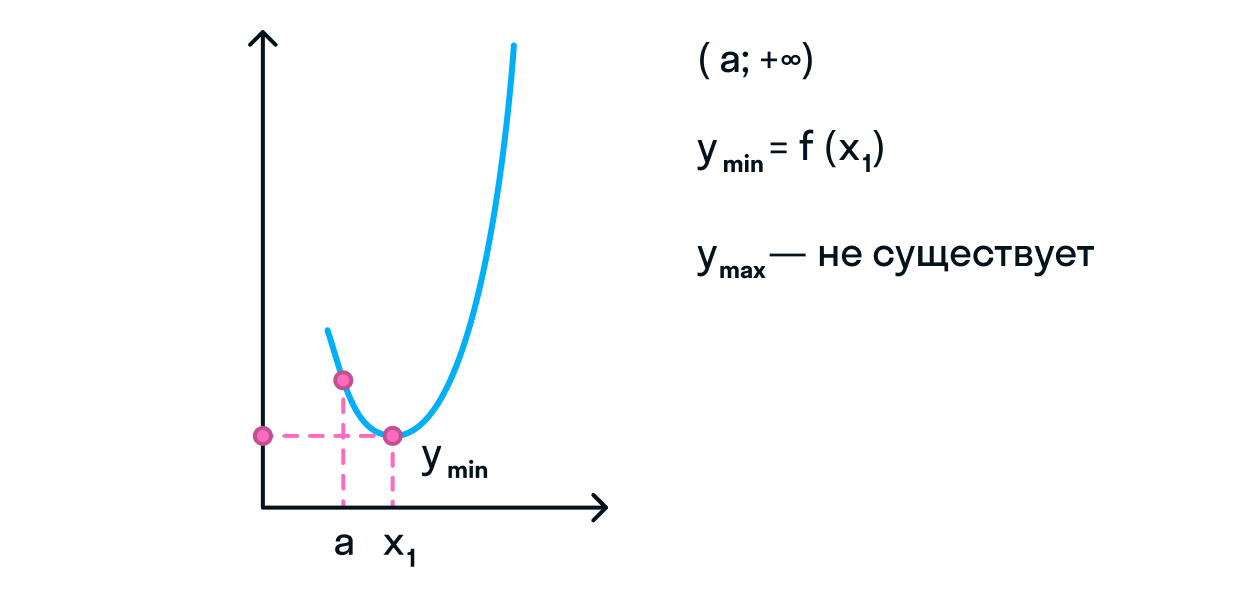
Задача 3
Необходимо найти наибольшее и наименьшее значение функции
на всём промежутке области определения.
Решение:
-
ОДЗ:
-
Найдём стационарные точки:
-
Точка
входит в промежуток области определения и является точкой минимума.
-
Так как
— парабола, ветви которой направлены вверх, мы не можем определить точку
максимума.
Cегодня мы на славу потрудились и разобрали множество важных вопросов:
-
что такое функция, какой она бывает;
-
что такое наименьшее и наибольшее значение функции;
-
как определить
и
на отрезке;
-
как находить наименьшее и наибольшее значение функции на интервале;
-
что такое предел и производная.
Вот и ещё одна тема по математике стала понятнее! А если всё же остались вопросы, спешим ещё раз пригласить вас на уроки математики в Skysmart — мы постараемся ответить на них, закрепить материал и попрактиковаться в решении задач. Обещаем, будет увлекательно и безумно интересно!
Судя по всему, то, о чем Вы говорите — аппроксимация функции. В Википедии более подробна статья про интерполяцию.
По сути, Ваша задача сводится к 2м шагам:
1. По точкам и общим зависимостям выбирается форма функции (например, полиномиальная, экспоненциальная и.т.п).
2. Строится модель, в которой задаётся функция с неизвестными параметрами. Задача — найти такие параметры, чтобы минимизировать функцию невязки(часто это квадрат разности между реальными значениями в заданых точках и значениями модельной функции, см. МНК).
Если известны некоторые значения x и y на графике, то можно найти коэффициент и свободный член данной функции. Допустим линейная зависимость y=kx+b. Например нам известно, что при x = 2, y = 5 и при х = 3, у = 4,5. Составим систему уравнений, подставив известные значения х и у: {2k+b=5; 3k+b=4,5}, решив систему, нетрудно догадаться, что k=-0,5; b=6;
В итоге наша функция принимает вид y=-0,5x+6
Да, это численные методы. Ищите по словам «Аппроксимация» и «Интерполяция». Из книг могу порекомендовать: Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. У меня бумажное издание 1989 года. В Гугле можно найти в DJVU. Примеры на Бейсике позволяет запрограммировать нужный метод на вашем любимом языке программирования, даже не вникая в их суть. А вообще если есть время и желание, разберитесь, это довольно интересно 🙂
Вывести уравнение прямой по координатам двух точек
По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.
Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.
Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.
Алгоритм решения данной задаче на языке программирования будет таков:
- Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .
- Получить значения координат ( x2, y2 ) второй точки.
- Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .
- Вычислить значение b по формуле b = y2 — k * x2 .
- Вывести на экран полученное уравнение.
Аппроксимация функции одной переменной
Калькулятор использует методы регрессии для аппроксимации функции одной переменной.
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной
Линейная регрессия
Коэффициент линейной парной корреляции:
Средняя ошибка аппроксимации:
Квадратичная регрессия
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:
,
где
Средняя ошибка аппроксимации:
Кубическая регрессия
Система уравнений для нахождения коэффициентов a, b, c и d:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Степенная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Показательная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Гиперболическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Логарифмическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Экспоненциальная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Вывод формул
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Для функции вида частные производные равны:
,
Подставив производные, получим:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
Как найти функцию зная только точки?
![]()
![]()
Судя по всему, то, о чем Вы говорите — аппроксимация функции. В Википедии более подробна статья про интерполяцию.
По сути, Ваша задача сводится к 2м шагам:
1. По точкам и общим зависимостям выбирается форма функции (например, полиномиальная, экспоненциальная и.т.п).
2. Строится модель, в которой задаётся функция с неизвестными параметрами. Задача — найти такие параметры, чтобы минимизировать функцию невязки(часто это квадрат разности между реальными значениями в заданых точках и значениями модельной функции, см. МНК).
[spoiler title=”источники:”]
http://planetcalc.ru/5992/
http://qna.habr.com/q/5823
[/spoiler]
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
![]()
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
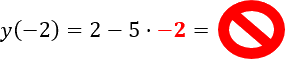
Правильно
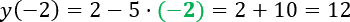
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
![]()
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
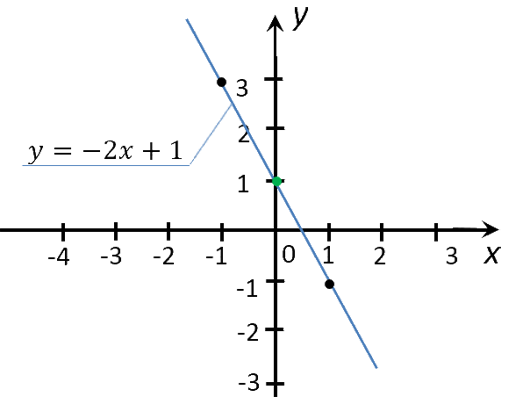
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
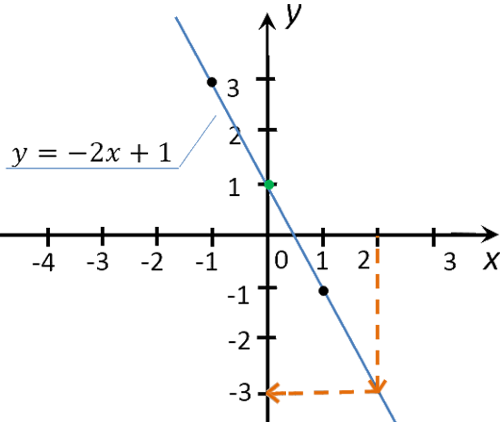
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры

Профиль
Благодарили: 0
Сообщений: 1

Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= – x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov

Профиль
Благодарили: 0
Сообщений: 1

Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов

Профиль
Благодарили: 0
Сообщений: 1

Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
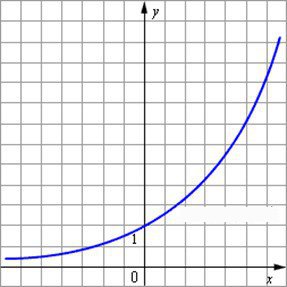 определите вид графика
определите вид графика
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов

Профиль
Благодарили: 0
Сообщений: 3

Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова

Профиль
Благодарили: 0
Сообщений: 11

Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
Как по точкам найти функцию
Во многих случаях данные статистики или измерений какого-либо процесса бывают представлены в виде набора дискретных значений. Но для того, чтобы на их основе построить непрерывный график, нужно по этим точкам найти функцию. Сделать это можно путем интерполяции. Для этого хорошо подходит полином Лагранжа.
Вам понадобится
- – бумага;
- – карандаш.
Инструкция
Определите степень полинома, который будет использован для интерполирования. Он имеет вид: Кn*Х^n + К(n-1)*Х^(n-1) +… + К0*Х^0. Число n здесь на 1 меньше количества известных точек с различными Х, через которые должна проходить результирующая функция. Поэтому просто пересчитайте точки и отнимите от полученного значения единицу.
Определите общей вид искомой функции. Поскольку Х^0 = 1, то она примет вид: f(Хn) = Кn*Х^n + К(n-1)*Х^ (n-1) +… + К1*Х + К0, где n – найденное на первом шаге значение степени полинома.
Начните составление системы линейных алгебраических уравнений с целью нахождения коэффициентов интерполирующего полинома. Исходный набор точек задает ряд соответствий значений координат Хn искомой функции по оси абсцисс и оси ординат f(Хn). Поэтому поочередная подстановка величин Хn в полином, значение которого будет равно f(Хn), позволяет получить нужные уравнения:
Кn*Хn^n + К(n-1)*Хn^ (n-1) +… + К1*Хn + К0 = f(Хn)
Кn*Х(n-1)^n + К(n-1)*Х(n-1)^ (n-1) +… + К1*Х(n-1) + К0 = f(Х(n-1))
…
Кn*Х1n + К(n-1)*Х1^ (n-1) + … + К1*Х1 + К0 = f(Х1).
Представьте систему линейных алгебраических уравнений в удобном для решения виде. Вычислите значения Хn^n… Х1^2 и Х1…Хn, а затем подставьте их в уравнения. При этом значения (также известные) перенесите в левую часть уравнений. Получится система вида:
Сnn*Кn + Сn(n-1)*К(n-1) +… + Сn1*К1 + К0 – Сn = 0
С(n-1)n*Кn + С(n-q)(n-1)*К(n-1) +… + С(n-1)1*К1 + К0 – С(n-1) = 0
…
С1n*Кn + С1(n-1)*К(n-1) +… + С11*К1 + К0 – С1 = 0
Здесь Сnn = Хn^n, а Сn = f(Хn).
Решите систему линейных алгебраических уравнений. Используйте любой известный способ. Например, метод Гаусса или Крамера. В результате решения будут получены значения коэффициентов полинома Кn…К0.
Найдите функцию по точкам. Подставьте коэффициенты Кn…К0, найденные в предыдущем шаге, в полином Кn*Х^n + К(n-1)*Х^ (n-1) +… + К0*Х^0. Данное выражение и будет являться уравнением функции. Т.е. искомая f(Х) = Кn*Х^n + К(n-1)*Х^ (n-1) +… + К0*Х^0.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
