- Определение прямой пропорциональности
- График прямой пропорциональности
- Примеры
Определение прямой пропорциональности
Если машина движется со скоростью 50 км/ч, пройденное расстояние (в километрах) в зависимости от времени (в часах) s = 50t. Время мы определяем как $tgeq0$. Но механика позволяет нам рассчитать не только будущее положение тела, но и прошлое, подставив в формулу $t lt 0$ и запросто «прокрутив» время назад. Поэтому в общем случае, если движение было и остаётся постоянным, мы получаем:
$${left{ begin{array}{c} – infty lt tlt + infty \ s = 50t end{array} right.}$$
Можно представить себе не только отрицательное время («поход в прошлое»). Ещё проще ввести отрицательные координаты: направо идём – координата растёт, становится положительной, поворачиваем налево – уменьшается, становится отрицательной.
В задачах, связанных с экономикой, величины также могут уходить в «плюс» и «минус»: покупки/продажи, кредиты/депозиты, доходы/затраты, прибыли/убытки . Часто эти величины изменяются на какую-то постоянную сумму с течением времени.
Если обобщить формулы, описывающие подобные зависимости, то получаем:
$${left{ begin{array}{c}- infty lt x lt + infty – аргумент, quad любое quad действительное quad число \ k = const ≠ 0 quad – параметр, quad константа \ y = kx quad – функцияend{array} right.}$$
Функция такого вида называется прямой пропорциональностью.
Если $k gt 0$, то чем больше x, тем больше y – функция возрастает.
Если $k lt 0$, то чем больше x, тем больше y – функция убывает.
График прямой пропорциональности
Графиком прямой пропорциональности является прямая, проходящая через начало координат.
Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:
Алгоритм построения графика прямой пропорциональности
- Выбрать произвольное значение аргумента $x_*neq 0$
- Вычислить соответствующее значение функции $y_*=kx_*$
- Отметить на координатной плоскости точку $(x_*,y_* )$
- Провести прямую через начало координат (0;0) и точку $(x_*,y_* )$
Эта прямая – график прямой пропорциональности y=kx.
Например: построим график функции y = 2x
Примеры
Пример 1. Постройте графики прямых пропорциональностей.
Укажите, возрастает или убывает функция.
$k = 1 gt 0$ – функция возрастает
$k = 3 gt 0$ – функция возрастает
$k = frac{1}{3} gt 0$ – функция возрастает
$k = -1 lt 0$ – функция убывает
$k = -2 lt 0$ – функция убывает
$k = -frac{1}{2} lt 0$ – функция убывает
Пример 2. Известно, что график прямой пропорциональности проходит через точку A(5;22). Проходит ли этот график через точки B(7;32,4)и C(9;39,6)?
Точка A определяет коэффициент пропорциональности:
$$ k= frac{y_A}{x_A} = frac{22}{5} = 4,4 $$
При $x = 7:y = 4,4 cdot 7 = 30,8 neq 32,4 Rightarrow$ B не принадлежит графику.
При $x = 9:y = 4,4 cdot 9 = 39,6 Rightarrow C$ принадлежит графику.
Пример 3. Является ли прямой пропорциональностью функция, проходящая через точки:
а) A(1,5;2,75) и B(12;22)
Найдём коэффициенты пропорциональностей для каждой из точек:
$$ k_A = frac{y_A}{x_A} = frac{2,75}{1,5} stackrel{text{ × 4}}{=} frac{11}{6} = frac{15}{6} $$
$$ k_B = frac{y_B}{x_B} = frac{22}{12} = frac{11}{6} = frac{15}{6} $$
$k_A = k_B Rightarrow$ прямая AB $y=1 frac{5}{6} x$ является прямой пропорциональностью.
б) A(3;4,5) и B(5;8)
Найдём коэффициенты пропорциональностей для каждой из точек:
$$ k_A = frac{y_A}{x_A} = frac{2,75}{1,5} = frac{4,5}{3} = 1,5 $$
$$ k_B = frac{y_B}{x_B} = frac{8}{5} = 1,6 $$
$k_A neq k_B Rightarrow$ прямая AB не является прямой пропорциональностью.
Прямая пропорциональность и её график
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение прямой пропорциональности
Для начала напомним следующее определение:
Определение
Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть:
[frac{y}{x}=k]
Отсюда мы видим, что $y=kx$.
Определение
Функция вида $y=kx$ называется прямой пропорциональностью.
Прямая пропорциональность является частным случаем линейной функции $y=kx+b$ при $b=0$. Число $k$ называется коэффициентом пропорциональности.
Примером прямой пропорциональности может служить второй закон Ньютона: Ускорение тела прямо пропорционально приложенной к нему силе:
[F=ma]
Здесь масса — коэффициент пропорциональности.
Исследование функции прямой пропорциональности $f(x)=kx$ и её график
Вначале рассмотрим функцию $fleft(xright)=kx$, где $k > 0$.
- Область определения — все числа.
- Область значения — все числа.
- $fleft(-xright)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
- Функция проходит через начало координат.
- $f’left(xright)={left(kxright)}’=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
- $f^{”}left(xright)=k’=0$. Следовательно, функция не имеет точек перегиба.
- ${mathop{lim}_{xto -infty } kx }=-infty $, ${mathop{lim}_{xto +infty } kx }=+infty $
- График (рис. 1).
Рис. 1. График функции $y=kx$, при $k>0$
Теперь рассмотрим функцию $fleft(xright)=kx$, где $k
- Область определения — все числа.
- Область значения — все числа.
- $fleft(-xright)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
- Функция проходит через начало координат.
- $f’left(xright)={left(kxright)}’=k
- $f^{”}left(xright)=k’=0$. Следовательно, функция не имеет точек перегиба.
- ${mathop{lim}_{xto -infty } kx }=+infty $, ${mathop{lim}_{xto +infty } kx }=-infty $
- График (рис. 2).
Рис. 2. График функции $y=kx$, при $k
Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $left(x_0, y_0right)$ и провести прямую через эту точку и начало координат.
Задачи на построение графиков функции прямой пропорциональности
Задача 1
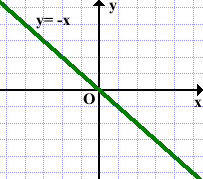
Построить график функции $y=-x$
Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=-1$. Проведем прямую через точки $left(1,-1right) и (0, 0)$. Получим
Задача 2
Построить график функции $y=2x$
Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=2$. Проведем прямую через точки $left(1,2right) и (0, 0)$. Получим
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 02.02.2023
Прямая пропорциональность — базовые понятия
Определение
Пропорциональностью в алгебре называют зависимость между парой величин, при которой изменение одной из них приводит к изменению другой во столько же раз.
Пропорциональность бывает двух видов:
- прямая;
- обратная.
Пример
Предположим, что скорость движения автомобиля составляет 50 км/ч. По определению, скоростью является расстояние, преодолеваемое за единицу времени. В данном случае транспортное средство проезжает 50 километров в течение 1 часа.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если автомобиль движется в течение еще одного часа с такой же скоростью 50 км/ч, то он преодолеет расстояние в 100 км.
Согласно примеру, увеличение времени в 2 раза сопровождается увеличением пройденного расстояния во столько же раз, то есть в 2 раза. Величины времени и расстояния будут прямо пропорциональными. Они обладают взаимосвязью, которую называют прямой пропорциональностью.
Определение
Прямая пропорциональность – это взаимосвязь между двумя величинами, при которой увеличение одной из них приводит к увеличению другой во столько же раз и, наоборот, при уменьшении одной величины в какое-то число раз, другая величина уменьшается во столько же раз.
Предположим, что вначале водитель планировал проехать 100 км за 2 часа, но после того, как он преодолел 50 км, произошла остановка. В таком случае, уменьшая расстояние в 2 раза, получим, что время уменьшится тоже в 2 раза.
Особенностью прямо пропорциональных величин является стабильность их отношений. Таким образом, во время изменения значений прямо пропорциональных величин, их отношение остается постоянным. Рассмотренная ситуация характеризуется изменением расстояния с 50 км при значении времени в 1 час. Отношение расстояния ко времени равно 50 и определяется формулой:
(frac{50}{1}=50)
После увеличения времени движения автомобиля в 2 раза, оно составит 2 часа. Таким образом, расстояние также увеличилось в 2 раза до 100 км. Отношение 100 км к 2 часам равно числу 50:
(frac{100}{2}=50)
Число 50 представляет собой коэффициент прямой пропорциональности. Эта величина демонстрирует, какое расстояние соответствует одному часу движения. В условиях рассматриваемого примера данный коэффициент является скоростью движения автомобиля, исходя из ее определения.
С помощью прямо пропорциональных характеристик можно составлять пропорции. Например, записанные ранее отношения составляют пропорционально:
(frac{50}{1}=frac{100}{2})
Представленное выражение читают таким образом: 50 км так относятся к 1 часу, как 100 км относятся к 2 часам.
Линейное уравнение относительно двух переменных x и y имеет такой вид:
ax + by + c = 0
(aneq 0)
(bneq 0)
Известно, что график записанного равенства является прямая линия, любая точка на которой имеет два числа в виде координат x и y, то есть абсциссы и ординаты. Каждая точка этой прямой соответствует заданному уравнению. Если выразить y через x, получим:
by = -ax – c
Принимая во внимание, что (bneq 0), можно поделить на него две части выражения:
(y=-frac{a}{b}x-frac{c}{b})
Сделать уравнение более удобным можно с помощью следующих обозначений:
(-frac{a}{b}=k)
(-frac{c}{b}=m)
Таким образом:
y = kx + m
Данным способом была выведена линейная функция y от x в общем виде. В этом случае были применены новые обозначения:
- x — в виде независимой переменной или аргумента;
- y — представляет собой зависимую переменную или функцию;
- k и m — являются параметрами, полностью и однозначно определяющими конкретную линейную функцию.
В том случае, когда m = 0, уравнение примет вид:
y = kx
Данная функция представляет собой прямую пропорциональность. Она определяется с помощью единственного параметра k.
Исследование функции прямой пропорциональности и ее график
Определение
Функция, которая обладает видом y = kx, где k — число (k≠0), является функцией прямой пропорциональности.
Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции
y = kx + m, если m=0
График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.
Прямая пропорциональность характеризуется следующими свойствами:
- областью определения является множество действительных чисел: D(y): x∈(-∞;+∞) (или x∈R);
- областью значений является множество действительных чисел: D(y): y∈(-∞;+∞) (или y∈R);
- нуль функции (y=0) при x=0;
- если k>0, функция y = kx возрастает, а при k<0 — убывает;
Если k>0, график функции пересекает первую и третью координатные четверти. Функция будет обладать положительными значениями, если значения аргумента положительные:
y > 0 при x > 0.
Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:
y < 0 при x < 0.
Если k < 0, то функция будет иметь график, проходящий через вторую и четвертую координатную четверть. Функция будет характеризоваться положительными значениями, если значения аргумента отрицательные:
y > 0 при x < 0.
Функция будет характеризоваться отрицательными значениями, если значения аргумента положительные:
y < 0 при x > 0.
Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.
В качестве примера можно рассмотреть такие функции:
- y = 2x в виде прямой пропорциональности;
- y = 2x + 1 в виде линейной функции;
- y = 2x – 1 в виде линейной функции.
Можно построить график рассматриваемых функций. Каждая из них обладает коэффициентом k = 2. Для первой функции m = 0, для второй: m = 1, для третьей: m = -1. Данные величины вытекают из стандартной записи линейного уравнения:
y = kx + m
Необходимо представить данные в виде таблицы:
График примет такой вид:
Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.
Примеры задач на прямую пропорциональность
Задача 1
Требуется определить соотношение между угловыми коэффициентами, согласно графику:
Решение:
(k_{1}=frac{y_{1}}{x})
(k_{2}=frac{y_{2}}{x})
x = x;
(y_{1}> y_{2})
Таким образом:
(k_{1}>k_{2})
Ответ: (k_{1}>k_{2})
Задача 2
Требуется построить график прямой пропорциональности при том, что на данном графике есть точка с координатами (2;8).
Решение:
Построить прямую можно через пару точек. Первая будет обладать координатами (0;0), исходя из того, что любой график прямой пропорциональности пересекает точку (0;0). Вторая точка дана в условии задачи (2;8).
Задачу можно решить другим способом. Согласно координатам точки (2;8), получим:
x=2 и y=8
Данные выражения подходят для уравнения вида:
y = kx
Можно подставить известные значения и определить k:
8 = 2k
k = 4
Таким образом, уравнение примет вид:
y = 4x
С помощью данного уравнения можно построить график:
Функция прямая пропорциональность
Определение
Функция вида y=kx, где k — число (k≠0), называется функцией прямой пропорциональности (или функция прямая пропорциональность).
Число k называется коэффициентом пропорциональности. О переменной y говорят, что она пропорциональна переменной x.
Прямая пропорциональность — частный случай линейной функции y=kx+b (при b=0).
Графиком прямой пропорциональности является прямая, проходящая через начало координат — точку O (0;0).
Для построения графика прямой пропорциональности достаточно взять одну точку, вторая — точка O.
Свойства функции прямой пропорциональности
1) Область определения — множество действительных чисел:
D(y): x∈(-∞;+∞) (или x∈R).
2) Область значений — множество действительных чисел:
D(y): y∈(-∞;+∞) (или y∈R).
3) Нуль функции (y=0) при x=0.
4) При k>0 функция y=kx возрастает, при k<0 — убывает.
5) При k>0 график функции проходит через I и III координатные четверти.
Функция принимает положительные значения при положительных значениях аргумента:
y>0 при x>0.
Функция принимает отрицательные значения при отрицательных значениях аргумента:
y<0 при x<0.
При k<0 график функции проходит через II и IV координатные четверти.
Функция принимает положительные значения при отрицательных значениях аргумента:
y>o при x<0.
Функция принимает отрицательные значения при положительных значениях аргумента:
y<0 при x>0.
Число k называется угловым коэффициентом прямой y=kx.
k=tg α, где α — угол, который прямая образует с положительным направлением оси Ox.
Чтобы сравнить угловые коэффициенты прямых, сравниваем углы между прямыми и положительным направлением оси абсцисс.
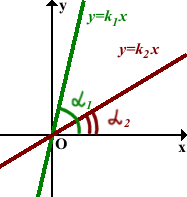
При k1>0, k2>0
так как α1>α2, то k1>k2.
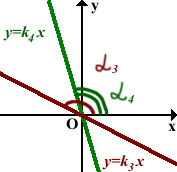
При k3<0, k4<0
так как α3>α4, то k4>k3.
В качестве иллюстрации рассмотрим графики четырёх функций прямой пропорциональности.
Графики функций y=x и y= -x являются биссектрисами соответственно I и III, II и IV координатных четвертей. Эти графики легко построить на листе в клеточку: каждую клеточку делим по диагонали:
Пользуясь тем, что можем на него разделить обе части уравнения:
Для удобства приняли следующие обозначения: , получаем:
Таким образом, была получена линейная функция у от х в общем виде. Мы ввели некоторые новые обозначения: х называем независимой переменной, или аргументом, у называем зависимой переменной, или функцией. k и m – параметры, которые полностью и однозначно определяют конкретную линейную функцию.
Рассмотрим частный случай линейной функции, когда , в таком случае . Данная функция называется прямой пропорциональностью. Она определяется единственным параметром k. Нам следует изучить влияние данного параметра на график функции прямой пропорциональности и на саму функцию.
- Рассмотрим примеры:
- Пример 1:
- Пусть известно, что турист двигается со скоростью 2 км/ч от некоторого пункта А к другому пункту В. В таком случае пройденный им путь будет подчиняться закону:
- (1)
- Если известно, что пассажир едет на поезде от некоторого пункта А к другому пункту В, а поезд движется со скоростью 60 км/ч, то в каждый момент времени можно определить удаление пассажира от начального пункта по формуле:
- (2)
В общем виде обе эти формулы можно представить как . Не важно, что подразумевают под собой переменные х и у, важно только, что одна из них независимая, например время, а вторая зависимая, например расстояние.
- Вернемся к нашим примерам. В общем виде формулы 1 и 2 можно представить как
- Отсюда – это одна из физических интерпретаций углового коэффициента.
- Если перейти к формуле прямой пропорциональности, то
- Рассмотрим примеры:
- Пример 2:
- (3) и (4) – обе функции это прямая пропорциональность. Построим графики этих функций, для этого составим таблицы:
- Таблица для функции 3;
Таблица для функции 4;

- Угловой коэффициент является аналогом скорости в равномерном прямолинейном движении.
- Одна из основных задач – это уметь находить угловой коэффициент в различных выражениях.
- Пример 3 – найти угловой коэффициент:
- Отсюда очевидно, что
- Отсюда очевидно, что
Отметим также, что если , то угол между графиком функции и положительным направлением оси х тупой и функция убывает, а если k>0 – угол острый и функция возрастает, это видно из графика в примере 2.
Физический аналог этому такой: если турист ушел из дома и его скорость равна 2км/ч, то в каждый момент времени расстояние от него до дома увеличивается, а если сказать, что расстояние выражается как , это значит, что он возвращается домой и расстояние сокращается.
- Сформулируем свойства прямой пропорциональности:
- — График любой такой прямой проходит через начало координат, так как в уравнении при независимо от значения у будет равен нулю;
- — Рассмотрим несколько функций:
- – прямая пропорциональность;
- – линейная функция;
- – линейная функция;
Построим графики данных функций. У каждой из них . У первой , у второй , у третьей . Напомним, что параметры k и m определяются из стандартного вида линейного уравнения
- Составим таблицы для построения графиков:
- Таблица для первой функции;
- Таблица для второй функции;
- Таблица для третьей функции;

Как мы видим, построенные прямые параллельны, причиной тому является равенство их угловых коэффициентов. Есть теорема, которая гласит:
- Пример 3 – построить графики функций:
- Сразу отметим, что прямые не будут параллельны, так как их угловые коэффициенты не равны.
- Для построения каждого графика нам достаточно выбрать одну точку, так как вторая уже известна – это точка (0; 0).
- Итак, для первого графика возьмем точку (1; 1)
- Для второго графика возьмем точку (1; 2)
- Для третьего графика (1; -1)
- Для четвертого (1; -2)
- По графику очень хорошо видно, что прямая пошла круче, чем прямая , угол прямой менее острый, при одинаковых значениях аргумента значение функции больше чем , но в обоих случаях угол острый и функция возрастает.
- Обе прямые и имеют тупой угол наклона, обе функции убывают, но у прямой менее тупой и эта функция убывает быстрее.
- Пример 4 – определить соотношение между угловыми коэффициентами:
- отсюда
- Итак, роль углового коэффициента – это скорость роста функции.
- Рассмотрим некоторые типовые задачи.
- Пример 5:
- Построить график прямой пропорциональности, если известно, что ему принадлежит точка с координатами (2; 8)
- Для построения прямой нам нужно две точки, первая из них (0; 0), так как все графики прямой пропорциональности проходят через точку (0; 0), а вторая точка задана – это точка (2; 8).
- Можно поступить иначе. Из заданной точки (2; 8) мы понимаем, что х=2 и у=8 удовлетворяет нашему уравнению вида , подставим эти значения и найдем k:
, отсюда . Итак, нам задано уравнение , которое мы легко можем построить.
Пример 6:
Построить график прямой пропорциональности и по нему ответить на множество вопросов.
Начнем с построения графика. Первая точка нам известна – для любого графика прямой пропорциональности это точка (0; 0). Для второй точки возьмем , тогда :
- По графику требуется определить значение функции при следующих значениях аргумента: , , , ;
- Кроме того, по заданному значению функции определить значение аргумента:
- , ,
- Определить по графику решение неравенств:
- и
- y0
- Пример 7 – найти наибольшее и наименьшее значение функции, если они существуют:
- 1)Задана функция , причем
- 2),
- Построим график функции :
- Для первого случая х меняется в пределах , значит, у меняется в пределах , значит на этом интервале минимум функции равен нулю, а максимум трем.
- Для второго случая х меняется в пределах , значит, функция меняется в пределах , значит, минимальное значение функции на этом интервале есть и оно равно трем, а максимального значения функция не достигает.
- Последний тип задач – по заданному графику определить угловой коэффициент.
- Пример 8 – определить угловой коэффициент:
- Задан график прямой пропорциональности.
- Мы видим, что график проходит через точку (1; 2), значит пара чисел х=1, у=2 удовлетворяет функции вида , значит, можем подставить значения в уравнение и найти k:
- Итак, нам задан график функции
Вывод: в данном уроке мы рассмотрели частный случай линейной функции – прямую пропорциональность. Мы сформулировали свойства данной функции и основные типовые задачи, связанные с данной темой.
Список рекомендованной литературы
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
Рекомендованное домашнее задание
- Задание 1: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 299, ст.68;
- Задание 2: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 300, ст.68;
- Задание 3: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 305, ст.68;
Источник: https://interneturok.ru/lesson/algebra/7-klass/glava-2-lineynaya-funktsiya/pryamaya-proportsionalnost-i-eyo-grafik
Прямая пропорциональность и её график

- Прямая
- пропорциональность
- и
- её график

- ПОВТОРЕНИЕ
- Что такое функция ?
- Какая переменная называется независимой, зависимой ?
- Что такое аргумент и значение функции ?
- Что такое область определения функции ?

Способы задания функции.
- Аналитический (с помощью формулы)
- Графический (с помощью графика)
- Табличный (с помощью таблицы)

ГРАФИК ФУНКЦИИ
- Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции.

- 1) 2) 3)
- 4) 5) 6)
- 7) 8) 9)
- 5

ВЫПОЛНИТЕ ЗАДАНИЕ
Постройте график функции y = 2x+1,
где 0 ≤ х ≤ 4 . Составьте таблицу.
По графику найдите значение функции при х=2,5 . При каком значении аргумента значение функции равно 8 ?
5

- Прямая пропорциональная зависимость
- Определение
- Прямой пропорциональностью называется
- функция, которую можно задать формулой
- вида у=kх, где х- независимая переменная,
- k — не равное нулю число.
- (k- коэффициент прямой пропорциональности)
- 5

- Прямая пропорциональная зависимость y=kx
- График прямой пропорциональ-
- ности- прямая , проходящая через
- начало координат (точку О(0,0))
- Чтобы построить
- график функции y=kx,
- достаточно двух точек,
- одна из которых О (0,0)
- При k 0
- график расположен в I и III
- координатных четвертях.
- При k
- график расположен в II и IV
- координатных четвертях.
- 5
- 5

- Графики функций прямой пропорциональности
- k
- k0
- y
- x
- k
- k0
- 5

Задание
- Определите, на каком из графиков изображена функция прямой пропорциональности.
5
5
Задание
- Определите, график какой функции изображен на рисунке.
- Выберите формулу
из трех предложенных.
5
2) y = 0,5x
5
- Устная работа.
- Назовите точки ,
- Может ли график функции,
- принадлежащие графику
- заданной формулой у= kх ,
- где k
- функции
- у= — 2х.
- проходить через точку
- А(9;45)
- а) А(0;4)
- б) В(2;-4)
- В(-1;100)
- В случае утвердительного
- в) С(4;-2)
- ответа найти значение k.
- г) D(0;0)
- II уровень
- I уровень
- 5
- Определите, какие из точек А(6,-2), В(-2,-10),С(1,-1),Е(0,0) принадлежат графику прямой пропорциональности, заданной формулой
- у = 5х
- 1) А(6;-2) -2 = 5 6
- — 2 = 30 — неверно .
- Точка А не принадлежит графику функции у=5х.
- 2) В(-2;-10) -10 = 5 (-2)
- -10 = -10 — верно.
- Точка В принадлежит графику функции у=5х.
- 3) С(1;-1) -1 = 5 1
- -1 = 5 — неверно
- Точка С не принадлежит графику функции у=5х.
- 4) Е (0;0) 0 = 5 0
- 0 = 0 — верно.
- Точка Е принадлежит графику функции у=5х
- 5
ТЕСТ
1 вариант
№ 1. Какие из функций, заданные формулой, являются прямой пропорциональной зависимостью?
- 2 вариант
- А. y = 5x
- В. y = x 2 /8
- A. y = 3x 2 +5
- B. y = 8/x
- C. y = 7x(x-1)
- D. y = x+1
- C. y = 7(x + 9)
- D. y = 10x
0 k 1 вариант 2 вариант у I I I III 0 х V V I IV 17 » width=»640″
- № 2. Выпишите номера прямых y = kx , где
- k 0
- k
- 1 вариант
- 2 вариант
- у
- I
- I I
- III
- 0
- х
- V
- V I
- IV
- 17
- № 3. Определите, какие из точек
- принадлежaт графику прямой пропорциональности, заданной формулой
- А(6 -2),В(-2 -10)
- У= -1/3 Х
- С(1,-1),Е(0,0)
- 1 вариант
- 2 вариант
- №
- Правильный
- №
- Правильный
- ответ
- ответ
- 1
- 1
- y =10x
- y =5x
- III
- 2
- VI и IV
- 2
- 3
- А
- E
- 3
- Выполните задание:
- Покажите схематически, как расположен график функции, заданной формулой:
- y =1,7 x
- у=-3,1 х
- у=0,9 х
- у=-2,3 х
ЗАДАНИЕ
Из следующих графиков выберите только графики прямой пропорциональности.
- 1) 2) 3)
- 4) 5) 6)
- 7) 8) 9)
- 22
- Функции
- 2. у = 6/х
- 3. у = 2х
- 4. у = — 1,5х
- 5. у = — 5/х
- 6. у = 5х
- 7. у = 2х – 5
- 8. у = — 0,3х
- 9. у = 3/х
- 10. у = -х/3 + 1
- у=kх (прямая пропорциональность)
- и выпишите их
- 22
- Функции прямой пропорциональности
- у
- х
- У = 2х
- У = -1,5х
- У = 5х
- У = -0,3х
22
- Линейные функции, не являющиеся функциями прямой пропорциональности
- у
- 6
- 3
- -3
- -6
- 1) у = 2х + 3
- 2) у = 2х – 5
- у = 2х + 3
- у = 2х — 5
- х
- -6 -4 -2 0 2 4 6
- 25
Домашнее задание:
п.15 стр.65-67,
- № 307;
- № 308.
- 25
Еще раз давайте повторим. Что вы узнали нового? Чему научились?
Что показалось особенно трудным?
25
- Понравился урок и тема понята:
- Урок не понравился и тема не понятна:
- Понравился урок, но не всё ещё понятно:
- 25
Спасибо за урок!
25
Источник: https://kopilkaurokov.ru/matematika/presentacii/priamaiaproportsionalnostiieioghrafik
Прямая и обратная пропорциональность — формулы, свойства и графики функций

Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.

Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.

- Эта зависимость описывается следующей формулой:
- y = k * x.
- Здесь k и называется коэффициентом пропорциональности.

Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k < 0 (справа).

Свойства функции прямой пропорциональности

Основные свойства следующие:
- область определения, значений составляют все действительные числа;
- является нечетной;
- возрастает при всех значениях x, если k > 0;
- если коэффициент со знаком «-», т. е. если k < 0, то убывает;
- если k > 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k < 0, то прямая находится во 2 – 4 четвертях и образует тупой угол с осью Х.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.

Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
- Функция задается формулой:

где k – любое действительное число, кроме 0.
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).

Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
- Нужно построить график функции y = 8/x.
- Вот так выглядит таблица для данной функции:
- Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
Основные следующие:
- области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
- если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
- оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Источник: https://nauka.club/matematika/pryamaya-i-obratnaya-proportsionalnost.html
Прямая пропорциональность и её график
- Вопросы занятия:
- · ввести понятие «прямая пропорциональность»;
- · привести примеры, когда прямая пропорциональность встречается в повседневной жизни;
- · построить график прямой пропорциональности;
- · определить от чего зависит расположение графика в координатной плоскости.
- Материал урока
- Давайте рассмотрим пример.
- Пример.

Обратите внимание, что если переменную t увеличить, например, в 2 раза, то и переменная H также увеличится в 2 раза. То есть:

Также заметим, что зависимость высоты растения от времени его роста мы задали формулой вида:

- В рассматриваемом примере: k = 2,5, а переменная t является независимой.
- Сформулируем определение.
- Определение.

С прямой пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Например,

Или,

Теперь давайте построим график прямой пропорциональности:

Видим, что все точки лежат на одной прямой, которая проходит через начало координат. Для убедительности можем даже приложить линейку.
- Таким образом, можем сформулировать определение.
- Определение.
- Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.
Нам известно, что прямая определяется двумя точками. А значит, для построения графика функции y = kx достаточно указать любую точку графика этой функции, которая отличается от точки с координатами: (0, 0), то есть от начала координат.
Например,

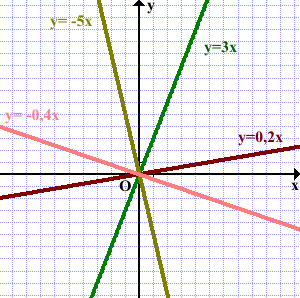
А теперь посмотрите на рисунок, на котором изображены графики прямой пропорциональности.

Обратите внимание, что графики тех функций, которые имеют положительный коэффициент k расположены в первой и третьей координатных четвертях, а которые имеют отрицательный коэффициент k – во второй и четвёртой четвертях. То есть расположение графика функции y= kx в координатной плоскости зависит от коэффициента k.
Источник: https://videouroki.net/video/13-priamaia-proportsional-nost-i-ieio-ghrafik.html
Прямая и обратная пропорциональность
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Прямая пропорциональность
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
- Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:
- Это отношение можно прочитать следующим образом:
- Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
- Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
- Запишем чему равно отношение тридцати рублей к одному килограмму
- Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Обратная пропорциональность
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.
Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.
Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.
Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.
- Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.
- и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.
- К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:
Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.
Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным
Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км
Источник: http://spacemath.xyz/pryamaya_proporcionalnost/
Прямая пропорциональность и ее график — Гипермаркет знаний
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Прямая пропорциональность и ее график
Прямая пропорциональность и её график
Среди линейных функций у = kx + m особо выделяют случай, когда m = 0; в этом случае Линейная функция принимает вид у = kx и ее называют прямой пропорциональностью. Это название объясняется тем, что две величины у и х называют прямо пропорциональными, если их отношение равно конкретному числу, отличному от нуля. Здесь , это число k называют коэффициентом пропорциональности.
- Многие реальные ситуации моделируются с помощью прямой пропорциональности.
- Например, путь s и время t при постоянной скорости, 20 км/ч связаны зависимостью s = 20t; это — прямая пропорциональность, причем k = 20.
- Другой пример:
стоимость у и число х батонов хлеба по цене 5 руб. за батон связаны зависимостью у = 5х; это — прямая пропорциональность, где k = 5.
Доказательство. Осуществим его в два этапа.
1. у = kx — частный случай линейной функции, а графиком линейной функции является прямая; обозначим ее через I.
2. Пара х = 0, у = 0 удовлетворяет уравнению у — kx, а потому точка (0; 0) принадлежит графику уравнения у = kx, т. е. прямой I.
Следовательно, прямая I проходит через начало координат. Теорема доказана.
Надо уметь переходить не только от аналитической модели у = kx к геометрической (графику прямой пропорциональности), но и от геометрической модели к аналитической. Рассмотрим, например, прямую на координатной плоскости хОу, изображенную на рисунке 50.
Она является графиком прямой пропорциональности, нужно лишь найти значение коэффициента k. Так как у , то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к ее абсциссе.
Прямая проходит через точку Р(3; 6), а для этой точки имеем: Значит, k = 2, а потому заданная прямая линия служит графиком прямой пропорциональности у = 2х.
График линейной функции у = kx обычно строят так: берут точку (1; k) (если х = 1, то из равенства у = kx находим, что у = k) и проводят прямую через эту точку и начало координат. Впрочем, в случае необходимости точку (1; k) можно заменить другой точкой, более удобной. На рисунке 51 изображены графики линейных функций
Обратите внимание: от коэффициента пропорциональности зависит угол, который построенная прямая образует с положительным направлением оси х. Если k > О, то этот угол острый (так обстоит дело на рис.
51 с прямыми l1 l2, 13); если k < 0, то этот угол тупой (так обстоит дело на рис. 51 с прямой I4). Далее, если k > О, то чем больше k, тем больше угол.
Так, на рисунке 51 для прямой I3 имеем , для прямой I1 имеем k = 1, для прямой I2 имеем k = 2; при увеличении коэффициента k увеличивается и угол между прямой и положительным направлением оси абсцисс.
- Поэтому коэффициент k в записи у = kx называют не только коэффициентом прямой пропорциональности, но и угловым коэффициентом.
- На рисунке 52 изображены графики линейных функций у = 2х — 4, у = 2х + 6. Оба они параллельны графику прямой
- пропорциональности у = 2х, только первая прямая (у = 2х — 4) получается из прямой у = 2х сдвигом вниз на 4 единицы масштаба, а вторая прямая(у = 2х + 6) получается из прямой у = 2х сдвигом вверх на 6 единиц масштаба.
- Справедлив следующий общий результат, который мы оформим в виде теоремы.

Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
конспект урока
опорный каркас презентация урока
акселеративные методы интерактивные технологии Практика
задачи и упражнения самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи фишки для любознательных шпаргалки учебники основные и дополнительные
словарь терминов прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год методические рекомендации программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Источник: http://edufuture.biz/index.php?title=%D0%9F%D1%80%D1%8F%D0%BC%D0%B0%D1%8F_%D0%BF%D1%80%D0%BE%D0%BF%D0%BE%D1%80%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%B8_%D0%B5%D0%B5_%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA
Внеклассный урок — Линейная функция. Прямая пропорциональность. Обратная пропорциональность
- Линейная функция
- Линейная функция – это функция, которую можно задать формулой y = kx + b,
- где x – независимая переменная, k и b – некоторые числа.
- Графиком линейной функции является прямая.
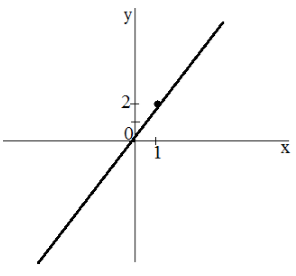
Число k называют угловым коэффициентом прямой – графика функции y = kx + b.
- Если k > 0, то угол наклона прямой y = kx + b к оси х острый; если k < 0, то этот угол тупой.
Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются. А если угловые коэффициенты одинаковы, то прямые параллельны.
График функции y = kx + b, где k ≠ 0, есть прямая, параллельная прямой y = kx.
Прямая пропорциональность.
Прямой пропорциональностью называется функция, которую можно задать формулой y = kx, где х – независимая переменная, k – не равное нулю число. Число k называют коэффициентом прямой пропорциональности.
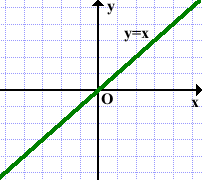
График прямой пропорциональности представляет собой прямую, проходящую через начало координат (см.рисунок).
Прямая пропорциональность является частным случаем линейной функции.
Свойства функции y = kx:
1. Область определения функции — множество всех действительных чисел.2. Это нечетная функция.3. Переменные изменяются прямо пропорционально на всей числовой прямой: при возрастании аргумента функция пропорционально возрастает, при убывании аргумента функция пропорционально убывает.
- Обратная пропорциональность
- Обратной пропорциональностью называется функция, которую можно задать формулой:
- k y = — x
- где x – независимая переменная, а k – не равное нулю число.
Графиком обратной пропорциональности является кривая, которую называют гиперболой (см.рисунок).
Для кривой, которая является графиком этой функции, оси x и y выступают в роли асимптот. Асимптота – это прямая, к которой приближаются точки кривой по мере их удаления в бесконечность.
k Свойства функции y = —: x
1. Область определения функции — множество всех действительных чисел, кроме нуля.2. Это нечетная функция.3. При возрастании аргумента функция пропорционально убывает, при убывании аргумента функция пропорционально возрастает.
Источник: http://raal100.narod.ru/index/0-275
Прямая пропорциональность и ее график
Слайд 1
Прямая пропорциональность и её график
Слайд 2
Что такое аргумент и значение функции ? Какая переменная называется независимой, зависимой ? Что такое функция ? ПОВТОРЕНИЕ Что такое область определения функции ?
- Слайд 3
- Способы задания функции. Аналитический (с помощью формулы) Графический ( с помощью графика) Табличный (с помощью таблицы)
- Слайд 4
- Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции. ГРАФИК ФУНКЦИИ
- Слайд 5
- 1) 2) 3) 4) 5) 6) 7) 8) 9)
- Слайд 6
ВЫПОЛНИТЕ ЗАДАНИЕ Постройте график функции y = 2 x +1, где 0 ≤ х ≤ 4 . Составьте таблицу. По графику найдите значение функции при х=2,5 . При каком значении аргумента значение функции равно 8 ?
- Слайд 7
- Определение Прямой пропорциональностью называется функция, которую можно задать формулой вида у= k х , где х — независимая переменная, k — не равное нулю число. ( k- коэффициент прямой пропорциональности) Прямая пропорциональная зависимость
- Слайд 8
8 График прямой пропорциональ — ности — прямая , проходящая через начало координат (точку О(0,0)) Чтобы построить график функции y= kx , достаточно двух точек, одна из которых О (0,0) При k > 0 график расположен в I и III координатных четвертях. При k< 0 график расположен в II и IV координатных четвертях. Прямая пропорциональная зависимость y= kx
- Слайд 9
- Графики функций прямой пропорциональности y x k>0 k>0 k
- Слайд 10
- Задание Определите, на каком из графиков изображена функция прямой пропорциональности.
- Слайд 12
Задание Определите, график какой функции изображен на рисунке. Выберите формулу из трех предложенных.
- Слайд 13
- 2) y = 0,5x
- Слайд 14
Устная работа. Может ли график функции, заданной формулой у= k х , где k < 0, проходить через точку А(9;45) В(-1;100) В случае утвердительного ответа найти значение k . II уровень Назовите точки , принадлежащие графику функции у= – 2х. а) А(0;4) б) В(2;-4) в) С(4;-2) г) D( 0;0 ) I уровень
Слайд 15
Определите, какие из точек А(6,-2), В(-2,-10),С(1,-1),Е(0,0) принадлежат графику прямой пропорциональности, заданной формулой у = 5х 1) А(6;-2) -2 = 5 6 — 2 = 30 — неверно . Точка А не принадлежит графику функции у=5х.
2) В(-2;-10) -10 = 5 (-2) -10 = -10 — верно. Точка В принадлежит графику функции у=5х. 3) С(1;-1) -1 = 5 1 -1 = 5 — неверно Точка С не принадлежит графику функции у=5х. 4) Е (0;0) 0 = 5 0 0 = 0 — верно.
Точка Е принадлежит графику функции у=5х
Слайд 16
ТЕСТ 1 вариант 2 вариант №1. Какие из функций, заданные формулой, являются прямой пропорциональной зависимостью? А . y = 5x В . y = x 2 /8 C. y = 7x(x-1) D . y = x+1 A. y = 3x 2 +5 B. y = 8/x C. y = 7(x + 9) D. y = 10x
- Слайд 17
- №2. Выпишите номера прямых y = kx , где k > 0 1 вариант k< 0 2 вариант х у 0 I I I III V V I IV
- Слайд 18
- №3. Определите, какие из точек принадлеж a т графику прямой пропорциональности, заданной формулой У= -1 /3 Х А(6 -2) ,В(-2 -10) 1 вариант С(1,-1),Е(0,0) 2 вариант
- Слайд 19
- y =5x y =10x III А VI и IV E 1 2 3 1 2 3 № Правильный ответ Правильный ответ №
- Слайд 20
- Выполните задание : Покажите схематически, как расположен график функции, заданной формулой : y =1,7 x у =-3 ,1 х у=0,9 х у=-2,3 х
- Слайд 21
- ЗАДАНИЕ Из следующих графиков выберите только графики прямой пропорциональности .
- Слайд 22
- 1) 2) 3) 4) 5) 6) 7) 8) 9)
- Слайд 23
Функции у = 2х + 3 2. у = 6/ х 3. у = 2х 4. у = — 1,5х 5. у = — 5/ х 6. у = 5х 7. у = 2х – 5 8. у = — 0,3х 9. у = 3/ х 10. у = — х /3 + 1 Выберите функции вида у= k х (прямая пропорциональность) и выпишите их
- Слайд 24
- Функции прямой пропорциональности У = 2х У = -1,5х У = 5х У = -0,3х у х
- Слайд 25
- у Линейные функции, не являющиеся функциями прямой пропорциональности 1) у = 2х + 3 2) у = 2х – 5 х -6 -4 -2 0 2 4 6 6 3 -3 -6 у = 2х + 3 у = 2х — 5
- Слайд 26
Домашнее задание: п.15 стр.65-67, № 307; № 308.
Слайд 27
Еще раз давайте повторим. Что вы узнали нового? Чему научились? Что показалось особенно трудным?
- Слайд 28
- Понравился урок и тема понята: Понравился урок, но не всё ещё понятно: Урок не понравился и тема не понятна:
- Слайд 29
- Спасибо за урок!
Источник: https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/01/12/pryamaya-proportsionalnost-i-ee-grafik
Прямая и обратная пропорциональность
Пропорциональность – это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность – это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
- Рассмотрим пример прямой пропорциональности на формуле пути:
- s = vt
- где s – это путь, v – скорость, а t – время.
- При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
Скорость v = 5 км/чВремя t (ч)
| 1 | 2 | 4 | 8 | 16 |
| 5 | 10 | 20 | 40 | 80 |
Путь s (км)
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| s | = v, следовательно, | 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5 |
| t | 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
Время t = 2 чСкорость v (км/ч)
| 5 | 15 | 45 | 90 |
| 10 | 30 | 90 | 180 |
Расстояние s (км)
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| s | = t, следовательно, | 10 | = | 30 | = | 90 | = | 180 | = 2 |
| v | 5 | 15 | 45 | 90 |
- Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
- Формула прямой пропорциональности:
- y = kx
- где y и x – это переменные величины, а k – это постоянная величина, называемая коэффициентом прямой пропорциональности.
- Коэффициент прямой пропорциональности – это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
- Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность – это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
- Рассмотрим пример обратной пропорциональности на формуле пути:
- s = vt
- где s – это путь, v – скорость, а t – время.
- При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
Путь s = 120 кмСкорость v (км/ч)
| 10 | 20 | 40 | 80 |
| 12 | 6 | 3 | 1,5 |
Время t (ч)
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
- В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
- s = vt, следовательно 10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120
- Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
- Формула обратной пропорциональности:
- где y и x – это переменные величины, а k – это постоянная величина, называемая коэффициентом обратной пропорциональности.
- Коэффициент обратной пропорциональности – это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
- Формула коэффициента обратной пропорциональности:
- xy = k
Источник: https://naobumium.info/algebra/proportsionalnost.php









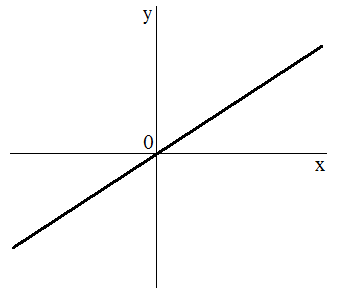
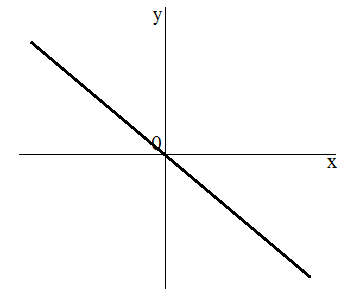
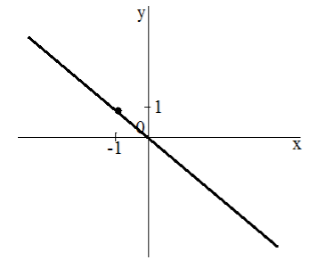
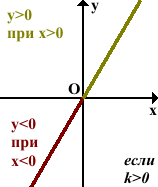
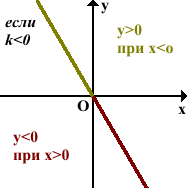









 Число k называют угловым коэффициентом прямой – графика функции y = kx + b.
Число k называют угловым коэффициентом прямой – графика функции y = kx + b. 
