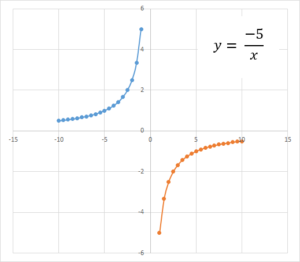Функция y = k/x и её график. Гипербола
Определение обратной пропорциональности
Допустим, что у нас есть 1000 руб. Спрашивается, сколько тетрадей мы сможем купить, в зависимости от их цены. Составим таблицу:
Цена 1 тетради, руб.
Графическое представление полученных результатов:
Результат вполне ожидаемый: чем больше цена, тем меньше то количество, которое мы можем себе позволить за определённую ограниченную сумму.
Можно привести и другие примеры, где зависимость между величинами будет аналогичной:
- время, которое придётся потратить на дорогу между двумя городами (при заданном расстоянии), в зависимости от скорости;
- длина фанерного листа в зависимости от ширины при заданной площади;
- время заполнения бассейна (заданный объём) в зависимости от количества открытых труб, и т.п.
Если обобщить формулы, описывающие подобные зависимости, то получаем:
$$<left< begin -infty lt x lt +infty – аргумент, quad любое quad действительное quad число \ k = const neq 0-параметр, quad константа \ y = frac – функция end right.>$$
Функция такого вида называется обратной пропорциональностью .
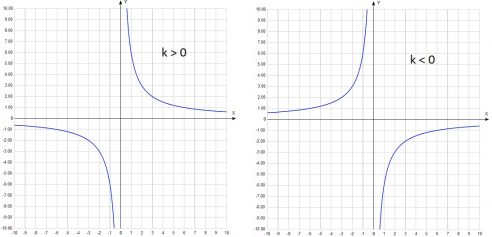
Если $k gt 0$, то чем больше x, тем меньше y – функция убывает.
Если $k lt 0$, то чем больше x, тем больше y – функция возрастает.
(Сравните с прямой пропорциональностью – см. §37 справочника для 7 класса)
График обратной пропорциональности
Графиком обратной пропорциональности является кривая, которую называют гиперболой.
Чтобы построить гиперболу, нужно 1) составить таблицу, в которой рассчитать значения y=k/x для некоторых значений x, 2) отметить полученные точки на координатной плоскости и 3) соединить их плавной кривой.
Гипербола
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac<1>-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color <frac<1>>) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment
Гипербола: формулы, примеры решения задач
Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:
,
где a и b – длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как и .
На чертеже ветви гиперболы – бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:
.
Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки и , где
,
называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:
.
Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет – это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:
.
Результат – каноническое уравнение гиперболы:
Если – произвольная точка левой ветви гиперболы () и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:
.
Если – произвольная точка правой ветви гиперболы () и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:
.
На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами гиперболы (на чертеже – прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы
,
где – расстояние от левого фокуса до точки любой ветви гиперболы, – расстояние от правого фокуса до точки любой ветви гиперболы и и – расстояния этой точки до директрис и .
Пример 4. Дана гипербола . Составить уравнение её директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:
.
Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке “Эллипс” это пример 7.
Характерной особенностью гиперболы является наличие асимптот – прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями
.
На чертеже асимптоты – прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:
, где .
В том случае, когда угол между асимптотами – прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.
Решение. Дробь в уравнении асимптот гиперболы – это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.
.
Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
[spoiler title=”источники:”]
http://tutomath.ru/8-klass/kak-postroit-giperbolu.html
http://function-x.ru/curves_hyperbola.html
[/spoiler]
Добавлено: 9 декабря 2021 в 15:07

Гипербола — одно из наиболее сложных понятий в школьном курсе математики за 8 класс, точнее уже алгебры. Возможно, играет роль сбивающий с толку «синоним» из курса литературы, возможно, сложно понять смысл слова «асимптота», но школьнику сложно освоить построение и в сравнении с параболой. Чтобы раз и навсегда разобраться с этим вопросом, мы начнем не с школьного определения гиперболы, а с построения графика. Более того, этот график не будет гиперболой.
Прямая пропорциональность
Большинство школьников хорошо понимают понятие «прямая пропорциональность», поскольку оно согласуется с их бытовым опытом. Чем больше вы работаете, тем лучше оценки, то есть уровень оценок прямо пропорционален времени обучения. С математической точки зрения эта зависимость выглядит следующим образом.
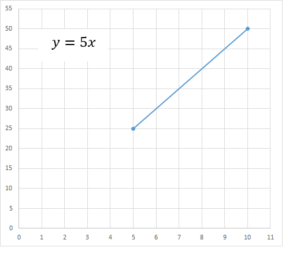
Пример: у бога грома Тора есть молот (этот инструмент называется «Мьёльнир»), который, будучи брошенным, всегда возвращается к своему хозяину. Но летает Мьёльнир с постоянной скоростью — за секунду он преодолевает 5 км. В первый раз Тор бросил молот (в Локи) и поймал через 5 секунд (Локи увернулся). Во второй раз Тор бросил молот и поймал через 10 секунд (вновь не попал в бога хитрости). Какое расстояние молот пролетел в первый и второй раз.
Решение
В нашей задаче изменяется время полета молота — обозначим эту величину «х». Расстояние полета Мьёльнира будет «y». В нашем случае эти две величины связаны постоянной скоростью полета молота — то есть коэффициентом пропорциональности k, который для данной задачи равен 5.
Если нанести эти данные на график, где по оси абсцисс будет x, а по оси ординат — y, то получится прямая с определенным наклоном, угол которого относительно оси абсцисс зависит от коэффициента k и для нашего случая составляет 45°. При отрицательном значении k прямая будет наклонена под 135°к оси х.
Если экстраполировать (продлить по тому же закону) обе стороны прямой, то можно сделать простой вывод: чем дольше летит молот, тем больше он пролетает.
Гипербола с примерами
Обратная пропорциональность
Внимательный читатель уже понял, что если есть прямая пропорциональность, то должна быть и обратная, при которой с возрастанием х будет убывать у (чем больше траты, тем меньше денег). Правильно, такая зависимость существует и выражается следующим образом:
Проанализируем указанное выше выражение:
- х может быть любым, кроме 0 (потому что НА 0 ДЕЛИТЬ НЕЛЬЗЯ);
- при k = 0 при любом значении х у = 0.
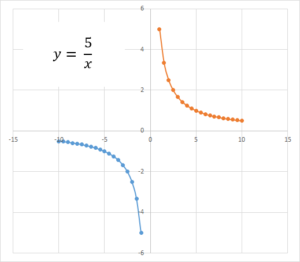
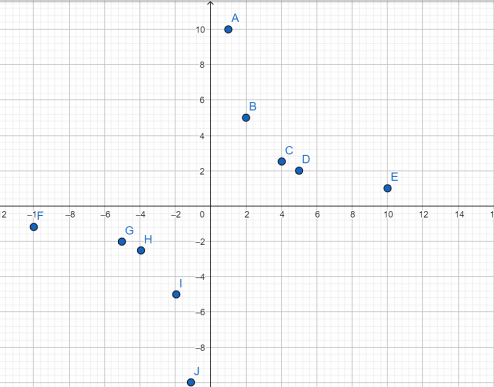
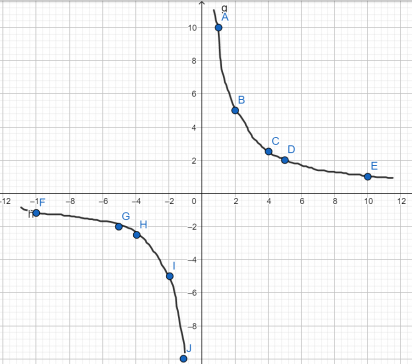
Рассмотрим все остальные случаи, то есть условие при k≠0. Примем коэффициент пропорциональности k = 5 (как в предыдущем примере) и подставив значения х от -10 до 10, нанесем полученные точки на график.
| х | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 |
| у | -0,5 | -1 | -1,25 | -2,5 | -5 | 5 | 2,5 | 1,25 | 1 | 0,5 |
Гипербола с примерами
Полученная совокупность точек и называется гиперболой.
Чем примечательна гипербола?
Гипербола с примерами
Если мы проанализируем полученный график, то увидим, что гипербола состоит из двух ветвей с достаточно характерными особенностями:
- ветви симметричны;
- каждая ветвь симметрична относительно прямой, лежащей под углом 45° к оси абсцисс;
- ветви находятся в I и III четвертях.
Если мы продолжим подставлять значения х в уравнение , то заметим, что ветви приближаются к осям х и у, но не пересекают их. Вот почему так происходит:
- х не может принимать значение 0 по математическим соображениям;
- k не может принимать значение 0 (мы сами исключили этот вариант);
- у не может обращаться в 0.
Внимание: исключение значения k = 0 является неким самообманом, поэтому каноническое уравнение гиперболы отличается от школьного.
Оси абсцисс и ординат выполняют для гиперболы роль асимптоты — линии, к которой кривая бесконечно приближается, но не может коснуться. Говорят, что ветви гиперболы асимптотически приближаются к осям x и y. Асимптоты есть и у других кривых.
Попробуем рассмотреть нашу обратную пропорциональность пристальней — поменяем знак коэффициента k.
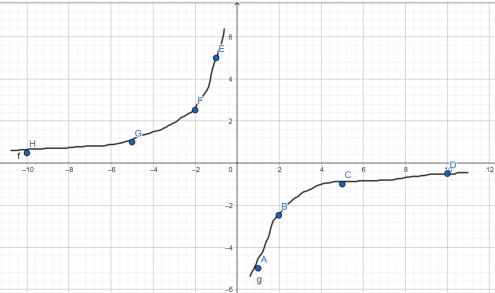
Подставим значения х от -10 до 10, нанесем полученные точки на график.
| х | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 |
| у | 0,5 | 1 | 1,25 | 2,5 | 5 | -5 | -2,5 | -1,25 | -1 | -0,5 |
Теперь ветви гиперболы располагаются во II и IV координатных четвертях.
Гипербола с примерами
Отметим несколько закономерностей:
- гипербола имеет две асимптоты;
- ветви гиперболы симметричны относительно друг друга;
- для всех положительных вариантов х ветви размещаются в I или II четвертях;
- для всех отрицательных вариантов х ветви размещаются в III или IV четвертях;
- для всех положительных вариантов k ветви размещаются в I и III четвертях;
- для всех отрицательных вариантов k ветви размещаются во II и IV четвертях;
- чем меньше |x|, тем больше |y|;
- если точка (х, у) принадлежит одной из ветвей гиперболы, точка (-х, -у) будет принадлежать второй его ветви (так как они симметричны).
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.
Занимайтесь на курсах подготовки к ЕГЭ и ОГЭ (ГИА) в паре TwoStu и получите максимум баллов на ЕГЭ и ОГЭ!
09
Янв 2022
Категория: 10 Графики функций
2022-01-09
2022-09-11
Задача 1. На рисунке изображён график функции Найдите
Решение: + показать
Задача 2. На рисунке изображён график функции вида где числа
и
— целые. Найдите значение
, при котором
Решение: + показать
Задача 3. На рисунке изображён график функции вида где
– целые числа. Найдите
Решение: + показать
Задача 4. На рисунке изображён график функции Найдите
Решение: + показать
Задача 5. На рисунке изображены графики функций и
и которые пересекаются в точках
и
. Найдите ординату точки
Решение: + показать
Вы можете пройти тест “Гиперболы”
Автор: egeMax |
Нет комментариев
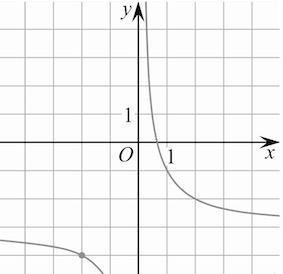
Графиком функции у=kx, где k≠0 число, а х – переменная, является кривая, которую называют гиперболой.
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
Свойства гиперболы (у=kx)
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
- Область определения – любое число, кроме нуля.
- Область значения – любое число, кроме нуля.
- Функция не имеет наибольших или наименьших значений.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Построить график функции у=10x.
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.
Теперь для построения гиперболы соединим точки плавной линией.
Построить график функции у=−5x.
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
Задание OM1104o
Установите соответствие между графиками функций и формулами, которые их задают.

2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1102o
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 11.4k
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
- Определение и функция гиперболы
-
Алгоритм построения гиперболы
- Пример 1
- Пример 2
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Здесь:
- x – независимая переменная;
- k ≠ 0;
- при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
- при k < 0 график находится во II и IV четвертях.
На рисунке ниже изображен пример гиперболы.
- Линии графика (зеленым цветом) называются его ветвями.
- Оси абсцисс и ординат (Ox и Oy) являются асимптотами гиперболы, т.е. ветви бесконечно к ним приближаются, но никогда их не коснутся и не пересекут.
- Ось симметрии (синим цветом) – это прямая:
- y = x (при k > 0)
- y = -x (при k < 0)
Смещение асимптот
Допустим у нас есть функция, заданная формулой:
В этом случае:
- x = a – это вертикальная асимптота графика (при a ≠ 0) вместо оси Oy;
- y = b – горизонтальная асимптота (при b ≠ 0) вместо оси Ox.
Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):
Алгоритм построения гиперболы
Пример 1
Дана функция y = 4/x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
| x | y | Расчет y |
| 0,5 | 8 | 4 / 0,5 = 8 |
| 1 | 4 | 4 / 1 = 4 |
| 2 | 2 | 4 / 2 = 2 |
| 4 | 1 | 4 / 4 = 1 |
| 8 | 0,5 | 4 / 8 = 0,5 |
Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.
Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.
| x | y | Расчет y |
| -0,5 | -8 | 4 / -0,5 = -8 |
| -1 | -4 | 4 / -1 = -4 |
| -2 | -2 | 4 / -2 = -4 |
| -4 | -1 | 4 / -4 = -1 |
| -8 | -0,5 | 4 / -8 = -0,5 |
Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.
Пример 2
Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:
Решение
Так как k < 0, график будет располагаться во второй и четвертой четвертях.
Теперь определяемся с асимптотами, в нашем случае это x = 3 и y = 4 (см. информацию выше про их смещение).
Составим таблицу соответствия значений x и y.
| x II четв. | y II четв. | x IV четв. | y IV четв. |
| -1 | 4,5 | 3,5 | 0 |
| 1 | 5 | 4 | 2 |
| 2 | 6 | 5 | 3 |
| 2,5 | 8 | 7 | 3.5 |
Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.