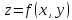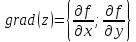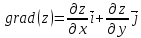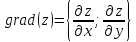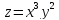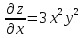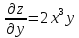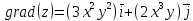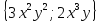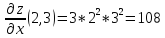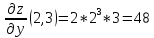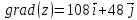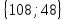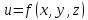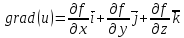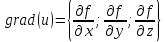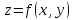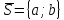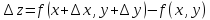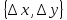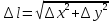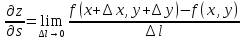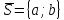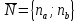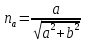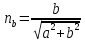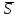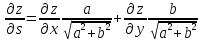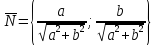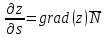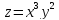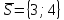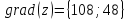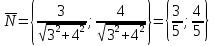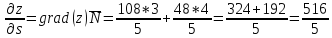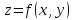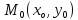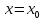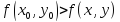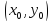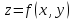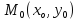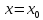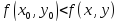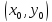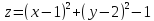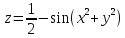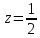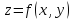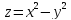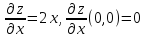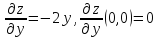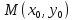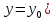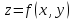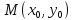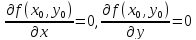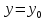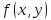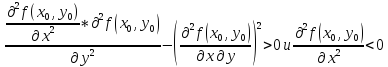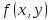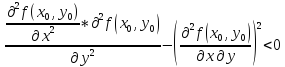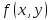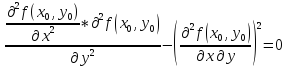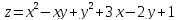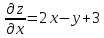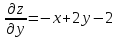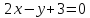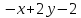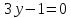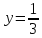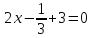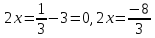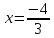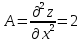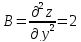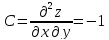Как найти значение градиента функции

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Градиент функции

Как найти?

Постановка задачи

Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $

План решения

Градиент функции $ f(x,y,z) $ – это вектор, каждая координата которого является частной производной первого порядка этой функции:

$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$

1. Берём частные производные первого порядка от функции $ f(x,y,z) $:
   $$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$
2. Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
   $$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$
3. Подставляем, полученные данные в формулу градиента функции:
   $$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$

Примеры решений

Пример 1

Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $

Решение

Находим частные производные первого порядка функции трёх переменных: $$ frac{partial f}{partial x} = 1; frac{partial f}{partial y} = frac{2y}{z^2+y^2}; frac{partial f}{partial z} = frac{2z}{z^2+y^2} $$ Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ grad f = (1,1,1) $$

Пример 2

Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $

Решение

Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$

Ответ

$$ grad f = (3,1,frac{pi}{2}) $$

Приветствую всех. Сегодня на занятии хотелось бы затронуть немало важную тему, связанную одновременно с дифференциальным исчислением и векторной алгеброй. Мы постараемся как можно меньше углубляться в теоретические тезисы и побольше сделаем упор на решение практических задач. Незамедлительно начнём.

Определение слова “градиент” в математике нужно усвоить.

Градиент – это вектор показывающий направление наибольшего возрастания функции. Модуль вектора градиента показывает скорость изменения функции.

Запишем формулу для нахождения вектора градиента:

При нашем раскладе можно с теорией закончить, этого будет достаточно.

Разберём простенький примерчик для начала.

Никто ведь не забыл как брать частные производные? Если подзабыли, ссылочка (на статью) будет в конце урока.

Было слишком уж просто для нас, возьмём что-нибудь посложнее.

Такого плана примеры уже устно не решишь, хотя… Нет, всё же возможно.

Не будем перенапрягаться сильно, рассмотрим последний пример и пойдём отдыхать.

Берёмся за дело.

Не отчаиваемся что уже конец практики, у вас всегда есть возможность найти похожие задачки в интернете или взять в библиотеке задачник по высшей математике. Практикуйтесь, практикуйтесь, и ещё раз практикуйтесь. Спасибо за внимание.

Другие темы:

Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.

Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле

∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},

где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).

Иногда градиент обозначается так: grad⁡F(x,y,z)operatorname{grad} F(x,y,z).

Градиент функции в данной точке показывает направление наибольшего роста функции.

Пример 1

Найти градиент функции F(x,y,z)=ln⁡(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).

Вычислим частные производные:
∂F∂x=∂∂xln⁡(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},

∂F∂y=∂∂yln⁡(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},

∂F∂z=∂∂zln⁡(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.

Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):

∇F(M)=17  i+27  j+37  k=17  OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.

Производная по направлению

Пусть FF – функция на плоскости или в пространстве.

Производной функции FF по направлению вектора amathbf{a} в точке MM называется число

∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},

если производная в правой части существует.

Пример 2

Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).

Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):

F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.

Длина вектора amathbf{a}:

∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.

Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}

Выражение производной по направлению через градиент

Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства

F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)

следует, что

ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).

Таким образом,

∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.

Пример 2′2′

Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.

Частные производные:

∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,

∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,

∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.

Градиент:

∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.

Скалярное произведение:

(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.

Производная по направлению:

∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.

Тест по теме “Градиент функции. Производная по направлению”

Лекция
15.
«Дифференцирование функции
нескольких переменных»

1. Градиент
   функции двух переменных и производная
   по направлению.

Определение.
Градиентом функции

называется
вектор

.

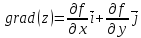
Иначе,
этот вектор может быть записан следующим
образом:

или

или

Как
видно из определения градиента функции,
компонентами вектора градиента являются
частные производные функции.

Пример.
Вычислить градиент функции

в
точке A(2,3).

Решение.
Вычислим частные производные функции.

В
общем виде градиент функции имеет вид:

=

Подставим
координаты точки A(2,3)
в выражения частных производных

В
градиент функции в
точке A(2,3)
имеет вид:

=

Аналогично
можно определить понятие градиента
функции трех переменных:

Определение.
Градиентом функции от трех переменных

называется
вектор

Иначе,
этот вектор может быть записан следующим
образом:

Определение
производной по направлению.

Пусть
задана функция двух переменных

и
произвольный вектор

Рассмотрим
приращение этой функции, взятое вдоль
данного вектора

Т.е.
вектор

коллинеарный по отношению к вектору
.
Длина приращения аргумента

Производной
по некоторому направлению называется
предел отношения приращения функции
вдоль данного направления на длину
приращения аргумента, когда длина
приращения аргумента стремиться к 0.

Формула
для вычисления производной по направлению.

Исходя
из определения градиента, производную
функции по направлению, можно посчитать
следующим образом.

Пусть

некоторый
вектор. Вектор с тем же направлением,
но единичной
длины назовем

Координаты
этого вектора вычисляются следующим
образом:

Из
определения производной по направлению
,
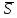
производная по направлению

может быть вычислена по следующей
формуле:

Правая
часть этой формулы представляет собой
скалярное произведение двух векторов

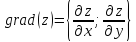
И

Поэтому,
производную по направлению можно
представить в виде следующей формулы:

Из
этой формулы следует несколько важных
свойств вектора градиента.

1. Производная
   в данной точке по направлению вектора
   S имеет наибольшее значение, если
   направление вектора S совпадает с
   направлением градиента; это наибольшее
   значение производной равно |
   |.

2. Производная
   по направлению вектора, перпендикулярного
   к вектору
   

   равна нулю.

Первое
свойство градиента следует из того
очевидного факта,
что скалярное произведение двух векторов
принимает наибольшее значение, когда
вектора совпадают по направлению. Второе
свойство следует из того, что скалярное
произведение перпендикулярных векторов
равно нулю. Кроме того, из первого
свойства следует геометрический смысл
градиента – градиент это вектор, вдоль
направления, которого производная по
направлению наибольшая. Так как
производная по направлению определяет
тангенс угла наклона касательной к
поверхности функции, то градиент
направлен вдоль наибольшего наклона
касательной.

Пример
2. Для
функции (из примера 1)

Вычислить
производную по направлению

в
точке A(2,3).

Решение.
Для вычисления производной по направлению
надо вычислить вектор градиента в
указанной точке и единичный вектор
направления
(т.е.
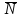
нормализовать вектор
).

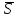
Вектор
градиента был вычислен в примере 1:

Вычисляем
единичный вектор направления:

Вычисляем
производную по направлению:

#2.
Максимум и минимум функции нескольких
переменных.

Определение.
Функция

Имеет
максимум в точке

(т. е. при

и
),
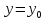
если

для
всех точек
,
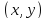
достаточно близких к точке

и отличных от нее.

Определение.
Совершенно аналогично говорят, что
функция

Имеет
минимум в точке

(т. е. при

и
),
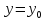
если

для
всех точек
,
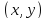
достаточно близких к точке

и отличных от нее.

Максимум
и минимум функции называются экстремумами
функции, т. е. говорят, что функция имеет
экстремум в данной точке, если эта
функция имеет максимум или минимум в
данной точке.

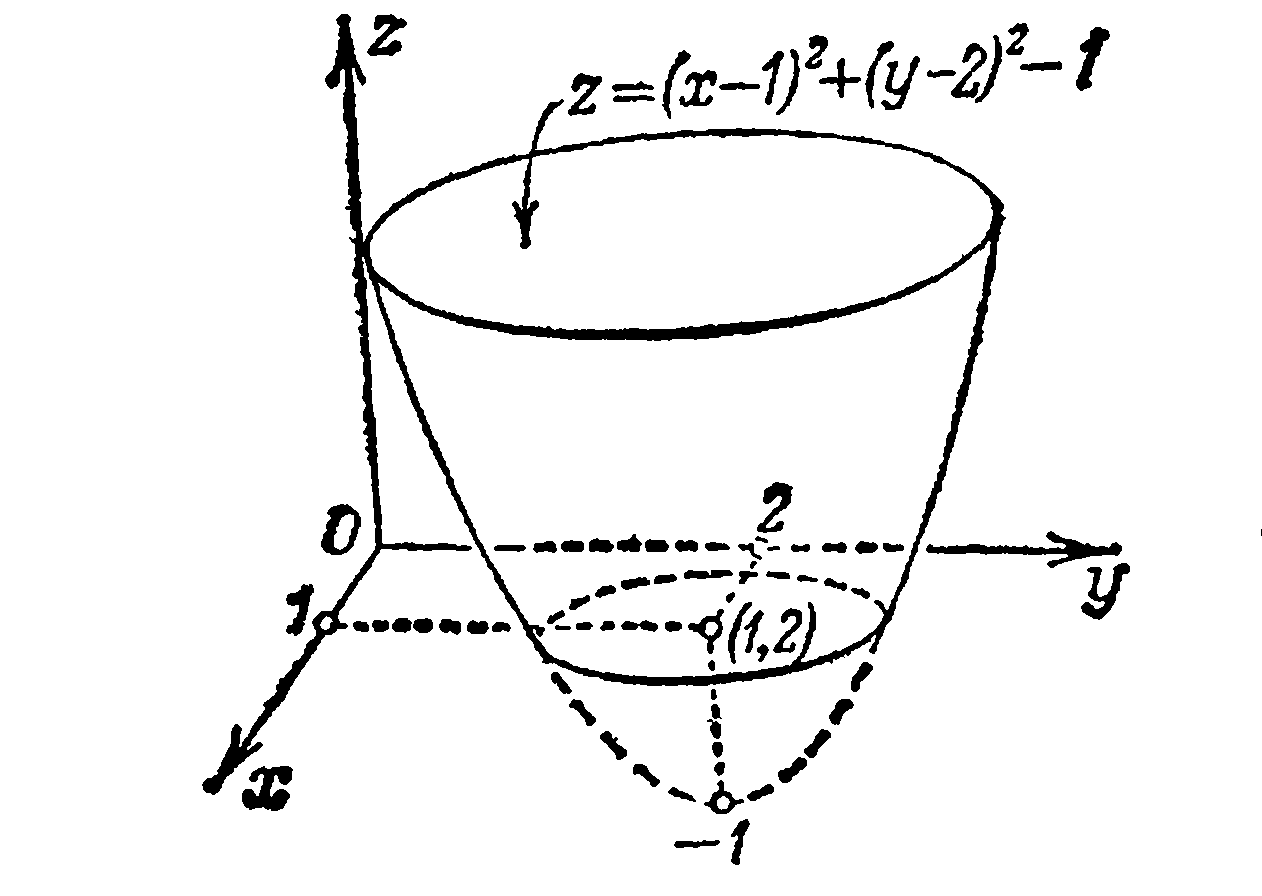
Например,
функция

Имеет
очевидный минимум z
= -1 при x
= 1 и y
= 2.

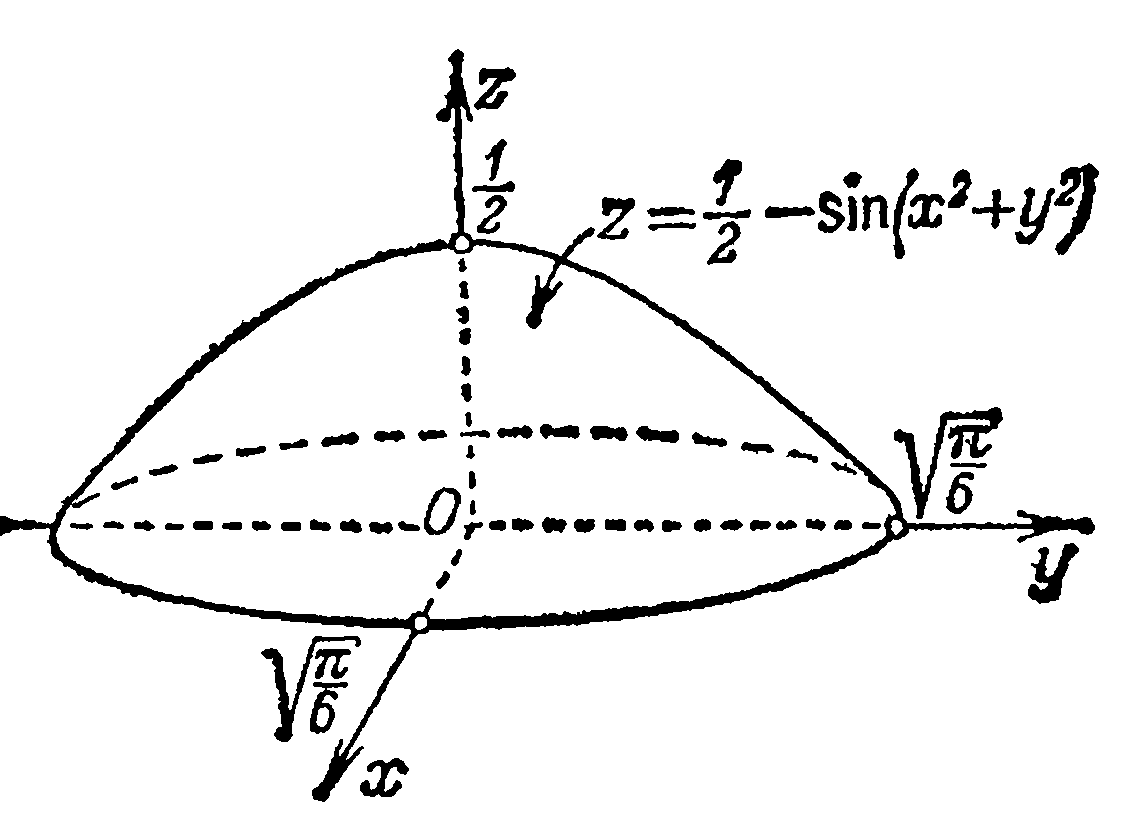
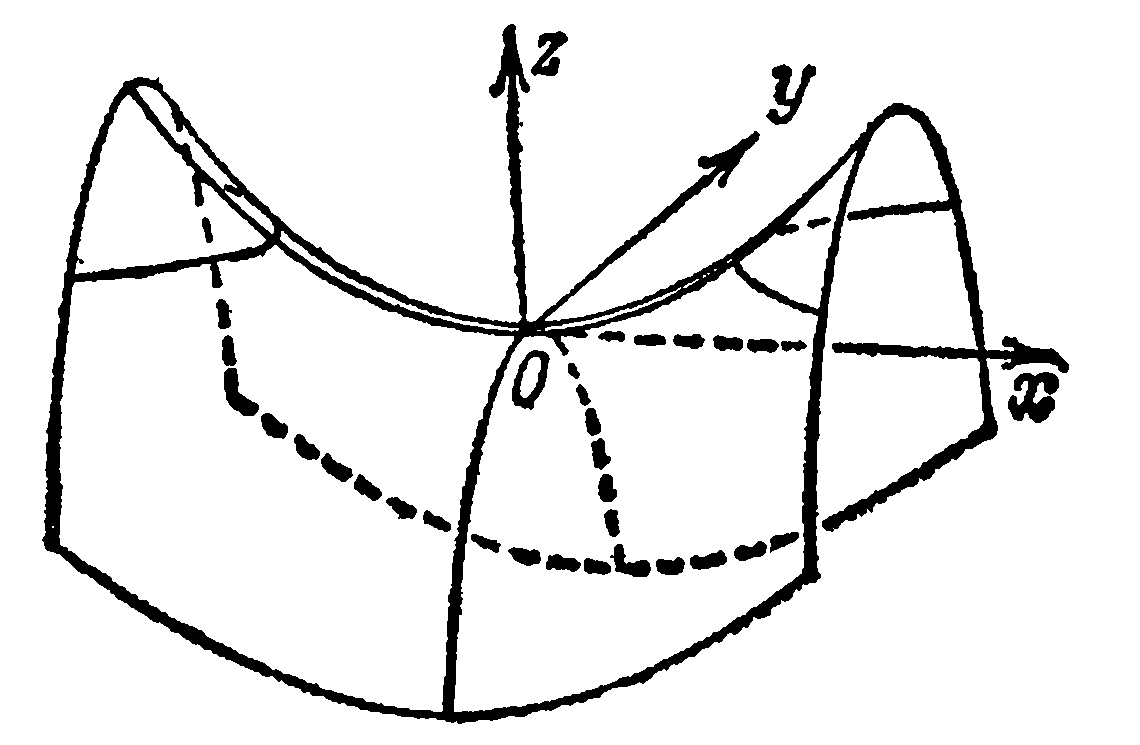
Функция

Имеет
максимум в точке

при x
= 0 и y
= 0.

Теорема.
(необходимые условия экстремума).

Если
функция

достигает экстремума при
,
,
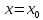
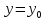
то каждая частная производная первого
порядка от z
или обращается в нуль при этих значениях
аргументов, или не существует.

Замечание.
Эта теорема не является достаточной
для исследования вопроса об экстремальных
значениях функции. Можно привести
примеры функций, которые в некоторых
точках имеет нулевые частные производные,
но не имеет экстремума в этих точка.

Пример.
Функции, которая имеет нулевые частные
производные, но не имеет экстремума.

В
точке
.

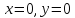
В
самом деле:

Достаточные
условия экстремума.

Теорема.
Пусть в некоторой области, содержащей
точку

,

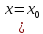
функция

имеет непрерывные
частные производные до третьего порядка
включительно; пусть, кроме того, точка

является
критической точкой функции
,
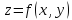
т.е.

Тогда
при
,

1. 
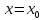
   имеет максимум,
   если

1. 
   имеет минимум,
   если

1. 
   не имеет ни
   минимума, ни максимума, если

1. 
   может иметь
   экстремум, а может и не иметь – требуется
   дополнительное исследование, если

Пример 3.2. Исследовать
на максимум и на минимум функцию

Решение.

1. Найдем
   критические точки, т.е. точки, в которых
   первые частные производные равны нулю
   или не существуют.

Сначала вычисляем
сами частные производные.

Приравниваем
частные производные нулю и решаем
следующую систему линейных уравнений

= 0

Умножаем второе
уравнение на 2 и складываем с первым.
Получится уравнение только от y.

Находим

и подставляем
в первое уравнение

Преобразуем

Находим

Следовательно,
точка ()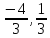
является критической.

1. Вычислим
   вторые производные второго порядка и
   подставим в них координаты критической
   точки.

В нашем случае,
подставлять значения критических точек
не надо, так как вторые производные
являются числами.

В итоге имеем:

Следовательно,
найденная критическая точка, является
точкой экстремума. Более того, так как

то эта точка
минимума.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рассмотрим функцию $z=f(x,y)$, которая определена в некоторой области в пространстве $Oxy$.

Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $frac{partial z}{partial x} ;frac{partial z}{partial y} $.

«Градиент заданной функции» 👇

Рассмотрим функцию $w=f(x,y,z)$, которая определена в некоторой области в пространстве $Oxyz$.

Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $frac{partial z}{partial x} ;frac{partial z}{partial y} $.

Перечислим некоторые свойства градиента:

• Производная заданной функции в заданной точке по направлению некоторого вектора $overrightarrow{s} $ имеет наибольшее значение, если направление данного вектора $overrightarrow{s} $ совпадает с направлением градиента. При этом данное наибольшее значение производной совпадает с длиной вектора градиента, т.е. $|overrightarrow{gradw} |$.

• Производная заданной функции по направлению вектора, который перпендикулярен к вектору градиента, т.е. $overrightarrow{gradw} $, равна 0. Так как $varphi =frac{pi }{2} $, то $cos varphi =0$; следовательно, $frac{partial w}{partial s} =|overrightarrow{gradw} |cdot cos varphi =0$.