Хеш-функция, что это такое?
Время на прочтение
8 мин
Количество просмотров 117K

Приветствую уважаемого читателя!
Сегодня я хотел бы рассказать о том, что из себя представляет хеш-функция, коснуться её основных свойств, привести примеры использования и в общих чертах разобрать современный алгоритм хеширования SHA-3, который был опубликован в качестве Федерального Стандарта Обработки Информации США в 2015 году.
Общие сведения
Криптографическая хеш-функция – это математический алгоритм, который отображает данные произвольного размера в битовый массив фиксированного размера.
Результат, производимый хеш-функцией, называется «хеш-суммой» или же просто «хешем», а входные данные часто называют «сообщением».
Для идеальной хеш-функции выполняются следующие условия:
а) хеш-функция является детерминированной, то есть одно и то же сообщение приводит к одному и тому же хеш-значению
b) значение хеш-функции быстро вычисляется для любого сообщения
c) невозможно найти сообщение, которое дает заданное хеш-значение
d) невозможно найти два разных сообщения с одинаковым хеш-значением
e) небольшое изменение в сообщении изменяет хеш настолько сильно, что новое и старое значения кажутся некоррелирующими
Давайте сразу рассмотрим пример воздействия хеш-функции SHA3-256.
Число 256 в названии алгоритма означает, что на выходе мы получим строку фиксированной длины 256 бит независимо от того, какие данные поступят на вход.
На рисунке ниже видно, что на выходе функции мы имеем 64 цифры шестнадцатеричной системы счисления. Переводя это в двоичную систему, получаем желанные 256 бит.
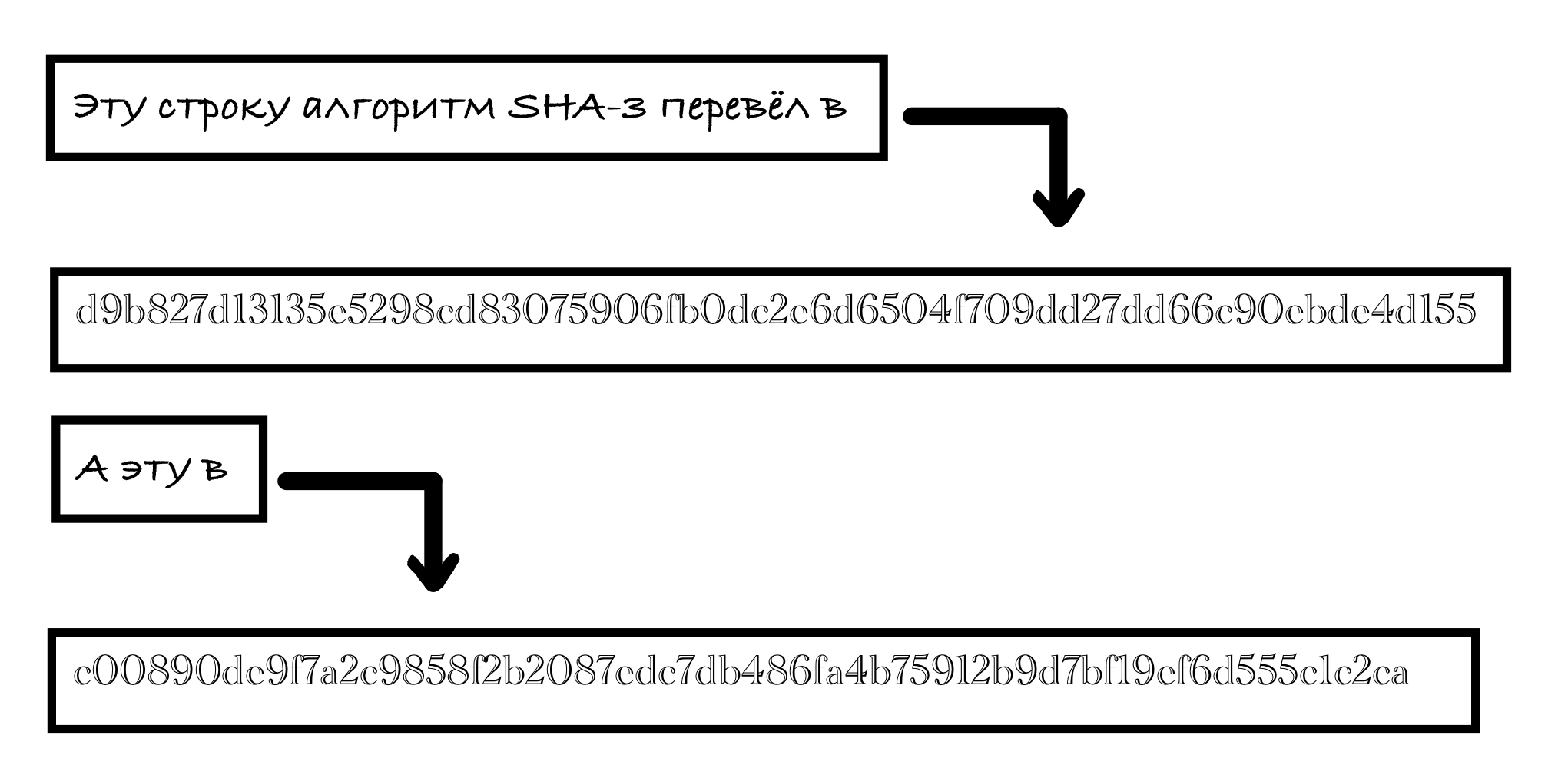
Любой заинтересованный читатель задаст себе вопрос: “А что будет, если на вход подать данные, бинарный код которых во много раз превосходит 256 бит?”
Ответ таков: на выходе получим все те же 256 бит!
Дело в том, что 256 бит – это соответствий, то есть
различных входов имеют свой уникальный хеш.
Чтобы прикинуть, насколько велико это значение, запишем его следующим образом:
Надеюсь, теперь нет сомнений в том, что это очень внушительное число!
Поэтому ничего не мешает нам сопоставлять длинному входному массиву данных массив фиксированной длины.
Свойства
Криптографическая хеш-функция должна уметь противостоять всем известным типам криптоаналитических атак.
В теоретической криптографии уровень безопасности хеш-функции определяется с использованием следующих свойств:
Pre-image resistance
Имея заданное значение h, должно быть сложно найти любое сообщение m такое, что
Second pre-image resistance
Имея заданное входное значение , должно быть сложно найти другое входное значение
такое, что
Collision resistance
Должно быть сложно найти два различных сообщения и
таких, что
Такая пара сообщений и
называется коллизией хеш-функции
Давайте чуть более подробно поговорим о каждом из перечисленных свойств.
Collision resistance. Как уже упоминалось ранее, коллизия происходит, когда разные входные данные производят одинаковый хеш. Таким образом, хеш-функция считается устойчивой к коллизиям до того момента, пока не будет обнаружена пара сообщений, дающая одинаковый выход. Стоит отметить, что коллизии всегда будут существовать для любой хеш-функции по той причине, что возможные входы бесконечны, а количество выходов конечно. Хеш-функция считается устойчивой к коллизиям, когда вероятность обнаружения коллизии настолько мала, что для этого потребуются миллионы лет вычислений.
Несмотря на то, что хеш-функций без коллизий не существует, некоторые из них достаточно надежны и считаются устойчивыми к коллизиям.
Pre-image resistance. Это свойство называют сопротивлением прообразу. Хеш-функция считается защищенной от нахождения прообраза, если существует очень низкая вероятность того, что злоумышленник найдет сообщение, которое сгенерировало заданный хеш. Это свойство является важным для защиты данных, поскольку хеш сообщения может доказать его подлинность без необходимости раскрытия информации. Далее будет приведён простой пример и вы поймете смысл предыдущего предложения.
Second pre-image resistance. Это свойство называют сопротивлением второму прообразу. Для упрощения можно сказать, что это свойство находится где-то посередине между двумя предыдущими. Атака по нахождению второго прообраза происходит, когда злоумышленник находит определенный вход, который генерирует тот же хеш, что и другой вход, который ему уже известен. Другими словами, злоумышленник, зная, что пытается найти
такое, что
Отсюда становится ясно, что атака по нахождению второго прообраза включает в себя поиск коллизии. Поэтому любая хеш-функция, устойчивая к коллизиям, также устойчива к атакам по поиску второго прообраза.
Неформально все эти свойства означают, что злоумышленник не сможет заменить или изменить входные данные, не меняя их хеша.
Таким образом, если два сообщения имеют одинаковый хеш, то можно быть уверенным, что они одинаковые.
В частности, хеш-функция должна вести себя как можно более похоже на случайную функцию, оставаясь при этом детерминированной и эффективно вычислимой.

Применение хеш-функций
Рассмотрим несколько достаточно простых примеров применения хеш-функций:
• Проверка целостности сообщений и файлов
Сравнивая хеш-значения сообщений, вычисленные до и после передачи, можно определить, были ли внесены какие-либо изменения в сообщение или файл.
• Верификация пароля
Проверка пароля обычно использует криптографические хеши. Хранение всех паролей пользователей в виде открытого текста может привести к массовому нарушению безопасности, если файл паролей будет скомпрометирован. Одним из способов уменьшения этой опасности является хранение в базе данных не самих паролей, а их хешей. При выполнении хеширования исходные пароли не могут быть восстановлены из сохраненных хеш-значений, поэтому если вы забыли свой пароль вам предложат сбросить его и придумать новый.
• Цифровая подпись
Подписываемые документы имеют различный объем, поэтому зачастую в схемах ЭП подпись ставится не на сам документ, а на его хеш. Вычисление хеша позволяет выявить малейшие изменения в документе при проверке подписи. Хеширование не входит в состав алгоритма ЭП, поэтому в схеме может быть применена любая надежная хеш-функция.
Предлагаю также рассмотреть следующий бытовой пример:
Алиса ставит перед Бобом сложную математическую задачу и утверждает, что она ее решила. Боб хотел бы попробовать решить задачу сам, но все же хотел бы быть уверенным, что Алиса не блефует. Поэтому Алиса записывает свое решение, вычисляет его хеш и сообщает Бобу (сохраняя решение в секрете). Затем, когда Боб сам придумает решение, Алиса может доказать, что она получила решение раньше Боба. Для этого ей нужно попросить Боба хешировать его решение и проверить, соответствует ли оно хеш-значению, которое она предоставила ему раньше.
Теперь давайте поговорим о SHA-3.

SHA-3
Национальный институт стандартов и технологий (NIST) в течение 2007—2012 провёл конкурс на новую криптографическую хеш-функцию, предназначенную для замены SHA-1 и SHA-2.
Организаторами были опубликованы некоторые критерии, на которых основывался выбор финалистов:
• Безопасность
Способность противостоять атакам злоумышленников
• Производительность и стоимость
Вычислительная эффективность алгоритма и требования к оперативной памяти для программных реализаций, а также количество элементов для аппаратных реализаций
• Гибкость и простота дизайна
Гибкость в эффективной работе на самых разных платформах, гибкость в использовании параллелизма или расширений ISA для достижения более высокой производительности
В финальный тур попали всего 5 алгоритмов:
• BLAKE
• Grøstl
• JH
• Keccak
• Skein
Победителем и новым SHA-3 стал алгоритм Keccak.
Давайте рассмотрим Keccak более подробно.
Keccak
Хеш-функции семейства Keccak построены на основе конструкции криптографической губки, в которой данные сначала «впитываются» в губку, а затем результат Z «отжимается» из губки.
Любая губчатая функция Keccak использует одну из семи перестановок которая обозначается
, где
перестановки представляют собой итерационные конструкции, состоящие из последовательности почти одинаковых раундов. Число раундов
зависит от ширины перестановки и задаётся как
где
В качестве стандарта SHA-3 была выбрана перестановка Keccak-f[1600], для неё количество раундов
Далее будем рассматривать
Давайте сразу введем понятие строки состояния, которая играет важную роль в алгоритме.
Строка состояния представляет собой строку длины 1600 бит, которая делится на и
части, которые называются скоростью и ёмкостью состояния соотвественно.
Соотношение деления зависит от конкретного алгоритма семейства, например, для SHA3-256
В SHA-3 строка состояния S представлена в виде массива слов длины
бит, всего
бит. В Keccak также могут использоваться слова длины
, равные меньшим степеням 2.
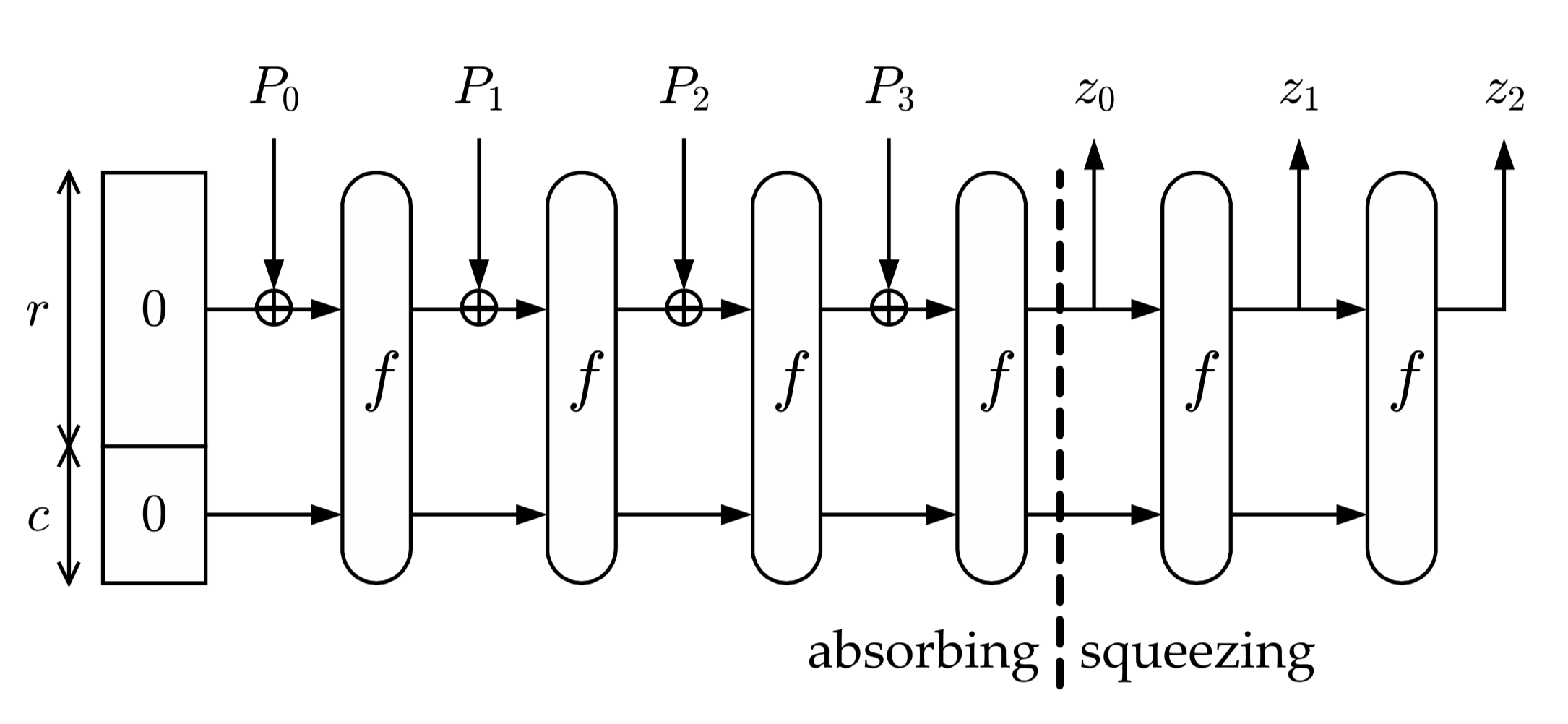
Алгоритм получения хеш-функции можно разделить на несколько этапов:
• С помощью функции дополнения исходное сообщение M дополняется до строки P длины кратной r
• Строка P делится на n блоков длины
• «Впитывание»: каждый блок дополняется нулями до строки длиной
бит (b = r+c) и суммируется по модулю 2 со строкой состояния
, далее результат суммирования подаётся в функцию перестановки
и получается новая строка состояния
, которая опять суммируется по модулю 2 с блоком
и дальше опять подаётся в функцию перестановки
. Перед началом работы криптографической губки все элементы
равны 0.
• «Отжимание»: пока длина результата меньше чем
, где
– количество бит в выходном массиве хеш-функции,
первых бит строки состояния
добавляется к результату
. После каждой такой операции к строке состояния применяется функция перестановок
и данные продолжают «отжиматься» дальше, пока не будет достигнуто значение длины выходных данных
.
Все сразу станет понятно, когда вы посмотрите на картинку ниже:
Функция дополнения
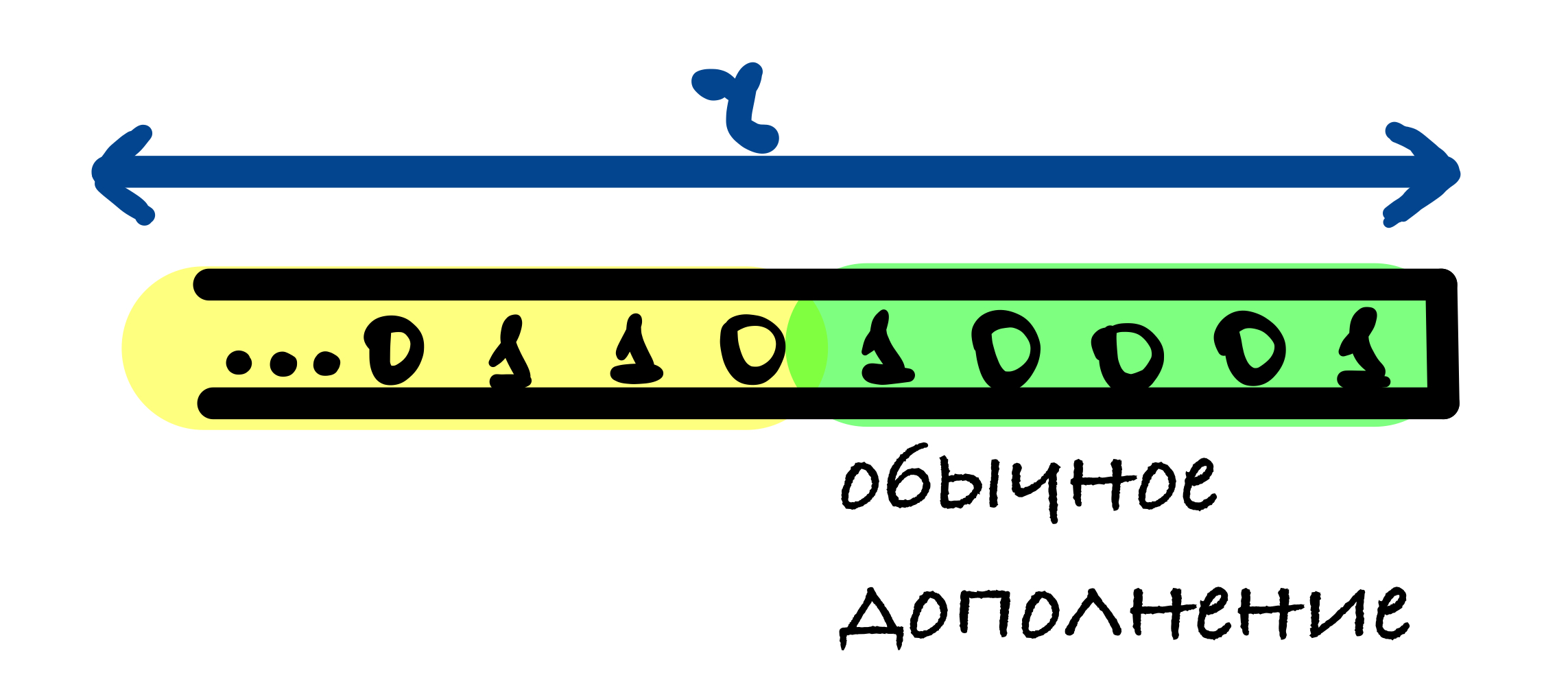
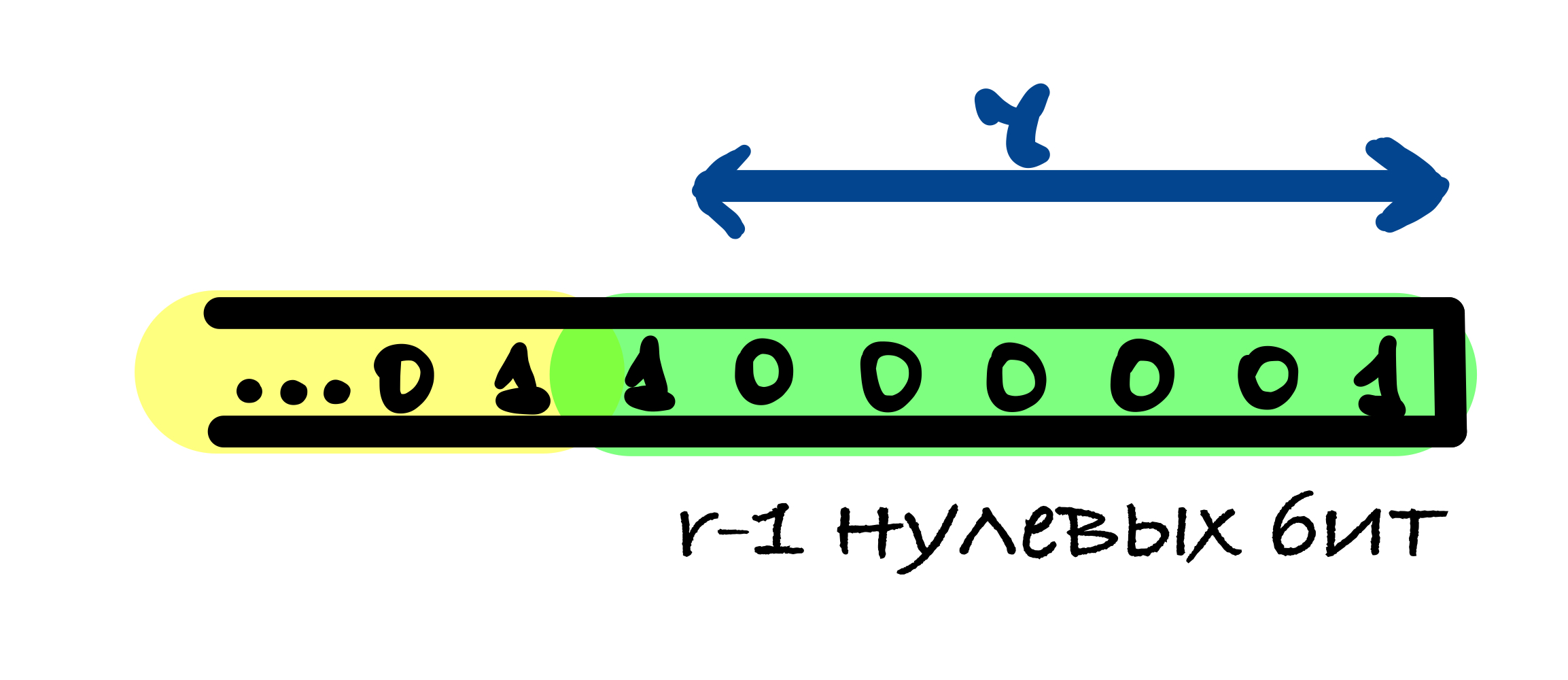
В SHA-3 используется следующий шаблон дополнения 10…1: к сообщению добавляется 1, после него от 0 до r – 1 нулевых бит и в конце добавляется 1.
r – 1 нулевых бит может быть добавлено, когда последний блок сообщения имеет длину r – 1 бит. В этом случае последний блок дополняется единицей и к нему добавляется блок, состоящий из r – 1 нулевых бит и единицы в конце.
Если длина исходного сообщения M делится на r, то в этом случае к сообщению добавляется блок, начинающийся и оканчивающийся единицами, между которыми находятся r – 2 нулевых бит. Это делается для того, чтобы для сообщения, оканчивающегося последовательностью бит как в функции дополнения, и для сообщения без этих бит значения хеш-функции были различны.
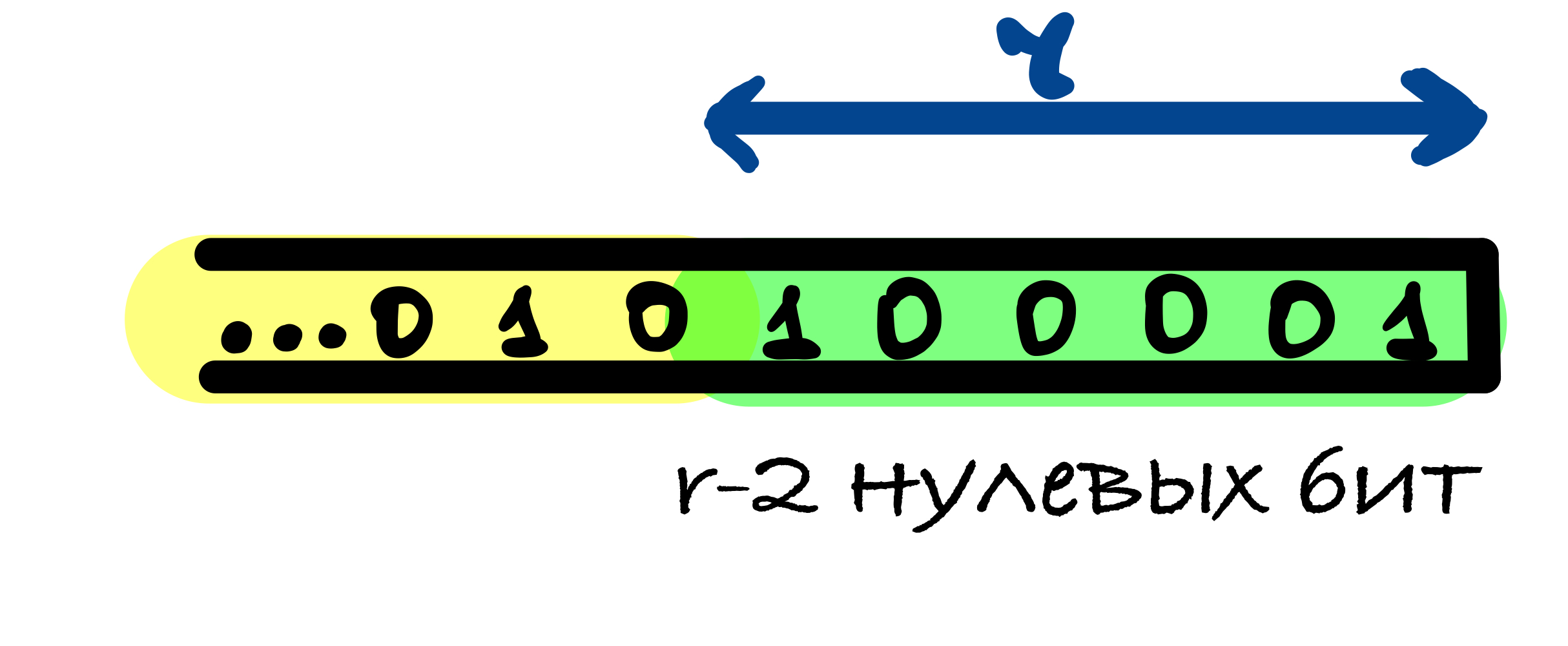
Первый единичный бит в функции дополнения нужен, чтобы результаты хеш-функции от сообщений, отличающихся несколькими нулевыми битами в конце, были различны.
Функция перестановок
Базовая функция перестановки состоит из раундов по пять шагов:
-
Шаг
-
Шаг
-
Шаг
-
Шаг
-
Шаг
Тета, Ро, Пи, Хи, Йота
Далее будем использовать следующие обозначения:
Так как состояние имеет форму массива
, то мы можем обозначить каждый бит состояния как
Обозначим результат преобразования состояния функцией перестановки
Также обозначим функцию, которая выполняет следующее соответствие:
– обычная функция трансляции, которая сопоставляет биту
бит
,
где – длина слова (64 бит в нашем случае)
Я хочу вкратце описать каждый шаг функции перестановок, не вдаваясь в математические свойства каждого.
Шаг
Эффект отображения можно описать следующим образом: оно добавляет к каждому биту
побитовую сумму двух столбцов
и
Схематическое представление функции:
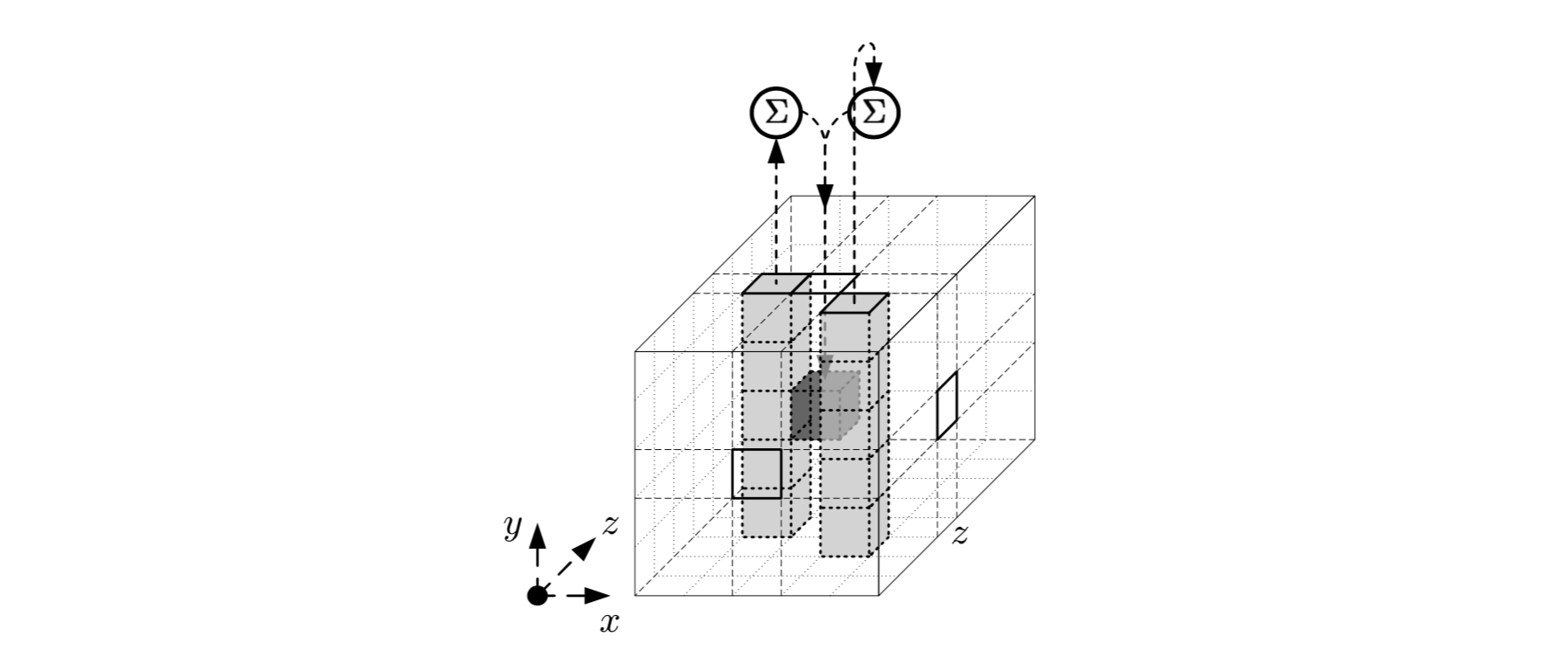
Псевдокод шага:

Шаг
Отображение направлено на трансляции внутри слов (вдоль оси z).
Проще всего его описать псевдокодом и схематическим рисунком:

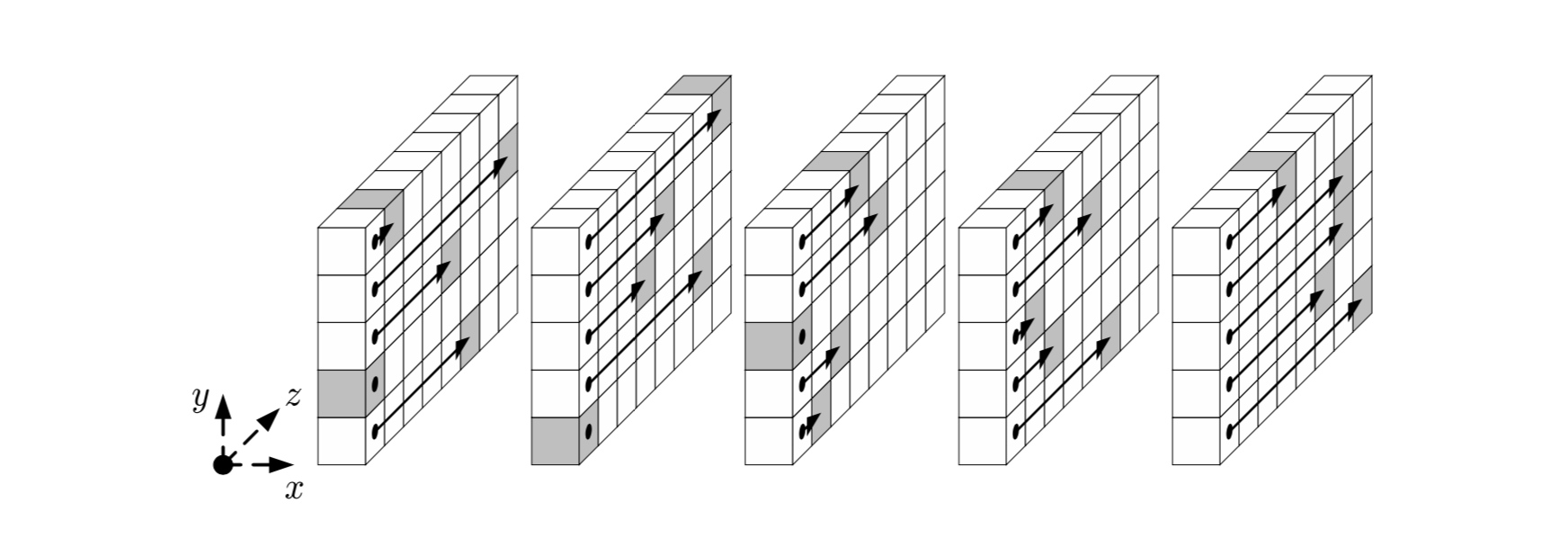
Шаг
Шаг представляется псевдокодом и схематическим рисунком:


Шаг
Шаг является единственный нелинейным преобразованием в
Псевдокод и схематическое представление:

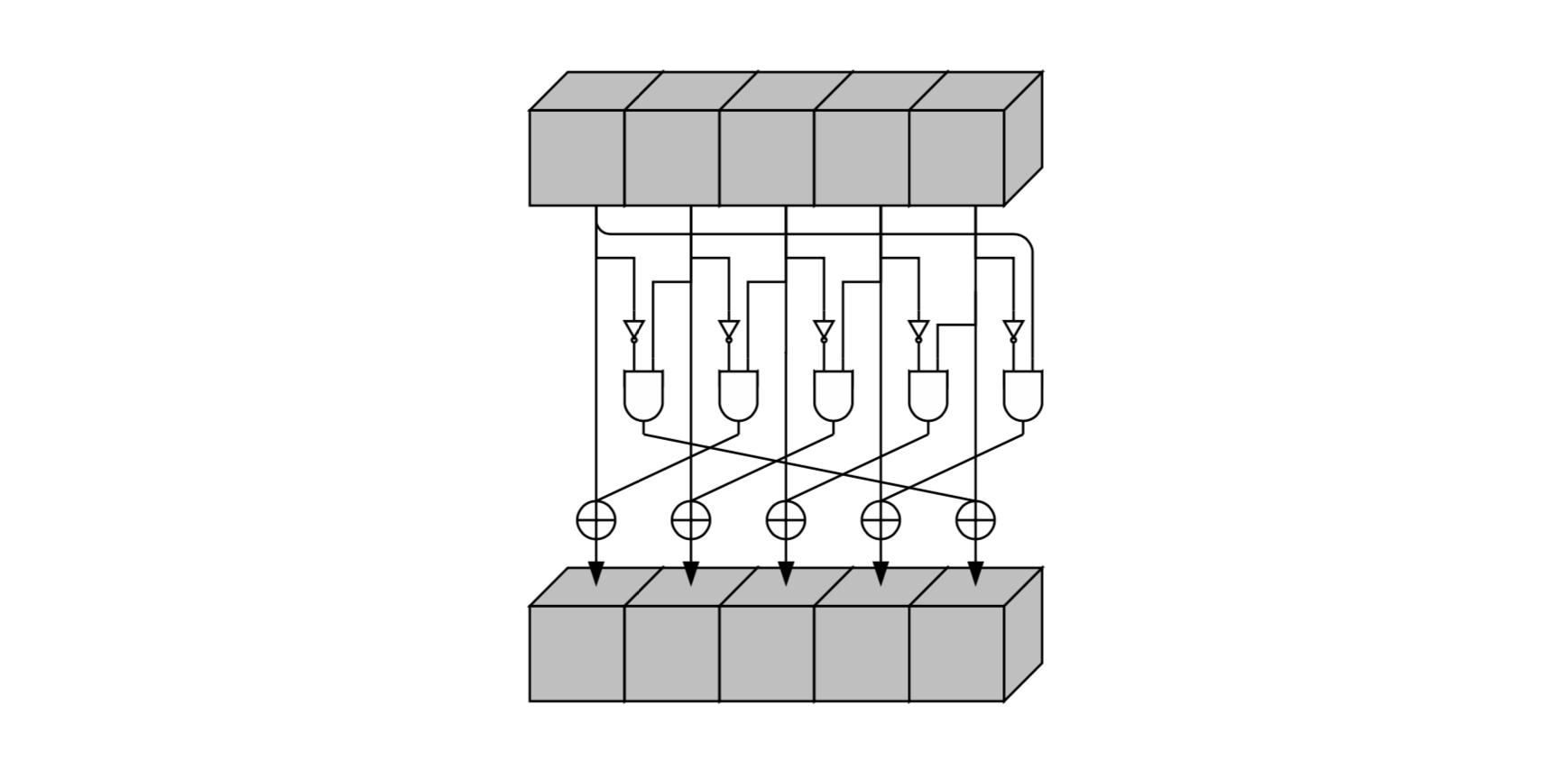
Шаг
Отображение состоит из сложения с раундовыми константами и направлено на нарушение симметрии. Без него все раунды
были бы эквивалентными, что делало бы его подверженным атакам, использующим симметрию. По мере увеличения
раундовые константы добавляют все больше и больше асимметрии.
Ниже приведена таблица раундовых констант для
бит

Все шаги можно объединить вместе и тогда мы получим следующее:


Где константы являются циклическими сдвигами и задаются таблицей:
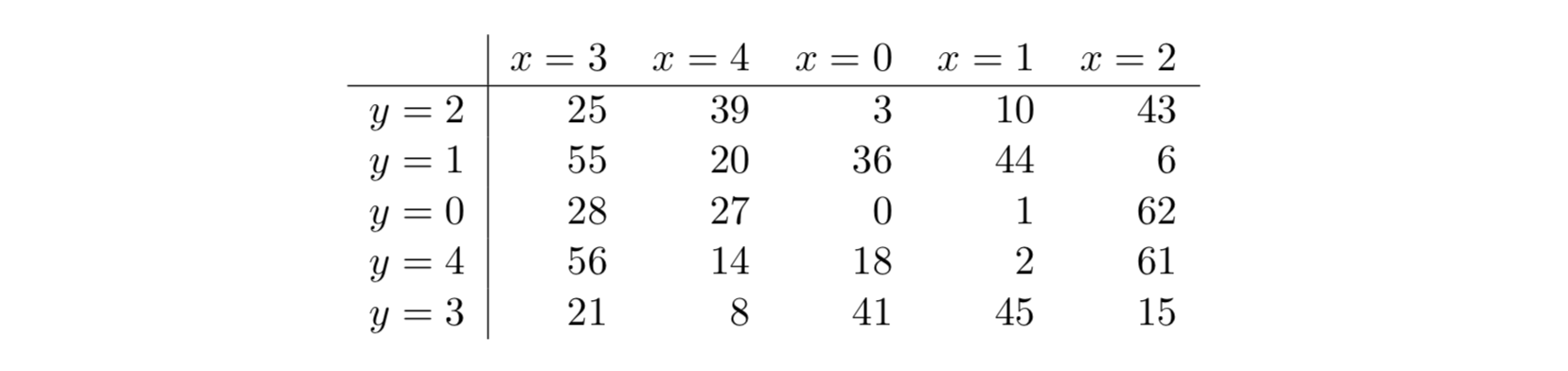
Итоги
В данной статье я постарался объяснить, что такое хеш-функция и зачем она нужна
Также в общих чертах мной был разобран принцип работы алгоритма SHA-3 Keccak, который является последним стандартизированным алгоритмом семейства Secure Hash Algorithm
Надеюсь, все было понятно и интересно
Всем спасибо за внимание!
Хеш-функция (англ. hash function от hash — «превращать в фарш», «мешанина»[1]), или функция свёртки — функция, осуществляющая преобразование массива входных данных произвольной длины в выходную битовую строку установленной длины, выполняемое определённым алгоритмом. Преобразование, производимое хеш-функцией, называется хешированием. Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования называется «хешем», «хеш-кодом», «хеш-суммой», «сводкой сообщения».
Хеш-функции применяются в следующих случаях:
- при построении ассоциативных массивов;
- при поиске дубликатов в последовательностях наборов данных;
- при построении уникальных идентификаторов для наборов данных;
- при вычислении контрольных сумм от данных (сигнала) для последующего обнаружения в них ошибок (возникших случайно или внесённых намеренно), возникающих при хранении и/или передаче данных;
- при сохранении паролей в системах защиты в виде хеш-кода (для восстановления пароля по хеш-коду требуется функция, являющаяся обратной по отношению к использованной хеш-функции);
- при выработке электронной подписи (на практике часто подписывается не само сообщение, а его «хеш-образ»);
- и др.
В общем случае (согласно принципу Дирихле) нет однозначного соответствия между хеш-кодом и исходными данными. Возвращаемые хеш-функцией значения менее разнообразны, чем значения входного массива. Случай, при котором хеш-функция преобразует более чем один массив входных данных в одинаковые сводки, называется «коллизией». Вероятность возникновения коллизий используется для оценки качества хеш-функций.
Существует множество алгоритмов хеширования, различающихся различными свойствами. Примеры свойств:
- разрядность;
- вычислительная сложность;
- криптостойкость.
Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшим примером хеш-функции может служить «обрамление» данных циклическим избыточным кодом (англ. CRC, cyclic redundancy code).
История[править | править код]
Шифровка сообщений без возможности однозначной расшифровки, а только с целью подтверждения авторского приоритета, применялась издавна.
Галилео Галилей наблюдал кольца Сатурна, которые принял за «ушки». Не будучи уверен, но желая утвердить свой приоритет, он опубликовал сообщение с перестановленными буквами: smaismrmilmepoetaleumibunenugttauiras. В 1610 году он раскрыл исходную фразу: Altissimum planetam tergeminum obseruaui, что в переводе с латинского языка означает «высочайшую планету тройною наблюдал». Таким образом, на момент публикации первого сообщения исходная фраза не была раскрыта, но была создана возможность подтвердить её позже.
В середине 1650-х Христиан Гюйгенс разглядел кольца и опубликовал сообщение с буквами, расставленными по алфавиту: aaaaaaacccccdeeeeeghiiiiiiillllmmnnnnnnnnnooooppqrrstttttuuuuu. Через некоторое время была опубликована и исходная фраза: Annulo cingitur, tenui plano, nusquam cohaerente, ad eclipticam inclinato — «Окружен кольцом тонким, плоским, нигде не подвешенным, наклоненным к эклиптике». От применения хеш-функции, включая и цель позднее подтвердить некоторое нераскрытое сообщение, данный случай отличается только тем, что выходное сообщение не имеет фиксированной длины, а определяется длиной входного. Фактически, расстановка букв исходного сообщения по алфавиту является некоторой хеш-функцией, но только с результатом нефиксированной длины.
В январе 1953 года Ханс Петер Лун (нем. Hans Peter Luhn) (сотрудник фирмы IBM) предложил «хеш-кодирование». Дональд Кнут считает, что Ханс первым выдвинул систематическую идею «хеширования».
В 1956 году Арнольд Думи (англ. Arnold Dumey) в своей работе «Computers and automation» первым описал идею «хеширования» такой, какой её знает большинство программистов сейчас. Думи рассматривал «хеширование» как решение «проблемы словаря», предложил использовать в качестве «хеш-адреса» остаток от деления на простое число[2].
В 1957 году в журнале «IBM Journal of Research and Development» была опубликована статья Уэсли Питерсона (англ. W. Wesley Peterson) о поиске текста в больших файлах. Эта работа считается первой «серьёзной» работой по «хешированию». В статье Уэсли определил «открытую адресацию», указал на уменьшение производительности при удалении. Спустя шесть лет была опубликована работа Вернера Бухгольца (нем. Werner Buchholz), в которой было проведено обширное исследование «хеш-функций». В течение нескольких последующих лет «хеширование» широко использовалось, однако никаких значимых работ не публиковалось.
В 1967 году «хеширование» в современном значении упомянуто в книге Херберта Хеллермана «Принципы цифровых вычислительных систем»[3]. В 1968 году Роберт Моррис (англ. Robert Morris) опубликовал в журнале «Communications of the ACM» большой обзор по «хешированию». Эта работа считается «ключевой» публикацией, вводящей понятие о «хешировании» в научный оборот, и закрепившей термин «хеш», ранее применявшийся только специалистами (жаргон).
До начала 1990-х годов в русскоязычной литературе в качестве эквивалента термину «хеширование» благодаря работам Андрея Петровича Ершова использовалось слово «расстановка», а для «коллизий» использовался термин «конфликт» (А. П. Ершов использовал «расстановку» с 1956 года). В русскоязычном издании книги Никлауса Вирта «Алгоритмы и структуры данных» 1989 года также используется термин «расстановка». Предлагалось также назвать метод другим русским словом: «окрошка». Однако ни один из этих вариантов не прижился, и в русской литературе используется преимущественно термин «хеширование»[4].
Виды «хеш-функций»[править | править код]
«Хорошая» хеш-функция должна удовлетворять двум свойствам:
- быстрое вычисление;
- минимальное количество «коллизий».
Введём обозначения:
То есть:
.
В качестве примера «плохой» хеш-функции можно привести функцию с 


Рассмотрим несколько простых и надёжных реализаций «хеш-функций».
«Хеш-функции», основанные на делении[править | править код]
1. «Хеш-код» как остаток от деления на число всех возможных «хешей»[править | править код]
Хеш-функция может вычислять «хеш» как остаток от деления входных данных на 
,
где 
При этом очевидно, что при чётном 





2. «Хеш-код» как набор коэффициентов получаемого полинома[править | править код]
Хеш-функция может выполнять деление входных данных на полином по модулю два. В данном методе 




При правильном выборе 
«Хеш-функции», основанные на умножении[править | править код]
Обозначим символом 

Выберем некую константу 


В этом случае на компьютере с двоичной системой счисления 


Одним из преимуществ хеш-функций, основанных на делении и умножении, является выгодное использование неслучайности реальных ключей. Например, если ключи представляют собой арифметическую прогрессию (например, последовательность имён «Имя 1», «Имя 2», «Имя 3»), хеш-функция, использующая умножение, отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшит количество коллизий по сравнению со случайной ситуацией[4].
Одной из хеш-функций, использующих умножение, является хеш-функция, использующая хеширование Фибоначчи. Хеширование Фибоначчи основано на свойствах золотого сечения. В качестве константы 



Хеширование строк переменной длины[править | править код]
Вышеизложенные методы применимы и в том случае, если необходимо рассматривать ключи, состоящие из нескольких слов, или ключи переменной длины.
Например, можно скомбинировать слова в одно при помощи сложения по модулю 
Хеширование Пирсона — алгоритм, предложенный Питером Пирсоном (англ. Peter Pearson) для процессоров с 8-битовыми регистрами, задачей которого является быстрое преобразование строки произвольной длины в хеш-код. На вход функция получает слово 

Алгоритм можно описать следующим псевдокодом, который получает на вход строку 

h := 0 for each c in W loop index := h xor c h := T[index] end loop return h
Среди преимуществ алгоритма:
- простоту вычисления;
- отсутствие таких входных данных, для которых вероятность коллизии наибольшая;
- возможность модификации в идеальную хеш-функцию[5].
В качестве альтернативного способа хеширования ключей 


[4]
Идеальное хеширование[править | править код]
Идеальной хеш-функцией (англ. perfect hash function) называется такая функция, которая отображает каждый ключ из набора 
Описание[править | править код]
- Функция
называется идеальной хеш-функцией для
, если она инъективна на
.
- Функция
называется минимальной идеальной хеш-функцией для
, если она является идеальной хеш-функцией и
.
- Для целого
функция
называется
-идеальной хеш-функцией (k-PHF) для
, если для каждого
имеем
.
Идеальное хеширование применяется, если требуется присвоить уникальный идентификатор ключу без сохранения какой-либо информации о ключе. Пример использования идеального (или скорее 
Универсальное хеширование[править | править код]
Универсальным хешированием называется хеширование, при котором используется не одна конкретная хеш-функция, а происходит выбор хеш-функции из заданного семейства по случайному алгоритму. Универсальное хеширование обычно отличается низким числом коллизий, применяется, например, при реализации хеш-таблиц и в криптографии.
Описание[править | править код]
Предположим, что требуется отобразить ключи из пространства 
![[m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b649f5418f2ac84d66063f41319368b0926ccec4)


![H={h:Uto [m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07dbe0dc6d02fc97f45867f07178c7000d6343b9)
Методы борьбы с коллизиями[править | править код]
Коллизией (иногда конфликтом[2] или столкновением) называется случай, при котором одна хеш-функция для разных входных блоков возвращает одинаковые хеш-коды.
Методы борьбы с коллизиями в хеш-таблицах[править | править код]
Большинство первых работ, описывающих хеширование, посвящено методам борьбы с коллизиями в хеш-таблицах. Тогда хеш-функции применялись при поиске текста в файлах большого размера. Существует два основных метода борьбы с коллизиями в хеш-таблицах:
- метод цепочек (метод прямого связывания);
- метод открытой адресации.
При использовании метода цепочек в хеш-таблице хранятся пары «связный список ключей» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; если хеш-код был получен ранее (для другого ключа), ключ добавляется в существующий список ключей, парный хеш-коду; иначе создаётся новая пара «список ключей» — «хеш-код», и ключ добавляется в созданный список. В общем случае, если имеется 



При использовании метода открытой адресации в хеш-таблице хранятся пары «ключ» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; пара «ключ» — «хеш-код» сохраняется в таблице. В этом случае при поиске по таблице по сравнению со случаем, в котором используются связные списки, ссылки не используются, выполняется последовательный перебор пар «ключ» — «хеш-код», перебор прекращается после обнаружения нужного ключа. Последовательность, в которой просматриваются ячейки таблицы, называется последовательностью проб[4].
Криптографическая соль[править | править код]
Для защиты паролей и цифровых подписей от подделки создано несколько методов, работающих даже в том случае, если криптоаналитику известны способы построения коллизий для используемой хеш-функции. Одним из таких методов является добавление к входным данным так называемой криптографической «соли» — строки случайных данных; иногда «соль» добавляется и к хеш-коду. Добавление случайных данных значительно затрудняет анализ итоговых хеш-таблиц. Данный метод, к примеру, используется при сохранении паролей в UNIX-подобных операционных системах.
Применение хеш-функций[править | править код]
Хеш-функции широко используются в криптографии.
Хеш используется как ключ во многих структурах данных — хеш-таблицаx, фильтрах Блума и декартовых деревьях.
Криптографические хеш-функции[править | править код]
Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того, чтобы хеш-функция 
Данные требования не являются независимыми:
- обратимая функция нестойка к коллизиям первого и второго рода;
- функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.
Не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.
Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n бит в среднем за примерно 

Криптографические хеш-функции должны иметь лавинный эффект — при малейшем изменении аргумента значение функции сильно изменяется. В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа[8].
Хеширование часто используется в алгоритмах электронно-цифровой подписи, где шифруется не само сообщение, а его хеш-код, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев вместо паролей хранятся значения их хеш-кодов.
Контрольные суммы[править | править код]
Алгоритмы вычисления контрольных сумм — несложные, быстрые и легко реализуемые аппаратно алгоритмы, используемые для защиты данных от непреднамеренных искажений, в том числе — от ошибок аппаратуры. С точки зрения математики такие алгоритмы являются хеш-функциями, вычисляющими контрольный код. Контрольный код применяется для обнаружения ошибок, которые могут возникнуть при передаче и хранении информации.
Алгоритмы вычисления контрольных сумм по скорости вычисления в десятки и сотни раз быстрее, чем криптографические хеш-функции, и значительно проще в аппаратном исполнении.
Платой за столь высокую скорость является отсутствие криптостойкости — возможность легко «подогнать» сообщение под заранее известную контрольную сумму. Также обычно разрядность контрольных сумм (типичное число: 32 бита) ниже, чем разрядность криптографических хешей (типичные числа: 128, 160 и 256 бит), что означает возможность возникновения непреднамеренных коллизий.
Простейшим алгоритмом вычисления контрольной суммы является деление сообщения (входных данных) на 32- или 16-битовые слова с последующим суммированием слов. Такой алгоритм применяется, например, в протоколах TCP/IP.
Как правило, алгоритмы вычисления контрольных сумм должны обнаруживать типичные аппаратные ошибки, например, должны обнаруживать несколько подряд идущих ошибочных бит до заданной длины. Семейство алгоритмов так называемых «циклических избыточных кодов» удовлетворяет этим требованиям. К ним относится, например, алгоритм CRC32, применяемый в устройствах Ethernet и в формате сжатия данных ZIP.
Контрольная сумма, например, может быть передана по каналу связи вместе с основным текстом (данными). На приёмном конце контрольная сумма может быть рассчитана заново и может сравниваться с переданным значением. Если будет обнаружено расхождение, то при передаче возникли искажения, и можно запросить повторную передачу.
Пример применения хеширования в быту — подсчёт количества чемоданов, перевозимых в багаже. Для проверки сохранности чемоданов не требуется проверять сохранность каждого чемодана, достаточно посчитать количество чемоданов при погрузке и выгрузке. Совпадение чисел будет означать, что ни один чемодан не потерян. То есть, число чемоданов является хеш-кодом.
Данный метод можно дополнить для защиты передаваемой информации от фальсификации (метод MAC). В этом случае хеширование производится криптостойкой функцией над сообщением, объединённым с секретным ключом, известным только отправителю и получателю сообщения. Криптоаналитик, перехватив сообщение и значение хеш-функции, не сможет восстановить код, то есть не сможет подделать сообщение (см. имитозащита).
Геометрическое хеширование[править | править код]
Геометрическое хеширование (англ. geometric hashing) — метод, широко применяемый в компьютерной графике и вычислительной геометрии для решения задач на плоскости или в трёхмерном пространстве, например для нахождения ближайших пар точек среди множества точек или для поиска одинаковых изображений. Хеш-функция в данном методе обычно получает на вход какое-либо метрическое пространство и разделяет его, создавая сетку из клеток. Хеш-таблица в данном случае является массивом с двумя или более индексами и называется «файлом сетки» (англ. grid file). Геометрическое хеширование применяется в телекоммуникациях при работе с многомерными сигналами[9].
Ускорение поиска данных[править | править код]
Хеш-таблицей называется структура данных, позволяющая хранить пары вида «ключ» — «хеш-код» и поддерживающая операции поиска, вставки и удаления элемента. Хеш-таблицы применяются с целью ускорения поиска, например, при записи текстовых полей в базе данных может рассчитываться их хеш-код, и данные могут помещаться в раздел, соответствующий этому хеш-коду. Тогда при поиске данных надо будет сначала вычислить хеш-код текста, и сразу станет известно, в каком разделе их надо искать. То есть искать надо будет не по всей базе, а только по одному её разделу, а это ускоряет поиск.
Бытовым аналогом хеширования в данном случае может служить размещение слов в словаре в алфавитном порядке. Первая буква слова является его хеш-кодом, и при поиске просматривается не весь словарь, а только слова, начинающиеся на нужную букву.
Примечания[править | править код]
- ↑ Вирт2, 2010, с. 256.
- ↑ 1 2 Вирт, 1989.
- ↑ Herbert Hellerman. Digital Computer System Principles. N.Y.: McGraw-Hill, 1967, 424 pp.
- ↑ 1 2 3 4 5 6 7 Кнут, 2007.
- ↑ Pearson, Peter K. (June 1990), Fast Hashing of Variable-Length Text Strings, Communications of the ACM Т. 33 (6): 677, doi:10.1145/78973.78978, <http://epaperpress.com/vbhash/download/p677-pearson.pdf>
- ↑ Djamal Belazzougui, Fabiano C. Botelho, Martin Dietzfelbinger. Hash, displace, and compress (неопр.). — Springer Berlin / Heidelberg, 2009.
- ↑
Miltersen, Peter Bro Universal Hashing (англ.) (PDF). Архивировано 24 июня 2009 года. - ↑ Шнайер, 2002.
- ↑ Wolfson, H.J. & Rigoutsos, I (1997). Geometric Hashing: An Overview. IEEE Computational Science and Engineering, 4(4), 10-21.
Литература[править | править код]
- Брюс Шнайер. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. — М.: Триумф, 2002. — ISBN 5-89392-055-4.
- Дональд Кнут. Искусство программирования. Том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е издание. — М.: «Вильямс», 2007. — С. 824. — ISBN 0-201-89685-0.
- Никлаус Вирт. Алгоритмы и структуры данных. — М.: «Мир», 1989. — ISBN 5-03-001045-9.
- Никлаус Вирт. Алгоритмы и структуры данных. Новая версия для Оберона. — М.: «ДМК Пресс», 2010. — ISBN 978-5-94074-584-6.
Ссылки[править | править код]
- Информация по электронной цифровой подписи
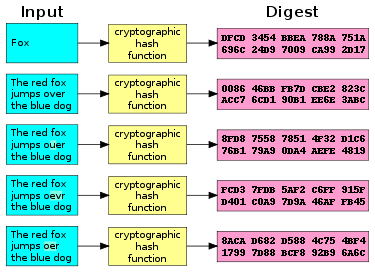
A cryptographic hash function (specifically SHA-1) at work. A small change in the input (in the word “over”) drastically changes the output (digest). This is the so-called avalanche effect.
| Secure Hash Algorithms |
|---|
| Concepts |
| hash functions · SHA · DSA |
| Main standards |
| SHA-0 · SHA-1 · SHA-2 · SHA-3
|
|
A cryptographic hash function (CHF) is a hash algorithm (a map of an arbitrary binary string to a binary string with fixed size of 
Cryptographic hash functions have many information-security applications, notably in digital signatures, message authentication codes (MACs), and other forms of authentication. They can also be used as ordinary hash functions, to index data in hash tables, for fingerprinting, to detect duplicate data or uniquely identify files, and as checksums to detect accidental data corruption. Indeed, in information-security contexts, cryptographic hash values are sometimes called (digital) fingerprints, checksums, or just hash values, even though all these terms stand for more general functions with rather different properties and purposes.[2]
Noncryptographic hashes are used in hash tables and to detect accidental errors, their construction frequently provides no resistance to a deliberate attack. For example, a denial-of-service attack on hash tables is possible if the collisions are easy to find, like in the case of linear cyclic redundancy check (CRC) functions.[3]
Properties[edit]
Most cryptographic hash functions are designed to take a string of any length as input and produce a fixed-length hash value.
A cryptographic hash function must be able to withstand all known types of cryptanalytic attack. In theoretical cryptography, the security level of a cryptographic hash function has been defined using the following properties:
- Pre-image resistance
- Given a hash value h, it should be difficult to find any message m such that h = hash(m). This concept is related to that of a one-way function. Functions that lack this property are vulnerable to preimage attacks.
- Second pre-image resistance
- Given an input m1, it should be difficult to find a different input m2 such that hash(m1) = hash(m2). This property is sometimes referred to as weak collision resistance. Functions that lack this property are vulnerable to second-preimage attacks.
- Collision resistance
- It should be difficult to find two different messages m1 and m2 such that hash(m1) = hash(m2). Such a pair is called a cryptographic hash collision. This property is sometimes referred to as strong collision resistance. It requires a hash value at least twice as long as that required for pre-image resistance; otherwise collisions may be found by a birthday attack.[4]
Collision resistance implies second pre-image resistance but does not imply pre-image resistance.[5] The weaker assumption is always preferred in theoretical cryptography, but in practice, a hash-function which is only second pre-image resistant is considered insecure and is therefore not recommended for real applications.
Informally, these properties mean that a malicious adversary cannot replace or modify the input data without changing its digest. Thus, if two strings have the same digest, one can be very confident that they are identical. Second pre-image resistance prevents an attacker from crafting a document with the same hash as a document the attacker cannot control. Collision resistance prevents an attacker from creating two distinct documents with the same hash.
A function meeting these criteria may still have undesirable properties. Currently, popular cryptographic hash functions are vulnerable to length-extension attacks: given hash(m) and len(m) but not m, by choosing a suitable m′ an attacker can calculate hash(m ∥ m′), where ∥ denotes concatenation.[6] This property can be used to break naive authentication schemes based on hash functions. The HMAC construction works around these problems.
In practice, collision resistance is insufficient for many practical uses. In addition to collision resistance, it should be impossible for an adversary to find two messages with substantially similar digests; or to infer any useful information about the data, given only its digest. In particular, a hash function should behave as much as possible like a random function (often called a random oracle in proofs of security) while still being deterministic and efficiently computable. This rules out functions like the SWIFFT function, which can be rigorously proven to be collision-resistant assuming that certain problems on ideal lattices are computationally difficult, but, as a linear function, does not satisfy these additional properties.[7]
Checksum algorithms, such as CRC32 and other cyclic redundancy checks, are designed to meet much weaker requirements and are generally unsuitable as cryptographic hash functions. For example, a CRC was used for message integrity in the WEP encryption standard, but an attack was readily discovered, which exploited the linearity of the checksum.
Degree of difficulty[edit]
In cryptographic practice, “difficult” generally means “almost certainly beyond the reach of any adversary who must be prevented from breaking the system for as long as the security of the system is deemed important”. The meaning of the term is therefore somewhat dependent on the application since the effort that a malicious agent may put into the task is usually proportional to their expected gain. However, since the needed effort usually multiplies with the digest length, even a thousand-fold advantage in processing power can be neutralized by adding a dozen bits to the latter.
For messages selected from a limited set of messages, for example passwords or other short messages, it can be feasible to invert a hash by trying all possible messages in the set. Because cryptographic hash functions are typically designed to be computed quickly, special key derivation functions that require greater computing resources have been developed that make such brute-force attacks more difficult.
In some theoretical analyses “difficult” has a specific mathematical meaning, such as “not solvable in asymptotic polynomial time”. Such interpretations of difficulty are important in the study of provably secure cryptographic hash functions but do not usually have a strong connection to practical security. For example, an exponential-time algorithm can sometimes still be fast enough to make a feasible attack. Conversely, a polynomial-time algorithm (e.g., one that requires n20 steps for n-digit keys) may be too slow for any practical use.
Illustration[edit]
When a user creates an account on a website, they are typically asked to create a password. Rather than storing the password in plain text, which would make it vulnerable to theft in the event of a data breach, the website will typically use a cryptographic hash function to generate a unique hash of the password.
An illustration of the potential use of a cryptographic hash is as follows: Alice poses a tough math problem to Bob and claims that she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, computes its hash, and tells Bob the hash value (whilst keeping the solution secret). Then, when Bob comes up with the solution himself a few days later, Alice can prove that she had the solution earlier by revealing it and having Bob hash it and check that it matches the hash value given to him before. (This is an example of a simple commitment scheme; in actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution.)
Applications[edit]
Verifying the integrity of messages and files[edit]
An important application of secure hashes is the verification of message integrity. Comparing message digests (hash digests over the message) calculated before, and after, transmission can determine whether any changes have been made to the message or file.
MD5, SHA-1, or SHA-2 hash digests are sometimes published on websites or forums to allow verification of integrity for downloaded files,[8] including files retrieved using file sharing such as mirroring. This practice establishes a chain of trust as long as the hashes are posted on a trusted site – usually the originating site – authenticated by HTTPS. Using a cryptographic hash and a chain of trust detects malicious changes to the file. Non-cryptographic error-detecting codes such as cyclic redundancy checks only prevent against non-malicious alterations of the file, since an intentional spoof can readily be crafted to have the colliding code value.
Signature generation and verification[edit]
Almost all digital signature schemes require a cryptographic hash to be calculated over the message. This allows the signature calculation to be performed on the relatively small, statically sized hash digest. The message is considered authentic if the signature verification succeeds given the signature and recalculated hash digest over the message. So the message integrity property of the cryptographic hash is used to create secure and efficient digital signature schemes.
Password verification[edit]
Password verification commonly relies on cryptographic hashes. Storing all user passwords as cleartext can result in a massive security breach if the password file is compromised. One way to reduce this danger is to only store the hash digest of each password. To authenticate a user, the password presented by the user is hashed and compared with the stored hash. A password reset method is required when password hashing is performed; original passwords cannot be recalculated from the stored hash value.
Standard cryptographic hash functions are designed to be computed quickly, and, as a result, it is possible to try guessed passwords at high rates. Common graphics processing units can try billions of possible passwords each second. Password hash functions that perform key stretching – such as PBKDF2, scrypt or Argon2 – commonly use repeated invocations of a cryptographic hash to increase the time (and in some cases computer memory) required to perform brute-force attacks on stored password hash digests. A password hash requires the use of a large random, non-secret salt value which can be stored with the password hash. The salt randomizes the output of the password hash, making it impossible for an adversary to store tables of passwords and precomputed hash values to which the password hash digest can be compared.
Proof-of-work[edit]
A proof-of-work system (or protocol, or function) is an economic measure to deter denial-of-service attacks and other service abuses such as spam on a network by requiring some work from the service requester, usually meaning processing time by a computer. A key feature of these schemes is their asymmetry: the work must be moderately hard (but feasible) on the requester side but easy to check for the service provider. One popular system – used in Bitcoin mining and Hashcash – uses partial hash inversions to prove that work was done, to unlock a mining reward in Bitcoin, and as a good-will token to send an e-mail in Hashcash. The sender is required to find a message whose hash value begins with a number of zero bits. The average work that the sender needs to perform in order to find a valid message is exponential in the number of zero bits required in the hash value, while the recipient can verify the validity of the message by executing a single hash function. For instance, in Hashcash, a sender is asked to generate a header whose 160-bit SHA-1 hash value has the first 20 bits as zeros. The sender will, on average, have to try 219 times to find a valid header.
File or data identifier[edit]
A message digest can also serve as a means of reliably identifying a file; several source code management systems, including Git, Mercurial and Monotone, use the sha1sum of various types of content (file content, directory trees, ancestry information, etc.) to uniquely identify them. Hashes are used to identify files on peer-to-peer filesharing networks. For example, in an ed2k link, an MD4-variant hash is combined with the file size, providing sufficient information for locating file sources, downloading the file, and verifying its contents. Magnet links are another example. Such file hashes are often the top hash of a hash list or a hash tree which allows for additional benefits.
One of the main applications of a hash function is to allow the fast look-up of data in a hash table. Being hash functions of a particular kind, cryptographic hash functions lend themselves well to this application too.
However, compared with standard hash functions, cryptographic hash functions tend to be much more expensive computationally. For this reason, they tend to be used in contexts where it is necessary for users to protect themselves against the possibility of forgery (the creation of data with the same digest as the expected data) by potentially malicious participants.[citation needed]
Content-addressable storage[edit]
Content-addressable storage (CAS), also referred to as content-addressed storage or fixed-content storage, is a way to store information so it can be retrieved based on its content, not its name or location. It has been used for high-speed storage and retrieval of fixed content, such as documents stored for compliance with government regulations. Content-addressable storage is similar to content-addressable memory.
CAS systems work by passing the content of the file through a cryptographic hash function to generate a unique key, the “content address”. The file system’s directory stores these addresses and a pointer to the physical storage of the content. Because an attempt to store the same file will generate the same key, CAS systems ensure that the files within them are unique, and because changing the file will result in a new key, CAS systems provide assurance that the file is unchanged.
CAS became a significant market during the 2000s, especially after the introduction of the 2002 Sarbanes–Oxley Act which required the storage of enormous numbers of documents for long periods and retrieved only rarely. Ever-increasing performance of traditional file systems and new software systems have eroded the value of legacy CAS systems, which have become increasingly rare after roughly 2018. However, the principles of content addressability continue to be of great interest to computer scientists, and form the core of numerous emerging technologies, such as peer-to-peer file sharing, cryptocurrencies, and distributed computing.
Hash functions based on block ciphers[edit]
There are several methods to use a block cipher to build a cryptographic hash function, specifically a one-way compression function.
The methods resemble the block cipher modes of operation usually used for encryption. Many well-known hash functions, including MD4, MD5, SHA-1 and SHA-2, are built from block-cipher-like components designed for the purpose, with feedback to ensure that the resulting function is not invertible. SHA-3 finalists included functions with block-cipher-like components (e.g., Skein, BLAKE) though the function finally selected, Keccak, was built on a cryptographic sponge instead.
A standard block cipher such as AES can be used in place of these custom block ciphers; that might be useful when an embedded system needs to implement both encryption and hashing with minimal code size or hardware area. However, that approach can have costs in efficiency and security. The ciphers in hash functions are built for hashing: they use large keys and blocks, can efficiently change keys every block, and have been designed and vetted for resistance to related-key attacks. General-purpose ciphers tend to have different design goals. In particular, AES has key and block sizes that make it nontrivial to use to generate long hash values; AES encryption becomes less efficient when the key changes each block; and related-key attacks make it potentially less secure for use in a hash function than for encryption.
Hash function design[edit]
Merkle–Damgård construction[edit]
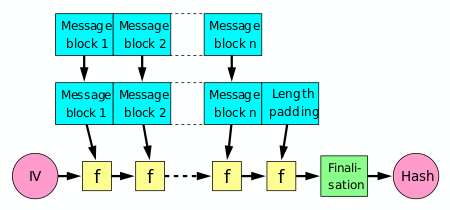
The Merkle–Damgård hash construction
A hash function must be able to process an arbitrary-length message into a fixed-length output. This can be achieved by breaking the input up into a series of equally sized blocks, and operating on them in sequence using a one-way compression function. The compression function can either be specially designed for hashing or be built from a block cipher. A hash function built with the Merkle–Damgård construction is as resistant to collisions as is its compression function; any collision for the full hash function can be traced back to a collision in the compression function.
The last block processed should also be unambiguously length padded; this is crucial to the security of this construction. This construction is called the Merkle–Damgård construction. Most common classical hash functions, including SHA-1 and MD5, take this form.
Wide pipe versus narrow pipe[edit]
A straightforward application of the Merkle–Damgård construction, where the size of hash output is equal to the internal state size (between each compression step), results in a narrow-pipe hash design. This design causes many inherent flaws, including length-extension, multicollisions,[9] long message attacks,[10] generate-and-paste attacks,[citation needed] and also cannot be parallelized. As a result, modern hash functions are built on wide-pipe constructions that have a larger internal state size – which range from tweaks of the Merkle–Damgård construction[9] to new constructions such as the sponge construction and HAIFA construction.[11] None of the entrants in the NIST hash function competition use a classical Merkle–Damgård construction.[12]
Meanwhile, truncating the output of a longer hash, such as used in SHA-512/256, also defeats many of these attacks.[13]
Use in building other cryptographic primitives[edit]
Hash functions can be used to build other cryptographic primitives. For these other primitives to be cryptographically secure, care must be taken to build them correctly.
Message authentication codes (MACs) (also called keyed hash functions) are often built from hash functions. HMAC is such a MAC.
Just as block ciphers can be used to build hash functions, hash functions can be used to build block ciphers. Luby-Rackoff constructions using hash functions can be provably secure if the underlying hash function is secure. Also, many hash functions (including SHA-1 and SHA-2) are built by using a special-purpose block cipher in a Davies–Meyer or other construction. That cipher can also be used in a conventional mode of operation, without the same security guarantees; for example, SHACAL, BEAR and LION.
Pseudorandom number generators (PRNGs) can be built using hash functions. This is done by combining a (secret) random seed with a counter and hashing it.
Some hash functions, such as Skein, Keccak, and RadioGatún, output an arbitrarily long stream and can be used as a stream cipher, and stream ciphers can also be built from fixed-length digest hash functions. Often this is done by first building a cryptographically secure pseudorandom number generator and then using its stream of random bytes as keystream. SEAL is a stream cipher that uses SHA-1 to generate internal tables, which are then used in a keystream generator more or less unrelated to the hash algorithm. SEAL is not guaranteed to be as strong (or weak) as SHA-1. Similarly, the key expansion of the HC-128 and HC-256 stream ciphers makes heavy use of the SHA-256 hash function.
Concatenation[edit]
Concatenating outputs from multiple hash functions provide collision resistance as good as the strongest of the algorithms included in the concatenated result.[citation needed] For example, older versions of Transport Layer Security (TLS) and Secure Sockets Layer (SSL) used concatenated MD5 and SHA-1 sums.[14][15] This ensures that a method to find collisions in one of the hash functions does not defeat data protected by both hash functions.[citation needed]
For Merkle–Damgård construction hash functions, the concatenated function is as collision-resistant as its strongest component, but not more collision-resistant.[citation needed] Antoine Joux observed that 2-collisions lead to n-collisions: if it is feasible for an attacker to find two messages with the same MD5 hash, then they can find as many additional messages with that same MD5 hash as they desire, with no greater difficulty.[16] Among those n messages with the same MD5 hash, there is likely to be a collision in SHA-1. The additional work needed to find the SHA-1 collision (beyond the exponential birthday search) requires only polynomial time.[17][18]
Cryptographic hash algorithms[edit]
There are many cryptographic hash algorithms; this section lists a few algorithms that are referenced relatively often. A more extensive list can be found on the page containing a comparison of cryptographic hash functions.
MD5[edit]
Main article: MD5
MD5 was designed by Ronald Rivest in 1991 to replace an earlier hash function, MD4, and was specified in 1992 as RFC 1321. Collisions against MD5 can be calculated within seconds which makes the algorithm unsuitable for most use cases where a cryptographic hash is required. MD5 produces a digest of 128 bits (16 bytes).
SHA-1[edit]
SHA-1 was developed as part of the U.S. Government’s Capstone project. The original specification – now commonly called SHA-0 – of the algorithm was published in 1993 under the title Secure Hash Standard, FIPS PUB 180, by U.S. government standards agency NIST (National Institute of Standards and Technology). It was withdrawn by the NSA shortly after publication and was superseded by the revised version, published in 1995 in FIPS PUB 180-1 and commonly designated SHA-1. Collisions against the full SHA-1 algorithm can be produced using the shattered attack and the hash function should be considered broken. SHA-1 produces a hash digest of 160 bits (20 bytes).
Documents may refer to SHA-1 as just “SHA”, even though this may conflict with the other Secure Hash Algorithms such as SHA-0, SHA-2, and SHA-3.
RIPEMD-160[edit]
RIPEMD (RACE Integrity Primitives Evaluation Message Digest) is a family of cryptographic hash functions developed in Leuven, Belgium, by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel at the COSIC research group at the Katholieke Universiteit Leuven, and first published in 1996. RIPEMD was based upon the design principles used in MD4 and is similar in performance to the more popular SHA-1. RIPEMD-160 has, however, not been broken. As the name implies, RIPEMD-160 produces a hash digest of 160 bits (20 bytes).
Whirlpool[edit]
Whirlpool is a cryptographic hash function designed by Vincent Rijmen and Paulo S. L. M. Barreto, who first described it in 2000. Whirlpool is based on a substantially modified version of the Advanced Encryption Standard (AES). Whirlpool produces a hash digest of 512 bits (64 bytes).
SHA-2[edit]
SHA-2 (Secure Hash Algorithm 2) is a set of cryptographic hash functions designed by the United States National Security Agency (NSA), first published in 2001. They are built using the Merkle–Damgård structure, from a one-way compression function itself built using the Davies–Meyer structure from a (classified) specialized block cipher.
SHA-2 basically consists of two hash algorithms: SHA-256 and SHA-512. SHA-224 is a variant of SHA-256 with different starting values and truncated output. SHA-384 and the lesser-known SHA-512/224 and SHA-512/256 are all variants of SHA-512. SHA-512 is more secure than SHA-256 and is commonly faster than SHA-256 on 64-bit machines such as AMD64.
The output size in bits is given by the extension to the “SHA” name, so SHA-224 has an output size of 224 bits (28 bytes); SHA-256, 32 bytes; SHA-384, 48 bytes; and SHA-512, 64 bytes.
SHA-3[edit]
SHA-3 (Secure Hash Algorithm 3) was released by NIST on August 5, 2015. SHA-3 is a subset of the broader cryptographic primitive family Keccak. The Keccak algorithm is the work of Guido Bertoni, Joan Daemen, Michael Peeters, and Gilles Van Assche. Keccak is based on a sponge construction which can also be used to build other cryptographic primitives such as a stream cipher. SHA-3 provides the same output sizes as SHA-2: 224, 256, 384, and 512 bits.
Configurable output sizes can also be obtained using the SHAKE-128 and SHAKE-256 functions. Here the -128 and -256 extensions to the name imply the security strength of the function rather than the output size in bits.
BLAKE2[edit]
BLAKE2, an improved version of BLAKE, was announced on December 21, 2012. It was created by Jean-Philippe Aumasson, Samuel Neves, Zooko Wilcox-O’Hearn, and Christian Winnerlein with the goal of replacing the widely used but broken MD5 and SHA-1 algorithms. When run on 64-bit x64 and ARM architectures, BLAKE2b is faster than SHA-3, SHA-2, SHA-1, and MD5. Although BLAKE and BLAKE2 have not been standardized as SHA-3 has, BLAKE2 has been used in many protocols including the Argon2 password hash, for the high efficiency that it offers on modern CPUs. As BLAKE was a candidate for SHA-3, BLAKE and BLAKE2 both offer the same output sizes as SHA-3 – including a configurable output size.
BLAKE3[edit]
BLAKE3, an improved version of BLAKE2, was announced on January 9, 2020. It was created by Jack O’Connor, Jean-Philippe Aumasson, Samuel Neves, and Zooko Wilcox-O’Hearn. BLAKE3 is a single algorithm, in contrast to BLAKE and BLAKE2, which are algorithm families with multiple variants. The BLAKE3 compression function is closely based on that of BLAKE2s, with the biggest difference being that the number of rounds is reduced from 10 to 7. Internally, BLAKE3 is a Merkle tree, and it supports higher degrees of parallelism than BLAKE2.
Attacks on cryptographic hash algorithms[edit]
There is a long list of cryptographic hash functions but many have been found to be vulnerable and should not be used. For instance, NIST selected 51 hash functions[19] as candidates for round 1 of the SHA-3 hash competition, of which 10 were considered broken and 16 showed significant weaknesses and therefore did not make it to the next round; more information can be found on the main article about the NIST hash function competitions.
Even if a hash function has never been broken, a successful attack against a weakened variant may undermine the experts’ confidence. For instance, in August 2004 collisions were found in several then-popular hash functions, including MD5.[20] These weaknesses called into question the security of stronger algorithms derived from the weak hash functions – in particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128, and RIPEMD-160 (both strengthened versions of RIPEMD).[21]
On August 12, 2004, Joux, Carribault, Lemuel, and Jalby announced a collision for the full SHA-0 algorithm.[16] Joux et al. accomplished this using a generalization of the Chabaud and Joux attack. They found that the collision had complexity 251 and took about 80,000 CPU hours on a supercomputer with 256 Itanium 2 processors – equivalent to 13 days of full-time use of the supercomputer.[citation needed]
In February 2005, an attack on SHA-1 was reported that would find collision in about 269 hashing operations, rather than the 280 expected for a 160-bit hash function. In August 2005, another attack on SHA-1 was reported that would find collisions in 263 operations. Other theoretical weaknesses of SHA-1 have been known:[22][23] and in February 2017 Google announced a collision in SHA-1.[24] Security researchers recommend that new applications can avoid these problems by using later members of the SHA family, such as SHA-2, or using techniques such as randomized hashing[25] that do not require collision resistance.
A successful, practical attack broke MD5 used within certificates for Transport Layer Security in 2008.[26]
Many cryptographic hashes are based on the Merkle–Damgård construction. All cryptographic hashes that directly use the full output of a Merkle–Damgård construction are vulnerable to length extension attacks. This makes the MD5, SHA-1, RIPEMD-160, Whirlpool, and the SHA-256 / SHA-512 hash algorithms all vulnerable to this specific attack. SHA-3, BLAKE2, BLAKE3, and the truncated SHA-2 variants are not vulnerable to this type of attack.[citation needed]
Attacks on hashed passwords[edit]
A common use of hashes is to store password authentication data. Rather than store the plaintext of user passwords, a controlled access system stores the hash of each user’s password in a file or database. When someone requests access, the password they submit is hashed and compared with the stored value. If the database is stolen (an all too frequent occurrence[27]), the thief will only have the hash values, not the passwords.
However, most people choose passwords in predictable ways. Lists of common passwords are widely circulated and many passwords are short enough that all possible combinations can be tested if fast hashes are used.[28]
The use of cryptographic salt prevents some attacks, such as building files of precomputing hash values, e.g. rainbow tables. But searches on the order of 100 billion tests per second are possible with high-end graphics processors, making direct attacks possible even with salt.[29]
[30]
The United States National Institute of Standards and Technology recommends storing passwords using special hashes called key derivation functions (KDFs) that have been created to slow brute force searches.[31]: 5.1.1.2 Slow hashes include pbkdf2, bcrypt, scrypt, argon2, Balloon and some recent modes of Unix crypt. For KSFs that perform multiple hashes to slow execution, NIST recommends an iteration count of 10,000 or more.[31]: 5.1.1.2
See also[edit]
- Avalanche effect
- Comparison of cryptographic hash functions
- Cryptographic agility
- CRYPTREC
- File fixity
- HMAC
- Hash chain
- Length extension attack
- MD5CRK
- Message authentication code
- NESSIE
- PGP word list
- Random oracle
- Security of cryptographic hash functions
- SHA-3
- Universal one-way hash function
References[edit]
Citations[edit]
- ^ Menezes, van Oorschot & Vanstone 2018, p. 33.
- ^ Schneier, Bruce. “Cryptanalysis of MD5 and SHA: Time for a New Standard”. Computerworld. Archived from the original on 2016-03-16. Retrieved 2016-04-20.
Much more than encryption algorithms, one-way hash functions are the workhorses of modern cryptography.
- ^ Aumasson 2017, p. 106.
- ^ Katz & Lindell 2014, pp. 155–157, 190, 232.
- ^ Rogaway & Shrimpton 2004, in Sec. 5. Implications.
- ^ Duong, Thai; Rizzo, Juliano. “Flickr’s API Signature Forgery Vulnerability”.
- ^ Lyubashevsky et al. 2008, pp. 54–72.
- ^ Perrin, Chad (December 5, 2007). “Use MD5 hashes to verify software downloads”. TechRepublic. Retrieved March 2, 2013.
- ^ a b Lucks, Stefan (2004). “Design Principles for Iterated Hash Functions”. Cryptology ePrint Archive. Report 2004/253.
- ^ Kelsey & Schneier 2005, pp. 474–490.
- ^ Biham, Eli; Dunkelman, Orr (24 August 2006). A Framework for Iterative Hash Functions – HAIFA. Second NIST Cryptographic Hash Workshop. Cryptology ePrint Archive. Report 2007/278.
- ^ Nandi & Paul 2010.
- ^ Dobraunig, Christoph; Eichlseder, Maria; Mendel, Florian (February 2015). Security Evaluation of SHA-224, SHA-512/224, and SHA-512/256 (PDF) (Report).
- ^ Mendel et al., p. 145:Concatenating … is often used by implementors to “hedge bets” on hash functions. A combiner of the form MD5
- ^ Harnik et al. 2005, p. 99: the concatenation of hash functions as suggested in the TLS… is guaranteed to be as secure as the candidate that remains secure.
- ^ a b Joux 2004.
- ^ Finney, Hal (August 20, 2004). “More Problems with Hash Functions”. The Cryptography Mailing List. Archived from the original on April 9, 2016. Retrieved May 25, 2016.
- ^ Hoch & Shamir 2008, pp. 616–630.
- ^ Andrew Regenscheid, Ray Perlner, Shu-Jen Chang, John Kelsey, Mridul Nandi, Souradyuti Paul, Status Report on the First Round of the SHA-3 Cryptographic Hash Algorithm Competition
- ^ XiaoyunWang, Dengguo Feng, Xuejia Lai, Hongbo Yu, Collisions for Hash Functions MD4, MD5, HAVAL-128, and RIPEMD
- ^ Alshaikhli, Imad Fakhri; AlAhmad, Mohammad Abdulateef (2015), “Cryptographic Hash Function”, Handbook of Research on Threat Detection and Countermeasures in Network Security, IGI Global, pp. 80–94, doi:10.4018/978-1-4666-6583-5.ch006, ISBN 978-1-4666-6583-5
- ^ Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu, Finding Collisions in the Full SHA-1
- ^ Bruce Schneier, Cryptanalysis of SHA-1 (summarizes Wang et al. results and their implications)
- ^ Fox-Brewster, Thomas. “Google Just ‘Shattered’ An Old Crypto Algorithm – Here’s Why That’s Big For Web Security”. Forbes. Retrieved 2017-02-24.
- ^ Shai Halevi and Hugo Krawczyk, Randomized Hashing and Digital Signatures
- ^ Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, MD5 considered harmful today: Creating a rogue CA certificate, accessed March 29, 2009.
- ^ Swinhoe, Dan (April 17, 2020). “The 15 biggest data breaches of the 21st century”. CSO Magazine.
- ^ Goodin, Dan (2012-12-10). “25-GPU cluster cracks every standard Windows password in <6 hours”. Ars Technica. Retrieved 2020-11-23.
- ^ Claburn, Thomas (February 14, 2019). “Use an 8-char Windows NTLM password? Don’t. Every single one can be cracked in under 2.5hrs”. www.theregister.co.uk. Retrieved 2020-11-26.
- ^ “Mind-blowing GPU performance”. Improsec. January 3, 2020.
- ^ a b Grassi Paul A. (June 2017). SP 800-63B-3 – Digital Identity Guidelines, Authentication and Lifecycle Management. NIST. doi:10.6028/NIST.SP.800-63b.
Sources[edit]
- Harnik, Danny; Kilian, Joe; Naor, Moni; Reingold, Omer; Rosen, Alon (2005). “On Robust Combiners for Oblivious Transfer and Other Primitives”. Advances in Cryptology – EUROCRYPT 2005. Lecture Notes in Computer Science. Vol. 3494. pp. 96–113. doi:10.1007/11426639_6. ISBN 978-3-540-25910-7. ISSN 0302-9743.
- Hoch, Jonathan J.; Shamir, Adi (2008). “On the Strength of the Concatenated Hash Combiner When All the Hash Functions Are Weak”. Automata, Languages and Programming. Lecture Notes in Computer Science. Vol. 5126. pp. 616–630. doi:10.1007/978-3-540-70583-3_50. ISBN 978-3-540-70582-6. ISSN 0302-9743.
- Joux, Antoine (2004). “Multicollisions in Iterated Hash Functions. Application to Cascaded Constructions”. Advances in Cryptology – CRYPTO 2004. Lecture Notes in Computer Science. Vol. 3152. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 306–316. doi:10.1007/978-3-540-28628-8_19. ISBN 978-3-540-22668-0. ISSN 0302-9743.
- Kelsey, John; Schneier, Bruce (2005). “Second Preimages on n-Bit Hash Functions for Much Less than 2 n Work”. Advances in Cryptology – EUROCRYPT 2005. Lecture Notes in Computer Science. Vol. 3494. pp. 474–490. doi:10.1007/11426639_28. ISBN 978-3-540-25910-7. ISSN 0302-9743.
- Katz, Jonathan; Lindell, Yehuda (2014). Introduction to Modern Cryptography (2nd ed.). CRC Press. ISBN 978-1-4665-7026-9.
- Lyubashevsky, Vadim; Micciancio, Daniele; Peikert, Chris; Rosen, Alon (2008). “SWIFFT: A Modest Proposal for FFT Hashing”. Fast Software Encryption. Lecture Notes in Computer Science. Vol. 5086. pp. 54–72. doi:10.1007/978-3-540-71039-4_4. ISBN 978-3-540-71038-7. ISSN 0302-9743.
- Mendel, Florian; Rechberger, Christian; Schläffer, Martin (2009). “MD5 Is Weaker Than Weak: Attacks on Concatenated Combiners”. Advances in Cryptology – ASIACRYPT 2009. Lecture Notes in Computer Science. Vol. 5912. pp. 144–161. doi:10.1007/978-3-642-10366-7_9. ISBN 978-3-642-10365-0. ISSN 0302-9743.
- Nandi, Mridul; Paul, Souradyuti (2010). “Speeding Up the Wide-Pipe: Secure and Fast Hashing”. Progress in Cryptology – INDOCRYPT 2010. Lecture Notes in Computer Science. Vol. 6498. pp. 144–162. doi:10.1007/978-3-642-17401-8_12. ISBN 978-3-642-17400-1. ISSN 0302-9743.
- Rogaway, P.; Shrimpton, T. (2004). “Cryptographic Hash-Function Basics: Definitions, Implications, and Separations for Preimage Resistance, Second-Preimage Resistance, and Collision Resistance”. In Roy, B.; Mier, W. (eds.). Fast Software Encryption: 11th International Workshop, FSE 2004. Vol. 3017. Lecture Notes in Computer Science: Springer. pp. 371–388. ISBN 3-540-22171-9.
- Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (7 December 2018). “Hash functions”. Handbook of Applied Cryptography. CRC Press. pp. 33–. ISBN 978-0-429-88132-9.
- Aumasson, Jean-Philippe (6 November 2017). Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press. ISBN 978-1-59327-826-7. OCLC 1012843116.
External links[edit]
- Paar, Christof; Pelzl, Jan (2009). “11: Hash Functions”. Understanding Cryptography, A Textbook for Students and Practitioners. Springer. Archived from the original on 2012-12-08. (companion web site contains online cryptography course that covers hash functions)
- “The ECRYPT Hash Function Website”.
- Buldas, A. (2011). “Series of mini-lectures about cryptographic hash functions”. Archived from the original on 2012-12-06.
- Open source python based application with GUI used to verify downloads.
Хеш-функции чрезвычайно полезны и появляются практически во всех приложениях информационной безопасности.
Хеш-функция – это математическая функция, которая преобразует числовое входное значение в другое сжатое числовое значение. Входные данные для хеш-функции имеют произвольную длину, но выходные данные всегда имеют фиксированную длину.
Значения, возвращаемые хэш-функцией, называются дайджестом сообщения или просто хэш-значениями . На следующем рисунке проиллюстрирована хеш-функция –
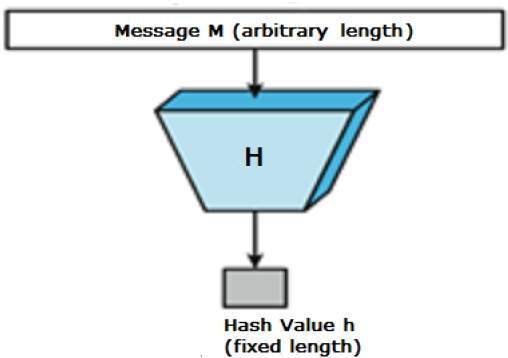
Особенности хеш-функций
Типичные особенности хеш-функций –
-
Выход фиксированной длины (значение хэша)
-
Хэш-функция охватывает данные произвольной длины до фиксированной длины. Этот процесс часто называют хэшированием данных .
-
В общем, хеш намного меньше, чем входные данные, поэтому хеш-функции иногда называют функциями сжатия .
-
Поскольку хэш представляет собой меньшее представление больших данных, его также называют дайджестом .
-
Хеш-функция с n-битным выходом называется n-битной хеш-функцией . Популярные хеш-функции генерируют значения от 160 до 512 бит.
-
-
Эффективность операции
-
Обычно для любой хеш-функции h с входом x вычисление h (x) является быстрой операцией.
-
Вычислительные хеш-функции намного быстрее, чем симметричное шифрование.
-
Выход фиксированной длины (значение хэша)
Хэш-функция охватывает данные произвольной длины до фиксированной длины. Этот процесс часто называют хэшированием данных .
В общем, хеш намного меньше, чем входные данные, поэтому хеш-функции иногда называют функциями сжатия .
Поскольку хэш представляет собой меньшее представление больших данных, его также называют дайджестом .
Хеш-функция с n-битным выходом называется n-битной хеш-функцией . Популярные хеш-функции генерируют значения от 160 до 512 бит.
Эффективность операции
Обычно для любой хеш-функции h с входом x вычисление h (x) является быстрой операцией.
Вычислительные хеш-функции намного быстрее, чем симметричное шифрование.
Свойства хеш-функций
Чтобы быть эффективным криптографическим инструментом, желательно, чтобы хеш-функция обладала следующими свойствами:
-
Сопротивление до изображения
-
Это свойство означает, что в вычислительном отношении должно быть трудно перевернуть хеш-функцию.
-
Другими словами, если хеш-функция h создала хеш-значение z, то будет трудно найти любое входное значение x, которое хэширует к z.
-
Это свойство защищает от злоумышленника, который имеет только хэш-значение и пытается найти входные данные.
-
-
Сопротивление второго изображения
-
Это свойство означает, что заданы входные данные и их хэш, должно быть трудно найти другой входной файл с тем же хешем.
-
Другими словами, если хеш-функция h для входа x создает хеш-значение h (x), то должно быть трудно найти любое другое входное значение y такое, что h (y) = h (x).
-
Это свойство хэш-функции защищает от злоумышленника, у которого есть входное значение и его хэш, и он хочет заменить другое значение допустимым значением вместо исходного входного значения.
-
-
Сопротивление столкновению
-
Это свойство означает, что должно быть трудно найти два разных входа любой длины, которые приводят к одному и тому же хешу. Это свойство также называется хеш-функцией без столкновений.
-
Другими словами, для хеш-функции h трудно найти любые два различных входа x и y, для которых h (x) = h (y).
-
Поскольку хеш-функция является функцией сжатия с фиксированной длиной хеш-функции, невозможно, чтобы хеш-функция не имела коллизий. Это свойство отсутствия столкновений только подтверждает, что эти столкновения трудно найти.
-
Это свойство очень мешает злоумышленнику найти два входных значения с одинаковым хешем.
-
Кроме того, если хеш-функция устойчива к столкновениям, она является второй устойчивой к изображениям.
-
Сопротивление до изображения
Это свойство означает, что в вычислительном отношении должно быть трудно перевернуть хеш-функцию.
Другими словами, если хеш-функция h создала хеш-значение z, то будет трудно найти любое входное значение x, которое хэширует к z.
Это свойство защищает от злоумышленника, который имеет только хэш-значение и пытается найти входные данные.
Сопротивление второго изображения
Это свойство означает, что заданы входные данные и их хэш, должно быть трудно найти другой входной файл с тем же хешем.
Другими словами, если хеш-функция h для входа x создает хеш-значение h (x), то должно быть трудно найти любое другое входное значение y такое, что h (y) = h (x).
Это свойство хэш-функции защищает от злоумышленника, у которого есть входное значение и его хэш, и он хочет заменить другое значение допустимым значением вместо исходного входного значения.
Сопротивление столкновению
Это свойство означает, что должно быть трудно найти два разных входа любой длины, которые приводят к одному и тому же хешу. Это свойство также называется хеш-функцией без столкновений.
Другими словами, для хеш-функции h трудно найти любые два различных входа x и y, для которых h (x) = h (y).
Поскольку хеш-функция является функцией сжатия с фиксированной длиной хеш-функции, невозможно, чтобы хеш-функция не имела коллизий. Это свойство отсутствия столкновений только подтверждает, что эти столкновения трудно найти.
Это свойство очень мешает злоумышленнику найти два входных значения с одинаковым хешем.
Кроме того, если хеш-функция устойчива к столкновениям, она является второй устойчивой к изображениям.
Разработка алгоритмов хеширования
В основе хеширования лежит математическая функция, которая работает с двумя блоками данных фиксированного размера для создания хеш-кода. Эта хеш-функция является частью алгоритма хеширования.
Размер каждого блока данных варьируется в зависимости от алгоритма. Обычно размеры блоков составляют от 128 до 512 бит. Следующая иллюстрация демонстрирует хэш-функцию –
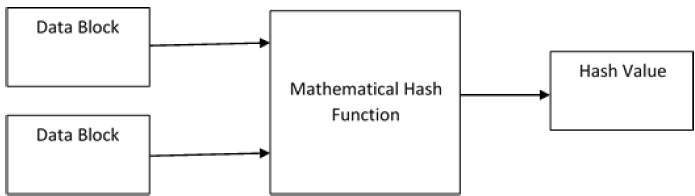
Алгоритм хеширования включает в себя раунды вышеуказанной хеш-функции, такие как блочный шифр. Каждый раунд требует ввода фиксированного размера, обычно это комбинация самого последнего блока сообщения и результата последнего раунда.
Этот процесс повторяется столько раз, сколько требуется для хеширования всего сообщения. Схема алгоритма хеширования изображена на следующей иллюстрации –
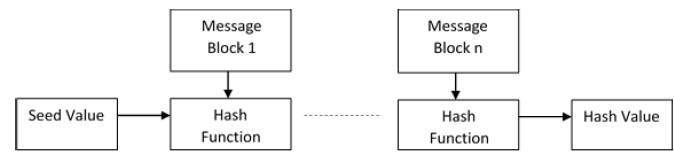
Поскольку значение хеш-функции первого блока сообщений становится входом для второй операции хеширования, выход которой изменяет результат третьей операции, и так далее. Этот эффект известен как лавинный эффект перемешивания.
Лавинный эффект приводит к существенно различающимся значениям хеш-функции для двух сообщений, которые отличаются даже одним битом данных.
Понимать разницу между хэш-функцией и алгоритмом правильно. Хеш-функция генерирует хеш-код, работая с двумя блоками двоичных данных фиксированной длины.
Алгоритм хеширования – это процесс использования хеш-функции, определяющий, как сообщение будет разбито и как результаты предыдущих блоков сообщений объединяются воедино.
Популярные хэш-функции
Давайте кратко рассмотрим некоторые популярные хеш-функции –
Дайджест сообщения (MD)
MD5 был самой популярной и широко используемой хэш-функцией в течение нескольких лет.
-
Семейство MD состоит из хеш-функций MD2, MD4, MD5 и MD6. Он был принят как Интернет-стандарт RFC 1321. Это 128-битная хеш-функция.
-
Дайджесты MD5 широко используются в мире программного обеспечения для обеспечения целостности передаваемого файла. Например, файловые серверы часто предоставляют предварительно вычисленную контрольную сумму MD5 для файлов, чтобы пользователь мог сравнить с ней контрольную сумму загруженного файла.
-
В 2004 году столкновения были обнаружены в MD5. Сообщалось, что аналитическая атака была успешной только через час с использованием компьютерного кластера. Эта атака столкновения привела к взлому MD5 и, следовательно, больше не рекомендуется для использования.
Семейство MD состоит из хеш-функций MD2, MD4, MD5 и MD6. Он был принят как Интернет-стандарт RFC 1321. Это 128-битная хеш-функция.
Дайджесты MD5 широко используются в мире программного обеспечения для обеспечения целостности передаваемого файла. Например, файловые серверы часто предоставляют предварительно вычисленную контрольную сумму MD5 для файлов, чтобы пользователь мог сравнить с ней контрольную сумму загруженного файла.
В 2004 году столкновения были обнаружены в MD5. Сообщалось, что аналитическая атака была успешной только через час с использованием компьютерного кластера. Эта атака столкновения привела к взлому MD5 и, следовательно, больше не рекомендуется для использования.
Безопасная хеш-функция (SHA)
Семейство SHA состоит из четырех алгоритмов SHA; SHA-0, SHA-1, SHA-2 и SHA-3. Хотя из одной семьи, есть структурно разные.
-
Первоначальная версия – SHA-0, 160-битная хеш-функция, была опубликована Национальным институтом стандартов и технологий (NIST) в 1993 году. Она имела несколько слабых мест и не стала очень популярной. Позднее, в 1995 году, SHA-1 был разработан для исправления предполагаемых недостатков SHA-0.
-
SHA-1 является наиболее широко используемым из существующих хеш-функций SHA. Он используется в нескольких широко используемых приложениях и протоколах, включая протокол Secure Socket Layer (SSL).
-
В 2005 году был найден метод для выявления коллизий для SHA-1 в течение практического периода времени, что делает долгосрочную возможность использования SHA-1 сомнительной.
-
Семейство SHA-2 имеет еще четыре варианта SHA: SHA-224, SHA-256, SHA-384 и SHA-512 в зависимости от количества бит в их хэш-значении. О хэш-функции SHA-2 пока не сообщалось об успешных атаках.
-
Хотя SHA-2 – сильная хеш-функция. Хотя существенно отличается, его базовый дизайн все еще следует за дизайном SHA-1. Следовательно, NIST призвал к созданию новых конкурентоспособных конструкций хэш-функций.
-
В октябре 2012 года NIST выбрал алгоритм Keccak в качестве нового стандарта SHA-3. Keccak предлагает множество преимуществ, таких как эффективная производительность и хорошая устойчивость к атакам.
Первоначальная версия – SHA-0, 160-битная хеш-функция, была опубликована Национальным институтом стандартов и технологий (NIST) в 1993 году. Она имела несколько слабых мест и не стала очень популярной. Позднее, в 1995 году, SHA-1 был разработан для исправления предполагаемых недостатков SHA-0.
SHA-1 является наиболее широко используемым из существующих хеш-функций SHA. Он используется в нескольких широко используемых приложениях и протоколах, включая протокол Secure Socket Layer (SSL).
В 2005 году был найден метод для выявления коллизий для SHA-1 в течение практического периода времени, что делает долгосрочную возможность использования SHA-1 сомнительной.
Семейство SHA-2 имеет еще четыре варианта SHA: SHA-224, SHA-256, SHA-384 и SHA-512 в зависимости от количества бит в их хэш-значении. О хэш-функции SHA-2 пока не сообщалось об успешных атаках.
Хотя SHA-2 – сильная хеш-функция. Хотя существенно отличается, его базовый дизайн все еще следует за дизайном SHA-1. Следовательно, NIST призвал к созданию новых конкурентоспособных конструкций хэш-функций.
В октябре 2012 года NIST выбрал алгоритм Keccak в качестве нового стандарта SHA-3. Keccak предлагает множество преимуществ, таких как эффективная производительность и хорошая устойчивость к атакам.
RIPEMD
RIPEND – это аббревиатура для дайджеста сообщения оценки примитивов RACE. Этот набор хеш-функций был разработан открытым исследовательским сообществом и широко известен как семейство европейских хеш-функций.
-
В комплект входят RIPEND, RIPEMD-128 и RIPEMD-160. Также существуют 256 и 320-битные версии этого алгоритма.
-
Оригинальный RIPEMD (128 бит) основан на принципах проектирования, используемых в MD4 и обеспечивает сомнительную безопасность. 128-разрядная версия RIPEMD пришла в качестве быстрой замены для устранения уязвимостей в оригинальной версии RIPEMD.
-
RIPEMD-160 является улучшенной версией и наиболее широко используемой версией в семействе. 256 и 320-битные версии снижают вероятность случайного столкновения, но не имеют более высокого уровня безопасности по сравнению с RIPEMD-128 и RIPEMD-160 соответственно.
В комплект входят RIPEND, RIPEMD-128 и RIPEMD-160. Также существуют 256 и 320-битные версии этого алгоритма.
Оригинальный RIPEMD (128 бит) основан на принципах проектирования, используемых в MD4 и обеспечивает сомнительную безопасность. 128-разрядная версия RIPEMD пришла в качестве быстрой замены для устранения уязвимостей в оригинальной версии RIPEMD.
RIPEMD-160 является улучшенной версией и наиболее широко используемой версией в семействе. 256 и 320-битные версии снижают вероятность случайного столкновения, но не имеют более высокого уровня безопасности по сравнению с RIPEMD-128 и RIPEMD-160 соответственно.
джакузи
Это 512-битная хеш-функция.
-
Он взят из модифицированной версии Advanced Encryption Standard (AES). Одним из дизайнеров был Винсент Раймен, один из создателей AES.
-
Три версии Whirlpool были выпущены; а именно, WHIRLPOOL-0, WHIRLPOOL-T и WHIRLPOOL.
Он взят из модифицированной версии Advanced Encryption Standard (AES). Одним из дизайнеров был Винсент Раймен, один из создателей AES.
Три версии Whirlpool были выпущены; а именно, WHIRLPOOL-0, WHIRLPOOL-T и WHIRLPOOL.
Применение хеш-функций
Существует два непосредственных применения хеш-функции на основе ее криптографических свойств.
Хранение пароля
Хэш-функции обеспечивают защиту для хранения паролей.
-
Вместо того, чтобы хранить пароль в открытом виде, в основном все процессы входа в систему хранят хеш-значения паролей в файле.
-
Файл паролей состоит из таблицы пар в форме (идентификатор пользователя, h (P)).
-
Процесс входа изображен на следующей иллюстрации –
Вместо того, чтобы хранить пароль в открытом виде, в основном все процессы входа в систему хранят хеш-значения паролей в файле.
Файл паролей состоит из таблицы пар в форме (идентификатор пользователя, h (P)).
Процесс входа изображен на следующей иллюстрации –
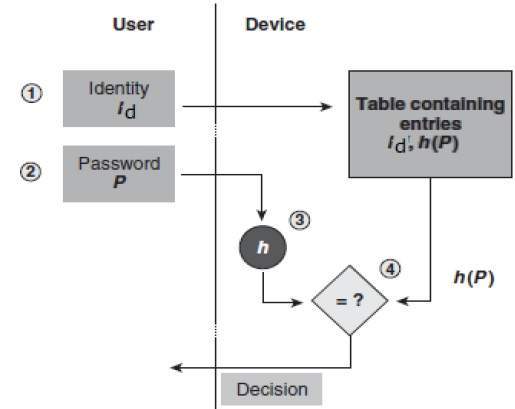
-
Злоумышленник может видеть только хэши паролей, даже если он получил доступ к паролю. Он не может войти в систему с использованием хеш-кода и не может получить пароль из хеш-значения, поскольку хеш-функция обладает свойством сопротивления до изображения.
Злоумышленник может видеть только хэши паролей, даже если он получил доступ к паролю. Он не может войти в систему с использованием хеш-кода и не может получить пароль из хеш-значения, поскольку хеш-функция обладает свойством сопротивления до изображения.
Проверка целостности данных
Проверка целостности данных является наиболее распространенным применением хэш-функций. Он используется для генерации контрольных сумм в файлах данных. Это приложение предоставляет пользователю гарантию правильности данных.
Процесс изображен на следующей иллюстрации –
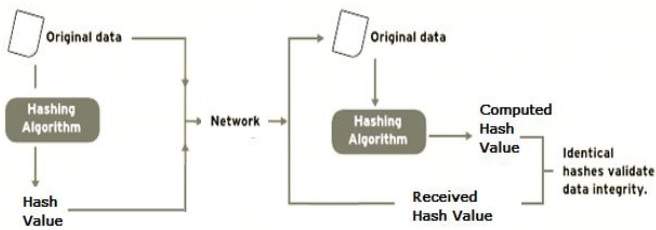
Проверка целостности помогает пользователю обнаружить любые изменения, внесенные в исходный файл. Это, однако, не дает никаких гарантий относительно оригинальности. Злоумышленник, вместо того, чтобы изменять данные файла, может изменить весь файл и вычислить все вместе новый хэш и отправить его получателю. Это приложение проверки целостности полезно, только если пользователь уверен в оригинальности файла.
Привет, Вы узнаете про хеширование, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
хеширование, хэш-функции, криптографическая соль, кукушкино хеширование , настоятельно рекомендую прочитать все из категории Криптография и криптоанализ, Стеганография и Стегоанализ.
Для очень большого количества технологий безопасности (например, аутентификации, ЭЦП) применяются односторонние функции шифрования, называемые также хэш-функциями. Основное назначение подобных функций – получение из сообщения произвольного размера его дайджеста – значения фиксированного размера. Дайджест может быть использован в качестве контрольной суммы исходного сообщения, обеспечивая таким образом (при использовании соответствующего протокола) контроль целостности информации.
Хеш-функция (англ. hash function от hash — «превращать в фарш», «мешанина» ), или функция свертки — функция, осуществляющая преобразование массива входных данных произвольной длины в выходную битовую строку установленной длины, выполняемое определенным алгоритмом. Преобразование, производимое хеш-функцией, называется
хеширование м. Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования называется «хешем», «хеш-кодом», «хеш-суммой», «сводкой сообщения».
Хеш – это своего рода это отражение в искаженном зеркале нейкой информации, по которому практически однозначно можно сравнивать первоисточники (не считая редких коллизий.)
Хеш-функции применяются в следующих случаях:
- при построении ассоциативных массивов;
- при поиске дубликатов в сериях наборов данных;
- при построении уникальных идентификаторов для наборов данных;
- при вычислении контрольных сумм от данных (сигнала) для последующего обнаружения в них ошибок (возникших случайно или внесенных намеренно), возникающих при хранении и/или передаче данных;
- при сохранении паролей в системах защиты в виде хеш-кода (для восстановления пароля по хеш-коду требуется функция, являющаяся обратной по отношению к использованной хеш-функции);
- при выработке электронной подписи (на практике часто подписывается не само сообщение, а его «хеш-образ»);
- и др.
В общем случае (согласно принципу Дирихле) нет однозначного соответствия между хеш-кодом и исходными данными. Возвращаемые хеш-функцией значения менее разнообразны, чем значения входного массива. Случай, при котором хеш-функция преобразует более чем один массив входных данных в одинаковые сводки, называется «коллизией». Вероятность возникновения коллизий используется для оценки качества хеш-функций.
Существует множество алгоритмов хеширования, отличающихся различными свойствами. Примеры свойств:
- разрядность;
- вычислительная сложность;
- криптостойкость.
Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшим примером хеш-функции может служить «обрамление» данных циклическим избыточным кодом (англ. CRC, cyclic redundancy code).
Основные свойства
хэш-функции :
- 1) на вход хэш-функции подается сообщение произвольной длины;
- 2) на выходе хэш-функции формируется блок данных фиксированной длины;
- 3) значения на выходе хэш-функции распределены по равномерному закону;
- 4) при изменении одного бита на входе хэш-функции существенно изменяется выход.
Кроме того, для обеспечения устойчивости хэш-функции к атакам она должна удовлетворять следующим требованиям:
1) если мы знаем значение хэш-функции h, то задача нахождения сообщения M такого, что Н(М)=h, должна быть вычислительно трудной;
2) при заданном сообщении M задача нахождения другого сообщения M’, такого, что Н(М)=H(M’), должна быть вычислительно трудной
Если хэш-функция будет удовлетворять перечисленным свойствам, то формируемое ею значение будет уникально идентифицировать сообщения, и всякая попытка изменения сообщения при передаче будет обнаружена путем выполнения хэширования на принимающей стороне и сравнением с дайджестом, полученным на передающей стороне.
Еще одной особенностью хэш-функций является то, что они не допускают обратного преобразования – получить исходное сообщения по его дайджесту невозможно. Поэтому их называют еще односторонними функциями шифрования.
Хэш-функции строятся по итеративной схеме, когда исходное сообщение разбивается на блоки определенного размера, и над ними выполняются ряд преобразований с использованием как обратимых, так и необратимых операций. Как правило, в состав хэширующего преобразования включается сжимающая функция, поскольку его выход зачастую по размеру меньше блока, подаваемого на вход. На вход каждого цикла хэширования подается выход предыдущего цикла, а также очередной блок сообщения. Таким образом, на каждом цикле выход хэш-функции hi представляет собой хэш первых i блоков.
Если вспомнить, насколько рандомизируют входное сообщение блочные шифры, можно в качестве функции хэш-преобразования использовать какой-нибудь блочный шифр. То, что блочные шифры являются обратимыми преобразованиями, не противоречит свойствам хэш-функции, поскольку блочный шифр необратим по ключу шифрования, и, если в качестве ключа шифрования использовать выход предыдущего шага хэш-преобразования, а в качестве шифруемого сообщения очередной блок сообщения (или наоборот), то можно получить хэш-функцию с хорошими криптографическими характеристиками. Такой подход использован, например, в российском стандарте хэширования – ГОСТ Р 34.11-94. Эта хэш-функция формирует 256-битное выходное значение, используя в качестве преобразующей операции блочный шифр ГОСТ 28147-89 (рис.2.17). Функция хэширования H получает на вход хэш, полученный на предыдущем шаге (значение h0 произвольное начальное число), а также очередной блок сообщения mi. Ее внутренняя структура представлена на рис.2.18. Здесь в блоке шифрующего преобразования для модификации hi в si используется блочный шифр ГОСТ 28147-89. Перемешивающее преобразование представляет собой модифицированную перестановку Фейштеля. Для последнего блока mN (N – общее количество блоков сообщения) выполняется набивка до размера 256 бит с добавлением истинной длины сообщения. Параллельно подсчитывается контрольная сумма сообщения S и суммарная длина L, которые участвуют в финальной функции сжатия.
Рис.2.17. Общая схема хэшироваения по ГОСТ Р 34.11 – 94
Рис.2.18. Структура функции хэширования в ГОСТ Р 34.11-94
Основным недостатком хэш-функций на основе блочных шифров является невысокая скорость их работы. Поэтому были спроектированы ряд специализированных алгоритмов, которые, обеспечивая аналогичную стойкость к атакам, выполняют гораздо меньшее количество операций над входными данными и обеспечивают большую скорость работы. Примерами подобного рода алгоритмов являются : MD2, MD4, MD5, RIPEMD –160, SHA. Рассмотрим подробнее структуру алгоритма хэширования SHA (Secure Hash Algorithm), который описан в стандарте SHS и обеспечивает безопасность электронной цифровой подписи DSA, формируя 160-битный дайджест сообщения.
Сначала сообщение разбивается на блоки длиной 512 бит. Если длина сообщения не кратна 512, к последнему блоку приписывается справа 1, после чего он дополняется нулями до 512 бит. В конец последнего блока записывается код длины сообщения. В результате сообщение приобретает вид n 512-разрядных блоков M1,M2,…,Mn.
Алгоритм SHA использует 80 логических функций f0,f1,…,f79, которые производят операции над тремя 32-разрядными словами (B,C,D):
|
ft(B,C,D) = (B Ù C) Ú ((Ø B) Ù D) |
для 0 £t £19 |
|
ft(B,C,D) = B Å C Å D |
для 20 £ t £39 |
|
ft(B,C,D) = (B Ù C) Ú (B Ù D) Ú (C Ù D) |
для 40 £ t £ 59 |
|
ft(B,C,D) = B Å C Å D |
для 60 £ t £ 79 |
В алгоритме используются также специальным образом инициализированные 4 константы Ki и 5 начальных значений Hi.
Делим массив M на группы из 16 слов W0, W1,…,W15 (W0 самое левое слово).
Для t = 16 – 79 Wt = S1(Wt-3 Å Wt-8 Å Wt-14 Å Wt-16)
Sk означает операцию циклического сдвига влево на k разрядов.
Пусть теперь A = H0, B = H1, C = H2, D = H3, E = H4.
for t = 0 to 79 do
TEMP = S5(A) + ft(B,C,D) + E + Wt + Ki.
E = D; D = C; C = S30(B); B = A; A = TEMP;
Пусть H0 = H0 + A; H1 = H1 + B; H2 = H2 + C; H3 = H3 + D; H4 = H4 + E.
Графически один цикл SHA представлен на рис.2.19.
Рис.2.19. Один цикл преобразования SHA
В результате обработки массива М будет получено 5 слов H0, H1, H2, H3, H4 с общей длиной 160 бит, которые и образуют дайджест сообщения.
Из приведенных данных ясно, что сложность американского стандарта хэширования ниже, чем у российского. Российский стандарт предполагает выполнение четырех шифрований за один цикл выработки хэша, или в общей сложности 128 раундов. Каждый раунд шифрования требует примерно полтора десятка элементарных машинных операций, что существенно увеличивает затраты машинного времени на выполнение линейных перемешивающих операций. Один раунд выработки хэша SHA гораздо проще: он весь может быть реализован примерно за 15-20 команд, общее количество раундов всего 80, и за один цикл выработки хэша обрабатывается вдвое больше исходных данных — 512 против 256 в ГОСТ P34.ll -94. Таким образом, можно предположить, что быстродействие программных реализаций SHA будет примерно в 3-6 раз быстрее, чем у отечественного стандарта.
Основная задача хэш-функций – генерация дайджестов, уникальных для конкретного документа. Если для двух различных входных блоков хэш-функция дает одинаковый дайджест, такая ситуация называетсяхэш-коллизией. Из теоремы, носящей название «парадокс дней рождения», следует, что для n–битного хэш-значения необходимо в среднем 2n/2 различных входных сообщений, чтобы возникла коллизия. Это делает практически невозможным изменение документа при его подписи с помощью, например, алгоритма SHА путем простого подбора, поскольку при таком подходе потребуется сгенерировать около 280 различных сообщений, чтобы получить аналогичное подменяемому по получаемому дайджесту. Эта цифра недостижима для современного уровня технологий.
Виды «хеш-функций»
«Хорошая» хеш-функция должна удовлетворять двум свойствам:
- быстрое вычисление;
- минимальное количество «коллизий».
Введем обозначения:
То есть:
.
В качестве примера «плохой» хеш-функции можно привести функцию с , которая десятизначному натуральному числу
сопоставляет три цифры, выбранные из середины двадцатизначного квадрата числа
. Казалось бы, значения «хеш-кодов» должны равномерно распределяться между «000» и «999», но для «реальных» данных это справедливо лишь в том случае, если «ключи» не имеют «большого» количества нулей слева или справа .
Рассмотрим несколько простых и надежных реализаций «хеш-функций».
«Хеш-функции», основанные на делении
1. «Хеш-код» как остаток от деления на число всех возможных «хешей»
Хеш-функция может вычислять «хеш» как остаток от деления входных данных на :
,
где — количество всех возможных «хешей» (выходных данных).
При этом очевидно, что при четном значение функции будет четным при четном
и нечетным — при нечетном
. Также не следует использовать в качестве
степень основания системы счисления компьютера, так как «хеш-код» будет зависеть только от нескольких цифр числа
, расположенных справа, что приведет к большому количеству коллизий . Об этом говорит сайт https://intellect.icu . На практике обычно выбирают простое
; в большинстве случаев этот выбор вполне удовлетворителен.
2. «Хеш-код» как набор коэффициентов получаемого полинома
Хеш-функция может выполнять деление входных данных на полином по модулю два. В данном методе должна являться степенью двойки, а бинарные ключи (
) представляются в виде полиномов, в качестве «хеш-кода» «берутся» значения коэффициентов полинома, полученного как остаток от деления входных данных
на заранее выбранный полином
степени
:
При правильном выборе гарантируется отсутствие коллизий между почти одинаковыми ключами .
«Хеш-функции», основанные на умножении
Обозначим символом количество чисел, представимых машинным словом. Например, для 32-разрядных компьютеров, совместимых с IBM PC,
.
Выберем некую константу так, чтобы
была взаимно простой с
. Тогда хеш-функция, использующая умножение, может иметь следующий вид:
В этом случае на компьютере с двоичной системой счисления является степенью двойки, и
будет состоять из старших битов правой половины произведения
.
Одним из преимуществ хеш-функций, основанных на делении и умножении, является выгодное использование неслучайности реальных ключей. Например, если ключи представляют собой арифметическую прогрессию (например, последовательность имен «Имя 1», «Имя 2», «Имя 3»), хеш-функция, использующая умножение, отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшит количество коллизий по сравнению со случайной ситуацией .
Одной из хеш-функций, использующих умножение, является хеш-функция, использующая хеширование Фибоначчи. Хеширование Фибоначчи основано на свойствах золотого сечения. В качестве константы здесь выбирается целое число, ближайшее к
и взаимно простое с
, где
— это золотое сечение .
Хеширование строк переменной длины
Вышеизложенные методы применимы и в том случае, если необходимо рассматривать ключи, состоящие из нескольких слов, или ключи переменной длины.
Например, можно скомбинировать слова в одно при помощи сложения по модулю или операции «исключающее или». Одним из алгоритмов, работающих по такому принципу, является хеш-функция Пирсона.
Хеширование Пирсона — алгоритм, предложенный Питером Пирсоном (англ. Peter Pearson) для процессоров с 8-битовыми регистрами, задачей которого является быстрое преобразование строки произвольной длины в хеш-код. На вход функция получает слово , состоящее из
символов, каждый размером 1 байт, и возвращает значение в диапазоне от 0 до 255. При этом значение хеш-кода зависит от каждого символа входного слова.
Алгоритм можно описать следующим псевдокодом, который получает на вход строку и использует таблицу перестановок
:
h := 0 for each c in W loop index := h xor c h := T[index] end loop return h
Среди преимуществ алгоритма:
- простоту вычисления;
- отсутствие таких входных данных, для которых вероятность коллизии наибольшая;
- возможность модификации в идеальную хеш-функцию .
В качестве альтернативного способа хеширования ключей , состоящих из
символов (
), можно предложить вычисление
Идеальное хеширование
Идеальной хеш-функцией (англ. perfect hash function) называется такая функция, которая отображает каждый ключ из набора во множество целых чисел без коллизий. В математике такое преобразование называется инъективным отображением.
Описание
- Функция
называется идеальной хеш-функцией для
, если она инъективна на
.
- Функция
называется минимальной идеальной хеш-функцией для
, если она является идеальной хеш-функцией и
.
- Для целого
функция
называется
-идеальной хеш-функцией (k-PHF) для
, если для каждого
имеем
.
Идеальное хеширование применяется, если требуется присвоить уникальный идентификатор ключу без сохранения какой-либо информации о ключе. Пример использования идеального (или скорее -идеального) хеширования: размещение хешей, связанных с данными, хранящимися в большой и медленной памяти, в небольшой и быстрой памяти. Размер блока можно выбрать таким, чтобы необходимые данные считывались из медленной памяти за один запрос. Подобный подход используется, например, в аппаратных маршрутизаторах. Также идеальное хеширование используется для ускорения работы алгоритмов на графах, если представление графа не умещается в основной памяти .
Универсальное хеширование
Универсальным хешированием называется хеширование, при котором используется не одна конкретная хеш-функция, а происходит выбор хеш-функции из заданного семейства по случайному алгоритму. Универсальное хеширование обычно отличается низким числом коллизий, применяется, например, при реализации хеш-таблиц и в криптографии.
Описание
Предположим, что требуется отобразить ключи из пространства в числа
. На входе алгоритм получает данные из некоторого набора
размерностью
. Набор заранее неизвестен. Как правило, алгоритм должен обеспечить наименьшее число коллизий, чего трудно добиться, используя какую-то определенную хеш-функцию. Число коллизий можно уменьшить, если каждый раз при хешировании выбирать хеш-функцию случайным образом. Хеш-функция выбирается из определенного набора хеш-функций, называемого универсальным семейством
.
Методы борьбы с коллизиями
Коллизией (иногда конфликтом или столкновением) называется случай, при котором одна хеш-функция для разных входных блоков возвращает одинаковые хеш-коды.
Методы борьбы с коллизиями в хеш-таблицах
Большинство первых работ, описывающих хеширование, посвящено методам борьбы с коллизиями в хеш-таблицах. Тогда хеш-функции применялись при поиске текста в файлах большого размера. Существует два основных метода борьбы с коллизиями в хеш-таблицах:
- метод цепочек (метод прямого связывания);
- метод открытой адресации.
При использовании метода цепочек в хеш-таблице хранятся пары «связный список ключей» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; если хеш-код был получен ранее (для другого ключа), ключ добавляется в существующий список ключей, парный хеш-коду; иначе создается новая пара «список ключей» — «хеш-код», и ключ добавляется в созданный список. В общем случае, если имеется ключей и
списков, средний размер хеш-таблицы составит
. В этом случае при поиске по таблице по сравнению со случаем, в котором поиск выполняется последовательно, средний объем работ уменьшится примерно в
раз.
При использовании метода открытой адресации в хеш-таблице хранятся пары «ключ» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; пара «ключ» — «хеш-код» сохраняется в таблице. В этом случае при поиске по таблице по сравнению со случаем, в котором используются связные списки, ссылки не используются, выполняется последовательный перебор пар «ключ» — «хеш-код», перебор прекращается после обнаружения нужного ключа. Последовательность, в которой просматриваются ячейки таблицы, называется последовательностью проб .
криптографическая соль Соль (криптография)
Для защиты паролей и цифровых подписей от подделки создано несколько методов, работающих даже в том случае, если криптоаналитику известны способы построения коллизий для используемой хеш-функции. Одним из таких методов является добавление к входным данным так называемой криптографической «соли» — строки случайных данных; иногда «соль» добавляется и к хеш-коду. Добавление случайных данных значительно затрудняет анализ итоговых хеш-таблиц. Данный метод, к примеру, используется при сохранении паролей в UNIX-подобных операционных системах.
Применение хеш-функций
Хеш-функции широко используются в криптографии.
Хеш используется как ключ во многих структурах данных — хеш-таблицаx, фильтрах Блума и декартовых деревьях.
Криптографические хеш-функции
Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того, чтобы хеш-функция считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
Данные требования не являются независимыми:
- обратимая функция нестойка к коллизиям первого и второго рода;
- функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.
Не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.
Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно вычислений хеш-функции. Поэтому n-битовая хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для нее близка к
.
Криптографические хеш-функции должны иметь лавинный эффект — при малейшем изменении аргумента значение функции сильно изменяется. В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа .
Хеширование часто используется в алгоритмах электронно-цифровой подписи, где шифруется не само сообщение, а его хеш-код, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев вместо паролей хранятся значения их хеш-кодов.
Контрольные суммы
Алгоритмы вычисления контрольных сумм — несложные, быстрые и легко реализуемые аппаратно алгоритмы, используемые для защиты данных от непреднамеренных искажений, в том числе — от ошибок аппаратуры. С точки зрения математики такие алгоритмы являются хеш-функциями, вычисляющими контрольный код. Контрольный код применяется для обнаружения ошибок, которые могут возникнуть при передаче и хранении информации.
Алгоритмы вычисления контрольных сумм по скорости вычисления в десятки и сотни раз быстрее, чем криптографические хеш-функции, и значительно проще в аппаратном исполнении.
Платой за столь высокую скорость является отсутствие криптостойкости — возможность легко «подогнать» сообщение под заранее известную контрольную сумму. Также обычно разрядность контрольных сумм (типичное число: 32 бита) ниже, чем разрядность криптографических хешей (типичные числа: 128, 160 и 256 бит), что означает возможность возникновения непреднамеренных коллизий.
Простейшим алгоритмом вычисления контрольной суммы является деление сообщения (входных данных) на 32- или 16-битовые слова с последующим суммированием слов. Такой алгоритм применяется, например, в протоколах TCP/IP.
Как правило, алгоритмы вычисления контрольных сумм должны обнаруживать типичные аппаратные ошибки, например, должны обнаруживать несколько подряд идущих ошибочных бит до заданной длины. Семейство алгоритмов так называемых «циклических избыточных кодов» удовлетворяет этим требованиям. К ним относится, например, алгоритм CRC32, применяемый в устройствах Ethernet и в формате сжатия данных ZIP.
Контрольная сумма, например, может быть передана по каналу связи вместе с основным текстом (данными). На приемном конце, контрольная сумма может быть рассчитана заново и может сравниваться с переданным значением. Если будет обнаружено расхождение, то при передаче возникли искажения, и можно запросить повторную передачу.
Пример применения хеширования в быту — подсчет количества чемоданов, перевозимых в багаже. Для проверки сохранности чемоданов не требуется проверять сохранность каждого чемодана, достаточно посчитать количество чемоданов при погрузке и выгрузке. Совпадение чисел будет означать, что ни один чемодан не потерян. То есть, число чемоданов является хеш-кодом.
Данный метод можно дополнить для защиты передаваемой информации от фальсификации (метод MAC). В этом случае хеширование производится криптостойкой функцией над сообщением, объединенным с секретным ключом, известным только отправителю и получателю сообщения. Криптоаналитик, перехватив сообщение и значение хеш-функции, не сможет восстановить код, то есть не сможет подделать сообщение (см. имитозащита).
Геометрическое хеширование
Геометрическое хеширование (англ. geometric hashing) — метод, широко применяемый в компьютерной графике и вычислительной геометрии для решения задач на плоскости или в трехмерном пространстве, например для нахождения ближайших пар точек среди множества точек или для поиска одинаковых изображений. Хеш-функция в данном методе обычно получает на вход какое-либо метрическое пространство и разделяет его, создавая сетку из клеток. Хеш-таблица в данном случае является массивом с двумя или более индексами и называется «файлом сетки» (англ. grid file). Геометрическое хеширование применяется в телекоммуникациях при работе с многомерными сигналами .
Ускорение поиска данных Хеш-таблица
Хеш-таблицей называется структура данных, позволяющая хранить пары вида «ключ» — «хеш-код» и поддерживающая операции поиска, вставки и удаления элемента. Хеш-таблицы применяются с целью ускорения поиска, например, при записи текстовых полей в базе данных может рассчитываться их хеш-код, и данные могут помещаться в раздел, соответствующий этому хеш-коду. Тогда при поиске данных надо будет сначала вычислить хеш-код текста, и сразу станет известно, в каком разделе их надо искать. То есть искать надо будет не по всей базе, а только по одному ее разделу, а это ускоряет поиск.
Бытовым аналогом хеширования в данном случае может служить размещение слов в словаре в алфавитном порядке. Первая буква слова является его хеш-кодом, и при поиске просматривается не весь словарь, а только слова, начинающиеся на нужную букву.
кукушкино хеширование
Перейти к навигацииПерейти к поиску

Пример кукушкиного хеширования. Стрелки показывают альтернативное положение ключа. Новое значение, которое вставляется в ячейку A, выталкивая A в альтернативную ячейку, занимаемую ключом B, значение B переносится в альтернативное место, которое в настоящее время не занято. Вставка нового значения в ячейку H завершается неудачей — H входит в цикл (вместе с W), так что только что вставленный элемент должен быть вытолкнут.
Кукушкино хеширование — это схема в программировании для решения коллизий значений хеш-функций в таблице с постоянным временем выборки в худшем случае[en]. Имя происходит от поведения некоторых видов кукушек, когда птенец кукушки выталкивает яйца или других птенцов из гнезда сразу после того, как вылупится. Аналогичное происходит в кукушкином хеше, когда вставка нового ключа в таблицу может вытолкнуть старый ключ в другое место в таблице.
Кукушкино хеширование было впервые описано Расмусом Пажом и Флеммингом Фришем Родлером в 2001 .
Операции
Кукушкино хеширование является видом открытой адресации , в которой каждая непустая ячейка хеш-таблицы содержит ключ или пару ключ–значение . Хеш-функция используется для определения места для каждого ключа, и его присутствие в таблице (или значение, ассоциированное с ним) может быть найдено путем проверки этой ячейки в таблице. Однако открытая адресация страдает от коллизий, которые случаются, когда более одного ключа попадают в одну ячейку. Основная идея кукушкиного хеширования заключается в разрешении коллизий путем использования двух хеш-функций вместо одной. Это обеспечивает два возможных положения в хеш-таблице для каждого ключа. В одном из обычных вариантов алгоритма хеш-таблица разбивается на две меньшие таблицы меньшего размера и каждая хеш-функция дает индекс в одну из этих двух таблиц. Можно обеспечить также для обеих хеш-функций индексирование внутри одной таблицы.
Выборка требует просмотра всего двух мест в хеш-таблице, что требует постоянного времени в худшем случае (см. «O» большое и «o» малое). Это контрастирует с многими другими алгоритмами хеш-таблиц, которые не обеспечивают постоянное время выборки в худшем случае. Удаление также может быть осуществлено очищением ячейки, содержащей ключ за постоянное время в худшем случае, что осуществляется проще, чем в других схемах, таких как линейное зондирование.
Когда вставляется новый ключ и одна из двух ячеек пуста, ключ может быть помещен в эту ячейку. В случае же, когда обе ячейки заняты, необходимо переместить другие ключи в другие места (или, наоборот, на их прежние места), чтобы освободить место для нового ключа. Используется жадный алгоритм — ключ помещается в одну из возможных позиций, «выталкивая» любой ключ, который был в этой позиции. Вытолкнутый ключ затем помещается в его альтернативную позицию, снова выталкивая любой ключ, который мог там оказаться. Процесс продолжается, пока не найдется пустая позиция. Возможен, однако, случай, когда процесс вставки заканчивается неудачей, попадая в бесконечный цикл или когда образуется слишком длинная цепочка (длиннее, чем заранее заданный порог, зависящий логарифмически от длины таблицы). В этом случае хеш-таблица перестраивается на месте[en] с новыми хеш-функциями:
| Нет необходимости размещения новой таблицы для повторного хеширования — мы можем просто просматривать таблицу для удаления и повторной вставки всех ключей, которые находятся не в той позиции, в которой должны были бы стоять.
Pagh & Rodler, «Cuckoo Hashing» |
Теория
Ожидаемое время вставки постоянно , даже если принимать во внимание возможную необходимость перестройки таблицы, пока число ключей меньше половины емкости хеш-таблицы, т.е. коэффициент загрузки меньше 50 %.
Чтобы обеспечить это, используется теория случайных графов — можно образовать неориентированный граф, называемый «кукушкиным графом», в котором вершинами являются ячейки хеш-таблицы, а ребра для каждого хешируемого соединяют два возможных положения (ячейки хеш-таблицы). Тогда жадный алгоритм вставки множества значений в кукушкину хеш-таблицу успешно завершается тогда и только тогда, когда кукушкин граф для этого множества значений является псевдолесом, графом максимум с одним циклом в каждой компоненте связности. Любой порожденный вершинами подграф с числом ребер, большим числа вершин, соответствует множеству ключей, для которых число слотов в хеш-таблице недостаточно. Если хеш-функция выбирается случайно, кукушкин граф будет случайным графом в модели Эрдеша – Реньи[en]. С высокой степенью вероятности для случайного графа, в котором отношение числа ребер к числу вершин ограничено сверху 1/2, граф является псевдолесом и алгоритм кукушкиного хеширования располагает успешно все ключи. Более того, та же теория доказывает, что ожидаемый размер компонент связности кукушкиного графа мал, что обеспечивает постоянное ожидаемое время вставки .
Пример
Пусть даны следующие две хеш-функции:

Столбцы в следующих двух таблицах показывают состояние хеш-таблицы после вставки элементов.
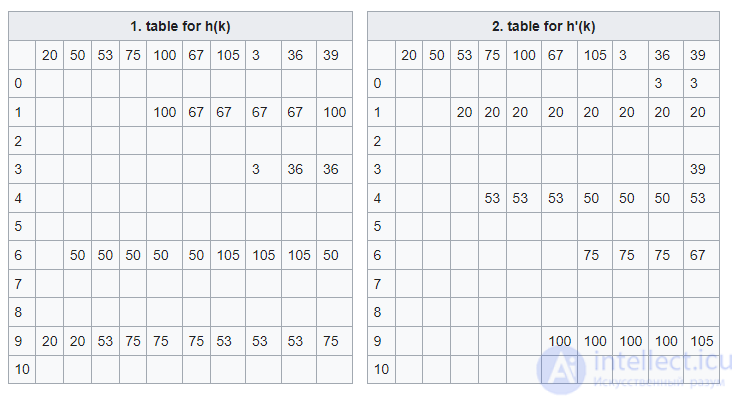
Циклы
Если вы хотите вставить элемент 6, вы получите бесконечный цикл. В последней строке таблицы мы находим ту же начальную ситуацию, что и в начале.
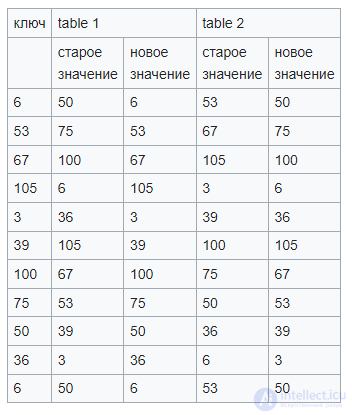
Вариации
Изучались некоторые вариации кукушкиного хеширования, в основном с целью улучшить использование пространства путем увеличения коэффициента загрузки[en]. В этих вариантах может достигаться порог загрузки больше 50 %. Некоторые из этих методов могут быть использованы для существенного уменьшения числа необходимых перестроек структуры данных.
От обобщения кукушкиного хеширования, использующего более двух хеш-функций, можно ожидать лучшего использования хеш-таблицы, жертвуя некоторой скоростью выборки и вставки. Использование трех хеш-функций повышает коэффициент загрузки до 91 % . Другое обобщение кукушкиного хеширования, называемое блочным кукушкиным хешированием, содержит более одного ключа на ячейку. Использование двух ключей на ячейку позволяет повысить загрузку выше 80 % .
Еще один изучавшийся вариант — кукушкино хеширование с запасом. «Запас» — это массив ключей постоянной длины, который используется для хранения ключей, которые не могут быть успешно вставлены в главную хеш-таблицу. Эта модификация уменьшает число неудач до обратно-полиномиальной функции со степенью, которая может быть произвольно большой, путем увеличения размера запаса. Однако большой запас означает более медленный поиск ключа, которого нет в основной таблице, либо если он находится в запасе. Запас можно использовать в комбинации с более чем двумя хеш-функциями или с блоковым кукушкиным хешированием для получения как высокой степени загрузки, так и малого числа неудач вставки . Анализ кукушкиного хеширования с запасом распространился и на практические хеш-функции, не только случайные модели хеш-функций, используемые в теоретическом анализе хеширования .
Некоторые исследователи предлагают использовать в некоторых кэшах процессора упрощенное обобщение кукушкиного хеширования, называемого несимметричным ассоциативным кэшем.
Сравнение с аналогичными структурами
Есть другие алгоритмы, которые используют несколько хеш-функций, в частности фильтр Блума, эффективная по памяти структура данных для нечетких множеств. Альтернативная структура данных для задач с теми же нечеткими множествами, основанная на кукушкином хешировании, называемая кукушкиным фильтром, использует даже меньшую память и (в отличие от классических фильтров Блума) позволяет удаление элемента, не только вставку и проверку существования. Однако теоретический анализ этих методов проведен существенно слабее, чем анализ фильтров Блума .
Исследования, проведенные Жуковским, Хеманом и Бонзом , показали, что кукушкино хеширование существенно быстрее метода цепочек для малых хеш-таблиц, находящихся в кэше современных процессоров. Кеннет Росс[10] показал блочную версию кукушкиного хеширования (блок содержит более одного ключа), который работает быстрее обычных методов для больших хеш-таблиц в случае высокого коэффициента загрузки. Скорость работы блочной версии кукушкиной хеш-таблицы позднее исследовал Аскитис[11] по сравнению с другими схемами кэширования.
Обзор Мутцемахера представляет открытые проблемы, связанные с кукушкиным хешированием.
См. также
- Хеш-таблица
- Криптографическая хеш-функция
- Хеш-функция облегченной криптографии
- хеширование в программировании на языке си , хеширование в программировании ,
- скользящий хеш , rolling hash , прокручивающий хеш , кольцевой хеш ,
- Совершенная функция хеширования
- Линейное зондирование
- Двойное хеширование
- Коллизия хеш-функции
- Хеширование
- Квадратичное зондирование
- Хеширование «Классики»
К сожалению, в одной статье не просто дать все знания про хеширование. Но я – старался.
Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое хеширование, хэш-функции, криптографическая соль, кукушкино хеширование
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Криптография и криптоанализ, Стеганография и Стегоанализ


![h(K)=left[Mleftlfloor {frac {A}{w}}*Krightrfloor right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3477baf1616abe639668f7aa485598339f9ad0df)
