Что такое значение функции? Как найти значение функции?
Рассмотрим значение функции в математике на примере.
Значение функции в математике
Значение функции – это значение зависимой переменной.
Часто функцию в общем виде записывают как
y = f(x)
здесь игрек представляет значение функции.
Примеры значений функции
Простой пример значения функции:
y = x + 5
Что такое значение в этой функции?
Значение в этой функции представлено игреком.
Как узнать, что именно игрек, а не икс и не число пять, в этой функции покажет её значение?
Значение функции есть значение зависимой переменной.
Значение функции есть значение переменной, которое получается в результате математического действия.
В нашем случае к переменной икс прибавляется 5. Значит икс есть аргумент.
Значение же игрека получается в результате данного математического действия. Игрек и будет представлять значение функции.
Значение функции – это то, чему равна функция.
Пример. Пусть дана функция:
y = 5x
Функцией здесь является игрек. Чтоб найти значение функции, т.е. значение игрека, нужно подставить допустимое значение аргумента x. Так и сделаем. Пусть икс равен 4, тогда
20 = 5 * 4
откуда получаем, что значение функции при икс = 4 будет равно 20-ти.
Итак, значение функции это х или у? Значение функции это y.
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
![]()
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
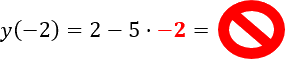
Правильно
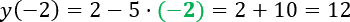
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
![]()
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
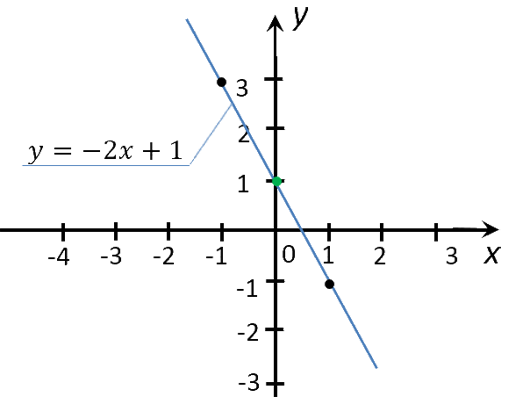
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
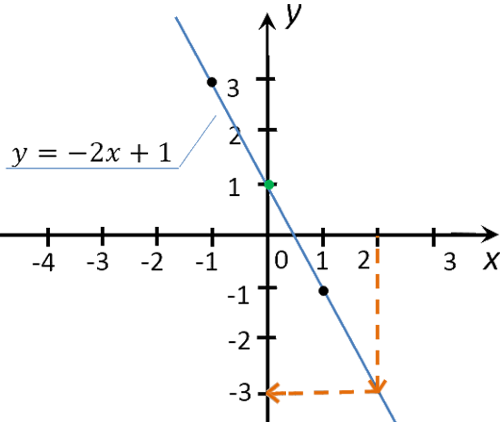
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры

Профиль
Благодарили: 0
Сообщений: 1

Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= – x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov

Профиль
Благодарили: 0
Сообщений: 1

Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов

Профиль
Благодарили: 0
Сообщений: 1

Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
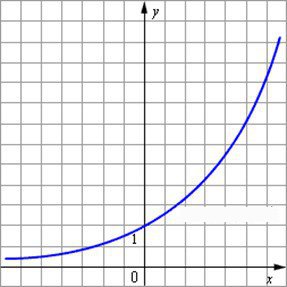 определите вид графика
определите вид графика
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов

Профиль
Благодарили: 0
Сообщений: 3

Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова

Профиль
Благодарили: 0
Сообщений: 11

Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
На чтение 4 мин Просмотров 5.3к.
Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.
Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.
1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.
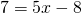
Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):
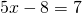
Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):
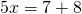
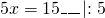
Обе части уравнения делим на число, стоящее перед иксом:
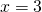
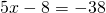
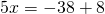
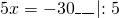
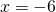
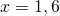
2) При каком значении аргумента значение функции
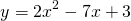
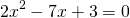
Решаем квадратное уравнение.
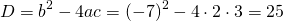
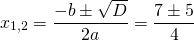
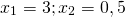
При y=0 x=3 и x=0,5.
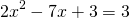
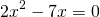
Это — неполное квадратное уравнение. Общий множитель x выносим за скобки
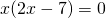
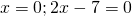
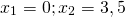
При y=3 x=0 и x=3,5.
Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.
В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.
Рассмотрим, как по данному графику функции найти y по x.

1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.
Аргумент — это x, функция — y.
Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.
Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.
От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).
Следовательно, при x=1 y=2.
Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.
Получаем, что при x=3 y=4.
Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.
При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.
Записываем: при x=-1 y=0.
При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.
2) На рисунке 2 изображен график функции y=f(x).
Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.

Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.
При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.
Пишем: при x=1 y=2.
При x равном -1 и -5 идем сначала вверх, затем — вправо.
При иксах равных 3; 5 и 7 идём вниз и влево.
Обратите внимание: различным значениям икса может соответствовать одно значение y:
Дана следующая функция y=f(x) :
y = 2x – 10, если x > 0
y = 0, если x = 0
y = 2 * |x| – 1, если x
Требуется найти значение функции по переданному x .
- Получить с клавиатуры значение x .
- Если x больше 0, то вычислить выражение 2*x-10 , результат присвоить переменной y .
- Иначе если x равен 0, то присвоить y значение 0.
- Иначе присвоить y результат выражения 2*|x|-1 .
var x , y : integer ;
begin
readln ( x ) ;
if x > 0 then y : = 2 * x – 10
else
if x = 0 then y : = 0
else y : = 2 * abs ( x ) – 1 ;
writeln ( y ) ;
end .
main ( ) <
int x , y ;
scanf ( “%d” , & x ) ;
if ( x > 0 ) y = 2 * x – 10 ;
else
if ( x == 0 ) y = 0 ;
else
y = 2 * abs ( x ) – 1 ;
printf ( “%d
” , y ) ;
>
x = input ( )
x = int ( x )
if x > 0 :
y = 2 *x – 10
elif x == 0 :
y = 0
else :
y = 2 * abs ( x ) – 1
В КуМир функция взятия модуля от числа возвращает вещественное значение. Поэтому используется функция int(), чтобы привести к целому, иначе присвоение невозможно.
График линейной функции, его свойства и формулы

О чем эта статья:
Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х – 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
Если k > 0 и b
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x – 2.
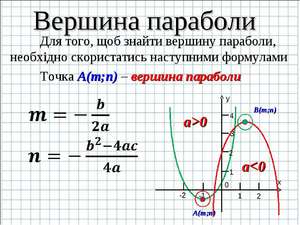
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b – второй коэффициент, c – свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
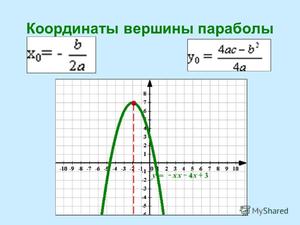
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n – корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 – первый корень;
- 5 – второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
Прямые на координатной плоскости

Линейная функция
Линейной функцией называют функцию, заданную формулой
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
График линейной функции
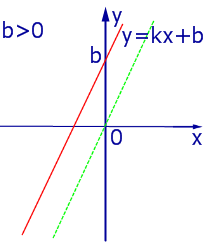
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
 |
| Рис.1 |
 |
| Рис.2 |
 |
| Рис.3 |
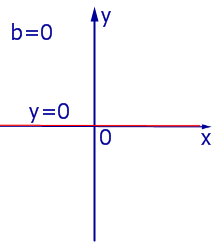
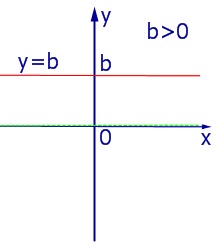
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
 |
| Рис.4 |
 |
| Рис.5 |
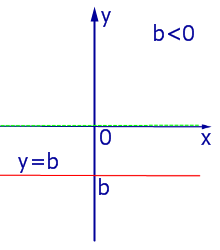 |
| Рис.6 |
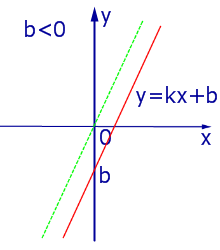
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
имеющие одинаковые угловые коэффициенты и разные свободные члены  , параллельны .
, параллельны .
имеющие разные угловые коэффициенты  , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.
y = kx + b1 и 
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
 |
| Рис.10 |
 |
| Рис.11 |
 |
| Рис.12 |
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .
При  прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат
Прямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
 |
| Рис.13 |
 |
| Рис.14 |
 |
| Рис.15 |
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа.
В случае, когда  уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .


что и требовалось.
В случае, когда  получаем:
получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).
В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости:

В случае, когда  уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.
Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) .
Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) .
Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
- параллельной к прямой
- перпендикулярной к прямой (8).
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

Итак, уравнение прямой, параллельной к прямой
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly
http://www.resolventa.ru/spr/algebra/degree1.htm
[/spoiler]
Вычисление значений функции
Онлайн калькулятор поможет найти значения функции в заданном интервале, построить таблицу значений функции онлайн, табулировать функцию.
Вычисляет значения функции одной переменной y для заданных значений переменной x. Функция задается при помощи формулы, пример:
Построить таблицу значений функции f(x)=x/(x+1) на отрезке от 0 до 6 с шагом в единицу.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

