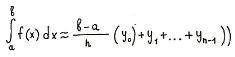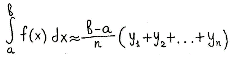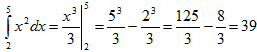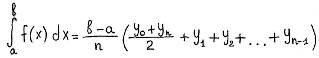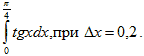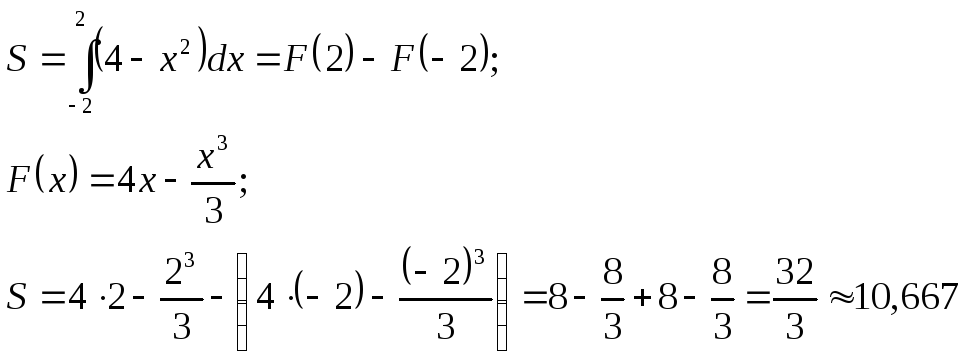Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 мая 2021 года; проверки требуют 4 правки.
Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0. (Для формулы средних прямоугольников равен 1).
Если отрезок ![{displaystyle left[a,bright]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)
- Формуле левых прямоугольников:
- Формуле правых прямоугольников:
- Формуле прямоугольников (средних):
Составные квадратурные формулы[править | править код]
В случае разбиения отрезка интегрирования на 
- Для левых прямоугольников:
- Для правых прямоугольников:
- Для средних прямоугольников:
Формулу с вычислением значения в средней между двумя узлами точке можно применять лишь тогда, когда подынтегральная функция задана аналитически, либо каким-нибудь иным способом, допускающим вычисление значения в произвольной точке. В задачах, где функция задана таблицей значений остаётся лишь вычислять среднее значение между интегралами, посчитанными по формулам левых и правых прямоугольников соответственно, что приводит к составной квадратурной формуле трапеций.
Поскольку составные квадратурные формулы являются ни чем иным, как суммами, входящими в определение интеграла Римана, при 

Метод средних прямоугольников
Составные формулы для равномерных сеток[править | править код]
Равномерную сетку можно описать следующим набором формул:
где 
Для равномерных сеток формулы прямоугольников можно записать в виде следующих формул Котеса:
- Составная формула левых прямоугольников:
- Составная формула правых прямоугольников:
- Составная формула средних прямоугольников:
Т.е. соответствует формуле трапеций.
Погрешность методов[править | править код]
Для формул правых и левых прямоугольников погрешность составляет
Для формулы прямоугольников (средних)
Для составных формул правых и левых прямоугольников на равномерной сетке:
Для составной формулы прямоугольников:
Пример реализации[править | править код]
Формула средних прямоугольников для аналитически заданной функции, написанная на С
double InFunction(double x) { //Подынтегральная функция return sin(x); } double CalcIntegral(double a, double b, int n) { double result = 0, h = (b - a) / n; for(int i = 0; i < n; i++) { result += InFunction(a+h/2+i*h); } result *= h; return result; }
См. также[править | править код]
- Формула Симпсона
- Метод трапеций
- Список квадратурных формул
Учебно-воспитательные задачи:
- Дидактическая цель. Познакомить учащихся с методами
приближённого вычисления определённого интеграла. - Воспитательная цель. Тема данного занятия имеет большое
практическое и воспитательное значение. Наиболее просто к идее численного
интегрирования можно подойти, опираясь на определение определённого
интеграла как предела интегральных сумм. Например, если взять какое-либо
достаточно мелкое разбиение отрезка [a; b] и построить для
него интегральную сумму, то её значение можно приближённо принять за
значение соответствующего интеграла. При этом важно быстро и правильно
производить вычисления с привлечением вычислительной техники.
Основные знания и умения. Иметь понятие о приближённых методах
вычисления определённого интеграла по формулам прямоугольников и трапеций.
Обеспечение занятия
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод
прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора). - Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится
вычислять определённые интегралы, для которых невозможно найти первообразную. В
этом случае применяют приближённые методы вычисления определённых интегралов.
Иногда приближённый метод применяют и для “берущихся” интегралов, если
вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого
вычисления интеграла заключается в том, что кривая
заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.
Последовательность занятия.
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
План занятия
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных
методов интегрирования, геометрический смысл определённого интеграла.
- Выполнение практической работы.
Решение многих технических задач сводится к вычислению определённых
интегралов, точное выражение которых сложно, требует длительных вычислений и не
всегда оправдано практически. Здесь бывает вполне достаточно их приближённого
значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение
которой неизвестно. В этом случае можно заменить данную линию более простой,
уравнение которой известно. Площадь полученной таким образом криволинейной
трапеции принимается за приближённое значение искомого интеграла.
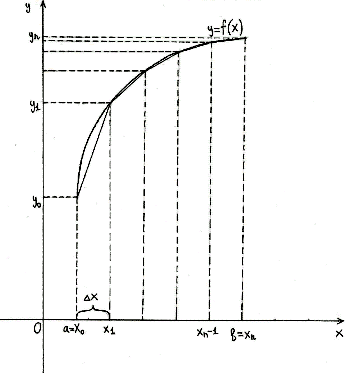
Простейшим приближённым методом является метод прямоугольников. Геометрически
идея способа вычисления определённого интеграла по формуле прямоугольников
состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой
площадей прямоугольников, одна сторона которых равна
, а друга –
.
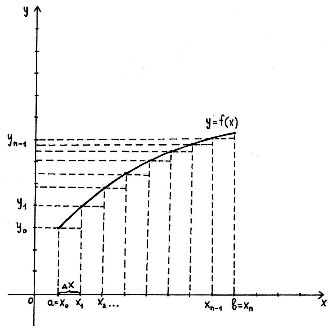
Если суммировать площади прямоугольников, которые показывают площадь
криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
[Рисунок1]
то получим формулу:
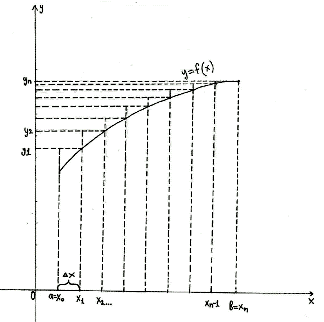
Если с избытком
[Рисунок2],
то
Значения у0, у1,…, уn находят из
равенств ,
к
=
0, 1…,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла
, нужно:
- разделить отрезок интегрирования [a, b] на n равных частей
точками х0=а,
х1, х2,…, х
n
-1,
х
n
=
b
; - вычислить значения подынтегральной функции
в
точках деления, т.е. найтиу
0
=
f (x0),
у
1
=
f (x1),
у
2
=
f (x2),
у
n
-1
=
f (xn-1),
у
n
=
f (xn)
; - воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Пример 1. Вычислить по формуле прямоугольников
. Найти
абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных
частей. Тогда а
=
0,
b =
3
,
х
k = a + k
х
х0 = 2 + 0
= 2
х1 = 2 + 1
= 2,5
х2 = 2 + 2
=3
х3 = 2 + 3
= 3
х4 = 2 + 4
= 4
х5 = 2 + 5
= 4,5
f (x0) = 22 = 4
f
(x
1
)
= 2
,5
2
=
6,25
f
(x
2
)
=
32
=
9
f
(x
3
)
=
3,52
=
12,25
f
(x
4
)
=
42
=
16
f
(x
5
)
=
4,52
=
20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти
точное значение интеграла:
Вычисления проходили долго и мы получили довольно-таки грубое округление.
Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться
техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х
[2
;5
]
с заданным шагом
х = 0,1.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (2). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (2,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А32, до значения х=5). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской
раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется
4. Теперь необходимо скопировать функцию из ячейки В2.
Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В33 может быть найдено приближённое значение интеграла.
Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции (f(x)).
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция – функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В
ячейке В33 появляется приближённое значение искомого интеграла с недостатком
(37,955) .
Сравнивая полученное приближённое значение с истинным значением интеграла (39),
можно видеть, что ошибка приближения метода прямоугольников в данном случае
равна
=
|39 – 37
,
955| = 1
,045
Пример 2. Используя метод прямоугольников, вычислить
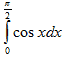
заданным шагом х =
0,05.
Решение:
- Для нахождения определённого интеграла значения подынтегральной функции
f(x) должны быть введены в рабочую таблицу Excel в диапазоне
с
заданным шагомх
= 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
интегрирования (0). В ячейку А3 вводится второе значение аргумента –
левая граница диапазона плюс шаг построения (0,05). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=1,55). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2. Здесь должно оказаться значение косинуса, соответствующее
значению аргумента в ячейке А2. Для получения значения косинуса
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку
Вставка функции (
f
х
)
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция – функцию COS.
Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя
указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле
вправо, чтобы открыть столбец данных (А). Указываем значение
аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В
ячейке В2 появляется 1. Теперь необходимо скопировать функцию из
ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В
результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла.
Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции(
(
f
х
))
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция – функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В
ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).
Сравнивая полученное приближённое значение с истинным значением интеграла
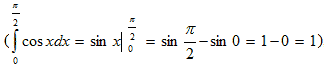
видеть, что ошибка приближения метода прямоугольников в данном случае равна
Метод трапеций обычно даёт более точное значение интеграла, чем метод
прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций
и приближённое значение определённого интеграла находится как сумма площадей
трапеций
[Рисунок3]
Пример 3. Методом трапеций найти
с шагом
х = 0,1.
Решение.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (0). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (0,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=3,1). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение (в примере синуса). Для этого табличный курсор
необходимо установить в ячейку В2. Здесь должно оказаться значение синуса,
соответствующее значению аргумента в ячейке А2. Для получения значения
синуса воспользуемся специальной функцией: нажимаем на панели инструментов
кнопку Вставка функции f(x). В появившемся диалоговом окне
Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические.
Справа в поле Функция – функцию SIN. Нажимаем кнопку ОК.
Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле
окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец
данных (А). Указываем значение аргумента синуса щелчком мыши на
ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
формулу в диапазон В2:В33. В результате должна быть получена таблица данных
для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла
по методу трапеций. Для этого в ячейку В34 вводим формулу =
0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели
инструментов кнопки Вставка функции (f(x)). В появившемся
диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем
Математические. Справа в поле Функция – функцию Сумм. Нажимаем кнопку ОК.
Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон
суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке
В34 появляется приближённое значение искомого интеграла с недостатком (1,997)
.
Сравнивая полученное приближённое значение с истинным значением интеграла
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
- Решение упражнений.
- Вычислить
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить
разделив отрезок [0;4] на 40 равных частей. - Вычислить
разделив отрезок [0;8] на 40 равных частей. - Вычислить
7
Лекция 7
Вычисление
определённых интегралов
Для функции вида
y=f(x)
значением
интеграла в пределах [a,
b]
при условии, что на этом интервале
f(x)>0,
является
площадь под кривой f(x),
ограниченная вертикальными прямыми
x=a
и x=b
(рис. 1).
Рис. 1. Графическая
интерпретация определённого интеграла.
Все численные
методы решения задач, связанных с
вычислением определённых интегралов,
основаны на графической интерпретации
данной задачи. Иными словами, вычислить
определённый интеграл одним из численных
методов, значит найти площадь под кривой,
образованной подынтегральной функцией,
в заданных пределах интегрирования.
Общеизвестно, что
аналитически определённый интеграл
вычисляется с использованием первообразных:
. (1)
Однако первообразные
известны или достаточно легко выводятся
для простых функций. Для функционалов
со сложными структурами приходится
прибегать к численным методам.
Среди методов
численного интегрирования рассмотрим
методы прямоугольников, трапеций и
парабол (Симпсона).
Метод прямоугольников,
как и все другие методы, основан на
разбиении исходного интервала
интегрирования [a,
b]
на равные, малые по величине подынтервалы,
на которых рассчитывается площадь
простейшей геометрической фигуры, в
данном случае – прямоугольника.
Шаг интегрирования
(ширина подынтервала) (x)
напрямую
зависит от количества подынтервалов
(n):
. (2)
Графическая
иллюстрация метода прямоугольников
представлена на рис. 2.
Рис. 2. Графическая
иллюстрация метода прямоугольников.
Алгоритм метода
прямоугольников следующий.
-
Выбирается шаг
интегрирования (количество подынтервалов). -
По соотношению
(3) рассчитывается сумма площадей на
всех подынтервалах:
, (3)
где
здесь и
далее
.
Задание 1.
Для функции вида
вычислить определённый интеграл в
пределах [–2;
2] двумя
способами: аналитически и методом
прямоугольников при n=8.
Рассчитать погрешности численного
метода.
Аналитическое
решение:
Численное решение
представлено в табл. 1.
Таблица 1
Вычисление определённого интеграла методом прямоугольников
-
xi
f(xi)
f(xi)x
–2,0
0,00
0,000
–1,5
1,75
0,875
–1,0
3,00
1,500
–0,5
3,75
1,875
0,0
4,00
2,000
0,5
3,75
1,875
1,0
3,00
1,500
1,5
1,75
0,875
f(xi)x
10,5
Абсолютная
погрешность метода: |10,500–10,667|=0,167.
Относительная
погрешность:
.
Очевидно, что чем
меньше шаг интегрирования, тем меньшую
погрешность даёт метод. Однако в данной
постановке погрешность всё равно будет
достаточно высокой. Для уменьшения
ошибки можно модифицировать метод
прямоугольников.
Модификация
метода прямоугольников
заключается в том, что высота прямоугольника
на каждом участке интегрирования
определяется не значением функции в
крайней точке участка, а значением
функции, вычисленном в середине
подынтервала (рис. 3).
Рис. 3. Графическая
иллюстрация модификации метода
прямоугольников.
В этом случае в
алгоритме формула (3) изменяется:
. (4)
Задание 2.
Для функции вида
вычислить определённый интеграл в
пределах [–2;
2]
модифицированным методом прямоугольников.
Рассчитать погрешности данного метода.
Численное решение
представлено в табл. 2.
Таблица 2
Вычисление определённого интеграла модифицированным методом прямоугольников
-
xi+0,5x
f(xi+0,5x)
f(xi+0,5x)x
–1,75
0,9375
0,46875
–1,25
2,4375
1,21875
–0,75
3,4375
1,71875
–0,25
3,9375
1,96875
0,25
3,9375
1,96875
0,75
3,4375
1,71875
1,25
2,4375
1,21875
1,75
0,9375
0,46875
f(xi+0,5x)x
10,75
Абсолютная
погрешность метода: |10,750–10,667|=0,083.
Относительная
погрешность:
.
В методе
трапеций,
как следует из названия, формой каждого
участка под заданной кривой является
не прямоугольник, а трапеция (рис. 4).
Соответственно, и площадь каждого
участка вычисляется по формуле площади
трапеции.
Формула для
вычисления определённого интеграла
выглядит следующим образом:
. (5)
Задание 3.
Для функции вида
вычислить определённый интеграл в
пределах [–2;
2] методом
трапеций. Рассчитать погрешности данного
метода.
Численное решение
представлено в табл. 3.
Таблица 3
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим задачу, в которой требуется вычислить определённый интеграл $int^b_a f(x)dx$, при этом функция $f(x)$ является непрерывной на промежутке $left[a;bright]$. Обычно, если существует возможность, интегралы вычисляются через нахождение первообразной, но так как это не всегда возможно, прибегают к использованию приближённых методов.
К наиболее часто используемым приближённым методам относят:
- Метод прямоугольников;
- Метод трапеций;
- Метод Симпсона или иначе метод парабол.
В данной статье мы подробно расcмотрим метод прямоугольников.
Сущность метода прямоугольников
Рассмотрим нахождение определённого интеграла от функции $f(x)$ с точки зрения геометрии. Интеграл $int^b_a f(x)dx$ в данном случае есть не что иное, как площадь фигуры, ограниченной сверху графиком $f(x)$, по бокам прямыми $x=a$ и $x=b$, а снизу осью абсцисс.

Рисунок 1. Метод средних прямоугольников
Для того чтобы найти площадь всей фигуры, можно воспользоваться определением интеграла и разбить всю фигуру на равные сегменты одной и той же длины. Точки на оси абсцисс, которые будут разбивать фигуру, обозначим как $x_i$. Нулевая точка при разбиении $x_0=a$, а конечная точка $x_n=b$. Для того чтобы вычислить длину одного сегмента, воспользуемся формулой:
$Δx_i=frac{b-a}{n}$
В методе средних прямоугольников каждый сегмент заменяется на прямоугольник, за высоту которого принимается ордината середины отрезка. Получается, что площадь одного такого прямоугольника равна $S_i= frac{b-a}{n} cdot f(ξ_i)$, а площадь всей фигуры будет равна:
«Метод прямоугольников» 👇
$int^b_a f(x)dx=frac{b-a}{n}cdot (f( ξ_0)+f( ξ_1)+…+f( ξ_{n-1})$, где $x_i≤ ξ_i≤x_{i+1}$
Эта формула позволяет не вычислять напрямую площадь искомой фигуры, ограниченной кривой линией, а заменить её приблизительной площадью ступенчатой фигуры, состоящей из прямоугольников.
При использовании метода средних прямоугольников так как $ξ_i=frac{x_i+x_{i+1}}{2}=x_{i+frac{1}{2}}$, тогда $f( ξ_i)=f(x_{i+frac{1}{2}})$ обозначим как $y_{i+ frac{1}{2}}$,
и формула примет вид:
Определение 1
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_{frac{1}{2}} + y_{frac{3}{2}} + y_{n- frac{1}{2}}left(1right)$
Эта формула называется формулой средних прямоугольников.
Методы левых и правых прямоугольников
Данные методы отличаются от метода средних прямоугольников тем, что здесь в качестве ординаты для элементарного прямоугольника выбирается либо крайнее левое значение функции $f(x)$ (и тогда метод называется методом левых прямоугольников), либо крайнее правое, и тогда метод носит название метода правых прямоугольников.
Определение 2
Формула для применения метода левых прямоугольников выглядит так:
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_0 + y_1 + y_{n- 1})left(2right)$
Определение 3
Формула для метода правых прямоугольников:
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_1 + y_2 + y_n)left(3right)$
Формулы $(1), (2), (3)$ иначе также называются квадратурными составными формулами.
Погрешность метода прямоугольников
Для того чтобы оценить общую погрешность метода прямоугольников, необходимо рассмотреть каждый из элементарных сегментов кривой по отдельности. Общая погрешность в таком случае представляет собой сумму погрешностей всех погрешностей сегментов.
Итак, рассмотрим, чему равна погрешность на одном сегменте.
Площадь одного сегмента вычисляется по приближённой формуле:
$int^{x_i}_{x_{i-1}} f(x)dx≈f(x_{i-1}+frac{x_i-x_{i-1}}{2}) cdot (x_i-x_{i-1})left(4right)$
Погрешность будем определять по разнице со значением первообразной, вычисленной с помощью формулы Ньютона-Лейбница:
$δ_i= int^{x_i}_{x_{i-1}} f(x)dx – f(x_{i-1}+frac{x_{i}-x_{i-1}}{2}) cdot (x_i-x_{i-1})left(5right)$
Так как в левой части равенства $x_{i}-x_{i-1}$ есть не что иное как $int^x{i}_{x_{i-1}}dx$ — длина элементарного отрезка, его можно заменить на $dx$. Перепишем правую часть равенства $(4)$, используя это:
$f(x_{i-1}+frac{x_i-x_{i-1}}{2}) cdot (x_i-x_{i-1})=int^{x_i}_{x_{i-1}} f(x_{i-1}+ frac{x_{i}-x_{i-1}}{2})dx$
$δ_i=int^{x_i}_{x_{i-1}} f(x)dx – int^{x_i}_{x_{i-1}} f(x_{i-1}+ frac{x_{i}-x_{i-1}}{2})dx =int^{x_i}_{x_{i-1}}(f(x)-f(x_{i-1}+ frac{x_i-x_{i-1}}{2})dx left(6right)$
Допуская, что фунцкия $f(x)$ дважды дифференцируема в точке $x=x_{i}-x_{i-1}$ и вокруг неё, разложим её в бесконечную сумму степенных функций, используя ряды Тейлора и формулу Лагранжа:
$f(x)=f(x_{i-1}+frac{Δx}{2})+f’(x_{i-1}+frac{Δx}{2}) cdot (x-(x_{i-1}+frac{Δx}{2}))+f’’(ε_i) cdot frac{(x-(x_{i-1}+frac{Δx}{2}))^2}{2}$
Применим полученное для подстановки:
$f(x)-f(x_{i-1}+ frac{Δx}{2})=f’(x_{i-1}+frac{Δx}{2}) cdot(x-(x_{i-1} + frac{Δx}{2}))+f’’(ε_i) cdot frac{(x-(x_{i-1}+frac{Δx}{2}))^2}{2}left(7right)$
Проинтегрируем $(7)$:
$int^{x_{i}}_{x_{i-1}}(f(x)-f(x_{i-1}+ frac{Δx}{2})dx= int^{x_{i}}_{x_{i-1}}f’(x_{i-1}+frac{Δx}{2}) cdot(x-(x_{i-1}+frac{ Δx}{2}))dx+ int^{x_{i}}_{x_{i-1}} f’’(ε_i) cdot frac{x-(x_{i-1}+ frac{Δx}{2}))^2}{2}dx$
В конечном итоге для элементарного сегмента $left[x_{i-1};x_iright]$ имеем:
$δ_i=int^x{i}_{x_{i-1}} (f(x)-f(x_{i-1}+frac{Δx}{2}))=frac{f’’(ε_i) cdot h^3}{24}$ и наконец,
$|δ_i|≤max_{xin left[x_{i-1};x_iright]}|f’’(x)| cdot frac{h^3}{24}.$
Для всей же фигуры погрешность полученной площади составит:
$δ_i=sum^n_{i=1}int^{x_i}_{x_{i-1}}(f(x)-f(x_{i-1}+frac{Δx}{2}))dx$
и в конечном виде:
Определение 4
$|δ_i|≤max_{xin left[a;bright]}|f’’(x)| cdot frac{(b-a)^3}{24n^2}$
Данная формула используется для получения погрешности при использовании формулы для средних прямоугольников.
Формула для погрешности методов правых и левых прямоугольников выводится аналогичным способом и имеет следующий вид:
Определение 5
$|δ_i|≤max_{xin left[a;bright]}|f’(x)| cdot frac{(b-a)^2}{2n}$
Погрешность, полученная с использованием метода правых или левых прямоугольников для вычисления интегралов больше, чем погрешность при использовании метода средних прямоугольников. Поэтому более предпочтительным для приближённого интегрирования является именно метод средних прямоугольников.
Пример 1
Вычислить интеграл $int_1^2 frac{dx}{x}=ln2$ с точностью до $0, 001$ используя формулу средних прямоугольников.
Разобьём нашу функцию на 10 равных сегментов.
В начале оценим погрешность вычисления:
$|δ_n|≤max_{xin left[a;bright]}|(frac{1}{x})’| cdot frac{(2-1)^3}{24 cdot 10^2}$
В данном случае погрешность меньше либо равна:
$|δ_n|≤0.000042$, следовательно, в данном случае для разбиения можно использовать 10 сегментов.
Разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=frac{2-1}{10}=0,1$ и вычислим значение подынтегральной функции $y(x)=frac{1}{x}$ в середине каждого отрезка:
$x_frac{1}{2}=1,05; y_frac{1}{2}=0,9524;$
$x_frac{3}{2}=1,15; y_frac{3}{2}=0,8696;$
$x_frac{5}{2}=1,25; y_frac{5}{2}=0,8;$
$x_frac{7}{2}=1,35; y_frac{7}{2}=0,7407;$
$x_frac{9}{2}=1,45; y_frac{9}{2}=0,6897;$
$x_frac{11}{2}=1,55; y_frac{11}{2}=0,6452;$
$x_frac{13}{2}=1,65; y_frac{13}{2}=0,6061;$
$x_frac{15}{2}=1,75; y_frac{15}{2}=0,5714;$
$x_frac{17}{2}=1,85; y_frac{17}{2}=0,5405;$
$x_frac{19}{2}=1,95; y_frac{19}{2}=0,5128;$
Сумма всех вычисленных значений функции $f(x)$ составит $6.9284$, а само значение составит:
$int_1^2 frac{dx}{x}=frac{6,9284}{10}=0.69284$ — что отвечает требуемому условию о погрешности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Метод прямоугольников.
Вычисление определенных интегралов по формуле Ньютона-Лейбница не всегда возможно. Многие подынтегральные функции не имеют первообразных в виде элементарных функций, поэтому мы во многих случаях не можем найти точное значение определенного интеграла по формуле Ньютона-Лейбница. С другой стороны, точное значение не всегда и нужно. На практике нам часто достаточно знать приближенное значение определенного интеграла с некоторой заданной степенью точности (например, с точностью до одной тысячной). В этих случаях нам на помощь приходят методы численного интегрирования, такие как метод прямоугольников, метод трапеций, метод Симпсона (парабол) и т.п.
В этой статье подробно разберем метод прямоугольников для приближенного вычисления определенного интеграла.
Сначала остановимся на сути этого метода численного интегрирования, выведем формулу прямоугольников и получим формулу для оценки абсолютной погрешности метода. Далее по такой же схеме рассмотрим модификации метода прямоугольников, такие как метод правых прямоугольников и метод левых прямоугольников. В заключении рассмотрим подробное решение характерных примеров и задач с необходимыми пояснениями.
Навигация по странице.
Суть метода прямоугольников.
Пусть функция y = f(x) непрерывна на отрезке [a; b] . Нам требуется вычислить определенный интеграл .
Обратимся к понятию определенного интеграла. Разобьем отрезок [a;b] на n частей точками . Внутри каждого отрезка выберем точку . Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения , то любая из интегральных сумм является приближенным значением интеграла .
Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму (далее мы покажем, какую именно интегральную сумму берут в методе прямоугольников).
Метод средних прямоугольников.
Формула метода средних прямоугольников.
Если отрезок интегрирования [a;b] разбить на РАВНЫЕ части длины h точками (то есть ) и в качестве точек выбрать СЕРЕДИНЫ элементарных отрезков (то есть ), то приближенное равенство можно записать в виде . Это и есть формула метода прямоугольников. Ее еще называют формулой средних прямоугольников из-за способа выбора точек .
называют шагом разбиения отрезка [a;b] .
Приведем графическую иллюстрацию метода средних прямоугольников.
Из чертежа видно, что подынтегральная функция y=f(x) приближается кусочной ступенчатой функцией на отрезке интегрирования.
С геометрической точки зрения для неотрицательной функции y=f(x) на отрезке [a;b] точное значение определенного интеграла представляет собой площадь криволинейной трапеции, а приближенное значение по методу прямоугольников – площадь ступенчатой фигуры.
Оценка абсолютной погрешности метода средних прямоугольников.
Перейдем к оценке абсолютной погрешности метода прямоугольников. Сначала оценим погрешность на элементарном интервале. Погрешность метода прямоугольников в целом будет равна сумме абсолютных погрешностей на каждом элементарном интервале.
На каждом отрезке имеем приближенное равенство . Абсолютную погрешность метода прямоугольников на i -ом отрезке вычисляем как разность между точным и приближенным значением определенного интеграла: . Так как есть некоторое число и , то выражение в силу четвертого свойства определенного интеграла можно записать как . Тогда абсолютная погрешность формулы прямоугольников на i -ом элементарном отрезке будет иметь следующий вид
Если считать, что функция y = f(x) имеет в точке и некоторой ее окрестности производные до второго порядка включительно, то функцию y = f(x) можно разложить в ряд Тейлора по степеням с остаточным членом в форме Лагранжа:
По свойствам определенного интеграла равенства можно интегрировать почленно:
где .
Таким образом, и .
Абсолютная погрешность формулы прямоугольников на отрезке [a; b] равна сумме погрешностей на каждом элементарном интервале, поэтому
и .
Полученное неравенство представляет собой оценку абсолютной погрешности метода прямоугольников.
Метод левых прямоугольников и метод правых прямоугольников.
Перейдем к модификациям метода прямоугольников.
– это формула метода левых прямоугольников.
– это формула метода правых прямоугольников.
Отличие от метода средних прямоугольников заключается в выборе точек не в середине, а на левой и правой границах элементарных отрезков соответственно.
Абсолютная погрешность методов левых и правых прямоугольников оценивается как .
Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов.
Перейдем к решению примеров, в которых требуется вычислить приближенное значение определенного интеграла методом прямоугольников.
В основном, встречаются два типа задач. В первом случае задается количество интервалов, на которые разбивается отрезок интегрирования. Во втором случае задается допустимая абсолютная погрешность.
Формулировки задач примерно следующие:
- вычислить приближенно определенный интеграл методом прямоугольников, разбив отрезок интегрирования на n частей;
- Методом прямоугольников найти приближенное значение определенного интеграла с точностью до одной сотой (одной тысячной и т.п.).
Разберем каждый случай.
Сразу оговоримся, что в примерах подынтегральные функции будем брать такие, чтобы можно было найти их первообразные. В этом случае мы сможем вычислить точное значение определенного интеграла и сравнить его с приближенным значением, полученным по методу прямоугольников.
Вычислить определенный интеграл методом прямоугольников, разбив отрезок интегрирования на 10 частей.
В нашем примере a = 4, b = 9, n = 10 , .
Внимательно посмотрим на формулу прямоугольников .
Чтобы ее применить, нам нужно вычислить шаг h и значения функции в точках .
Вычислим шаг: .
Так как , то .
Для i = 1 имеем . Находим соответствующее значение функции .
Для i = 2 имеем . Находим соответствующее значение функции .
И так продолжаем вычисления до i = 10 .
Для удобства представим результаты в виде таблицы.
Подставляем полученные значения в формулу прямоугольников:
Значение исходного определенного интеграла можно вычислить по формуле Ньютона-Лейбница:
.
Первообразная подынтегральной функции была найдена интегрированием по частям.
Как видите, точное значение определенного интеграла отличается от значения, полученного по методу прямоугольников для n = 10 , менее чем на шесть сотых долей единицы.
Вычислите приближенное значение определенного интеграла методами левых и правых прямоугольников с точностью до одной сотой.
По условию имеем a = 1, b = 2 , .
Чтобы применить формулы правых и левых прямоугольников нам необходимо знать шаг h , а чтобы вычислить шаг h необходимо знать на какое число отрезков n разбивать отрезок интегрирования. Так как в условии задачи нам указана точность вычисления 0.01 , то число n мы можем найти из оценки абсолютной погрешности методов левых и правых прямоугольников.
Нам известно, что . Следовательно, если найти n , для которого будет выполняться неравенство , то будет достигнута требуемая степень точности.
Найдем – наибольшее значение модуля первой производной подынтегральной функции на отрезке [1; 2] . В нашем примере это сделать достаточно просто.
Графиком функции производной подынтегральной функции является парабола, ветви которой направлены вниз, на отрезке [1; 2] ее график монотонно убывает. Поэтому достаточно вычислить модули значения производной на концах отрезка и выбрать наибольшее:
В примерах со сложными подынтегральными функциями Вам может потребоваться теория раздела наибольшее и наименьшее значение функции.
Таким образом:
Число n не может быть дробным (так как n – натуральное число – количество отрезков разбиения интервала интегрирования). Поэтому, для достижения точности 0.01 по методу правых или левых прямоугольников, мы можем брать любое n = 9, 10, 11, … Для удобства расчетов возьмем n = 10 .
Формула левых прямоугольников имеет вид , а правых прямоугольников . Для их применения нам требуется найти h и для n = 10 .
Итак,
Точки разбиения отрезка [a; b] определяются как .
Для i = 0 имеем и .
Для i = 1 имеем и .
И так далее до i = 10 .
Полученные результаты удобно представлять в виде таблицы:
Подставляем в формулу левых прямоугольников:
Подставляем в формулу правых прямоугольников:
Вычислим точное значение определенного интеграла по формуле Ньютона-Лейбница:
Очевидно, точность в одну сотую соблюдена.
Во многих случаях нахождение наибольшего значения модуля первой производной (или второй производной для метода средних прямоугольников) подынтегральной функции на отрезке интегрирования является очень трудоемкой процедурой.
Поэтому можно действовать без использования неравенства для оценки абсолютной погрешности методов численного интегрирования. Хотя оценки предпочтительнее.
Для методов правых и левых прямоугольников можно использовать следующую схему.
Берем произвольное n (например, n = 5 ) и вычисляем приближенное значение интеграла. Далее удваиваем количество отрезков разбиения интервала интегрирования, то есть, берем n = 10 , и вновь вычисляем приближенное значение определенного интеграла. Находим разность полученных приближенных значений для n = 5 и n = 10 . Если абсолютная величина этой разности не превышает требуемой точности, то в качестве приближенного значения определенного интеграла берем значение при n = 10 , предварительно округлив его до порядка точности. Если же абсолютная величина разности превышает требуемую точность, то вновь удваиваем n и сравниваем приближенные значения интегралов для n = 10 и n = 20 . И так продолжаем до достижения требуемой точности.
Для метода средних прямоугольников действуем аналогично, но на каждом шаге вычисляем треть модуля разности полученных приближенных значений интеграла для n и 2n . Этот способ называют правилом Рунге.
Вычислим определенный интеграл из предыдущего примера с точностью до одной тысячной по методу левых прямоугольников.
Не будем подробно останавливаться на вычислениях.
Для n = 5 имеем , для n = 10 имеем .
Так как , тогда берем n = 20 . В этом случае .
Так как , тогда берем n = 40 . В этом случае .
Так как , то, округлив 0.01686093 до тысячных, утверждаем, что значение определенного интеграла равно 0.017 с абсолютной погрешностью 0.001 .
В заключении остановимся на погрешности методов левых, правых и средних прямоугольников более детально.
Из оценок абсолютных погрешностей видно, что метод средних прямоугольников даст большую точность, чем методы левых и правых прямоугольников для заданного n . В то же время, объем вычислений одинаков, так что использование метода средних прямоугольников предпочтительнее.
Если говорить о непрерывных подынтегральных функциях, то при бесконечном увеличении числа точек разбиения отрезка интегрирования приближенное значение определенного интеграла теоретически стремиться к точному. Использование методов численного интегрирования подразумевает использование вычислительной техники. Поэтому следует иметь в виду, что при больших n начинает накапливаться вычислительная погрешность.
Еще заметим, если Вам требуется вычислить определенный интеграл с некоторой точностью, то промежуточные вычисления проводите с более высокой точностью. Например, Вам требуется вычислить определенный интеграл с точностью до одной сотой, тогда промежуточные вычисления проводите с точностью как минимум до 0.0001 .
При вычислении определенного интеграла методом прямоугольников (методом средних прямоугольников) пользуемся формулой и оцениваем абсолютную погрешность как .
Для метода левых и правых прямоугольников пользуемся формулами и соответственно. Абсолютную погрешность оцениваем как .
Метод прямоугольников
Не всегда имеется возможность вычисления интегралов по формуле Ньютона-Лейбница. Не все подынтегральные функции имеют первообразные элементарных функций, поэтому нахождение точного числа становится нереальным. При решении таких задач не всегда необходимо получать на выходе точные ответы. Существует понятие приближенного значения интеграла, которое задается методом числового интегрирования типа метода прямоугольников, трапеций, Симпсона и другие.
Данная статья посвящена именно этому разделу с получением приближенных значений.
Будет определена суть метода Симпсона, получим формулу прямоугольников и оценки абсолютной погрешности, метод правых и левых треугольников. На заключительном этапе закрепим знания при помощи решения задач с подробным объяснением.
Суть метода прямоугольников
Если функция y = f ( x ) имеет непрерывность на отрезке [ a ; b ] и необходимо вычислить значение интеграла ∫ a b f ( x ) d x .
Необходимо воспользоваться понятием неопределенного интеграла. Тогда следует разбить отрезок [ a ; b ] на количество n частей x i – 1 ; x i , i = 1 , 2 , . . . . , n , где a = x 0 x 1 x 2 . . . x n – 1 x n = b . В промежутке отрезка x i – 1 ; x i , i = 1 , 2 , . . . , n выберем точку со значением ζ i . Из определения имеем, что существует определенный тип интегральных сумм при бесконечном уменьшении длины элементарного отрезка, который уже разбили. Это выражается формулой λ = m a x i = 1 , 2 , . . . , n ( x i – x i – 1 ) → 0 , тогда получаем, что любая из таких интегральных сумм – приближенное значение интеграла ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i – x i – 1 ) .
Суть метода прямоугольников выражается в том, что приближенное значение считается интегральной суммой.
Метод средних прямоугольников
Если разбить интегрируемый отрезок [ a ; b ] на одинаковые части точкой h , то получим a = x 0 , x 1 = x 0 + h , x 2 = x 0 + 2 h , . . . , x – 1 = x 0 + ( n – 1 ) h , x n = x 0 + n h = b , то есть h = x i – x i – 1 = b – a n , i = 1 , 2 , . . . , n . Серединами точек ζ i выбираются элементарные отрезки x i – 1 ; x i , i = 1 , 2 , . . . , n , значит ζ i = x i – 1 + h 2 , i = 1 , 2 , . . . , n .
Тогда приближенное значение ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i – x i – 1 ) записывается таким образом ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i – 1 + h 2 . Данная формула называется формулой метода прямоугольников.
Такое название метод получает из-за характера выбора точек ζ i , где шаг разбиения отрезка берется за h = b – a n .
Рассмотрим на приведенном ниже рисунке данный метод.
Чертеж явно показывает, что приближение к кусочной ступенчатой функции
y = f x 0 + h 2 , x ∈ [ x 0 ; x 1 ) f x 1 + h 2 , x ∈ [ x 1 ; x 2 ) . . . f x n – 1 + h 2 , x ∈ [ x n – 1 ; x n ] происходит на всем пределе интегрирования.
С геометрической стороны мы имеем, что неотрицательная функция y = f ( x ) на имеющемся отрезке [ a ; b ] имеет точное значение определенного интеграла и выглядит как криволинейная трапеция, площадь которой необходимо найти. Рассмотрим на рисунке, приведенном ниже.
Оценка абсолютной погрешности метода средних прямоугольников
Для оценки абсолютной погрешности необходимо выполнить ее оценку на заданном интервале. То есть следует найти сумму абсолютных погрешностей каждого интервала. Каждый отрезок x i – 1 ; x i , i = 1 , 2 , . . . , n имеет приближенное равенство ∫ x i – 1 x i f ( x ) d x ≈ f x i – 1 + h 2 · h = f x i – 1 + h 2 · ( x i – x i – 1 ) . Абсолютная погрешность данного метода треугольников δ i , принадлежащей отрезку i , вычисляется как разность точного и приближенного определения интеграла . Имеем, что δ i = ∫ x i – 1 x i f ( x ) d x – f x i – 1 + h 2 · x i – x i – 1 . Получаем, что f x i – 1 + h 2 является некоторым числом, а x i – x i – 1 = ∫ x i – 1 x i d x , тогда выражение f x i – 1 + h 2 · x i – x i – 1 по 4 свойству определения интегралов записывается в форме f x i – 1 + h 2 · x i – x i – 1 = ∫ x – 1 x f x i – 1 + h 2 d x . Отсюда получаем, что отрезок i имеет абсолютную погрешность вида
δ i = ∫ x i – 1 x i f ( x ) d x – f x i – 1 + h 2 · x i – x i – 1 = = ∫ x i – 1 x i f ( x ) d x – ∫ x i – 1 x i x i – 1 + h 2 d x = ∫ x i – 1 x i f ( x ) = – f x i – 1 + h 2 d x
Если взять, что функция y = f ( x ) имеет производные второго порядка в точке x i – 1 + h 2 и ее окрестностях, тогда y = f ( x ) раскладывается в ряд Тейлора по степеням x – x i – 1 + h 2 с остаточным членом в форме разложения по Лагранжу. Получаем, что
f ( x ) = f x i – 1 + h 2 + f ‘ x i – 1 + h 2 · x – x i – 1 + h 2 + + f ” ( ε i ) x – x i – 1 + h 2 2 2 ⇔ ⇔ f ( x ) = f ( x i – 1 + h 2 ) = f ‘ x i – 1 + h 2 · x – x i – 1 + h 2 + + f ” ( ε i ) x – x i – 1 + h 2 2 2
Исходя из свойства определенного интеграла, равенство может интегрироваться почленно. Тогда получим, что
∫ x i – 1 x i f ( x ) – f x i – 1 + h 2 d x = ∫ x i – 1 x i f ‘ x i – 1 + h 2 · x – x i – 1 + h 2 d x + + ∫ x i – 1 x i f ” ε i · x – x i – 1 + h 2 2 2 d x = = f ‘ x i – 1 + h 2 · x – x i – 1 + h 2 2 2 x i – 1 x i + f ” ε i · x – x i – 1 + h 2 3 6 x i – 1 x i = = f ‘ x i – 1 + h 2 · x i – h 2 2 2 – x i – 1 – x i – 1 + h 2 2 2 + + f ” ε i · x i – h 2 3 6 – x i – 1 – x i – 1 + h 2 3 6 = = f ‘ x i – 1 + h 2 · h 2 8 – h 2 8 + f ” ( ε i ) · h 3 48 + h 3 48 = f ” ε i · h 3 24
где имеем ε i ∈ x i – 1 ; x i .
Отсюда получаем, что δ i = ∫ x i – 1 x i f ( x ) – f x i – 1 + h 2 d x = f ” ε i · h 3 24 .
Абсолютная погрешность формулы прямоугольников отрезка [ a ; b ] равняется сумме погрешностей каждого элементарного интервала. Имеем, что
δ n = ∑ i = 1 n ∫ x i – 1 x i f ( x ) – f x i – 1 + h 2 d x и δ n ≤ m a x x ∈ [ a ; b ] f ” ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f ” ( x ) = b – a 3 24 n 2 .
Неравенство является оценкой абсолютной погрешности метода прямоугольников.
Метод левых прямоугольников и метод правых прямоугольников
Для модификации метода рассмотрим формулы.
∫ a b f ( x ) d x ≈ h · ∑ i = 0 n – 1 f ( x i ) является формулой левых треугольников.
∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) является формулой правых треугольников.
Рассмотрим на примере рисунка, приведенного ниже.
Отличием метода средних прямоугольников считается выбор точек не по центру, а на левой и правой границах данных элементарных отрезков.
Такая абсолютная погрешность методов левых и правых треугольников можно записать в виде
δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b – a ) 2 2 n
Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов
Необходимо рассмотреть решение примеров, где нужно вычислять примерное значение имеющегося определенного интеграла при помощи метода прямоугольников. Рассматривают два типа решения заданий. Суть первого случая – задание количества интервалов для разбивания отрезка интегрирования. Суть второго заключается в наличии допустимой абсолютной погрешности.
Формулировки задач выглядят следующим образом:
- произвести приближенное вычисление определенного интеграла при помощи метода прямоугольников, разбивая на nколичество отрезков интегрирования;
- найти приближенное значение определенного интеграла методом прямоугольников с точностью до одной сотой.
Рассмотрим решения в обоих случаях.
В качестве примера выбрали задания, которые поддаются преобразованию для нахождения их первообразных. Тогда появляется возможность вычисления точного значения определенного интеграла и сравнения с приближенным значением при помощи метода прямоугольников.
Произвести вычисление определенного интеграла ∫ 4 9 x 2 sin x 10 d x при помощи метода прямоугольников, разбивая отрезок интегрирования на 10 частей.
Из условия имеем, что a = 4 , b = 9 , n = 10 , f ( x ) = x 2 sin x 10 . Для применения ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f x i – 1 + h 2 необходимо вычислить размерность шага h и значение функции f ( x ) = x 2 sin x 10 в точках x i – 1 + h 2 , i = 1 , 2 , . . . , 10 .
Вычисляем значение шага и получаем, что
h = b – a n = 9 – 4 10 = 0 . 5 .
Потому как x i – 1 = a + ( i – 1 ) · h , i = 1 , . . . , 10 , тогда x i – 1 + h 2 = a + ( i – 1 ) · h + h 2 = a + i – 0 . 5 · h , i = 1 , . . . , 10 .
Так как i = 1 , то получаем x i – 1 + h 2 = x 0 + h 2 = a + ( i – 0 . 5 ) · h = 4 + ( 1 – 0 . 5 ) · 0 . 5 = 4 . 25 .
После чего необходимо найти значение функции
f x i – 1 + h 2 = f x 0 + h 2 = f ( 4 . 25 ) = 4 . 25 2 sin ( 4 . 25 ) 10 ≈ – 1 . 616574
При i = 2 получаем x i – 1 + h 2 = x 1 + h 2 = a + i – 0 . 5 · h = 4 + ( 2 – 0 . 5 ) · 0 . 5 = 4 . 75 .
Нахождение соответствующего значения функции получает вид
f x i – 1 + h 2 = f x 1 + h 2 = f ( 4 . 75 ) = 4 . 75 2 sin ( 4 . 75 ) 10 ≈ – 2 . 254654
Вычисления производятся до i = 10 .
Представим эти данные в таблице, приведенной ниже.
| i | 1 | 2 | 3 | 4 | 5 |
| x i – 1 + h 2 | 4 . 25 | 4 . 75 | 5 . 25 | 5 . 75 | 6 . 25 |
| f x i – 1 + h 2 | – 1 . 616574 | – 2 . 254654 | – 2 . 367438 | – 1 . 680497 | – 0 . 129606 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i – 1 + h 2 | 6 . 75 | 7 . 25 | 7 . 75 | 8 . 25 | 8 . 75 |
| f x i – 1 + h 2 | 2 . 050513 | 4 . 326318 | 5 . 973808 | 6 . 279474 | 4 . 783042 |
Значения функции необходимо подставить в формулу прямоугольников. Тогда получаем, что
∫ 4 9 x 2 sin x 10 d x ≈ h · ∑ i = 1 n f x i – 1 + h 2 = = 0 . 5 · – 1 . 616574 – 2 . 25654 – 2 . 367438 – 1 . 680497 – 0 . 129606 + + 2 . 050513 + 4 . 326318 + 5 . 973808 + 6 . 279474 + 4 . 783042 = = 7 . 682193
Исходный интеграл можно вычислить при помощи формулы Ньютона-Лейбница. Получаем, что
∫ 4 9 x 2 · sin x 10 d x = – 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x 4 9 = = 7 5 cos 4 – 4 5 sin 4 – 79 10 cos 9 + 9 5 sin 9 ≈ 7 . 630083
Находим первообразную выражения – 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x соответствующую функции f ( x ) = x 2 sin x 10 . Нахождение производится методом интегрирования по частям.
Отсюда видно, что определенный интеграл отличается от значения, полученном при решении методом прямоугольников, где n = 10 , на 6 долей единицы. Рассмотрим на рисунке, приведенном ниже.
Вычислить приближенного значение определенного интеграла ∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x при помощи метода левых и правых прямоугольников с точностью до одной сотой.
Из условия мы имеем, что a = 1 , b = 2 и f ( x ) = – 0 . 03 x 3 + 0 . 26 x – 0 . 26 .
Для применения формулы правых и левых прямоугольников нужно знать размерность шага h , а для его вычисления разбиваем отрезок интегрирования на n отрезков. По условию имеем, что точность должна быть до 0 , 01 , тогда нахождение n возможно при помощи оценки абсолютной погрешности методов левых и правых прямоугольников.
Известно, что δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b – a ) 2 2 n . Для достижения необходимой степени точности необходимо найти такое значение n , для которого неравенство m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b – a ) 2 2 n ≤ 0 . 01 будет выполнено.
Найдем наибольшее значение модуля первой производной, то есть значение m a x x ∈ [ a ; b ] f ‘ ( x ) подынтегральной функции f ( x ) = – 0 . 03 x 3 + 0 . 26 x – 0 . 26 , определенной на отрезке [ 1 ; 2 ] . В нашем случае необходимо выполнить вычисления:
f ‘ ( x ) = – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ‘ = – 0 . 09 x 2 + 0 . 26
Парабола является графиком подынтегральной функции с ветвями, направленными вниз, определенная на отрезке [ 1 ; 2 ] , причем с монотонно убывающим графиком. Необходимо произвести вычисление модулей значений производных на концах отрезков, а из них выбрать наибольшее значение. Получаем, что
f ‘ ( 1 ) = – 0 . 09 · 1 2 + 0 . 26 = 0 . 17 f ‘ ( 2 ) = – 0 . 09 · 2 2 + 0 . 26 = 0 . 1 → m a x x ∈ [ 1 ; 2 ] f ‘ ( x ) = 0 . 17
Решение сложных подынтегральных функций подразумевает обращение к разделу наибольше и наименьшее значение функции.
Тогда получаем, что наибольшее значение функции имеет вид:
m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b – a ) 2 2 n ≤ 0 . 01 ⇔ ⇔ 0 . 17 · ( 2 – 1 ) 2 2 n ≤ 0 . 01 ⇔ 0 . 085 n ≤ 0 . 01 ⇔ n ≥ 8 . 5
Дробность числа n исключается, так как n является натуральным числом. Чтобы прийти к точности 0 . 01 , используя метод правых и левых прямоугольников, не обходимо выбирать любое значение n . Для четкости расчетов возьмем n = 10 .
Тогда формула левых прямоугольников примет вид ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n – 1 f ( x i ) , а правых – ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Для применения их на практике необходимо найти значение размерности шага h и f ( x i ) , i = 0 , 1 , . . . , n , где n = 10 .
h = b – a n = 2 – 1 10 = 0 . 1
Определение точек отрезка [ a ; b ] производится с помощью x i = a + i · h , i = 0 , 1 , . . . , n .
При i = 0 , получаем x i = x 0 = a + i · h = 1 + 0 · 0 . 1 = 1 и f ( x i ) = f ( x 0 ) = f ( 1 ) = – 0 . 03 · 1 3 + 0 . 26 · 1 – 0 . 26 = – 0 . 03 .
При i = 1 , получаем x i = x 1 = a + i · h = 1 + 1 · 0 . 1 = 1 . 1 и f ( x i ) = f ( x 1 ) = f ( 1 . 1 ) = – 0 . 03 · ( 1 . 1 ) 3 + 0 . 26 · ( 1 . 1 ) – 0 . 26 = – 0 . 01393 .
Вычисления производятся до i = 10 .
Вычисления необходимо представить в таблице, приведенной ниже.
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| x i | 1 | 1 . 1 | 1 . 2 | 1 . 3 | 1 . 4 | 1 . 5 |
| f ( x i ) | – 0 . 03 | – 0 . 01393 | 0 . 00016 | 0 . 01209 | 0 . 02168 | 0 . 02875 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i | 1 . 6 | 1 . 7 | 1 . 8 | 1 . 9 | 2 |
| f ( x i ) | 0 . 03312 | 0 . 03461 | 0 . 03304 | 0 . 02823 | 0 . 02 |
Подставим формулу левых треугольников
∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x ≈ h · ∑ i = 0 n – 1 f ( x i ) = = 0 . 1 · – 0 . 03 – 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + + 0 . 02875 + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 = = 0 . 014775
Подставляем в формулу правых треугольников
∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x ≈ h · ∑ i = 1 n f ( x i ) = = 0 . 1 · – 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + 0 . 02875 + + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 + 0 . 02 = 0 . 019775
Произведем вычисление по формуле Ньютона-Лейбница:
∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x = = – 0 . 03 x 4 4 + 0 . 13 x 2 – 0 . 26 x 1 2 = 0 . 0175
Рассмотрим рисунок, приведенный ниже.
Замечание
Нахождение наибольшего значения модуля первой производной является трудоемкой работой, поэтому можно исключить использование неравенства для оценивания абсолютной погрешности и методов численного интегрирования. Разрешено применять схему.
Берем значение n = 5 для вычисления приближенного значения интеграла. Необходимо удвоить количество отрезков интегрирования, тогда n = 10 , после чего производится вычисление примерного значения. необходимо найти разность этих значений при n = 5 и n = 10 . Когда разность не соответствует требуемой точности, то приближенным значением считается n = 10 с округлением до десятка.
Когда погрешность превышает необходимую точность, то производится удваивание n и сравнивание приближенных значений. Вычисления производятся до тех пор, пока необходимая точность не будет достигнута.
Для средних прямоугольников выполняются аналогичные действия, но вычисления на каждом шаге требуют разности полученных приближенных значений интеграла для n и 2 n . Такой способ вычисления называется правилом Рунге.
Произведем вычисление интегралов с точностью до одной тысячной при помощи метода левых прямоугольников.
При n = 5 получаем, что ∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x ≈ 0 . 0116 , а при n = 10 – ∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x ≈ 0 . 014775 . Так как имеем, что 0 . 0116 – 0 . 014775 = 0 . 003175 > 0 . 001 , возьмем n = 20 . Получаем, что ∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x ≈ 0 . 01619375 . Имеем 0 . 014775 – 0 . 01619375 = 0 . 00141875 > 0 . 001 , возьмем значение n = 40 , тогда получим ∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x ≈ 0 . 01686093 . Имеем, что 0 . 1619375 – 0 . 01686093 = 0 . 00066718 0 . 001 , тогда после округления значения проверим, что ∫ 1 2 ( – 0 . 03 x 3 + 0 . 26 x – 0 . 26 ) d x равняется значению 0 , 017 с погрешностью 0 , 001 . Из оценок абсолютных погрешностей видно, что данный метод дает максимальную точность в отличие от метода левых и правых координат для заданного n . Отдается предпочтение методу средних прямоугольников.
Непрерывные подынтегральные функции при бесконечном разделении на отрезки данное приближенно число стремится к точному. Чаще всего такой метод выполняется при помощи специальных программ на компьютере. Поэтому чем больше значение n , тем больше вычислительная погрешность.
Для наиболее точного вычисления необходимо выполнять точные промежуточные действия, желательно с точностью до 0 , 0001 .
Итоги
Для вычисления неопределенного интеграла методом прямоугольников следует применять формулу такого вида ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i – 1 + h 2 и оценивается абсолютная погрешность с помощью δ n ≤ m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · b – a 3 24 n 2 .
Для решения с помощью методов правых и левых прямоугольников применяют формулы, имеющие вид, ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n – 1 f ( x i ) и ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Абсолютная погрешность оценивается при помощи формулы вида δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · b – a 2 2 n .
Метод прямоугольников
Вы будете перенаправлены на Автор24
Рассмотрим задачу, в которой требуется вычислить определённый интеграл $int^b_a f(x)dx$, при этом функция $f(x)$ является непрерывной на промежутке $left[a;bright]$. Обычно, если существует возможность, интегралы вычисляются через нахождение первообразной, но так как это не всегда возможно, прибегают к использованию приближённых методов.
К наиболее часто используемым приближённым методам относят:
- Метод прямоугольников;
- Метод трапеций;
- Метод Симпсона или иначе метод парабол.
В данной статье мы подробно расcмотрим метод прямоугольников.
Сущность метода прямоугольников
Рассмотрим нахождение определённого интеграла от функции $f(x)$ с точки зрения геометрии. Интеграл $int^b_a f(x)dx$ в данном случае есть не что иное, как площадь фигуры, ограниченной сверху графиком $f(x)$, по бокам прямыми $x=a$ и $x=b$, а снизу осью абсцисс.
Рисунок 1. Метод средних прямоугольников
Для того чтобы найти площадь всей фигуры, можно воспользоваться определением интеграла и разбить всю фигуру на равные сегменты одной и той же длины. Точки на оси абсцисс, которые будут разбивать фигуру, обозначим как $x_i$. Нулевая точка при разбиении $x_0=a$, а конечная точка $x_n=b$. Для того чтобы вычислить длину одного сегмента, воспользуемся формулой:
В методе средних прямоугольников каждый сегмент заменяется на прямоугольник, за высоту которого принимается ордината середины отрезка. Получается, что площадь одного такого прямоугольника равна $S_i= frac cdot f(ξ_i)$, а площадь всей фигуры будет равна:
$int^b_a f(x)dx=fraccdot (f( ξ_0)+f( ξ_1)+. +f( ξ_)$, где $x_i≤ ξ_i≤x_$
Готовые работы на аналогичную тему
Эта формула позволяет не вычислять напрямую площадь искомой фигуры, ограниченной кривой линией, а заменить её приблизительной площадью ступенчатой фигуры, состоящей из прямоугольников.
При использовании метода средних прямоугольников так как $ξ_i=frac><2>=x_<2>>$, тогда $f( ξ_i)=f(x_<2>>)$ обозначим как $y_<2>>$,
и формула примет вид:
Эта формула называется формулой средних прямоугольников.
Методы левых и правых прямоугольников
Данные методы отличаются от метода средних прямоугольников тем, что здесь в качестве ординаты для элементарного прямоугольника выбирается либо крайнее левое значение функции $f(x)$ (и тогда метод называется методом левых прямоугольников), либо крайнее правое, и тогда метод носит название метода правых прямоугольников.
Формула для применения метода левых прямоугольников выглядит так:
$int^b_a f(x)dx=fraccdot (y_0 + y_1 + y_)left(2right)$
Формула для метода правых прямоугольников:
$int^b_a f(x)dx=fraccdot (y_1 + y_2 + y_n)left(3right)$
Формулы $(1), (2), (3)$ иначе также называются квадратурными составными формулами.
Погрешность метода прямоугольников
Для того чтобы оценить общую погрешность метода прямоугольников, необходимо рассмотреть каждый из элементарных сегментов кривой по отдельности. Общая погрешность в таком случае представляет собой сумму погрешностей всех погрешностей сегментов.
Итак, рассмотрим, чему равна погрешность на одном сегменте.
Площадь одного сегмента вычисляется по приближённой формуле:
Погрешность будем определять по разнице со значением первообразной, вычисленной с помощью формулы Ньютона-Лейбница: $δ_i= int^_> f(x)dx – f(x_+frac-x_><2>) cdot (x_i-x_)left(5right)$
Так как в левой части равенства $x_-x_$ есть не что иное как $int^x_>dx$ — длина элементарного отрезка, его можно заменить на $dx$. Перепишем правую часть равенства $(4)$, используя это:
Допуская, что фунцкия $f(x)$ дважды дифференцируема в точке $x=x_-x_$ и вокруг неё, разложим её в бесконечную сумму степенных функций, используя ряды Тейлора и формулу Лагранжа:
Применим полученное для подстановки: $f(x)-f(x_+ frac<Δx><2>)=f’(x_+frac<Δx><2>) cdot(x-(x_ + frac<Δx><2>))+f’’(ε_i) cdot frac<(x-(x_+frac<Δx><2>))^2><2>left(7right)$
В конечном итоге для элементарного сегмента $left[x_;x_iright]$ имеем:
Для всей же фигуры погрешность полученной площади составит:
и в конечном виде:
Данная формула используется для получения погрешности при использовании формулы для средних прямоугольников.
Формула для погрешности методов правых и левых прямоугольников выводится аналогичным способом и имеет следующий вид:
Погрешность, полученная с использованием метода правых или левых прямоугольников для вычисления интегралов больше, чем погрешность при использовании метода средних прямоугольников. Поэтому более предпочтительным для приближённого интегрирования является именно метод средних прямоугольников.
Вычислить интеграл $int_1^2 frac=ln2$ с точностью до $0, 001$ используя формулу средних прямоугольников.
Разобьём нашу функцию на 10 равных сегментов.
В начале оценим погрешность вычисления:
В данном случае погрешность меньше либо равна:
$|δ_n|≤0.000042$, следовательно, в данном случае для разбиения можно использовать 10 сегментов.
Разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=frac<2-1><10>=0,1$ и вычислим значение подынтегральной функции $y(x)=frac<1>$ в середине каждого отрезка:
Сумма всех вычисленных значений функции $f(x)$ составит $6.9284$, а само значение составит:
$int_1^2 frac=frac<6,9284><10>=0.69284$ — что отвечает требуемому условию о погрешности.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 25 02 2021
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/metod-prjamougolnikov/
http://spravochnick.ru/matematika/metod_pryamougolnikov/
[/spoiler]