Как найти значение косинуса 30 градусов

Косинус 30 градусов равен синусу 60 градусов.

cos30°=sin60°=√3/2 или же cos(π/6).

Никогда не любил эти синусы и косинусы потому что никогда и ничего в этом не понимал, как только в школе начали изучать эти темы так тут же мои оценки по этому предмету ухудшились.

автор вопроса выбрал этот ответ лучшим

novachok88
[1.9K]

2 месяца назад

Значение косинуса 30 градусов равно √3/2 или примерно 0.86602540378 (округлено до 11 знаков после запятой).

Это значение можно найти на многих калькуляторах или в таблицах значений тригонометрических функций. Косинус 30 градусов можно также выразить через геометрическую интерпретацию: он равен отношению прилежащего катета к гипотенузе в прямоугольном треугольнике, у которого угол между гипотенузой и прилежащим катетом равен 60 градусам, а все его стороны равны в соответствующих пропорциях.

Также можно использовать тригонометрическое тождество cos(30°) = sin(60°) = √3/2, которое следует из свойств треугольников и определений тригонометрических функций.

moreljuba
[62.5K]

6 лет назад

Между синусом и косинусом есть определённая зависимость. Так вот если мы говорим о косинусе угла в тридцать градусов, то он будет равен синусу угла в 60 градусов или же отношению корня из трёх к двойке. а вот наглядно:

Если раздедим, то получим приблизительно 0,866.

Вадим1965
[0]

3 года назад

Ни один из авторов не предложил РЕШЕНИЯ задачи: Используя единичную полуокружность, найти cos30. В ответах нет даже упоминания единичной полуокружности. А эта задача имеет решение. И оно очень простое. Надо зеркально отразить вниз единичный треугольник через катет х. Получится равносторонний единичный треугольник. Значит хорда будет равна 1. А ее половина – 0,5. Это синус 30. Косинус найдем по Основному тригонометрическому тожлеству! Вот решение задачи. А копировать таблицу Брадиса в качестве ответа – это неприлично!

Бархатные лапки
[382K]

6 лет назад

Помню эти задачки по геометрии с косинусами, сейчас даже не верится, что я могла их решать, сейчас напрочь все вылетело из головы (а может и правильно, в жизни мне они никак еще не пригодились).

Хорошо, хоть в интернете можно найти эту информацию и заодно освежить свои познания в геометрии.

Novasagova
[27.2K]

6 лет назад

Я конечно, не очень сильно люблю математику, но все – таки, некоторые знания с учебного курса остались.

Есть два варианта узнать, сколько равен косинус 30 градусов.

Первый способ – это посмотреть в таблицу, в которой ответ – это корень трех, который делится на два.

А вот точная формула:

Nelli4ka
[114K]

6 лет назад

Возьмем прямоугольный треугольник с углом в 30 градусов:

Косинус – это ничто иное, как отношение прилежащего к искомому углу (в данном случае это угол А) катета (АС) к гипотенузе (АВ). Уже из рисунка видно, что

cos(30°) = (√3)/2;

а также cos(30°) = cos(π/6)

и cos(30°) = sin(60°).

Alexgroovy
[14.6K]

6 лет назад

Косинус является одной из основных тригонометрических функций. На письме обозначается латинскими буквами cos. В прямоугольном треугольнике косинус угла со значением менее 90 градусов равен отношению прилежащего катета к гипотенузе.

Значение cos (30°) = cos (π/6) = (√3)/2.

РУДЬКО
[257K]

6 лет назад

Это совсем не сложно. Как известно, косинус 30 градусов равняется синусу 60 градусов, который в свою очередь равняется половине корня квадратного из трёх.

.Для большей наглядности, можно обратиться к рисунку

В принципе, это значение надо просто запомнить.

Помощни к
[56.9K]

7 лет назад

Калькулятор Яндекса выдает такое значение:

Но для решения задач эта цифра не всегда удобна.

В школе мы использовали таблицу специальных значений. 30 градусов – это как раз значение угла из таблицы. А вот и сама таблица значений косинуса (cos 30 = √3/2):

Для решения задач по геометрии и других задач обычно используют округленное значение, равное 0,8660.

Можно попробовать высчитать и более точное значение, если оно нужно для расчетов. Даже с помощью обычного калькулятора или онлайн калькулятора.

Птичка2014
[25.4K]

6 лет назад

Не любила в школе тригонометрию.

Существует всем известная таблица косинусов, синусов, тангенсов и катангенсов, которую просто надо запомнить. Из таблицы видно, что косинус 30 градусов = корень трех деленное на два.

Знаете ответ?

Источник

Найдем, чему равен косинус 30 градусов.

Утверждение.

$[cos {30^o} = frac{{sqrt 3 }}{2}]$

Рассмотрим прямоугольный треугольник ABC с острым углом 30 градусов:

∠C=90º, ∠A=30º.

Так как катет, лежащий против угла 30 градусов, равен половине гипотенузы, то

$[BC = frac{1}{2}AB.]$

Обозначим BC=a, тогда AB=2a (a>0).

По теореме Пифагора,

$[A{B^2} = B{C^2} + A{C^2}.]$

Значит,

$[{(2a)^2} = {a^2} + A{C^2}]$

$[A{C^2} = 4{a^2} - {a^2} = 3{a^2}]$

$[AC = sqrt {3{a^2}} = asqrt 3 .]$

По определению, косинуса острого угла прямоугольного треугольника

$[cos angle A = frac{{AC}}{{AB}}.]$

Подставляем:

$[cos angle A = frac{{asqrt 3 }}{{2a}} = frac{{sqrt 3 }}{2}.]$

Таким образом,

$[cos {30^o} = frac{{sqrt 3 }}{2}.]$

Что и требовалось доказать.

Если перевести 30 градусов в радианы:

$[{30^o} = frac{pi }{6},]$

получим значение косинуса пи на 6:

$[cos frac{pi }{6} = frac{{sqrt 3 }}{2}.]$

Источник

The value of cos 30 degrees in trigonometry is √3/2. In a right-angled triangle, cosine is the ratio of the base and hypotenuse. When the angle of the right-angled triangle is 30°, the value of cos 30° is required. In fraction form, the value of cos 30° is √3/2, and in decimal form, the value is 0.8660. Let’s understand how the value of cos 30° is obtained with examples.

What is the Value of Cos 30 Degrees?

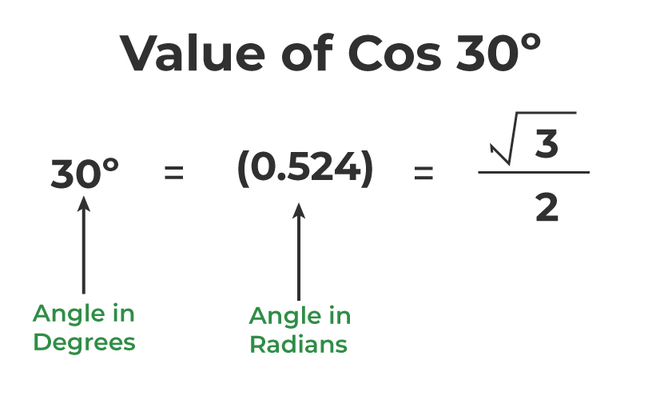
The value of cos 30 degrees in decimals is 0.8660. Converting degree to radian, that is, θ in radians = θ × π/180° or θ × Pi/180°. Therefore, converting cos 30° in radians will give cos (30 × π/180°), and the final value in radians will become cos(π/6) or cos(0.5235). Following are the values of cos 30° in different forms,

Cos 30° in decimal = 0.8660
Cos 30° in radians = cos(π/6) or cos(0.5235)
Cos 30° in fraction = √3/2
Cos (-30°) = 0.8660

Methods to Find the Value of Cos30 Degrees

In order to find the value of cos 30 degrees, the unit circle is taken into account. While looking at the unit circle, it is noticed that the value of cos 30° in the first quadrant is positive and is given as 0.8660. There are two ways to find out the value of cos 30°. The methods are mentioned below:

Using Trigonometric Functions
Using Unit Circle

Cos 30 Degrees in Terms of Trigonometric Functions

Trigonometric functions are also called circular functions or trigonometric ratios. The relationship between angles and sides is represented by these trigonometric functions. The representation of the value of cos 30° using trigonometric functions are:

Cos 30° = ± √(1 – sin² 30°)
Cos 30° = ± 1/√(1 + tan² 30°)
Cos 30° = ± cot 30°/√(1 + cot² 30°)
Cos 30° = 1/sec 30°

Cos 30 Degrees Using Unit Circle

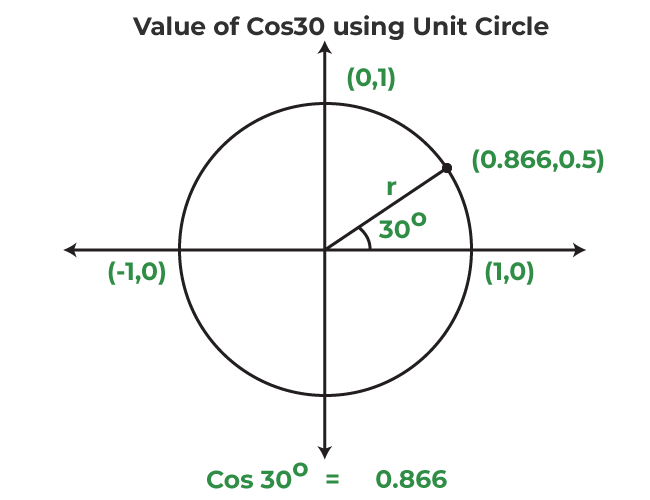
In order to find the value of cos 30 degrees using a unit circle, the following steps are required to be followed:

Rotate the ‘r’ from 0 degrees to 30 degrees in the unit circle.
The value of ‘r’ will be 0.8660 in the x-coordinate and 0.5 in the y-coordinate.
Therefore, the value of cos 30° = x = 0.8660.

Cos 30 Degrees Proof

There are two approaches to deriving the value of cos 30 degrees, they are:

Theoretical approach
Practical approach

Theoretical Approach

In the theoretical approach, the value of cos 30 degrees is obtained by observing the sides of the right-angled triangle and using Pythagoras theorem. It can be seen that if the angle of the right angle triangle is 30, we can find out the length of the opposite side, which will be half the length of the hypotenuse, but in order to find the value of cos 30, we require the length of the adjacent side as well (base of the triangle).

Applying Pythagoras theorem:

OA² = OB² + AB²

d² = OB² + (d/2)²

d² = OB² + d²/4

OB² = d² – d²/4

OB² = 3d²/4

OB = √3d/2

The value of cosine can be found by finding the ratio of the base to its hypotenuse; therefore, in this case, cos 30 degrees will be:

Cos 30° = OB/OA

Cos 30° = √3d/2 × 1/d

Cos 30° = √3/2

Practical Approach

The value of cos 30 degrees can also be observed using the practical approach. In the practical approach, the right-angled triangle is drawn, making an angle of 30 degrees, and then the value of cos 30° is observed. Following are the steps to draw the triangle:

Take a point O and draw and line.
Using the line as the baseline, make a 30-degree angle from the protector.
Draw a line from that angle found. Take any random length and draw an arc to decide where the line shall stop. Name it, Point A.
Draw the perpendicular (Vertical line) to the base from the intersection formed by the arc and the line. They will meet at B.

Value of Sin 30°

Value of Tan 30°

Solved Examples on Value of Cos 30 Degrees

Example 1: In a right-angled triangle, the base to the angle of 30° is 9m. Find the length of the Hypotenuse.

Solution:

Given: Base = 9m

Cos = √3/2

B/H = √3/2

9/H = √3/2

H = (9 × 2) / √3

H = 6√3m

Example 2: In a right-angled triangle, the hypotenuse is 16m. and one angle is 30°, find the other two sides of the triangle.

Solution:

Given, Hypotenuse = 16, angle = 30°

Cos 30 = B/H

B/H = √3/2

B/16 = √3/2

B = 8√3m

Third side is calculated using Pythagoras theorem.

P²+ B² = H²

P² + (8√3)² = 16²

P² + 192 = 256

P²= 64

p = 8m

Sides of triangle are – 8m, 8√3m, 16m.

Example 3: Find the value of 4cos 30°/sin 30°.

Solution:

The value of cos 30° in fractions is √3/2, and the value of sin 30 in fractions is 1/2. Therefore, it can be written as,

4 cos 30°/sin 30° = 4[√3/2 × 2]

= 4 × √3

= 4√3

Example 4: Find the value of sin 60° multiplied by cos 30°.

Solution:

The value of cos 30° in fractions is √3/2, and the value of sin 60° in fractions is √3/2. Therefore, it can be written as,

sin 60° × cos 30° = [√3/2 × √3/2]

sin 60° × cos 30° = 3/4

FAQs on Value of Cos 30 Degrees

Question 1: What is the value of cos 30° in terms of cot 30°?

Answer:

Any trigonometric function can be represented in terms of another trigonometric function. The value of cos θ in terms of cot θ is written as,

Cos θ = ± cot θ/√(1 + cot² θ)

Therefore, the value of cos 30 in terms of cot 30° can be written as:

Cos 30° = ± cot 30°/√(1 + cot² 30°).

Question 2: How to find the value of cos 30 degrees from a practical approach?

Answer:

The value of cos 30 can be found using a practical approach by drawing a right-angled triangle having an angle of 30 with the help of a compass, protector, and ruler. After the triangle is drawn, take the ratio of the adjacent side to the hypotenuse. The value obtained is the value of cos 30.

Cos 30° = 0.8660.

Question 3: Write the alternate forms of the value of cos 30 degrees.

Answer:

Below table explains the alternate forms of cos 30 degrees along with the value in decimals.

Forms Formula for cos 30 degrees Value of cos 30 degree

Trigonometric ratio √3/2 0.8660254

Circular system π/6 0.8660254

Centesimal system cos 33(1/3)^g 0.8660254

Question 4: What is the value of cos 30° in terms of cosec 30°?

Answer:

Any trigonometric function can be represented in terms of another trigonometric function. The value of cos θ in terms of cosec θ is written as,

Cos θ = ± [√(cosec² θ – 1)/cosec θ]

Therefore, the value of cos 30 in terms of cot 30 can be written as:

Cos 30° = ± [√(cosec² 30° – 1)/cosec 30°].

Last Updated :
02 Sep, 2022

Like Article

Save Article

Источник

Многих девятиклассников и восьмиклассников кидает в дрожь, когда учитель спрашивает чему равен косинус 60 градусов и строго наказывает учить “табличку”. А для того чтобы ее выучить, достаточно один раз понять, откуда берутся эти значения в табличке.

Начнем с определений. Без них конечно вообще невозможно понять, что такое синус, косинус и тангенс. На то они и определения…

Вспомним как называются стороны прямоугольного треугольника, а также понятия противолежащая и прилежащая стороны.

Что такое синусы и косинусы. Откуда взялись табличные значения синусов и косинусов для 30°, 60° и 45°

Выходит, что синус и косинус это отношения, т.е. безразмерный числовой коэффициент. Этот числовой коэффициент является связующим звеном между сторонами и углами в прямоугольном треугольнике.

Аналогично, тангенс является отношением сторон прямоугольного треугольника, а также отношением синуса к косинусу одного и того же угла.

Из определений синуса и косинуса острого угла прямоугольного треугольника можно заметить:

Это нам понадобится для вывода синуса и косинуса углов 30 и 60 градусов.

А теперь посмотрим, откуда берутся значения синуса и косинуса для углов 30, 60, 45 градусов…

Итак, во-первых, вспоминаем, что против угла 30° в прямоугольном треугольнике лежит катет равный половине гипотенузы (1/2с). Далее выражаем второй катет через “с” по теореме Пифагора. Найденные значения подставляем в определение синуса и косинуса. “с” сокращается и остаются числовые значения.

Угол 60° является вторым острым углом прямоугольного треугольника с углом 30°, а значит его косинус равен синусу 30°, аналогично синус 60° равен косинусу 30°.

Далее по определению находим тангенс этих углов.

Не трудно догадаться, если синус и косинус 45° равны, то тангенс 45° равен 1 🙂

Вывод этих формул поможет не только запомнить значения синуса и косинуса основных углов, но и научит решать простейшие задачи.

Сами задачи посмотрим в следующей статье завтра

А пока…

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

canva.com

Источник

Значения тригонометрических функций синуса, косинуса, тангенса при α=30°

Рассмотрим равносторонний треугольник АВС. Пусть, каждая из его сторон будет равна a. Согласно свойствам равностороннего треугольника, все его углы равны, в том числе угол ∠В=60°.

Значения синуса, косинуса и тангенса мы можем вычислить, если найдем соотношение соответствующих сторон для угла 30 градусов в прямоугольном треугольнике. Так как значение этих тригонометрических функций зависит исключительно от градусной меры угла, то вычисленные нами соотношения и будут значениями синуса 30, косинуса 30 и тангенса 30 градусов.

Сначала совершим дополнительные построения. Из вершины А на сторону BC проведем медиану AO.

Медиана АО в равностороннем треугольнике одновременно является биссектрисой и высотой.

Тогда треугольник АОВ – прямоугольный с углом ∠ВАО=30°. (Угол В равен 60 градусам, ∠ВOA прямой и равен 90 градусам, следовательно, ∠ВАО = 180 – 90 – 60 = 30 градусов)

Значення тригонометричних функцій синуса, косинуса, тангенса при α=30°

Розглянемо рiвнобiчний трикутник АВС. Хай, кожна з його сторін буде рівна а. Згідно з властивостями рівностороннього трикутника, всі його кути рівні, у тому числі кут ∠В=60°.

Значення синуса, косинуса і тангенса ми можемо обчислити, якщо знайдемо співвідношення відповідних сторін для кута 30 градусів в прямокутному трикутнику. Оскільки значення цих тригонометричних функцій залежить виключно від градусної міри кута, то обчислені нами співвідношення і будуть значеннями синуса 30, косинуса 30 і тангенса 30 градусів.

Спочатку зробимо додаткові побудови. З вершини А на сторону BC проведемо медіану АO.

Медіана АО у рівносторонньому трикутнику одночасно є бісектрисою і висотою.

Тоді тикутник АОВ – прямокутний з кутом ∠ВАО=30°. (Кут В дорівнює 60 градусам ∠ВOA прямій і дорівнює 90 градусам, отже ∠ВАО = 180 – 90 – 60 = 30 градусів)

Для полученного прямоугольного треугольника вычислим значения тригонометрических функций его углов. Сделаем это сначала для угла 30 градусов.

Величина гипотенузы нам известна и равна a. Катет OB равен a/2 , так как AO – медиана треугольника ABC. Найдем катет AO.

По теореме Пифагора:

АВ²=АО²+ОВ²;

АО²=АВ²-ОВ²

подставим в полученное выражение значение гипотенузы (мы приняли, что оно равно а)

АО²=a²– (а/2)²

АО²=3a²/4

AO=√( 3a²/4 ) =a√3/2

Теперь мы вычислили все стороны прямоугольного треугольника ABO. Учитывая, что AB = a, OB = a/2, AO = a√3/2, из соотношений сторон прямоугольного треугольника рассчитаем полученные значения. Согласно определению синуса, косинуса и тангенса:

sin 30 = OB / AB (по определению синуса – отношение противолежащего катета к гипотенузе)

cos 30 = AO / AB (по определению косинуса – отношение прилежащего катета к гипотенузе)

tg 30 = OB / AO (по определению тангенса – отношение противолежащего катета к прилежащему)

Откуда:

Так как треугольник ABC – равносторонний, то BO равно AB/2, а значение AO вычислено выше. В результате получаем табличные значения sin 30, cos 30 и tg 30 градусов

Для отриманого прямокутного трикутника обчислимо значення тригонометричних функцій його кутів. Зробимо це спочатку для кута 30 градусів.

Величина гіпотенузи нам відома і рівна а. Катет OB рівний a/2, оскільки АO – медіана трикутника ABC. Знайдемо катет АТ.

По теоремі Піфагора:

АВ²=АО²+ОВ²;

АО²=АВ²-ОВ²

пiдставимо в одержане рiвняння значення гiпотенузи (намi прийнято, що воно равно а)

АО²=a²– (а/2)²

АО²=3a²/4

AO=√( 3a²/4 ) =a√3/2

Тепер ми обчислили всі сторони прямокутного трикутника ABO. Враховуючи, що AB = a, OB = a/2, AO = a√3/2, iз спiввiдношень сторiн прямокутного трикутника розрахуємо одержанi значення. Згiдно визначенню сiнуса, косiнуса та тангенса:

sin 30 = OB / AB (за визначенням синуса – відношення катета, що протилежить, до гіпотенузи)

cos 30 = AO / AB (за визначенням косинуса – відношення прилеглого катета до гіпотенузи)

tg 30 = OB / AO (за визначенням тангенса – відношення катета, що протилежить, до прилеглого)

Звiдки маємо:

Враховуючи, що трикутник ABC – рiвнобiчний, то BO равно AB/2, а значення AO розраховано вище. В результатi одержуємо табличнi значення sin 30, cos 30 и tg 30 градусiв

То есть:
Тангенс 30 градусов равен корню из трех на три
Синус 30 градусов равен одной второй или 0,5
Косинус 30 градусов равен корню из трех на два

Источник

What is the Value of Cos 30 Degrees?

Methods to Find the Value of Cos30 Degrees