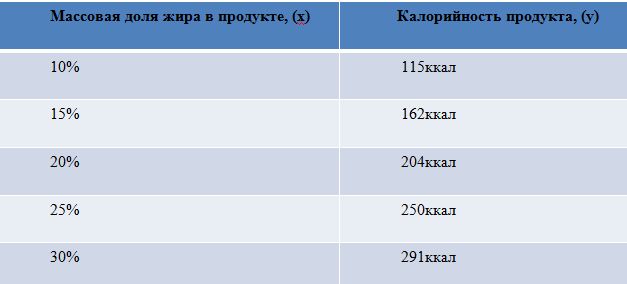
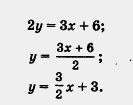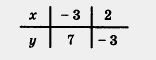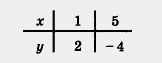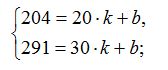построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Обновлено: 19.05.2023
Так как функция линейная, то будет возрастать (или убывать) на всем множестве определения, поэтому достаточно найти значение функции на концах отрезка.
Ответ: наибольшее значение 1, наименьшее -5.
- Написать правильный и достоверный ответ;
- Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;
- Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Применяя эту формулу, зная конкретное значение (x), можно вычислить соответствующее значение (y).
Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.
В жизни существует множество ситуаций, которые можно описать математической моделью с помощью линейных функций.
на овощной базе хранится (700) т картофеля. Каждый день запасы пополняют на (30) т. Сколько картофеля станет на овощной базе через (2); (4); (10) дней?
После (x) дней количество (y) картофеля на овощной базе можно записать в виде формулы (y = 700 + 30x).
Если функцию (y = kx + m) надо исследовать только для значений (x) из некоторого множества (X), то записывают y = kx + m , x ∈ X .
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
b) y = 1 3 x + 1, x ∈ − 6 ; 3 , концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Наибольшее и наименьшее значения функции на множестве
(основные определения)
Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x) .
Определение 1. Значение f (x0) функции y = f (x) в точкеназывают наибольшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наибольшее значение функции f (x) на множестве X часто обозначают
Определение 2. Значение f (x0) функции y = f (x) в точке называют наименьшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наименьшее значение функции f (x) на множестве X часто обозначают
Определение 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .
Пример 1. Минимальным значением функции y = x 2 на множестве является число 0 (рис. 1).
Максимального значения функция y = x 2 на множестве не имеет.
Пример 2. Максимальным значением функции y = – x 2 на множестве является число 0 (рис. 2).
Минимального значения функция y = – x 2 на множестве не имеет.
Пример 3. Функция y = x на множестве не имеет ни максимального, ни минимального значений (рис. 3).
Пример 4. Функция y = arctg x на множестве не имеет ни максимального, ни минимального значений (рис. 4).
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса
Как мы видели в примерах 1 – 4, даже такие хорошо известные функции, как
не имеют наибольших или наименьших значений на множестве. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.
Теорема Вейерштрасса. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.
Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.
Примеры решения задач
| y = 2x 3 + 3x 2 – 36x + 30 | (1) |
Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:
| y (2) = – 14 , |
| y (– 2) = 98 , |
| y (4) = 62 . |
Ответ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наменьшее значение функции (1) на отрезке [–2, 4] равно – 14 .
на отрезке [–1, 27] .
Решая уравнение y’ = 0 , получим
Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0, и , причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, и , а также на концах отрезка x = – 1 и x = 27 , получим:
| y (0) = 0 , |
| y (– 1) = – 1 , |
| y (27) = 99 . |
Ответ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наменьшее значение функции (3) на отрезке [–1, 27] равно – 1 .
Решение. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:
В точке x = 0 производная функции (5) не существует. Критическими точками являются точки
Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:
| y (0) = – 4 , |
| y (3) = – e 3 , |
| y (5) = e 5 , |
| y (– 1) = – 5e , |
| y (6) = 2e 6 . |
Ответ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6 , а наменьшее значение функции (5) на отрезке [–1, 6] равно – e 3 .
| y = (x – 27) e 28 – x | (6) |
на отрезке [23, 40] .
В некоторых задачах нужно найти наибольшее и наименьшее значения функции. Если неизвестен алгоритм и основные правила, то простое задание превращается в изнурительный труд, который очень редко приносит положительные результаты. В интернете существует множество информации, но не вся она достоверна. Самое страшное — применение неверных методик нахождения.
Общая информация
Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
- Нахождение области определения функции (ОДФ).
- Понятие дифференциала и основные методы его нахождения.
- Умение решать уравнения.
- Знание графиков простых функций.
- Основные типы функций, полуинтервал и интервал.
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Область определения
Обозначение интервалов
Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:
Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
- Алгебраические: рациональные и иррациональные.
- Тригонометрические: sin, cos, tg и ctg.
- Трансцендентные: степенные, показательные и логарифмические.
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
- Найти корни уравнения знаменателя, приравнивая его к 0.
- Определить интервал, значения из которого может принимать аргумент.
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.
Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x – 1) * (x + 1) * (10 – x)^(1/2)]). Решать ее необходимо по такому алгоритму:
- Знаменатель является сложным. Он состоит из двух выражений: (x – 1) * (x + 1) и (10 – x)^(1/2).
- Первое выражение (решить уравнение): (x – 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
- Второе (неравенство): (10 – x) a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.
Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.
Примеры решений
Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:
- D(y): все множество Z.
- Отрезок входит в D(y).
- Производная: y’ = [x^2 + 6x + 9]’ = 2x + 6 (существует во всех точках).
- Стационарные точки (y’ = 0): 2x + 6 = 0. Отсюда, x = -3.
- Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 – 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
- Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.
Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
- D(z) — все значения от бесконечно малого до бесконечно большого чисел.
- Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
- Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
- Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.
Читайте также:
- Обработка кокеток план урока
- Счастлив ли мечтатель белые ночи кратко
- План урока рог1аллин терахьдешнаш 6 класс
- Почему в русских школах учат немецкий язык
- Проект по вокалу в доу
§ 9 ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК
1. Преобразование уравнения ах + by + с = 0 к виду у = kx + m
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 8, при всей его чёткости и определённости математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + by + с = 0, затем ах2 + by + с = 0? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим.
Рассмотрим сначала уравнение Зх — 2у + 6 = 0 (см. пример 2 из § 8), т. е. 2у = Зх + 6.
Умножив обе части уравнения на ½ получим …
Впрочем, тот же результат мы получили бы, если обе части исходного уравнения почленно разделили на 2. Обычно предпочитают в подобных случаях говорить не об умножении, а о почленном делении обеих частей уравнения на одно и то же число.
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем у = 9. Видите, как легко и быстро найдены точки (0; 3), (-2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 8.
Точно так же уравнение 5х — 2у = 0 (см. пример 4 из § 8) можно было преобразовать к виду 2у = 5х и, далее, у = 2,5х; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению. Наконец, уравнение Зх + 2у — 16 = 0 из того же примера можно было преобразовать к виду 2у = 16 — Зх и, далее, у — 8 — -х.
Из этого уравнения можно найти решения (0; 8) и (2; 5), которые ему удовлетворяют.
Рассмотрим теперь указанные преобразования в общем виде.
Случаи, когда в уравнении ах + by + с = 0 коэффициенты а и b равны нулю, мы рассмотрели в § 8. Там же мы отметили, что в случае, когда а Ф О, b = 0, графиком уравнения является прямая, параллельная оси у.
Рассмотрим случай, когда b ≠ 0. Имеем ах + by + с = 0; (1) bу = -ах – с;
Введя обозначения … получаем у = kx + m.
Таким образом, линейное уравнение (1) с двумя переменными х и у в случае, когда b ≠ 0, можно преобразовать к виду у = kx + m (2) где k, m — числа (коэффициенты).
Это частный вид линейного уравнения. Зная, чему равен х, по правилу у = kx + m всегда можно найти, чему равен у. Будем называть уравнение (2) линейной функцией.
С помощью уравнения (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например, у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
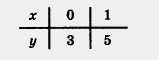
Обычно эти результаты оформляют в виде таблицы:
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3 соответственно в точках х = 0, х = 1, х = -1, х = 3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаём одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Частным случаем теоремы 1 из § 8 является следующая теорема.
ТЕОРЕМА 2. Графиком линейной функции у = kx + m является прямая.
ПРИМЕР 1. Построить график линейной функции у = 2х + 3.
Решение: Составим таблицу:
х I 0 I 1
У I 3 I 5
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведём через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 34).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = kx + m, где k, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными x и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между хну. Это неважно, главное — понимать, что во всех случаях речь идёт о математической модели у = kx + m.
2. Линейные функции как математические модели реальных ситуаций
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведём примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдёт х дней, то количество у угля на складе (в тоннах) выразится формулой у = 500 + ЗОх. Таким образом, линейная функция у = ЗОх + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
- при х = 2 имеем у = 560 (в уравнение у = ЗОх + 500 подставили х = 2 и получили у = 560);
- при х = 4 имеем у = 620;
- при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 — ЗОх. С помощью этой модели нетрудно ответить на вопрос задачи:
- если х = 2, то у = 440 (в уравнение у = 500 — ЗОх подставили х = 2 и получили у = 440);
- если х = 4, то у = 380;
- если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до пункта В, а затем продолжил движение в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от пункта А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у = 15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
- если х = 2, то у = 23 (в уравнение у = 15 + 4х подставили х = 2 и получили у = 23);
- если х = 4, то у = 31;
- если х = 6, то у = 39.
Итак, в каждой из рассмотренных ситуаций математической моделью служит линейная функция. Но (внимание!), строго говоря, все три составленные модели не совсем точны, они не учитывают тех ограничений на переменную, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, …, поскольку х — число дней. Следовательно, уточнённая математическая модель первой ситуации выглядит так:
у = 500 + ЗОх, где х — натуральное число.
Вторую ситуацию необходимо уточнить условием у > 0. Это значит, что независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, …, 16. Действительно, если х = 16, то по формуле у = 500 — ЗОх находим у = 500 — 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придётся прекратить. Следовательно, уточнённая математическая модель второй ситуации выглядит так:
у = 500 — ЗОх, у > 0 или у = 500 — ЗОх, где х = 1, 2, 3, …, 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (х = 0, х = 2, х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было принять разумные ограничения для х, скажем, 0 < х < 6 (т.е. турист идёт не более 6 ч).
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0; 6] координатной прямой (рис. 35). Значит, уточнённая модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0; 6].
Условимся вместо фразы «х принадлежит множеству X» писать х е X (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. Множество натуральных чисел обычно обозначают буквой N. Значит, вместо фразы «х — натуральное число» мы можем использовать соотношение х е N.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового множества X, то пишут у = kx + m, х ∈ Х.
А теперь запишем более точные математические модели для рассмотренных выше трёх ситуаций.
- Первая ситуация: у = 500 + ЗОх, х е N.
- Вторая ситуация: у = 500 — ЗОх, х е {1, 2, 3, …, 16}.
- Третья ситуация: у = 15 + 4х, х е [0; 6].
3. Построение графика линейной функции на заданном промежутке
Построить график линейной функции:
Решение: а) Составим таблицу для линейной функции у = -2х + 1:
х | -3 | 2
y I 7 I -3
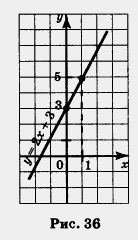
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведём через них прямую линию. Это график уравнения у = -2х + 1. Далее выделим отрезок, соединяющий построенные точки (рис. 36). Этот отрезок и есть график линейной функции у = -2х + 1, где х е [-3; 2].
Обычно говорят, что мы построили график линейной функции у = -2х + 1 на отрезке [-3; 2].
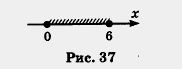
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и графиком её служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3; 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (-3; 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 5. Точно так же и точки (-3; 7) и (2; -3) придётся отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = -2х + 1, которые лежат между точками, отмеченными кружочками (рис. 37). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 38). Это непринципиально: главное — понимать, о чём идёт речь.
ПРИМЕР 3. На координатной прямой отмечены точки А(-4), В(-3). Найти наибольшее и наименьшее значения линейной функции у = х/2 + 4 на отрезке [0; 6].
Решение: Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведём через них прямую — график линейной функции
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0; 6], т. е. для х е [0; 6]. Соответствующий отрезок графика выделен на чертеже. Обратим внимание, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции у = х/2 + 4 на отрезке [0; 6]. Обычно используют такую запись:
Замечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 40 части прямой, равна 4 — это и есть наименьшее значение линейной функции у — iх + 4 на отрезке [0; 6]. Обычно используют такую запись:
Ответ: унаиб = 7, унаим = 4.
ПРИМЕР 4. Найти унаиб и унаим для линейной функции у = -1,5х + 3,5:
- а) на отрезке [1; 5];
- б) на интервале (1; 5);
- в) на полуинтервале [1; 5);
- г) на луче [0; +оо);
- д) на луче (~°°; 3].
Решение
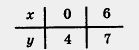
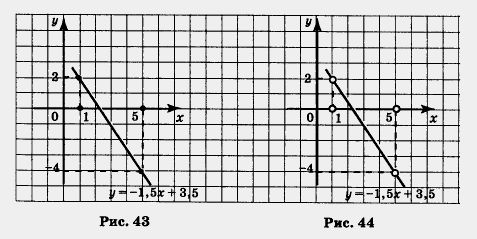
Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (1; 2) и (5; -4) и проведём через них прямую (рис. 41—45). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1; 5] (рис. 41), из интервала (1; 5) (рис. 42), из полуинтервала [1; 5) (рис. 43), из луча [0; +°°) (рис. 44), из луча (~°°; 3] (рис. 45).
а) С помощью рисунка 41 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим = -4 (этого значения линейная функция достигает при х = 5).
б) В отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены (рис. 42). Среди остальных точек графика нет ни точки с наименьшей ординатой, ни точки с наибольшей ординатой. Значит, ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет.
в) С помощью рисунка 43 заключаем, что унаиб 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим не существует (рис. 44).
д) унаим = -1 (этого значения линейная функция достигает при х — 3), а унаиб не существует (рис. 45).
4. Свойства линейной функции
ПРИМЕР 5. Построить график линейной функции у = 2х — 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0;
б) при каких значениях х будет у > 0;
в) при каких значениях х будет у < 0?
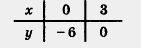
Решение: Составим таблицу для линейной функции у = 2х — 6:
Через точки (0; -6) и (3; 0) проведём прямую — график линейной функции у = 2х — 6 (рис. 46).
- а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у — 0.
- б) у > 0 при х > 3. В самом деле, если х > 3, то соответствующая часть прямой расположена выше оси х, значит, ординаты соответствующих точек прямой положительны.
- в) у < 0 при х < 3. В самом деле, если х < 3, то соответствующая часть прямой расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны.
Обратите внимание, что в этом примере мы с помощью графика решили:
- а) уравнение 2х — 6 = 0 (получили х = 3);
- б) неравенство 2х — 6 > 0 (получили х > 3);
- в) неравенство 2х — 6 < 0 (получили х < 3).
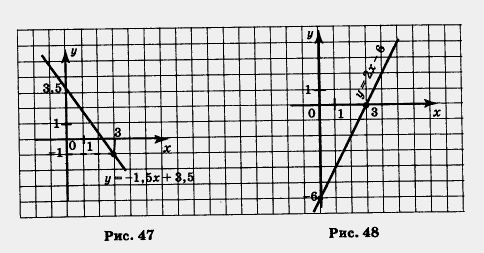
Рассмотрим график линейной функции, изображённый на рисунке 47, а. Если двигаться по этому графику слева направо, то ординаты точек графика всё время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если к > 0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображённый на рисунке 47, б. Если двигаться по этому графику слева направо, то ординаты точек графика всё время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < 0, то линейная функция у = kx + m убывает.
ПРИМЕР 6. На рисунке 48 изображён график движения автомобиля между пунктами 1 и 2. По оси t отмечено время (в часах), по оси S — расстояние до пункта 1. Требуется охарактеризовать весь процесс движения словами.
Решение: Точка А соответствует началу движения. До пункта 2 автомобиль доехал за 1 1/3 ч — об этом можно судить по абсциссе точки D. Пройденное расстояние равно 50 км — об этом можно судить по ординате точки D. Значит, можно вычислить скорость движения автомобиля: v = 50 : 4/3 = 37,5 км/ч.
На участке графика DE ордината постоянна, т. е. расстояние от пункта 1 не менялось. Это значит, что автомобиль не двигался (стоял в пункте 2). Причём он стоял в промежутке от 1^ ч до 2-| ч (это абсциссы точек D и Е). Остановка длилась, таким образом, 1 ч 20 мин.
На обратный путь после остановки автомобиль потратил столько же времени, сколько на путь от 1 до 2, значит обратно он ехал с той же скоростью.
Вопросы для самопроверки
- Что такое линейная функция?
- Что является графиком линейной функции?
- Сколько точек достаточно взять для построения графика линейной функции?
- Опишите процесс построения графика линейной функции у = 2х + 3, где х е [0; 2]. Что изменится, если х е (0; 2)?
- Дана линейная функция у = kx + m, х е X, где X — некоторый числовой промежуток. Что такое унаим, унаиб?
- Дано: у = 2х + 3, х е [0; +оо). Найдите, если возможно, унаим, унаиб. Что изменится, если х е (0; +оо)? если х е (—оо; 0]? если X € (-оо; 0)?
- Как с помощью графика линейной функции у = kx + m, где k Ф 0, решить: а) уравнение kx + m = 0; б) неравенство kx + m > 0; в) неравенство kx + m < 0?
- В каком случае линейная функция возрастает, а в каком — убывает? Как об этом можно судить по графику линейной функции?
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Линейная функция и ее график
Линейная функция и ее график
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 28, при всей его четкости и определенности математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + Ьу + с = О, затем ахг + Ьу + с = О? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала уравнение 3x – 2у + 6 = 0 (см. пример 2 из § 28).
Имеем:
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем: у = 9.
Видите, как легко и быстро найдены точки (0; 3), (- 2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 28.
Точно так же уравнение Ьх – 2у = 0 (см. пример 4 из § 28) можно было преобразовать к виду 2у =16 -3x . далее у = 2,5x; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению.
Наконец, уравнение 3x + 2у – 16 = 0 из того же примера можно преобразовать к виду 2y = 16 -3x и далее нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют.
Рассмотрим теперь указанные преобразования в общем виде.
Имеем:
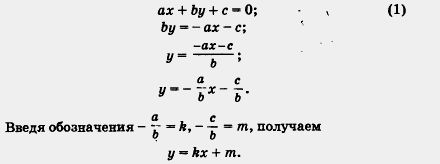
Таким образом, линейное уравнение (1) с двумя переменными х и у всегда можно преобразовать к виду
y = kx + m,(2) где k,m — числа (коэффициенты), причем .
Этот частный вид линейного уравнения будем называть линейной функцией.
С помощью равенства (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например,
у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
Обычно эти результаты оформляют в виде таблицы:
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3, соответственно, в точках х = 0, х = 1, х = -1,х=-3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаем одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Обратите внимание: линейная функция – это специальный вид линейного уравнения с двумя переменными. Графиком уравнения у — kx + т, как всякого линейного уравнения с двумя переменными, является прямая — ее называют также графком линейной функции y = kx + тп. Таким образом, справедлива следующая теорема.
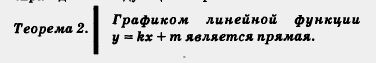
Пример 1. Построить график линейной функции у = 2х + 3.
Решение. Составим таблицу:
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведем через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 36).
Замечание. В § 25 мы уже говорили о том, как обстоит дело в математике с новыми понятиями, новыми терминами. Часто бывает так: ввели новое понятие, работают с ним, но затем, по мере дальнейшего изучения математики, начинают осознавать, что введенное понятие требует уточнения, развития. Именно так обстояло дело с понятием «тождество». Точно так же обстоит дело и с понятием «функция». Мы еще довольно долго будем привыкать к нему, набираться опыта, работать с этим понятием пока не придем к строгому определению (зто будет в 9 классе).
Практические задания
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.Приведем примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдет х дней, то количество у угля на складе (в тоннах) выразится формулой у — 500 + ЗОд:. Таким образом, линейная функция у = З0x + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
при х = 2 имеем у = 560 (в уравнение у = ЗОд: + 500 подставили
х = 2 и получили у = 560);
при х = 4 имеем у = 620;
при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4,10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 – З0x. С помощью этой модели нетрудно ответить на вопрос задачи:
если х = 2, то у = 440 (в уравнение у = 500 – З0x подставили
х — 2 и получили у = 440);
если х = 4, то у = 380;
если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до Б, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
если х = 2, то у = 23 (в уравнение у = 15 + 4д: подставили х = 2
и получили у = 23);
если д: = 4, то у = 31;
если х = 6, то у = 39.
На самом деле во всех математических моделях этих трех ситуаций мы допустили неточности, поскольку ничего не сказали о тех ограничениях на х, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, …, поскольку х — число дней.
Следовательно, уточненная математическая модель первой ситуации выглядит так:
у = 500 + З0x, где х — натуральное число.
Во второй ситуации независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, …, 16. Действительно, если х = 16, то по формуле у = 500 – З0x находим: у = 500 – 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придется прекратить. Следовательно, уточненная математическая модель второй ситуации выглядит так:
у = 500 – ЗОд:, где х = 1, 2, 3, …. 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (напр., значение х = 0, значение х = 2, значение х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было сделать разумные ограничения на х, скажем, 0 < х < 6 (т. е. турист идет не более 6 ч).
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0, 6] (рис. 37). Значит, уточненная модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0, 6].
Условимся вместо фразы «х принадлежит множеству X» писать (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового промежутка X, то пишут:
Пример 2. Построить график линейной функции:
Решение, а) Составим таблицу для линейной функции y = 2x + 1
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведем через них прямую линию. Это — график уравнения у = -2x: + 1. Далее, выделим отрезок, соединяющий построенные точки (рис. 38). Этот отрезок и есть график линейной функции у = -2х+1, гдехе [-3, 2].
Обычно говорят так: мы построили график линейной функции у = – 2х + 1 на отрезке [- 3, 2].
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и ее графиком служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3, 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (- 3, 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 26. Точно так же и точки (- 3; 7) и B; – 3) придется отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = – 2х + 1, которые лежат между точками, отмеченными кружочками (рис. 40). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 41). Это непринципиально, главное, понимать, о чем идет речь.
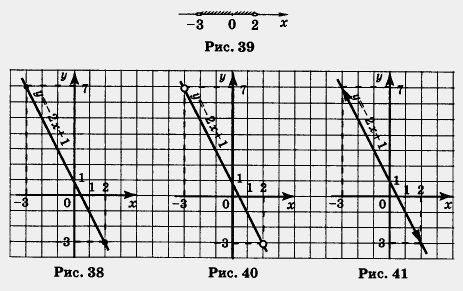
Пример 3. Найти наибольшее и наименьшее значения линейной функции на отрезке [0, 6].
Решение. Составим таблицу для линейной функции
Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведем через них прямую — график линейной х функции (рис. 42).
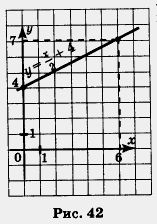
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0, 6], т. е. для х е [0, 6].
Соответствующий отрезок графика выделен на чертеже. Замечаем, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции на отрезке [0, 6]. Обычно используют такую запись: унаиб =7.
Отмечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 42 части прямой, равна 4 — это и есть наименьшее значение линейной функции на отрезке [0, 6].
Обычно используют такую запись: yнаим. = 4.
Пример 4. Найти унаиб и yнаим. для линейной функции y = -1,5x + 3,5
а) на отрезке [1,5]; б) на интервале (1,5);
в) на полуинтервале [1, 5); г) на луче [0, + со);
д) на луче (- со, 3].
Решение. Составим таблицу для линейной функции у = -l,5x + 3,5:
Построим на координатной плоскости хОу точки (1; 2) и (5; – 4) и проведем через них прямую (рис. 43-47). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1,5] (рис. 43), из интервала A, 5) (рис. 44), из полуинтервала [1, 5) (рис. 45), из луча [0, + со) (рис. 46),из луча(- со, 3] (рис. 47).
а) С помощью рисунка 43 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим. = – 4 (этого значения линейная функция достигает при х = 5).
б) Используя рисунок 44, делаем вывод: ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет. Почему? Дело в том, что, в отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены.
в) С помощью рисунка 45 заключаем, что yнаиб. = 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) Используя рисунок 46, делаем вывод: унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим. не существует.
д) С помощью рисунка 47 делаем вывод: yнаим = -1 (этого значения линейная функция достигает при х = 3), а унаиб., не существует.
Пример 5. Построить график линейной функции
у = 2х – 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0?
б) при каких значениях х будет у > 0?
в) при каких значениях х будет у < 0?
Ре ш е ни е. Составим таблицу для линейной функции у = 2х- 6:
Через точки (0; – 6) и (3; 0) проведем прямую — график функции у = 2х – 6 (рис. 48).
а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у = 0.
б) у > 0 при х > 3. В самом деле если х > 3, то прямая расположена выше оси ж, значит, ординаты соответствующих точек прямой положительны.
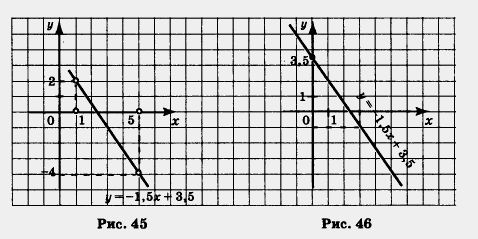
в) у < 0 при х < 3. В самом деле если х < 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны. A
Обратите внимание, что в этом примере мы с помощью графика решили:
а) уравнение 2х – 6 = 0 (получили х = 3);
б) неравенство 2х – 6 > 0 (получили х > 3);
в) неравенство 2x – 6 < 0 (получили х < 3).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = кх + m, где к, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными х и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между х и у. Это неважно, главное, понимать, что во всех случаях речь идет о математической модели у = кх + m
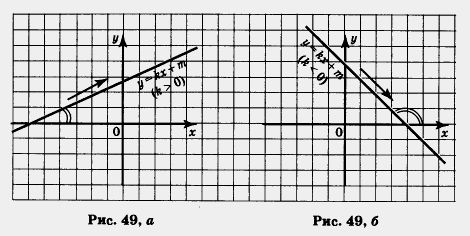
Рассмотрим график линейной функции, изображенный на рисунке 49, а. Если двигаться по этому графику слева направо, то ординаты точек графика все время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если k>0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображенный на рисунке 49, б. Если двигаться по этому графику слева направо, то ординаты точек графика все время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < О, то линейная функция у = kx + m убывает.
Линейная функция в жизни
А теперь давайте подведем итог этой темы. Мы с вами уже познакомились с таким понятие, как линейная функция, знаем ее свойства и научились строить графики. Так же, вы рассматривали частные случаи линейной функции и узнали от чего зависит взаимное расположение графиков линейных функций. Но, оказывается, в нашей повседневной жизни мы также постоянно пересекаемся с этой математической моделью.
Давайте мы с вами подумаем, какие реальные жизненные ситуации связаны с таким понятием, как линейные функции? А также, между какими величинами или жизненными ситуациями, возможно, устанавливать линейную зависимость?
Многие из вас, наверное, не совсем представляют, зачем им нужно изучать линейные функции, ведь это вряд ли пригодится в дальнейшей жизни. Но здесь вы глубоко ошибаетесь, потому что с функциями мы сталкиваемся постоянно и повсюду. Так как, даже обычная ежемесячная квартплата также является функцией, которая зависит от многих переменных. А к этим переменным относится метраж площади, количество жильцов, тарифов, использование электроэнергии и т.д.
Конечно же, самыми распространенными примерами функций линейной зависимости, с которыми мы с вами сталкивались – это уроки математики.
Мы с вами решали задачи, где находили расстояния, которые проезжали машины, поезда или проходили пешеходы при определенной скорости движения. Это и есть линейные функции времени движения. Но ведь эти примеры применимы не только в математике, они присутствуют в нашей повседневной жизни.
Калорийности молочных продуктов зависит жирности, а такая зависимость, как правило, является линейной функцией. Так, например, при увеличении сметане процента жирности, увеличивается и калорийность продукта.
Теперь давайте сделаем подсчеты и найдем значения k и b, решив систему уравнений:
Теперь давайте выведем формулу зависимости:
y = 8,7x + 30
В итоге мы получили линейную зависимость.
Чтобы знать скорость распространения звука в зависимости от температуры, возможно, узнать, применив формулу: v = 331 +0,6t, где v – скорость (в м/с), t – температура. Если мы начертим график этой зависимости, то увидим, что он будет линейным, то есть представлять прямую линию.
И таких практических использований знаний в применении линейной функциональной зависимости можно перечислять долго. Начиная от платы за телефон, длины и роста волос и даже пословиц в литературе. И этот список можно продолжать до бесконечности.
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно нами строится выражение этих значений в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x), чтобы вам не нужно было искать это самостоятельно онлайн.
Основные определения
Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.
Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Минимальное значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или то, что больше всего, значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы можем определить наибольшее или найти наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с интервалом, не имеющим конца. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения (мало и много). В этих случаях определить или найти наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
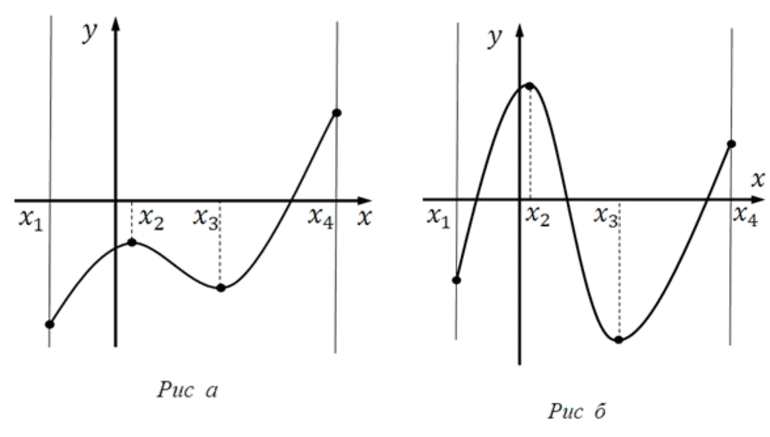
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
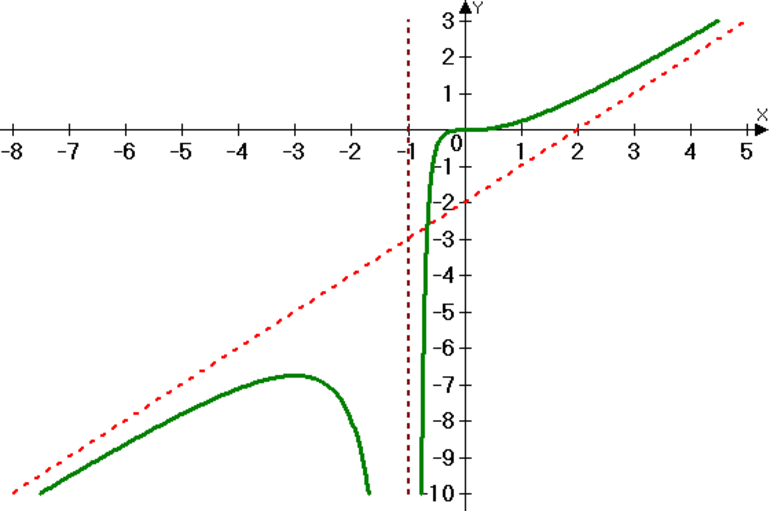
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
Как найти наибольшее и наименьшее значение функции на отрезке?
В этом пункте мы приведем последовательность действий, которую нужно выполнить, чтобы найти наибольшее значение функции на некотором отрезке или как найти наименьшее значение функции.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] – max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] – max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный (квадратичный) трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определяться с наименьшим значением функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.