Как найти значение линейной функции в точке - Сайт, где вы сможете решить свои вопросы

Определение

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
Областью значений также является множество всех действительных чисел.
Функция не имеет ни наибольших, ни наименьших значений.
При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
При k=0 прямая параллельна оси х.
Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

у=2х – 1=2×0 – 1= –1;

у=2х – 1=2×3 – 1= 5.

Вписываем в таблицу значения у:

Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.

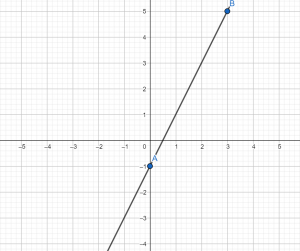
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

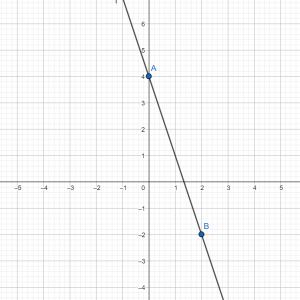
Пример №3

Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

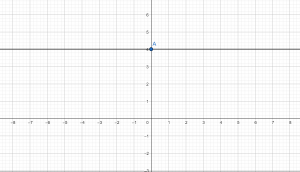
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.

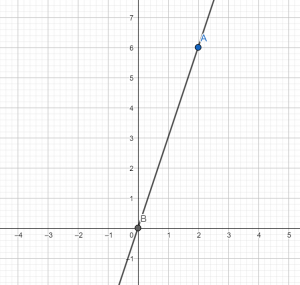
Задание OM1106o

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ГРАФИКИ:

КОЭФФИЦИЕНТЫ:

1) k>0, b<0 2) k>0, b>0 3) k<0, b<0

ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>90⁰) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.

У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<90⁰). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

Ответ: 213

pазбирался: Даниил Романович | обсудить разбор

Задание OM1103o

Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x

Б) y = -3x

В) y = (1/3)x

Графики:

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

y = kx + b

График данной функции зависит от k и b.

если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1

Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 6.1k

Источник

Содержание:

Рассмотрим уравнение с двумя неизвестными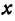

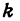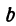где и —заданные числа. Этому уравнению удовлетворяет бесконечное множество пар чисел 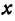и .

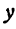Например, уравнению

удовлетворяют следующие пары:

и т. д.

Для того чтобы найти пару чисел, удовлетворяющих уравнению 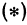, нужно придать произвольное числовое значение и подставить в уравнение 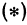, тогда получит определенное числовое значение. Например, если 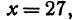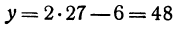. Очевидно, что пара чисел 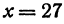и 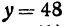удовлетворяет уравнению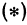. Так же и в случае уравнения (1) можно придать произвольное числовое значение и получить для соответствующее числовое значение.

Так как в данном уравнении может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то называют независимой переменной величиной или аргументом.

Для получаются также различные значения, но уже в зависимости от выбранного значения ; поэтому называют зависимым переменным или функцией.

Функцию , определяемую уравнением (1), называют линейной функцией.

Пример:

Вычислить значения линейной функции, определяемой уравнением 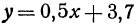, при следующих значениях независимого переменного: .

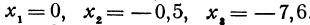Решение:

Если 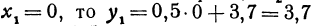; если 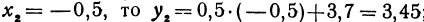; если .

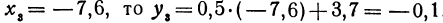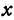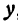Покажем, что если принять пару чисел и , удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).

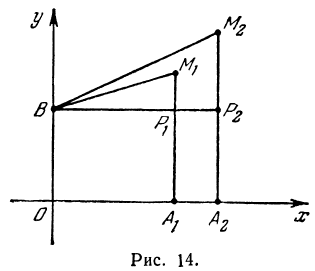
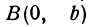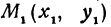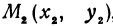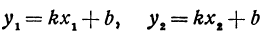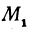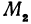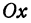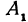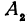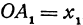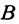В самом деле, рассмотрим точку и точки и , координаты которых удовлетворяют уравнению (1), т. е. . Обозначим проекции точек , и на ось через , и , тогда , Проведем из точки прямую, параллельную оси 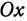. При этом получим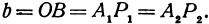

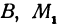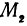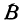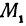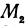Предположим, что точки и , не лежат на родной прямой. Соединяя точку с точками , и , получим два прямоугольных треугольника 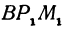и 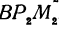, из которых имеем:

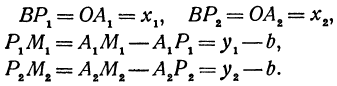
Но так как 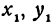и 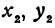удовлетворяют уравнению (1), то

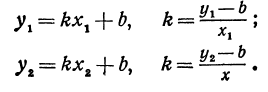
Иначе говоря,

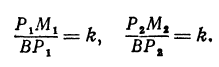
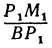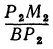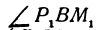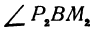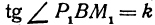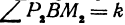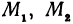Выражения и являются отношениями противоположных катетов к прилежащим для углов и . Следовательно, и — а поэтому и так как углы острые. Это значит, что точки и 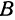лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точк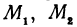и и 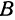лежат на одной прямой. Обозначим угол 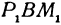через 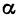. Этот угол образован прямой 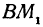с положительным направлением оси .

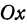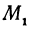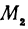Так как и — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси 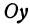отрезок 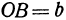и образующей с положительным направлением оси 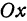угол 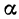такой, что .

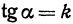Число 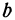называется начальной ординатой, число 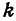— угловым коэффициентом прямой.

Предыдущие рассуждения позволяют сделать вывод: линейная функция 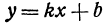определяет на плоскости прямую, у которой начальная ордината равна 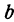, а угловой коэффициент .

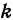Например, линейная функция 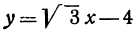определяет на координатной плоскости прямую, отсекающую на оси 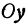отрезок —4 и наклоненную к оси 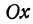под углом в 60°, так как .

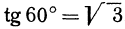Если имеем определенную прямую, отсекающую на оси 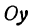отрезок 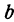и наклоненную к оси 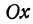под углом 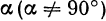тангенс которого равен 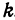, то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному 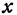найдется только одна точка, а следовательно, и одно значение .

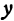Очевидно, имеет место и такое предложение: Всякой прямой, отсекающей на оси 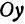отрезок 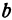и наклоненной к оси 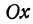под углом, тангенс которого равен числу 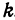, соответствует линейная функция .

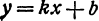Координаты любой, точки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение 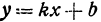называют уравнением прямой.

Таким образом, всякая линейная функция является уравнением некоторой прямой.

Отметим частные случаи.

1. Пусть 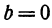, т. е. линейная функция определяется уравнением

Прямая, определяемая этим уравнением, проходит через начало координат. Здесь 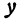пропорционален 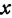, т. е. если 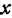увеличить (уменьшить) в несколько раз, то и 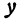увеличится (уменьшится) во столько же раз.

2. Пусть 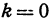, т. е. 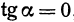, откуда 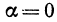. Линейная функция определяется уравнением

Этому уравнению соответствует прямая, параллельная оси 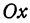и отстоящая от нее на расстояние .

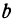На основании всего сказанного в этом параграфе легко решаются следующие задачи.

Пример:

Даны точк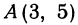и и 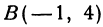. Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид

Решение:

Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки 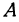в уравнение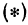, получим 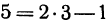. Это тождество, следовательно, точка 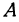лежит на прямой. Подставляя координаты точки 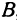, получаем 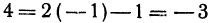. Отсюда видно, что точка 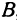не лежит на прямой.

Пример:

Построить прямую, уравнение которой

Решение:

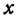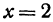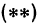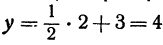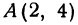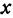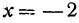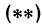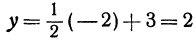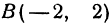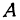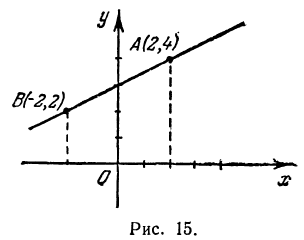
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим произвольное значение, например , и найдем из уравнения значение . Значит, точка лежит на прямой. Это первая точка. Теперь дадим какое-нибудь другое значение, например , и вычислим у из уравнения . Получим. Точка лежит на прямой. Это вторая точка. Строим точки и 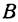(рис. 15) и проводим через них прямую, это и есть искомая прямая.

Основное свойство линейной функции

Рассмотрим линейную функцию 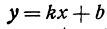. Найдем значение этой функции при :

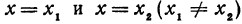Здесь первое и второе значения 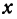различны, они отличаются друг от друга на величину 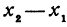Величину разности , на которую изменяется 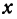при переходе от 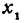к 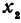, назовем приращением независимого переменного 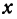. Эту величину часто будем обозначать через 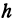, так что 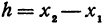. Найдем, насколько изменилось значение 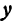при изменении 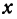, на 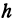. Для этого вычтем из 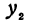значение :

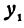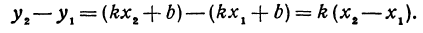
Таким образом,

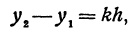
т. е. приращение линейной функции пропорционально приращению независимого переменного.

Это и есть основное свойство линейной функции.

Заметим, что 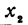, может быть больше, а может быть и меньше, чем 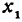. Поэтому 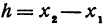может быть как положительным, так и отрицательным числом, иначе говоря, приращение 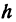независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине.

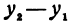Пример:

Найдем приращение функции 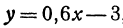, если приращение независимого переменного .

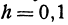Решение:

По основному свойству 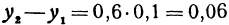. Приращение этой же функции 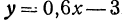, если 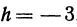, будет равно 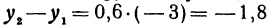. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.

Пример:

Найдем приращение функции 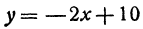при изменении 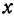на . Решение:

Будем иметь

Задачи на прямую

Пример:

Найти угол 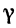между двумя прямыми, заданными уравнениями

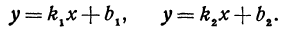
Решение:

При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).

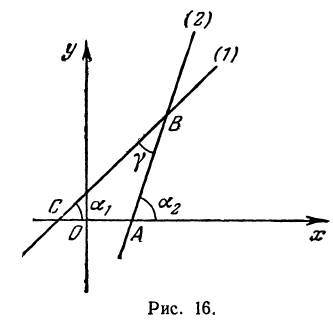
Угол 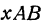является внешним по отношению к треугольнику 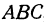, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е. 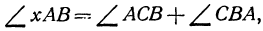откуда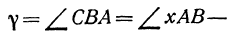 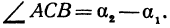Но углы 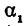и 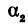, непосредственно неизвестны, а известны их тангенсы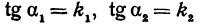. Поэтому напишем

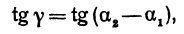
или

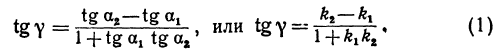
Заказать решение задач по высшей математике

Пример:

Найти угол между прямыми, заданными уравнениями 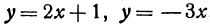. Здесь ;

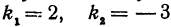Решение:

Применяя формулу (1), получим:

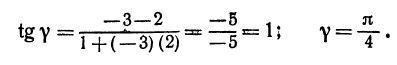
Если же будем считать, ч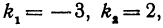то то

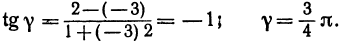
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.

Если заданы две параллельные прямые, то углы 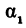и 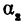, равны, как соответственные, следовательно, тангенсы их тоже равны

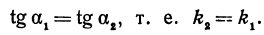
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.

Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 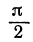. Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):

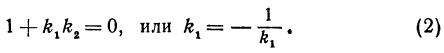
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.

Пример:

Найдем угол между прямыми, заданными уравнениями 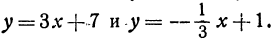Здесь угловые коэффициенты (первый равен 3, а второй 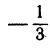) обратны по величине и противоположны по знаку.

Решение:

Следовательно, рассматриваемые прямые перпендикулярны.

Пример:

Даны две точки: 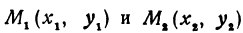, где 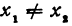, (т. е. эти точки не лежат на одной прямой, параллельной оси 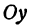). Написать уравнение прямой, проходящей через точк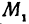и и .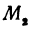

Решение:

Искомая прямая не параллельна оси 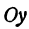, поэтому ее уравнение можно написать в виде 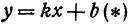. Значит, для решения задачи надо определить числа 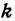и 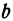. Так как прямая проходит через точк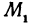и , и 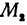, то координаты этих точек должны удовлетворять уравнению 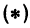, т. е.

В уравнениях 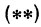и 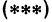все числа, кроме 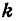и , и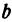звестны, поэтому эти уравнения можно рассматривать как систему уравнений относительно 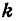и .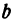

Решая систему, находим:

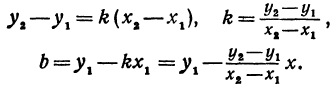
Подставляя найденные выражения в уравнение 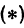, получим

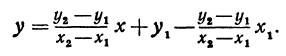
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси 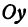. Полученному уравнению можно придать форму, удобную для запоминания, а именно:

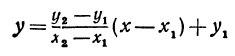
или

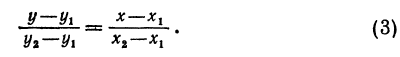
Пример:

Написать уравнение прямой, проходящей через данную точку 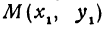и образующей с осью 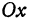угол .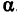

Решение:

Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла 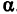. Обозначим 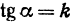. Значит, уравнение прямой можно написать в виде 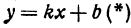, где пока число 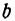неизвестно.

Так как прямая должна проходить через точку 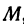, то координаты точки 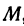удовлетворяют этому уравнению, т. е.

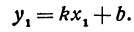
Находим отсюда неизвестное 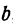, получим 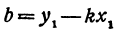. Подставляя найденное в уравнение 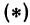, будем иметь

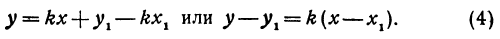
Это и есть уравнение прямой, проходящей через точку 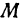в заданном направлении.

Если в уравнении (4) менять направление, не меняя точку 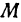, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 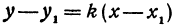, в котором 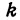переменное, а 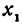и 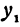не меняются, называется уравнением пучка прямых, проходящих через точку .

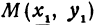Пример:

Напишем уравнение прямой, проходящей через точку 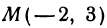и образующей с осью 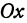угол 45°.

Решение:

Так как 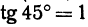, то угловой коэффициент равен 1; 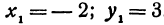. Уравнение прямой запишется в виде

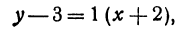
или

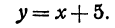
Общее уравнение прямой. Неявная линейная функция

Рассмотрим уравнение первой степени с двумя неизвестными

Решим его относительно :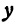

т. е. мы получили линейную функцию, где ,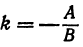

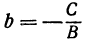
Уравнения (1) и (2) равносильны, поэтому пара чисел 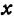и 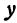, удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).

Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой. Рассмотрим особо случай, когда 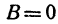, так как на нуль делить нельзя. Уравнение (1) примет вид 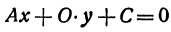или 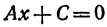, откуда 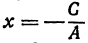. Поэтому, каков бы ни был 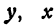всегда равен 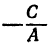. Это имеет место для прямой, параллельной оси 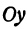; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу. Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.

Из уравнения (1) (если 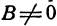) можно определить 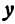, т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.

Система двух уравнений первой степени

Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке). Рассмотрим систему двух уравнений

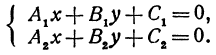
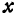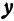Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения и , которые удовлетворяют и первому и второму уравнениям. Но так как 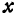и 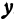определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.

Пример:

Найдем точку пересечения двух прямых:

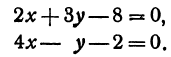
Решение:

Решая эту систему, получим: 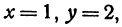т. е. прямые пересекаются в точке (1, 2) (рис. 17).

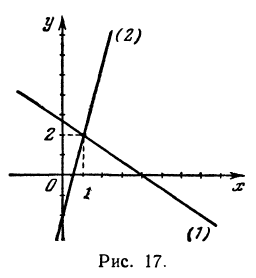
Пример:

Найдем точку пересечения двух прямых:

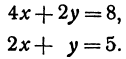
Решение:

Решая эту систему, получим: 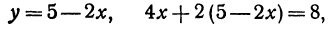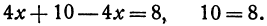Последнее равенство нелепо, значит, прямые не пересекаются, т. е. они параллельны.

Пример:

Найдем точку пересечения данных прямых

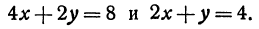
Решение:

Решая эту систему, получим:

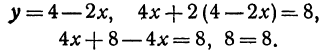
Полученное равенство всегда справедливо, т. е. справедливо при любом значении 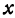. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.

Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.

Примеры применения линейной функции

Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.

Пример:

Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 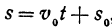, где 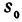— начальное расстояние, 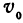—скорость, 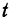— время; это, как мы уже знаем, есть линейная функция.

Пример:

Закон Ома записывается в ви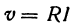де , где 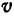— напряжение, 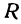— сопротивление и 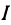—ток. Если 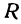не изменяется, то 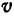является линейной функцией тока .

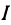Пример:

Если стоимость провоза единицы товара по железной дороге равна 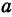руб. за километр, то стоимость 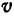провоза 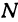единиц товара на 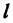км равна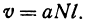

Если же стоимость товара на месте равна 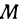руб., то после перевозки за него надо заплатить

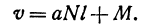
Здесь 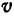— линейная функция .

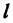Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.

Пример:

Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А к В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В —200 т. Перевозка одной тонны нефти на один километр обходится в 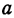руб.

Решение:

Обозначим расстояние от А до предполагаемого пункта С через 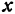. Тогда расстояние от города В до С равно 300 — 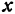. Стоимость перевозки одной тонны нефти из С в А равна 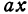руб., а перевозки 400 т—400 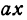руб. Аналогично перевозка нефти из С в В будет стоить 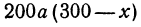руб. Стоимость всех перевозок, которую обозначим через 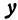, будет выражаться так:

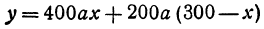
или

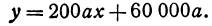
Это линейная функция. Если примем 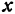за абсциссу, а 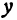за ординату точки, то полученная линейная функция опредеяет уравнение некоторой прямой. Угловой коэффициент ее равен 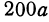, т. е. положителен, следовательно, эта прямая образует с осью 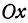острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина 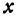заключена между 0 и 300, т. е. 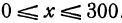. При 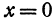величина у принимает значение 60000а, а при 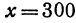— значение 120000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.

Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе А; если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к А, тем выгодней.

Квадратичная функция
Тригонометрические функции
Производные тригонометрических функции
Производная сложной функции
Функции нескольких переменных
Комплексные числ
Координаты на прямой
Координаты на плоскости

Источник

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось (y) в точке (b).
Примеры:

Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Примеры:
Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

Примеры:
Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Примеры:

Пример (ЕГЭ)

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k<0).

Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.

(k=-frac{AC}{BC}=-frac{1}{3}). Получается (g(x)=-frac{1}{3}x+3).

Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.

Способ 2

Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу (f(x)=kx+b) и решить получившуюся систему уравнений.

Пример (ЕГЭ)

Обозначим жирные точки какими-нибудь буквами и найдем их координаты.

(A(-2;2)) и (B(2;-5)) подставим эти значения вместо (x) и (f(x)) в формулу (f(x)=kx+b):

Получим:

(begin{cases}2=-2k+b\-5=2k+bend{cases})

Теперь найдем (k) и (b), решив эту систему.

Для этого сложим уравнения друг с другом, чтобы исчезло (k):

(2+(-5)=-2k+b+2k+b)
(-3=2b)
(b=-1,5)

Теперь подставим найденное (b) во второе уравнение системы и найдем (k):

(-5=2k-1,5)
(-5+1,5=2k)
(-3,5=2k)
(k=-1,75)

Получается (f(x)=-1,75x-1,5). Остается последний шаг – вычислим при каком иксе функция, то есть (f(x)), равна (16):

(16=-1,75x-1,5)
(17,5=-1,75x)
(x=-10).

Ответ: (-10).

Пример (ЕГЭ)

Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.

Функция (f(x)) возрастает, значит (k>0). (k=+frac{AC}{BC}=frac{4}{4}=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

(begin{cases}4=-2k+b\1=-4k+bend{cases})

Вычтем второе уравнение из первого, чтоб убрать (b):

(4-1=-2k+b-(-4k+b))
(3=2k)
(k=1,5)

Найдем (b):

(4=-2cdot 1,5+b)
(4=-3+b)
(b=7)

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

(x+1=1,5x+7)
(x-1,5x=7-1)
(-0,5x=6)
(x=6:(-0,5))
(x=-12).

Ответ: (-12).

Картинку в хорошем качестве, можно скачать нажав на кнопку “скачать статью”.

Смотрите также:
Как определить a, b и c по графику параболы

Скачать статью

Источник

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х – 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x – 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x – 2.

Алгоритм определения формулы линейной функции по графику

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна

Алгоритм определения формулы линейной функции по графику”

На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.

1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1

2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.

Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :

Это ВПР задание 8) это ответ:

ВНИМАНИЕ : задание на сегодня 16 апреля

Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 687 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 315 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 593 156 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

16. Линейная функция и её график

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

16.09.2020

201

11

31.03.2020

1171

30

16.03.2020

227

1

16.03.2020

191

1

08.03.2020

282

6

20.02.2020

1254

72

21.01.2020

180

0

09.12.2019

424

13

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

30.09.2020 16236

DOCX 549.2 кбайт

155 скачиваний

Оцените материал:

Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 5 лет и 3 месяца

Подписчики: 0

Всего просмотров: 38997

Всего материалов: 37

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

В приграничных пунктах Брянской области на день приостановили занятия в школах

Время чтения: 0 минут

Минобрнауки создаст для вузов рекомендации по поддержке молодых семей

Время чтения: 1 минута

Курские власти перевели на дистант школьников в районах на границе с Украиной

Время чтения: 1 минута

РДШ организовало сбор гуманитарной помощи для детей из ДНР

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Линейная функция, ее свойства и график

теория по математике 📈 функции

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.

Областью значений также является множество всех действительных чисел.

Функция не имеет ни наибольших, ни наименьших значений.

При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.

При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.

При k=0 прямая параллельна оси х.

Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

у=2х – 1=2 × 0 – 1= –1;

у=2х – 1=2 × 3 – 1= 5.

Вписываем в таблицу значения у:

Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5),

Проводимость – способность живой ткани проводить возбуждение.

Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

Пример №3

Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

График данной функции зависит от k и b.

если k 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках

коэффициент b определяет сдвиг по оси y, если b 0, то выше ноля в точке y = b

если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k

pазбирался: Даниил Романович | обсудить разбор | оценить

[spoiler title=”источники:”]

http://infourok.ru/algoritm-opredeleniya-formuly-linejnoj-funkcii-po-grafiku-4463697.html

Линейная функция, ее свойства и график

[/spoiler]

Источник

В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.

Линейной функцией называется функция вида y=kx+b

В уравнении функции число , которое мы умножаем на называется коэффициентом наклона.

Например, в уравнении функции y=-2x+3 ;

в уравнении функции y=-2+3x ;

в уравнении функции y=-x ;

в уравнении функции y=5 .

Графиком линейной функции является прямая линия.

1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции , удобно взять x=0 и x=3 , тогда ординаты эти точек будут равны y=2 и y=3 .

Получим точки А(0;2) и В(3;3). Соединим их и получим график функции :

2. В уравнении функции y=kx+b коэффициент отвечает за наклон графика функции:

Коэффициент отвечает за сдвиг графика вдоль оси :

На рисунке ниже изображены графики функций y=2x+3 ; ; y=x+3

Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.

Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3 ; ; y=-x+3

На этот раз во всех функциях коэффициент меньше нуля, и все графики функций наклонены влево.

Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3 ; y=2x ; y=2x-2

Теперь во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)

График функции y=2x (b=0) пересекает ось OY в точке (0;0) – начале координат.

График функции y=2x-2 (b=-2) пересекает ось OY в точке (0;-2)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b .

Если k<0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b<0, то график функции y=kx+b имеет вид:

Если k<0 и b<0, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны

Если b=0, то график функции y=kx проходит через начало координат:

Это график прямой пропорциональности.

3. Отдельно отмечу график уравнения x=a . График этого уравнения представляет собой прямую линию, параллельую оси все точки которой имеют абсциссу x=a .

Например, график уравнения x=3 выглядит так:

Внимание! Уравнение x=a не является функцией, так как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции $y=k_1{x}+b_1$ параллелен графику функции $y=k_2{x}+b_2$ , если k_1=k_2

5. Условие перпендикулярности двух прямых:

График функции $y=k_1{x}+b_1$ перпендикулярен графику функции $y=k_2{x}+b_2$ , если или $k_1=-1/{k_2}$

6. Точки пересечения графика функции с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k . То есть точка пересечения с осью OX имеет координаты ( -b/k ;0):

Рассмотрим решение задач.

1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции y=kx+b два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции y=kx+b параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид y=-4x+b

б) Нам осталось найти b. Известно, что график функции y=-4x+b проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

отсюда b=-10

Таким образом, нам надо построить график функции

Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой y=kx+b . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y=kx+b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k=3 . Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой y=3x-2 .

3. Постройте график уравнения

Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя.

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений: