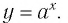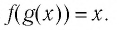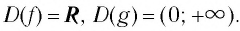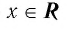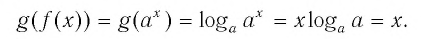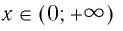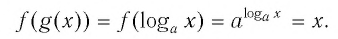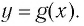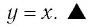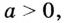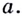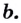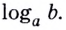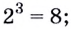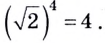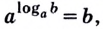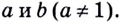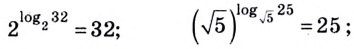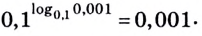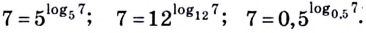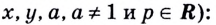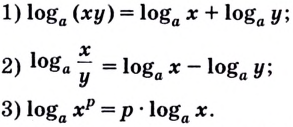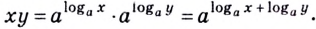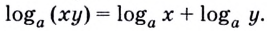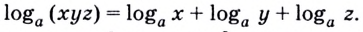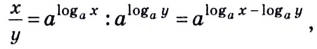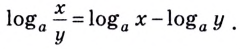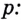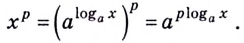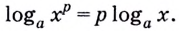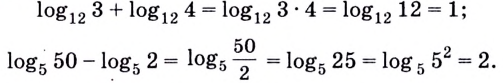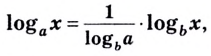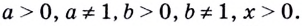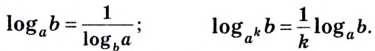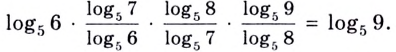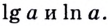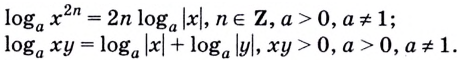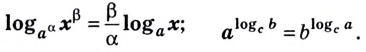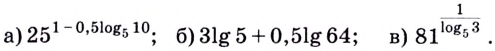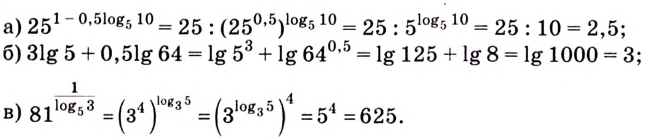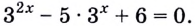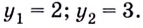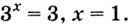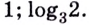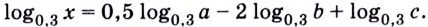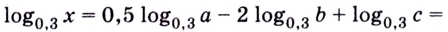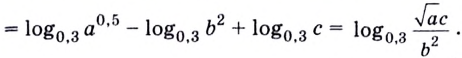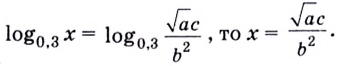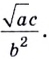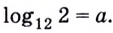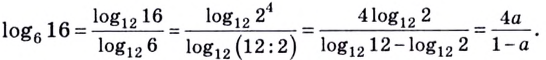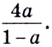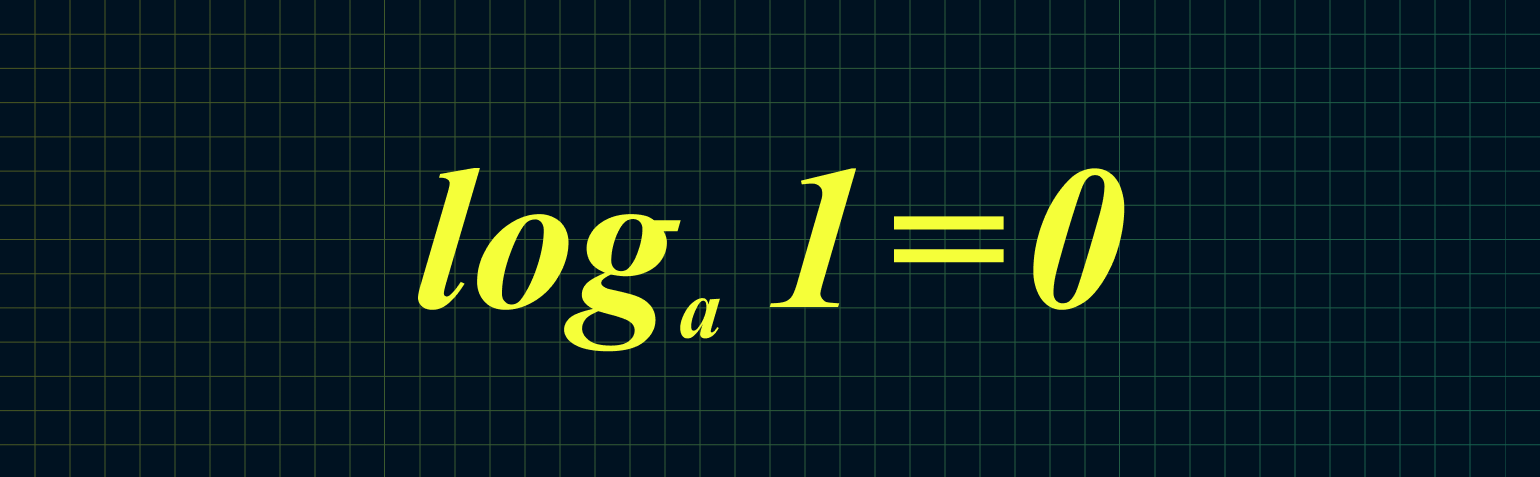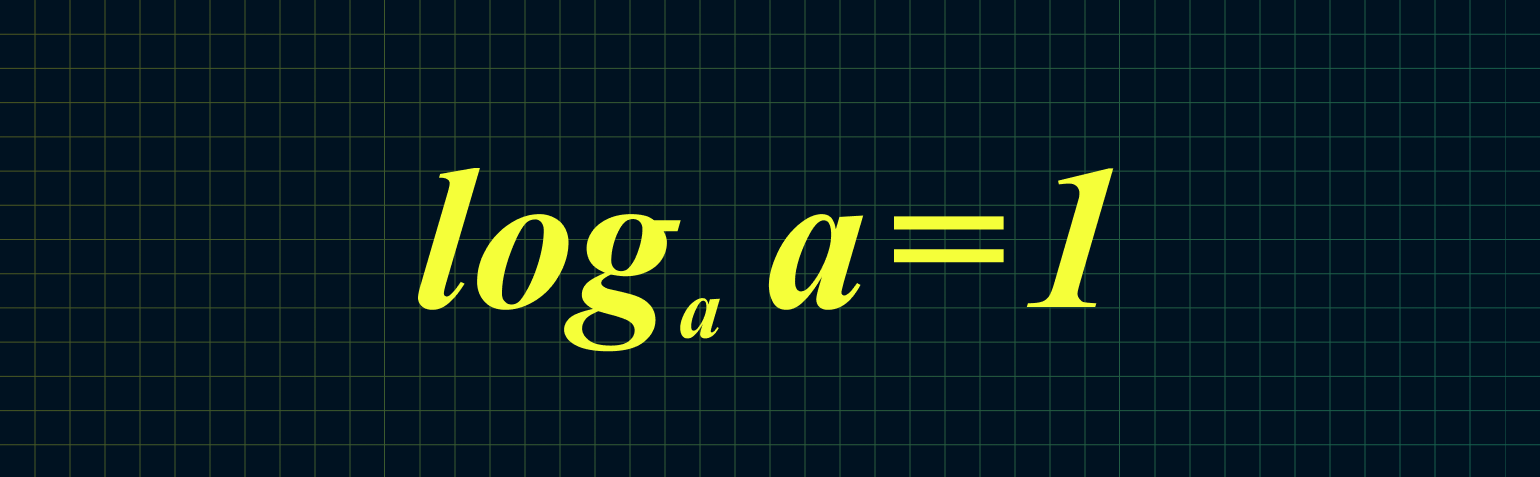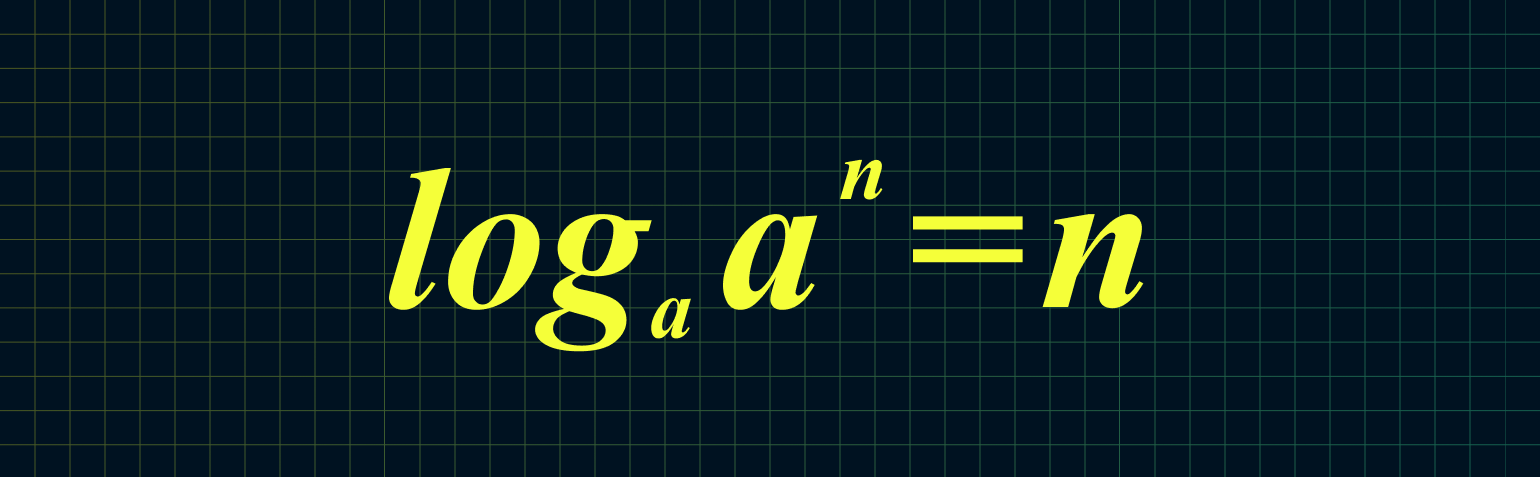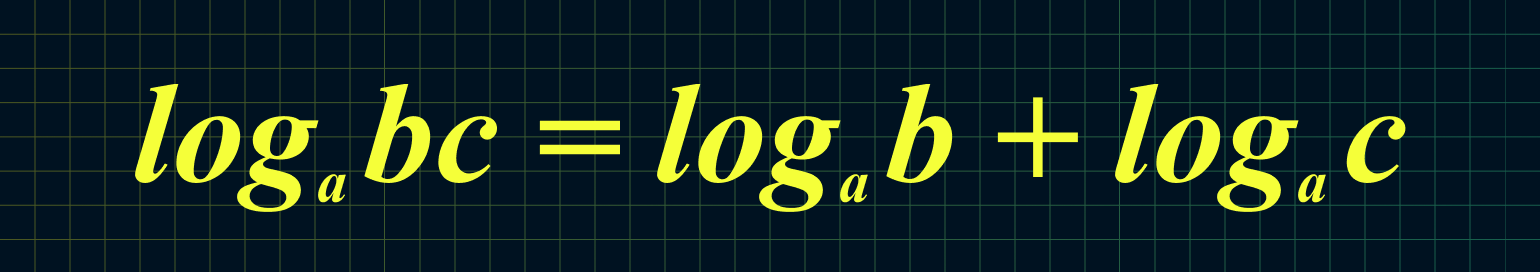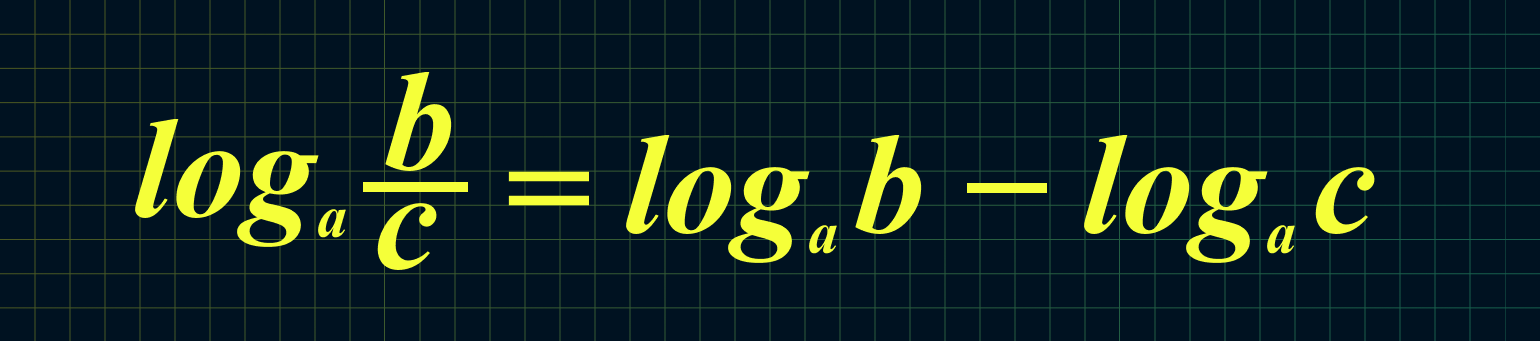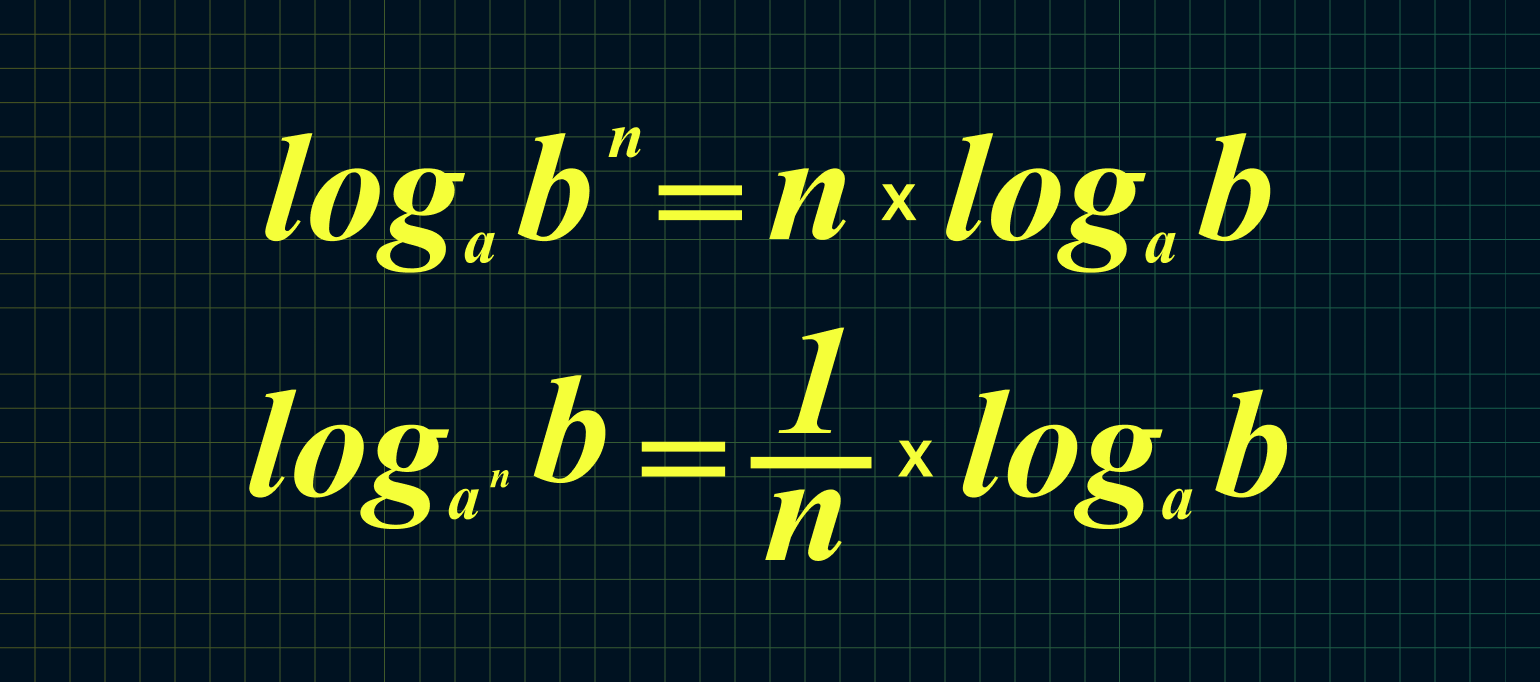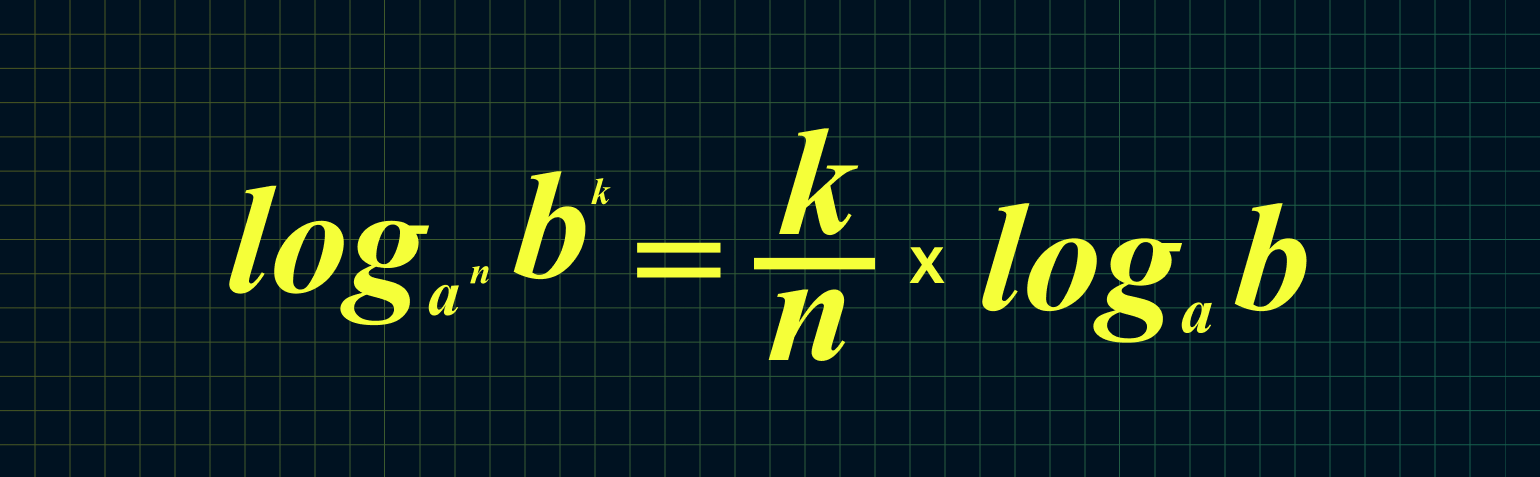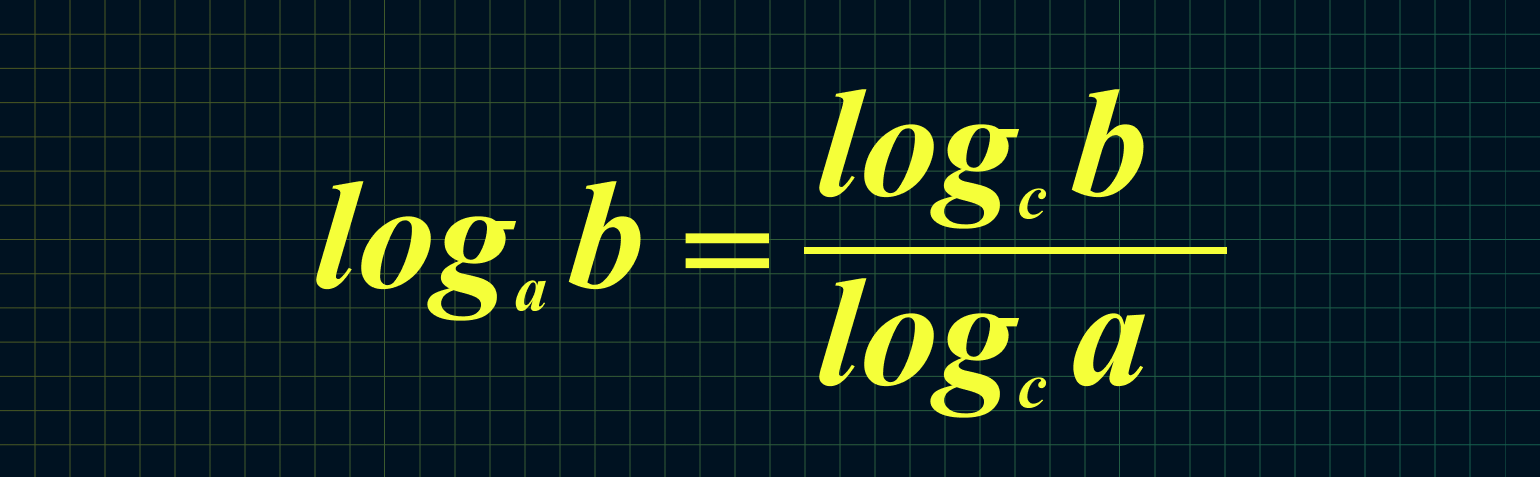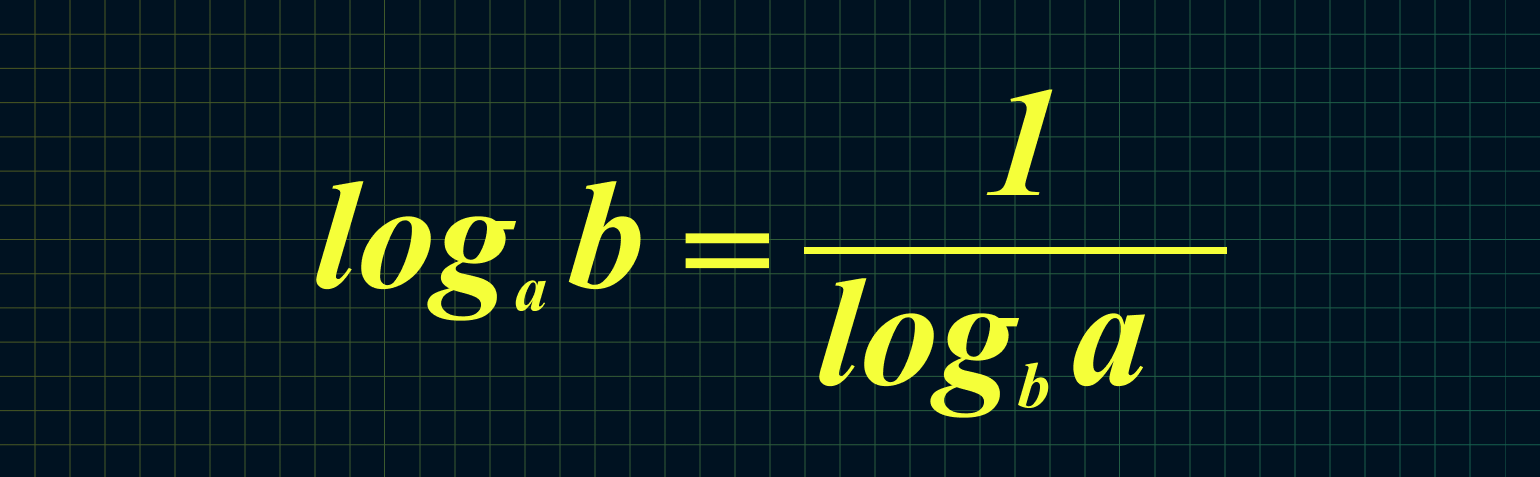Логарифм по основанию (a) от (b) – это число (t), которое показывает, в какую степень нужно возвести (a), чтобы получить (b).
Ограничения: числа (a) и (b) такие, что (a>0, ane 1, b>0).
Таким образом, верно основное логарифмическое тождество [Large{{color{royalblue}{a^t=b quadLeftrightarrowquad
log_a{b}=t}}}]
Т.к. мы имеем право возводить в любую степень, то (tin
mathbb{R}).
(blacktriangleright) Если (a,b,c) – числа, удовлетворяющие ограничениям: (a,b,c>0, ane 1), то справедливы следующие формулы:
[begin{array}{|ccc|}
hline textbf{(1)} log_a1=0&&textbf{(2)} log_aa=1\
&&\
textbf{(3)} log_{a^n}{b^m}=frac mnlog_ab&&textbf{(4)}
a^{log_bc}=c^{log_ba}\
&&\
textbf{(5)} log_a{bc}=log_ab+log_ac&&textbf{(6)}
log_a{dfrac bc}=log_ab-log_ac\
&&\
textbf{(7)} log_abcdot log_bc=log_ac & text{или}
&textbf{(7′}) log_bc=dfrac{log_ac}{log_ab}\
&&\
hline
end{array}]
Заметим, что при выполнении ограничений данные формулы верны в обе стороны!
Некоторые частные случаи, которыми удобно пользоваться:
(blacktriangleright) Частные случаи формул (3) и (4): [m=log_a{a^m} text{и} b=a^{log_ab}]
С помощью первой формулы нагляднее видно, как заменить число на логарифм по нужному основанию:
(4=log_2{2^4}=log_2{16});
а с помощью второй – как заменить число на степень с нужным основанием:
(4=3^{log_34}).
(blacktriangleright) Частные случаи формул (7) и (7’): [log_abcdot log_ba=1 text{и}
log_ab=dfrac1{log_ba}]
Пример:
(log_3{25}+dfrac2{log_{frac15}3}={small{text{(применили}}}
{small{text{ формулу}}}
(2))=log_3{25}+2log_3{dfrac15}=log_3{25}+log_3{dfrac1{25}}=log_3{left(25cdotdfrac1{25}right)}=0)
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 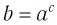
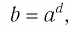
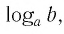
Таким образом, равенство 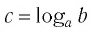
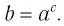
Определение:
Пусть 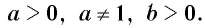
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 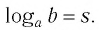
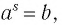
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 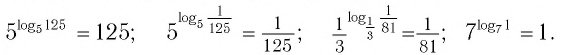
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 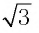
б) Записать число -5 в виде логарифмов по основанию 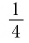
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 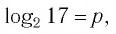
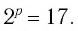
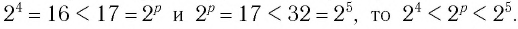
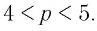
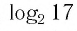
Ответ:
Пример:
Решить уравнение:
Решение:
а) Поскольку 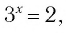
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 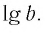
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
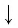
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
Доказательство:
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 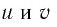
Следствие 2. При любом целом 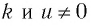
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 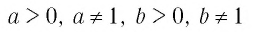
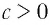
Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 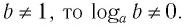
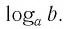
Способ 2. Пусть 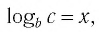
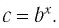
Откуда имеем
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




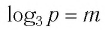
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 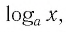
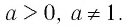
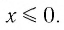
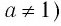
Определение:
Логарифмической функцией называется функция вида 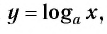
Область определения логарифмической функции — это естественная область определения выражения 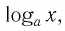
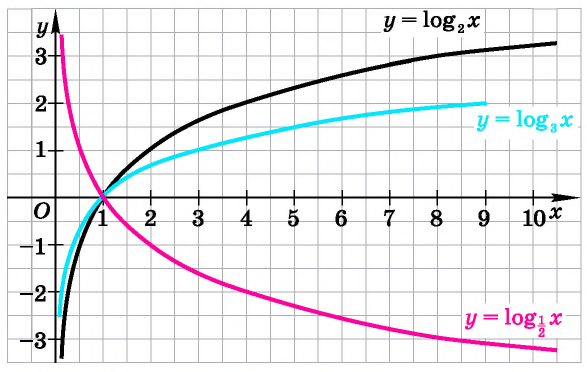
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 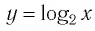
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 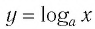
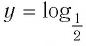
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 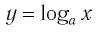
Теорема (о свойствах логарифмической функции 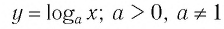
- Областью определения логарифмической функции является интервал
- Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
- Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
- График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
- Значение аргумента х = 1 является нулем логарифмической функции.
- 6. При а > 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
и принимает положительные значения на интервале (0; 1).
- Логарифмическая функция не является ни четной, ни нечетной.
- При а > 1 логарифмическая функция возрастает на всей области определения. При 0 < а < 1 логарифмическая функция убывает на всей области определения.
- Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 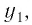
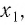
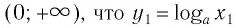
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а > 1 график логарифмической функции лежит в IV координатном угле, когда 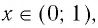
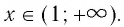
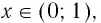
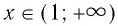
Область определения логарифмической функции — интервал 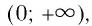
На рисунке 35 видно, что при а > 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 < а < 1 логарифмическая функция убывает на области определения (свойство 8).
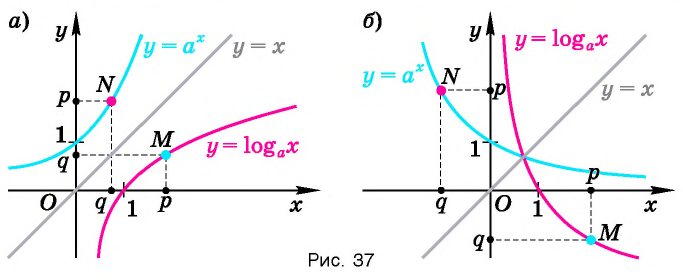
Пусть точка 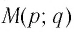
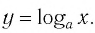
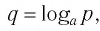
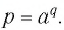
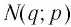
Заметим, что точки 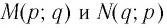
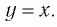
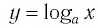
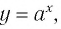
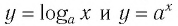
Последнее утверждение дает возможность, зная график функции 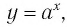
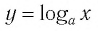
▲ Симметричность графиков функций 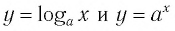
Функции 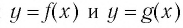
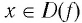
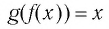
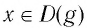
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 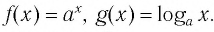
Для любого
Для любого
Покажем, что графики взаимно обратных функций 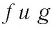
Пусть точка 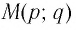
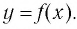
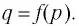
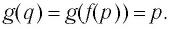
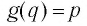
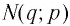
Таким образом, каждой точке М на графике функции 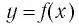
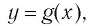
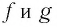
- Заказать решение задач по высшей математике
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида 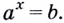
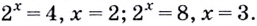
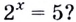
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 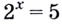
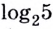
Рассмотрим общий случай-.
Пусть 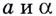
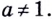
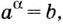
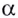
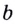
Логарифмом числа 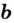
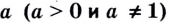
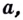
Логарифм числа 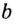
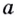
Примеры:
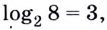
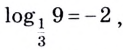
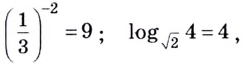
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 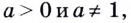
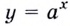
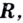
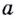
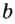
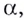
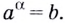
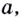
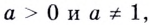
Полезно помнить, что для каждого
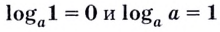
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если 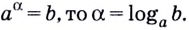
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных
Например:
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например:
Докажем ещё несколько важных свойств логарифмов (для положительных
1) По основному логарифмическому тождеству и основному свойству степени
Итак, 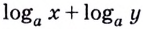
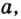
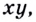
Эту формулу можно обобщить на три и более множителя:
Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
отсюда
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества 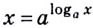
Итак,
Доказанные формулы можно использовать и справа налево, например:
В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
где
Докажем эту формулу. Поскольку положительные числа 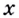
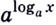
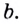
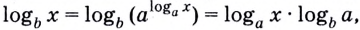
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
Докажите их самостоятельно.
Пример №4
Упростите выражение 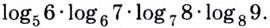
Решение:
Сведём все логарифмы к основанию 5. Имеем:
Особенно часто используют логарифмы по основаниям 10 и 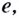
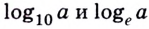
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:
Докажите их самостоятельно.
Пример №5
Вычислите:
Решение:
Пример №6
Решите уравнение:
Решение:
Пусть 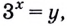
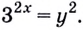
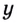
Получим: 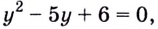
Поскольку 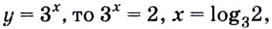
Ответ.
Пример №7
Найдите 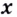
Решение:
Поскольку
Ответ.
Пример №8
Вычислите 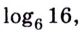
Решение:
Ответ.
- Корень из числа – нахождение и вычисление
- Теория множеств – виды, операции и примеры
- Числовые множества
- Вектор – определение и основные понятия
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем
Логарифмом положительного числа (c) по основанию (a) ((a>0, aneq1)) называется показатель степени (b), в которую надо возвести основание (a), чтобы получить число (c) ((c>0)), т.е.
(a^{b}=c) (Leftrightarrow) (log_{a}{c}=b)
Объясним проще. Например, (log_{2}{8}) равен степени, в которую надо возвести (2), чтоб получить (8). Отсюда понятно, что (log_{2}{8}=3).
|
Примеры: |
(log_{5}{25}=2) |
т.к. (5^{2}=25) |
||
|
(log_{3}{81}=4) |
т.к. (3^{4}=81) |
|||
|
(log_{2})(frac{1}{32})(=-5) |
т.к. (2^{-5}=)(frac{1}{32}) |
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание – подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм – нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например, вычислите логарифм: а) (log_{4}{16}) б) (log_{3})(frac{1}{3}) в) (log_{sqrt{5}}{1}) г) (log_{sqrt{7}}{sqrt{7}}) д) (log_{3}{sqrt{3}})
а) В какую степень надо возвести (4), чтобы получить (16)? Очевидно во вторую. Поэтому:
(log_{4}{16}=2)
б) В какую степень надо возвести (3), чтобы получить (frac{1}{3})? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).
(log_{3})(frac{1}{3})(=-1)
в) В какую степень надо возвести (sqrt{5}), чтобы получить (1)? А какая степень делает любое число единицей? Ноль, конечно!
(log_{sqrt{5}}{1}=0)
г) В какую степень надо возвести (sqrt{7}), чтобы получить (sqrt{7})? В первую – любое число в первой степени равно самому себе.
(log_{sqrt{7}}{sqrt{7}}=1)
д) В какую степень надо возвести (3), чтобы получить (sqrt{3})? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень – это степень (frac{1}{2}).
(log_{3}{sqrt{3}}=)(frac{1}{2})
Пример: Вычислить логарифм (log_{4sqrt{2}}{8})
Решение:
|
(log_{4sqrt{2}}{8}=x) |
Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: |
|
|
((4sqrt{2})^{x}=8) |
Что связывает (4sqrt{2}) и (8)? Двойка, потому что и то, и другое число можно представить степенью двойки: |
|
|
({(2^{2}cdot2^{frac{1}{2}})}^{x}=2^{3}) |
Слева воспользуемся свойствами степени: (a^{m}cdot a^{n}=a^{m+n}) и ((a^{m})^{n}=a^{mcdot n}) |
|
|
(2^{frac{5}{2}x}=2^{3}) |
Основания равны, переходим к равенству показателей |
|
|
(frac{5x}{2})(=3) |
Умножим обе части уравнения на (frac{2}{5}) |
|
|
(x=1,2) |
Получившийся корень и есть значение логарифма |
Ответ: (log_{4sqrt{2}}{8}=1,2)
Зачем придумали логарифм?
Чтобы это понять, давайте решим уравнение: (3^{x}=9). Просто подберите (x), чтобы равенство сработало. Конечно, (x=2).
А теперь решите уравнение: (3^{x}=8).Чему равен икс? Вот в том-то и дело.
Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как (x=log_{3}{8}).
Хочу подчеркнуть, что (log_{3}{8}), как и любой логарифм – это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: (1,892789260714…..)
Пример: Решите уравнение (4^{5x-4}=10)
Решение:
|
(4^{5x-4}=10) |
(4^{5x-4}) и (10) никак к одному основанию не привести. Значит тут не обойтись без логарифма.
Воспользуемся определением логарифма: |
|
|
(log_{4}{10}=5x-4) |
Зеркально перевернем уравнение, чтобы икс был слева |
|
|
(5x-4=log_{4}{10}) |
Перед нами линейное уравнение. Перенесем (4) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу. |
|
|
(5x=log_{4}{10}+4) |
Поделим уравнение на 5 |
|
|
(x=)(frac{log_{4}{10}+4}{5}) |
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают. |
Ответ: (frac{log_{4}{10}+4}{5})
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы ((a>0, aneq1)). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание – число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).
То есть, (ln{a}) это то же самое, что и (log_{e}{a}), где (a) – некоторое число.
Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).
То есть, (lg{a}) это то же самое, что и (log_{10}{a}), где (a) – некоторое число.
Основное логарифмическое тождество
У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:
Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.
Вспомним краткую запись определения логарифма:
если (a^{b}=c), то (log_{a}{c}=b)
То есть, (b) – это тоже самое, что (log_{a}{c}). Тогда мы можем в формуле (a^{b}=c) написать (log_{a}{c}) вместо (b). Получилось (a^{log_{a}{c}}=c) – основное логарифмическое тождество.
Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.
Пример: Найдите значение выражения (36^{log_{6}{5}})
Решение:
|
(36^{log_{6}{5}}=) |
Сразу пользоваться свойством (a^{log_{a}{c}}=c) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что (36=6^{2}) |
|
|
(=(6^{2})^{log_{6}{5}}=) |
Зная формулу ((a^{m})^{n}=a^{mcdot n}), а так же то, что множители можно менять местами, преобразовываем выражение |
|
|
(=6^{2cdotlog_{6}{5}}=6^{log_{6}{5}cdot2}=(6^{log_{6}{5}})^{2}=) |
Вот теперь спокойно пользуемся основным логарифмическим тождеством. |
|
|
(=5^{2}=25) |
Ответ готов. |
Ответ: (25)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что (log_{2}{4}) равен двум. Тогда можно вместо двойки писать (log_{2}{4}).
Но (log_{3}{9}) тоже равен (2), значит, также можно записать (2=log_{3}{9}) . Аналогично и с (log_{5}{25}), и с (log_{9}{81}), и т.д. То есть, получается
(2=log_{2}{4}=log_{3}{9}=log_{4}{16}=log_{5}{25}=log_{6}{36}=log_{7}{49}…)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как (log_{2}{8}), или как (log_{3}{27}), или как (log_{4}{64})… Здесь мы как аргумент пишем основание в кубе:
(3=log_{2}{8}=log_{3}{27}=log_{4}{64}=log_{5}{125}=log_{6}{216}=log_{7}{343}…)
И с четверкой:
(4=log_{2}{16}=log_{3}{81}=log_{4}{256}=log_{5}{625}=log_{6}{1296}=log_{7}{2401}…)
И с минус единицей:
(-1=) (log_{2})(frac{1}{2})(=) (log_{3})(frac{1}{3})(=) (log_{4})(frac{1}{4})(=) (log_{5})(frac{1}{5})(=) (log_{6})(frac{1}{6})(=) (log_{7})(frac{1}{7})(…)
И с одной третьей:
(frac{1}{3})(=log_{2}{sqrt[3]{2}}=log_{3}{sqrt[3]{3}}=log_{4}{sqrt[3]{4}}=log_{5}{sqrt[3]{5}}=log_{6}{sqrt[3]{6}}=log_{7}{sqrt[3]{7}}…)
И так далее.
Любое число (a) может быть представлено как логарифм с основанием (b): (a=log_{b}{b^{a}})
Пример: Найдите значение выражения (frac{log_{2}{14}}{1+log_{2}{7}})
Решение:
|
(frac{log_{2}{14}}{1+log_{2}{7}})(=) |
Превращаем единицу в логарифм с основанием (2): (1=log_{2}{2}) |
|
|
(=)(frac{log_{2}{14}}{log_{2}{2}+log_{2}{7}})(=) |
Теперь пользуемся свойством логарифмов: |
|
|
(=)(frac{log_{2}{14}}{log_{2}{(2cdot7)}})(=)(frac{log_{2}{14}}{log_{2}{14}})(=) |
В числителе и знаменателе одинаковые числа – их можно сократить. |
|
|
(=1) |
Ответ готов. |
Ответ: (1)
Смотрите также:
Логарифмические уравнения
Логарифмические неравенства
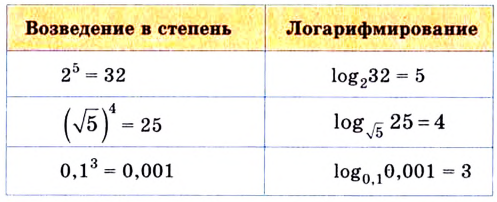
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
$$ log_{2}(32)=5;$$
Аналогично, глядя в таблицу получим, что:
$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)
$$log_{a}(b)=c;$$
$$a^{c}=b.$$
Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм – это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
$$log_{2}(5)=???$$
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
$$log_{2}(5)=2,32192809…$$
Или логарифм шести по основанию 4:
$$log_{4}(6)= 1.2924812…$$
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:
$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$
Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:
$$ log_{4}(6) in (1;2). $$
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).
$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$
Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
$$log_{3}(frac{1}{3})=-1;$$
Так как (вспоминайте определение отрицательной степени)
$$3^{-1}=frac{1}{3};$$
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- (x) и будет искомым значением логарифма.
Давайте разберем на примерах.
Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))
- Сначала представим аргумент и основание в виде степени тройки:
$$ 3=3^1, qquad 9=3^2;$$ - Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$ - В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(frac{1}{125})=-3.$$
Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, qquad 4=2^2;$$ - В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=frac{2}{6}=frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=frac{1}{3}.$$
Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))
- Представим аргумент и основание в виде степени двойки:
$$ 8=2^3 qquad 1=2^0;$$ - В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 qquad 15= ???;$$
(15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.
$$16=2*2*2*2=2^4,$$
(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.
$$ 48=6*8=3*2*2*2*2,$$
Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается – (lg(a)).
Пример 6
$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию (e). Обозначение – (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.
$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$
Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.
$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$
Пример 10. Формула (5,6). Свойства степени.
$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
Логично, что будет выполняться и такое соотношение:
$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$
И если (m=n), то:
$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$
Пример 11. Формулы (7,8). Переход к другому основанию.
$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$
#статьи
- 6 окт 2022
-
0
Стыдные вопросы о логарифмах: всё, что нужно знать программисту
Объясняем, почему не стоит бояться логарифмов и как их считать в Python.
Иллюстрация: Оля Ежак для Skillbox Media
Журналист, изучает Python. Любит разбираться в мелочах, общаться с людьми и понимать их.
Прежде чем начать обсуждение, давайте немного освежим знания и решим несколько стандартных задачек:
- Чему равен log3 81?
- А lg 2 × lb 10?
- А сумма log216 2 + log216 3?
Если вы легко прорешали все три примера в уме, не пользуясь калькулятором, — можете сразу переходить к заключительной главе. Для тех же, кто слегка подзабыл школьные годы чудесные, — буквально пять минут ликбеза.
По большому счёту, логарифм — это просто перевёрнутая степень. Рассмотрим выражение 23 = 8. В нём:
- 2 — основание степени;
- 3 — показатель степени;
- 8 — результат возведения в степень.
У возведения в степень существует два обратных выражения. В одном мы ищем основание (это извлечение корня), в другом — показатель (это логарифмирование).
Таким образом, выражение 23 = 8 можно превратить в log2 8 = 3.
Закрепляем знания: логарифм — это число, в которое нужно возвести 2 (основание степени), чтобы получить 8 (результат возведения в степень).
Форма записи неинтуитивна, и поначалу можно легко спутать основание со степенью. Чтобы избежать этого, можно использовать следующее правило:
Основание у логарифма, как и у возведения в степень, находится внизу.
Чтобы лучше запомнить структуру записи, посмотрите на эти выражения и постарайтесь понять их смысл:
- log3 9 = 2
- log4 64 = 3
- log5 625 = 4
- log7 343 = 3
- log10 100 = 2
- log2 128 = 7
- log2 0,25 = −2
- log625 125 = 0,75
В общем виде запись logAB читается так: логарифм B по основанию A.
Главная часть любого логарифма — его основание. Именно наличие общего основания у нескольких логарифмических функций позволяет проводить с ними различные операции.
Основанием натурального логарифма является число Эйлера (e) — иррациональное число, приблизительно равное 2,71828.
На всякий случай напомним, что такое иррациональные числа. Так называют числа, которые нельзя записать в виде обыкновенной дроби с целыми числителем и знаменателем. При этом знаменатель не должен быть равен нулю.
Например, 0,333… — рациональное число, потому что его можно записать как 1/3. А вот число Пи или корень из 2 — иррациональны.
Так как натуральные логарифмы часто используются, для них ввели особый способ записи: ln x — это то же самое, что loge x.
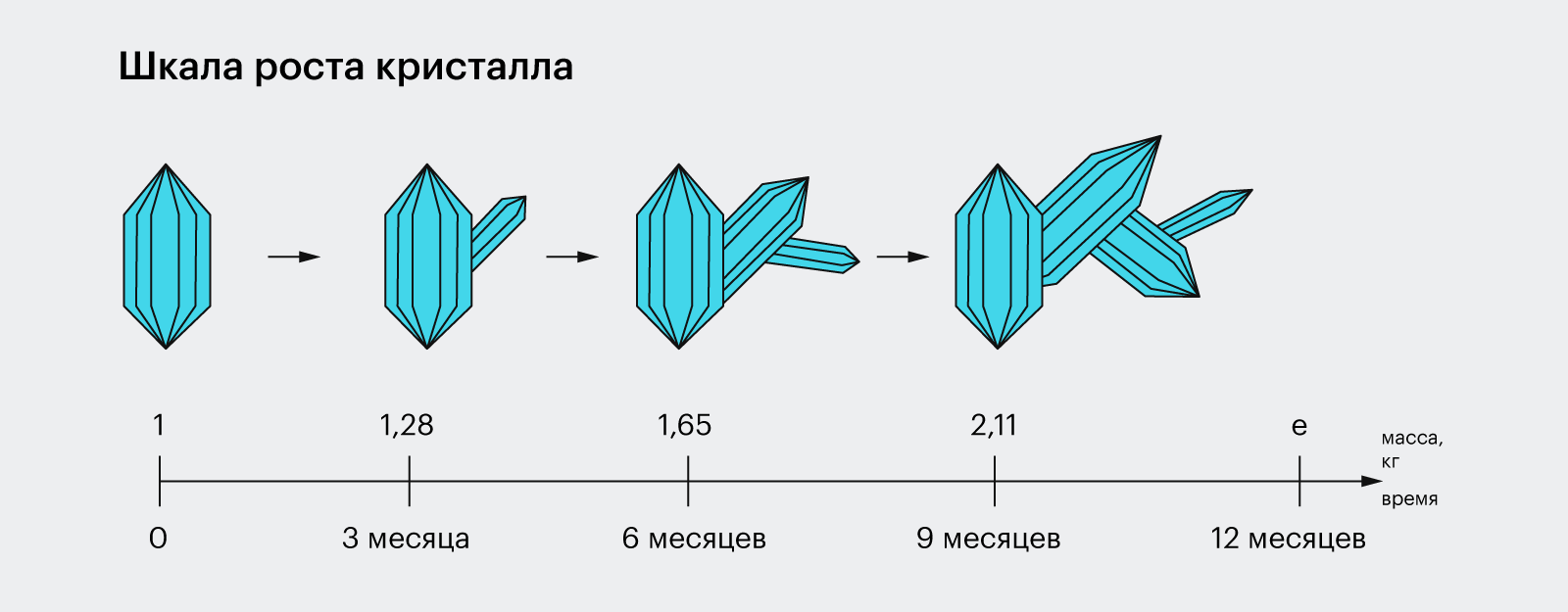
Представим кристалл, который весит 1 кг и растёт со скоростью 100% в год. Можно ожидать, что через год он будет весить 2 кг, но это не так.
Каждая новая выращенная часть начнёт растить свою собственную. Когда в кристалле будет 1,1 кг, он будет расти со скоростью 1,1 кг в год, а когда в нём будет 1,5 кг — со скоростью 1,5 кг в год. Математики подсчитали, что через год масса кристалла составит e, или ≈ 2,71828 кг.
Такой рост называется экспоненциальным. По экспоненте размножаются бактерии, увеличиваются популяции, приумножаются доходы, растут снежные комья, распадается радиоактивное вещество и остывают напитки.
Чтобы узнать, какой массы достигнет кристалл через три, пять, десять лет, нужно возвести e в соответствующую степень.
e3 ≈ 20,0855 кг
e5 ≈ 148,4132 кг
e10 ≈ 22 026,4658 кг
Но как рассчитать, когда кристалл будет весить тонну? Составим уравнение:
ex = 1000
Нам известны основание степени и результат возведения в степень — осталось найти её показатель. Ничего не напоминает? Это ведь и есть логарифм x = loge 1000! Или, если использовать сокращённую запись, x = ln 1000.
Подставим в калькулятор и выясним, что x ≈ 6,9. Именно столько лет потребуется кристаллу, чтобы его масса достигла тонны.
Десятичный логарифм — логарифм, основание которого равно 10. Он обозначается lg x и очень удобен, потому что с ним легко вычислять круглые числа.
Двоичный логарифм — логарифм, основание которого равно 2. Он обозначается lb x и часто используется программистами, потому что компьютеры думают и считают в двоичной системе.
Список операций, которые можно совершать с логарифмами, ограничен. Если вы запомните все и научитесь их выполнять, то сможете щёлкать логарифмические задачки, как семечки.
У всех логарифмов есть ограничения. Их основание и аргумент должны быть больше нуля, при этом основание не может быть равно единице. На математическом языке это звучит так:
Перейдём к свойствам логарифмов. Они работают в обе стороны, и их применяют как слева направо, так и справа налево.
1. Логарифм единицы по любому основанию всегда равен нулю:
Например: log17 1 = 0
2. Логарифм, где число и основание совпадают, равен единице:
Например: log17 17 = 1
3. Основное логарифмическое тождество:
Например: log17 175 = 5
4. Логарифм произведения чисел равен сумме их логарифмов:
Например: log5 12,5 + log5 10 = log5 (12,5 × 10) = log5 125 = 3
5. Логарифм дроби равен разности логарифмов числителя и знаменателя:
Например: log3 63 − log3 7 = log3 63/7 = log3 9 = 2
6. Если основание или аргумент возведены в степень, то их можно удобно выносить перед логарифмом:
Из этих двух формул следует:
Например: log23 49 = 9/3 × log2 4 = 3 × 2 = 6
7. Если нам неудобно основание логарифма, то его можно изменить:
Например: log25 125 = log5 125/log5 25 = 3/2 = 1,5
Из этой формулы следует, что мы можем поменять местами основание и аргумент вот так:
Например: log16 4 = 1/log4 16 = 1/2 = 0,5
А теперь возвращаемся к задачам, которые мы дали в начале статьи.
Пример 1
log3 81
Вспомните, что 81 — это 92. А 9 — это 32. Таким образом:
log3 81 = log3 92 = log3 32+2 = log3 34
Теперь логарифм не представляет для нас никаких сложностей. Воспользуемся свойством степени и вынесём четвёрку.
log3 34 = 4 × log3 3 = 4 × 1 =4
Ответ: 4.
Пример 2
lg 2 × lb 10
Переведём сокращённые записи в полный вид:
lg 2 × lb 10 = log10 2 × log2 10
Приведём оба логарифма к одному основанию.
log10 2 × log2 10 = 1/log2 10 × log2 10 = log2 10/log2 10 = 1
Ответ: 1.
Пример 3
log216 2 + log216 3
Воспользуемся свойством суммы.
log216 2 + log216 3 = log216 2 × 3 = log216 6
Представим 216 в виде степени числа 6 и вынесем с помощью свойства степени.
log216 6 = log63 6 = 1/3 × log6 6 = 1/3 × 1 = 1/3
Ответ: 1/3.
Чтобы работать с логарифмическими выражениями в Python, необходимо импортировать модуль math:
import math
И теперь посчитаем log2 8, используя метод math.log (b, a):
print (math.log (8, 2)) >>> 3.0
Обратите внимание на два момента. Во-первых, мы сначала передаём функции аргумент и только потом — основание. Во-вторых, функция всегда возвращает тип данных float, даже если результат целочисленный.
Если мы не передаём функции основание, то логарифм по умолчанию считается натуральным:
#math.e — метод для вызова числа Эйлера. print (math.log (math.e)) >>> 1.0
Для подсчёта десятичного и двоичного логарифма есть отдельные методы:
#Для десятичного. print (math.log10 (100)) >>> 2.0 #Для двоичного. print (math.log2 (512)) >>> 9.0
Ещё в Python есть специфичный метод, который прибавляет к аргументу единицу и считает натуральный логарифм от получившегося числа:
x = math.e print (math.log1p (x-1)) >>> 1.0
Когда х близок к нулю, этот метод даёт более точные результаты, чем math.log (1+x). Сравните:
x = 0.00001 print (math.log(x+1)) >>> 9.999950000398841e-06 print (math.log1p(x)) >>> 9.99995000033333e-06
Это все основные инструменты для работы с логарифмами в Python.

Научитесь: Профессия Python-разработчик
Узнать больше
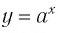
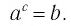
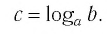
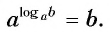
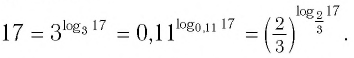
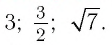
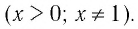
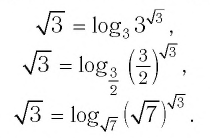
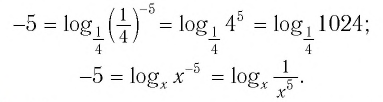
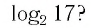
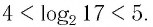
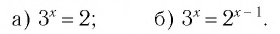
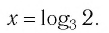
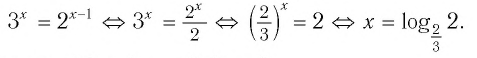
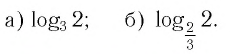
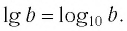
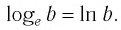
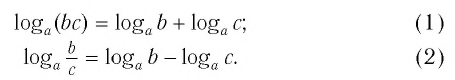
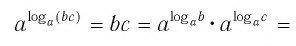
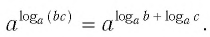
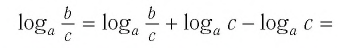
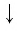
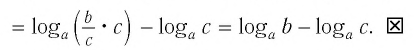

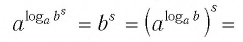
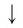
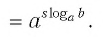
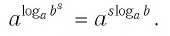

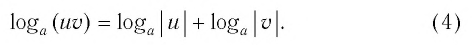
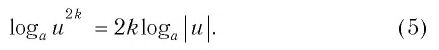
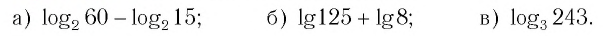
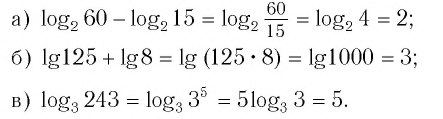
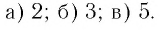

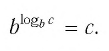
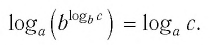
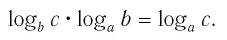

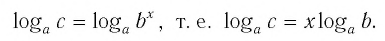
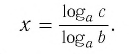
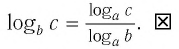

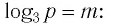
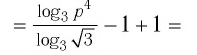
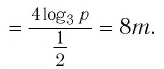
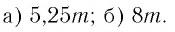

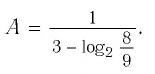
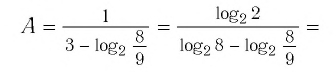
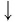
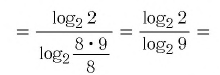
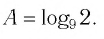
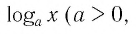
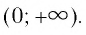
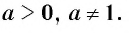
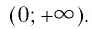
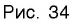
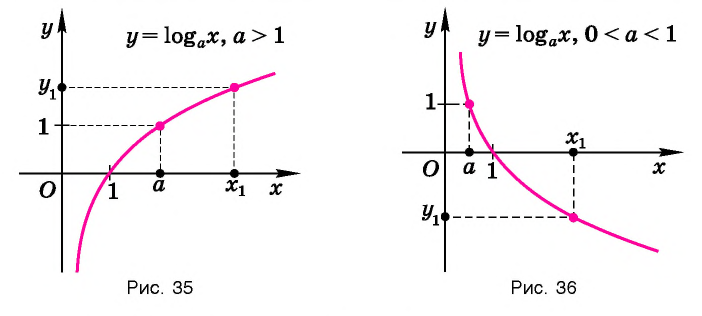
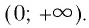
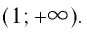 И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале 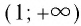 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).