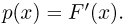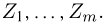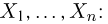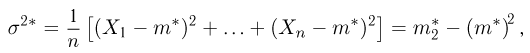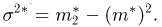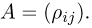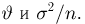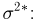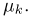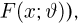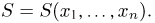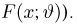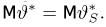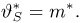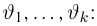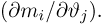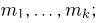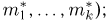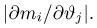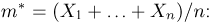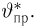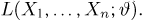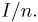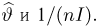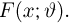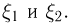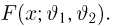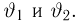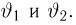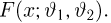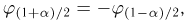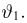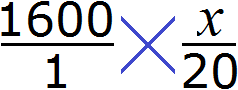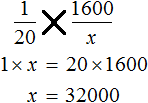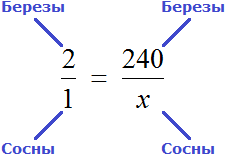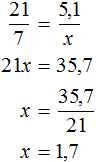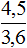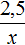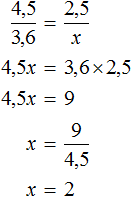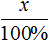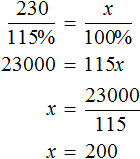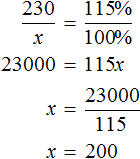Как найти неизвестное значение при помощи простых математических действий
Нередко возникают ситуации, когда вам нужно определить значение неизвестной величины. Это может быть что-то простое, например, определить скорость движения тела, или что-то более сложное, например, определить величину силы тяжести на планете.
Счастливо, при помощи простых математических действий, вы можете решить большинство этих проблем самостоятельно. Вот несколько способов, которые вы можете использовать, чтобы найти неизвестное значение.
Используйте уравнения
Если у вас есть уравнение, в котором участвует неизвестное значение, вы можете легко решить его, используя фундаментальные законы математики. Например, если у вас есть следующее уравнение:
2x + 3 = 7
То вы можете выразить значение x, используя следующие шаги:
2x + 3 = 7 (изначальное уравнение)
2x = 4 (вычтите 3 с обеих сторон)
x = 2 (разделите на 2 с обеих сторон)
Теперь вы знаете, что x равен 2.
Используйте пропорции
Если две величины пропорциональны друг другу, вы можете использовать пропорции, чтобы найти значение неизвестной. Например, если вы знаете, что a пропорционально b и c, вы можете записать это отношением:
a/b = c/d
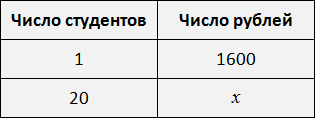
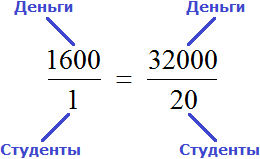
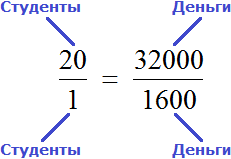
Теперь, если вы знаете значения b и c, вы можете использовать этот принцип, чтобы найти a. Просто умножьте b на c, а затем разделите на d:
a = (b * c) / d
Используйте формулы
Многие научные и математические концепции могут быть представлены в виде формул, которые вы можете использовать, чтобы найти неизвестные значения. Например, формула для вычисления скорости может быть записана следующим образом:
v = d/t
Здесь v – это скорость, d – расстояние и t – время. Если вы знаете значения d и t, вы можете использовать эту формулу, чтобы найти значение v.
Итог
Конечно, это только начало того, что вы можете сделать с помощью математических действий. Если вы будете продолжать изучать математику, вы найдете множество других способов для определения неизвестных значений. Однако, если вы запомните эти основы, вы сможете решать многие практические задачи в жизни.
Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.
Нахождение неизвестного слагаемого
Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9 . Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x. Согласно первоначальному условию, это число вместе с 4 образуют 9 , значит, можно записать уравнение 4 + x = 9 . Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x ? Для этого надо использовать правило:
Для нахождения неизвестного слагаемого надо вычесть известное из суммы.
В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a + b = c , то c − a = b и c − b = a , и наоборот, из выражений c − a = b и c − b = a можно вывести, что a + b = c .
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.
Возьмем то уравнение, что у нас получилось выше: 4 + x = 9 . Согласно правилу, нам нужно вычесть из известной суммы, равной 9 , известное слагаемое, равное 4 . Вычтем одно натуральное число из другого: 9 – 4 = 5 . Мы получили нужное нам слагаемое, равное 5 .
Обычно решения подобных уравнений записывают следующим образом:
- Первым пишется исходное уравнение.
- Далее мы записываем уравнение, которое получилось после того, как мы применили правило вычисления неизвестного слагаемого.
- После этого пишем уравнение, которое получилось после всех действий с числами.
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:
4 + x = 9 , x = 9 − 4 , x = 5 .
Мы можем проверить правильность полученного ответа. Подставим то, что у нас получилось, в исходное уравнение и посмотрим, выйдет ли из него верное числовое равенство. Подставим 5 в 4 + x = 9 и получим: 4 + 5 = 9 . Равенство 9 = 9 верное, значит, неизвестное слагаемое было найдено правильно. Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки. Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.
Нахождение неизвестного вычитаемого или уменьшаемого
Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.
Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.
Например, у нас есть уравнение x – 6 = 10 . Неизвестно уменьшаемое. Согласно правилу, нам надо прибавить к разности 10 вычитаемое 6 , получим 16 . То есть исходное уменьшаемое равно шестнадцати. Запишем все решение целиком:
x − 6 = 10 , x = 10 + 6 , x = 16 .
Проверим получившийся результат, добавив получившееся число в исходное уравнение: 16 – 6 = 10 . Равенство 16 – 16 будет верным, значит, мы все подсчитали правильно.
Переходим к следующему правилу.
Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.
Воспользуемся правилом для решения уравнения 10 – x = 8 . Мы не знаем вычитаемого, поэтому нам надо из 10 вычесть разность, т.е. 10 – 8 = 2 . Значит, искомое вычитаемое равно двум. Вот вся запись решения:
10 – x = 8 , x = 10 – 8 , x = 2 .
Сделаем проверку на правильность, подставив двойку в исходное уравнение. Получим верное равенство 10 – 2 = 8 и убедимся, что найденное нами значение будет правильным.
Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.
Нахождение неизвестного множителя
Посмотрим на два уравнения: x · 2 = 20 и 3 · x = 12 . В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a · b = c при a и b , не равных 0 , c : a = b , c : b = c и наоборот.
Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2 . Проводим деление натуральных чисел и получаем 10 . Запишем последовательность равенств:
x · 2 = 20 x = 20 : 2 x = 10 .
Подставляем десятку в исходное равенство и получаем, что 2 · 10 = 20 . Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x · 0 = 11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на 0 , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от 0 . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Решим с его помощью уравнение x : 3 = 5 . Перемножаем между собой известное частное и известный делитель и получаем 15 , которое и будет нужным нам делимым.
Вот краткая запись всего решения:
x : 3 = 5 , x = 3 · 5 , x = 15 .
Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5 . Верное числовое равенство – свидетельство правильного решения.
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Для нахождения неизвестного делителя нужно разделить делимое на частное.
Возьмем простой пример – уравнение 21 : x = 3 . Для его решения разделим известное делимое 21 на частное 3 и получим 7 . Это и будет искомый делитель. Теперь оформляем решение правильно:
21 : x = 3 , x = 21 : 3 , x = 7 .
Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21 : 7 = 3 , так что корень уравнения был вычислен верно.
Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на 0 . Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как 0 : x = 0 , то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0 , с делимым, отличным от 0 , решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5 : x = 0 , которое не имеет ни одного корня.
Последовательное применение правил
Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.
У нас есть уравнение вида 3 · x + 1 = 7 . Вычисляем неизвестное слагаемое 3 · x , отняв от 7 единицу. Получим в итоге 3 · x = 7 − 1 , потом 3 · x = 6 . Это уравнение решить очень просто: делим 6 на 3 и получаем корень исходного уравнения.
Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :
( 2 · x − 7 ) : 3 − 5 = 2 , ( 2 · x − 7 ) : 3 = 2 + 5 , ( 2 · x − 7 ) : 3 = 7 , 2 · x − 7 = 7 · 3 , 2 · x − 7 = 21 , 2 · x = 21 + 7 , 2 · x = 28 , x = 28 : 2 , x = 14 .
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = – 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
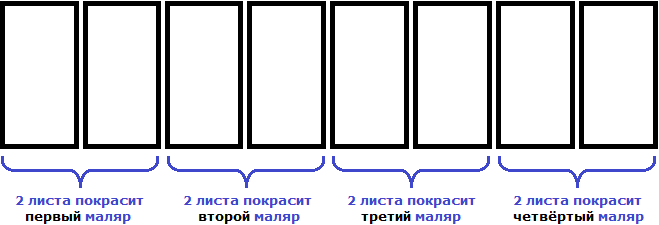
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства позволяет узнать чему равно x
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда .
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда .
Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве вместо числа 15 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Теперь представим, что в равенстве вместо числа 5 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение и подставим вместо x
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда .
Вернемся к исходному уравнению и подставим вместо x найденное значение 2
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы вычли из обеих частей уравнения число 10 . В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2
Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 4x , а в правой части число 4
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения .
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.
Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 5
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения равен 5 . Значит эти уравнения равносильны.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 9
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно . Теперь найдем значение переменной B . То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно
Видим, что значение переменной B , как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение . Чему равен корень этого уравнения?
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . Это есть произведение минус единицы и переменной x
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом:
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения равен 5 . Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения на минус единицу:
После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10
Корень этого уравнения, как и уравнения равен 5
Значит уравнения и равносильны.
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1 .
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения на −1 можно записать подробно следующим образом:
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения на −1 , мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2
Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5
Уравнения вида мы решали выражая неизвестное слагаемое:
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю:
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x , левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s .
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения определить время. Для этого нужно выразить переменную t .
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение примет следующий вид
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение примет вид .
Отсюда .
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
[/spoiler]
Так же как и теория вероятностей, математическая статистика имеет свои ключевые понятия, к которым относятся: генеральная совокупность, теоретическая функция распределения, выборка, эмпирическая функция распределения, статистика. Именно с определения этих понятий, а также с установления связи между ними и объектами, изучаемыми в теории вероятностей, мы начнем изложение математической статистики, предварительно дав краткое описание задач, которые собираемся решать. Кроме того, в последнем параграфе главы остановимся на некоторых распределениях, наиболее часто встречающихся в математической статистике.
Задачи математической статистики
Математическая статистика, являясь частью общей прикладной математической дисциплины «Теория вероятностей и математическая статистика», изучает, как и теория вероятностей, случайные явления, использует одинаковые с ней определения, понятия и методы и основана на той же самой аксиоматике А.Н. Колмогорова.
Однако задачи, решаемые математической статистикой, носят специфический характер. Теория вероятностей исследует явления, заданные полностью их моделью, и выявляет еще до опыта те статистические закономерности, которые будут иметь место после его проведения. В математической статистике вероятностная модель явления определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется тем, что нам позволено проводить «пробные» испытания и на их основе восстанавливать недостающую информацию.
Попытаемся показать различие этих двух взаимосвязанных дисциплин на простейшем примере — последовательности независимых одинаковых испытаний, или схеме Бернулли (часть 1, гл.4). Схему Бернулли можно трактовать как подбрасывание несимметричной монеты с вероятностью выпадения «герба» (успеха) р и «цифры» (неудачи) 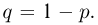
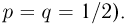
часть 1, гл.4, параграфы 2-4) и т.д. В математической статистике значения р и q неизвестны заранее, но мы можем произвести серию подбрасываний монеты. Цель проведения испытаний как раз и заключается либо в определении р и q, либо в проверке некоторых априорных суждений относительно их значений. Таким образом, судя уже по этому простейшему примеру, задачи математической статистики являются в некотором смысле обратными задачам теории вероятностей.
В математической статистике обычно принято выделять два основных направления исследований.
Первое направление связано с оценкой неизвестных параметров. Возвращаясь к нашему примеру, предположим, что мы произвели п подбрасываний монеты и установили, что в 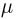
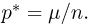
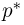
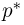
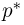
Второе направление в математической статистике связано с проверкой некоторых априорных предположений, или статистических гипотез. Так, до опыта мы можем предположить, что монета симметрична, т.е. высказать гипотезу о равенстве 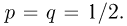
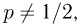
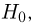
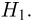
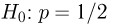
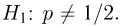
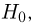
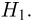
на ошибки первого и второго рода. Ошибка первого рода состоит в том, что мы принимаем конкурирующую гипотезу 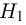
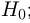
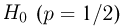
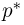
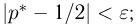
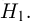
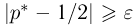
Далее мы увидим, что задача проверки статистических гипотез наиболее полно решается для случая двух простых гипотез. Можно поставить и задачу проверки нескольких гипотез (в примере с монетой можно взять, например, три гипотезы: 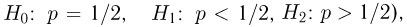
Условно математическую статистику можно подразделить на исследование байесовских и небайесовских моделей.
Байесовские модели возникают тогда, когда неизвестный параметр является случайной величиной и имеется априорная информация о его распределении. При байесовском подходе на основе опытных данных априорные вероятности пересчитываются в апостериорные. Применение байесовского подхода фактически сводится к использованию формулы Байеса (см. часть 1, гл. 3, параграф 5), откуда, собственно говоря, и пошло его название. Байесовский подход нами будет применяться только как вспомогательный аппарат при доказательстве некоторых теорем.
Небайесовские модели появляются тогда, когда неизвестный параметр нельзя считать случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели мы будем рассматривать в дальнейшем изложении.
В заключение этого параграфа отметим, что в математической статистике употребляют также понятия параметрических и непараметрических моделей. Параметрические модели возникают тогда, когда нам известна с точностью до параметра (скалярного или векторного) функция распределения наблюдаемой характеристики и необходимо по результатам испытаний определить этот параметр (задача оценки неизвестного параметра) или проверить гипотезу о принадлежности его некоторому заранее выделенному множеству значений (задача проверки статистических гипотез). Все приведенные выше примеры с подбрасыванием монеты представляют собой параметрические модели. Примеры непараметрических моделей мы рассмотрим позже.
Основные понятия математической статистики
Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.
Генеральная совокупность. Будем предполагать, что у нас имеются N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики X. Характеристика X, вообще говоря, может быть и векторной (например, линейные размеры объекта), однако для простоты изложения мы ограничимся только скалярным случаем, тем более что переход к векторному случаю никаких трудностей не вызывает. Совокупность этих N объектов назовем генеральной совокупностиью.
Поскольку все наши статистические выводы мы будем делать, основываясь только на значениях числовой характеристики X, естественно абстрагироваться от физической природы самих объектов и отождествить каждый объект с присущей ему характеристикой X. Таким образом, с точки зрения математической статистики генеральная совокупность представляет собой N чисел, среди которых, конечно, могут быть и одинаковые.
Выборка. Для того чтобы установить параметры генеральной совокупности, нам позволено произвести некоторое число п испытаний. Каждое испытание состоит в том, что мы случайным образом выбираем один объект генеральной совокупности и определяем его значение X. Полученный таким образом ряд чисел 

Заметим, что сам процесс выбора можно осуществлять различными способами: выбрав объект и определив его значение, изымать этот объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность и может полноправно участвовать в дальнейших испытаниях (выборка с возвращением) и т.д.
Разумеется, если бы мы смогли провести сплошное обследование всех объектов генеральной совокупности, то не нужно было бы применять никакие статистические методы и саму математическую статистику можно было бы отнести к чисто теоретическим наукам. Однако такой полный контроль невозможен по следующим причинам. Во-первых, часто испытание сопровождается разрушением испытуемого объекта; в этом случае мы имеем выборку без возвращения. Во-вторых, обычно необходимо исследовать весьма большое количество объектов, что просто невозможно физически. Наконец, может возникнуть такое положение, когда многократно измеряется один и тот же объект, но каждый замер производится со случайной ошибкой, и цель последующей статистической обработки заключается именно в уточнении характеристик объекта на основе многократных наблюдений; при этом результат каждого наблюдения надо считать новым объектом генеральной совокупности (простейшим примером такой ситуации является многократное подбрасывание монеты с целью определения вероятности выпадения «герба»). Следует помнить также, что выборка обязательно должна удовлетворять условию репрезентативности или, говоря более простым языком, давать обоснованное представление о генеральной совокупности.
С ростом объема N генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Мы, как обычно это делается в математической статистике, будем рассматривать случай бесконечно большого объема генеральной совокупности и поэтому, употребляя слово «выборка», не будем указывать, какая она — с возвращением или без него.
Теоретическая функция распределения. Пусть 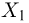
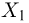
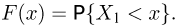
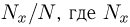
В случае выборки 
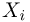


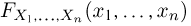

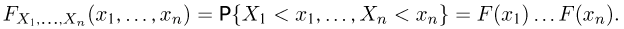
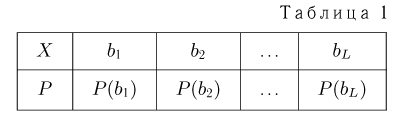
В дальнейшем, как правило, мы будем предполагать, что F(x) является функцией распределения либо дискретной, либо непрерывной наблюдаемой случайной величины X. В первом случае будем оперировать рядом распределения случайной величины X, записанным в виде табл. 1, а во втором — плотностью распределения
Простейшие статистические преобразования
Прежде чем переходить к детальному анализу наблюденных статистических данных, обычно проводят их предварительную обработку. Иногда результаты такой обработки уже сами по себе дают наглядную картину исследуемого явления, в большинстве же случаев они служат исходным материалом для получения более подробных статистических выводов.
Вариационный и статистический ряды. Часто бывает удобно пользоваться не самой выборкой 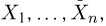
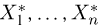
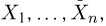
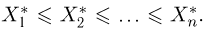

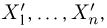
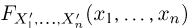
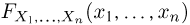
Для 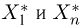
Пример 1. Измерение проекции вектора скорости молекул водорода на одну из осей координат дало (с учетом направления вектора) результаты 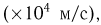
Вариационный ряд этой выборки приведен в табл. 3. Крайними членами вариационного ряда 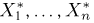
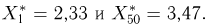
Если среди элементов выборки 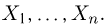
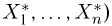
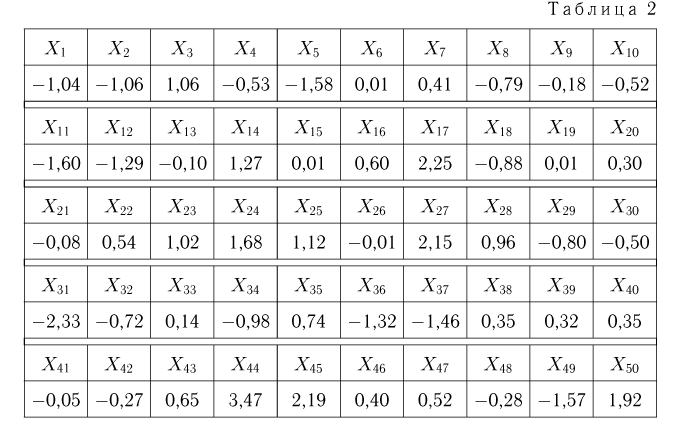
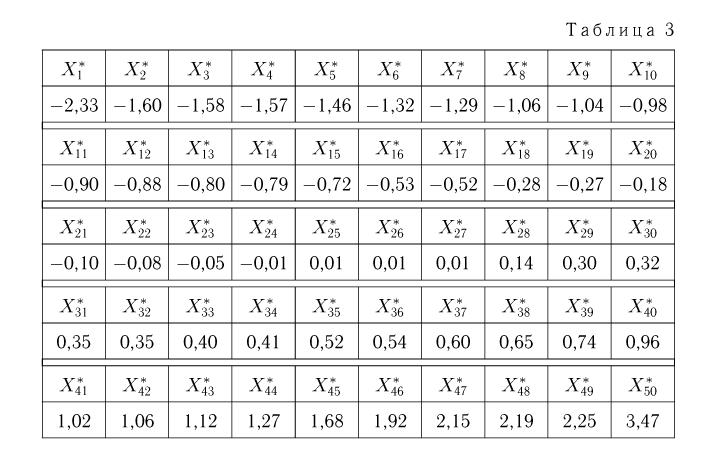
ряда (табл.4), в котором 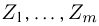
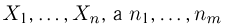
Пример 2. В течение минуты каждую секунду регистрировалось число попавших в счетчик Гейгера частиц. Результаты наблюдений приведены в табл. 5.
Статистический ряд выборки представлен в табл. 6.

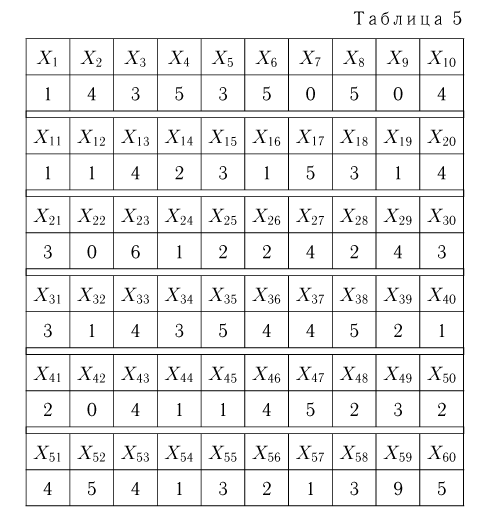
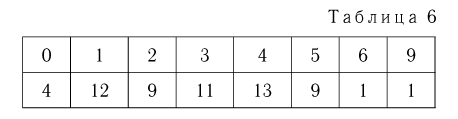
Статистики. Для получения обоснованных статистических выводов необходимо проводить достаточно большое число испытаний, т.е. иметь выборку достаточно большого объема п. Ясно, что не только использование такой выборки, но и хранение ее весьма затруднительно. Чтобы избавиться от этих трудностей, а также для других целей, полезно ввести понятие статистики, общее определение которой формулируется следующим образом. Назовем статистикой 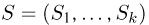
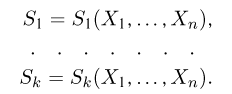
Как функция от случайного вектора 
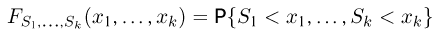
определяется для дискретной наблюдаемой случайной величины X формулой
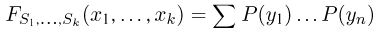
и для непрерывной — формулой
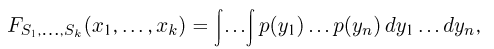
где суммирование или интегрирование производится по всем возможным значениям 
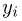
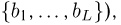
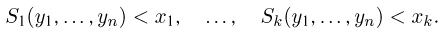
Пример 3. Пусть выборка 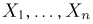
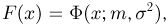
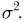
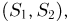
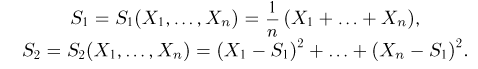
Тогда
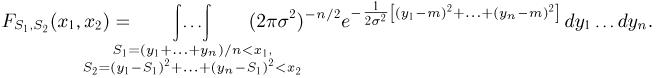
Мы, однако, не будем вычислять записанный интеграл, а воспользуемся тем фактом (см. пример 29, часть 1, гл.6, параграф 7), что любое линейное преобразование переводит нормально распределенный вектор в вектор, снова имеющий нормальное распределение, причем ортогональное преобразование переводит вектор с независимыми координатами, имеющими одинаковые дисперсии, в вектор с также независимыми и имеющими те же самые дисперсии координатами.
Из курса теории вероятностей известно, что статистика 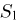
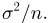
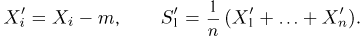
Очевидно, что
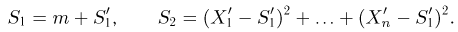
Пусть теперь А — линейное ортогональное преобразование пространства 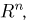
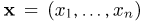
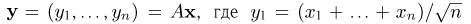
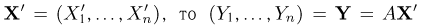
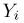
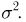
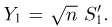
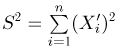
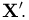
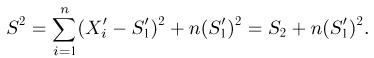
С другой стороны, в силу ортогональности преобразования А
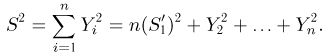
Отсюда, в частности, следует, что
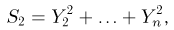
т.е. 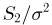
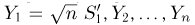
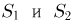
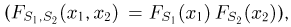
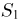
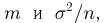
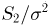
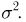
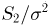
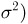
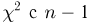
Отметим, что проведенные рассуждения будут нами постоянно использоваться в гл. 4, посвященной статистическим задачам, связанным с нормально распределенными наблюдениями.
Важный класс статистик составляют так называемые достаточные статистики. Не давая пока строгого математического определения, скажем, что статистика S является достаточной, если она содержит всю ту информацию относительно теоретической функции распределения F(x), что и исходная выборка 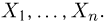
Эмпирическая функция распределения. Пусть мы имеем выборку 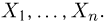
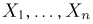
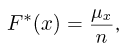
где 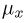
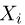
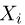
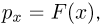
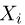
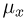
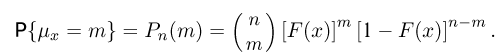
Функция 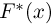
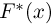
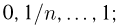
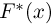
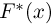
Построение эмпирической функции распределения 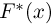
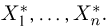
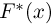
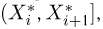
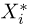
Пример 4. График эмпирической функции распределения, построенной по вариационному ряду из табл. 3, приведен на рис. 1.
Если выборка задана статистическим рядом (см. табл. 4), то эмпирическая функция распределения также постоянна на интервалах 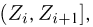
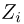
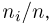
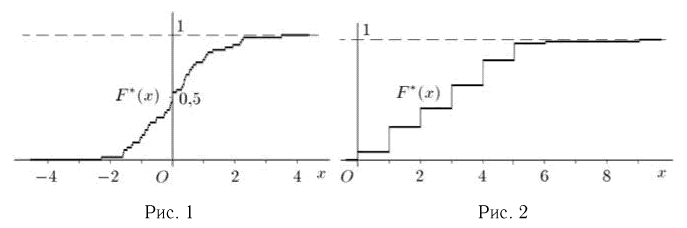
Пример 5. График эмпирической функции распределения, построенной по статистическому ряду из табл. 6, приведен на рис. 2.
Гистограмма, полигон. Для наглядности выборку иногда преобразуют следующим образом. Всю ось абсцисс делят на интервалы 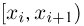
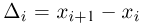
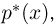
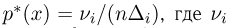
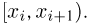
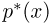
При наблюдении дискретной случайной величины вместо гистограммы часто используют полигон частот. Для этого по оси абсцисс откладывают все возможные значения 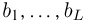


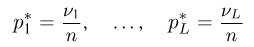
(полигон относительных частот). Для большей наглядности соседние точки соединяются отрезками прямой.
Для непрерывной наблюдаемой случайной величины полигоном относительных частот иногда называют ломаную линию, соединяющую середины отрезков, составляющих гистограмму.
Пример 6. Построим гистограмму и полигон относительных частот выборки, представленной в табл. 2. Для этого выберем интервалы одинаковой длины 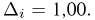
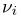
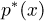
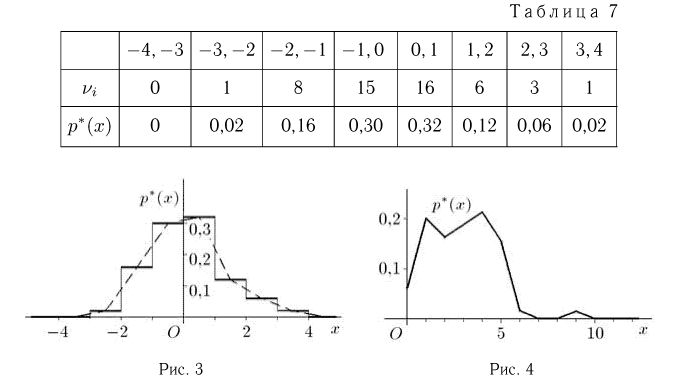
Пример 7. Построим полигон относительных частот выборки, приведенной в табл. 5. Возможные значения наблюдаемой случайной величины X (числа частиц, попавших в счетчик Гейгера) представляют собой неотрицательные целые числа. Воспользовавшись статистическим рядом из табл. 6, получаем полигон относительных частот, изображенный на рис. 4.
Предельное поведение эмпирической функции распределения.
Предположим, что по выборке 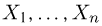
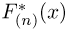
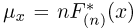
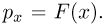
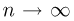
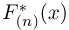
Теорема Гливенко-Кантелли. При 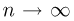
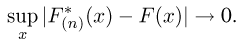
Смысл теоремы Гливенко-Кантелли заключается в том, что при увеличении объема выборки п у эмпирической функции распределения исчезают свойства случайности и она приближается к теоретической функции распределения.
Аналогично, если п велико, то значение гистограммы 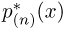
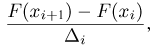
где 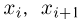
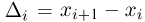
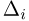
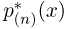
Выборочные характеристики. Эмпирическая функция распределения 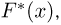
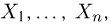
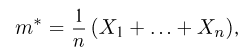
второй момент
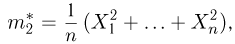
дисперсию
момент k-го порядка
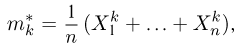
центральный момент k-го порядка
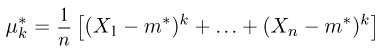
и т.д. Соответствующие характеристики называются выборочными (выборочное среднее, выборочный второй момент, выборочная дисперсия и т.п.). Ясно, что выборочные характеристики как функции от случайных величин 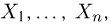
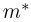
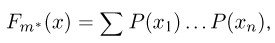
где суммирование ведется по всем 
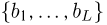
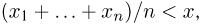
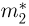
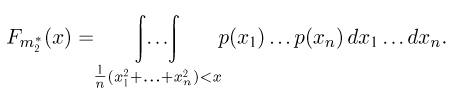
Наряду с выборочной дисперсией 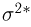
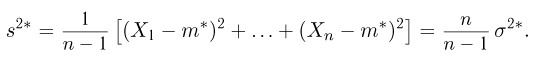
Характеристику 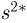
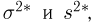
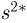
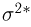
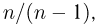
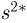
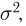
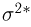
Пример 8. Подсчитаем выборочное среднее и выборочные дисперсии для выборки, приведенной в табл. 2:
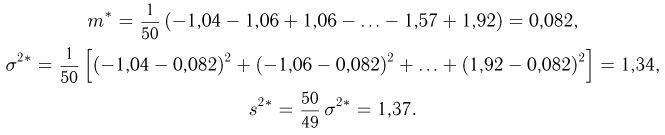
Для подсчета выборочной дисперсии 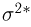
Основные распределения математической статистики
Наиболее часто в математической статистике используются: нормальное распределение, 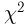
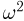
Нормальное распределение. Одномерное стандартное нормальное распределение (стандартный нормальный закон) задается своей плотностью распределения (см. часть 1, гл.5, параграф 4)
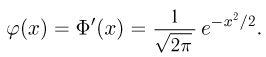
Значения функции Ф(x) и плотности 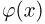
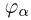
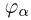
Общее одномерное нормальное распределение характеризуется двумя параметрами: средним (математическим ожиданием) т и дисперсией 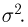
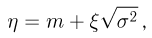
где случайная величина 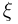
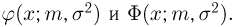
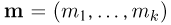
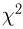
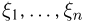
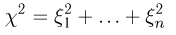
носит название 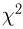
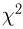
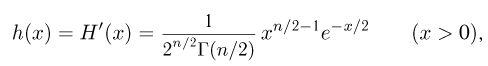
где 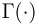
Значения функции 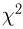
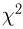
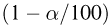
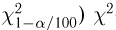

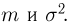
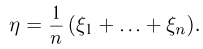
Тогда случайная величина
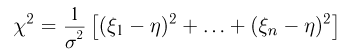
имеет 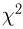
Еще одна схема, в которой появляется 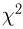
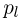
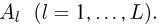
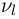
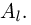
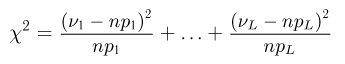
при 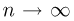
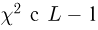
t-распределение. Пусть 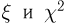
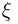
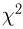
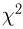
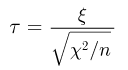
называется t-распределением с п степенями свободы, t-распределение имеет плотность распределения
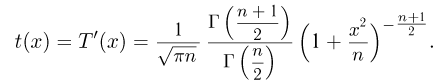
Значения функции t-распределения и 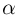
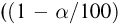
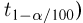
Далее, пусть 
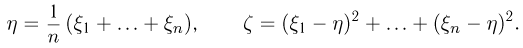
Тогда случайные величины 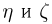
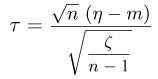
имеет t-распределение с n-1 степенями свободы (доказательство этого см. в примере 3).
F-распределение. Пусть 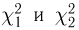
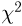
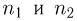
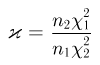
носит название F-распределения с параметрами 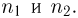
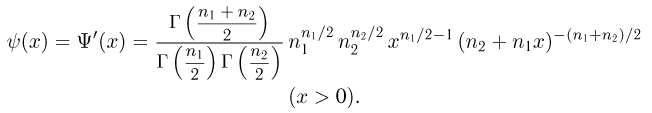
Значения 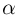
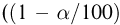
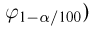
Распределение Колмогорова. Функция распределения Колмогорова имеет вид
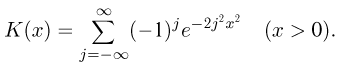
Распределение Колмогорова является распределением случайной величины
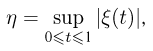
где 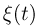
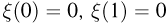
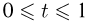
Значения функции распределения Колмогорова приведены в [1], табл.6.1. Квантили распределения Колмогорова будем обозначать через
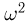
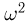
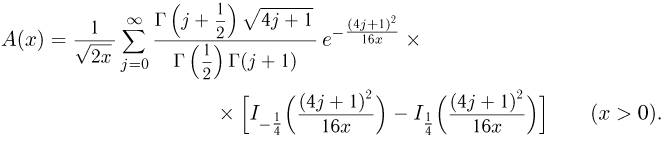
Здесь 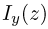
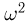
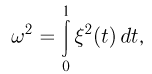
где 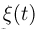
Значения функции 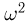
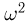
Оценки неизвестных параметров
Как уже говорилось в гл. 1, одним из двух основных направлений в математической статистике является оценивание неизвестных параметров. В этой главе мы дадим определение оценки, опишем те свойства, которые желательно требовать от оценки, и приведем основные методы построения оценок. Завершается глава изложением метода построения доверительных интервалов для неизвестных параметров.
Статистические оценки и их свойства
Предположим, что в результате наблюдений мы получили выборку 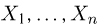
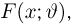


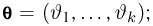
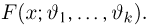
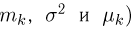

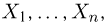
Оценкой неизвестного параметра 
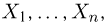
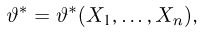
зависящую только от выборки 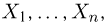
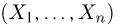
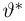
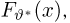
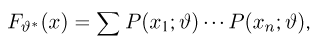
где суммирование ведется по всем переменным 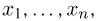
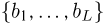
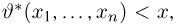
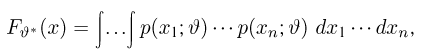
где интегрирование ведется по области, выделяемой неравенством 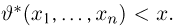
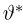
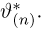
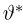


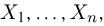

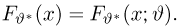
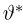
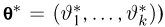
Пример:
Предположим, что проведено п испытаний в схеме Бернулли с неизвестной вероятностью успеха 
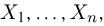
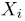
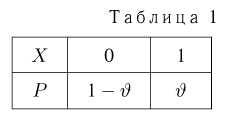
В качестве оценки 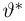
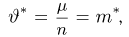
где
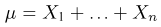
представляет собой суммарное число успехов в п испытаниях Бернулли. Статистика 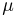


Пример:
Выборка 
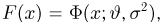


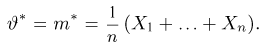
Функция распределения 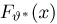
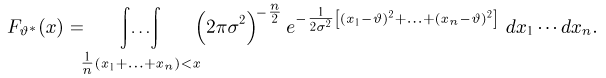
Однако вместо непосредственного вычисления написанного n-мерного интеграла заметим, что статистика
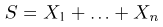
распределена по нормальному закону с параметрами 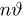
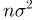
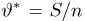
Разумеется, на практике имеет смысл использовать далеко не любую оценку.
Пример:
Как и в примере 1, рассмотрим испытания в схеме Бернулли. Однако теперь в качестве оценки неизвестной вероятности успеха 
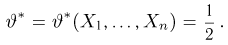
Такая оценка будет хороша лишь в том случае, когда истинное значение 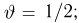

Приведенный пример показывает, что желательно употреблять только те оценки, которые по возможности принимали бы значения, наиболее близкие к неизвестному параметру. Однако в силу случайности выборки в математической статистике мы, как правило, не застрахованы полностью от сколь угодно большой ошибки. Значит, гарантировать достаточную близость оценки 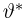

Опишем теперь те свойства, которые мы хотели бы видеть у оценки.
Главное свойство любой оценки, оправдывающее само название «оценка», — возможность хотя бы ценой увеличения объема выборки до бесконечности получить точное значение неизвестного параметра 
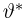

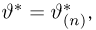
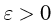

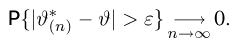
Отметим, что правильнее было бы говорить о состоятельности последовательности оценок 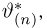
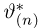
Пример:
Оценка 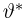

Пример:
Пусть выборка 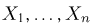
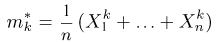
сходится к теоретическому моменту 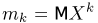
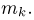
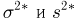
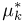
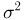
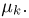
Пример:
Выборка 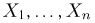
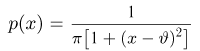
с неизвестным параметром 

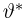

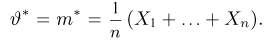
Однако 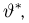


Из курса теории вероятностей известно (см. часть 1, гл.7, параграф 1), что мерой отклонения оценки 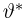

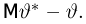
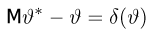
называется смещением оценки 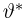
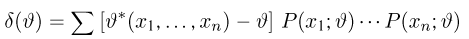
в дискретном случае и
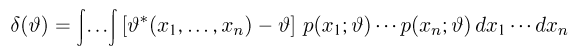
в непрерывном, где суммирование или интегрирование ведется по всем возможным значениям
Оценка 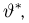
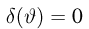
при всех 
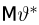
Пример:
Оценка 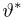

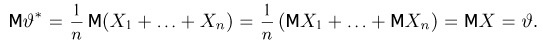
Пример:
Выборочные моменты 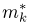
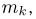
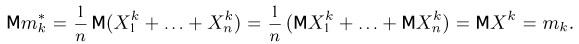
Вычислим теперь математическое ожидание выборочной дисперсии
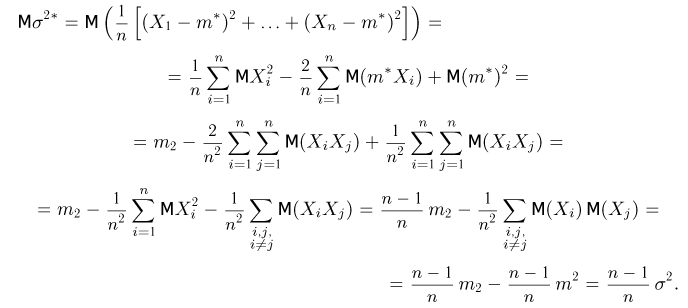
Таким образом, 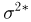
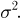
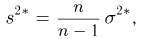
то
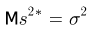
и 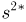
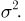
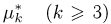
Пример:
Пусть 
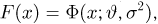

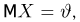
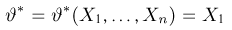
является несмещенной. Очевидно, однако, что она не является состоятельной.
Примеры 8 и 9 показывают, что состоятельная оценка может быть сметенной и, наоборот, несмещенная оценка не обязана быть состоятельной.
Рассматривая несколько оценок неизвестного параметра 

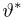
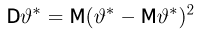
(дисперсия, как и распределение оценки, зависит от неизвестного параметра 
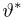

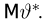
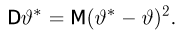
Имеется несколько подходов к нахождению несмещенных оценок с минимальной дисперсией. Это связано с тем, что такие оценки существуют не всегда, а найти их бывает чрезвычайно сложно. Здесь мы изложим понятие эффективности оценки, основанное на неравенстве Рао-Крамера.
Теорема:
Неравенство Рао-Крамера. Пусть 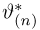
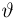
где 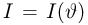
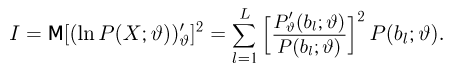
а в непрерывном — формулой
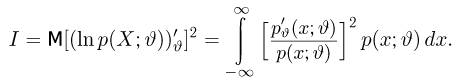
Прежде чем переходить к доказательству теоремы, заметим, что по неравенству Рао-Крамера дисперсия любой несмещенной оценки не может быть меньше 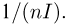
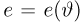
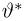
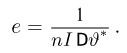
Ясно, что эффективность любой оценки 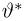
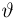
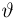
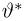
Несмещенная оценка 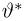
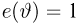
Доказательство теоремы 1. Доказательство этой и всех остальных теорем будем проводить (если не сделано специальной оговорки) для непрерывного случая. Это связано с тем, что непрерывный случай, как правило, более сложен, и читатель, усвоивший доказательство для непрерывного случая, легко проведет его для дискретного.
Как мы увидим из хода доказательства, условия регулярности семейства 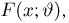
функция 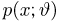
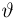
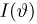
Приступим теперь к собственно доказательству теоремы. Заметим прежде всего, что, дифференцируя тождество
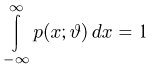
(в силу сформулированного условия это можно делать), получаем
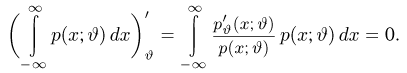
Далее, в силу несмещенности оценки 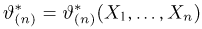
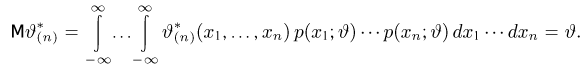
Дифференцируя это равенство по 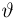
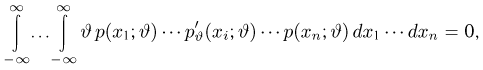
полученное из (1) и (2), находим
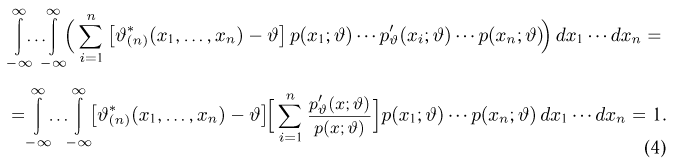
Воспользовавшись неравенством Коши-Буняковского
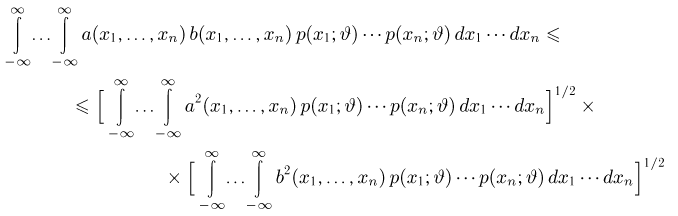
при
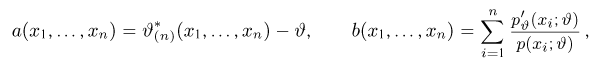
имеем
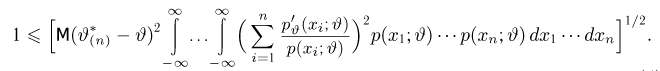
Заметим теперь, что в силу тождества (2)
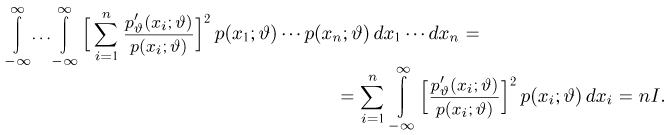
Тогда неравенство (5) можно переписать в виде 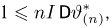
Замечание:
Для превращения используемого при доказательстве теоремы 1 неравенства Коши-Буняковского, в равенство необходимо и достаточно существование таких функций 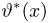
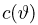
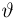
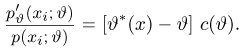
При этом оценка 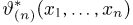
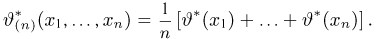
Обозначая
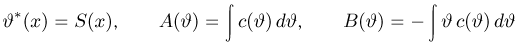
и интегрируя уравнение (6), получаем, что необходимым условием существования эффективной оценки является возможность представления плотности распределения 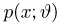
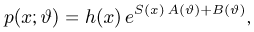
где 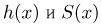
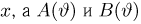
Аналогичное представление для ряда распределения 
Экспоненциальные семейства играют в математической статистике важную роль. В частности, как мы показали, только для этих семейств могут существовать эффективные оценки, которые к тому же определяются формулой
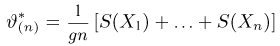
(появление множителя 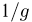
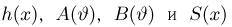
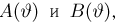
Замечание:
Неравенство Рао-Крамера можно обобщить на случай смещенных оценок:
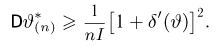
И в этом случае неравенство превращается в равенство только тогда, когда семейство распределений экспоненциально.
Пример:
Рассмотрим оценку 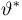
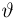
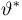
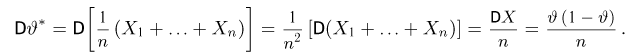
Найдем информацию Фишера (напомним, что в данном случае наблюдаемая величина X принимает всего два значения 0 и 1 с вероятностями 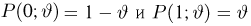
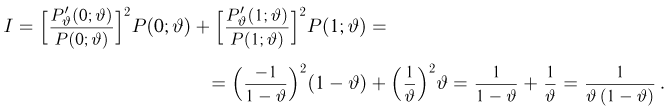
Таким образом, 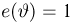
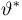
Пример:
Рассмотрим оценку 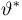
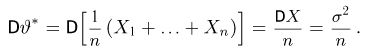
Далее,
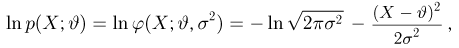
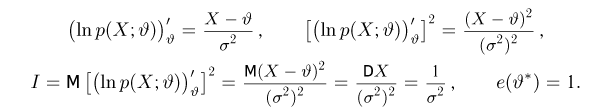
И в этом примере оценка 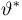
Пример:
Оценим неизвестную дисперсию 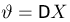
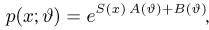
где
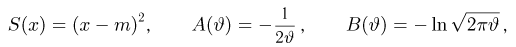
т.е. по отношению к неизвестной дисперсии 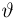
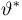
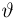
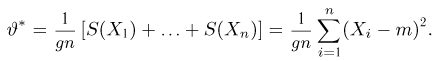
С другой стороны, нетрудно видеть, что 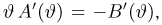
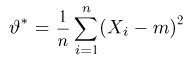
и, значит, ее эффективность. Впрочем, эффективность оценки 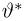
Пусть теперь мы оцениваем не дисперсию, а среднее квадратичное отклонение 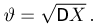
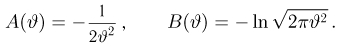
Поэтому равенство 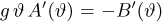
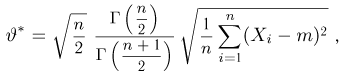
равную корню квадратному из оценки дисперсии с точностью до постоянного множителя 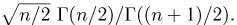
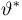

Пример:
Пусть выборка 
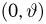

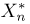

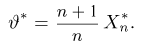
Функция распределения 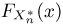
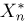
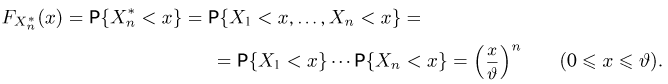
Тогда
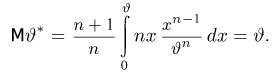
Значит, оценка 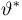
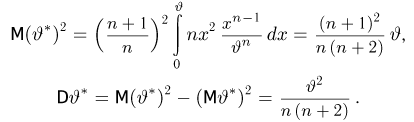
Мы видим, что дисперсия оценки 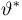
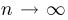
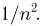
В заключение этого параграфа отметим, что эффективные по Рао-Крамеру оценки существуют крайне редко. Правда, как мы увидим в параграфе 4, эффективность по Рао-Крамеру играет существенную роль в асимптотическом анализе оценок, получаемых методом максимального правдоподобия. Кроме того, существуют обобщения неравенства Рао-Крамера (например, неравенство Бхаттачария [7]), позволяющие доказывать оптимальность более широкого класса оценок.
В следующем параграфе мы рассмотрим другой подход к определению оценок с минимальной дисперсией, базирующийся на достаточных статистиках.
Наиболее распространенные методы нахождения оценок приводятся в параграфах 3-6.
Наконец, в параграфе 7 описан подход к построению доверительных интервалов для неизвестных параметров.
Достаточные оценки
Первый шаг в поисках другого (не основанного на неравенстве Рао-Крамера) принципа построения оценок с минимальной дисперсией состоит во введении понятия достаточной статистики (отметим, что достаточные статистики играют в современной математической статистике весьма важную роль, причем как при оценке неизвестных
параметров, так и при проверке статистических гипотез). Назовем k-мерную статистику
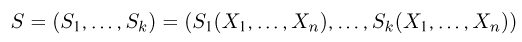
достаточной для параметра 
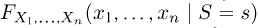
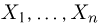
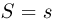
Пример:
Пусть 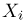
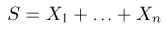
— общее число успехов в п испытаниях Бернулли. Покажем, что она является достаточной для вероятности успеха 
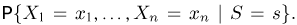
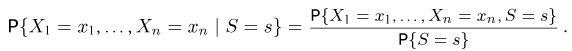
Если 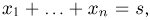
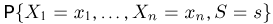
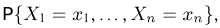
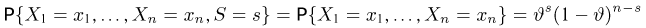
(напомним еще раз, что каждое 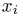
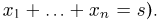
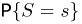
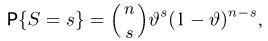
то из (9) получаем, что
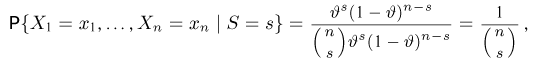
т. е. не зависит от 
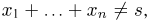
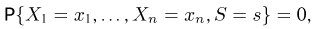
откуда
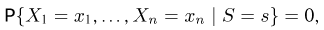
т. е. опять-таки не зависит от 
Очевидно, что использовать приведенное выше определение для проверки достаточности конкретных статистик весьма сложно, особенно в непрерывном случае. Простой критерий достаточности задается следующей теоремой.
Теорема:
Факторизационная теорема Неймана-Фишера. Для того чтобы статистика 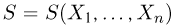

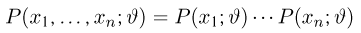
в дискретном случае или плотность распределения
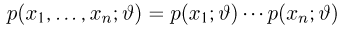
в непрерывном случае выборки 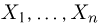
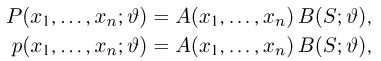
где функция 
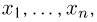
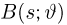
Доказательство:
Для простоты изложения ограничимся только дискретным случаем. По определению условной вероятности,
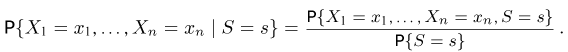
Очевидно, что числитель в правой части (II) совпадает с вероятностью 
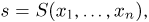
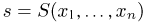
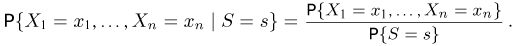
Теперь, если S — достаточная статистика, то левая часть (12) не зависит от 
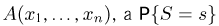
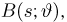
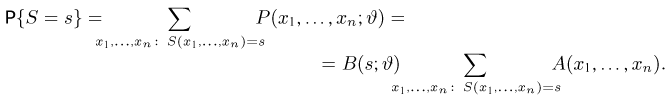
Подставляя последнее равенство в (12), имеем
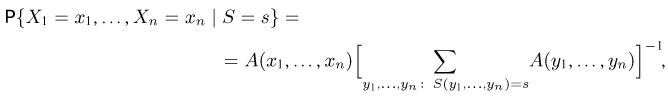
т.е. не зависит от 
Замечание к теореме 2. Очевидно, что представление (10) справедливо с точностью до функции 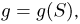
Пример:
Пусть 
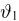
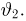
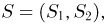
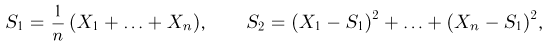
является достаточной для (двумерного) параметра 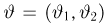
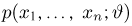

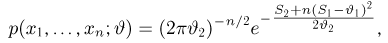
т.е. имеет вид (10), где
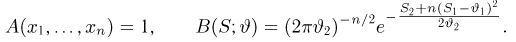
Пример:
Пусть 
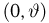
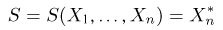
является (одномерной) достаточной статистикой для 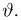
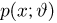
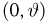
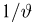
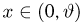

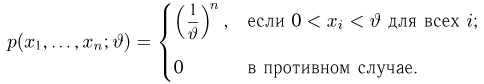
В частности, область изменения каждого аргумента 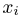
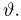
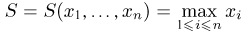
и положим
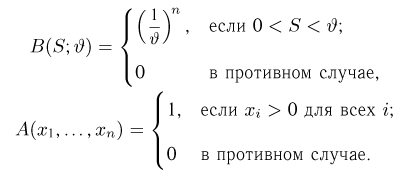
С учетом введенных функций.
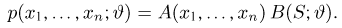
Здесь уже при определении функции 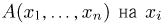
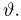



является достаточной для параметра
Пример:
Покажем, что для экспоненциального семейства (7) существует одномерная достаточная статистика. Этот факт легко установить, если подставить выражение (7) в формулу для плотности распределения выборки
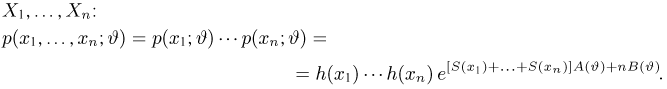
Полагая теперь
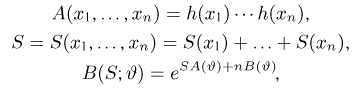
видим, что одномерная статистика
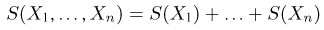
является достаточной для параметра 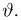
Как уже говорилось в гл. 1, смысл достаточной статистики S заключается в том, что она включает в себя всю ту информацию о неизвестном параметре 

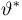
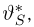
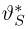
Начиная с этого момента и до конца параграфа будем для простоты предполагать, что неизвестный параметр 
Пусть имеется некоторая оценка 
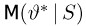

Теорема:
Улучшение оценки по достаточной статистике. Пусть S — достаточная статистика, а 
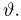
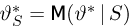
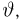
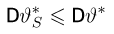
при всех
Доказательство:
В силу достаточности статистики 5 условное распределение, а значит, и условное математическое ожидание оценки 


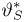
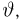
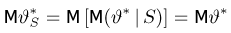
для условного математического ожидания немедленно следует несмещенность оценки
Наконец,
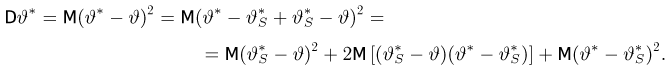
Используя опять свойство условного математического ожидания, получаем
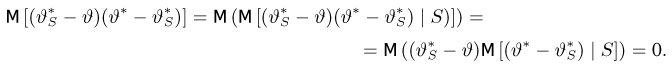
Поэтому
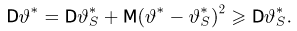
Замечание:
Неравенство (13) превращается для некоторого 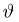
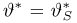
Замечание:
Утверждение теоремы остается в силе и для смещенной оценки 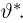
Смысл теоремы 3 заключается в том, что взятие условного математического ожидания, т. е. переход к оценке 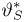

Пример:
Пусть 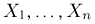
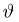
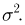
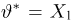
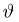
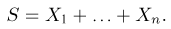
Нетрудно показать, что статистика S является достаточной для параметра 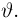
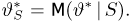
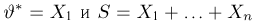
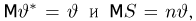
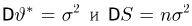
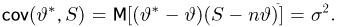

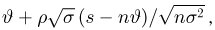
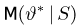
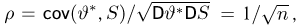

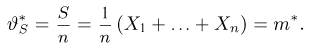
Иными словами, мы из совсем плохой оценки 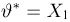
Рассмотренный пример приоткрывает нам те возможности, которые несет с собой теорема 3. Однако, прежде чем сделать последний шаг, введем еще одно определение. Назовем статистику 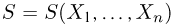
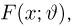
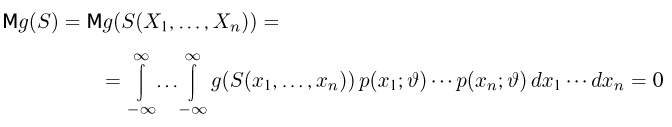
при всех 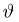
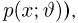
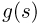
Теорема:
Минимальность дисперсии оценки, зависящей от полной достаточной статистики. Пусть S — полная достаточная статистика, 
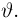
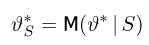
является единственной несмещенной оценкой с минимальной дисперсией.
Доказательство теоремы немедленно вытекает из предыдущих результатов. Действительно, в силу теоремы 3 оценка с минимальной дисперсией обязательно должна находиться среди оценок, зависящих только от достаточной статистики S; в противном случае ее можно было бы улучшить с помощью условного математического ожидания. Но среди оценок, зависящих только от S, может быть максимум одна несмещенная. В самом деле, если таких оценок две: 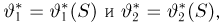
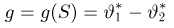
имеет при всех значениях 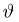
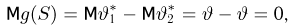
что в силу полноты статистики S влечет за собой равенство 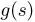
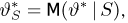
Перейдем к обсуждению полученных результатов.
Условие полноты статистики S, как мы видим, сводится к единственности несмещенной оценки 
Сравнение размерностей полной статистики S и оцениваемого параметра 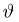
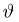
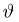


Сформулируем очевидное следствие из теоремы 4. которое удобно применять во многих частных случаях.
Следствие из теоремы 4. Если оценка 
Пример:
Пусть 
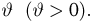
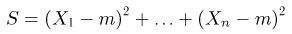
является достаточной для параметра 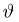
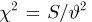
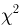
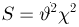
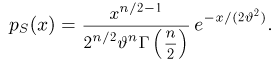
Пусть теперь 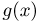
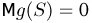
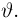
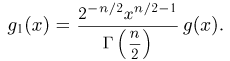
Тогда
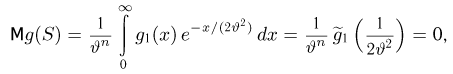
что 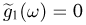
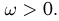
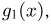
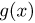
Рассмотрим теперь оценку
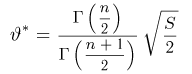
(см. пример 12) неизвестного среднего квадратичного отклонения 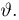
Пример:
Рассмотрим оценку
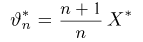
параметра 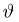
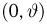
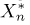
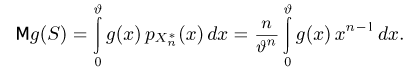
Отсюда, в частности, следует, что если 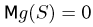
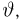
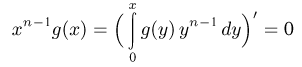
при всех х. Поэтому 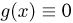
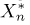
Таким образом, в силу следствия из теоремы 4 и в этом примере оценка 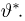
Метод моментов
Пусть мы имеем выборку 
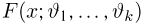
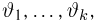
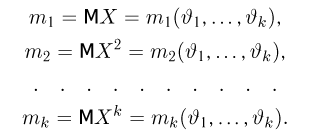
Суть метода моментов заключается в следующем: так как выборочные моменты являются состоятельными оценками теоретических моментов (см. пример 8), мы можем в написанной системе равенств при большом объеме выборки п теоретические моменты 
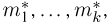
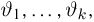
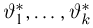

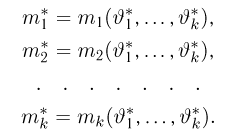
Можно показать, что при условии непрерывной зависимости решения этой системы от начальных условий 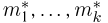
Теорема:
Асимптотическая нормальность оценок, полученных методом моментов. При некоторых условиях, наложенных на семейство 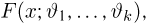
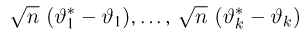
при 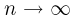

Доказательство:
Будем полагать, что выполнены следующие условия: а) параметры 
б) существует теоретический момент 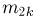
в) функция
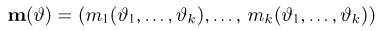
дифференцируема по 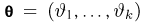
Доказательство теоремы проведем для одномерного случая, предоставляя общий случай читателю. Оно является комбинацией следующих результатов: теоремы о дифференцируемости обратного отображения и центральной предельной теоремы. Действительно, поскольку существует дисперсия DX, то при каждом истинном значении 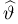
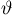
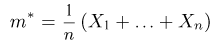
асимптотически при 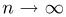
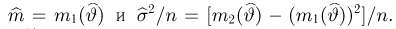

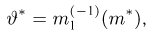
где 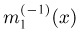
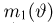
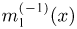
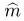
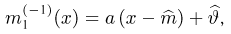
причем 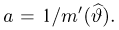
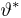
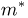
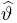
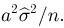
Пример:
Найдем методом моментов оценку неизвестной вероятности успеха 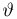
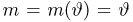
Итак, оценка 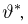
Пример:
Выборка 
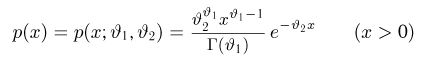
с двумя неизвестными параметрами 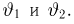
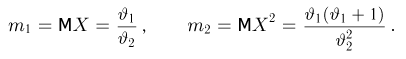
Отсюда для определения оценок 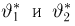
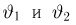
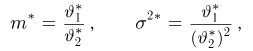
решение которой имеет вид
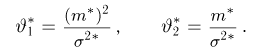
Вообще говоря, в методе моментов не обязательно использовать первые k моментов. Более того, можно рассматривать моменты не обязательно целого порядка. Иногда для использования в методе моментов привлекают более или менее произвольные функции 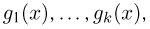
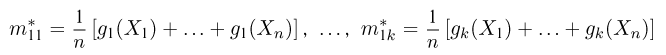
функций 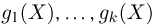
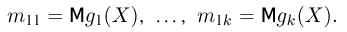
Пример:
Пусть выборка 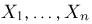
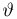
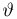
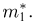
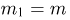
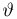
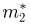
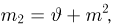
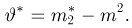
Следует отметить, что оценки, полученные методом моментов, обычно имеют эффективность существенно меньше единицы и даже являются смещенными. Иногда из-за своей простоты они используются в качестве начального приближения для нахождения более эффективных оценок.
Метод максимального правдоподобия
Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок. Пусть по-прежнему выборка 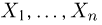
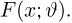
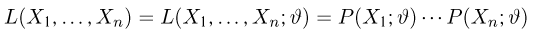
в дискретном случае и
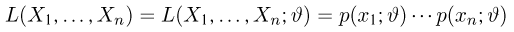
в непрерывном называется функцией правдоподобия. Отметим,что в функции правдоподобия 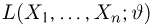

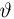

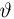
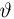
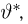
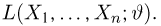
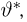
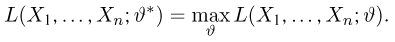
При практической реализации метода максимального правдоподобия удобно пользоваться не самой функцией правдоподобия, а ее логарифмом.
Уравнением правдоподобия называется уравнение
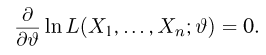
Если функция правдоподобия дифференцируема по 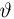
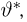
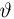
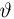
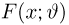
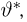
Пример:
Найдем оценку неизвестной вероятности успеха 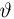
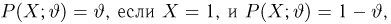
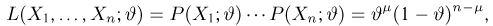
где 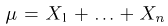
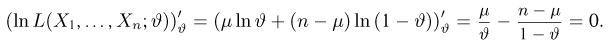
Решая это уравнение, имеем
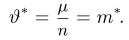
Поскольку
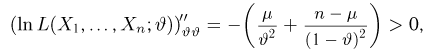
то 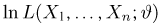
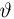
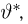
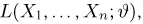
Оказывается, имеется тесная связь между эффективными оценками и оценками, полученными методом максимального правдоподобия. А именно, справедлива следующая теорема.
Теорема:
Совпадение эффективной оценки с оценкой максимального правдоподобия. Если (естественно, при условиях регулярности теоремы 1) существует эффективная оценка 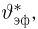
Доказательство теоремы 6 представляет собой дальнейшее уточнение доказательства теоремы 1. Действительно, как следует из замечания 1 к теореме 1, из существования эффективной оценки 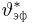
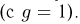
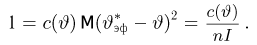
Поэтому из условия строгой положительности информации I вытекает строгая положительность 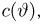
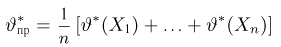
уравнения правдоподобия
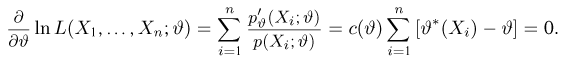
Это решение совпадает с эффективной оценкой 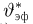
В общем случае оценка максимального правдоподобия может быть не только неэффективной, но и смещенной. Тем не менее она обладает свойством асимптотической эффективности в следующем смысле.
Теорема:
Асимптотическая эффективность оценки максимального правдоподобия. При некоторых условиях на семейство 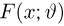
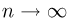
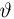
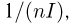
Доказательство:
Сначала сформулируем условия теоремы (см. [9]), которые, как мы увидим далее, гарантируют возможность дифференцируемости под знаком интеграла и разложения 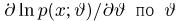
а) для (почти) всех х существуют производные
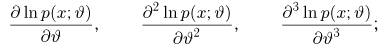
б) при всех 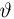
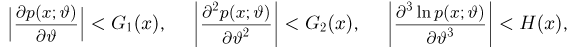
где функции 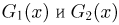
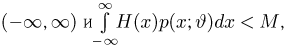
в) информация I конечна и положительна для всех
Обозначим через 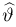
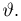
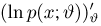
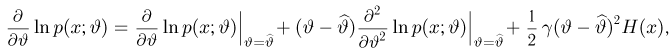
причем 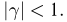
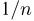
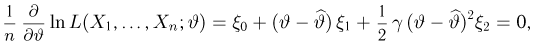
где случайные величины 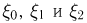
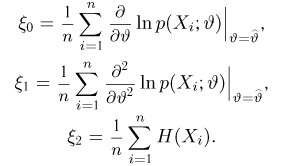
Рассмотрим поведение 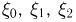
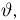
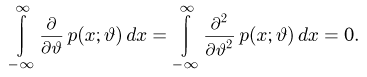
Поэтому
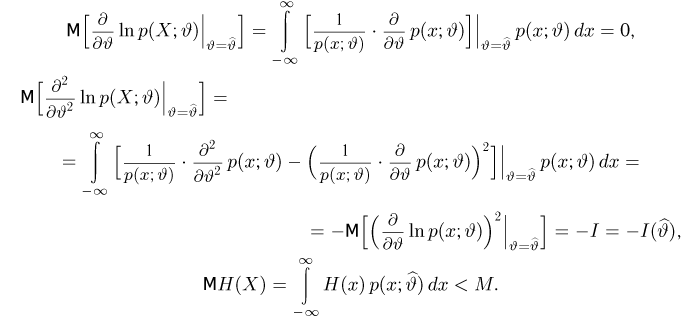
Вернемся к уравнению (14) и воспользуемся сначала тем фактом, что при 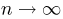
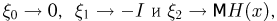
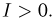
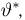
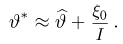
Величина 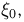
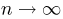
Поэтому оценка 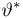
Замечание:
Доказанная теорема гарантирует, что среди всех решений уравнения правдоподобия существует по крайней мере одно 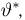
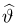
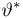
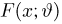
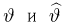
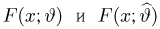
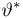
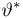
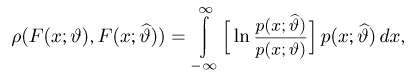
поскольку в силу закона больших чисел именно к расстоянию Кульбака-Лейблера при 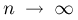
здесь 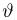
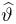
В случае, когда семейство 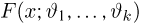
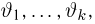
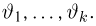
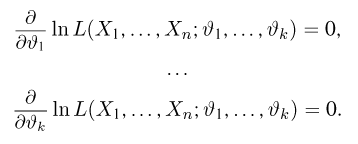
Пример:
Выборка 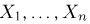
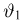
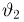
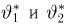
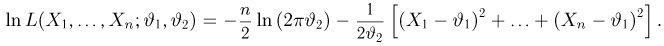
Система уравнений правдоподобия имеет вид
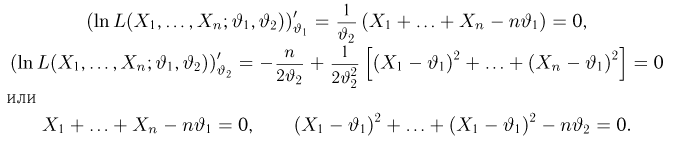
Таким образом,
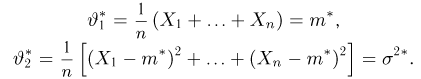
Читателю предлагается самостоятельно показать, что 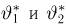
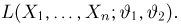
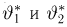
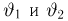
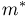
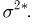
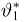
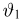
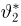
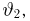
Оказывается, однако, что если мы в качестве оценки параметра 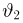
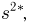
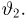
Метод минимального расстояния
Суть этого метода заключается в следующем. Предположим, что любым двум функциям распределения 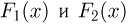
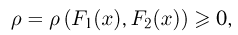
называемое расстоянием, причем 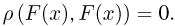
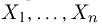
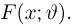
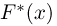
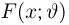
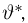
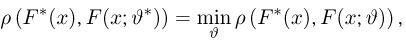
т. е. такое значение 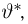
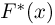
Приведем примеры некоторых наиболее часто встречающихся в математической статистике расстояний.
Равномерное расстояние (расстояние Колмогорова) определяется формулой
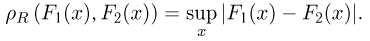
Расстояние 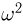
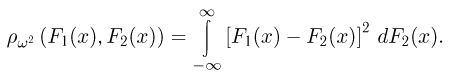
Расстояние 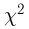
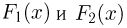
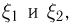
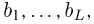
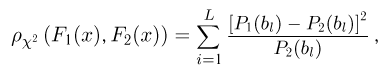
где вероятности 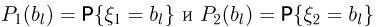
Использование приведенных выше расстояний для получения оценок весьма сложно в вычислительном плане, и поэтому они употребляются крайне редко. Здесь мы упомянули об этих расстояниях только потому, что применение оценок, полученных с их помощью, позволяет упростить вычисление уровней значимости критериев при проверке сложных непараметрических статистических гипотез, поскольку такие оценки естественным образом связаны с соответствующими критериями (см. параграф 5 гл. 3).
Метод номограмм
Еще одним методом, позволяющим, пользуясь только номограммами (специальным образом разлинованными листами бумаги, которые в математической статистике носят название вероятностной бумаги), весьма просто и быстро оценить неизвестные параметры, является метод номограмм. Его сущность состоит в следующем. Пусть мы имеем выборку 
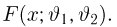
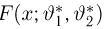
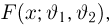
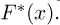
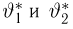
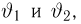
Казалось бы, мы пришли к не менее сложной задаче: найти «чрезвычайно простой» способ приближения эмпирической функции распределения функцией распределения из семейства 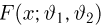
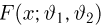
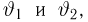
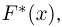
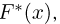
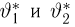
Практическая реализация метода номограмм происходит следующим образом. Сначала выборку 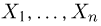
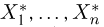
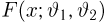
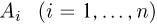
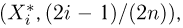
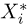
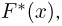
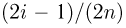
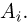
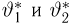
Пример 26. Предполагая в примере 1 из гл. 1, что проекция вектора скорости молекул водорода распределена по нормальному закону, оценим с помощью метода номограмм неизвестное математическое ожидание 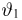
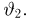
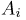
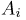
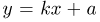
Оценка 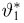
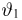
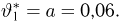
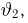
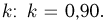
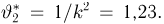
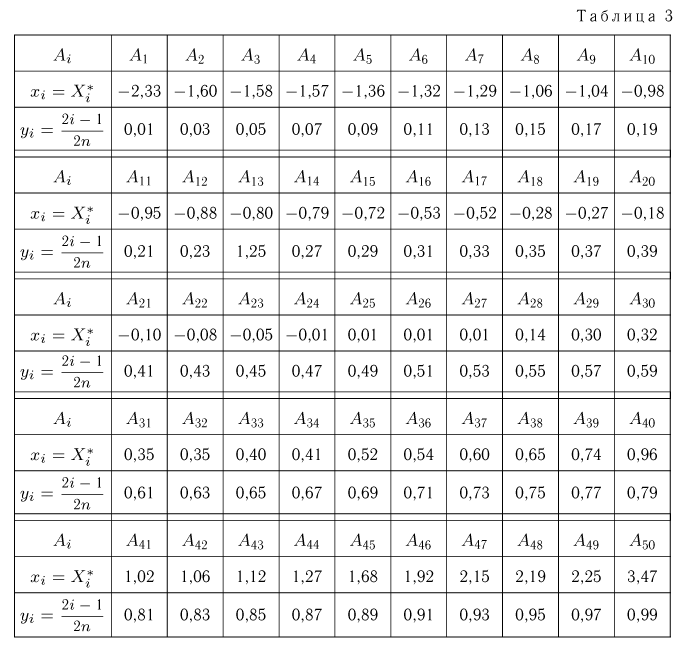
правдоподобия (см. пример 18, а также пример 8 из гл. 1): 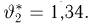
Следует отметить, что с помощью метода номограмм можно судить также о правильности выбора семейства 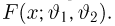
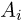
Доверительные интервалы
Полученные в предыдущих параграфах оценки неизвестных параметров естественно называть точечными, поскольку они оценивают неизвестный параметр одним числом или точкой. Однако, как мы знаем, точечная оценка не совпадает с оцениваемым параметром и более разумно было бы указывать те допустимые границы, в которых может находиться неизвестный параметр 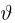
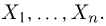

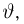
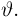
Доверительной вероятностью назовем такую вероятность 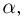
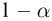
Задавшись доверительной вероятностью 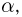

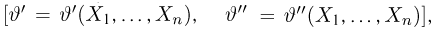
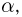
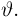
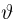
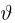
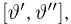
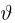

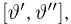
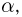
Доверительные интервалы определим, следуя Ю. Нейману, опираясь на точечные оценки. По заданной оценке 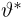
Итак, пусть у нас имеется выборка 
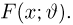
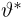
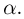
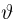
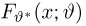
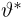
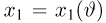
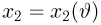
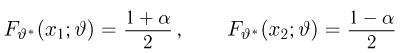
(напомним, что 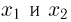
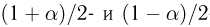
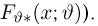
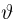
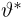
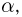
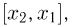
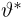
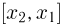
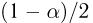
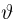
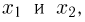
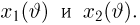
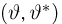
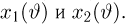

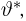
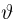
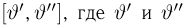

Именно интервал 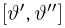
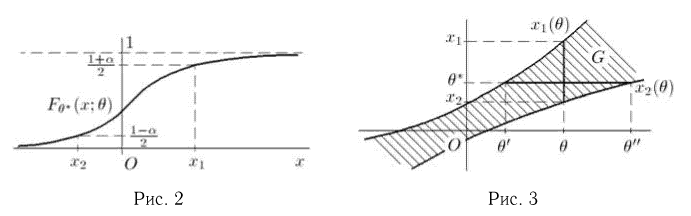
Пример 27. Построим симметричный доверительный интервал доверительной вероятности а для неизвестной вероятности успеха 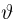
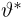
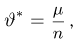
где 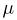
При малом объеме выборки п процедура построения доверительных интервалов трудоемка, поскольку она практически сводится к перебору значений неизвестного параметра. Поэтому существуют специальные таблицы (см. [1], табл. 5.2), которые по наблюденным значениям числа успехов 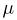

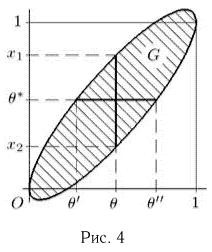
При больших объемах выборки п пользуются тем фактом, что в силу интегральной теоремы Муавра-Лапласа оценка 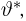
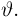
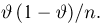
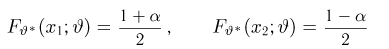
связаны с 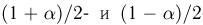
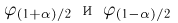
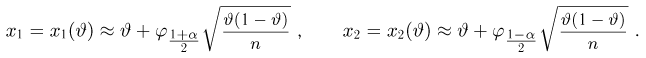
Учитывая, что 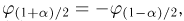
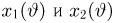
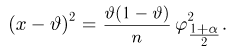
Последнее уравнение, как нетрудно видеть, представляет собой уравнение эллипса (рис. 4) (физически непонятный выход эллипса за полосу 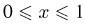
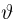
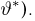
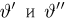
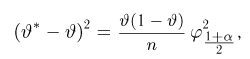
откуда окончательно получаем
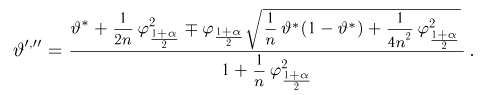
Пример:
Построим симметричный доверительный интервал доверительной вероятности а для неизвестного среднего 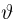
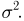
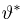
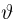
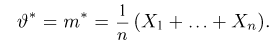
Оценка 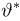
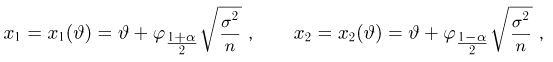
т.е. 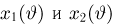
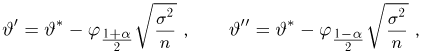
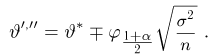
Пример:
Как и в предыдущем примере, предположим, что выборка 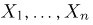
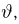
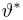
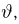
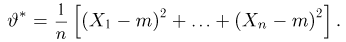
Тогда случайная величина 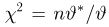
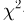
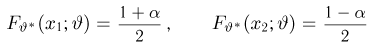
определяются формулами
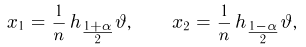
где 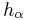
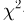
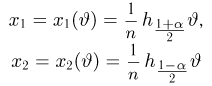
представляют собой уравнения двух лучей, исходящих из начала координат (рис.6), и, значит, границы симметричного доверительного интервала доверительной вероятности а для неизвестной дисперсии 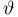
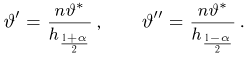
Пример:
Рассмотрим, наконец, случай, когда в выборке из нормальной генеральной совокупности неизвестны оба параметра: среднее 
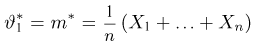
и выборочной дисперсией
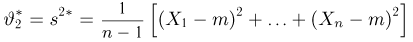
(см. пример 25).
Построение доверительного интервала 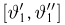
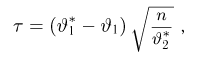
которая, как говорилось в параграфе 4 гл. 1, имеет t-распределение с п — 1 степенями свободы. Обозначим через 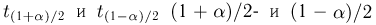
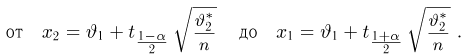
Продолжая рассуждения, как и в случае известной дисперсии, и учитывая равенство 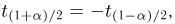
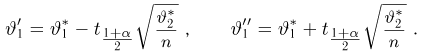
Доверительный интервал 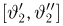
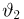
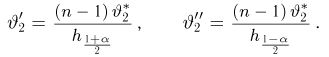
При этом нужно учитывать, что квантили 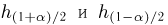
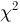
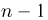
В заключение отметим, что в современной математической статистике доверительные интервалы строят так же, основываясь на критериях значимости.
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Генеральная совокупность
Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.
Как решить задачу с помощью пропорции
Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.
Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.
Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.
В результате имеем следующее решение:
Для подобных задач решение можно записывать с помощью пропорции.
Пропорция по определению есть равенство двух отношений. К примеру, равенство является пропорцией. Эту пропорцию можно прочесть следующим образом:
a так относится к b, как c относится d
Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.
Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:
Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:
Теперь соединим полученные отношения знаком равенства:
Мы получили пропорцию. Её можно прочесть следующим образом:
Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам.
То есть по 1600 рублей каждому. Если выполнить деление в обеих частях равенства , то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.
Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?
В таком случае пропорция приняла бы вид
. То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:
Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам
Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:
Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x. Вычислив обе части равенства, получим 32000 = x или x = 32000. Иными словами, мы найдём значение неизвестной величины, которое искали.
Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как и
. Воспользовавшись основным свойством пропорции, можно найти значение x
Задача 2. Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?
Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:
100 : 2 = 50 км на каждый час движения
300 км : 50 = 6 часов
Либо можно составить пропорцию «сто километров так относятся к двум часам, как триста километров к неизвестному числу часов»:
Отношение одноименных величин
Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.
Так, в пропорции можно поменять местами крайние члены. Тогда получится пропорция
.
Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.
Перевернем пропорцию . Тогда получим пропорцию
. Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы
Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.
Условие задачи запишем следующим образом:
Составим таблицу на основе этого условия:
Составим пропорцию, используя данные таблицы:
Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:
Изначально, мы имели дело с пропорцией , которая составлена из отношений величин разной природы. В числителях отношений располагались суммы денег, а в знаменателях количество студентов:
Поменяв местами крайние члены, мы получили пропорцию . Эта пропорция составлена из отношений величин одной природы. В первом отношении содержатся количества студентов, а во втором — суммы денег:
Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин. Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.
Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.
Пример 2. В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?
Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:
Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез
Соединим эти отношения знаком равенства, получим следующую пропорцию:
«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»
Используя основное свойство пропорции, находим значение x
Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:
Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:
Значит в саду посадили 120 сосен.
Пример 3. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?
Можно разделить 34,2 на 225 и полученный результат выразить в процентах:
Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:
Либо составить пропорцию в которой отношения составлены из одноименных величин:
Задачи на прямую пропорциональность
Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.
Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?
Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.
Покажем, что расстояние увеличилось в два раза:
Аналогично покажем, что время увеличилось во столько же раз
Соединим эти отношения знаком равенства, получим пропорцию:
«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»
Если выполнить деление в обеих частях равенства , то обнаружим что расстояние и время были увеличены в одинаковое число раз.
2 = 2
Задача 2. За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?
Решение
Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.
В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:
Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы
Соединим эти отношения знаком равенства, получим пропорцию .
Воспользуемся основным свойством пропорции и найдем x
Значит за 9 ч можно смолоть 81 т пшеничной муки.
Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.
Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 т. Тогда отношение нового значения времени работы мельницы к старому значению равно отношению нового значения массы перемолотой муки к старому значению
Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:
3 = 3
Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:
Применительно к нашей задаче значения переменных
будут следующими:
Где впоследствии стало равно 81.
Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.
Решение
Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.
Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.
Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.
Запишем отношение, показывающее во сколько раз увеличилось количество коров:
Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:
Соединим эти отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.
Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений и
, затем вычислим значение x
Определим сколько силоса и концентратов нужно заготовить для 18 коров:
Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.
Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на стакана вишни?
Решение
Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:
Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:
Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x
Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.
Определим количество стаканов сахара для 10 стаканов вишни и стакана вишни
Задачи на обратную пропорциональность
Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.
В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.
Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.
Допустим, что нужно покрасить забор, состоящий из 8 листов
Один маляр будет красить все 8 листов сам
Если маляров будет 2, то каждый покрасит по 4 листа.
Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.
Если маляров будет 4, то каждый покрасит по 2 листа
Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.
Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:
В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:
Соединим эти отношения знаком равенства, получим пропорцию
«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»
Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
Решение
Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.
Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих
Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)
Соединим полученные отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит 18 рабочих выполнят необходимую работу за 20 дней.
Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.
Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в раза). В результате количество дней, необходимых для выполнения работы, уменьшилось во столько же раз. Новыми значениями стали 18 рабочих и 20 дней. Тогда отношение нового количества рабочих к старому количеству
равно отношению старого количества дней к новому количеству
Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:
Применительно к нашей задаче значения переменных
будут следующими:
Где впоследствии стало равно 20.
Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
Решение
Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:
5 ч 10 мин = 300 мин + 10 мин = 310 мин
Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.
Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:
Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x, а в знаменателе старое время, равное трёхсот десяти минутам
Соединим полученные отношения знаком равенства, получим пропорцию . Отсюда найдём значение x
410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.
Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?
Решение
Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим
12 дней − 4 дня = 8 дней
На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x.
Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:
Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:
Соединим эти отношения знаком равенства, получим пропорцию . Отсюда можно вычислить значение x
Значит 5 рабочих прибыло дополнительно.
Масштаб
Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.
Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.
Уменьшим 800 000 см в сто тысяч раз:
800 000 см : 100 000 см = 8 см
8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.
Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:
8 : 800 000
Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.
В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.
Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000
Примеры:
1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.
К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.
Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000
8 см × 100 000 = 800 000 см
Получаем 800 000 см или 8 км, если перевести сантиметры в километры.
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.
Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.
Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:
Эту пропорцию можно прочитать так:
1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.
Из этой пропорции узнаём, что значение x равно 800000 см.
Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.
Решение
Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x
В 1 км содержится 100000 см. Тогда в 8 500 000 см будет
Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:
Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:
Отсюда x равен 8 500 000 см или 85 км.
Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000
Решение
Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.
А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте
7 400 000 : 2 000 000 = 3,7 см
Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.
Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:
Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:
Отсюда находим x равный 3,7 см
Задачи для самостоятельного решения
Задача 1. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Решение
Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.
Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.
Задача 2. На некотором участке железнодорожного пути старые рельсы длиной в 8 м заменили новыми длиной в 12 м. Сколько потребуется новых двенадцатиметровых рельсов, если сняли 360 старых рельсов?
Решение
Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.
Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью
Ответ: для замены старых рельсов потребуется 240 новых.
Задача 3. 60% учеников класса пошли в кино, а остальные 12 человек – на выставку. Сколько учащихся в классе?
Решение
Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников 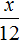
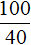
Ответ: в классе 30 учащихся.
Задача 4. Расстояние на карте между городами 18 см. Какое действительное расстояние между городами, если масштаб карты 1 : 500 000?
Решение
Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.
Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами
18 см × 500 000 = 9 000 000 см
Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет
Запишем решение с помощью пропорции:
Ответ: расстояние между городами 90 км.
Задача 5. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч
Решение
Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.
Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:
Запишем отношение, показывающее что время движения уменьшилось во столько же раз:
Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x
Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.
Задача 6. Перевыполнив план на 15%, завод выпустил за месяц 230 станков. Сколько станков должен был выпустить за месяц завод по плану?
Решение
Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков
А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана
Составим пропорцию из имеющихся отношений и найдём значение x
Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%
Ответ: по плану завод должен был выпустить 200 станков.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

План урока:
Понятие уравнения
Что такое корень уравнения?
Решение уравнений с одной переменной
Линейное уравнение с одной переменной
Примеры задач
Понятие уравнения
Уравнение являются одним из основных понятий алгебры и всей математики. Сам термин «алгебра» возник от названия книги «Китаб аль-джебрваль-мукабала», написанной великим ученым аль-Хорезми в 830 году, в которой он рассматривал способы решения уравнений.
Уравнение – это разновидность равенства. При этом в нем должна находиться хотя бы одна переменная, но их количество может быть любым. Дадим определение понятия уравнения:
В качестве примера уравнений можно привести следующие равенства:
- x=5;
- a+b+c=9;
- dg+98=(j+f)·k;
- L²+V²= 25²;
- 5z+3z=100.
Во всех приведенных примерах вместо переменной можно подставлять действительные числа, однако в старших классах мы познакомимся и с более сложными уравнениями, где в качестве переменных величин выступают такие математические объекты, как функции и вектора.
Уравнения – это не просто абстрактные математические конструкции. Часто они появляются при описании окружающего мира на формальном языке математики. Пусть доходы семьи за месяц обозначаются буквой Д, а расходы – Р. Разница в доходах и расходах семьи идет на сбережения (С). Формально такую ситуацию можно описать уравнением:
Д – Р=С.
Что такое корень уравнения?
Как и в любое буквенное выражение, в уравнение можно подставлять различные значения переменных. В зависимости от них оно будет превращаться либо в верное равенство, либо в неверное. Подставим r=6 в уравнение
(r+2)·r=48
и получим запись
(6+2)·6=48.
Очевидно, что это равенство верное. Но если подставить значение r=1, то получится ошибочное равенство
(1+2)·1=48.
Число 6 будет называться корнем уравнения (r+2)·r=48, а число 1 им не является.
Дадим строгое определение понятию корня уравнения:
Слово набор используется для того, чтобы охватить определением уравнения с несколькими переменными. Так, переменных две, то следует указывать пару чисел, которые могут обернуть выражение в равенство. Так, для уравнения
M+W=10;
корнем является набор M=4; W=6. Однако по отдельности ни число 6, ни число 4 не является корнем уравнения.
Именно поиск корней уравнения и является целью при его решении:
Встает вопрос – а сколько корней может быть у уравнения? Их число может быть абсолютно разным. Возможно записать уравнение, имеющее любое наперед заданное количество корней. Покажем, как это сделать. Уравнение
y–1=0
имеет ровно один корень, равный единице. Теперь умножим его левую часть на выражение (y–2):
(y–2)·(y–1)=0.
Произведение нескольких чисел может равняться нулю только тогда, когда хотя бы одно из них равняется нулю. Поэтому корнями данного уравнения будут числа 1 и 2. Чтобы построить уравнение с 3 корнями, допишем слева ещё одно выражение в скобках:
(y–3)·(y–2)·(y–1)=0.
Теперь имеем три корня: 1, 2 и 3. Добавляя слева подобные выражения, можно получить уравнение с любым количеством корней. Например, ровно 7 корней будет иметь уравнение
(y–7)·(y–6)·(y–5)·(y–4)·(y–3)·(y–2)·(y–1)=0.
Есть ещё два особых случая. Первый из них – это уравнения с бесконечным количеством корней. Примером подобного равенства является z=z.Очевидно, что при любом значении z оно будет верным, поэтому у него бесчисленное множество корней.
Второй особый случай – это уравнения, вообще не имеющие ни единого корня.Доказать их существование можно, просто приведя пример:
y²= –5.
Действительно, если мы возведем в квадрат любое действительное число, мы получим неотрицательное число, поэтому приведенное уравнение не имеет решения.
Однако в данном случае стоит отметить, что количество корней может зависеть от того, какие числа допускается подставлять в записанное выражение. Дело в том, что математики в XVI веке придумали новое понятие – «мнимые числа». Их особенность заключается в том, что при умножении на себя они дают отрицательное число!Например, число «мнимая единица», которая обозначается символом i, при возведении в квадрат дает –1:
i² = –1.
Мнимые числа были специально введены в алгебру для того, чтобы из отрицательных чисел можно было извлекать квадратный корень. Однако со временем область их применения в математике сильно расширилась. Более того, мнимые числа даже используются на практике. Оказалось, что с их помощью удобно описывать процессы в электрических цепях и квантовые явления. Более подробно мнимые числа будут изучены в старших классах и институте. Пока же мы будем учитывать только действительные корни уравнений.
Иногда уравнение записывается так, что в него нельзя подставлять некоторые числа. Часто это связано с недопустимостью деления на ноль. Так, в уравнение
(9-d)/(p-5)=9dx
нельзя подставлять значение p=5. В таком случая говорят, что число 5 не входит в область определения уравнения.
Решение уравнений с одной переменной
Рассмотрим простейшее уравнение вида
z=b,
где z– это переменная, а b – произвольное действительное число. Приведем примеры простейших уравнений:
- e=7;
- L=9;
- f= –10,68;
- y=0.
Очевидно, что единственным корнем уравнения z=b является число b.
Для решения всех остальных уравнений их постепенно упрощают, сводя к одному или нескольким простейшим. Для этого из исходного уравнения с помощью некоторого набора правил получают эквивалентное, или равносильное, уравнение.
Например, уравнения 2y+5=15 и 4z=20 равносильны друг другу, так как имеют единственный корень, равный 5.Убедиться в этом можно подстановкой:
2·5+5 = 15;
4·5 = 20.
Какими же способами можно получить из одного уравнение другое, равносильное ему? Во-первых, и в левой, и в правой части можно делать стандартные алгебраические процедуры:
- складывать подобные слагаемые;
- раскрывать скобки;
- выносить общий множитель за скобки.
Например, запись 5d+4d=5z+5k будет эквивалента равенству 9d=5(z+k). Здесь в левой части сложили подобные слагаемые, а в правой вынесли множитель 5 за скобки:
5d+4d = 5z+5k
9d = 5z+5k
9d = 5(z+k).
Во-вторых, к левой и правой части можно добавлять любое одинаковое выражение. Равносильными будут уравнения y+9=10 и y+10=11, так как обе части были увеличены ровно на единицу:
y+9 = 10
y+9+1 = 10+1
y+10 = 11.
Но добавлять можно и выражения, содержащие переменные, поэтому эквивалентны друг другу будут уравнения r+6=8 и r+6+r²=8+r².
Однако здесь можно совершить логическую ошибку, если забыть про области определения уравнений. Приведем пример. Уравнение
N+7=9
имеет единственный корень, равный 2:
2+7 = 9
Теперь добавим к его частям выражение 1/(N-2):
N+7+1/(N–2)=9+1/(N–2).
Подумайте, сколько решений имеет получившееся уравнение? Оказывается, ни одного! При подстановке N=2 получаем деление на ноль, а потому число 2 теперь не может являться корнем уравнения:
N+7+1/(N–2) = 9+1/(N–2);
2+7+1/(2–2) = 9+1/(2–2) (подставили N = 2);
9+1/0 = 9+1/0 (получили деление на ноль).
Но если бы мы добавили к обеим частям дробь 1/(N-3), то получили бы равносильное уравнение:
N+7+1/(N–3) = 9+1/(N–3);
2+7+1/(3–2) = 9+1/(3–2) (подставили N = 3);
9+1/1 = 9 + 1/1;
9+1 = 9+1;
10 = 10.
Добавлять можно не только положительные, но и отрицательные числа. В таком случае мы вычитаем из частей уравнения одинаковое выражение. Из уравнения h+10=20 вычтем число 4 и получим h+6=16:
h+10 = 20;
h+10 – 4= 20 – 4;
h+6 = 16.
На этом свойстве уравнений построен специальный прием, который называют переносом слагаемого из одной части в другую. Пусть дано уравнение L+2=5. Вычитая из обеих частей число 2, получаем запись L= 5–2:
L+2 = 5;
L+2–2 = 5–2;
L = 5–2.
Мы перенесли двойку из левой части в правую, при этом она поменяла знак с плюса на минус. Подобным образом можно перенести любое слагаемое.
Покажем перенос слагаемых на нескольких примерах:
3d²+7 = 2d²+10;
3d² = 2d²+10–7(перенесли 7 вправо);
3d² –2d² = 10–7(перенесли 2d² влево);
d² = 3 (сложили подобные слагаемые).
Ещё один пример:
4F–9+2G = 5+2G–2F;
4F–9+2G+2F = 5+2G (перенесли влево слагаемое –2F);
4F+2F = 5+2G+9–2G (перенесли вправо –9 и 2G);
2F = 14 (сложили подобные слагаемые).
В-третьих, обе части уравнения можно умножить или поделить на одинаковое число или выражение. Так, эквивалентны равенства 3p=7 и 6p=14:
3p = 7;
2·3p = 2·7;
6p = 14.
Но здесь стоит соблюдать осторожность и учитывать области определения уравнений. Приведем пример ошибки. Уравнение
x/(x+2)+2/(x+2)=0
умножим на (х+2). В результате получим:
x/(x+2)+2/(x+2) = 0;
(x/(x+2)+2/(x+2))·(х+2) = 0·(x+2);
(х+2)·x/(x+2)+ (х+2)· 2/(x+2) = 0·(x+2);
х+2=0
и корень, равный (–2). Однако если подставить его в исходное уравнение, то получим выражение, не имеющее смысла из-за деления на ноль:
x/(x+2)+2/(x+2) = 0;
–2/(–2+2)+2/(–2+2) = 0; (подставили x = –2)
-2/0+2/0 = 0.
Этих методов достаточно для решения простых уравнений. Существуют и иные способы их преобразования (логарифмирование, возведение в степень и т.п.), которые будут рассмотрены в старших классах.
С помощью эквивалентных преобразований можно решить самые сложные задачи, постепенно упрощая выражение. Пусть есть уравнение
(2x+1)(3x–2)–6x(x+4)= 67–2x.
Решим его. Попробуем сначала раскрыть скобки в левой части:
(6x²–4x+3 –2) – (6x²+24x) = 67–2х
6x²–4x+3x–2–6x²–24x = 67–2х.
Далее перенесем слагаемое (-2x) в левую часть, а (-2) в правую. В результате в одной части у нас будут только слагаемые с переменной, а в другой – числа:
6x²–4x+3x–6x²–24x–67+2x=67+2.
Приведем подобные слагаемые. 6x² и –6x² сократятся:
–23x=69.
Теперь поделим обе части на –23:
x = –3
Получили простейшее уравнение, единственный корень которого равен -3. Так как каждое наше преобразование было равносильным, то и исходное уравнение имеет единственный корень –3. Подставив его туда, можно проверить себя:
(2x+1)·(3x–2)–6x·(x+4) = 67–2x;
(2·(–3)+1)·(3·(–3)–2)–6·(–3)·(–3+4) = 67–2·(–3) (подставили х = –3);
(–6+1)·(–9–2)–(–18)·1 = 67–(–6);
(–5)·(–11)+18 = 67+6;
55+18=73;
73 = 73.
Линейное уравнение с одной переменной
Существует много разновидностей уравнений: квадратные, кубические, логарифмические, тригонометрические и т.п. Наиболее простыми являются линейные уравнения.
Примеры линейных уравнений:
- 2x=9;
- 5F=¼;
- 6d=-1,5;
- ¾L=0,96.
Возможны 3 случая:
- a=0 и b=0;
- a=0, но b≠0;
- a≠0.
В первом случае имеем уравнение 0·x=0. При любом значении переменной мы будем получать верное равенство 0=0, поэтому уравнение будет иметь бесконечное множество корней.
Во втором случае имеем уравнение 0·x=b. Левая часть при любом значении x будет равняться нулю, а правая нет, поэтому уравнение не будет иметь ни одного решения.
В третьем случае обе части уравнения поделим на a. Тогда получим равносильное равенство x=b/a. Получаем ровно один корень.
Примеры задач
Уравнения активно используются для решения разнообразных задач. При этом используется следующий алгоритм:
- неизвестная величина в задаче обозначается буквой, то есть принимается за переменную величину;
- на основании условий задачи записывается уравнение;
- решая его, находят значение неизвестной величины.
Рассмотрим несколько примеров.
№1. Фирме принадлежит два офиса. Их общая площадь составляет 508 м². Известно, что одно из помещений занимает площадь в три раза больше, чем второе. Какова площадь каждого здания?
Обозначим как x площадь меньшего офиса. Тогда второе помещение занимает площадь 3x. Их сумма равна 508 м². Это условие можно представить следующим уравнением:
x+3x=508.
Найдем корень уравнения:
x+3x=508;
4x=508;
x=508/4;
x=127.
Получаем, что площадь меньшего офиса составляет 127 м². Тогда второе помещение занимает 3·127=381 м². Результат можно проверить: 127+381=508. Оба условия задачи соблюдены.
Попробуем решить задачу, составив иное уравнение. Обозначим x площадь первого помещения, но площадь второго выразим как (508-x). Тогда уравнение и его выглядеть так:
3x = 508–x; (так как площадь двух помещений отличаются в три раза)
3x+x=508;
4x=508;
x=127.
Из приведенного примера ясно, что условия задачи можно использовать по-разному, а потому и исходные уравнения могут получаться различными. Однако на ответ задачи это не влияет. Более того, можно было принять за неизвестное площадь второго офиса, а не первого.
№ 2. У металлурга есть два слитка. В первом содержится 20% золота, а во втором – 60%. Масса первого самородка на 4 кг меньше, чем масса второго. Металлург сплавил их и получил новый слиток, в котором содержалось 45% золота. Сколько весил каждый из слитков до их сплавления?
Примем за x кг массу первого самородка. Тогда второй должен весить (x+4) кг. Новый слиток весит столько же, сколько первый и второй самородки вместе взятые: x+(x+4).
Теперь оценим массу золота в каждом слитке. В первом его содержится 0,2x (20% от x). Во втором самородке 0,6(x+4) драгоценного металла, а в новом слитке содержится 0,45(x+(x+4)) килограмм золота. Так как количество золота при переплавке не изменяется, то должно выполняться уравнение:
0,2х+0,6(х+4)=0,45(х+(х+4)).
Раскроем скобки:
0,1х+0,6х+2,4=0,45(х+х+4);
0,1х+0,4х+1,2=0,45х+0,45х+1,8.
Теперь перенесем все слагаемые с неизвестной величиной влево, а числа – вправо:
0,1x+0,4х–0,45х–0,45х=1,8–2,4.
Приведем подобные слагаемые:
–0,1х=–0,6.
Получили линейное уравнение, его корень равен
х=(–0,6)/(–0,1)=6.
Первый самородок весит 6 кг. Значит, второй слиток имеет массу 6+4=10 кг, а новый слиток, получившийся после сплавления первых двух, весит 16 кг.