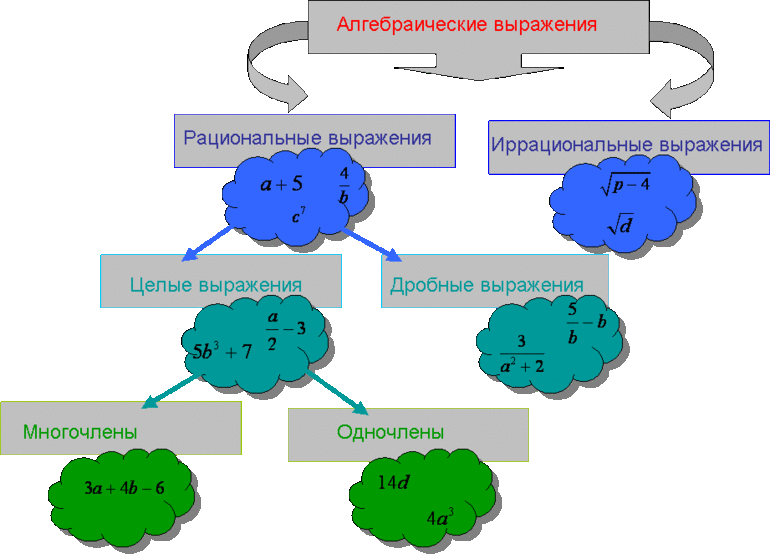
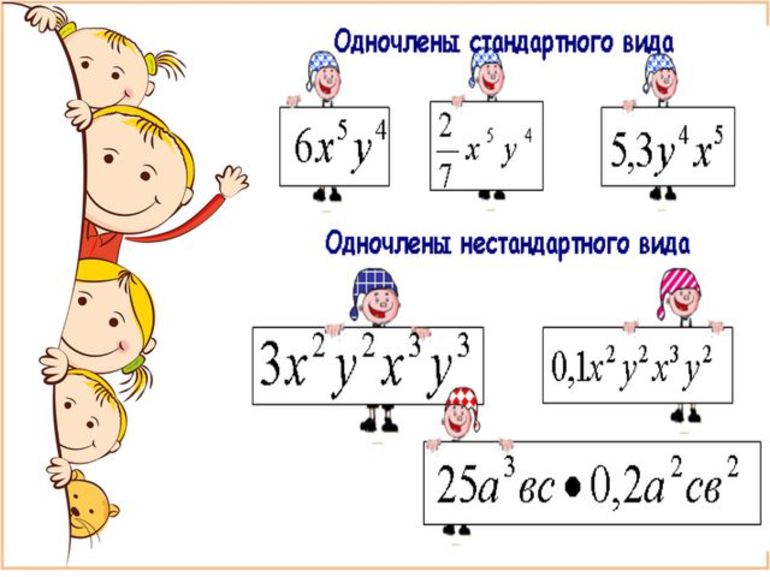
Произведение чисел, переменных и их степеней называется одночленом.
Уже знакомые нам одночлены:
Выражения
6⋅a⋅y
;
0,25×3
;
abbc
;
8,43
;
16c⋅−12d
;
38x2y
тоже являются одночленами.
При записи одночленов между числами и переменными знак умножения не ставится
Одночленом также считается:
– одна переменная, например, (x), т. к.
x=1⋅x
;
– число, например, (3), так как
3=3⋅x0
(одно число также является одночленом).
Некоторые одночлены можно упростить.
Упростим одночлен
6xy2⋅(−2)x3y
, используя свойство умножения степеней:
(=)
6⋅(−2)xx3y2y=−12x4y3
(числа перемножаются, а показатели у одинаковых букв складываются).
Стандартный вид одночлена
Если в одночлене первым записан числовой множитель, а произведение одинаковых степеней переменных записано в виде одной степени, то такой вид одночлена называют стандартным видом.
Запишем одночлен
10⋅12abbb
в стандартном виде:
10⋅12abbb=5⋅2⋅12ab3=5ab3
.
(Коэффициенты перемножаются между собой, переменные — между собой.)
Если одночлен записан в стандартном виде, то его числовой множитель, называется коэффициентом одночлена.
Одночлен
5ab3
имеет коэффициент (5), одночлен
−12x4y3
имеет коэффициент (-12).
Коэффициенты (1) и (-1) обычно не записываются.
Степенью одночлена называется сумма показателей степеней всех переменных.
Чтобы определить степень одночлена, нужно сложить показатели степеней всех переменных (букв).
−12x4y3
является одночленом седьмой степени ((4 + 3 = 7));
(6a) — одночлен первой степени (переменная (a) в первой степени);
(7) — одночлен нулевой степени.
|
Одночлен |
Стандартный вид |
Коэффициент |
Степень |
|
2a2x |
2a2x1 |
(2) |
(2+1=3) |
|
−3ab⋅a2b |
−3a3b2 |
(-3) |
(3+2=5) |
|
ab⋅(−1) |
−a1b1 |
(-1) |
(1+1=2) |
|
(x) |
1×1 |
(1) |
(1) |
|
(2) |
(2) |
(2) |
(0) |
Подобные одночлены
Одночлены, у которых произведения переменных равны, хотя их порядок может отличаться, называются подобными одночленами.
Подобными одночленами являются:
(6xy) и (xy);
(5) и (-3);
Подобными одночленами не являются
x2y
и
xy2
.
Если у подобных одночленов равные коэффициенты, они называются равными (одинаковыми) одночленами.
В этом можно убедиться, записав одночлены в стандартном виде.
Из пяти одночленов
8xy3;xy3;8y3x;2⋅4xyyy;8x3y
равными являются только три
8xy3;8y3x;2⋅4xyyy
.
В этом можно убедиться, если записать все одночлены в стандартном виде и расположить переменные в одинаковом порядке:
.
Если у подобных одночленов коэффициенты являются противоположными числами, одночлены называются противоположными.
Противоположными являются одночлены:
(3ac) и (-3ac);
(9ba) и (-9ba).
Важность понятия
Пик развития математики пришёлся на XVI век, когда учёные разных стран начали обобщать известные сведения и формулировать различные теоремы и доказательства. Но перед этим появились такие понятия, как одночлен и многочлен. Запись уравнения или любой другой формулы, в которой не использовалось сложение или вычитание, получило название одночлен. А суммирование нескольких таких выражений или их разность назвали многочленом.
Карл Фридрих Гаусс, считающийся королём математиков, утверждал, что коэффициенты многочлена могут быть не только вещественными, но и комплексными. Свои доказательства этому он привёл в основной теореме алгебры. Из-за этого роль неизвестных в выражениях начала меняться. Буквенные обозначения стали не только символами, подменяющими числовые значения, но и начали заменять функции.
Таким образом, было принято, что любое математическое выражение состоит из совокупности одночленов. Ими могут быть:
- единственные числа;
- буквы;
- буквенно-числовые произведения.
Изучение уравнений и равенств, состоящих из нескольких одночленов, стало главным объектом в развитии классической алгебры. С их преобразованием связаны такие разделы, как теория групп, анализ функций, изучение комплексных чисел, алгебраическая геометрия.
Над одночленами можно выполнять различные действия. Их можно возводить в корень с разным основанием, перемножать или делить между собой, возводить в степень. Это позволяет выполнять упрощения и приведения выражений к стандартной форме, что впоследствии облегчает вычисление многочленов.
Впервые с понятием «одночлен» знакомят учеников в среднеобразовательной школе в седьмом классе на уроке алгебры. Изучение видов одночленов и правил действий над ними является стартовой площадкой для понимания сущности многочлена, то есть фактически основ алгебры.
С помощью одночлена можно описать простые события, при которых происходит умножение. Это могут быть как количественно известные параметры, так и переменные или неизвестные. Для того чтобы понять важность введения в математике термина «одночлен», лучше всего провести аналогию с фруктами. Яблоко и груши — это отдельный вид деревьев, но их всех объединяет одинаковое свойство, поэтому их называют «фруктами». Так и с формулами: они хотя и разные, но обладают общими свойствами. Поэтому и придумали название — одночлен.
Общие сведения
Алгебраическое выражение, в состав которого входит переменная и постоянная часть, объединённая произведением, принято называть одночленом. Фактически эта запись представляет умножение чисел и степеней неизвестных с натуральным показателем. Каждое неопределённое или известное число занимает одну позицию. Количество таких позиций неограниченно.
Если перед буквенным значением стоит цифра, то её называют коэффициентом одночлена. Он может быть как положительным, так и отрицательным. Когда коэффициент не указан, в зависимости от знака он принимается равным единице или минус единице. При этом понятие коэффициент зачастую применительно и к числу. Например, считают, что у числа девять он равен девяти.
Наиболее типичные записи рассматриваемого вида выражений имеют следующий вид:
- 23 — это обыкновенный одночлен, в составе которого нет переменных;
- 12 * f — выражение, состоящее из буквенного и цифрового числа;
- -5 * d2 — запись, содержащая степень;
- 12 * 3 5/6 * x2 * y4 — пример сложного порядка;
- x * y — формула, в которой все коэффициенты равны единице.
Это всё стандартные виды одночлена, то есть выражения записаны в таком состоянии, что их упростить уже невозможно. Например, формула a3 * 1*3 * b * 3 * а * b3 хоть и является одночленом, но не считается записью стандартного вида. Всё дело в том, что её можно упростить. Кроме этого, её нужно переписать таким образом, чтобы числовой множитель стоял на первом месте, затем неизвестные и основания со степенными показателями. После преобразования получится выражение: 9 * a4 * b4. Этот вид записи уже является стандартным. В нём одночленами считаются числа, переменные и степени.
В алгебре часто используется понятие «степень одночлена». Под ним понимают сумму показателей переменных значений, входящих в состав выражения. Примечательно что нуль, входящий в состав одночлена, степени не имеет, при этом если степень не указана, то она принимается нулевой. Когда выражения похожи друг на друга, они считаются подробными. Например, 5 * d2* k10 и 1/8 * d2 * k10 — подобны.
Действия над выражениями
После умножения одночленов получается также одночлен, указываемый в стандартной записи. Для того чтобы выполнить операцию произведения, используют свойства умножения, а также правила действия со степенями. Умножить одно выражение на другое, значит, определить сумму слагаемых множителя, каждое из которых равно умножаемому.
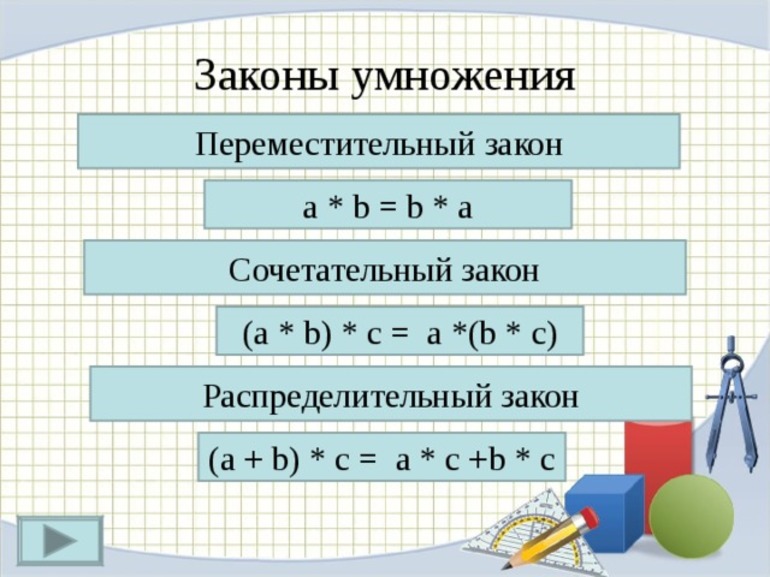
Существует три закона умножения:
- Сочетательный. Если нужно умножить два одночлена на третий, то можно сначала посчитать произведение первого на третий, а после результат умножить на второй член.
- Переместительный. От перестановки множителей итог не изменится.
- Распределительный. Для того чтобы умножить одночлен на сумму, нужно его отдельно перемножить с каждым суммирующимся членом, а после сложить результат. То есть одночлен превратится в многочлен. При этом этот закон справедлив и для разницы.
При умножении сложных выражений типовой операцией является упрощение записи. Но преобразовать возможно не все выражения. Например, пусть необходимо выполнить умножение одночленов: 2 * c * p3 * s5 (-7 * c3 * p2) = -14 * с2 * p5 * s5.
Деление происходит аналогичным образом. При этом действует правило, согласно которому частное одночленов можно упростить, но лишь в том случае, если делимое и делитель содержат одинаковые буквенные или числовые коэффициенты. В этом случае из показателя делителя отнимается значение степени делимого, коэффициент которого делят на количественный показатель делителя. Например, 12 * p3 * d4 * r6: 4 * p * d2 * r3 = 3 * p2 * d2 * r3.
Возведение в степень выполняют согласно правилам свойств степеней. Так как операция возведения это не что иное, как умножение члена самого на себя столько раз, сколько показывает число в показателе. Например, (3*с)3 = (3*с) * (3*с) *(3*с). Используя правило умножения, выражение можно представить как (3 * 3 * 3) * (с * с * с). Последнюю запись же можно упростить до вида: (3 * 3 * 3) * (с * с * с) = 33 * c3 = 9 * c * p3.
Таким образом, для того чтобы возвести выражение в степень, необходимо каждый множитель отдельно возвести в степень, а затем результаты перемножить. Это правило действует и для любых степеней, показатель которых натуральный. Закон применим и для дробного отношения, только после возведения числитель делят на знаменатель.
Принцип преобразования
Пусть имеется сложный одночлен, состоящий из ненулевых степеней, квадратов, дробных чисел и букв следующего вида: 5 * 7 * a * m * c7 * 3 *2/9 * 2 (1/7) * am * bn * c * x5 * 120. Тут следует обратить внимание, что дроби в выражении могут быть любого типа, кроме случая, когда в знаменателе будет стоять буква. Такая запись неудобна для восприятия и дальнейшего использования из-за хаотично расставленных подобных членов. Поэтому нужно преобразовать её к стандартному виду.
В основе способа упрощения одночлена лежат следующие принципы:
- Если в записи встречается число, то оно обязательно пишется впереди и должно быть единственным в выражении.
- Каждая буква, встречающаяся в формуле, должна повторяться только один раз, записанная в своей степени.
- Буквы в одночлене записывают в алфавитном порядке.
При этом математиками было решено не писать знак умножения между числовым и буквенным множителем, а также между буквенными множителями, перемножающимися между собой.
Решения одночленов
Примеры для самостоятельной работы по преобразованию многочленов помогут понять, как правильно выполняются простые арифметические действия, что важно для решения последующих задач, связанных с многочленами.
Можно выделить следующие виды типовых заданий:
- Пусть дан многочлен: 14 a7b13mt. Нужно определить степень одночлена, то есть сумму степеней входящих в выражение. Для рассматриваемого примера она будет равна: 7 + 13 + 1 + 6 = 20.
- Необходимо записать результат перемножения двух выражений: 12a7c5d * 3b9c6d7k. Решение задания будет следующим: 12a7c5d * 3b9c6d7k = 36a7b9c11d8k.
-
Нужно найти ответ, получающийся после деления 16 a7b5k14m на 8 a5bk3. Итак, при делении получится следующее: 16 a7b5k14m / 8 a5bk3 = 2a2b4k11m.
-
Сложение и вычитание одночленов допускается только в том случае, если буквенная часть у них одинаковая, включая степени. Например, 2 a7b5ck + 7a7b5ck = 9 a7b5ck или 9 p5 — 3p5 = 6p5. То есть действие выполняется только над коэффициентами.
-
Дан многочлен вида: 2a7b5kz3. Нужно возвести его в пятую степень. Согласно правилу, каждый член выражения возводится в степень отдельно. При этом следует помнить правило, что при возведении степени в степень показатели перемножаются. Ответ будет выглядеть следующим образом: (2a7b5kz3)5 = 32a35 b25k5z15.
При выполнении различных действий с одночленом нужно знать всего лишь несколько правил и быть предельно аккуратным при вычислении. Особенно это важно для длинных выражений, состоящих из различного вида членов.
Упрощение на онлайн-калькуляторе
Привести одночлены к удобному виду, значит, упростить их до стандартной записи. Однако зачастую приходится иметь дело с выражениями большого порядка. При этом они могут включать в себя одновременно различные арифметические операции. Выполнять тождественные преобразования самостоятельно бывает довольно трудно, причём возникает вероятность допущения ошибки.
Поэтому использовать специализированные сайты, которые умеют быстро и безошибочно упрощать одночлены любого вида, не зазорно. Порталы предлагают свои услуги бесплатно и для решения примеров не требуют даже регистрации. Что интересно, кроме быстрого расчёта, пользователь, зашедший на такой ресурс, сможет увидеть всю цепочку упрощения, а при желании на страницах онлайн-калькулятора ознакомиться с теорией и основными определениями.
Из всего множества сайтов можно выделить следующие три:
- Kontrolnaya-rabota. Сервис хоть и ориентирован на учащихся старших классов, но по своим возможностям довольно функционален. Так, с его помощью можно преобразовать даже комплексные выражения. Всё, что требуется от пользователя, это правильно ввести выражение и нажать кнопку «Упростить».
- Umath. Программа даёт возможность упростить любое алгебраическое выражение. На сайте можно найти всю необходимую теорию. Ограничений в размере формулы нет.
- Mathforyou. Используя этот онлайн-калькулятор, пользователь сможет выполнить различные действия над выражением, содержащим числовое и символьное обозначение. Для правильного вычисления нужно предварительно ознакомиться с правилами ввода математической формулы, указанными тут же на сайте.
Рекомендованные сайты имеют российский домен, а программы написаны русскими программистами. Поэтому проблем с пониманием, как пользоваться приложениями, возникнуть не должно. Интерфейс онлайн-калькуляторов не содержит нагромождения ненужной информации и интуитивно понятен. Ответ вычисляется буквально за несколько секунд, а используемые алгоритмы исключают возникновение ошибки.
Определение одночлена
Одночлен – это алгебраическое выражение, которое является произведением чисел, переменных и их степеней.
Одночленами также считают все числа, любые переменные и их степени.
Например:
Являются одночленами
Не являются одночленами
$ 5m^2 n $
$ left(frac{3}{4}right)^2 k $
$8^3$
$ -34m^7 pm^4 z$
abcde
$a^2 b+1$
$ 4(k+n)^2 $
$ 500-m^4+2m^2 $
$ 10p^2+k $
Стандартный вид одночлена – представление одночлена в виде произведения, в котором на первом месте стоит числовой множитель (коэффициент одночлена), а все остальные множители являются степенями различных переменных.
Степень одночлена – это сумма показателей всех переменных, в него входящих.
Например:
$x^2cdot23xy$ – одночлен нестандартного вида, с коэффициентом 23 и степенью 4 (x в кубе и y в первой степени);
$-frac{3}{15}a^3 b^2$ – одночлен стандартного вида, с коэффициентом $left(-frac{3}{15}right)$ и степенью 5 (a в кубе и b в квадрате);
9 – одночлен стандартного вида, с коэффициентом 9 и степенью 0;
a – одночлен стандартного вида, с коэффициентом 1 и степенью 1.
Число 0, а также одночлены, тождественно равные нулю (например, $0 cdot x^3, 0cdot mn$), называются нуль-одночленами. Считают, что нуль-одночлен степени не имеет. Одночлены с одинаковой буквенной частью (например, $2ab^3 c^2 и -frac{7}{5}ab^3 c^2$) называются подобными.
Приведение одночлена к стандартному виду
Любой одночлен можно преобразовать так, чтобы получился одночлен стандартного вида.
Алгоритм приведения одночлена к стандартному виду
- Определить коэффициент одночлена: перемножить все числовые множители и записать результат первым множителем.
- Используя свойства степеней, найти общую степень для каждой из переменных одночлена.
Если в одночлен в качестве множителей входят несколько переменных, их принято записывать по алфавиту. Но это не является обязательным.
Примеры
Пример 1. Преобразуйте выражение в одночлен стандартного вида, найдите его коэффициент и степень:
а) $ frac{1}{2}x^5y^4c cdot (-5xy^2 c^3) = frac{1}{2} cdot (-5) cdot c^{1+3} cdot x^{5+1} cdot y^{4+2} = -2,5c^4 x^6 y^6 $
коэффициент (-2,5), степень 4+6+6 = 16
б) $ -(3m^4)^2 cdot (-m^3 kp)^3 = -3^2 cdot (-1)^3 cdot k^3 cdot m^{8+9} cdot p^3 = 9k^3 m^17 p^3 $
коэффициент 9, степень 3+17+3 = 23
в) $ (-2)^3 xy cdot 1,5(x^4 y)^2 = -8 cdot 1,5 cdot x^{1+8} cdot y^{1+2} = -12x^9 y^3 $
г) $ (8m^3 )^2 n^3 cdot frac{1}{(4mn)^3} = frac{8^2 m^6 n^3}{4^3 m^3 n^3} = frac{(2^3)^2}{(2^2)^3} cdot frac{m^6}{m^3} cdot frac{n^3}{n^3} = m^3$
коэффициент 1, степень 3
Пример 2. Запишите одночлен в стандартном виде и найдите его числовое значение:
а) $ frac{1}{2} xycdot frac{1}{4}x^2 при x = 2, y = 3 $
$ frac{1}{2}xy cdot frac{1}{4}x^2 = frac{1}{2} cdot frac{1}{4} cdot x^{1+2}cdot y = frac{1}{8} x^3 y $
Подставляем: $ frac{1}{8}cdot2^3cdot3 = 3 $
б) $ (-2a^2 b^3) cdot left(frac{0,5}{ab}right)^2 при a = 73,b = 3 $
$ (-2a^2 b^3) cdot left(frac{0,5}{ab}right)^2 = -2 cdot frac{1}{2}^2 cdot frac{a^2}{a^2} cdot frac{b^3}{b^2} = -frac{1}{2}b $
Подставляем: $ -frac{1}{2}cdot3 = -1,5 $
Пример 3. Представьте выражение в виде квадрата одночлена:
а) $ 16x^4 y^2 z^6 = 4^2cdot(x^2 )^2cdot y^2cdot(z^3 )^2 = (4x^2 yz^3 )^2 $
б) $ frac{49}{64}x^{12} y^4 z^{16} = (frac{7}{8} x^6 y^2 z^8 )^2 $
Пример 4*. Известно, что $ 5a^2 b^3 = 7$. Найдите значение выражения $ -frac{4}{49} a^6 b^9 $
Выразим произведение переменных через число: $ a^2 b^3 = frac{7}{5} $
Преобразуем выражение:
$$ -frac{4}{49} a^6 b^9 = -frac{4}{49} left(underbrace{a^2 b^3}_{=7/5text{}}right)^3 = -frac{4}{7^2} cdot left(frac{7}{5}right)^3 = -frac{4}{5^3} cdot frac{7^3}{7^2} = -frac{28}{125} $$
Ответ: $ -frac{28}{125} $
Алгебра
7 класс
Урок №15
Понятие одночлена
Перечень рассматриваемых вопросов:
• Алгебраические выражения.
• Одночлен; свойства одночленов.
• Числовые и буквенные множители.
• Нулевой одночлен.
Тезаурус:
Одночлен – алгебраическое выражение, являющееся произведением букв и чисел.
Множители одночлена – буквы и числа, входящие в состав одночлена.
Нулевой одночлен – одночлен, среди множителей которого есть число ноль.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Наверное, вы слышали достаточно известную фразу: «знание – источник, который надо постоянно пополнять». Поэтому сегодня мы пополним свои знания об алгебраических выражениях ещё одним термином – одночлены.
Мы знаем, что алгебраические выражения бывают буквенные и числовые.
Например, слева находятся выражения буквенные, так как в них содержатся буквы, а справа – числовые выражения, т.к. в них нет букв.
Обратите внимание на алгебраические выражения 12 · х и 124.
В них нет таких знаков арифметического действия, как сложение, вычитание или деление. Такие выражения называют одночленами.
Итак, одночлен – алгебраическое выражение, являющееся произведением букв и чисел.
Буквы и числа называют множителями одночлена.
Например:
10 · х · с – одночлен,
где 10 – числовой множитель одночлена,
x; c – буквенные множители одночлена.
Множители одночлена, записанные с помощью цифр, называют числовыми множителями одночлена, а множители, обозначенные буквами, называют буквенными множителями. При этом стоит отметить, что знак умножения между числовыми и буквенными множителями или между буквенными множителями очень часто не пишут.
Стоит отметить, что одночлен может состоять и только из буквы или цифры.
Например:
а
с
1,5
0 – нулевой одночлен.
Сформулируем некоторые свойства одночленов.
1 свойство. Два одночлена считаются равными, если они отличаются друг от друга лишь порядком множителей.
Пример:
(-12,3)acx = a(-12,3)xc
4xc ≠ -4xc, т.к. числовые множители разные
2 свойство. Два одночлена считаются равными, если один из них получен из другого заменой некоторых его числовых множителей их произведением.
Пример:
-24kx = 6 · x · (-24)k (т.к. -24 получено при умножении числа 6 на число -4)
-24kx ≠ 6 · x · 4 · k (т.к. -24 не получается при умножении числа 6 на число 4)
3 свойство. Одночлен считается равным нулю, если среди его множителей есть число ноль.
Пример: 2х · 0с = 0 – нулевой одночлен.
(-24)kx – ненулевой одночлен, т.к. среди его множителей нет нуля.
И, наконец, рассмотрим последнее свойство.
4 свойство. Два одночлена считаются равными, если один получен из другого путём опускания множителя один.
Пример:
7у · 1а = 7уа
Итак, сегодня мы получили представление о новом понятии – одночлен.
Это интересно!
Давайте зададимся вопросом, где мы можем встретить одночлены?
Везде.
Посмотрите на номера домов. Что это, как не одночлены?
Или цифры, из которых можно составить любые числа, что это, как не одночлены?
А буквы, из которых можно составить выражение, например, такое mc2. Это тоже одночлен.
Но внимательно всмотритесь в последний одночлен. Возможно, он вам где-нибудь встречался?
А если нет, то курс физики вас с ним познакомит, этот одночлен входит в состав знаменитой формулы Эйнштейна, по которой находят энергию. E = mc2.
Итак, понятие «одночлен» широко используется не только в математике, но и в других науках.
Разбор заданий тренировочного модуля.
1) Может ли периметр треугольника, с разными сторонами: а, b, c, быть выражен в виде одночлена?
Варианты ответа:
Да;
Нет;
Не всегда.
Решение: Для решения задания, нужно вспомнить формулу периметра. Периметр находится как сумма всех сторон многоугольника. По условию у нас есть три разных стороны: а, b, c. Следовательно, периметр треугольника – это выражение: а + b + c. А при записи одночлена использовать знак «+» нельзя. Следовательно, ответ – нет.
2) На заводе есть 3 цеха. В первом работают х человек, во втором в 2 раза больше, чем в первом, а в третьем в 1,5 раза больше чем во втором. Сколько человек работает в третьем цехе?Выберите правильное выражение (одночлен), которое характеризует ответ на поставленный вопрос.
Варианты ответа:
x + 2x + 1,5x
3x
3x2
Решение. Опишем условие задачи в виде следующей схемы:
По схеме найдём сначала количество рабочих во 2 цехе, это будет одночлен 2x.
Теперь остаётся найти количество рабочих в 3 цехе, это будет:
2x · 1,5 = 3х
Это и есть искомый ответ.
Ответ: 3x.
Содержание:
- § 1 Одночлен и его стандартный вид
- § 2 Разбор примеров по теме урока
§ 1 Одночлен и его стандартный вид
Одночленом называют алгебраическое выражение, состоящее из произведения чисел и переменных, возведенных в степень с натуральными показателями.
Например, выражения 4bс; 3,9k2х; (–2)3у7а4 являются одночленами, а вот выражения а – b; 4у2+7 одночленами не являются, т.к. нарушено условие определения, допускающее лишь произведение чисел и переменных. Все числа, любые переменные и их степени также считают одночленами. Например, одночленами являются 5; -2,3; а; с5 и другие. Обратите внимание на интересный случай, когда одночлен записан в виде, очень похожим на дробь, т.е. выражение, предполагающее деление.
А теперь давайте рассмотрим такой одночлен:
2а ∙ 3b∙ а3
Так как от перестановки мест множителей произведение не меняется, то его можно записать в таком виде:
2 ∙ 3 ∙ а ∙ а3 ∙ b
Выполнив умножение и применив свойства степени, получим выражение:
6а4b
Это тот же самый одночлен, только записанный в более коротком виде, где только один числовой множитель и каждая переменная встречается только один раз. В таком случае математики говорят, что одночлен записан в стандартномвиде. Причём числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена. Записывают его на первом месте. Если коэффициент одночлена равен 1, то его не пишут, но знают, что он есть. Если коэффициент равен –1, то пишут только знак минус. Число 1 не пишут. Привести к стандартному виду можно любой одночлен.
§ 2 Разбор примеров по теме урока
Пример 1. Записать в стандартном виде одночлен –3,2bа ∙ 2аb3.
Сначала применим переместительное свойство умножения. Получим^
–3,2 ∙ 2 ∙ а ∙ а ∙ b∙ b3
Перемножим все числовые множители и поставим их произведение на первое место, затем перемножим все имеющиеся степени с одним буквенным основанием, потом – с другим. Получим:
–6,4а2в4
Коэффициент одночлена –6,4.
Пример 2. Записать в стандартном виде одночлен:
3а3 с2 ∙ с6а7 = 3 ∙
∙ а3 ∙ а7 ∙ с2 ∙ с6 = 1 ∙ а10 ∙ с8 = а10с8
Коэффициент одночлена равен 1.
Пример 3. Записать в стандартном виде одночлен:
–0,2ус ∙ 5у5 = –0,2 ∙ 5 ∙ с ∙ у ∙ у5 = – 1су6 = –су6
Коэффициент одночлена равен –1.
Пример 4. Найти значение одночлена у2 ∙ у ∙ х3 если у = 2, х = –3.
Сначала приведём одночлен к стандартному виду, получим одночлен у3х3.
Значение одночлена – это значение алгебраического выражения у3х3. Подставим в одночлен вместо у число 2, а вместо х число –3. Получим:
у3х3 = 23 ∙ (–3)3 = 8 ∙ (–27) = –216.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007
- Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010