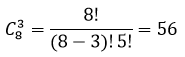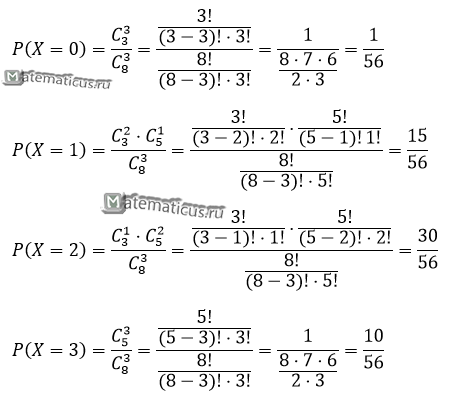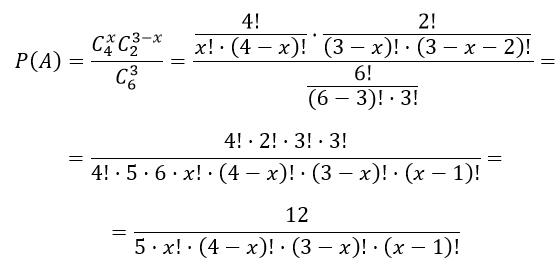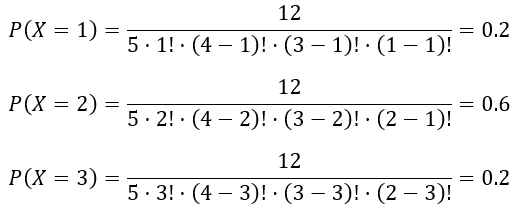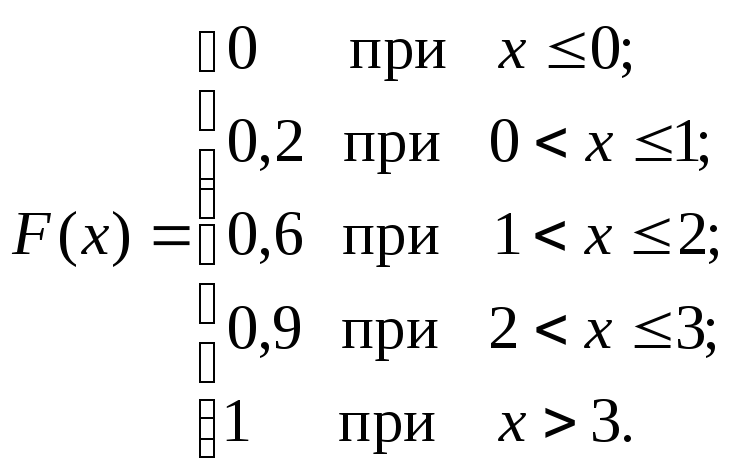Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
|
|
Полезная страница? Сохрани или расскажи друзьям
Дискретные случайные величины
Биномиальное распределение ДСВ
Пусть дискретная случайная величина $X$ – количество “успехов” в последовательности из $n$ независимых случайных экспериментов, таких что вероятность “успеха” в каждом из них равна $p$ (“неуспеха” – $q=1-p$).
Закон распределения $X$ имеет вид:
| $x_k$ | 0 | 1 | … | k | … | n |
| $p_k$ | $q^n$ | $ncdot p cdot q^{n-1}$ | $C_n^k cdot p^k cdot q^{n-k}$ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
$$
P(X=k) = C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}, k=0,1,2,…,n.
$$
Числовые характеристики биномиального распределения:
$$M(X)=np, quad D(X)=npq, sigma(X)=sqrt{npq}.$$
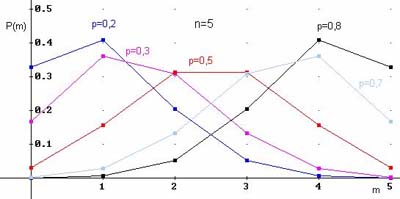
Примеры многоугольников распределения для $n=5$ и различных вероятностей:
Примеры решенных задач на биномиальный закон ДСВ
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии $pto 0$, $n to infty$, $np to lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | … | k | … |
| $p_k$ | $e^{-lambda}$ | $lambda e^{-lambda}$ | … | $frac{lambda^k}{k!}cdot e^{-lambda}$ | … |
Вероятности вычисляются по формуле Пуассона:
$$
P(X=k)=frac{lambda^k}{k!}cdot e^{-lambda}, k=0,1,2,…
$$
Числовые характеристики для распределения Пуассона:
$$M(X)=lambda, quad D(X)=lambda, sigma(X)=sqrt{lambda}.$$
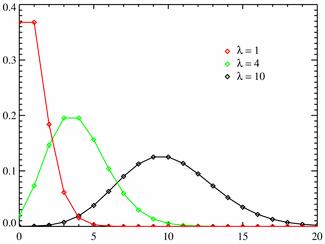
Разные многоугольники распределения при $lambda = 1; 4; 10$.
Примеры решенных задач на закон Пуассона
Геометрическое распределение ДСВ
Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ – количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.
Формула для вероятностей:
$$
P(X=k) = q^k cdot p, k=0,1,2,…,n,…
$$
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | … | k | … |
| $p_k$ | $p$ | $qcdot p$ | $q^2 cdot p$ | … | $q^k cdot p$ | … |
Числовые характеристики:
$$M(X)=frac{q}{p}, quad D(X)=frac{q}{p^2}.$$
Примеры решенных задач на геометрическое распределение
Гипергеометрическое распределение ДСВ
Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n le N$). Найти закон распределения случайной величины $X$ – равной числу белых шаров среди выбранных.
Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n lt K$, то до $n$). Вероятности вычисляются по формуле:
$$
P(X=k)=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}, quad 0le k le K.
$$
Числовые характеристики:
$$M(X)=frac{K}{N}cdot n, quad D(X)=frac{K}{N}cdot n cdot frac{N-n}{N} cdot frac{N-K}{N-1}.$$
Примеры задач на гипергеометрическое распределение
Решаем теорию вероятностей на отлично. Закажите сейчас!
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Плотность распределения величины $X$(везде $ lambda gt 0)$:
$$
f(x)=
left{
begin{array}{l}
0, x lt 0\
lambda e^{-lambda x}, xge 0 \
end{array}
right.
$$
Функция распределения величины $X$:
$$
F(x)=
left{
begin{array}{l}
0, x lt 0\
1- e^{-lambda x}, xge 0 \
end{array}
right.
$$
Числовые характеристики можно найти по формулам:
$$M(X)=frac{1}{lambda}, quad D(X)=frac{1}{lambda^2}, quad sigma= frac{1}{lambda}.$$
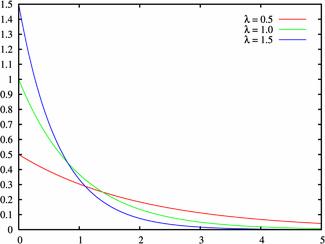
Плотность распределения при различных значениях $lambda gt 0$:
Примеры решенных задач на показательное распределение
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Плотность распределения на отрезке $(a;b)$:
$$
f(x)=
left{
begin{array}{l}
0, x le a\
frac {1}{b-a}, a lt x le b, \
0, x gt b, \
end{array}
right.
$$
Функция распределения:
$$
F(x)=
left{
begin{array}{l}
0, x le a\
frac {x-a}{b-a}, a lt x le b, \
1, x gt b, \
end{array}
right.
$$
Числовые характеристики равномерно распределенной случайной величины:
$$M(X)=frac{a+b}{2}, quad D(X)=frac{(b-a)^2}{12}, quad sigma=frac{b-a}{2sqrt{3}}.$$
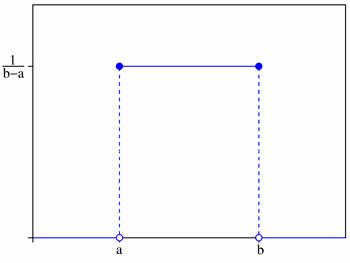
График плотности вероятностей:
Примеры решенных задач на равномерное распределение
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Плотность распределения нормальной случайной величины $X$ имеет вид:
$$f(x)= frac{1}{sigmasqrt{2pi}} expleft({-frac{(x-a)^2}{2sigma^2}}right). $$
При $a=0$ и $sigma=1$ эта функция принимает вид:
$$varphi(x)= frac{1}{sqrt{2pi}} e^{-x^2/2}.$$
Скачать таблицу для функции $varphi(x)$
Числовые характеристики для нормального распределения:
$$M(X)=a, quad D(X)=sigma^2.$$
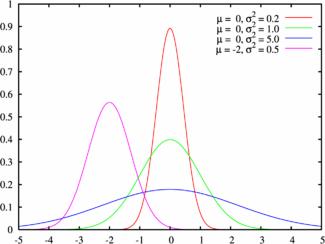
Пример графика плотности распределения для различных значений среднего и СКО:
Нормальный закон распределения случайной величины с параметрами $a=0$ и $sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.
Функция Лапласа определяется как:
$$Phi(x)= frac{1}{sqrt{2pi}}int_0^x e^{-t^2/2} dt$$
Скачать таблицу для функции Лапласа
Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(alpha, beta)$:
$$
P(alpha lt X lt beta) = Phileft( frac{beta-a}{sigma} right) – Phileft( frac{alpha-a}{sigma} right).
$$
Вероятность отклонения нормально распределенной случайной величины $X$ на величину $delta$ от математического ожидания (по модулю).
$$
P(|X -a|lt delta) = 2 Phileft( frac{delta}{sigma} right).
$$
Примеры решенных задач на нормальное распределение
Спасибо за ваши закладки и рекомендации
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:
Подробно решим теорию вероятностей. Закажите сейчас!
Полезные ссылки
|
|
Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х1, х2,…,хn этой величины и их вероятностями p1, p2,…,pn
Может быть задан аналитически, графически или таблично.
Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть
| X | x1 | x2 | …… | xn |
| P | p1 | p2 | …… | pn |
х1, х2,…,хn — значения дискретной случайной величины;
p1, p2,…,pn — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p1+p2+ … +pn=1
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли.Рассмотрим примеры
Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p1(6)=6/10=0,6;
p2(4)=4/10=0,4
Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x1=4; x2=6; x3=8; x1=2
Найдем их вероятности:
p1(4)=4/20=0,2;
p2(6)=6/20=0,3;
p3(8)=8/20=0,4;
p4(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины
| X | 4 | 6 | 8 | 2 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение
n=5+13+7=26
Вычислим вероятности:
p1(5)=5/25=0,2;
p2(13)=13/25=0,52;
p3(7)=7/25=0,28
Таблица имеет вид:
| X | 5 | 13 | 8 | 2 |
| P | 0.2 | 0.52 | 0.28 | 0.1 |
Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем:
при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные.
Составим таблицу распределения
| X | 0 | 1 | 2 | 3 |
| P | 0.018 | 0.268 | 0.536 | 0.178 |
Пример 5
В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.
Решение
Возможные варианты значений СВ X: 1, 2, 3
$n=C_6^3$ — числу способов, которыми можно выбрать три детали из шести;
$C_4^x$ — число способов, которыми из четырех деталей выбирают х деталей.
$C_2^{3 — x}$ — общее число способов отбора нестандартных деталей
Тогда вероятности события A вычисляются по формуле
Закон распределения дискретной случайной величины X для составления ряда распределения:
Получаем таблицу ряда распределения ДСВ
| X | 0 | 1 | 2 | 3 |
| P | 0 | 0.2 | 0.6 | 0.2 |
17118
Наиболее общей
формой задания случайной величины
является функция распределения.
Функцей
распределения (интегральной
функцией)
случайной величины X
называется функция действительной
переменной х,
определяемая равенством
F(x) =P(X<x), (40)
где P(X
< x) –
вероятность того, что случайная величина
X примет
значение, меньшее x.
Основные свойства функции распределения
1.
Функция
распределения является неубывающей,
т. е. если x1
< x2,
то
.
2.
.
3.
Если возможные значения случайной
величины
,
то
при
,
,
.
4.
Вероятность того, что значение случайной
величины X
окажется на заданном интервале (a;b)
определяется формулой
.
(41)
Функция
распределения F(x)
для дискретной случайной величины X,
которая может принимать значения x1,
x2,
…, xn
с соответствующими вероятностями, имеет
следующий вид:
,
(42)
где
символ означает,
что суммируются вероятности тех значений,
которые меньше x.
Пример
2.4. Найти
функцию распределения случайной
величины, если закон распределения
дискретной случайной величины задан
следующей таблицей:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,2 |
0,4 |
0,3 |
0,1 |
Решение.
1.
При
.
,
так как величина X
не принимает значений меньше 0.
2.
При
.
.
3.
При
.
.
4.
При
.
F(x)
==
P(X
= 0) + P(X
= 1) + P(X
= 2) = 0,2 + 0,4 + 0,3 =
= 0,9.
5.
При x >
3.
F(x)
= P(X
= 0) + P(X
= 1) + P(X
= 2) + P(X
= 3) = 0,2 + 0,4 + 0,3 +
+ 0,1 = 1.
График
функции F(x)
отражен на рис. 2.2.
Рис. 2.2
Вероятность
попадания случайной величины X
в интервал (2;5) равна P(2
< X <
5) = F(5)
– F(2) =
1 – 0,6 = 0,4.
Пример
2.5. Охотник
имеет 4 патрона и стреляет до первого
попадания в цель (или пока не израсходуются
патроны). Найти функцию распределения
числа израсходованных патронов, если
вероятность попадания при каждом
выстреле равна 0,25.
Решение.
Вероятность попадания
р = 0,25,
следовательно q = 0,75.
Случайная
величина X
(число израсходованных патронов) имеет
следующие значения: x1
= 1 (одно попадание), x2
= 2 (один промах и одно попадание), x3
= 3 (два промаха и одно попадание), x4
= 4 (три промаха и одно попадание или
четыре промаха).
Найдем
вероятность того, что стрельба закончится
при четвертом выстреле, т. е. первые три
выстрела дали промахи, а четвертый
выстрел – попадание. Так как события
независимы, то искомая вероятность p
= q · q · q · p
= q3 · p.
Тогда искомый закон распределения
запишем в виде следующей таблицы:
|
X |
1 |
2 |
3 |
4 |
|
P |
0,25 |
0,75 · 0,25 |
0,752 · 0,25 |
0,753 · 0,25 |
.
Функция
распределения имеет вид:
Задачи для самостоятельного решения
1.
Игральную кость подбрасывают 3 раза.
Найти закон распределения случайной
величины X
(число невыпадений единицы).
-
X
0
1
2
3
P
2.
В партии 6 деталей, из которых 4 стандартных.
Наудачу отобраны 3 детали. Найти функцию
распределения случайной величины X
(число стандартных деталей среди
отобранных).
-
X
0
1
2
3
P
3.
Две игральные кости бросают 2 раза.
Написать закон распределения случайной
величины X
(число выпадений четного числа очков
на двух игральных костях).
|
X |
0 |
1 |
2 |
|
P |
4.
Подбрасываются две монеты. Найти функцию
распределения случайной величины X
(число выпадений герба
на верхних сторонах монеты). Построить
график этой функции.
5.
Из 25 контрольных работ, среди которых
5 оценены на “отлично”, наугад извлекают
3 работы. Найти функцию распределения
случайной величины X
(число оцененных на “отлично” работ
среди извлеченных). Используя функцию
распределения, найти вероятность события
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
P-значение — это статистическая величина, которая помогает ученым определить, корректны ли их гипотезы. P-значения используются для определения того, подпадают ли результаты эксперимента в диапазон значений, нормальный для наблюдаемой величины. Обычно если P-значение для набора данных меньше, чем заранее определенное число (например 0,05), то ученые должны отклонить «нулевую гипотезу» своего эксперимента. Другими словами, они сделают вывод, что переменные в их эксперименте не оказывают достаточного эффекта на результаты. В настоящее время p-значения обычно можно найти в справочнике, если сначала посчитать значение хи-квадрат.
Шаги
-
1
Определите ожидаемые в вашем эксперименте результаты. Обычно когда ученые проводят эксперимент, у них уже есть идея того, какие результаты считать «нормальными» или «типичными». Это может быть основано на экспериментальных результатах прошлых опытов, на достоверных наборах данных, на данных из научной литературы, либо ученый может основываться на каких-либо других источниках. Для вашего эксперимента определите ожидаемые результаты и выразите их в виде чисел.
- Пример: допустим, более ранние исследования показали, что в вашей стране владельцы красных машин чаще получают штрафы за превышение скорости, чем владельцы синих. Например, средние результаты показывают предпочтение 2:1 красных машин перед синими. Наша задача — определить, относится ли полиция точно так же предвзято к цвету машин в вашем городе. Для этого мы будем анализировать штрафы, выданные за превышение скорости. Если мы возьмем случайный набор из 150 штрафов за превышение скорости, выданных либо владельцам красных, либо синих автомобилей, мы ожидаем, что 100 штрафов будет выписано владельцам красных автомобилей, а 50 — владельцам синих, если полиция в нашем городе так же предвзято относится к цвету машин, как это наблюдается по всей стране.
-
2
Определите наблюдаемые результаты вашего эксперимента. Теперь, когда вы определили ожидаемые результаты, необходимо провести эксперимент и найти действительные (или «наблюдаемые») значения. Вам снова необходимо представить эти результаты в виде чисел. Если мы создаем экспериментальные условия, и наблюдаемые результаты отличаются от ожидаемых, то у нас есть две возможности — либо это произошло случайно, либо это вызвано именно нашим экспериментом. Цель нахождения p-значения как раз и состоит в том, чтобы определить, отличаются ли наблюдаемые результаты от ожидаемых настолько, чтобы можно было не отвергать «нулевую гипотезу» — гипотезу о том, что между экспериментальными переменными и наблюдаемыми результатами нет никакой связи.
- Пример: допустим, в нашем городе мы случайно выбрали 150 штрафов за превышение скорости, которые были выданы либо владельцам красных, либо владельцам синих автомобилей. Мы определили, что 90 штрафов были выписаны владельцам красных автомобилей, и 60 — владельцам синих. Это отличается от ожидаемых результатов, которые равны 100 и 50, соответственно. Действительно ли наш эксперимент (в данном случае изменение источника данных с государственного уровня на городской) привел к данному изменению в результатах, или наша городская полиция относится к автомобилистам предвзято точно так же, как и в среднем по стране, а мы видим просто случайное отклонение? P-значение поможет нам это определить.
-
3
Определите число степеней свободы вашего эксперимента. Число степеней свободы — это степень изменяемости вашего эксперимента, которая определяется числом категорий, которые вы исследуете. Уравнение для числа степеней свободы — Число степеней свободы = n-1, где «n» — число категорий или переменных, которые вы анализируете в своем эксперименте.
- Пример: в нашем эксперименте две категории результатов: одна категория для владельцев красных машин и другая — для владельцев синих машин. Поэтому в нашем эксперименте у нас 2-1 = 1 степень свободы. Если бы мы сравнивали красные, синие и зеленые машины, у нас было бы 2 степени свободы и так далее.
-
4
Сравните ожидаемые и наблюдаемые результаты с помощью критерия хи-квадрат. Хи-квадрат (пишется «x2») — это числовое значение, которое измеряет разницу между ожидаемыми и наблюдаемыми значениями эксперимента. Уравнение для хи-квадрата следующее: x2 = Σ((o-e)2/e), где «o» — это наблюдаемое значение, а «e» — это ожидаемое значение.[1]
Суммируйте результаты данного уравнения для всех возможных результатов (смотри ниже).- Заметьте, что данное уравнение включает оператор суммирования Σ (сигма). Другими словами, вам необходимо подсчитать ((|o-e|-.05)2/e) для каждого возможного результата и сложить полученные числа, чтобы получить значение критерия хи-квадрат. В нашем примере у нас два возможных результата — либо машина, получившая штраф красная, либо синяя. Поэтому мы должны посчитать ((o-e)2/e) дважды — один раз для красных машин и один раз для синих машин.
- Пример: давайте подставим наши ожидаемые и наблюдаемые значения в уравнение x2 = Σ((o-e)2/e). Помните, что из-за оператора суммирования нам необходимо посчитать ((o-e)2/e) дважды — один раз для красных автомобилей и один раз — для синих. Мы выполним эту работу следующим образом:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3 .
-
5
Выберите уровень значимости. Теперь, когда мы знаем число степеней свободы нашего эксперимента и узнали значение критерия хи-квадрат, нам нужно сделать еще одну вещь перед тем, как мы найдем наше p-значение. Нам нужно определить уровень значимости. Говоря простым языком, уровень значимости показывает, насколько мы уверены в наших результатах. Низкое значение для значимости соответствует низкой вероятности того, что экспериментальные результаты вышли случайными и наоборот. Уровни значимости записываются в виде десятичных дробей (таких как 0,01), что соответствует вероятности того, что экспериментальные результаты мы получили случайно (в данном случае вероятность этого 1 %).
- По соглашению, ученые обычно устанавливают уровень значимости своих экспериментов равным 0,05, или 5 %.[2]
Это означает, что экспериментальные результаты, которые соответствуют такому критерию значимости, только с вероятностью 5 % могли получиться чисто случайно. Другими словами, существует 95 % вероятность, что результаты были вызваны тем, как ученый манипулировал экспериментальными переменными, а не случайно. Для большинства экспериментов 95 % уверенности наличия связи между двумя переменными достаточно, чтобы считать, что они «действительно» связаны друг с другом. - Пример: для нашего примера с красными и синими машинами, давайте последуем соглашению между учеными и установим уровень значимости в 0.05.
- По соглашению, ученые обычно устанавливают уровень значимости своих экспериментов равным 0,05, или 5 %.[2]
-
6
Используйте таблицу с данными распределения хи-квадрат, чтобы найти p-значение. Ученые и статисты используют большие таблицы для вычисления p-значения своих экспериментов. Данные таблицы обычно имеют вертикальную ось слева, соответствующую числу степеней свободы, и горизонтальную ось сверху, соответствующую p-значению. Используйте данные таблицы, чтобы сначала найти число ваших степеней свободы, затем посмотрите на ваш ряд слева направо, пока не найдете первое значение, большее вашего значения хи-квадрат. Посмотрите на соответствующее p-значение вверху вашего столбца. Нужное вам p-значение находится между этим числом и следующим за ним (тем, которое находится левее вашего).
- Таблицы с распределением хи-квадрат можно получить из множества источников — их можно просто найти онлайн, либо посмотреть в научных книгах или книгах по статистике. Если у вас нет под рукой таких книг, используйте картинку выше или какую-нибудь таблицу онлайн, которую можно просматривать бесплатно, например на сайте medcalc.org. Она расположена здесь.
- Пример: наше значение критерия хи-квадрат было равно 3. Поэтому давайте используем таблицу распределения хи-квадрат на изображении выше, чтобы найти приблизительное p-значение. Так как мы знаем, что в нашем эксперименте всего 1 степень свободы, выберем самую первую строку. Идем слева направо по данной строке, пока не встретим значение, большее 3, нашего значения критерия хи-квадрат. Первое, которое мы находим, это 3,84. Смотрим вверх нашего столбца и видим, что соответствующее p-значение равно 0,05. Это означает, что наше p-значение между 0,05 и 0,1 (следующее p-значение в таблице по возрастанию).
-
7
Решите, отклонить или оставить нулевую гипотезу. Так как вы определили приблизительное p-значение для вашего эксперимента, вам необходимо решить, отклонять ли нулевую гипотезу вашего эксперимента или нет (напоминаем, это гипотеза о том, что экспериментальные переменные, которыми вы манипулировали не повлияли на наблюдаемые вами результаты). Если p-значение меньше, чем уровень значимости — поздравляем, вы доказали, что очень вероятна связь между переменными, которыми вы манипулировали, и результатами, которые вы наблюдали. Если p-значение выше, чем уровень значимости, нельзя с уверенностью сказать, были ли наблюдаемые вами результаты результатом чистой случайности или манипуляцией данными переменными.
- Пример: наше p-значение находится между 0,05 и 0,1. Это явно не меньше, чем 0,05, поэтому, к сожалению, мы не можем отклонить нашу нулевую гипотезу. Это означает, что мы не достигли минимум 95 % вероятности того, чтобы сказать, что полиция в нашем городе выдает штрафы владельцам красных и синих автомобилей с такой вероятностью, которая достаточно сильно отличается от средней по стране.
- Другими словами, существует 5–10 % шанс, что наблюдаемые нами результаты — это не последствия смены места (анализа города, а не всей страны), а просто случайность. Так как заявленная нами точность не должна превышать 5 %, мы не можем сказать с уверенностью, что полиция нашего города менее предвзято относится к владельцам красных автомобилей — существует небольшая (но статистически значимая) вероятность, что это не так.
Реклама
Советы
- Научный калькулятор позволяет облегчить вычисления. Вы также можете использовать калькуляторы онлайн.
- Вы можете подсчитать p-значение с использованием некоторых компьютерных программ, включая как часто используемые программы электронных таблиц, так и более специализированное программное обеспечение.
Реклама
Об этой статье
Эту страницу просматривали 116 025 раз.
Была ли эта статья полезной?
Дискретные распределения вероятностей и их параметры
- Общие свойства дискретного распределения
- Функция распределения дискретной случайной величины
- Числовые характеристики дискретного распределения
- Таблица дискретных распределений, их параметров и числовых характеристик
- Примеры
п.1. Общие свойства дискретного распределения
Величина, которая в результате испытания может принимать то или иное числовое значение, называется случайной величиной.
Случайная величина называется дискретной, если она принимает не более чем счетное количество значений.
Дискретная случайная величина называется конечной, если она принимает конечное число значений.
Согласно данному определению дискретная величина может быть определена либо на бесконечном счетном множестве, либо на конечном множестве (которое всегда счетное).
Напомним, что счетным называется множество, которое эквивалентно множеству натуральных чисел, т.е. элементы которого можно пронумеровать (см. §11 справочника для 8 класса).
Например:
1) При подбрасывании игрального кубика мы получаем всего 6 исходов. Случайная величина X – выпавшее число очков – принимает конечное число значений (Omega=left{1;2;3;4;5;6right}), т.е. является дискретной конечной случайной величиной.
2) Случайная величина X – количество поступивших вызовов на сервер за сутки – не ограничена сверху и может принимать значения (Omega=left{1;2;3;…right})
Правило, устанавливающее связь между значениями случайной величины и вероятностью получения каждого из этих значений в испытании, называется законом распределения.
Случайная величина полностью описывается своим законом распределения.
Закон распределения может быть задан аналитически (формулой), таблично или графически.
Закон распределения конечной дискретной случайной величины, заданный в виде таблицы, называют рядом распределения.
Например:
В результате измерения температуры учеников школы получен следующий ряд распределения:
| t, °C | 36,3 | 36,4 | 36,5 | 36,6 | 36,7 | 36,8 | 36,9 | 37,0 | 37,1 |
| p(t) | 0,05 | 0,07 | 0,15 | 0,33 | 0,31 | 0,11 | 0,04 | 0,01 | 0,01 |
Значения (left{x_1,x_2,…,x_kright}), которые может принимать конечная случайная величина X, являются несовместными и образуют полную группу событий. Сумма их вероятностей: $$ sum_{i=1}^k p_i=1, p_igeq 0 $$
Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
Пусть в урне находится 2 белых и 3 черных шара. Мы достаем шар, смотрим на его цвет, возвращаем его обратно и все шары перемешиваем. Таким образом, событие A=«достали белый шар» каждый раз является независимым от предыдущих и имеет вероятность (p=frac25).
Пусть мы провели n=3 испытания. В 3 испытаниях можно получить от 0 до 3 белых шаров. Вероятность событий (kinleft{0;1;2;3right}) описывается биномиальным законом распределения (см. §40 справочника для 9 класса): $$ P_3(k)=C_3^k p^k q^{3-q}, k=overline{0;3} $$ Получаем закон распределения: begin{gather*} P_3(0)=C_3^0 p^0 q^{3-0}=q^3=left(frac35right)^3=frac{27}{125}\ P_3(1)=C_3^1 p^1 q^{3-1}=3pq^2=3cdot frac25cdot left(frac35right)^2=frac{54}{125}\ P_3(2)=C_3^2 p^2 q^{3-2}=3p^2q=3cdot left(frac25right)^2cdot frac35=frac{36}{125}\ P_3(3)=C_3^3 p^3 q^{3-3}=p^3=left(frac25right)^3=frac{8}{125} end{gather*}
| k | 0 | 1 | 2 | 3 |
| (P_3(k)) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) |
Сумма вероятностей: $$ sum_{k=0}^3 P(k)=frac{27+54+36+8}{125}=1 $$
п.2. Функция распределения дискретной случайной величины
Функцией распределения дискретной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины X не превышает граничное значение x: $$ F(x)=P(Xleq x) $$
Для дискретной случайной величины функция распределения будет ступенчатой кусочно-непрерывной функцией, область значений которой: (F(x)in[0;1]).
Слева на графике функции распределения будет нулевая «ступенька», а справа – единичная «ступенька».
Например:
Найдем из закона распределения случайной величины k, полученного в предыдущем примере для урны с шарами, функцию распределения.
| k | 0 | 1 | 2 | 3 |
| (P_3(k)) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) |
| (F(k)) | (frac{27}{125}) | (frac{27+54}{125}=frac{81}{125}) | (frac{81+36}{125}=frac{117}{125}) | (frac{117+8}{125}=1) |
Изобразим графически закон распределения в виде гистограммы:
Построим график для функции распределения: begin{gather*} F(k)= begin{cases} 0, kleq 0\ frac{27}{125}, 0lt kleq 1\ frac{81}{125}, 1lt klt 2\ frac{117}{125}, 2lt kleq 3\ 1, kgt 3 end{cases} end{gather*}
п.3. Числовые характеристики дискретного распределения
Числовыми характеристиками дискретного распределения являются математическое ожидание, дисперсия и среднее квадратичное отклонение (СКО).
Подробно о свойствах этих характеристик – см. §41 справочника для 9 класса.
Здесь мы приведем только основные определения.
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} $$ Математическое ожидание является средним значением величины X.
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ D(X)=M(X-M(X))^2 $$ На практике дисперсия рассчитывается по формуле: $$ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) $$
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ sigma(X)=sqrt{D(X)} $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Например:
Рассчитаем числовые характеристики для урны с шарами из предыдущего примера.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | ∑ |
| (p_i) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) | (1) |
| (x_i p_i) | (0) | (frac{54}{125}) | (frac{72}{125}) | (frac{24}{125}) | (1,2) |
| (x_i^2) | 0 | 1 | 4 | 9 | – |
| (x_i^2 p_i) | (0) | (frac{54}{125}) | (frac{144}{125}) | (frac{72}{125}) | (2,16) |
Получаем begin{gather*} M(X)=sum_{i=0}^3 x_i p_i=1,2=frac65\ D(X)=sum_{i=0}^3 x_i^2 p_i-M^2(X)=2,16-1,2^2=0,72=frac{18}{25}\ sigma(X)=sqrt{D(X)}=sqrt{frac{18}{25}}=frac{3sqrt{2}}{5} end{gather*} В научных статьях и технической документации принято записывать случайные величины в виде (x=M(X)pmsigma (X)).
В данном случае для числа вынутых белых шаров в 3 испытаниях можем записать: $$ k=frac{6pm 3sqrt{2}}{5} $$
п.4. Таблица дискретных распределений и их параметров
| Название | Принятое обозначение |
Плотность распределения |
Мат. ожидание |
Дисперсия |
| Дискретное равномерное | (U(N)) | begin{gather*} P(left{kright})=frac1N\ Ninmathbb{N}, kinleft{1,…,Nright} end{gather*} | (frac{N+1}{2}) | (frac{N^2-1}{12}) |
| Бернулли | (B(1,p)) | begin{gather*} P(0)=1-p=q\ P(1)=p\ kinleft{0;1right} end{gather*} | (p) | (pq) |
| Биномиальное | (B(n,p)) | begin{gather*} P(left{kright})=C_n^k p^k q^{n-k}\ ninmathbb{N}, k=inleft{0,1,…,nright} end{gather*} | (np) | (npq) |
| Пуассона | (Pois(lambda)) | begin{gather*} P(left{kright})=frac{lambda^k}{k!}e^{-lambda}\ lambdagt 0, k=inleft{0,1,…,nright} end{gather*} | (lambda) | (lambda) |
| Геометрическое | (Geopm(p)) | begin{gather*} P(left{kright})=pq^{k-1}\ k=inleft{0,1,2,…right} end{gather*} | (frac1p) | (frac{q}{p^2}) |
| Гипер-геометрическое | (HG(D,N,n)) | begin{gather*} P(left{kright})=frac{C_D^k C_{N_D}^{n-k}}{C_N^n} end{gather*} | (frac{nD}{N}) | $$frac{frac{nD}{N}left(1-frac DNright)(N-n)}{N-1}$$ |
п.5. Примеры
Пример 1. Выведите формулы для мат.ожидания и дисперсии дискретного равномерного распределения
Случайная величина имеет дискретное равномерное распределение, если она принимает конечное число N значений с равными вероятностями. Значения исходов (k_iinleft{1,…,Nright}). Вероятность каждого из исходов (p_i=frac1N, i=overline{1,N}).
Предварительно заметим, что по формуле суммы арифметической прогрессии: $$ sum_{i=1}^N k_i=1+2+…+N=frac{N(N+1)}{2} $$ А сумму квадратов можно найти по формуле Архимеда (доказательство – см. пример 2 в §25 справочника для 9 класса): $$ sum_{i=1}^N k_i^2=1^2+2^2+…+N^2=frac{N(N+1)(2N+1)}{6} $$ Найдем математическое ожидание: $$ M(X)=sum_{i=1}^N k_ip_i=sum_{i=1}^N k_icdot frac1N=frac1N(1+2+…+N)=frac1Ncdotfrac{N(N+1)}{2}=frac{N+1}{2} $$ Найдем дисперсию: begin{gather*} D(X)=sum_{i=1}^N k_i^2 p_i-M^2(X)=sum_{i=1}^N k_i^2cdotfrac1N-M^2(X)=\ =frac1Ncdotfrac{N(N+1)(2N_1)}{6}-left(frac{N+1}{2}right)^2=frac{(N+1)(2N+1)}{6}-frac{(N+1)^2}{4}=\ =frac{N+1}{2}left(frac{2N+1}{3}-frac{N+1}{2}right)=frac{N+1}{2}cdotfrac{4N+2-3N-3}{6}=frac{N+1}{2}cdotfrac{N-1}{6}=frac{N^2-1}{12} end{gather*} В частности, для игрального кубика: $$ N=6; p_i=frac16; M(X)=frac{6+1}{2}=3,5; D(X)=frac{6^2-1}{12}=2frac{11}{12} $$
Ответ: (M(X)=frac{N+1}{2}; D(X)=frac{N^2-1}{12})
Пример 2. Выведите формулы для мат.ожидания и дисперсии распределения Бернулли.
Случайная величина k имеет распределение Бернулли, если k принимает значения 1 или 0 с вероятностями p и 1-p соответственно. $$ P(0)=1-p=1, P(1)=p, kinleft{0;1right} $$
Закон распределения:
| (k_i) | 0 | 1 |
| (p_i) | 1-p | p |
Найдем математическое ожидание: $$ M(X)=0cdot (1-p)+1cdot p=p $$ Найдем дисперсию: begin{gather*} D(X)=(0^2cdot(1-p)+1^2cdot p)-M^2(X)=p-p^2=p(1-p)=pq end{gather*}
Типичным примером является бросание монеты, где (M(X)=p=0,5) и (D(X)=0,5cdot 0,5=0,25). Дисперсия максимальна для нефальшивой монеты.
Рассмотрим другой пример – бросание фальшивой монеты, для которой вероятность выпадения орла (k=1) равна p=0,7. Тогда (M(k)=p=0,7), дисперсия (D(k)=0,7cdot 0,3=0,21). Как и ожидалось, для фальшивой монеты средняя величина возрастает (70% бросков заканчивается выпадением орла). При этом дисперсия уменьшается.
Ответ: (M(X)=p, D(X)=pq)
Пример 3. Выведите формулы для мат.ожидания и дисперсии биномиального распределения.
Схема Бернулли – это последовательность независимых испытаний, в каждом из которых возможны только два исхода – «успех» и «неудача».
При этом вероятность успеха в каждом испытании постоянна и равна (pin(0;1)).
Вероятность неудачи в каждом испытании (q=1-p).
Вероятность того, что событие A появится в n испытаниях Бернулли ровно k раз, выражается биномиальным распределением: $$ P_n(k)=C_n^k p^k q^{n-k} $$
Математическое ожидание и дисперсию для одного опыта Бернулли мы получили в примере 2: (M(X)=p, D(X)=pq).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (X=X_1+X_2+…+X_n). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий (см. §41 справочника для 9 класса): begin{gather*} M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)=\ =underbrace{p+p+…+p}_{n раз}=np end{gather*} По свойству дисперсии суммы независимых событий (см. §41 справочника для 9 класса): begin{gather*} D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)=\ =underbrace{pq+pq+…+pq}_{n раз}=npq end{gather*} Например, пусть событие A=«уронить молоток на ногу» имеет вероятность p=0,1.
Тогда для n=100 забиваний гвоздей вы в среднем уроните молоток на ногу
(M(X)=np=100cdot 0,1=10) раз
Дисперсия этого события (D(X)=npq=100cdot 0,1cdot 0,9=9)
СКО (sigma(X)=sqrt{D(X)}=3)
По правилу «трех сигм» интервал оценки: begin{gather*} 10-3cdot 3lt Xlt 10+3cdot 3\ -17lt Xlt 37\ 0leq Xleq 36 end{gather*} Скорее всего (вероятность 99,72%), вы уроните молоток от 0 до 36 раз.
Ответ: (M(X)=np, D(X)=npq)
Пример 4. Выведите формулы для мат.ожидания и дисперсии распределения Пуассона.
Если проводится очень много испытаний Бернулли, для каждого из которых вероятность появления события A мала: (nrightarrowinfty, prightarrow 0, nprightarrowlambda), вероятность того, что событие A появится ровно k раз выражается распределением Пуассона: $$ p_k(lambda)=frac{lambda^k}{k!}e^{-lambda}, k=inleft{0,1,2,…right} $$
Распределение Пуассона получается из биномиального распределения предельным переходом (nrightarrowinfty, prightarrow 0, nprightarrowlambda).
Найдем математическое ожидание как предел мат. ожидания биномиального распределения: $$ M(X)=lim_{nprightarrowlambda}M_B(X)=lim_{nprightarrowlambda}(np)=lambda $$ Т.е. параметр (lambda) является средним числом удачных исходов.
Дисперсия, если учесть что (prightarrow 0), а значит (q=1-prightarrow 1) $$ D(X)=underset{qrightarrow 1}{lim_{nprightarrowlambda}} D_B(X)=underset{qrightarrow 1}{lim_{nprightarrowlambda}}(npq)=lambdacdot 1=lambda $$
Например, в городе размерами 10х10 км болеет гриппом 1000 человек.
С какой вероятностью в комнате размерами 10х10 м:
а) не окажется больных;
б) окажется 1 больной?
Площадь города в метрах (S=(10^4)^2=10^8) м2
Площадь комнаты в метрах (s_0=10^2) м2
Среднее количество больных в комнате: (lambda=Nfrac{s_0}{S}=10^3cdotfrac{10^2}{10^3}=10^{-3}=0,001)
а) вероятность того, что в комнате не окажется больных: $$ p_0=frac{0,001^0}{0!}e^{-0,001}=e^{-0,001}approx 1-0,001=0,999 $$ Здесь мы использовали формулу приближенных вычислений (e^xapprox 1+x, xrightarrow 0) (см. §52 данного справочника).
б) вероятность того, что в комнате окажется один больной: $$ p_1=frac{0,001^1}{1!}e^{-0,001}=0,000999approx 0,001 $$ Вероятность всех остальных случаев пренебрежимо мала.
Таким образом, при малых (lambda) вероятности (p_0approx 1-lambda, p_1approxlambda), т.е. фактически мы получаем распределение Бернулли.
Ответ: (M(X)=lambda , D(X)=lambda)