Функция распределения случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
– действительное число. Вероятность события,
состоящего в том, что
примет значение, меньшее
, то есть вероятность
события
обозначим через
. Разумеется, если
изменяется, то, вообще говоря, изменяется и
, то есть
– функция от
.
Функцией распределения называют функцию
, определяющую вероятность
того, что случайная величина
в результате испытания примет значение,
меньшее
, то есть:
Геометрически
это равенство можно истолковать так:
есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки
.
Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».
Функцию
распределения дискретной случайной величины
можно представить следующим соотношением:
Это
соотношение можно переписать в развернутом виде:
Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции
равна 1.
Свойства функции распределения
Свойство 1.
Значения
функции распределения принадлежат отрезку
:
Свойство 2.
– неубывающая функция, то есть:
,
если
Свойство 3.
Если возможные значения случайной величины
принадлежат интервалу
,
то:
1)
при
;
2)
при
Свойство 4.
Справедливо равенство:
Свойство 5.
Вероятность того, что непрерывная случайная
величина
примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.
Заметим, что было бы неправильным думать, что
равенство нулю вероятности
означает, что событие
невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство 6.
Если возможные значения непрерывной случайной величины
расположены на всей оси
,
то справедливы следующие предельные соотношения:
Свойство 7.
Функция распределения непрерывная слева, то есть:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Примеры решения задач
Пример 1
Дан ряд
распределения случайной величины
:
|
|
1 | 2 | 6 | 8 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти и изобразить ее функцию распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Будем задавать различные значения
и находить для них
1. Если
,
то, очевидно,
в том числе и при
2. Пусть
(например
)
Очевидно, что и
3. Пусть
(например
);
Очевидно, что и
4. Пусть
Очевидно, что и
5. Пусть
Итак:
График функции распределения
Пример 2
Случайная
величина
задана функцией распределения:
Найти
вероятность того, что в результате испытания
примет значение:
а) меньше
0,2;
б) меньше
трех;
в) не
меньше трех;
г) не
меньше пяти.
Решение
а) Так
как при
функция
, то
то есть
при
б)
в)
События
и
противоположны, поэтому
Отсюда:
г) сумма
вероятностей противоположных событий равна единице, поэтому
Отсюда, в
силу того что при
функция
, получим:
Пример 3
Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики функций f(x) и F(x);
4)
вычислить математическое ожидание и дисперсию X;
5)
определить вероятность того, что X примет значение из
интервала (a,b).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
и
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
3) Построим графики функций:
График плотности распределения
График функции распределения
4) Вычислим
математическое ожидание:
В нашем случае:
Вычислим дисперсию:
Искомая дисперсия:
5) Вероятность того, что
примет значение из интервала
:
Задачи контрольных и самостоятельных работ
Задача 1
Закон
распределения случайной величины X задан таблицей.
Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.
F(1)=
M[X]=
D[X]=
Задача 2
Случайная
величины X задана функцией распределения
Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)
Задача 3
Дискретная
случайная величина X задана рядом распределения. Найти:
1)
функцию распределения F(x) и ее график;
2)
математическое ожидание M(X);
3)
дисперсию D(X).
|
|
-5 | 5 | 25 | 45 | 65 |
|
|
0.2 | 0.15 | 0.3 | 0.25 | 0.1 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В задаче
дискретная случайная величина задана рядом распределения.
Найти
; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)
Задача 5
В задаче
непрерывная случайная величина X задана функцией
распределения F(x).
Найти a; f(x); M(X); D(X); P(X<0.2)
Начертить
графики функций f(x);F(x).
Задача 6
Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна
(
). Найти вероятность безотказной
работы устройства за время x больше либо равно T.
Задача 7
Функция
распределения непрерывной случайной величины задана выражением:
Найдите:
1)
параметр a;
2)
плотность вероятностей;
4) P(0<x<1)
Постройте
графики интегральной и дифференциальной функции распределения.
Задача 8
Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).
Задача 9
Дана
функция распределения F(х) случайной величины Х.
Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).
Задача 10
НСВ X имеет
плотность вероятности (закон Коши)
Найти:
а)
постоянную C=const;
б)
функцию распределения F(x);
в)
вероятность попадания в интервал -1<x<1
г)
построить графики f(x), F(x).
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
§4.
Функция
распределения
Ф ункция
ункция
распределения (интегральная)
Х
Х
Функцией
распределения F(X)
называется функция, которая для каждого
значения аргумента равна вероятности
того, с.в. Х примет значение меньшее, чем
аргумент (попадает в область, лежащую
слева от аргумента).
F(x)=P(X<x) (3)
Например:
Дискретная с.в. задана рядом распределения
|
ХI |
2 |
4 |
7 |
9 |
|
PI |
0.2 |
0.4 |
0.3 |
0.1 |

-3
0 2 П
4 6 7 9 12 X
F(-3)=P(X<-3)=0
F(П)=P(X<П)=P(X=2)=0,2
F(12)=P(X<12)=P(V)=1
F(6)=P(X<6)=0,2+0,4=0,6
Свойства
функции распределения:
1
область определения: Х Є
R
2
область значений: 0<=F(x)<=1
3
F(-∞)=0 [P(X<= -∞)=0]
4
F(+∞)=1 [P(X<=+∞)=P(V)=1]
F(x)
неубывающая функция:
X 1<X2
1<X2
F(X1)<=F(X2)


X1 X2 X
(X<x2)=(X<x1)+(x1
<X<x2)
несовместные
P

 (X<x2)=P(X<x1)+P(x1<X<x2)
(X<x2)=P(X<x1)+P(x1<X<x2)
F(x2)
>= F(x1)
>0
Неубывание
доказано.
Следствие:
Р(Х1<=X<Х2)
= F(X2)
– F(X1)
(4)
Замечание:
функция распределения F(x)
– универсальный способ задания закона
распределения. Он пригоден и для
дискретных и для непрерывных с.в.. С
ростом аргумента Х идет накопление
вероятности, т.е. функция F(X)
увеличивается. Для дискретных с.в. рост
происходит скачком при переходе через
очередное возможное значение XIДля
непрерывной с.в. F(X)
накапливается непрерывно.
Качественный
график функции распределения:

Непрерывная
с.в.
дискретная с.в.
Замечание
к формуле (4)
Пусть
с.в. непрерывна и функция F(X)
непрерывна.
Найдем
вероятность попадания в точку:
P(X=x1)=![]()
Для
непрерывной с.в. вероятность попадания
в точку равна нулю P(X=a)=0
Для
непрерывной с.в.
Р(α<X<β)=F(β)-F(α)
(5)
Например:
Дискретная с.в. задана рядом распределения
|
ХI |
2 |
4 |
5 |
7 |
||
|
PI |
0,1 |
0,3 |
0,2 |
0,4 |
Найти
значения функции распределения в
указанных точках. Построить функцию
распределения для всех значений
аргумента.

F(-3)=P(X<-3)=0
F(П)=Р(Х<П)=0,1
F(2L)=P(X<2L)=0.1+0.3+0.2=0.6
F(8)=P(X<8)=P(U)=1
F(50)=P(X<50)=P(U)=1

-∞<x<+∞
2<x<=2
F(x)=0 F(2)=P(X<2)=0
2<x<=4
F(x)=P(X<x)=P(x=2)=0,1
4<x<=5
F(x)=P(4<X<2)=0,4
5<x<=7
F(x)=0,6
7<x<
+∞ F(x)=1

0
при -∞<x<=2

0,1
2<=x<=4
F(X)
0,4 4<x<=5 В
точках разрыва
0,6
5<x<=7
значение
функции равно
1
7<x<+∞
пределу слева
С.в. задана функцией
распределения. Составить ряд распределения.

|
ХI |
1 |
2 |
4 |
6 |
7 |
10 |
|
PI |
0,1 |
0,2 |
0,2 |
0,2 |
0.1 |
0.2 |
Непрерывная с.в. задана функцией
распределения

0 -∞<X
<=0
F(X)
CX2
0< X<=3
1
3< X
< + ∞
1
С-?
Найти
С из условия непрерывности функции
F(X).
2
Найти вероятности попадания в указанные
интервалы.
3
Найти плотность распределения f(X).

1
Проверяя непрерывность в т. Х=0 и в т.
Х=3:
(Х=0)
![]()
![]()
F(0)=0
В т. Х=0 функция непрерывна
при любом С.
( Х=3)
Х=3)
![]()
![]()
![]() 9c=1
9c=1
c=1/9
F(3)=c*9


2
Р(-2<X<1)=F(1)
– F(2) = (CX2)X=1
– 0X=-2
= C = 1/9
Р(0<X<2)=F(2)
– F(0) = (CX2)X=1
– 0
= 4C = 4/9
Р(1<X<5)=F(5)
– F(1) =1- (CX2)X=1
= 1-1/9= 8/9
Р(0.5<X<2.5)=F(2.5)
– F(0.5) = (CX2)X=5/2
–
(CX2)X=1/2
= C(25/4 – 1/4) = 6C =
=
6/9=2/3
Р(2<X<9)=F(9)
– F(2) = 1 –
(CX2)X=2
= 1- 4C = 1 – 4/9 = 5/9
Р(X>2.5)=P(2,5<X<+∞)
= F(+∞) – F(2.5) = 1 – (CX2)X=5/2=
1 – 25/4 * 1/9 = 1 – 25/36 = 11/36
3
f(X) – ? f(X) = F1(X)
= 0 -∞<X<=0
2CX = 2X/9
0<X<3
0
3<X<+∞

Для
непрерывной случайной величины
X
задана
функция распределения F(x).
Необходимо:
-
Найти
значение параметра С из условия
непрерывности F(x),
Построить
график F(x).
-
Подсчитать
вероятности попаданий в указанные
интервалы. -
Найти
плотность распределения F(x)
и
построить ее график.

Рассматриваемая
случайная величина непрерывна. При
такой функции распределения все ее
возможные значения находятся только
на интервале (1<x4).
Вне
этого интервала возможных значений
нет.
-
Находим значение
параметра С. Используем условие
непрерывности
функции
распределения F(x).
Чтобы
функция была непрерывна, нужно, чтобы
предел слева, предел справа и значение
функции в точке совпадали.
В
точке
x=1
: F(1-0)= 0; F(1+0)= 0; F(1)=
0;
функция
непрерывна.
В
точке
x=4
: F(4-0)=
С(4-1)3
=27С;
F(4+0)=
1; F(4)=
27С;
функция
непрерывна,
если
27С
=1,
откуда получаем С=1/27.
График
F(x):
-
Находим
вероятности попаданий в указанные
интервалы
:
Если задана
функция распределения, то вероятность
попадания случайной величины в
заданный интервал подсчитывается по
известной формуле:
![]()
P(-7<X<2)
= F(2) – F(-7) = C(2-1)3
– 0 = 1/27.
P(1<X<3)
= F(3) – F(1) = C(3-1)3
– 0 = 8/27.
P(2<X<7)
= F(7) – F(2) = 1 – C(2-1)3
= 1 – 1/27 = 26/27.
P(X<2,5)
= P(-<X<2,5)
= F(2,5) – F(-)
= C(2,5-1)3
– 0 = 0,125.
P(X>1,5)
= P(1,5<X<+)
= F(+)
– F(1,5) = 1 – C(1,5-1)3
= 0,9954.
P(-4<X<40) = F(40) –
F(-4) = 1 – 0 = 1.
В
последнем случае
все
возможные значения случайной величины
лежат внутри интересующего нас
интервала, поэтому попадание в этот
интервал – достоверное
событие
и вероятность его равна 1.
-
Находим
плотность
распределения
случайной величины X
. По
определению, это первая производная
функции распределения.
f(x)
= F(x).
На разных
участках функция распределения задана
различными выражениями. Поэтому и
производная будет на разных участках
различной:
при
x
1 f(x)
= (0)
= 0.
при
1<x
<4
f(x)
= [C(x-1)3]
= 3C(x-1)2
= (x-1)2
/9.
при
4<x
f(x)
= (1)
= 0.
![]()
График
плотности распределения:
Когда мы проводим
наблюдения над случайной величиной, мы
можем обнаружить, что одни возможные
значения появляются чаще, другие реже.
Т.е., у одних значений вероятность
появления больше, у других меньше.
П
римеры:
-
Опыт
– бросание кубика.
Случайная
величина
Х
– выпавшее число очков.
Возможные
значения {1,
2, 3, 4, 5, 6 }.
-
Опыт
– трехкратное бросание монеты.
Случайная
величина
Х
–число выпавших гербов .
Возможные
значения { 0, 1, 2, 3 }.
-
Опыт
– лекция по теории вероятностей.
Случайная
величина
Х
– число присутствующих студентов.
Возможные
значения { 0, 1, 2, …, N }.
-
Опыт
– работа банковского служащего в
течение часа.
Случайная
величина
Х
– число обслуженных клиентов.
Возможные
значения { 0, 1, 2, …, N }.
О3
:Законом
распределения вероятностей случайной
величины Х
(дальше
везде
будем
говорить кратко
– Законом
распределения)
называется
всякое правило, устанавливающее
соответствие между
возможными значениями
случайной величины и
вероятностями
того, что она примет эти значения.
Это соответствие можно устанавливать
по-разному, в зависимости от того, с
какой случайной величиной мы работаем,
с дискретной
или с непрерывной.
Существуют три способа задания закона
распределения, которые мы далее по
очереди подробно рассмотрим.
Сейчас мы только перечислим их и отметим
главное: если закон распределения задан
(любым из этих способов) то мы можем
прогнозировать поведение случайной
величины. Точно предсказать
до опыта, какое именно значение примет
случайная величина, мы не можем в
принципе, но зато мы сможем подсчитывать
вероятность того, что она
примет то или иное значение, попадет в
интересующий нас интервал.
Способы
задания закона распределения:
-
Ряд
распределения; -
Функция
распределения
F(x)
(
иногда
ее еще называют
интегральная
Функция распределения)
-
Плотность
распределения
f(x)
(ее
еще называют также
дифференциальная
Функция распределения )
Следующая
схема показывает, когда применяется
каждый из этих способов:

Изменить примеры
Непрерывная случайная величина
Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.
Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).
Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $arcsin$ и $arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.
Примеры для других НСВ: Нормальный закон, Равномерный закон, Показательный закон.
Лучшее спасибо – порекомендовать эту страницу
Примеры решений
Задача 1. Случайная величина X задана дифференциальной функцией распределения
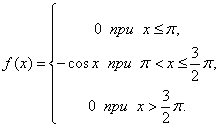
1) Определить вероятность попадания случайной величины X в интервал $[pi, 5/4 pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.
Задача 2. Случайная величина X задана плотностью вероятности:
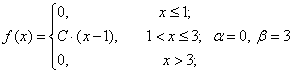
Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α < X < β);
д) построить графики f(x) и F(x).
Задача 3. Случайная величина Х задана функцией распределения F(x).
А) является ли случайная величина Х непрерывной?
Б) имеет ли случайная величина Х плотность вероятности f(X)? Если имеет, найти ее.
В) постройте схематично графики f(X) и F(X).
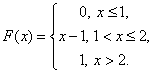
Задача 4. Дана функция распределения F(x) непрерывной случайной величины X.
1. Найти значения параметров a,b
2. Построить график функции распределения F(x)
3. Найти вероятность P(α < X < β)
4. Найти плотность распределения p(x) и построить ее график.
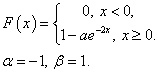
Задача 5. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: f(t)=2e-2t при t ≥ 0 и f(t)=0 при t<0.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 6. Функция распределения вероятностей случайной величины $X$ имеет вид:
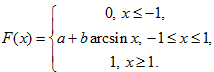
А) найти $a$ и $b$;
Б) найти плотность $f(x)$;
В) нарисовать график $F(x)$;
Г) нарисовать график $f(x)$;
Д) найти $M[X]$;
Е) найти $D[X]$.
Задача 7. Функция распределения вероятностей случайной величины $X$ имеет вид:
$$F(x)=A+B arctan (x/2), -infty lt x lt infty $$ (закон Коши).
А) определить постоянные $A$ и $B$;
Б) найти плотность распределения вероятностей
В) найти $P(-1 lt X lt 1)$;
Г) нарисовать график $F(x)$;
Д) нарисовать график $f(x)$.
Задача 8. Случайная величина $X$ имеет распределение Парето с плотностью вероятности $f(x)=4/23(23/x)^5$
при $23 le x$ и $f(x)=0$ при $x lt 23$.
Найдите $M(X)$ и $P(23lt X lt 27)$.
Задача 9. Непрерывная случайная величина задана интегральной функцией (функцией распределения) $F(x)$. Найти:
А) вероятность попадания случайной величины $X$ в интервал $(a;b)$.
Б) дифференциальную функцию (функцию плотности вероятностей) $f(x)$.
В) математическое ожидание, дисперсию и среднее квадратическое отклонение величины $X$.
Г) построить графики функций $F(x)$ и $f(x)$.
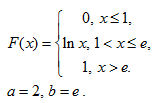
Задача 10. Случайная величина $X$ подчинена закону Лапласа $p(x)=acdot e^{-lambda |x|}$, $lambda gt 0.$ Найти $a$, $M(x)$, $D(x)$ и $F(x)$. Построить графики $p(x)$ и $F(x)$.
Задача 11. Случайная величина $X$ задана функцией распределения $F(x)$. Найти:
5) дифференциальную функцию $f(x)$ (плотность распределения),
6) математическое ожидание $M(X)$, дисперсию $D(X)$, среднее квадратическое отклонение $sigma(X)$.
7) Моду $Mo$ и медиану $Me$,
8) $P(1/2 lt X lt 2).$
Построить графики функции и плотности распределения.
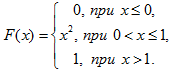
Задача 12. Случайная величина $Х$ подчинена закону Симпсона (закону равнобедренного треугольника) на участке от $-a$ до $+a$.
а) Написать выражение для плотности распределения.
б) Построить график функции распределения.
в) Определить числовые характеристики случайной величины Х.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
2.4.3. Функция ПЛОТНОСТИ распределения вероятностей
или дифференциальная функция распределения. Она представляет собой производную функции распределения: ![]() .
.
Примечание: для дискретной случайной величины такой функции не существует
В нашем примере:
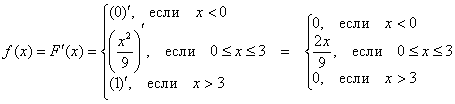
то есть, всё очень просто – берём производную от каждого куска, и порядок.
Но настоящий порядок состоит в том, что несобственный интеграл от ![]() с пределами интегрирования от «минус» до «плюс» бесконечности:
с пределами интегрирования от «минус» до «плюс» бесконечности:
![]() – равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то
– равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то ![]() – не является функцией распределения (несмотря на какие бы то ни было другие признаки).
– не является функцией распределения (несмотря на какие бы то ни было другие признаки).
Проверим «подлинность» наших функций. Если случайная величина ![]() принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности, делим интеграл на 3 части:
принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности, делим интеграл на 3 части:

Совершенно понятно, что левый и правый интегралы равны нулю и нам осталось вычислить средний интеграл:
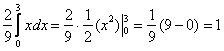 , что и требовалось проверить.
, что и требовалось проверить.
С вероятностной точки зрения это означает, что случайная величина ![]() достоверно примет одно из значений отрезка
достоверно примет одно из значений отрезка ![]() . Геометрически же это значит, что площадь между осью
. Геометрически же это значит, что площадь между осью ![]() и графиком
и графиком ![]() равна единице, и в данном случае речь идёт о площади треугольника
равна единице, и в данном случае речь идёт о площади треугольника ![]() . Сторона
. Сторона ![]() является фрагментом прямой
является фрагментом прямой ![]() и для её построения достаточно найти точку
и для её построения достаточно найти точку ![]() :
:
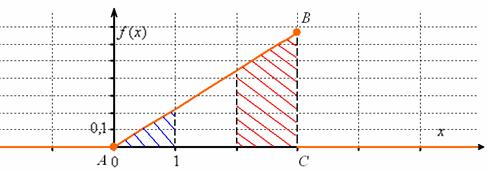
Ну вот, теперь всё наглядно – где бОльшая площадь, там и сконцентрированы более вероятные значения.
Так как функция плотности «собирает под собой» вероятности, то она неотрицательна ![]() и её график не может располагаться ниже оси
и её график не может располагаться ниже оси ![]() . В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).
. В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).
Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина ![]() примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
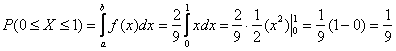 (синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка
(синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка ![]() ;
;
![]() (красная площадь) – вероятность того, что случайная величина примет значение из отрезка
(красная площадь) – вероятность того, что случайная величина примет значение из отрезка ![]() .
.
По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам и полуинтервалам, в частности:
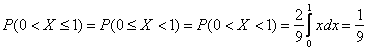
Этим же объяснятся аналогичная «вольность» с функцией ![]() .
.
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ![]() ?
?
А дело в том, что во многих задачах непрерывная случайная величина ИЗНАЧАЛЬНО задана функцией ![]() плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию
плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию ![]() (с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:
(с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:
Задача 105
Непрерывная случайная величина ![]() задана своей функцией распределения:
задана своей функцией распределения:
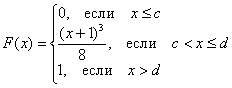
Найти значения ![]() и функцию
и функцию ![]() . Проверить, что
. Проверить, что ![]() действительно является функцией плотности распределения. Вычислить вероятности
действительно является функцией плотности распределения. Вычислить вероятности ![]() . Построить графики
. Построить графики ![]() .
.
Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце книги.
Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы:
1) когда дана функция ![]() , 2) когда дана функция
, 2) когда дана функция ![]() .
.
В первом случае не составляет особых трудностей отыскать функцию плотности распределения – почти всегда производные не то что простЫ, а примитивны (в чём мы только что убедились). Но вот когда НСВ задана функцией ![]() , то нахождение функции распределения – есть более кропотливый процесс:
, то нахождение функции распределения – есть более кропотливый процесс:
Задача 106
Непрерывная случайная величина ![]() задана функцией плотности распределения:
задана функцией плотности распределения:
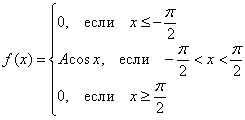
Найти значение ![]() и составить функцию распределения вероятностей
и составить функцию распределения вероятностей ![]() . Вычислить
. Вычислить ![]() .
.
Построить графики ![]() .
.
Решение: найдём константу ![]() . Это классика (в подавляющем большинстве задач вам не предложат готовую функцию плотности). Используем свойство
. Это классика (в подавляющем большинстве задач вам не предложат готовую функцию плотности). Используем свойство ![]() .
.
В данном случае:

На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
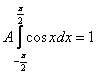 (*)
(*)
Пользуясь чётностью подынтегральной функции, вычислим интеграл:
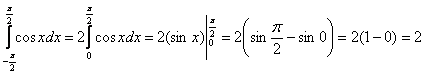 и подставим результат в уравнение (*):
и подставим результат в уравнение (*):
![]() , откуда выразим
, откуда выразим ![]()
Таким образом, функция плотности распределения:
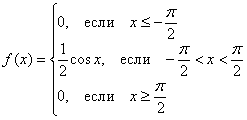
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
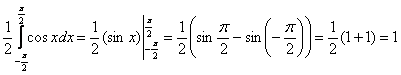 , отлично.
, отлично.
Обратите внимание, что только при ![]() и только при этом значении предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале
и только при этом значении предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале ![]() , т.е. условие неотрицательности действительно выполнено. Доверяй условию, да проверяй 😉 Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
, т.е. условие неотрицательности действительно выполнено. Доверяй условию, да проверяй 😉 Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
Теперь начинается самое интересное. Функции распределения вероятностей – есть интеграл:
![]()
Так как ![]() состоит из трёх кусков, то решение разобьётся на 3 шага:
состоит из трёх кусков, то решение разобьётся на 3 шага:
1) На промежутке ![]() , поэтому:
, поэтому: ![]()
2) На интервале ![]() , и мы прицепляем следующий вагончик:
, и мы прицепляем следующий вагончик:
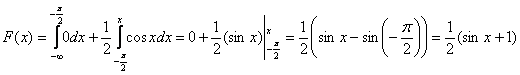
При подстановке верхнего предела интегрирования можно считать, что вместо «икс» мы подставляем «икс». Если же возник вопрос с пределом нижним, то вспоминаем график синуса либо его нечётность: ![]() .
.
3) И, наконец, на ![]() , и детский паровозик отправляется в путь:
, и детский паровозик отправляется в путь:

Внимание! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения 😉 К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. И такой пример я обязательно разберу ниже.
Записываем наши достижения под единую скобку:
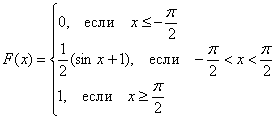
С высокой вероятностью всё правильно, но, тем не менее, устно возьмём производную: 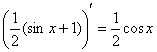 , а также «прозвоним» точки «стыка»:
, а также «прозвоним» точки «стыка»:
![]()
Правильность решения можно проконтролировать и в ходе построения графика, но, во-первых, он не всегда требуется, а во-вторых, до сего момента можно успеть «наломать дров». Ибо вероятности попадания чаще находят с помощью функции распределения:
![]()
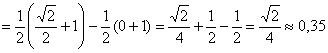 – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из промежутка
примет значение из промежутка ![]()
Второй способ состоит в вычислении интеграла:
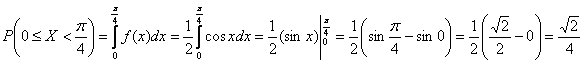 что, кстати, не труднее. И проверочка заодно получилась.
что, кстати, не труднее. И проверочка заодно получилась.
Выполним чертежи. График ![]() представляет собой
представляет собой косинусоиду, сжатую вдоль ординат в 2 раза. Тот редкий случай, когда функция плотности непрерывна:
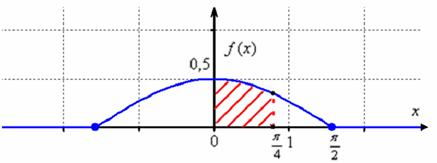
Значение ![]() численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала
численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала ![]() . Заметьте, что значения
. Заметьте, что значения ![]() по условию, невозможны.
по условию, невозможны.
Осталось изобразить функцию распределения. График ![]() представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на
представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на ![]() вверх:
вверх:
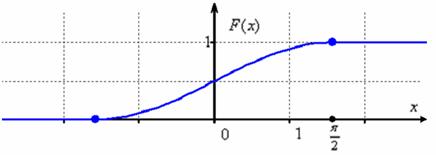
В принципе, тут можно было не заморачиваться преобразованием графиков, а найти несколько опорных точек и догадаться, как выглядит кривая (тригонометрическая таблица в помощь). Но «любительский» подход чреват тем, что график получится принципиально не точным. Так, в нашем примере в точке ![]() существует перегиб графика функции
существует перегиб графика функции ![]() , и велик риск неверно отобразить его выпуклость / вогнутость.
, и велик риск неверно отобразить его выпуклость / вогнутость.
Чертежи желательно расположить так, чтобы оси ординат (вертикальные оси) лежали ровненько одна под другой. Это будет хорошим тоном.
И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:
Задача 107
Задана плотность распределения вероятностей непрерывной случайной величины ![]() :
:
![]()
Требуется:
1) определить коэффициент ![]() ;
;
2) найти функцию распределения ![]() ;
;
3) построить графики ![]() ;
;
4) найти вероятность того, что ![]() примет значение из промежутка
примет значение из промежутка ![]()
и задачка поинтереснее:
Задача 108
Непрерывная случайная величина ![]() задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
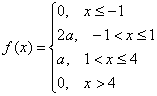
Найти значение ![]() и построить график плотности распределения. Найти функцию распределения вероятностей
и построить график плотности распределения. Найти функцию распределения вероятностей ![]() и построить её график. Вычислить вероятность
и построить её график. Вычислить вероятность ![]() .
.
Дерзайте! Свериться с решением можно внизу книги.
Следует отметить, что все эти задачи реально предлагают студентам-заочникам, и поэтому я не предлагаю вам ничего необычного.
И в заключение параграфа обещанные случаи с несобственными интегралами:
Задача 109
Непрерывная случайная величина ![]() задана своей плотностью распределения:
задана своей плотностью распределения:
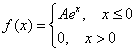
Найти коэффициент ![]() и функцию распределения
и функцию распределения ![]() . Построить графики.
. Построить графики.
Решение: по свойству функции плотности распределения:
![]()
В данной задаче ![]() состоит из 2 частей, поэтому:
состоит из 2 частей, поэтому:
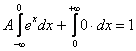
Правый интеграл равен нулю, а вот левый – есть «живой» несобственный интеграл с бесконечным нижним пределом:
![]()
Таким образом, наше уравнение превратилось в готовый результат:
![]()
и функция плотности:
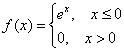
Функция ![]() , как нетрудно понять, отыскивается в 2 шага:
, как нетрудно понять, отыскивается в 2 шага:
1) На промежутке ![]() , следовательно:
, следовательно:
![]() – вот такая вот у нас замечательная экспонента. Как птица Феникс.
– вот такая вот у нас замечательная экспонента. Как птица Феникс.
2) На интервале ![]() и:
и:
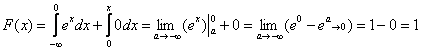 , что и должно получиться.
, что и должно получиться.
Для построения графиков найдём пару опорных точек: ![]() и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:
и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:

Заметьте, что теоретически случайная величина ![]() может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при
может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при ![]() .
.
В соответствующей статье сайта я рассмотрел ещё более интересный пример с функцией ![]() , где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.
, где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.
 2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?
2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?
 2.4.2. Вероятность попадания в промежуток
2.4.2. Вероятность попадания в промежуток
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
