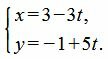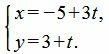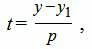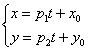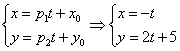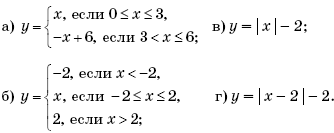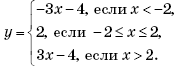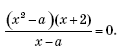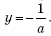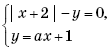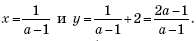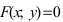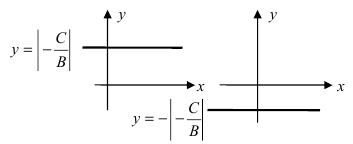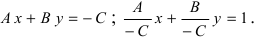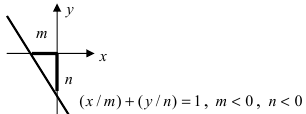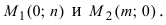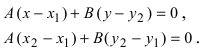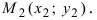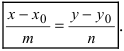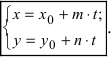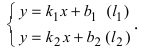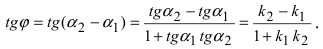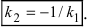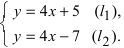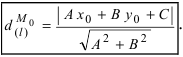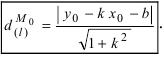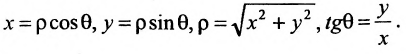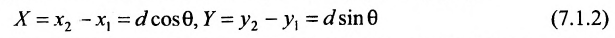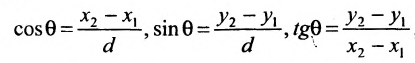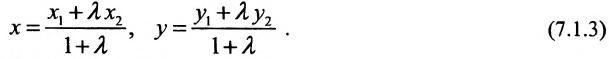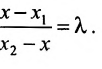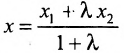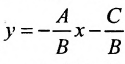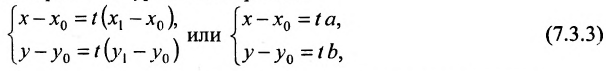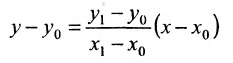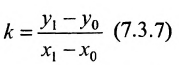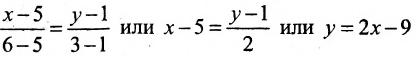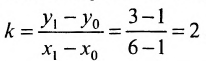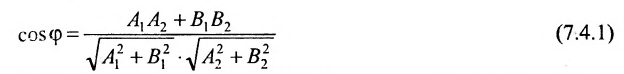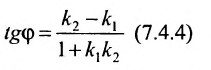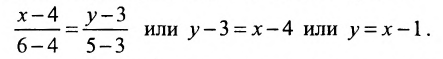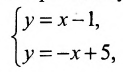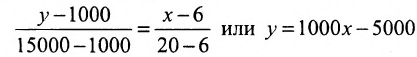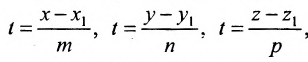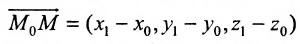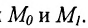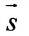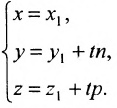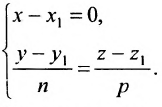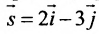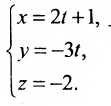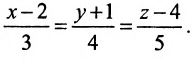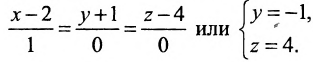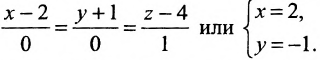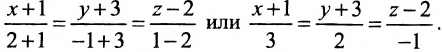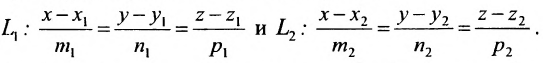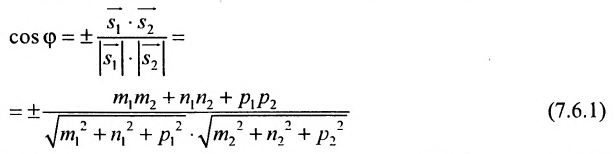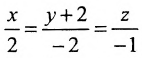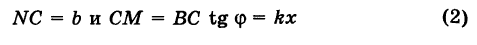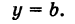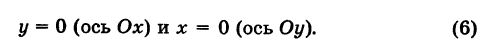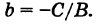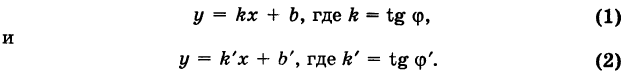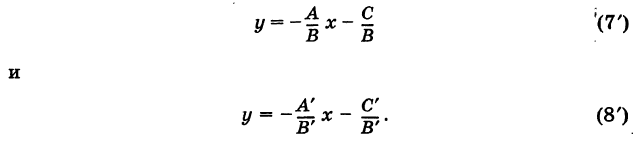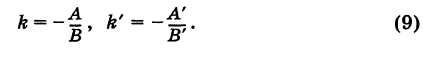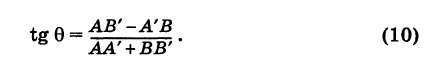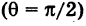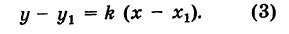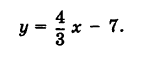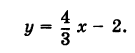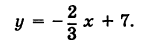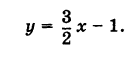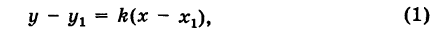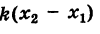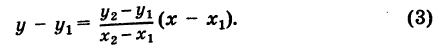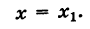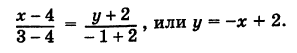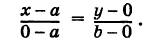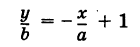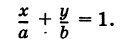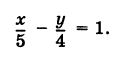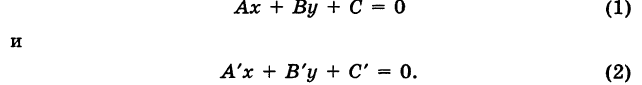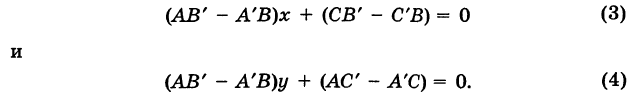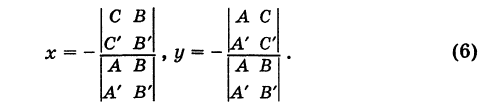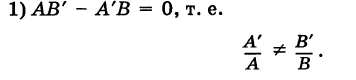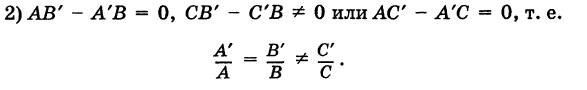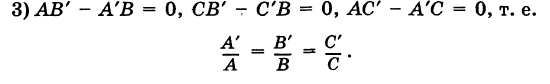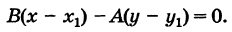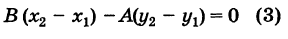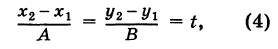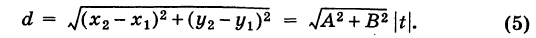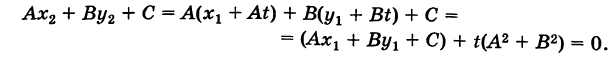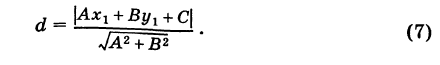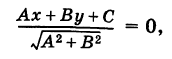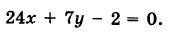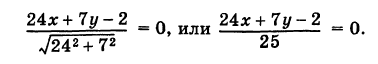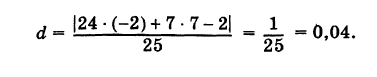Параметрическое уравнение прямой на плоскости
В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.
Параметрическое уравнение прямой L на плоскости представляется следующей формулой:
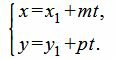 |
(1) |
Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.
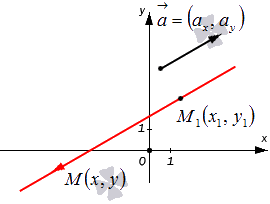
Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M1(x1, y1) при t=1, получим точку M2(x1+m, y1+p).
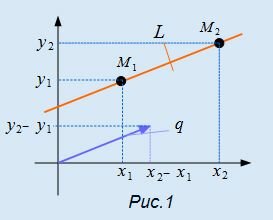
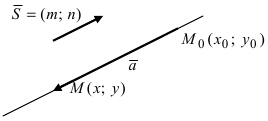
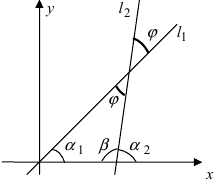
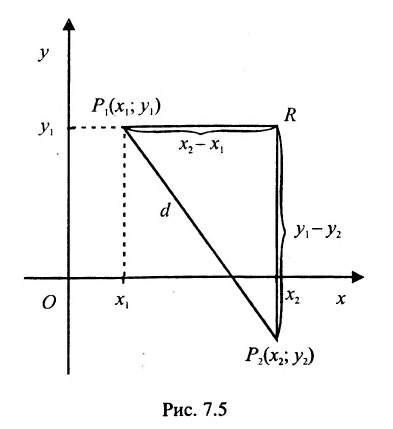
Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q=<m, p>, вычисляя разности соответствующих координатов точек M1 и M2: m=x2−x1, p=y2−y1(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).
Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x2−x1, p=y2−y1 в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M1(x1, y1) и M2(x2, y2):
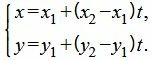 |
(2) |
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить параметрическое уравнение прямой.
Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
Пример 2. Прямая проходит через точки M1=(−5, 2) и M2=(−2, 3). Построить параметрическое уравнение прямой.
Решение. Воспользуемся формулой (2). Подставим координаты точек M1 и M2 в уравнение (2):
Упростим полученное уравнение:
Приведение параметрического уравнения на плоскости к каноническому виду
Выразим параметр t в (1) через переменные x и y:
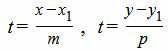 |
(3) |
Из выражений (3), можем записать каноническое уравнение прямой на плоскости:
 . . |
(4) |
Обратное преобразование смотрите здесь.
Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:
Привести данное уравнение прямой к каноническому виду.
Решение: Выразим параметр t через переменные x и y:
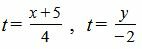 |
(5) |
Из выражений (5), можем записать:
Приведение параметрического уравнения на плоскости к общему виду
Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:
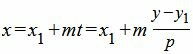 |
(6) |
Умножим обе части уравнения (6) на p и группируем элементы уравнения:
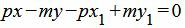 . . |
(7) |
Сделаем обозначения: A=p, B=−m, C=−px1+my1. Тогда получим общее уравнение прямой:
Обратное преобразование смотрите здесь.
Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:
 |
(9) |
Привести данное уравнение прямой к общему виду.
Решение: В уравнении (9) имеем: x1=−5, y1=0, m=4, p=−2. Подставим эти значения в формулу (7):
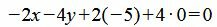 |
(10) |
Упростив выражение (10) получим общее уравнение прямой (9):
Параметрические уравнения прямой на плоскости: описание, примеры, решение задач
Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.
Вывод параметрических уравнений прямой на плоскости
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
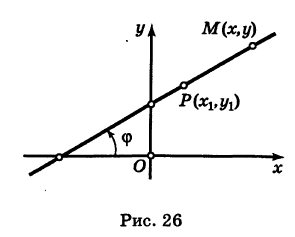
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.
Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x – x 1 , y – y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x – x 1 , y – y 1 ) и a → = ( a x , a y ) являются коллинеарными.
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x – x 1 , y – y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:
M 1 M → = λ · a → , где λ – некоторое действительное число.
Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.
В координатной форме оно имеет вид:
M 1 M → = λ · a → ⇔ x – x 1 = λ · a x y – y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ
Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ
Составление параметрических уравнений прямой на плоскости
Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.
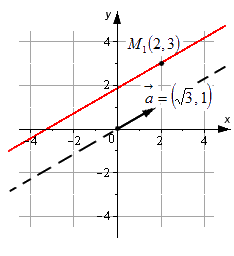
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .
Решение
На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ
Ответ: x = 2 + 3 · λ y = 3 + λ
Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .
К примеру, нам заданы направляющий вектор прямой a → = ( 2 , – 1 ) , а также точки М 1 ( 1 , – 2 ) и М 2 ( 3 , – 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = – 2 – λ или x = 3 + 2 · λ y = – 3 – λ .
Следует обратить внимание и на такой факт: если a → = ( a x , a y ) – направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .
Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.
Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = – 2 – 5 · λ . Тогда a → = ( 2 , – 5 ) – направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · – 5 ) = 2 μ , – 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор – 2 · a → = ( – 4 , 10 ) , ему соответствует значение μ = – 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 – 4 · λ y = – 2 + 10 · λ .
Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.
Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x – x 1 a x = y – y 1 a y .
Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y ⇔ x – x 1 a x = y – y 1 a y
При этом не должно смущать, если a x или a y будут равны нулю.
Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = – 2 – 4 · λ к каноническому уравнению.
Решение
Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = – 2 – 4 · λ
Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = – 2 – 4 · λ ⇔ λ = x – 3 0 λ = y + 2 – 4
Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:
x – 3 0 = y + 2 – 4
Ответ: x – 3 0 = y + 2 – 4
В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y ⇔ x – x 1 a x = y – y 1 a y ⇔ ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ A x + B y + C = 0
Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = – 1 + 2 · λ y = – 3 · λ
Решение
Для начала осуществим переход к каноническому уравнению:
x = – 1 + 2 · λ y = – 3 · λ ⇔ λ = x + 1 2 λ = y – 3 ⇔ x + 1 2 = y – 3
Полученная пропорция идентична равенству – 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: – 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .
Ответ: 3 x + 2 y + 3 = 0
Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.
Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.
Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x – x 1 a x = y – y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :
x – x 1 a x = y – y 1 a y = λ ⇔ λ = x – x 1 a x λ = y – y 1 a y
Разрешим полученные уравнения относительно переменных x и y :
x = x 1 + a x · λ y = y 1 + a y · λ
Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x – 2 5 = y – 2 2
Решение
Приравняем части известного уравнения к параметру λ : x – 2 5 = y – 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x – 2 5 = y – 2 2 = λ ⇔ λ = x – 2 5 λ = y – 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ
Ответ: x = 2 + 5 · λ y = 2 + 2 · λ
Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.
Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x – 3 y – 3 = 0 .
Решение
Заданное общее уравнение преобразуем в уравнение канонического вида:
4 x – 3 y – 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4
Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:
x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = – 1 3 + 4 · λ
Ответ: x = 3 · λ y = – 1 3 + 4 · λ
Примеры и задачи с параметрическими уравнениями прямой на плоскости
Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.
- В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.
Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.
Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 – 1 6 · λ y = – 1 + 2 · λ при λ = 3 .
Решение
Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 – 1 6 · 3 y = – 1 + 2 · 3 ⇔ x = 1 1 2 y = 5
Ответ: 1 1 2 , 5
Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .
Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.
Заданы точки М 0 ( 4 , – 2 ) и N 0 ( – 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = – 1 – 1 2 · λ .
Решение
Подставим координаты точки М 0 ( 4 , – 2 ) в заданные параметрические уравнения:
4 = 2 · λ – 2 = – 1 – 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .
Далее по аналогии проверим заданную точку N 0 ( – 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:
– 2 = 2 · λ 1 = – 1 – 1 2 · λ ⇔ λ = – 1 λ = – 4
Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( – 2 , 1 ) .
Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.
- В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.
Пример 8
Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y – 3 – 1 .
Решение
По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y – 3 – 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y – 3 – 1 , который запишем в виде: a → = ( 2 , – 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( – 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 – λ
Ответ: x = 1 2 + x · λ y = 2 3 – λ .
Задана точка М 1 ( 0 , – 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .
Решение
В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , – 2 ) . Запишем требуемые параметрические уравнения прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = – 7 + ( – 2 ) · λ ⇔ x = 3 · λ y = – 7 – 2 · λ
Ответ: x = 3 · λ y = – 7 – 2 · λ
- В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.
Пример 10
Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 – 3 4 · λ y = – 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.
Решение
Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:
x = 1 – 3 4 · λ y = – 1 + λ ⇔ λ = x – 1 – 3 4 λ = y + 1 1 ⇔ x – 1 – 3 4 = y + 1 1 ⇔ ⇔ 1 · x – 1 = – 3 4 · y + 1 ⇔ x + 3 4 y – 1 4 = 0
Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 – 3 4 · λ y = – 1 + λ имеет координаты 1 , 3 4 .
Параметрическое задание кривой















Параметрическое задание кривой
- Кривая параметрическая Н°1.Подход к делу problem. So до сих пор мы рассматривали только 2 вида назначений кривых: уравнение v = f (x) (явная задача) или уравнение F (x, y)= O (неявная задача)).Однако теоретическая механика очень естественно приводит к различным видам линий assignments. In дело в том, что
установка движения точки-это средство нахождения положения (то есть координат) любого момента времени t. Чтобы полностью определить движение точки, определите линию, на которой будет находиться точка move. So, в этом примере линии даны с использованием
So например, эквационный х = 2Т г = 3Т-2(1) Людмила Фирмаль
2 равенств (I).Конечно, очень легко получить более знакомые задачи в той же линии. Именно так. Для любого момента x 3x /будет t = — q, t y =-2. Это соединение X и y обеспечивает явное определение линии*).Видно, что эта задача получается путем исключения времени t из Формулы (1). В рассматриваемом
примере, тот факт, что переменная T показывает время не играет никакой роли. Например, предположим, что следующие X и y зависят от вспомогательных переменных: х = Т-ФЛ, г = т Изменение его даст вам различные точки(.x, комбинация которых состоит из нескольких линий. значение t обозначается равенством t = x-1 с соответствующим значением x, поэтому y =(x-I) 1 для
- любой точки линии, и я получил явную задачу линии. Из этого видно, что вы обрабатываете 1 пару болтов. Чтобы суммировать вышесказанное, пара уравнений Где t-вспомогательная переменная, определяющая lnnnu. Способ определения этой линии называется параметрическим, а переменная t называется
параметром. за исключением t, вы получаете нормальное (явное или неявное) уравнение для той же строки. Замечание. Если функция Людмила Фирмаль
и последовательным в интервале[i, b]), является непрерывной кривой, поскольку она также может Параметрические уравнения для окружностей и эллипсов. Рассмотрим окружность с радиусом R, центрированную вокруг начала координат
(рис.181).Положение любой точки M в этой окружности полностью определяется установкой угла f, который образуется осью Ox и радиусом OM. It естественно выразить координаты x и y точки M под этим углом. Из рисунков это сразу понятно (2) х = р COS в ТТ г = РС НТ. Эти уравнения (*) являются параметрическими
уравнениями окружности. Параметр T может быть изменен с-oo на — | — oo, но если вы хотите получить каждую точку круга по 1 разу, достаточно пройти t через зазор. Однако, это более удобно для обработки закрытых пробелов. Так, т, как правило,
изменяется в пределах 0 ^ / ^ 2ir, но точка с получает в 2 раза. T= 0 и в = 2ir. Чтобы получить нормальное уравнение окружности, необходимо исключить параметр T из (2).Это проще всего, если вы возьмете уравнение (2) на 2 квадрата и добавите результат. Очевидно, это приводит к известному уравнению Найти
параметрическое уравнение эллипса (3) Полезно помнить, что он получается из круга * * + > ■ = A (4)рисунок 181. Имеют диаметр с большой осью эллипса, иногда используют сжатие、 То есть любая точка M в эллипсе(3) берется из точки N в окружности (4). Б Ордината точки Н В соответствии с вышеизложенным
параметрическое уравнение окружности(4) имеет вид x = acos/, ^ = asin/.Но тогда понятно, что параметрическое уравнение (3) эллипса получается умножением. форма ординаты y имеет вид) (5) * = acosf, г = БС НТ. Чтобы получить все точки овала, достаточно
изменить Т выпускного вечера. Жуткий 0 ^ t ^кроме того, каждая точка эллипса, кроме точки (a, 0), получается только 1 раз, а точки(a, 0) — 2 раза (t = 0 и t = 2k).Если мы разделим первое уравнение (5) на a, а затем разделим 2-е уравнение на b, то полученное уравнение будет добавлено на 2 и станет каноническим уравнением эллипса(3).
Сравнение параметрических уравнений окружности и эллипса дает удобный метод построения любого числа точек в эллипсе. То есть, пара уравнений х-acoet, у = грех Т(6) U определяет окружность с радиусом A вокруг начала координат и пару уравнений х = б сое т, у = B грех Т(7) — Окружность b с тем же центром и радиусом; чтобы получить точку (l, y), как показывает уравнение (5), p / 82.Если
вы лежите на овале, вам нужно найти x Используйте первое выражение(6) и 2-е выражение (7) с y. но эти xn-y легко найти графически, так как в формулах (6) и (7) параметром T является угол наклона радиус-вектора точки относительно оси Ox. So, чтобы составить точку M (q, y) эллипса (5), нарисуйте окружность (6) и (7)
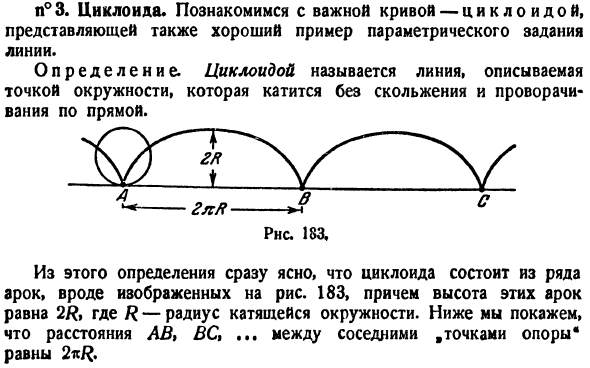
и нарисуйте луч на оси Ox под углом t от начала координат. Найдите точки A и B пересечения этого луча и ранее упомянутой окружности и проведите через них прямую линию, параллельную оси, вы получите точку M (см. Рисунок 182).П°3.Циклоида * важные
кривые-давайте познакомимся с циклоидой. Это также хороший пример параметрического определения линии. Определение циклоида представляет собой линию, которая представлена точкой окружности, которая катится без скольжения или вращения Из этого определения сразу видно, что циклоида состоит из ряда дуг, как
показано на рисунке 1. 183, высота этих арок равна 2R. R-радиус окружности. Ниже расстояние между соседними точками разворотаAB, BC,…равно 2π/?Это значение по умолчанию. Найдите параметрические уравнения циклоиды. В качестве оси Ox возьмите прямую линию, по которой катится круг, и для начала координат
возьмите положение точки M, которая представляет собой циклоиду острия в этой точке. Эта точка находится на оси Ox. Нарисуйте этот момент как первый момент, вращающийся круг в первый момент, а затем второй. t представляет собой угол, образованный в момент t радиусом вращающейся окружности, направленной
к точке A окружности, которая касается точки I и оси Ox, представляющей циклоиду. (Рисунок 184) радиус CXM и u ° С / а возьмем этот угол т. 184. Попробуйте параметр 8a Через него отрегулируйте точки x и y м-циклоиды. Что касается координат Y, то это довольно просто. г => ВМ = объявление = ОБК-CjZ)= /? — R cos t.
(8) Чтобы найти абсциссу X, нужно рассмотреть эквивалентность отрезка OA и дуги AM. OA = AM. (9 )) При таком равенстве окружность не будет скользить или вращаться. Следующий метод проверки эквивалентности очень очевиден(9): представьте себе катящийся круг, выполненный в виде деревянного кольца. Накройте этот обруч лентой, которая не растягивается, прибив ее правый край гвоздем
к точке O оси Ox, а левый край-к обручу. При вращении обруча лента начинает растекаться по оси Ox, и в момент t отсечение оси OA закрывается той частью ленты, которая упала вниз. С дугой AM обруч. Это*) доказывает(9). еще проще: t-значение угла AC% M, так как это Радиан、 AM = Rt Так… x = OB = OA-BA = AM-MD = Rt-Rsint (10) Если
сравнить (8)и(10), то получим параметрическое уравнение циклоиды х = р(т-Син т), г = р (- стоимость). Параметр Т может изменяться от-ОО до-Е-ОО. Пересечение начала координат и ближайших к нему справа циклоид соответствует значению Ox = t * 2.Это происходит потому, что круг качения приобретается после 1 rotation. In в этом случае
t будет n; = 2nR. In кроме того, из (11) видно, что координаты (π/,, 2/) находятся в высшей точке соответствующего cycloid. To будьте осторожны невозможно представить Y в качестве одной из основных функций Икс. И от x до y возможно| f = Arccos ^ l, но результат Формула очень трудоемкая. Параметрическое уравнение
проще. в N°4.Эвольвента circle. In в теории зацепления используется кривая, называемая эвольвентой окружности. Эвольвента окружности определения-это линия, которая описывается точкой нити и расстегивается от этой окружности, пока она прочно растянута. Предполагается, что нить неэластична и предварительно обмотана вокруг вышеуказанных кругов. Найти параметрическое
уравнение для эвольвенты circle. To сделайте это, поместите начало координат в центр круга и нарисуйте ось Ox Ноль ноль В тот момент, когда нить еще полностью обмотана вокруг окружности, точка окружности, в которой расположена точка, описывающая эвольвенту. Рисунок 185 эта точка обозначается A. 185 показывает положение потока виртуальной машины в некоторой точке в time. So, здесь B-
точка, в которой нить исчезает из окружности, а M-точка, в которой она описывает эвольвенту. Радиус окружности? Угол наклона оси Ox и Луча OB представлен через t. поскольку нить не является растяжимой、 Отрезок VM равен дуге AB окружности. То есть, BM = RT. обратите внимание, что нить остается прочно натянутой, поэтому она спускается по касательной от окружности. Таким образом,
нить VM перпендикулярна радиусу органического вещества. Поэтому углы AOB и MBD равны углам, где каждая сторона перпендикулярна друг другу. Следовательно,£МБД = T, и из треугольника МВС См = РТ грех ЦБ = стоимость РТ. Теперь вы можете легко найти X и y координаты точки м. Другими словами、 х = ое = ОД + де = ОД-ТСМ = стоимости Р + РТ грех г = ВС = ДК = ДБ-КБ = Р грех Т-РТ стоимость. Рисунок 185.Наконец. х = /?(потому что * — Ф — * грех/),; г = р (т Син-/ Кос Т), (’ Где: 0 f > = » K0(13) В точке M (x, y), соответствующей значению параметра T. To сделайте это, дайте
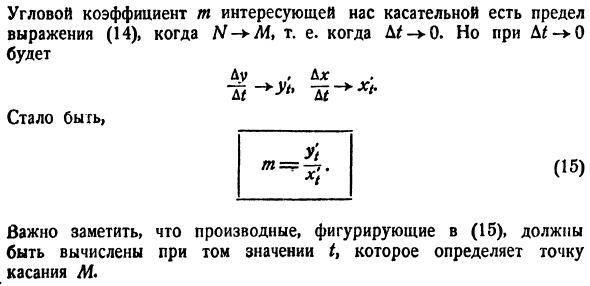
t приращение At и в результате получите ту же самую точку кривой AfCtf-J-A * » Y + AC) (13).Угловой коэффициент Т * Секущий MN равен или равен Важно отметить, что производная, фигурирующая в (15) , должна быть рассчитана для величины t, определяющей контакт M. Угловой коэффициент m интересующего тангенса является
пределом формулы (14) для N — + M, то есть, но так как D * — > 0 Вы будете Работать ДД: (15 )) Так… Образцы. Нарисуйте касательную к кривой + г = Тл-7т(16) Очки*)А!(2). Решение. Координаты точки M определяются из(16). xi = 17, y%=2.In сложение, x = bP—4/, y = 4P-7.So, t = 2 — Это X / = 20, yt = 25, угловой коэффициент Желаемый тангенс. Форма искомого уравнения имеет вид y-2 = 4 (l-17> Замечание.
Приведенная выше строка g:=?( * ), Y =φ (f), функция равна (t), φ (/).Если эти функции не только непрерывны, но и имеют непрерывные производные от y’0, то, как показывает уравнение (15), кривая имеет определенную касательную в каждой точке, и ее положение непрерывно изменяется с изменением контакта.
Кроме того, указанные касательные никогда не будут параллельны оси Oy. Учитывая, что координаты x и y полностью равны, линии x =
.Где f (/j u f ( / ) имеет непрерывную производную、 а В частности, под это определение подпадает линия y = f ( * ), где f (x) имеет непрерывную производную. Где роль параметра T-абсцисса ш=■»+*?> ми- Теперь зададим следующие общие вопросы: пусть
x и y зависят от вспомогательных переменных t, как показано в (13). в первом выражении (13) обозначим t из x, а затем присвоим его 2-му выражению, вы увидите, что y является функцией x, то есть y = f(x).Попробуйте найти производную этой функции. Для этого достаточно вспомнить, что интересующей нас производной является только угловой коэффициент касательной прямой y = / ( * ),
а ее параметрическим уравнением является уравнение (13).Таким образом, она задается формулой(15). Чтобы правильно понять это важное выражение, следует помнить, что точка дифференцирования t справа от (17) является значением параметра, и согласно формуле x = y (t) она соответствует точке дифференцирования x, где Y’x находится. Соотношения(17) легко получить с помощью чисто формальных
вычислений. dypy / ДТ Вау, х]’ Затем попробуйте найти 2-ю производную yx той же функции y = f (x).Это легко сделать, используя формулу (17).То есть он временно представляет y’X с Z. А затем… ** ух-з» (17) Значение (18) Однако, поскольку Z = yx = — m、 / ГМ-ГМ Узнайте, наконец, из (18)и (19) Образцы. Установите вогнутое направление
кривой х =(* + 3Т + л> г = 2Т * — (21) В точке Af (l). Решение. Из (21), x’f = 2t + 3, x? = 2,г = г г! = 12 /.Итак, если t = 1, то это выглядит так:= jc / = 2, y ’ 0, кривая точки M (21) направлена вогнутой поверхностью вверх.





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parametricheskie-uravnenija-prjamoj-na-ploskosti/
http://lfirmal.com/parametricheskoe-zadanie-krivoj/
[/spoiler]
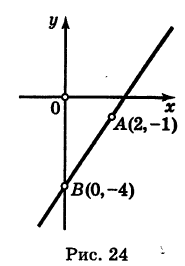
2.4. Параметрические уравнениЯ прямой
Если известна некоторая точка , принадлежащая прямой, и направляющий вектор
этой прямой, то параметрические уравнения данной прямой задаются системой:
В чём смысл? Параметр принимает все значения от «минус» до «плюс» бесконечности и каждому значению параметра соответствует конкретная точка
прямой
Задача 71
Составить параметрические уравнения прямой по точке и направляющему вектору
.
Решение закончилось, не успев начаться:
Как найти точки прямой? Возьмём какое-нибудь значение параметра, например, . Тогда соответствующая точка:
Обратная задача: как проверить, будет ли точка принадлежать данной прямой? Подставим её координаты параметрические уравнения:
Из обоих уравнений следует, что , значит, система совместна (имеет решение) и точка
действительно принадлежит данной прямой.
Рассмотрим более содержательные примеры:
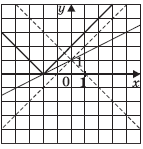
Задача 72
Составить параметрические уравнения прямой
Решение: по условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку. Найдём направляющий вектор:
Теперь нужно найти какую-нибудь точку, принадлежащую прямой, здесь проще всего обнулить «иксовую» координату , тогда:
Составим параметрические уравнения прямой:
Ответ:
И небольшое творческие задание для самостоятельного решения.
Задача 73
Составить параметрические уравнения прямой, если известна принадлежащая ей точка и вектор нормали
Решение и ответ в конце книги.
Укрепляем заложенный геометрический фундамент простейшими задачами с прямой:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Факультативный курс «Линейные уравнения и неравенства с параметрами»
Занятие № 6
Линейная функция и ее график
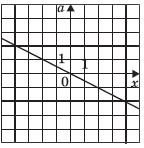
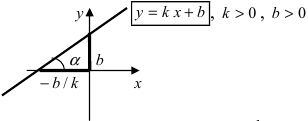
Линейной называется функция, задаваемая уравнением вида y = kx + b, где x — независимая переменная или аргумент, а k и b — произвольные действительные числа. Графиком линейной функции является прямая. Задавая конкретные значения параметров, мы выделяем из множества линейных функций одну или несколько функций, обладающих тем или иным свойством. Множество функций, обладающих указанным свойством, называют семейством функций, а множество их графиков — семейством графиков (семейством прямых).
Упражнение 1. Каким общим свойством будут обладать все графики функций, задаваемых уравнениями вида y = kx – 1?
Упражнение 2. Из множества линейных функций выделите семейство графиков, задаваемых уравнениями вида y = 2x + p.
Итак, задавая значение параметра b, мы выделяем семейство линейных функций, графики которых проходят через точку (0; b). Задавая значение параметра k, мы выделяем семейство линейных функций, графики которых параллельны прямой y = kx.
Упражнение 3. При каком значении k график функции y = kx + 2 проходит через точку A(1; 4), а при каких через точку B(–2; 0)?
Упражнение 4. График функции y = kx + b проходит через точки A(0; –4) и B(3; 5). Найдите значения k и b.
Упражнение 5. График функции y = kx + b проходит через точку B(3; 5) и параллелен графику функции y = 2x. Найдите значения k и b.
Полезно напомнить, что параметр k называют угловым коэффициентом. Если угловые коэффициенты равны, то прямые или параллельны (при b1 ≠ b2), или совпадают (при b1 = b2); если угловые коэффициенты различны — прямые пересекаются.
Упражнение 6. При каких значениях параметра a графики данных функций пересекаются:
а) y = (2a – 1)x и y = (4a + 3)x + 2a;
б) y = ax + 6a и y = ax?
Упражнение 7. При каких значениях параметра a графики данных функций параллельны:
а) y = (3 – a)x + 1 и y = (a – 1)x + 5;
б) y = (a – 3)x + 2a и y = (3 – 2a)x + a;
в) y = (a – 2)x + 6 – a и y = (2a – 3)x + 2a + 3?
Упражнение 8. При каких значениях параметра a графики данных функций совпадают:
а) y = 2ax + 7 и y = 4ax + 7;
б) y = (5a – 3)x + 2a – 1 и y = (a + 1)x + 14 + a;
в) y = (5a – 3)x + 3a и y = (5a + 1)x + 3a?
Упражнение 9. Проанализируйте, как изменяется наклон прямой в зависимости от параметра k, на примере функции y = kx (прямая пропорциональность).
Задание на дом
1. При каких значениях параметра a прямые y = –ax + 2 и будут: пересекаться, совпадать, параллельны?
2. Найдите значения параметра a, при которых прямая y = ax + 2 пройдет через точку пересечения прямых y = 5x – 7 и y = 3x + 1?
3. Постройте графики функций:
а) y = | x |; б) y = | x | + 1; в) y = | x + 1 |.
Занятие № 7
Линейная функция и ее график
Цель этого занятия — познакомить учащихся с «плавающей» и «вращающейся» прямыми, разобрать решение задач с параметрами, где используются эти понятия. Учащиеся 7-го класса более подробно изучают только линейную функцию, а также знакомы с графиками вида y = x2 и y = x3. Однако им еще не знакомы преобразования графиков, а также не известны другие функции. Поэтому, чтобы расширить представление учащихся о графиках, полезно познакомить их с кусочно-заданными функциями и способами построения их графиков и еще раз обратить внимание на понятие области определения функции.
Упражнение 1. Постройте графики функций:
а) y = 1,5x – 2, где –2 ≤ x ≤ 2,
(график — отрезок);
б) y = 1,5x – 2, где x ≤ 2,
(график — луч, идущий влево,
с началом в точке (2; 1));
в) y = 1,5x – 2, где x ≥ –2,
(график — луч, идущий вправо,
с началом в точке (–2; –5)).
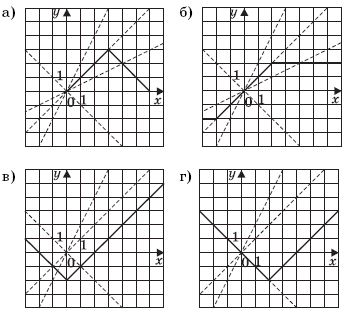
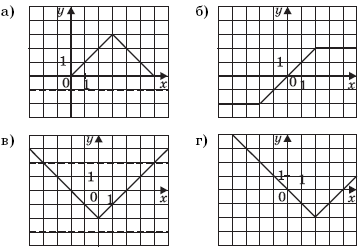
Упражнение 2. Постройте графики кусочно-заданных функций и графики функций, содержащих знак модуля:
а) в) y = | x | – 2;
б) г) y = | x – 2 | – 2.
Далее знакомим учащихся с понятиями «плавающей» и «вращающейся» прямых.
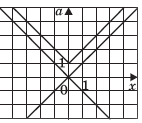
Упражнение 3. Постройте семейство прямых:
а) y = a;
б) y = ax.
Семейство прямых, задаваемых уравнением вида y = a — это прямые, параллельные оси абсцисс («плавающая» прямая). Семейство прямых, задаваемых уравнениями вида y = ax — это прямые, проходящие через начало координат («вращающаяся» прямая). Полезным будет вспомнить, что с увеличением a прямая вращается против часовой стрелки.
Упражнение 4. Сколько общих точек имеют графики функций из упражнения 2 и прямая
y = a в зависимости от значения параметра a?
Решение.
Ответ:
а) при a < 0 или a > 3 — нет точек пересечения;
при 0 ≤ a < 3 — две общие точки;
при a = 3 — одна общая точка;
б) при a < –2 или a > 2 — нет точек пересечения;
при –2 < a < 2 — одна общая точка;
при a = ±2 — бесконечное множество общих точек;
в) при a < –2 — нет точек пересечения;
при a = –2 — одна общая точка;
при a > –2 — две общие точки;
г) при a < –2 — нет точек пересечения;
при a = –2 — одна общая точка;
при a > –2 — две общие точки.
Упражнение 5. Сколько общих точек имеют графики функций из упражнения 2 и прямая
y = ax в зависимости от значений параметра a?
Решение.
Ответ:
а) при a < 0 или a > 1 — одна общая точка;
при 0 ≤ a < 1 — две общие точки;
при a = 1 — бесконечное множество общих точек;
б) при a ≤ 0 или a > 1 — одна общая точка;
при 0 < a < 1 — три общие точки;
при a = 1 — бесконечное множество общих точек;
в) при a ≤ –1 или a ≥ 1 — одна общая точка;
при –1 < a < 1 — две общие точки.
Комментарий. В данном примере нужно обратить внимание учащихся на то, что количество общих точек будет зависеть от того, параллельна ли прямая y = ax какому-либо участку графика или нет. Условие параллельности — равенство угловых коэффициентов.
г) при a < –1 или a ≥ 1 — одна общая точка;
при a = –1 — бесконечное множество общих точек;
при –1 < a < 1 — две общие точки.
Задание на дом
1. Сколько общих точек имеют прямая y = a и ломаная, задаваемая условием
2. Найдите все значения параметра a, при которых прямая y = ax пересечет в двух различных точках ломаную
3. Решите уравнение (a – 1)(a – 5)x = a – 1. Придумайте задачу с графиками функций, где пришлось бы решать данное уравнение.
Занятие № 8
Линейная функция и ее график
Упражнение 1. Найдите координаты точки пересечения прямых, заданных уравнениями
y = ax + 5 и y = 1,5x + 0,5b,
если известно, что график первой прямой проходит через точку A(–2; 3), а второй — через точку B(3; 4).
Упражнение 2. Найдите все значения параметра a, при которых графики функций
y = (2a – 3)x + a – 7 и y = (4a – 1)x + 5 – 3a
параллельны. Постройте графики этих функций при найденных значениях параметра a.
Статья опубликована при
поддержке медицинского центра “ЦРЧ”. “ЦРЧ” – это центр лазерной хирургии, подологии и проктологии. Центр предлагает Вам такие услуги, как лечение вросшего ногтя на пальце ноги, оперативная и консервативная ортопедия, мануальная терапия, удаление на коже лазером и другие. Узнать подробнее об услугах, цены и контакты Вы сможете на сайте, который располагается по адресу: http://www.rubca.net/.
Упражнение 3. Найдите общие точки функций
y = (4 – a)x + a и y = ax + 2.
Решение. Абсциссы общих точек двух графиков можно найти из уравнения
(4 – a)x + a = ax + 2.
Приведя уравнение к стандартному виду, получим:
(2a – 4)x = 2 – a.
Допустимые значения переменных — любые числа. Решим это уравнение относительно переменной x.
Если 2a – 4 = 0, то есть a = 2, то получим уравнение 0∙x = 0. Его корнями являются любые числа, поэтому графики функций совпадают. Общие точки графиков — прямая y = 2x + 2.
Если a ≠ 2, то x = –0,5, а ордината точки пересечения y = –0,5a + 2.
Ответ: при a = 2 координаты общих точек — (x; 2x + 2), где x — любое число;
при a ≠ 2 координаты общих точек —
(–0,5; –0,5a + 2).
Упражнение 4. При каких значениях параметров b и k графики функций y = kx – 4 и y = 2x + b
симметричны относительно:
а) оси абсцисс; б) оси ординат?
Ответ: а) при b = 4, k = –2; б) при b = –4, k = –2.
Упражнение 5. Сколько общих точек имеет график функции
с графиком функции:
а) y = ax; б) y = ax + 3?
Упражнение 6. При каких значениях параметра b графики функций y = | x | + x – 2 и y = b:
а) не пересекаются;
б) пересекаются более чем в одной точке?
Упражнение 7. При каких значениях параметра c графики функций
и y = cx пересекаются в одной точке?
Задание на дом
1. При каких значениях параметра c графики функций y = | x | + 2 и y = cx пересекаются в одной точке?
2. Найдите все значения параметра a, при которых точка пересечения прямых x – y = a и 0,2y – x = 3
лежит на оси абсцисс.
3. При каких значениях параметра p прямая
y = px + 2 образует с осями координат треугольник, площадь которого равна 16?
Занятие № 9
Уравнение с двумя переменными и
его график.
Координатная плоскость Oxa
Равенство, содержащее две переменные, называется уравнением с двумя переменными. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения. Соотнесение уравнения и геометрического места точек плоскости — один из самых важных шагов в развитии мышления учащихся.
Упражнение 1. Какие из пар чисел (–3; 9),
(–2; 4), (–1; 3), (0; 2), (1; –3), (2; 0), (3; 4) являются решениями уравнения:
а) x2 – y = 0; б) x + y = 2?
Упражнение 2. Постройте графики уравнений:
а) | x – 2 | = 0; б) 2x + 4y = 1;
в) | x – 1 | + (y + 2)2 = 0;
г) 2ax2 – 3x2 – 9y + 6ay = 0 при a = 1,5.
Ответ: а) прямая x = 2;
б) прямая y = –0,5x + 0,25;
в) точка (1; –2);
г) вся координатная плоскость.
Упражнение 3. Найдите все общие точки уравнений x2 – y = 0 и x + y = 2.
Ответ: (–2; 4), (1; 1).
Далее знакомим учащихся с графическим способом решения уравнений с параметром. При этом рассматриваем уравнение с параметрами как уравнение с двумя неизвестными, график которого существует, но только в плоскости Oxa. Сначала рассмотрим уравнение, которое может быть решено как графически, так и аналитически. Далее — уравнение, аналитический способ решения которого явно громоздкий.
Упражнение 4. Решите уравнение
(| x | – 4)(x + 2a) = 0.
Решение. Уравнение (| x | – 4)(x + 2a) = 0 можно решить как аналитически, так и графически. Разберем оба способа.
Способ I (аналитический). В данном случае произведение равно 0, если один из множителей равен 0, то есть | x | – 4 = 0 или x + 2a = 0. Отсюда x = ±4 или x = –2a.
Если –2a = ±4, то есть a = ±2, то уравнение имеет два корня: x = ±4,
Если a ≠ ±2, то три корня: x = ±4 или x = –2a.
Способ II (графический). Построим график уравнения в системе координат Oxa.
График уравнения — прямые x = 4, x = –4 и a = –0,5x. Проводим горизонтальные прямые
a = α. В зависимости от α находим решения уравнения как абсциссы точек пересечения прямой a = α с графиком уравнения (ось ординат не y,
а параметр a).
Ответ: при a = ±2 x = ±4;
при a ≠ ±2 x = ±4 и x = –2α
Упражнение 5. Решите уравнение
(x2 – a2)(a – 1 – | x |) = 0.
Решение. Построим график уравнения
(x2 – a2)(a – 1 – | x |) = 0
в системе координат Oxa. Это прямые a = x, a = –x и график функции a = | x | + 1. Проводим горизонтальные прямые a = α. В зависимости от α находим решения уравнения как абсциссы точек пересечения прямой a = α с графиком уравнения. Получаем, что при a < 0 уравнение имеет два корня: x = ±a; при a = 0 — один корень x = 0; при 0 < a < 1 — два корня: x = ±a; при a = 1 — три корня: x = 0 и x = ±a; при a > 1 — четыре корня: x = ±a и x = ±a + 1.
Ответ: при a < 0 или 0 < a < 1 x = ±a;
при a = 0 x = 0;
при a = 1 x = 0 и x = ±a;
при a > 1 = ±a и x = ±a + 1.
Обратим внимание учащихся на то, что графическим способом удобно находить количество решений уравнения с параметрами.
Упражнение 6. При каких значениях параметра a уравнение 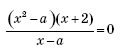
Решение.
Графиком уравнения будут парабола a = x2 и прямая x = –2. Необходимо также учесть область определения a ≠ x. Проводим горизонтальные прямые a = α и получаем, что уравнение будет иметь ровно три корня: при 0 < a < 1, 1 < a < 4, a > 4.
Ответ: при 0 < a < 1, или 1 < a < 4, или a > 4
уравнение имеет ровно три корня.
Задание на дом
1. Докажите, что уравнение
(a – | x – 1 |)(a + x2) = 0
при любых значениях параметра a имеет два различных корня.
2. Постройте графики уравнений:
а) | x – 1 | + (x + y)2 = 0; б) x2 = 4y2;
в)
3. При каких значениях параметра a две прямые ax – y = –2a и x – ay = 2 будут пересекаться, совпадать или будут параллельны?
Занятие № 10
Системы линейных уравнений
с двумя неизвестными
Одним из способов решения систем уравнений является графический способ.
Упражнение 1. Решите графически систему уравнений
Решение. Упростив формулу, задающую вторую функцию, получим: y = –x2, x ≠ ±2. Тогда график первого уравнения — прямая, а график второго уравнения — парабола с двумя выколотыми точками (x ≠ ±2).
Ответ: (–3; –9).
Упражнение 2. При каких значениях параметра a система
имеет единственное решение?
Решение. Решим задание графически. Построим в одной системе координат графики уравнений, входящих в систему, то есть y = | x | – 4 и
y = ax. Из рисунка видно, что графики будут иметь одну общую точку при a ≤ –1 или a ≥ 1.
Ответ: при a ≤ –1 или a ≥ 1 система имеет единственное решение.
Упражнение 3. При каких значениях параметра a система
имеет решения?
Решение. Графиком первого уравнения системы является пара точек на координатной плоскости: (1; 2) и (–1; 2). График второго уравнения — прямая y = 0,5ax – 1,5. Чтобы система имела решения, необходимо, чтобы прямая проходила через точки (1; 2) или (–1; 2). Подставляя координаты этих точек в уравнение прямой
y = 0,5ax – 1,5, получим:
0,5a – 1,5 = 2 или –0,5a – 1,5 = 2.
Откуда a = 7 или a = –7.
Ответ: при a = ±7 система имеет решения.
Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где
a2 + b2 > 0, то есть значение хотя бы одного из коэффициентов (параметров) должно быть отлично от нуля. Графиком линейного уравнения с двумя переменными является прямая линия.
Определение. Системой двух линейных уравнений с двумя переменными называется система вида
где a1, a2, b1, b2 — действительные числа, причем
и
Определение. Решением системы двух линейных уравнений с двумя переменными называется упорядоченная пара значений этих переменных, обращающая в верное равенство каждое уравнение системы.
Так как каждому уравнению системы можно поставить в соответствие прямую, то решением системы будут являться координаты точек пересечения этих прямых.
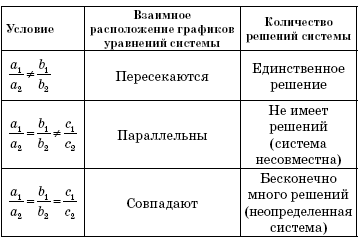
Две прямые на плоскости могут быть параллельны, пересекаться или совпадать. В связи с этим и системы линейных уравнений могут иметь единственное решение, не иметь решений или иметь бесконечное множество решений. Для ответа на вопрос о количестве решений системы уравнений полезно заполнить с учащимися таблицу.
Алгоритм определения количества решений системы линейных уравнений
Упражнение 4. Найдите все значения параметра a, при каждом из которых система уравнений
не имеет решения.
Решение. Система не имеет решений, если выполняются условия
То есть должно быть
Отсюда a2 = 4, a = ±2.
Если a = 2, то a2 + a – 2 = 4, то есть что неверно.
Если a = –2, то a2 + a – 2 = 0, то есть что верно.
Ответ: при a = –2 система не имеет решений.
Упражнение 5. Найдите все значения параметра a, при каждом из которых система уравнений
имеет бесконечно много решений.
Решение. Система имеет бесконечно много решений, если выполняются условия
то есть
Отсюда a2 – 3a = 0, то есть a = 0 или a = 3.
Если a = 3, то — верно.
Если a = 0, то — неверно.
Ответ: при a = –3 система имеет бесконечно много решений.
Упражнение 6. Найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение.
Решение. Система имеет единственное решение, если выполняется условие то есть
Отсюда a2 ≠ 16, a ≠ ±4.
Ответ: при a ≠ ±4 система имеет единственное решение.
Упражнение 7. Для каждого значения параметра a определите число решений системы уравнений
Задание на дом
1. При каких значениях параметра a система
имеет:
а) одно решение;
б) бесконечно много решений;
в) не имеет решений?
2. Постройте графики уравнений:
а) | x – 1 | + (x + y)2 = 0; б) x2 = 4y2;
в)
3. При каких значениях параметра a прямые ax – y = –2a и x – ay = 2 будут пересекаться, совпадать или будут параллельны?
Занятие № 11
Системы линейных уравнений
Упражнение 1. Числа a и b таковы, что система уравнений
имеет единственное решение (1; 1). Найдите a и b.
Решение. Если x = 1, y = 1 — решение системы, то при подстановке данных значений в систему получаем:
Отсюда a = 1, b = –1 или a = –1 и b = 1. Система должна иметь единственное решение. Проверим, выполняется ли условие 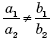
Если a = 1, b = –1, то 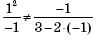
Если a = –1, b = 1, то 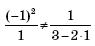
Ответ: при a = 1 и b = –1 система имеет единственное решение.
Упражнение 2. Найдите все значения параметра b, при каждом из которых система уравнений
имеет бесконечное множество решений, причем одно из этих решений x = 1, y = 3.
Упражнение 3. При каких значениях параметров a и b равносильны системы уравнений
Решение. Системы уравнений равносильны, если имеют одинаковые множества решений. Графиком каждого уравнения этих систем является прямая, причем прямые второй системы пересекаются 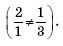
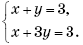
в уравнения с параметрами, получим: 3a = b + 1 и 6 = a2 + 2. Откуда a = 2, b = 5
или a = –2, b = –7. Проверим, пересекаются ли уравнения первой системы при найденных значениях параметров, то есть выполняется ли условие
Если a = 2, b = 5, то условие 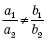
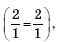
Если a = –2, b = –7, то получим: 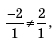
Ответ: при a = –2, b = –7 системы уравнений равносильны.
Упражнение 4. Решите систему уравнений
Упражнение 5. Решите систему уравнений
Решение. Выразим из второго уравнения переменную x и подставим в первое уравнение системы. Получим: 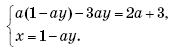
Преобразуем первое уравнение системы к виду: a(a + 3)y = –(a + 3). Допустимые значения переменных — любые числа. Коэффициент при y равен 0, если a = 0 или a = –3. При a = 0 получим уравнение 0жy = –3, которое не имеет корней. При a = –3 получим уравнение 0∙y = 0, которое имеет бесконечное множество корней, y— любое число. Если a ≠ 0 и a ≠ –3, то уравнение имеет единственный корень
Ответ: при a = 0 система не имеет решений;
при a = –3 x = 1 + 3y, y ∈ R;
при a ≠ 0 и a ≠ –3 x = 2, 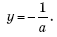
Упражнение 6. При каких значениях параметра a система
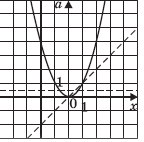
имеет единственное решение? Найдите это решение.
Решение. Решим задачу графически. Построим графики уравнений системы в одной системе координат и по рисунку определим, при каких значениях параметра a графики имеют одну общую точку. y = | x + 2 | — прямой угол с вершиной в точке (–2; 0). y = ax + 1 — «вращающаяся» прямая, центр вращения — (0; 1). Чтобы определить угловой коэффициент прямой y = ax + 1, проходящей через вершину «угла», подставим ее координаты в уравнение прямой. Получим: –2a + 1 = 0, отсюда
a = 0,5. Если a ≤ –1, то абсциссу точки пересечения находим из уравнения x + 2 = ax + 1.
Отсюда
Аналогично при a > 1.
Ответ: при a ≤ –1 решение системы точка 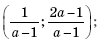
a > 1 — точка
Задание на дом
1. При каких значениях параметра p система уравнений
имеет решение?
2. При каких значениях параметра m система линейных уравнений
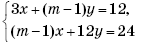
имеет одно решение, бесконечно много решений, не имеет решений?
3. Зная, что a < b, сравните:
а) 3a и 3b; б) –5a и –5b;
в) a – 4 и b – 4; г) 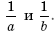
4. Верно ли, что если a < b, то:
а) a + 3 < b + 12; б) a – 6 < b – 2;
в) 2a < 2b + 2; г) –2a < –2b?
Окончание следует.
Овчинникова Т.
3.1. Основные сведения из теории
Пусть прямая задана каноническими
уравнениями
:
,
а плоскость –
общим уравнением
:
.
1. Угол между прямой и плоскостью равен
углу между направляющим вектором
прямой и нормальным вектором
плоскости и вычисляется по формуле
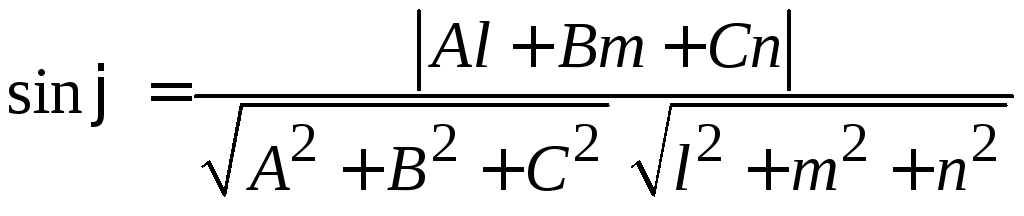
(3.1)
2. Условие параллельности прямой и
плоскости имеет вид
.
Оно равносильно условию ортогональности
векторов
и
3. Условие перпендикулярности прямой и
плоскости имеет вид
.
Оно равносильно условию коллинеарности
векторов
и
.
4. Условие принадлежности прямой
плоскости
записывается в виде
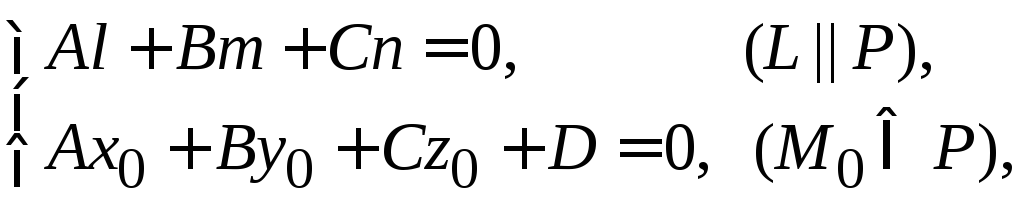
где
координаты точки
,
принадлежащей прямой.
3.2. Решение типовых задач
Задача 3.1. Найти острый угол между
прямойи плоскостью
.
Решение. Направляющий вектор прямой
равен.
Нормальный вектор плоскости равен.
По формуле (3.1)

.
Ответ:
Задача 3.2. При
каком значении
прямая
:

:
?
Решение. Согласно
условию задачи прямая
задана как линия пересечения двух
плоскостей. Нормальный вектор первой
плоскости равен,
нормальный вектор второй плоскости
равен.
Направляющий вектор прямой равен(см. формулу (2.6)):

Условие параллельности
прямой
и плоскости
это условие ортогональности направляющего
вектора прямойи нормального вектора плоскости
,
т. е..
Умножая, получаем
.
Таким образом, уравнение плоскости
будет
.
Ответ:
Задача 3.3. При каких значенияхи
прямая
лежит в плоскости
?
Решение. Прямая
будет параллельна плоскости, если ее
направляющий вектор
будет ортогонален нормальному вектору
плоскости,
т. е..
Запишем это условие:
Прямая будет принадлежать плоскости,
если координаты точки
,
через которую проходит прямая,
удовлетворяют уравнению плоскости:.
Отсюда получаем, что
При решении задачи мы воспользовались
формулой (3.2).
Ответ:
Задача 3.4. Найти точку пересечения
прямой:
и плоскости
:
Решение. Запишем уравнения прямой
в параметрическом виде
Подставляя выражения для
в уравнение плоскости
,
получим
Теперь следует подставить значение
параметра
в параметрические уравнения прямой
.
Находим.
Ответ:
Полезная
формула. Если прямаяпересекается с плоскостью
,
то точке пересечения
отвечает значение параметра
.
(3.3)
Задача 3.5. Найти уравнение плоскости,
проходящей через прямую:
перпендикулярно плоскости
:
Р
имеет два направляющих вектора
и
и проходит через точку
(рис. 3.1). Согласно формуле (1.9) ее уравнение
будет иметь вид

или
.
Окончательно:
.
Ответ:.
З
3.6.Известны
координаты вершин тетраэдра:
Найти уравнение и длину его высоты
.
Р
ешение.Данный тетраэдр мы
рассматривали в задаче 1.10. Уравнение
основанияимеет вид
.
В качестве направляющего векторавысоты
можно выбрать нормальный вектор грани
,
т. е.(рис. 3.2). Кроме того, нам известны
координаты точки,
через которую проходит высота.
Воспользуемся каноническими уравнениями
прямой (2.3). Тогда получим
:
.
Высоту
можно найти по формуле (1.5), определяющей
расстояние от точкидо грани
:
.

(Напомним, что
– это коэффициенты в общем уравнении
плоскости,
и они равны,
,
,
.)
Ответ: :
;

Задача 3.7. Даны прямые:
и
:
.
Найти уравнение плоскостипроходящей через прямую
параллельно прямой
Решение. Векторы
и
являются направляющими векторами
плоскости(рис. 3.3). Точка
принадлежит плоскости
.
Решаем задачу, используя формулу (1.9):

или
.
Окончательно:
.
Ответ: .
Задача 3.8. Составить уравнение
плоскости, проходящей через прямую:
и точку
.
Решение.Прямаяпроходит через точку
и ее направляющий вектор равен
.
Произвольная точкабудет принадлежать искомой плоскости
,
если векторы
и
компланарны:
(рис. 3.4), т. е.

Это и есть уравнение плоскости
.
Подставляем координаты:
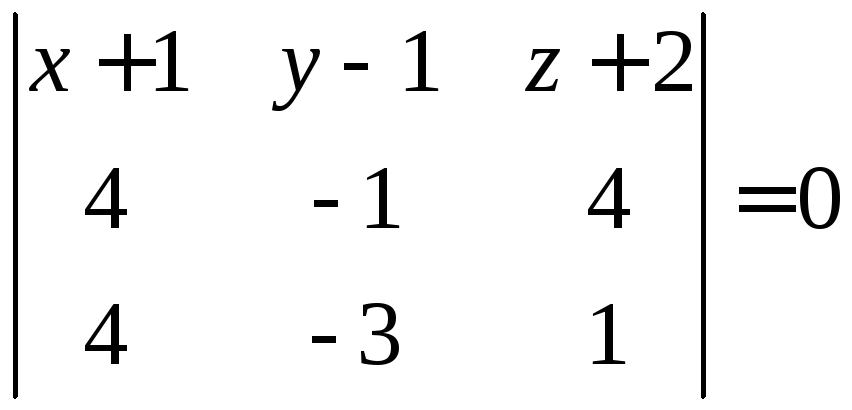
или
.
Окончательно:
.
Ответ: .
Полезная
формула. Уравнение
плоскости, проходящей через прямую
:
и точку
,
не лежащую на этой прямой, имеет вид

Задача 3.9. Доказать,
что прямые
:
:
лежат в одной плоскости и найти уравнение
этой плоскости.
Р
Первая прямая проходит через точку
и ее направляющий вектор
.
Вторая прямая проходит через точкуи ее направляющим вектором является
.
Очевидно, что прямые лежат в одной
плоскости, если векторы,
и
компланарны:
(рис. 3.5), т. е.

Подставим заданные координаты:

Это означает, что прямые
и
лежат в одной плоскости. Векторы
и
не коллинеарны. Следовательно, эти
прямые пересекаются.
Найдем уравнение
плоскости
,
в которой лежат прямыеи
.
Очевидн
что произвольная точкабудет принадлежать плоскости, если
векторы,
,
компланарны:
(рис. 3.6), т. е.

Это и есть уравнение искомой плоскости.
Подставляем координаты и вычисляем
определитель разложением по элементам
первой строки. Получаем
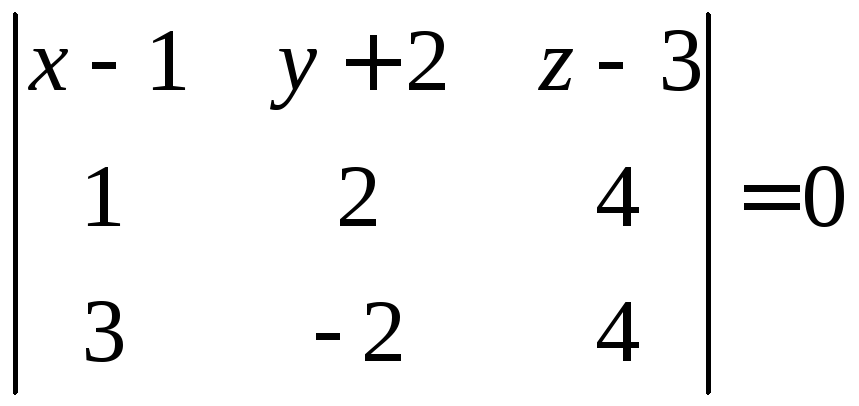
или
.
Окончательно:
.
Ответ: .
Полезные
формулы. Две прямые
:
:
лежат в одной плоскости, если
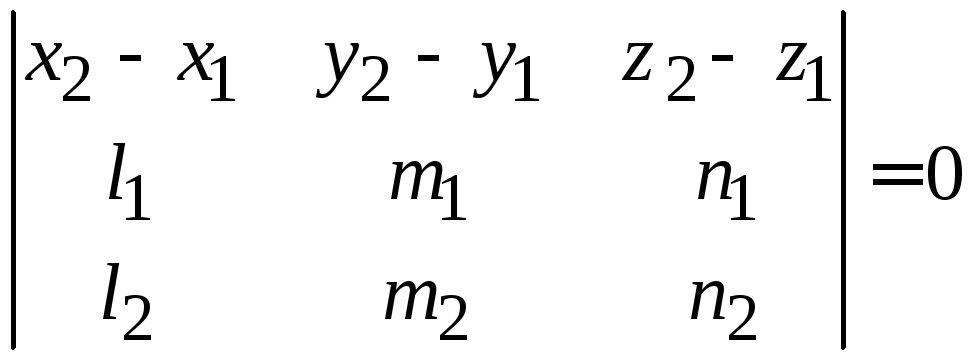
(3.5)
Если прямые пересекаются, то уравнением
этой плоскости будет

(3.6)
Замечание.
Прямые скрещиваются (т. е. не лежат в
одной плоскости) тогда и только тогда,
когда
и равенство (3.5) несправедливо.
Задача
3.10.Найти уравнение плоскости,
проходящей через две параллельные
прямые:
:
:
.
Р
ешение.Ясно, что направляющие
векторы этих прямых равны.
Первая прямая проходит через точку,
вторая
через точку.
Произвольная точкапринадлежит искомой плоскости
,
если векторы,
и
компланарны:
(рис. 3.7), т. е.
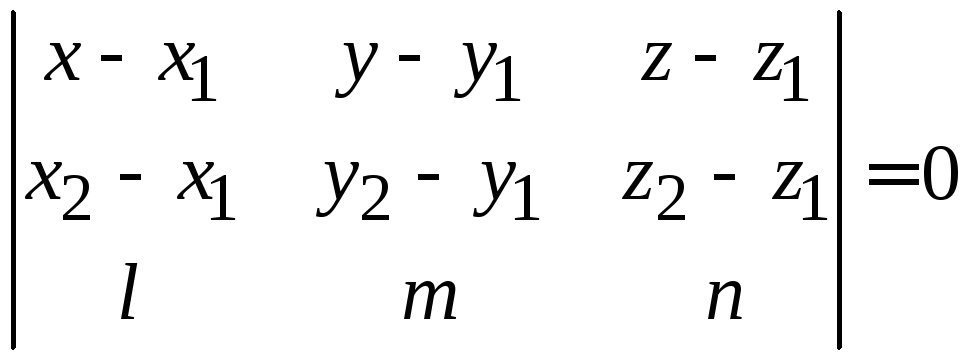
Подставляя заданные координаты, находим
уравнение плоскости

или
.
Окончательно:
.
Ответ: .
Полезная
формула. Уравнение плоскости, проходящей
через две параллельные прямые (,
)
:
:
,
имеет вид

(3.7)
Замечание. В задачах 1.3, 1.9, 3.5, 3.8–3.10
без труда можно указать два направляющих
вектора искомых плоскостей. Поэтому
решение этих задач аналогично решению
задачи 1.2. Если эти направляющие векторы
явно не обозначены в ходе решения, то
найдите их самостоятельно. Подумайте,
что общего в формулах (1.7)–(1.9), (3.4)–(3.7).
З
3.11.Найти координаты проекцииточки
на плоскость
:
.
Решение.Находим параметрические
уравнения прямой,
проходящей через точкуперпендикулярно плоскости
.
В качестве направляющего векторапрямой
можно выбрать нормальный вектор
плоскости
,
т. е. положить(рис. 3.8). Параметрические уравнения
прямойбудут (см. формулу (2.2)):
По формуле (3.3) находим значение параметра
,
при котором прямая пересекает плоскость.
Получим.
Подставим это значение в параметрические
уравнения прямой и вычислим координаты
точки
Ответ:
Задача 3.12.
Найти координаты
точки
,
симметричной точкеотносительно плоскости
:
.
Р
результатом решения предыдущей задачи.
Точка
– проекция
точки
на плоскость. Координаты точки
можно найти, используя соотношения:
(рис. 3.9). Следовательно,
Ответ:
Задача 3.13. Найти
координаты проекции
точки
на прямую
:
.
Р
Найдем уравнение плоскости
,
перпендикулярной прямойи проходящей через точку
.
В качестве нормального вектораплоскости
можно выбрать направляющий вектор
прямой
,
т. е. положить(рис. 3.10). Тогда уравнение плоскости
:
или
Параметрические уравнения прямой
имеют вид
Далее решаем аналогично задаче 3.11.
Координаты точки
находим с помощью формулы (3.3). Получаем
,
Ответ:
З
3.14.Найти координаты точки,
симметричной точкеотносительно прямой
:
Решение.
Воспользуемся результатом задачи 3.13.
Точка
проекция точки
на прямую
.
Координаты точки
можно найти, используя соотношения:
(рис. 3.11). Следовательно,
Ответ:
Задача 3.15. Найти расстояние между
параллельными прямыми
.
Р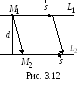
длину перпендикуляра ,
опущенного из точки
,
через которую проходит прямая,
на прямую.
Для этого построим параллелограмм со
сторонамии
(рис. 3.12). Здесь
– точка, через которую проходит прямая
,
анаправляющий вектор прямых (так как
прямые параллельны, то).
Площадьпараллелограмма вычисляется с помощью
векторного произведения векторови
:
.
Расстояние
получим, разделив площадь параллелограмма
на длину его стороны
:
Ответ:
Полезная
формула. Если заданы две параллельные
прямые
;
,
то расстояние
между
ними вычисляется по формуле

где
и
точки, через которые проходят прямые
и
соответственно,
их направляющий вектор.
Задача 3.16. Найти расстояние между
скрещивающимися прямыми:
Р
Прямая
проходит через точку
и ее направляющий вектор
.
Прямаяпроходит через точку
и ее направляющий вектор
.
Известно, что если прямые скрещиваются,
то существуют две параллельные плоскостии
такие, что прямая
лежит в плоскости
,
а прямая
в плоскости
.
Направляющие векторыи
будут направляющими векторами этих
плоскостей.
Построим параллелепипед,
сторонами которого являются векторы
(рис. 3.13). Найдем его объем. Для этого
вычислим смешанное произведение
Таким образом, объем
Теперь найдем площадь основания
параллелепипеда (см. решение задачи
3.15):

Расстояние
между
скрещивающимися прямыми будет равно
Ответ:
Полезная
формула. Если заданы две скрещивающиеся
прямые

то расстояние между ними вычисляется
по формуле
Здесь
и
– точки, через
которые проходят прямые
и
соответственно,
и
– их направляющие
векторы.
Замечание. Кратко опишем другой
способ решения задачи 3.16. Сначаланайдем
уравнение плоскости
(проделайте это самостоятельно). Оно
будет
.
Расстояние
равно расстоянию от точки
до плоскости
.
Теперь все следует из формулы (1.5):
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
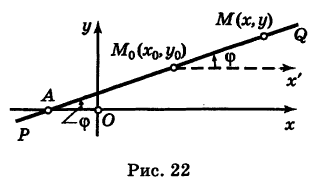
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 – линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) – ему не удовлетворяет;
б)
в) 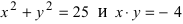
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 – уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
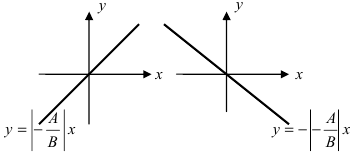
а) С = 0; 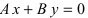
Рис. 20. Прямая, проходящая через начало координат.
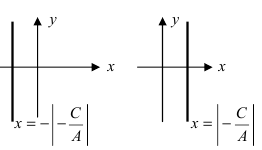
б) 5 = 0; Ах+С=0 – прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
в) А = 0; Ву+С=0 – прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
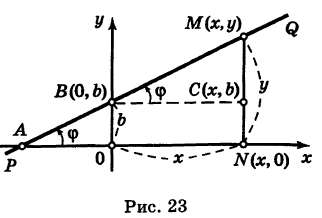
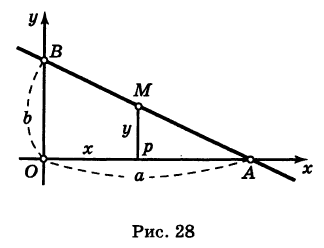
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 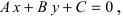
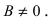
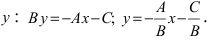
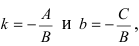
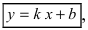
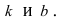
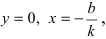
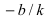
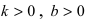
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 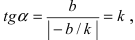
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 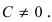
Обозначим через 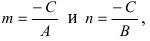
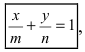
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 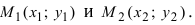
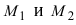
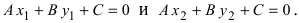
Пусть 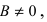
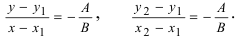
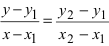
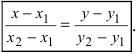
4. Уравнение прямой, проходящей через заданную точку 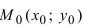
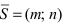
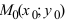
Определение: Вектор 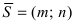
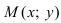
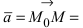
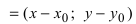
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 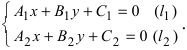
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
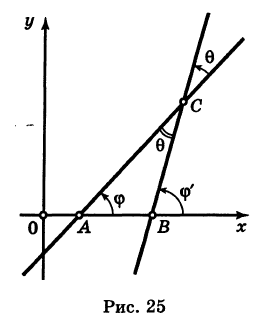
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 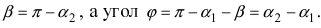
Наименьший угол между пересекающимися прямыми определим формулой 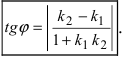
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 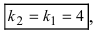
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 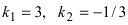
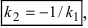
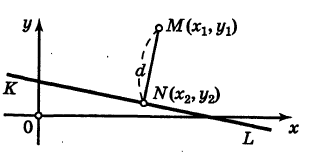
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 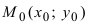
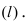
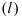
Если прямая 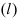
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 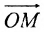
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая – второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси – координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую – осью ординат, обозначаемую Оу.
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 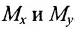
Координатами точки М в заданной системе называются числа 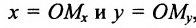
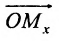
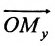
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у – М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
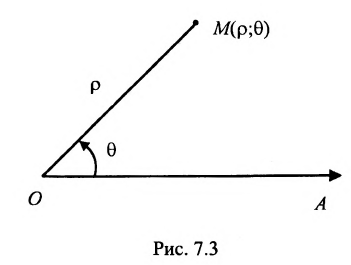
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 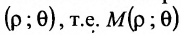
Декартова прямоугольная система координат связана с полярной системой формулами:
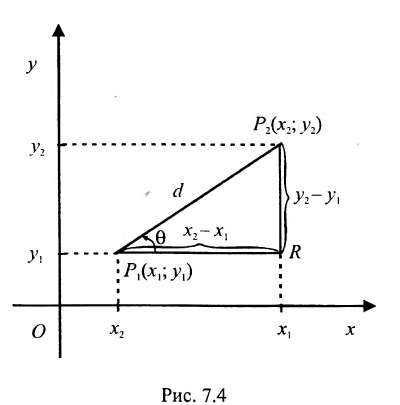
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками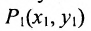
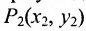
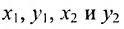
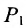
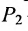
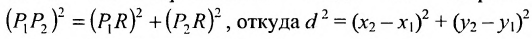
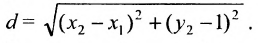
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 
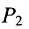
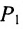
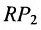
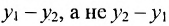
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 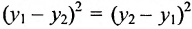
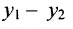
Если обозначить через 
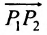
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u – произвольная ось, а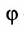
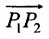
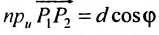
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая – второй. Обозначим их в заданном порядке через 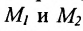
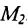
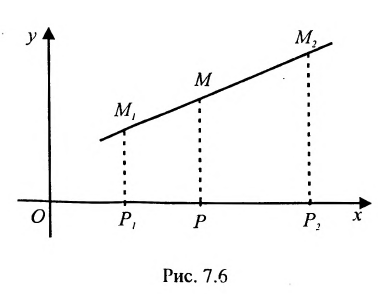
Определение 7.1.1. Число 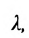
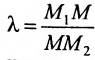
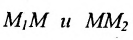
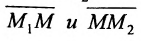
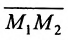
Число 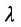
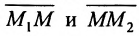
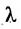
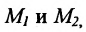
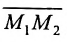
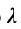
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 
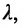
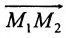
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 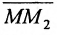
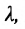
Доказательство:
Спроектируем точки 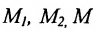
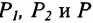
Подставив в (7.1.4) величины отрезков 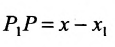
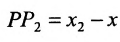
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 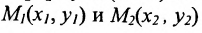
середина отрезка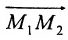
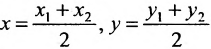
получаются из (7.1.3) при 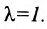
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 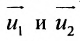
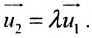
Для всех направляющих векторов 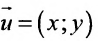
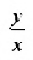
Действительно, если 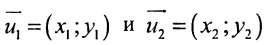
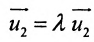
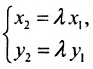
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
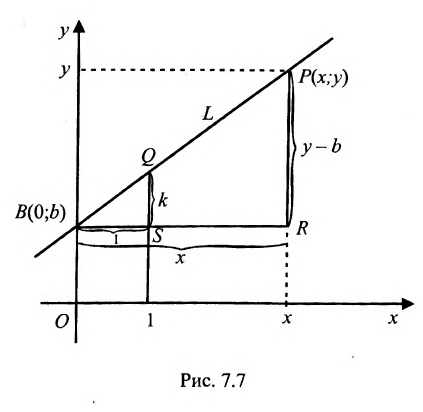
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
Доказательство: Пусть В = (О,b}- точка пересечения прямой L с осью у, а Р = (х,у) – любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р – прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 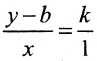
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
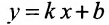
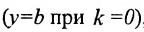
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Ах+Ву+С=0. (7.2.4)
Если 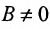
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
А х = —С,
или 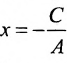
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 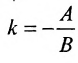
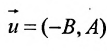
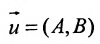
1. 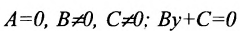
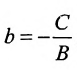
2. 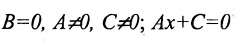
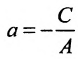
3. 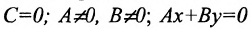
4. А=0; С=0; Ву-0 или у = 0 – это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 – это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 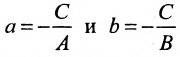
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 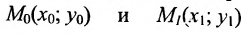
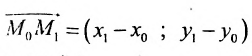
Геометрическое место концов всевозможных векторов вида 
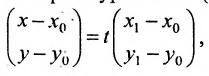
где 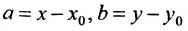
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
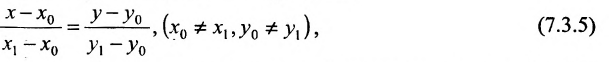
Если абсциссы точек 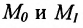
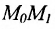
Если ординаты точек 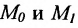
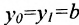
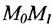
или
где
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 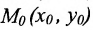
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 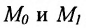
II способ. Зная координаты точек 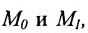
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 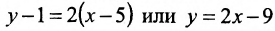
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
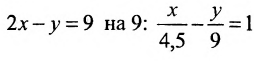
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 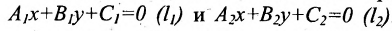
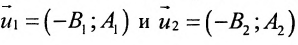
Если прямые параллельны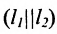
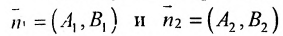
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые
Например, прямые 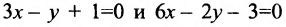
т. к.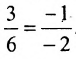
Если прямые перпендикулярны 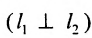
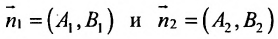
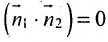
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 
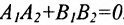
Например, прямые 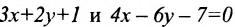
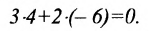
Если прямые заданы уравнениями вида 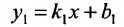
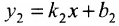
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
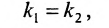
а для их перпендикулярности необходимо и достаточно, чтобы
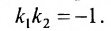
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ – это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 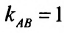
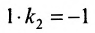
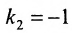
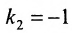
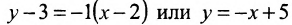
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
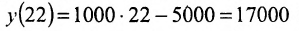
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 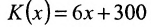
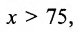
Прямая линия в пространстве
Системы координат в пространстве
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство
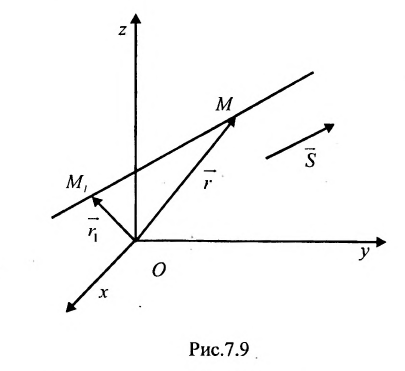
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 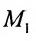
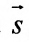
Вектор 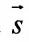
Итак, пусть прямая L проходит через точку 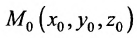
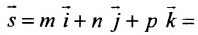
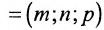
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 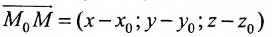
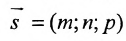
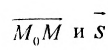
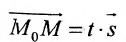
Уравнение 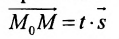
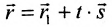
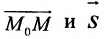
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 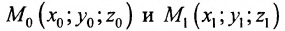
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 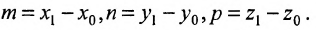
Пример:
Составить параметрические уравнения прямой, проходящей через точку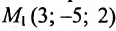
Решение:
В качестве направляющего вектора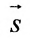
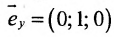
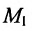
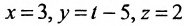
Пример:
Записать уравнения прямой 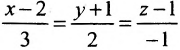
Обозначим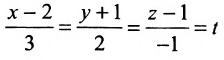
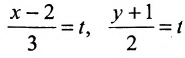
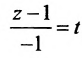
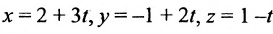
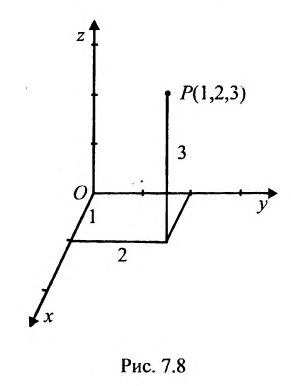
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 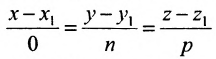
Аналогично, канонические уравнения
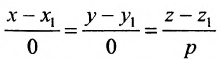
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 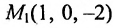
Решение:
Подставив координаты точки 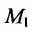
.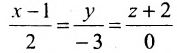
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 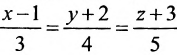
б) оси Ох;
в) оси Оу;
г) оси Oz.
Решение:
а) Поскольку направляющий вектор заданной прямой
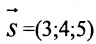
подставив координаты точки М(2; -1; 4) и вектора 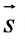
б) Поскольку единичный вектор оси О х: 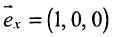
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 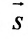
в) В качестве направляющего вектора 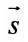
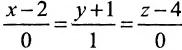
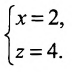
г) Единичный вектор оси Oz : 
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 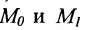
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 
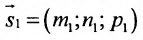
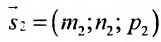
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 
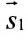
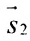
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 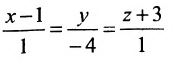
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 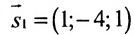
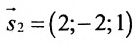
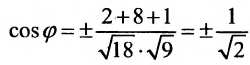
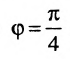
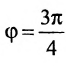
Вычисление уравнения прямой
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 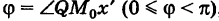
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
при х > 0.
Таким образом,
при х > 0.
Нетрудно проверить, что формула (3) остается справедливой также и при х < 0.
Мы доказали, что координаты любой точки М (х, у) прямой PQ удовлетворяют уравнению (3). Легко убедиться в обратном: если координаты какой-нибудь точки Ml 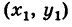
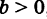
При k = 0 получаем уравнение прямой, параллельной оси Ох:
2) Если 
3) Если 
где а — абсцисса следа этой прямой на оси Ох (т. е. ее точки пересечения с осью Ох).
Замечание. Как частные случаи получаем уравнения осей координат:
Прямую легко построить по ее уравнению.
Пример:
Построить прямую, заданную уравнением
Решение:
Известно, что две точки вполне определяют положение прямой. Поэтому достаточно найти две точки, через которые проходит наша прямая. В данном уравнении b = -4. Следовательно, прямая проходит через точку В (0, -4). С другой стороны, координаты х и у любой точки, лежащей на нашей прямой, связаны заданным уравнением. Поэтому, задав абсциссу некоторой точки, лежащей на прямой, мы из уравнения прямой найдем ее ординату. Положим, например, х = 2; из уравнения прямой получим у = -1. Таким образом, наша прямая проходит через точки А (2, -1) и В (0, -4). Построив эти точки по их координатам и проведя через них прямую (рис. 24), мы получим искомую прямую.
Из предыдущего видно, что для произвольной прямой на плоскости можно составить ее уравнение; обратно, зная уравнение некоторой прямой, можно построить эту прямую. Таким образом, уравнение прямой полностью характеризует положение ее на плоскости.
Из формул (3) и (5) видно, что уравнение прямой есть уравнение первой степени относительно текущих координат х и у. Справедливо и обратное утверждение.
Теорема: Всякое невырожденное уравнение первой степени
представляет собой уравнение некоторой прямой линии на плоскости Оху (общее уравнение прямой линии).
Доказательство: 1) Пусть сначала В ^ 0. Тогда уравнение (7) можно представить в виде

2) Пусть теперь В = 0; тогда А 
х = -С/А.
Уравнение (9) представляет собой уравнение прямой, параллельной оси Оу и отсекающей на оси Ох отрезок a = -С/А.
Так как все возможные случаи исчерпаны, то теорема доказана.
- Заказать решение задач по высшей математике
Угол между двумя прямыми
Рассмотрим две прямые (не параллельные оси Оу)у заданные их уравнениями с угловыми коэффициентами (рис. 25):
Требуется определить угол 9 между ними. Точнее, под углом 0 мы будем понимать наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой (0 < 0 < я). Этот угол 9 (рис. 25) равен углу АСВ треугольника ABC. Далее, из элементарной геометрии известно, что внешний угол треугольника равен сумме внутренних, с ним не смежных. Поэтому ф’ = ф + 0, или
0 = ф’ – ф;
отсюда на основании известной формулы тригонометрии получаем
Заменяя tg ф и tg ф’ соответственно на к и k окончательно будем иметь
Формула (3) дает выражение тангенса угла между двумя прямыми через угловые коэффициенты этих прямых.
Выведем теперь условия параллельности и перпендикулярности двух прямых.
Если прямые (1) и (2) параллельны, то ф’ = ф и, следовательно,
k’ = к. (4)
Обратно, если выполнено условие (4), то, учитывая, что ф’ и ф заключаются в пределах от 0 до я, получаем
Ф’ – ф, (5)
и, следовательно, рассматриваемые прямые или параллельны, или сливаются (параллельность в широком смысле).
Правило 1. Прямые на плоскости параллельны (в широком смысле) тогда и только тогдау когда их угловые коэффициенты равны между собой.
Если прямые перпендикулярны, то 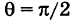
отсюда 1 + kk’ = 0 и
k’ = -l/k.
Справедливо также и обратное утверждение.
Правило 2. Две прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Пусть теперь уравнения прямых заданы в общем виде:
Ах + By + С = 0 (7)
и
А’х + В’у + С’ = 0. (8)
Отсюда, предполагая, что 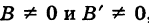
Следовательно, угловые коэффициенты этих прямых есть
Из формулы (3), производя несложные выкладки, находим тангенс угла между этими прямыми:
Отсюда получаем:
1) условие параллельности прямых (0 = 0)
2) условие перпендикулярности прямых
Отметим, в частности, что прямые
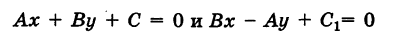
Для прямых, параллельных осям Ох и Оу, условно полагают 
Пример:
Определить угол между прямыми у = х и у = 1,001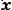
Решение:
По формуле (3) получаем
Так как для малых углов 0 справедливо приближенное равенство 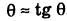
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая РМ образует угол ф с положительным направлением оси Ох (рис. 26) и проходит через заданную точку Р 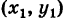
В этом случае, как мы видели, уравнение прямой имеет вид
у = kx + b, (1)
где k = tg ф — угловой коэффициент прямой, а Ь — длина отрезка, отсекаемого нашей прямой на оси Оу. Так как точка Р 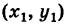
ух = kxt+ b. (2)
Вычитая из равенства (1) равенство (2), получим
Это и есть уравнение искомой прямой.
Если прямая, проходящая через точку Р 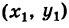
Если k — заданное число, то уравнение (3) представляет вполне определенную прямую. Если же k — переменный параметр, то это уравнение определит пучок прямых у проходящих через точку Р 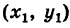
Пример:
Написать уравнение прямой, проходящей через точку Р (3, 2) и параллельной прямой:
Решение:
Так как искомая прямая параллельна данной прямой, то ее угловой коэффициент k = 4/3. Следовательно, на основании формулы (3) уравнение этой прямой имеет вид 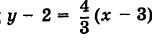
Пример:
Написать уравнение прямой, проходящей через точку Р (4, 5) и перпендикулярной к прямой:
Решение:
Так как искомая прямая перпендикулярна прямой с угловым коэффициентом k = -2/3, то ее угловой коэффициент k’ = -l/k = 3/2. Следовательно, на основании формулы (3) уравнение этой прямой таково:
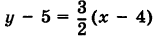
Уравнение прямой, проходящей через две данные точки
Известно, что через две не совпадающие между собой точки можно провести прямую, и притом только одну. Отыщем уравнение прямой, проходящей через точки 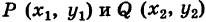
Предположим сначала, что 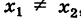
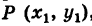
где k — неизвестный нам угловой коэффициент этой прямой. Однако так как наша прямая проходит также через точку Q 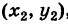
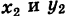
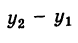
и, следовательно, при 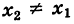
Подставляя выражение (2) для углового коэффициента k в уравнение (1), получим уравнение прямой PQ:
Это уравнение при 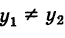
Если 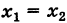
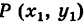
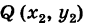
Пример:
Написать уравнение прямой, проходящей через точки Р(4, -2) и Q(3, -1).
Решение:
На основании уравнения (3) имеем
Уравнение прямой в «отрезках»
Выведем теперь уравнение прямой, положение которой на плоскости задано ненулевыми отрезками, отсекаемыми ею на осях координат. Предположим, например, что прямая АВ отсекает на оси Ох отрезок OA = а, а на оси Оу — отрезок О В = b (рис. 28), причем ясно, что тем самым положение прямой вполне определено.
Для вывода уравнения прямой АВ заметим, что эта прямая проходит через точки А (а, 0) и Б 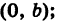
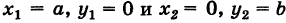
Отсюда
и окончательно
Это и есть так называемое уравнение прямой в «отрезках». Здесь х и у, как обычно, — координаты произвольной точки М (х, у), лежащей на прямой АВ (рис. 28).
Пример:
Написать уравнение прямой АВ, отсекающей на оси Ох отрезок OA = 5, а на оси Оу отрезок ОВ = -4.
Полагая в уравнении (1) а = 5 и b = -4, получим 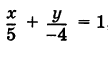
Примечание. Уравнение прямой, проходящей через начало координат или параллельной одной из осей координат, не может быть записано как уравнение прямой в «отрезках».
Точка пересечения двух прямых
Пусть имеем две прямые
Точка пересечения этих прямых лежит как на первой прямой, так и на второй. Поэтому координаты точки пересечения должны удовлетворять как уравнению первой, так и уравнению второй прямой. Следовательно, для того чтобы найти координаты точки пересечения двух данных прямых, достаточно решить совместно систему уравнений этих прямых.
Последовательно исключая из уравнений (1) и (2) неизвестные у и х, будем иметь
Отсюда если 
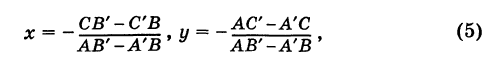
Для прямых (1) и (2) возможны следующие три случая.
На основании прямые не параллельны. Координаты их единственной точки пересечения определяются из формул (6).
Прямые параллельны и точки пересечения нет. Аналитически это видно из того, что по меньшей мере одно из уравнений (3) или (4) противоречиво и, значит, система (1) и (2) несовместна.
Прямые (1) и (2) сливаются, и, таким образом, существует бесчисленное множество точек пересечения. В этом случае левые части уравнений (1) и (2) отличаются только на постоянный множитель и, следовательно, система этих уравнений допускает бесконечно много решений.
Пример:
Решая совместно систему уравнений прямых
получаем х = 2 и у = 1. Следовательно, эти прямые пересекаются в точке N(2,1).
Расстояние от точки до прямой
Рассмотрим прямую KL, заданную общим уравнением
и некоторую точку М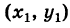
Уравнение перпендикуляра MN можно записать в виде
Отсюда для основания перпендикуляра N(x2, у2) будем иметь
и, следовательно,
где t — коэффициент пропорциональности. Поэтому
С другой стороны, учитывая, что точка N(*2, i/2) лежит на прямой KL, причем из (4) имеем 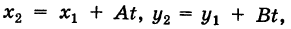
Следовательно,
Таким образом, в силу формулы (5) имеем
В частности, полагая 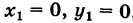
Замечание. Разделив обе части уравнения прямой (1) на 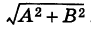
свободный член которого 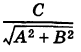
начала координат до прямой. Такое уравнение прямой будем называть нормированным.
Из формулы (7) получаем правило:
чтобы определить расстояние от точки до прямой, нужно в левую часть нормированного уравнения этой прямой подставить координаты данной точки и взять модуль полученного результата.
Пример:
Определить расстояние от точки М (-2, 7) до прямой
Решение:
Нормируя уравнение этой прямой, будем иметь
Отсюда искомое расстояние есть
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Обратная матрица – определение и нахождение
- Ранг матрицы – определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса – определение и вычисление