Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле
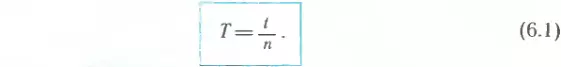
Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
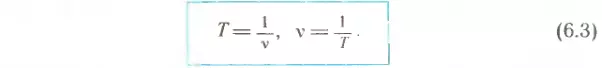
Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (lокр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,

Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
Видео, не по теме но интересно
1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Период вращения (обращения) — это минимальное время, за которое тело совершает один полный оборот, т.е. поворачивается на угол 2π
Для нахождения периода вращения надо время всех оборотов разделить на количество оборотов:
![]()
Период вращения – величина, обратная частоте вращения:
![]()
Единица измерения периода вращения (обращения) – секунда [1с]
Так как промежутку времени T соответствует угол поворота 2π, то период вращния можно поределить по формуле:
![]()
Обозначения:
T — период вращения
N — количество оборотов
t — время, за которое было совершено N оборотов
ν — частота вращения (обращения)
ω — угловая скорость
Содержание
- Как определить период обращения планеты вокруг солнца формула
- Что такое период обращения планеты вокруг солнца
- Как измерять период обращения планеты вокруг солнца
- Формула периода обращения планеты
- Большая полуось орбиты a
- Гравитационная постоянная G
- Масса солнца M
- Как вычислить период обращения Земли вокруг Солнца
- Общий итог
- Как определить период обращения планеты вокруг солнца формула
- Как можно определить период обращения планеты?
- Как найти значения переменных для расчета периода обращения планеты?
- Общий итог
- Как определить период обращения планеты вокруг солнца формула
- Период обращения планеты вокруг Солнца
- Формула определения периода обращения планеты вокруг Солнца
- Итог
Как определить период обращения планеты вокруг солнца формула
Спросите любого человека, знает ли он, сколько земных лет длится год на Плутоне, и вероятно, что он ответит: «Нет, конечно». И это нормально, потому что узнать период обращения планеты вокруг солнца может быть довольно сложным. Однако, если вы хотите стать космическим исследователем, то придется узнать, как определить период обращения планеты вокруг солнца формула. В этой статье мы разберемся, что означает период обращения планеты вокруг солнца, как его измерить и почему это так важно для нашего понимания космоса.
Что такое период обращения планеты вокруг солнца

Период обращения планеты вокруг солнца — это время, необходимое планете на то, чтобы совершить полный оборот вокруг своей оси и одновременно находясь на своей орбите вокруг солнца. Периоды обращения планет варьируются в зависимости от расстояния до солнца и их массы. Наибольший период обращения имеет планета Нептун (164.8 земных лет), а наименьший — Меркурий (88 земных дней).
Как измерять период обращения планеты вокруг солнца
Период обращения планеты может быть определен наблюдательным путем или математическими методами, основанными на измерениях расстояний, скоростей и времени. Но мы разберемся со всеми формулами.
Формула периода обращения планеты
Формула периода обращения планеты определяется, исходя из Закона Гравитации Ньютона:
T = 2 * π * (a³/GM)^(1/2),
Где:
- T — период обращения планеты вокруг солнца;
- π — константа Пи (3,14159265359);
- a — большая полуось орбиты планеты вокруг солнца;
- G — гравитационная постоянная (6,67 * 10⁻¹¹ Н * м²/кг²);
- M — масса солнца.
Давайте разберемся с каждой переменной.
Большая полуось орбиты a
Большая полуось орбиты — это расстояние от центра планеты до солнца в наиболее далекой точке орбиты. Это значение можно найти в таблицах данных планет.
Гравитационная постоянная G
Гравитационная постоянная — это фундаментальная константа физики, которая определяет силу гравитации между двумя объектами. Ее значение равно 6,67 * 10⁻¹¹ Н * м²/кг².
Масса солнца M
Масса солнца — это масса, которую имеет наша звезда, вокруг которой вращаются все планеты Солнечной системы. Его значение составляет 1,9891 * 10³⁰ кг.
Как вычислить период обращения Земли вокруг Солнца
Если вы хотите вычислить период обращения Земли вокруг Солнца, то вам нужно знать большую полуось орбиты Земли, гравитационную постоянную и массу Солнца.
По наблюдательным данным было определено расстояние от Земли до Солнца на равноденствие весны, которое составляет 149,6 миллионов километров. После того, как вы получили этот параметр, вы можете использовать формулу периода обращения:
T = 2 * π * (149,6 * 10⁶ км)^(3/2) / (6,67 * 10⁻¹¹ Н * м²/кг² * 1,9891 * 10³⁰ кг)^(1/2),
Упрощенный вычисленный ответ будет равен около 365 дням и 6 часам. Однако, для вычисления точного значения, необходимо принять в расчет множество факторов, например, орбита земли свойственна гравитационным влияниям солнца и луны.
Общий итог

Для определения периода обращения планеты вокруг солнца необходимо знать ее большую полуось, гравитационную постоянную и массу Солнца. Используя формулу, которая основана на Законе Гравитации Ньютона, можно вычислить период обращения любой планеты вокруг солнца. Эта формула играет важную роль в научных исследованиях, помогая ученым изучать космос и делать прогнозы о будущих космических миссиях и экспедициях.
Как определить период обращения планеты вокруг солнца формула
Система солнечных планет остается одной из самых загадочных частей космоса. Планеты кружат вокруг Солнца на определенных орбитах, и каждая планета имеет свой собственный период обращения вокруг Солнца. Но как определить этот период обращения и какую формулу использовать для расчета?
Как можно определить период обращения планеты?

Период обращения каждой планеты зависит от ее расстояния от Солнца. Чем дальше планета от нашей звезды, тем дольше ей требуется, чтобы набрать полный оборот.
Для определения периода обращения планеты необходимо использовать следующую формулу:
T = 2π√(a³/GM)
Где T — период обращения планеты, a — большая полуось орбиты планеты, G — гравитационная постоянная, M — масса Солнца.
Формула выше является математическим выражением закона всемирного тяготения Ньютона. Эта формула позволяет рассчитывать период обращения любой планеты вокруг Солнца, если известно ее расстояние от Солнца и масса нашей звезды.
Как найти значения переменных для расчета периода обращения планеты?

Для расчета периода обращения нам необходимо знать значения переменных из нашей формулы.
- Большая полуось орбиты планеты (a) — данное значение можно найти в таблицах планетных данных. Например, бóльшая полуось орбиты земли равна 149,6 миллионов километров.
- Гравитационная постоянная (G) — это константа, которая равна 6,674×10−11м³/(кг·с²). Значение этой постоянной не изменяется в разных условиях и является постоянным на всей территории Земли и вне ее.
- Масса Солнца (M) — Масса Солнца равна 1,989 × 10³⁰ килограммов.
Расчет периода обращения по этим значениям дает точный результат для каждой планеты, которую мы изучаем.
Общий итог
Расчет периода обращения каждой планеты вокруг Солнца может быть выполнен с помощью специальной формулы, которая учитывает различные значения, такие как большая полуось орбиты, гравитационную постоянную и массу Солнца. Нахождение этих значений в таблицах планетных данных, а также использование правильной формулы позволяет точно определить период обращения любой планеты. Это важный факт для изучения нашей солнечной системы и различия между планетами в ней.
Как определить период обращения планеты вокруг солнца формула
Космические объекты всегда привлекали внимание человека. Наблюдение за звездами, планетами и другими небесными телами является одним из самых увлекательных и захватывающих занятий. Многие из нас задумывались, как быстро движется огромные планеты вокруг нашей звезды- Солнца. В данной статье мы постараемся разобраться в этом вопросе и определить период обращения планеты вокруг солнца формула.
Период обращения планеты вокруг Солнца
Период обращения планеты вокруг Солнца – это время, за которое данная планета один раз совершит полный круг вокруг своей звезды. Это основной параметр, который определяет движение планеты вокруг своей оси. Более того, это важный параметр, позволяющий узнать о различиях в движениях различных планет.
От периода обращения планеты, в свою очередь, зависит расстояние между планетой и Солнцем. Если период обращения планеты большой, то планета удалится от Солнца. Если же период маленький, то планета будет находиться ближе к Солнцу.
Формула определения периода обращения планеты вокруг Солнца
Есть способ вычисления периода обращения планеты вокруг Солнца на основе нескольких известных данных.
Период обращения планеты T вокруг Солнца можно вычислить по следующей формуле:
T = D / V
где D – длина орбиты планеты (путь, который она пройдет вокруг своей звезды), а V – скорость движения планеты вдоль этой орбиты.

Обычно для такого вычисления берется во внимание среднее расстояние между планетой и Солнцем, а не максимальная или минимальная точка орбиты. Можно узнать среднее расстояние планеты от Солнца в астрономических единицах (АЕ). Одна астрономическая единица равна расстоянию от Земли до Солнца. Это расстояние составляет 149,6 миллионов километров. Использование астрономических единиц позволяет легче рассчитать расстояние и время.
Для вычисления скорости движения планеты используется закон движения с выстроенной орбиты. Согласно этому закону, планета находится на более удаленной от звезды стороне своей орбиты, когда она движется медленнее, и на более близкой, когда движется быстрее. Наилучшим способом определения скорости является использование угловых единиц, таких как градус, минуты и секунды.
Если у нас есть данные, представленные в километрах (километры в секунду), и мы хотим их перевести в угловые единицы, мы должны использовать формулу:
V = 2 * π * R / T
где R — среднее расстояние между планетой и Солнцем, T — период обращения планеты вокруг Солнца. Каждая скорость можно перевести в угловые единицы, используя различные формулы:
- 1 км/секунду = 1,67 х 10 ^ -5 градусов/секунду
- 1 км/секунду = 60 минут в градусе
- 1 минута в градусе = 60 секунд
Итог
Надеемся, что данная статья помогла вам понять, как определить период обращения планеты вокруг Солнца формула. Вычисление периода обращения планет — очень важно в науке. Знание этого параметра позволяет ученым и астрономам лучше понять движение планет вокруг своих звезд и вычислить определенные характеристики движения планет. Надеемся, вы получили максимум информации из данной статьи и она помогла вам раскрыть тему.
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения
— это время, за которое совершается один оборот.
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:
Итак,
чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов
.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения
— это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой
V
(читается: ню) и определяется по формуле:
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения
V
. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела
V
и радиус окружности r, по которой оно движется.
Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l
окр = 2
П
r, где
П
≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
. 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Отослано читателями из интернет-сайтов
Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Что называется равномерным движением по окружности?
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Интересные материалы:
Кто первым приветствует словами? Кто первым в российской литературе употребил слово обломовщина? Кто придумал слово этика? Кто придумал слово шапка? Кто придумал слово собака? Кто сделал перевод Слово о полку Игореве? Кто такие скептики простыми словами? Кто такие Цундере простыми словами? Кто такой бухгалтер своими словами? Кто такой интроверт простыми словами?
Номинальная скорость вращения
Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:
К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.
Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.
Рамка с током
Физиками было установлено, что если взять рамку и пропустить по ней ток, магнитное поле окажет влияние на электроны. В результате происходит их обращение. Вращательное действие силы характеризуется моментом энергии. Именно он и описывает действие материи.

Пусть в магнитном поле расположена прямоугольная рамка. По ней циркулирует ток против часовой стрелки. Вектор индукции направлен вверх. За направление магнитных линий принимается положительная нормаль. По правилу буравчика, если направление поступательного движения винта будет совпадать с направлением тока в проводнике, то вращение винта укажет расположение вектора магнитной индукции поля, создаваемого движением частиц.
Угол между нормалью и вектором обозначают буквой альфа. Естественно, что рамка стремится развернуться так, чтобы быть перпендикулярно полю. Но если она не совпадает с ним по направлению, на неё действует момент силы. Чтобы провести расчёты, необходимо выбрать ось относительно рамки.
Пусть она будет проходить параллельно длинным линиям прямоугольника. Для удобства длина её будет равняться a, а ширина b.
На такую установку будет действовать сила Ампера. Её определение звучит так: модуль вектора равен произведению магнитной индукции на силу тока в проводнике, его длине и синусу угла между направлением поля и заряженными частицами: F = B * I * L * sin (j). Она действует на все стороны рамки. При этом отличается только по направлению.
На рамку оказываются следующие воздействия:
- На дальнюю длинную сторону действует сила равная F1. Значит, на параллельную ей боковую грань воздействие будет противоположно по направлению -F2, поэтому силы принимаются по модулю. Так как значение тока везде одинаковое, можно записать: F = |F1| = |F2|.
- На короткие грани действуют силы, перпендикулярные проводнику. Они будут не поворачивать, а растягивать рамку. Соответственно, их можно обозначить как F3 и F4.
F1 и F2 создают нулевой момент. Они параллельны и направлены в противоположную сторону, образуют пару силы действующих в магнитном поле. Вычисляется она по формуле: M = F * d, где d — расстояние между воздействующими линиями энергии. Таким образом, момент силы в рамке будет определяться так: M = B * a * b * sin (j).
Если принять, что на прямоугольнике намотан провод с числом витков n, а произведение a * b — это площадь, формула примет окончательный вид: M = B * S * n * sin (j).
Общие сведения
Ещё в III—II тысячелетии на острове Магнезия были обнаружены камни, обладающие странными свойствами. Они имели способность притягивать к себе железные предметы. Эти вещества в честь острова получили название магниты. Так как их свойства сохраняются в течение длительного времени, их считают постоянными. Было установлено, что если такой камень разместить на поплавке и положить на него магнит, при его развороте он вернётся в начальное положение. Другими словами, он всегда стремится ориентироваться определённым образом.
Если взять 2 магнита, то, в зависимости от их расположения, они могут притягиваться друг к другу или отталкиваться. Этот эффект объясняется наличием у намагниченных веществ двух полюсов. В 1820 году Христиан Эрстед читал лекцию о тепловом действии тока. Он через проволоку пропускал электричество, демонстрируя, как она разогревается.
Во время эксперимента один из студентов обнаружил, что когда замыкалась цепь, стрелка у рядом находящегося компаса отклонялась. Это вращение и позволило обнаружить связь между электричеством и магнетизмом.
Учёный начал экспериментально изучать эффект. Он предположил, что, так как электрический ток — направленное движение в проводнике заряженных частиц, существует какая-то сила, возникающая вокруг проводящего тела. Обнаружить её можно с помощью компаса. Эту особую пространственную материю назвали магнитным полем. Воображаемые направления, вдоль которых бы расположились стрелки компасов, назвали силовыми линиями.
Опытным путём были установлены характеристики, описывающие движение заряженной частицы в магнитном поле.
К основным из них относят:
- Индукцию. Это плотность магнитных линий. С их помощью вещества разделяют на однородные и неоднородные. В первых магнитная индукция в каждой точке материи имеет одинаковое значение. Определяют её как отношение потока к площади поперечного сечения проводника.
- Проницаемость. Описывает способность среды создавать магнитные силы. Величиной, характеризующей это свойство, является абсолютное значение.
- Напряжённость. Изменяется в зависимости от силы тока в проводнике и его формы.
Описать магнитную материю можно численно и направлением. За её ориентацию принимается северная сторона, на которую указывает стрелка компаса.
Либо за неё можно принять расположение положительной нормали с током в рамке. Определяют её по правилу буравчика.
Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать ½, ¼ оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.
Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.
В этом случае находят применения такие характеристики, как:
- период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
- частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.
Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.
Переход от угловой к линейной скорости
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:
ν = 2*π*R / Т = 2*π*R* ν.
Так как ω = 2*π*ν, то получается:
Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.
К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:
а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.
Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.
Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.
Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.
Вписываемся в повороты: учитываем радиус и наклон
Если вам приходилось ехать на автомобиле или велосипеде или даже бежать трусцой, то наверняка вы заметили, что в крутой поворот проще вписаться, если поверхность дороги немного наклонена внутрь поворота. Из опыта известно, что чем больше наклон, тем проще вписаться в поворот. Это объясняется тем, что в таком случае на вас действует меньшая центростремительная сила. Центростремительная сила обеспечивается силой трения о поверхность дороги. Если поверхность дороги покрыта льдом, то сила трения становится меньше и потому часто не удается вписаться в поворот на обледеневшей дороге на большой скорости.
Представьте, что автомобилю с массой 1000 кг нужно вписаться в поворот с радиусом Юм, а коэффициент трения покоя (подробнее о нем см. главу6) равен 0,8. (Здесь используется коэффициент трения покоя, поскольку предполагается, что шины по поверхности дороги.) Какую максимальную скорость может развить этот автомобиль без риска не вписаться в поворот. Итак, сила трения покоя шин о поверхность дороги ( F_{трение,покоя} ) должна обеспечивать центростремительную силу:
где ( m ) — это масса автомобиля, ( v ) — его скорость, ( r ) — радиус, ( mu_п ) — коэффициент трения покоя, a ( g ) = 9,8 м/с2 — ускорение свободного падения под действием силы гравитации. Отсюда легко находим скорость:
(Обратите внимание, что максимальная безопасная скорость прохождения поворота не зависит от массы автомобиля. — Примеч. ред.)
Это выражение выглядит очень просто, а после подстановки в него численных значений получим:
Итак, максимальная скорость безопасного проезда при таком повороте равна 8,9 м/с. Пересчитаем в единицы “км/ч”, в которых скорость указана на спидометре, и сравним. Получается, что 8,9 м/с = 32 км/ч, а на спидометре всего 29 км/ч. Прекрасно, но далеко не все водители умеют так быстро рассчитывать безопасную скорость прохождения поворотов. Поэтому конструкторы дорог часто строят повороты с наклоном внутрь, чтобы обеспечить центростремительное ускорение не только за счет силы трения, но и за счет горизонтальной компоненты силы гравитации.
На рис. 7.3 показан пример поворота дороги с некоторым наклоном под углом ( theta ) к горизонтали. Предположим, что конструкторы решили полностью обеспечить центростремительное ускорение только за счет горизонтальной компоненты силы гравитации (т.е. без учета силы трения) ( F_нsintheta ), где ( F_н ) — это нормальная сила (подробнее о ней см. в главе 6). Тогда:

В вертикальном направлении на автомобиль действует сила гравитации ( mg ), которая уравновешивается вертикальной компонентой нормальной силы ( F_нcostheta ):
или, иначе выражая это соотношение, получим:
Подставляя это выражение в прежнее соотношение между центростремительной силой и нормальной силой, получим:
Поскольку ( sintheta/!costheta=tg,theta ) в то
Отсюда легко получаем, что угол наклона поворота дороги ( theta ) равен:
Именно это уравнение используют инженеры при проектировании дорог. Обратите внимание, что масса автомобиля не влияет на величину угла, при котором центростремительная сила полностью обеспечивается только горизонтальной компонентой нормальной силы. Попробуем теперь определить величину угла наклона поворота с радиусом 200 м для автомобиля, движущегося со скоростью 100 км/ч или 27,8 м/с:
Для обеспечения безопасного движения автомобиля со скоростью 100 км/ч в повороте с радиусом 200 м без учета силы трения, инженеры должны создать наклон около 22°. Отлично, из вас может получиться неплохой инженер-конструктор автомагистралей!
Угловая скорость
Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.
Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.
Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:
где:
- ω – угловая скорость (рад./с);
- ∆ϕ – изменение угла отклонения при повороте (рад.);
- ∆t – время, затраченное на отклонение ©.
Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.
Угловая скорость в конкретных случаях
На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.
Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
- S — расстояние (путь), пройденное материальной точкой или телом (м);
- T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

- неравномерную;
- среднюю;
- равномерно-переменную;
- поступательную;
- вращательную;
- ускоренную.
Сила Лоренца
Магнитное поле действует только на ту частицу, что подвергается воздействию силы Ампера. Пока электрон будет двигаться хаотично, никакого магнитного поля вокруг него не возникнет. Причём эта сила перпендикулярна проводнику и полю.
Получается, что причиной возникновения силы Ампера является какая-то материя, действующая на траекторию заряженных частиц, когда они начинают двигаться в поле.
Пусть в проводнике есть носители зарядов. Их массой в этом случае можно пренебречь. Так как частицами являются отрицательно заряженные электроны, движутся они противоположно направлению тока. На каждый заряд действует сила, которая в сумме даст силу Ампера.
Если взять воображаемое увеличительное стекло и посмотреть, что происходит в середине проводника, возможно было бы увидеть следующее: в окружности тела электрон перемещался бы встречно току и испытывал действие силы, перпендикулярной его движению. Именно она и называется силой Лоренца. Кратко её определение звучит так: равнодействующая всех энергий Ампера, действующих на заряженные частицы, которые перемещаются в поле. Обозначают её Fл.
Кинетическая сила возникает только при движении. Если частица нейтральная (нейтрон), воздействие на неё не оказывается. Чтобы рассчитать эту силу, нужно знать длину проводника и скорость перемещения носителей заряда. Время, которое потребуется электрону, чтобы сменить своё положение, определяют из равенства: t = L / V.
Всю совокупность прошедших частиц можно обозначить Qоб. Это общий заряд, прошедший через радиус проводника за t. Он будет равняться: Qоб = I * t = (I * L) / V.
Учитывая определение, можно утверждать, что Fa = Fл * N. Так как количество частиц, находящихся в проводнике, равняется всему заряду в нём N = Qоб / Q, можно записать: N = I * L / V * Q. Отсюда сила Ампера: Fa = Fл * (I * L) / (V * q). Если сделать подстановку Fа и выразить силу Лоренца, формула для её определения примет вид: Fл = Q * V * B * sin (j), то есть она пропорциональна скорости частицы в магнитном поле, вектору направления индукции и количеству зарядов. Причём сила Лоренца будет наибольшей, когда V перпендикулярно B.
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения
— это время, за которое совершается один оборот.
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:
Итак,
чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов
.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения
— это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой
V
(читается: ню) и определяется по формуле:
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения
V
. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела
V
и радиус окружности r, по которой оно движется.
Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l
окр = 2
П
r, где
П
≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
. 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Отослано читателями из интернет-сайтов
Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Номинальная скорость вращения
Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:
К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.
Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Угловая скорость
Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.
Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.
Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:
где:
- ω – угловая скорость (рад./с);
- ∆ϕ – изменение угла отклонения при повороте (рад.);
- ∆t – время, затраченное на отклонение ©.
Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.
Угловая скорость в конкретных случаях
На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.
Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.
Главное отличие между сидерическим и синодическим периодами

Как уже было сказано, сидерический — это реальный период обращения, а синодический — это кажущийся, однако в чем же главная разница между этими понятиями?
Вся разница заключается в количестве объектов, относительно которых измеряется временная характеристика. Понятие «сидерический период» принимает во внимание всего один относительный объект, например, Марс вращается вокруг Солнца, то есть движение рассматривается только относительно одной звезды. Синодический же временной период — это характеристика, которая учитывает относительное положение двух и более объектов, например, два одинаковых положения Юпитера относительно земного наблюдателя. То есть здесь необходимо учитывать положение Юпитера не только относительно Солнца, но и относительно Земли, которая также вращается вокруг Солнца.
Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать ½, ¼ оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.
Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.
В этом случае находят применения такие характеристики, как:
- период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
- частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.
Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.
Понятие о синодическом и сидерическом временных периодах

Вам будет интересно:Двусторонняя симметрия — это что такое? Кто имеет двустороннюю симметрию тела?
Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.
Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом. Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.
Сидерический временной период — это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.
Синодический период — это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.
Переход от угловой к линейной скорости
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:
ν = 2*π*R / Т = 2*π*R* ν.
Так как ω = 2*π*ν, то получается:
Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.
К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:
а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.
Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.
Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.
Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости 2) изменяется только направление его скорости 3) изменяются и модуль, и направление его скорости 4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии ( R_1 ) от центра вращающегося колеса, равна ( v_1 ). Чему равна скорость ( v_2 ) точки 2, находящейся от центра на расстоянии ( R_2=4R_1 )?
1) ( v_2=v_1 ) 2) ( v_2=2v_1 ) 3) ( v_2=0,25v_1 ) 4) ( v_2=4v_1 )
3. Период обращения точки по окружности можно вычислить по формуле:
1) ( T=2pi!Rv ) 2) ( T=2pi!R/v ) 3) ( T=2pi v ) 4) ( T=2pi/v )
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) ( omega=a^2R ) 2) ( omega=vR^2 ) 3) ( omega=vR ) 4) ( omega=v/R )
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза 2) уменьшилась в 2 раза 3) увеличилась в 4 раза 4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось 2) уменьшилось в 16 раз 3) уменьшилось в 4 раза 4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз 2) уменьшилось в 9 раз 3) уменьшилось в 3 раза 4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с 2) 3300 с 3) 3·10-4 с 4) 5·10-6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц 2) 2 Гц 3) 20 Гц 4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с 2) 7 с 3) 0,07 с 4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА А) линейная скорость Б) угловая скорость В) частота обращения
ФОРМУЛА 1) ( 1/T ) 2) ( v^2/R ) 3) ( v/R ) 4) ( omega R ) 5) ( 1/n )
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце. В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА A) угловая скорость Б) линейная скорость B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ 1) увеличилась 2) уменьшилась 3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Видео

- Как найти период обращения
- Как найти скорость частицы
- Как определить частоту
- — секундомер;
- — калькулятор;
- — справочные данные по орбитам планет.
- как найти обращения в тексте
Что такое линейная скорость?
Речь идет о физической величине, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Как правило, скорость обозначают буквой v¯, где символ черты говорит о том, что она является векторной величиной. Измеряется скорость в метрах в секунду (м/с), километрах в час (км/ч), милях в час (мил/ч) и других единицах, предполагающих отношение расстояния ко времени.
Вам будет интересно:«Почаще»: слитно или раздельно? Как написание зависит от части речи?
Вектор скорости v¯ показывает направление реального перемещения тела. Этим он отличается от вектора ускорения, который направлен в сторону действующей силы, но не в сторону движения тела, хотя они могут совпадать.
Вращение тел

Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
M = I*α.
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
ω = θ/t.
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
ω = α*t.
Для измерения всех угловых величин используются радианы.

