Как найти значение производной в неявной точке

Производная неявной функции онлайн

Неявная функция – это функция, например , заданная в виде уравнения:

F ( x , y ( x ) ) = 0

Как правило, вместо уравнения F ( x , y ( x ) ) = 0 пишут просто F ( x , y ) = 0 подразумевая, что есть функция от .

В качестве примера неявного задания функции, можно привести уравнение окружности:

уравнение декартового листа:

x 3 + y 3 = 3 ∙ a ∙ x ∙ y ( a = const ≠ 0 ) ,

и т.д. Все эти примеры можно записать в виде уравнения F ( x , y ) = 0 : уравнение окружности: F ( x , y ) = x 2 + y 2 − a 2 = 0 , уравнение декартового листа: F ( x , y ) = x 3 + y 3 − 3 ∙ a ∙ x ∙ y = 0 .

В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F ( x , y ) = 0 . Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа ). Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, – переменная, – функция, зависящая от .
Затем, вам необходимо ввести свое уравнение F ( x , y ) в наш онлайн калькулятор и получить решение вашей задачи.

Производная функции, заданной неявно

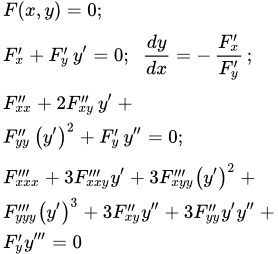
Производная первого порядка

Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .

Доказательство

Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.

Производные высших порядков

Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .

Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.

Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.

Продолжая дифференцирование, можно найти производную любого порядка.

Примеры

Пример 1

Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .

Решение по формуле 2

Находим производную по формуле (2):
(2) .

Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .

Находим производную по , считая постоянной.
;
;
;
.

Находим производную по переменной , считая переменную постоянной.
;
;
;
.

По формуле (2) находим:
.

Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.

Решение вторым способом

Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).

Подставим (из уравнения (П1)):
.
Умножим на :
.

Пример 2

Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .

Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.

Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .

Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :

;
.
Отсюда находим производную второго порядка.

Пример 3

Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .

Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;

Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .

Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.

Автор: Олег Одинцов . Опубликовано: 16-02-2017

Производная фукнции, заданной неявно: руководство, примеры

Как найти производную функции, заданной неявно

Будем учиться находить производные функций, заданных неявно. Что значит неявно? Сравним с обычной функцией. Обычная функция задана уравнением вида y=f(x) , где игрек, то есть функция, задан некоторым выражением, в котором присутствует икс. Таким образом, из переменных в левой части – только игрек, в правой – только икс. Если же функция задана неявно, то в левой части различные слагаемые с игреком “смешаны” с различными слагаемыми с иксом (или переменной, обозначенной другой буквой). Примеры функций, заданных неявно:

,

,

,

,

.

При этом и икс, и игрек могут быть в различных степенях, а в одном слагаемом могут быть и игрек, и икс.

Если функция задана неявно, то как получить игрек, то есть явную функцию? Просто: выразить игрек через другую переменную, то есть получить в левой части только игрек. А если нужно найти производную функции, заданной неявно, то есть получить в левой части только игрек со штрихом? Нужно сначала найти производные обеих частей уравнения, то есть продифференцировать их. А затем выразить производную игрека через производные других переменных.

Теперь приведенный выше “скелет” решения обрастет “мясом”, то есть необходимыми подробностями. Те слагаемые, в которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые, в которых присутствуют и икс, и игрек, нужно дифференцировать, пользуясь правилом дифференцирования сложной функции, то есть учитывать, что игрек – это функция от икса. Если совсем просто, то в полученной производной слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека. Например, производная слагаемого запишется как , производная слагаемого запишется как . Далее из всего этого нужно выразить этот “игрек штрих” и будет получена искомая производная функции, заданной неявно. Разберём это на примерах.

Решаем задачи вместе

Пример 1. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу, считая, что игрек – функция от икса:

.

Отсюда получаем производную, которая требуется в задании:

.

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.

y = f(x) . Так, например, заданные неявно функции

и

не выражаются через элементарные функции, то есть эти уравнения нельзя разрешить относительно игрека. Поэтому и существует правило дифференцирования функции, заданной неявно, которое мы уже изучили и далее будем последовательно применять в других примерах.

Пример 2. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу:

.

Выражаем игрек штрих и – на выходе – производная функции, заданной неявно:

.

Пример 3. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу:

.

Выражаем и получаем производную:

.

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.

Пример 4. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу:

.

Выражаем и получаем производную:

.

Пример 5. Найти производную функции, заданной неявно:

.

Решение. Переносим слагаемые в правой части уравнение в левую часть и справа оставляем ноль. Дифференцируем обе части уравнения по иксу:

Путь к ответу и в конец сам ответ:

Решить задачи самостоятельно, а затем посмотреть решения

Пример 6. Найти производную функции, заданной неявно:

Пример 7. Найти производную функции, заданной неявно:

Пример 8. Найти производную функции, заданной неявно:

[spoiler title=”источники:”]

http://1cov-edu.ru/mat_analiz/proizvodnaya/nayti/neyavnoy-funktsii/

http://function-x.ru/derivative7.html

[/spoiler]

Сначала
рассмотрим неявную функцию одного
переменного. Она определяется уравнением
(1), которое каждому х из некоторой
области Х сопоставляет определённое
у. Тогда на Х определяется этим уравнением
функция у=f(х).
Её называют неявной
или неявно
заданной.
Если уравнение (1) удаётся разрешить
относительно у, т.е. получить вид у=f(х),
то задание неявной функции становится
явным. Однако
разрешить уравнение удается не всегда
и в этом случае не всегда ясно –
существует ли вообще неявная функция
у=f(х),
определяемая уравнением (1) в некоторой
окрестности точки ( x₀,
y₀
).

Например,
уравнение
неразрешимо относительноy
и неясно – определяет ли оно неявную
функцию в некоторой окрестности точки
(1,0), например. Заметим, что существуют
уравнения, не определяющие никакой
функции (x²+y²+1=0).

Оказывается
справедливой следующая теорема:

Теорема«Существования и дифференцируемости
неявной функции» (без доказательства)

Пусть
дано уравнение
(1) и функция,
удовлетворяет условиям:

1. Сама
   функция
   и
   ее частные производные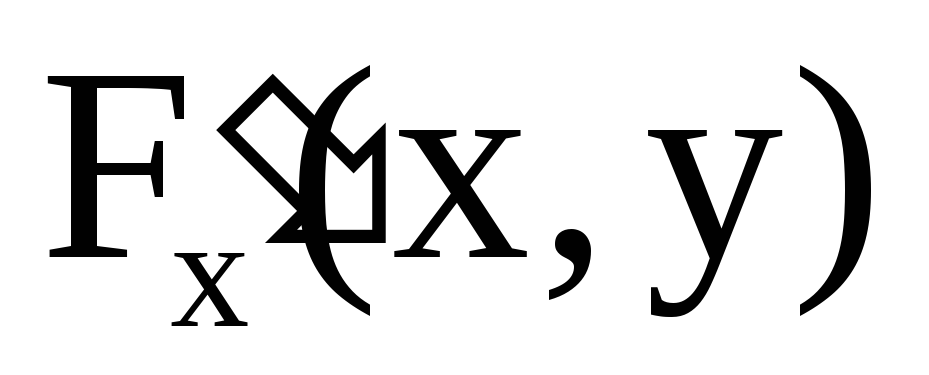инепрерывны в некоторой окрестности
   точки М₀
   (х₀,у₀);

2. ;

3. .

Тогда:

1. уравнение
   (1) при значении х близких к х₀
   определяет однозначную неявную функцию
   у=f(х);

2. ;

3. эта
   функция непрерывна в окрестности точки
   х₀;

4. она
   имеет непрерывную производную в этой
   окрестности, вычисляющуюся по формуле:

.
(2)

Геометрически
теорема утверждает, что в окрестности
точки
,
где выполняемы условия теоремы, неявная
функция, определяемая уравнением (1),
может быть задана в явном виде у=f(х),
т.к. каждому значению х соответствует
единственное у. Если даже мы не можем
найти выражение функции в явном виде,
мы уверены, что в некоторой окрестности
точки М₀
это уже
возможно в принципе.

Рассмотрим
тот же пример:
.
Проверим условия:

1),– и функция и её производные непрерывны
в окрестности точки (1,0) (как сумма и
произведение непрерывных).

2)
.

3)
.
Значит, неявная функция у=f(х)
существует в окрестности точки (1,0). Мы
не можем её выписать в явном виде, но
можем все-таки найти её производную,
которая будет даже непрерывной:

Рассмотрим
теперь неявную
функцию от нескольких переменных.
Пусть задано уравнение

. (2)

Если
каждой паре значений (х,у) из некоторой
области уравнение (2) сопоставляет одно
определённое значение z,
то говорят, что это уравнение неявно
определяет однозначную функцию от двух
переменных
.

Справедлива
и соответствующая теорема существования
и дифференцирования неявной функции
нескольких переменных.

Теорема
2: Пусть дано
уравнение
(2) и функцияудовлетворяет условиям:

1. ,

   ,,–
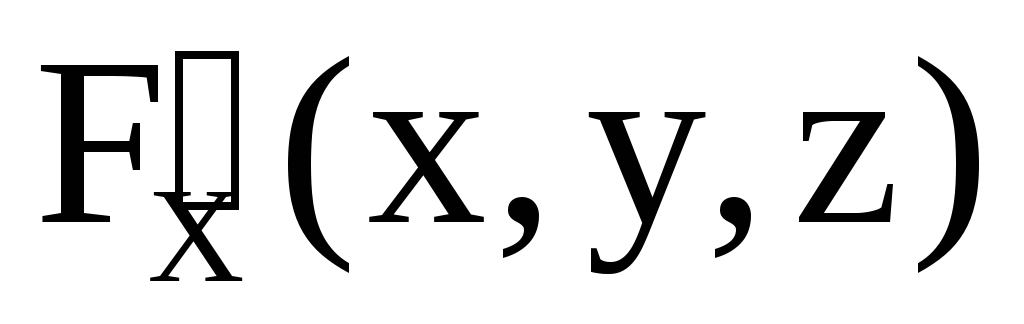   существуют и непрерывны в некоторой
   окрестности точки;

2. ;

3. .

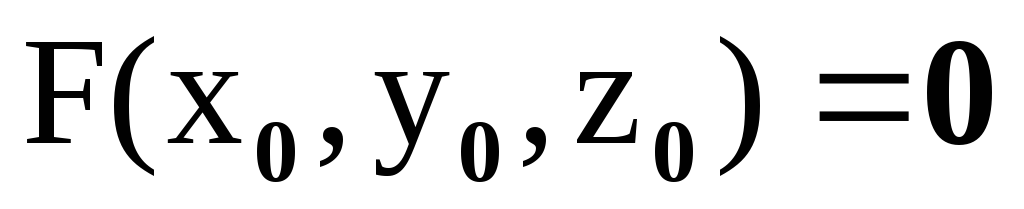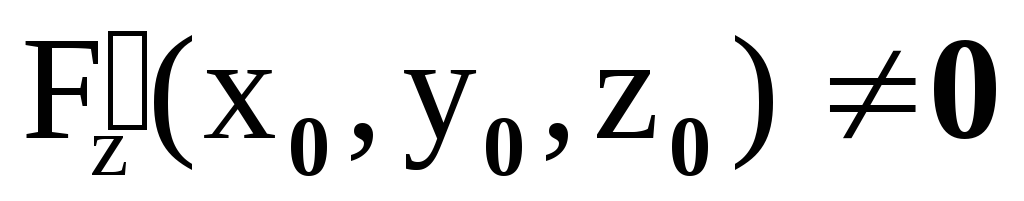Тогда:

1. в
   некоторой окрестности точки М₀
   уравнение (2) определяет z
   как однозначную функцию от х,у:
   ;

2. ;

3. функция
   непрерывна в этой окрестности;

4. неявная
   функция
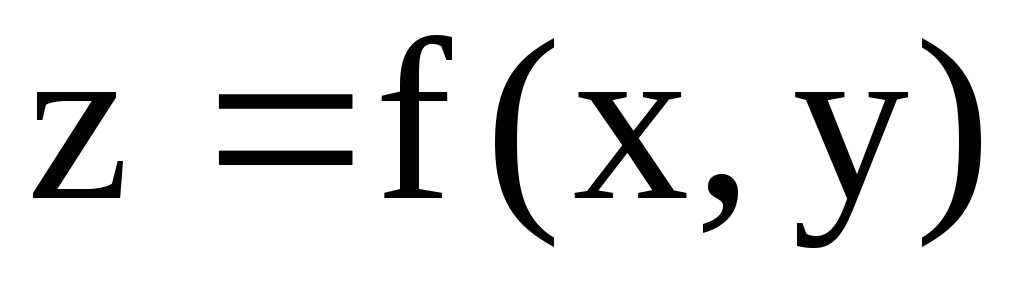   имеет непрерывные частные производные
   в этой окрестности, вычисляемые по
   формулам:.

Пример:
.
Это уравнение задаётz
как двузначную неявную функцию от х и
у
.
Если проверить условия теоремы в
окрестности точки, например, (0,0,1), то
видим выполнение всех условий:

1. –
   непрерывна,
   ,,–
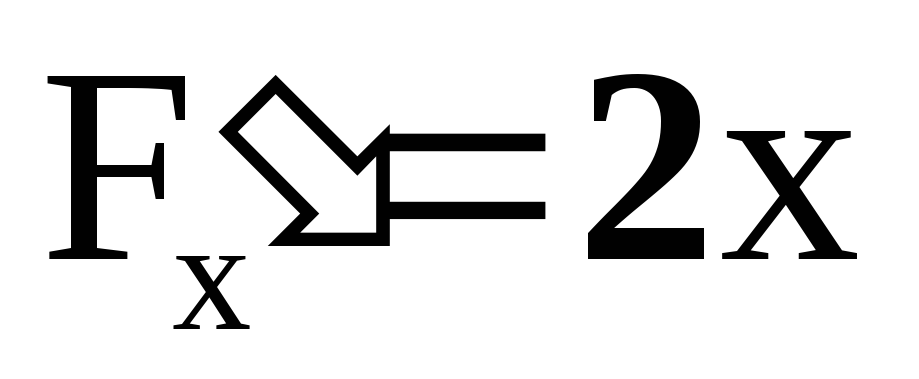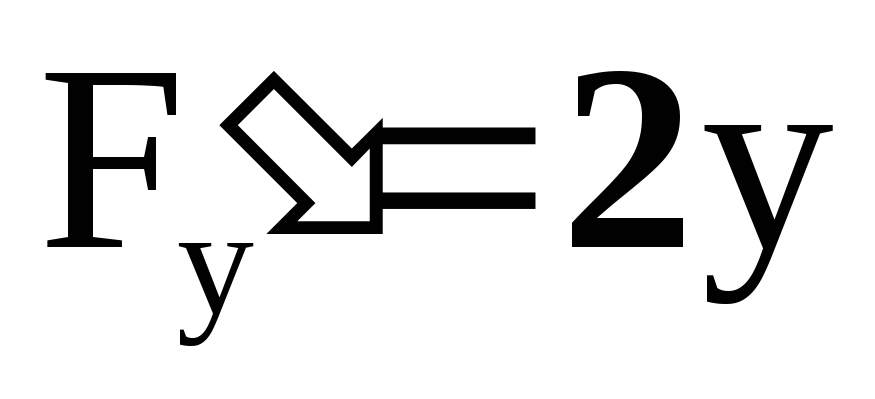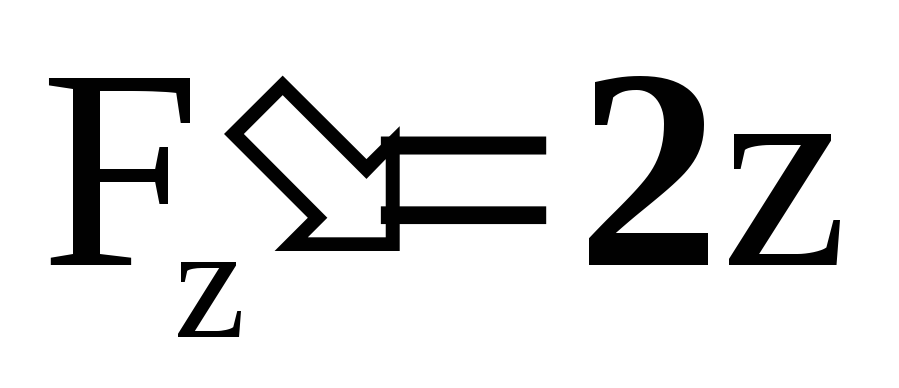   непрерывны также;

2. F(0,0,1)=1-1=0;

3. .

Значит,
неявная однозначная функция существует
в окрестности точки (0,0,1): Можно сказать
сразу, что это
,
задающая верхнюю полусферу.

Существуют
непрерывные частные производные
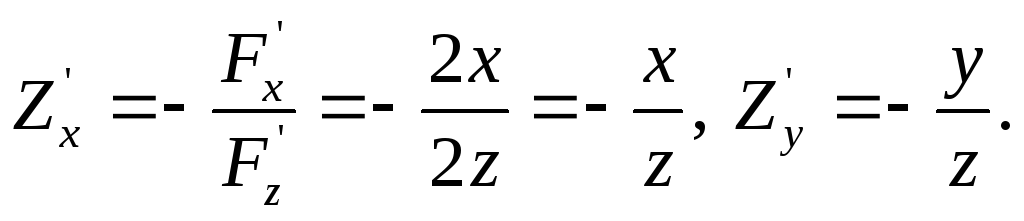Они, кстати, получаются такими же, если
дифференцировать неявную функцию,
выраженную в явном виде, непосредственно.

Определение
и теорема существования и дифференцирования
неявной функции большего числа аргументов
аналогичны.

Производная неявной функции

Формула

Рассмотрим функцию y(x), которая записывается неявным способом в общем виде $ F(x,y(x)) = 0 $. Производная неявной функции находится двумя способами:

1. Дифференцированием обеих частей уравнения
2. С помощью использования готовой формулы $ y’ = – frac{F’_x}{F’_y} $

Как найти?

Способ 1

Не требуется приводить функцию к явному виду. Нужно сразу приступать к дифференцированию левой и правой части уравнения по $ x $. Стоит обратить внимание, что производная $ y’ $ вычисляется по правилу дифференцирования сложной функции. Например, $ (y^2)’_x = 2yy’ $. После нахождения производной необходимо выразить $ y’ $ из полученного уравнения и разместить $ y’ $ в левой части.

Способ 2

Можно воспользоваться формулой, в которой используются в числителе и знаменателе частные производные неявной функции $ F(x,y(x)) = 0 $. Для нахождения числителя берем производную по $ x $, а для знаменателя производную по $ y $. 

Вторую производную неявной функции можно найти с помощью повторного дифференцирования первой производной неявной функции.

Примеры решений

Рассмотрим практические примеры решений на вычисление производной неявно заданной функции.

Пример 1

Найти производную неявной функции $ 3x^2y^2 -5x = 3y – 1 $

Решение

Воспользуемся способом №1. А именно продифференцируем левую и правую часть уравнения: $$ (3x^2y^2 -5x)’_x = (3y – 1)’_x $$ Не забываем при дифференцировании использовать формулу производной произведения функций: $$ (3x^2)’_x y^2 + 3x^2 (y^2)’_x – (5x)’_x = (3y)’_x – (1)’_x $$ $$ 6x y^2 + 3x^2 2yy’ – 5 = 3y’ $$ Далее выражаем y’ из уравнения: $$ 6x y^2 – 5 = 3y’ – 6x^2 yy’ $$ $$ 6x y^2 – 5 = y'(3-6x^2 y) $$ $$ y’ = frac{6x y^2 – 5}{3 – 6x^2y } $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y’ = frac{6x y^2 – 5}{3 – 6x^2y } $$

Пример 2

Функция задана неявно, найти производную $ 3x^4 y^5 + e^{7x-4y} -4x^5 -2y^4 = 0 $

Решение

Воспользуемся способом №2. Находим частные производные функции $ F(x,y) = 0 $ Положим $ y $ постоянной и продифференцируем по $ x $: $$ F’_x = 12x^3 y^5 + e^{7x-4y} cdot 7 – 20x^4 $$ $$ F’_x = 12x^3 y^5 + 7e^{7x-4y} – 20x^4 $$ Считаем теперь $ x $ константой и дифференцируем по $ y $: $$ F’_y = 15x^4 y^4 + e^{7x-4y} cdot (-4) – 8y^3 $$ $$ F’_y = 15x^4 y^4 – 4e^{7x-4y} – 8y^3 $$ Подставляем теперь в формулу $ y’ = -frac{F’_x}{F’_y} $ и получаем: $$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} – 20x^4}{15x^4 y^4 – 4e^{7x-4y} – 8y^3} $$

Ответ

$$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} – 20x^4}{15x^4 y^4 – 4e^{7x-4y} – 8y^3} $$

Дифференцирование функции, заданной неявно

Пусть дано уравнение F(x,y)=0, не разрешенное относительно y. Если существует y=f(x) такая, что F[x,f(x)]=0, то говорят, что уравнение F(x,y)=0 задает y как функцию от x неявно. Обычное задание функции y=f(x) называют явным.

При таком способе задания функции производную находим, дифференцируя уравнение F(x,y)=0, считая y функцией от x (по правилу дифференцирования сложной функции).

• Решение онлайн
• Видеоинструкция

Правила ввода функции, заданной в неявном виде

Примеры

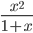≡ x^2/(1+y)

cos2(2x+y) ≡ (cos(2*x+y))^2

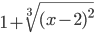≡ 1+(x-y)^(2/3)

см. также Производная от параметрической функции

Пример 1. Найти производную y’, не решая уравнения: x³ – x²y – x²y⁴ + 5 = 0 относительно y.

Решение. Так как в правой части уравнения стоит нуль, а производная постоянной равна нулю, то .

Применяя почленное дифференцирование, найдем 3x² – 2xy – x²y’ – 2xy⁴ – 4x²y³y’ = 0, откуда .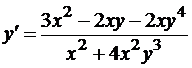

Пример 2. Найти y’ функции, заданной неявно уравнением y*lnx – x2ey + 1 = 0 (x>0).

Решение. 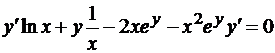(производную от e^y берем как производную сложной функции). Разрешая уравнение относительно y’ (что не всегда возможно), найдем .

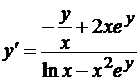Пример 3. Найти производную y’_x функции y(x), заданной неявно: x⁴ + x²y + y³ + 5 = 0.

Решение.

Продифференцируем уравнение по х, рассматривая у как функцию от х, и решим полученное уравнение относительно y’_x.

.

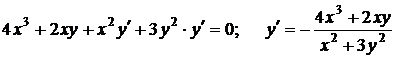Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Макеты страниц