15 марта 2011
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
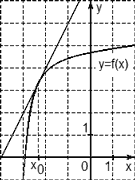
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
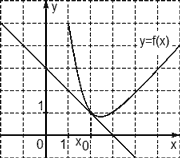
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
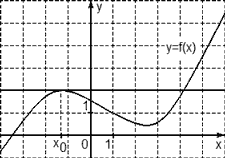
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
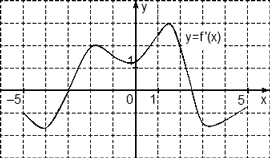
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
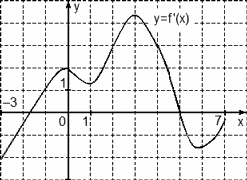
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
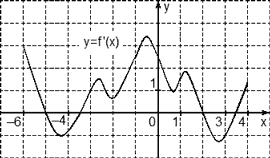
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
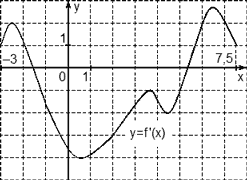
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
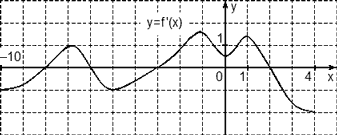
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции
- ЕГЭ 2022, задание 6. Касательная к графику функции
- Схема Бернулли. Примеры решения задач
- Решение задач B6: №362—377
- Четырехугольная пирамида: как найти координаты вершин
- Нестандартная задача B2: студенты, гонорары и налоги
Для исследования функции важно уметь определять угловой коэффициент касательной к ее графику.
Этот угловой коэффициент касательной называют производной.
Понятие производной часто используют и при решении многих других задач. Поэтому рассмотрим его подробнее.
Графический смысл производной
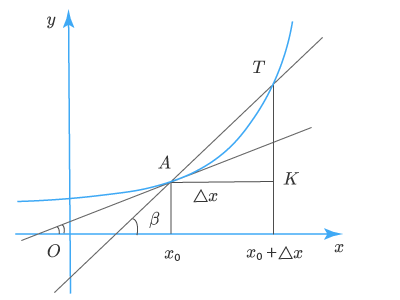
Пусть дан график функции y=f(x)y = f(x) и на нем точка АА, в которой существует касательная к графику:
Если абсцисса точки АА равна x0x_0, то ее ордината f(x0)f(x_0). Предоставим значению аргумента x0x_0 прирост ΔxΔx. Увеличенное значение аргумента х0+Δxх_0 + Δx на графике функции соответствует точка ТТ с абсциссой x0+Δxx_0 + Δx и ординатой f(x0+Δx)f(x_0 + Δx).
Через точки АА и ТТ проведем прямые АКАК и ТКТК, параллельные осям абсцисс и ординат; они пересекутся в некоторой точке КК. Тогда АК−ΔхАК – Δх – приращение аргумента, а ТК=ΔуТК = Δу – прирост функции на [x0;x0+Δx][x_0; x_0 + Δx].
Угловой коэффициент секущей ATAT равен тангенсу угла ββ, то есть отношению ΔуΔу к ΔxΔx:
tgβ=ΔyΔx=f(x0+Δx)−f(x0)Δxtgbeta =frac{Delta y}{Delta x}=frac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}
Если ΔxΔx бесконечно мало и стремится к нулю, то секущая АТАТ, поворачиваясь вокруг точки АА, приближается к касательной, проведенной в точке АА с графиком данной функции. То есть если kk – угловой коэффициент этой касательной и ΔxΔx стремится к нулю, то
f(x0+Δx)−f(x0)Δx→kfrac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}to k
Это число kk – производная функции f(x)f(x) в точке x0x_0.
Производной функции f(x)f(x) в точке x0x_0 называется число kk, которому соответствует дробь f(x0+Δx)−f(x0)Δxfrac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x} при Δх→0.
Производную функции f(x)f(x) в точке x0x_0 обозначают f′(x0)f'(x_0). Ее определение записывают также в виде равенства:
f′(x0)=limΔx→0 f(x0+Δx)−f(x0)Δx{f}'({{x}_{0}})=underset{Delta xto 0}{mathop{lim }},frac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}
или
f′(x0)=limΔx→0 ΔyΔx{f}'({{x}_{0}})=underset{Delta xto 0}{mathop{lim }},frac{Delta y}{Delta x}
Задача 1
Найдите производную функции f(x)=x2f(x) = x^2 в точке x=3x = 3.
Решение
Предоставим аргументу x=3x = 3 прирост ΔxΔx. Соответствующий прирост функции Δу=(3+Δx)2−33=6Δx+Δx2Δу = (3 + Δx)^2 – 33 = 6Δx+Δx^2.
Поэтому
ΔyΔx=6Δ+Δ2Δfrac{Delta y}{Delta x}=frac{6Delta +Delta {{}^{2}}}{Delta }
Если Δx→0Δx→0, то Δy/Δx→6Δy/Δx → 6.
Ответ: f′(3)=6f ‘(3) = 6.
Так решают задачу, пользуясь определением производной функции в точке.
Задача 2
Используя формулу (1/x)′=−1/x2(1/x)’ = – 1/x^2, запишите уравнение к графику функции у=1/xу = 1/x в точке с абсциссой x0=1/2x_0 = 1/2.
Уравнение касательной к графику функции у=f(x)у = f (x) в точке с абсциссой x0x^0 в общем виде записывается так:
y=f(x0)+f′(x0)(x−x0)y=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}})
Чтобы записать это уравнение для заданной функции, нужно найти значение f(x0)f(x_0), производную f′(x)f'(x) и значение f′(x0)f'(x_0). Для выполнения соответствующих вычислений удобно обозначить заданную функцию через f(x)f(x) и использовать табличное значение производной: (1/x)′=−1/x2.(1/x)’ = – 1/x^2.
Таким образом, если f(x)=1/xf(x) = 1/x, то f(x0)=f(1/2)=2f(x_0) = f(1/2) = 2.
Тогда f′(x0)=f′(1/2)=−4.f'(x_0) = f'(1/2) = -4.
Подставляя эти значения в уравнение касательной y=f(x0)+f′(x0)(x−x0)y=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}}) получаем
y=2−4(x−12).y=2-4left( x-frac{1}{2} right).
То есть у=−4x+4у = -4x + 4 – искомое уравнение касательной.
Тест на тему “Производная функции в точке”
- Приращение аргумента и приращение функции
- Определение производной
- Физический смысл производной
- Геометрический смысл производной
- Алгоритм поиска значения производной в заданной точке
- Алгоритм поиска уравнения производной
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x=x-x_0 $$ где (x) – произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0 )=f(x_0+triangle x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
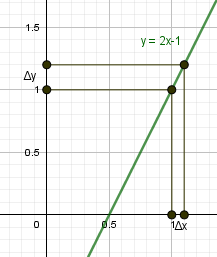 |
begin{gather*} y=2x-1\ x_0=1, x=1,1 end{gather*} Найдем приращение аргумента и функции. begin{gather*} triangle x= x-x_0=1,1-1=0,1gt 0\ \ f(x)=f(1,1)=2cdot 1,1-1=1,2\ f(x_0 )=f(1)=2cdot 1-1=1\ triangle y=f(x)-f(x_0 )=1,2-1=0,2gt 0 end{gather*} |
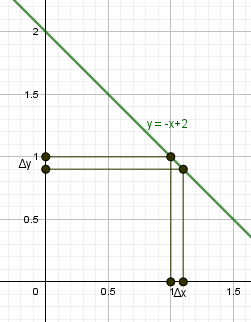 |
begin{gather*} y=-x+2\ x_0=1, x=1,1 end{gather*} Найдем приращение аргумента и функции. begin{gather*} triangle x= x-x_0=1,1-1=0,1gt 0\ \ f(x)=f(1,1)=-1,1+2=0,9\ f(x_0 )=f(1)=-1+2=1\ triangle y=f(x)-f(x_0)=0,9-1=-0,1lt 0 end{gather*} |
Если функция возрастает, приращение аргумента и приращение функции имеют один и тот же знак: $$ begin{cases} y=f(x) – text{возрастает}\ triangle xgt 0 end{cases} Rightarrow triangle ygt 0 $$ Если функция убывает, приращение аргумента и приращение функции имеют разные знаки: $$ begin{cases} y=f(x) – text{убывает}\ triangle xgt 0 end{cases} Rightarrow triangle ylt 0 $$
п.2. Определение производной
Производной функции (f(x)) в точке (x_0) называют предел отношения приращения функции в точке (x_0) к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x} $$
Например:
Найдем производную функции (f(x)=x^2-4) в точке (x_0=3)
Значение функции в точке: (f(x_0 )=3^2-4=5)
Пусть (triangle x) – некоторое приращение аргумента. Тогда: begin{gather*} f(x)=f(x_0+triangle x)=(x_0+triangle x)^2-4=(3+triangle x)^2-4=9+6triangle x+triangle x^2-4=\ =5+6triangle x+triangle x^2 end{gather*} Приращение функции: $$ triangle y=f(x)-f(x_0)=5+6triangle x+triangle x^2-5=6triangle x+triangle x^2=triangle x(6+triangle x) $$ Производная: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle x}{triangle y}=lim_{triangle xrightarrow 0}frac{triangle x(6+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(6+triangle x)=6+0=6 $$ Ответ: 6
п.3. Физический смысл производной
Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами (triangle x=) 300 км поезд преодолевает за (triangle t=)4 часа. Мы легко можем найти его среднюю скорость: $$ v_{cp}=frac{triangle x}{triangle t}, v_{cp}=frac{300}{4}=75 (text{км/ч}) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.
Мгновенная скорость это скорость тела в данный момент времени (t_0): $$ v(t_0)=lim_{triangle trightarrow 0}frac{triangle x}{triangle t}=x'(t_0) $$ где (triangle x=x-x_0) – путь тела за время (triangle t=t-t_0, x(t)) – уравнение движения.
Мгновенная скорость равна первой производной от уравнения движения при (t=t_0).
Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:
Производная функции (y=f(x)) в точке (x_0) равна скорости изменения функции в этой точке.
Или, ближе к физике/химии/биологии:
Производная уравнения процесса (s=f(t)) в момент времени (t_0) равна скорости протекания процесса в этот момент.
п.4. Геометрический смысл производной
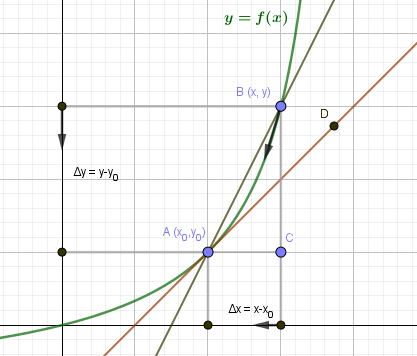
Пусть на плоскости задана кривая (y=f(x)).
Выберем на кривой две точки (A(x_0,y_0)) и (B(x,y)). Прямая AB будет секущей для кривой (y=f(x)). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_{AB}=tgangle A=frac{BC}{AC}=frac{triangle y}{triangle x} $$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: (triangle x=ACrightarrow 0). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:
Производная функции (y=f(x)) в точке (x_0) равна угловому коэффициенту касательной к графику этой функции в этой точке.
п.5. Алгоритм поиска значения производной в заданной точке
На входе: уравнение функции (y=f(x)), точка (x_0)
Шаг 1. Найти значение функции в заданной точке (y_0=f(x_0)).
Шаг 2. Задать приращение аргумента (triangle x=x-x_0), найти приращение функции (triangle y=f(x)-f(x_0)=f(x_0+triangle x)-f(x_0)).
Шаг 3. Найти предел (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=f'(x_0))
На выходе: значение производной в точке (x_0)
Например:
Найдем значение производной в точке (x_0=1) для функции (y=x^2-3).
Значение функции в заданной точке: (f(x_0)=1^2-3=-2)
Пусть (∆x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=((1+triangle x)^2-3)-(-2)=\ =1+2triangle x+(triangle x)^2-1=2triangle x+(triangle x)^2=triangle x(2+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2+triangle x)=2+0=2 end{gather*} Искомая производная в заданной точке: (f'(1)=2)
Ответ: 2
п.6. Алгоритм поиска уравнения производной
На входе: уравнение функции (y=f(x))
Шаг 1. Задать приращение аргумента (triangle x), найти выражение для приращения функции (triangle y=f(x+triangle x)-f(x)).
Шаг 2. Найти предел выражения (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=f'(x))
На выходе: уравнение производной (y ‘=f'(x)) в любой точке (x).
Например:
Найдем общее уравнение производной для функции (y=x^2-3).
Пусть (∆x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=((x+triangle x)^2-3)-(x^2-3)=\ =(x+triangle x)^2-x^2=(x+triangle x-x)(x+triangle x+x)=triangle x(2x+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2x+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2x+triangle x)=2x+0=2x end{gather*} Ответ: уравнение производной (y ‘=2x)
п.7. Примеры
Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) ( f'(1), text{если} f(x)=2x )
По условию (x_0=1)
Значение функции в заданной точке: (f(x_0 )=2cdot 1=2)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=2(1+triangle x)-2=2+2triangle x-2=2triangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{2triangle x}{triangle x}=2 end{gather*} Искомая производная в заданной точке: (f'(1)=2)
б) ( f'(3), text{если} f(x)=3x^2 )
По условию (x_0=3)
Значение функции в заданной точке: (f(x_0 )=3cdot 3^2=27)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=3(3+triangle x)^2-27=3(9+6triangle x+(triangle x)^2)-27=\ =27+18triangle x+3(triangle x)^2-27=3triangle x(6+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{3triangle x(6+triangle x)}{triangle x}=3lim_{triangle xrightarrow 0}(6+triangle x)=3(6+0)=18 end{gather*} Искомая производная в заданной точке: (f'(3)=18)
в) ( f'(-1), text{если} f(x)=4x-1 )
По условию (x_0=-1)
Значение функции в заданной точке: (f(x_0)=4cdot (-1)-1=-5)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=(4(-1+triangle x)-1)-(-5)=-5+4triangle x+5=4triangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{4triangle x}{triangle x}=4 end{gather*} Искомая производная в заданной точке: (f'(-1)=4)
г) ( f'(2), text{если} f(x)=x^3 )
По условию (x_0=2)
Значение функции в заданной точке: (f(x_0)=2^3=8)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=(2+triangle x)^3-8=\ =2^3+3cdot 2^2cdot triangle x+3cdot 2cdot (triangle x)^2+(triangle x)^3-8=\ =12triangle x+6(triangle x)^2+(triangle x)^3=triangle xcdot (12+6triangle x+(triangle x)^2 ) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle xcdot(12+6triangle x+(triangle x)^2)}{triangle x}=lim_{triangle xrightarrow 0}(12+6triangle x+(triangle x)^2)=12+0+0=12 end{gather*} Искомая производная в заданной точке: (f'(2)=12)
Ответ: а) 2; б) 18; в) 4; г) 12
Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции (y=f(x)):
a) ( f(x)=C), где C – постоянная величина
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=C-C=0 end{gather*} Отношение (frac{triangle y}{triangle x}=frac{0}{triangle x}=0)
Предел (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}0=0)
Производная (y ‘=C’=0)
Производная постоянной равна нулю: (C ‘=0)
б) ( f(x)=x)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=x+triangle x-x=triangle x end{gather*} Ищем предел: (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x}{triangle x}=lim_{triangle xrightarrow 0}1=1)
Производная (x ‘=1)
Производная аргумента равна единице: (x ‘=1)
в) ( f(x)=x^2)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=(x+triangle x)^2-x^2=(x+triangle x-x)(x+triangle x+x)=triangle x(2x+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2x+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2x+triangle x)=2x+0=2x end{gather*} Производная ((x^2) ‘=2x)
г) ( f(x)=x^3)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=(x+triangle x)^3-x^3=\ =(x+triangle x-x)((x+triangle x)^2+x(x+triangle x)+x^2)=triangle x((x+triangle x)^2+x(x+triangle x)+x^2) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x((x+triangle x)^2+x(x+triangle x)+x^2)}{triangle x}=\ =lim_{triangle xrightarrow 0}((x+triangle x)^2+x(x+triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 end{gather*} Производная ((x^3) ‘=3x^2)
д) ( f(x)=frac1x)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=frac{1}{x+triangle x}-frac1x=frac{x-(x+triangle x)}{x(x+triangle x)}=-frac{triangle x}{x(x+triangle x)} end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}left(-frac{triangle x}{triangle xcdot x(x+triangle x)}right)=-lim_{triangle xrightarrow 0}frac{1}{x(x+triangle x)}=-frac{1}{x(x+0)}=-frac{1}{x^2} end{gather*} Производная (left(frac1xright) ‘=-frac{1}{x^2})
e) ( f(x)=kx+b)
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=k(x+triangle x)+b-kx-b=ktriangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{ktriangle x}{triangle x}=lim_{triangle xrightarrow 0}k=k end{gather*} Производная ((kx+b) ‘=k)
ж) ( f(x)=sqrt{x})
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=sqrt{x+triangle x}-sqrt{x} end{gather*} Ищем предел, умножив числитель и знаменатель на сопряженное выражение: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{sqrt{x+triangle x}-sqrt{x}}{triangle x}= lim_{triangle xrightarrow 0}frac{(sqrt{x+triangle x}-sqrt{x})(sqrt{x+triangle x}+sqrt{x})}{triangle x(sqrt{x+triangle x}+sqrt{x})}=\ =lim_{triangle xrightarrow 0}frac{x+triangle x-x}{triangle x(sqrt{x+triangle x}+sqrt{x})}=lim_{triangle xrightarrow 0}frac{1}{(sqrt{x+triangle x}+sqrt{x})}=frac{1}{sqrt{x+0}+sqrt{x}}=frac{1}{2sqrt{x}} end{gather*} Производная ((sqrt{x}) ‘=frac{1}{2sqrt{x}})
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Если вы ничего не смыслите в том, что такое производная и какими методами можно её вычислить, то совершенно невозможно решать примеры по математике или задачи по физике. Ведь такое понятие, как производная, является одним из самых важных в математическом анализе.
В этой статье мы расскажем вам, что является производной, какой она имеет геометрический и физический смысл. В общем, мы с вами попытаемся понять производную.
Геометрический и физический смысл производной
Задаём функцию f(x) в интервале (a, b). А точки x и x0 этому интервалу принадлежат. Если изменится x, то и функция тоже изменится. Изменением аргумента является разность его значений x-x0. Записывается эта разность, как дельта икс и имеет название: приращение аргумента. Разность значений функций в двух точках называется приращением или изменением функции. Так каково определение производной?
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Можно записать ещё следующим образом:
Встаёт вопрос, для чего нужно находить такой предел? Вот и ответ:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Ещё в школе нас учили тому, что скорость – это частное пути x=f(t) и времени (t). Вычисляем среднюю скорость за какой-то временной промежуток:
Для того чтобы нам узнать какова скорость движения в момент t0, необходимо вычислить предел:
Сейчас мы разберем один пример, который продемонстрирует вам применение производной на практике. Допустим, тело движется по закону:
Нам необходимо рассчитать скорость в момент времени t=2c. Вычисляем производную:
Правила нахождения производных
Дифференцирование – это процесс нахождения производной. А дифференцируемая функция – это функция, которая имеет производную в данной точке.
Каким образом нам найти саму производную? Нам необходимо составить отношения приращения функции и аргумента, а после вычислить предел при условии стремящегося к нулю приращения аргумента. Но практика показывает, что такой путь вычисления является очень долгим. Всё, что нам необходимо, уже посчитано. И специально для вас, мы подготовили таблицу с производными элементарных функций.
После таблицы мы рассмотрим правила по вычисления производных. Коснёмся мы и вычисления производных сложных функций. Подробно разберём всё на примерах.
Правило первое: выносим константу
Вынести константы можно за знак производной. Причём делать это необходимо! Когда вы решаете примеры по математике, то всегда помните правило – если есть возможность упростить выражение, то делайте это.
Для примера вычислил с вами производную:
Правило второе: производная суммы функций
Производная суммы двух функций равняется сумме производных этих функций. Это касается и производной разности функций.
Сейчас мы с вами на практике рассмотрим пример доказательства этой теоремы.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
По следующей формуле мы сможем вычислить производную произведения двух дифференцируемых функций:
К примеру: необходимо найти производную функции:
Решение:
Необходимо сказать о том, каким образом вычисляются производные сложных функций.
Производная сложной функции равняется произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В примере, который указан выше, мы можем встретить выражение:
В этом примере промежуточным аргументом является 8x в пятой степени. Чтобы нам вычислить производную данного выражения, то для начала необходимо высчитать производную внешней функции по промежуточному аргументу, а после необходимо умножить на производную непосредственно сам промежуточный аргумент по независимой переменной.
Правило четвертое: производная частного двух функций
Ниже приведена формула для того, чтобы определить производную от частного двух функций:
Пример:
Решение:
В данной статье мы попытались рассказать о производных для тех, кто совершенно не знаком с этой темой. Когда вы будете решать примеры, то будьте очень внимательны, ведь в них часто можно встретить ловушки. Эта тема не так уж и проста, какой кажется на первый взгляд.
Вы можете обратиться в наш студенческий сервис по любым вопросам. Мы с удовольствием поможем решить для вас задачи любой сложности. А занимались вы раньше вычислением производных или нет, не имеет никакого значения. Мы помогаем всем!